Evaluation of Urban Intensive Land Use Degree with GEE Support: A Case Study in the Pearl River Delta Region, China
Abstract
1. Introduction
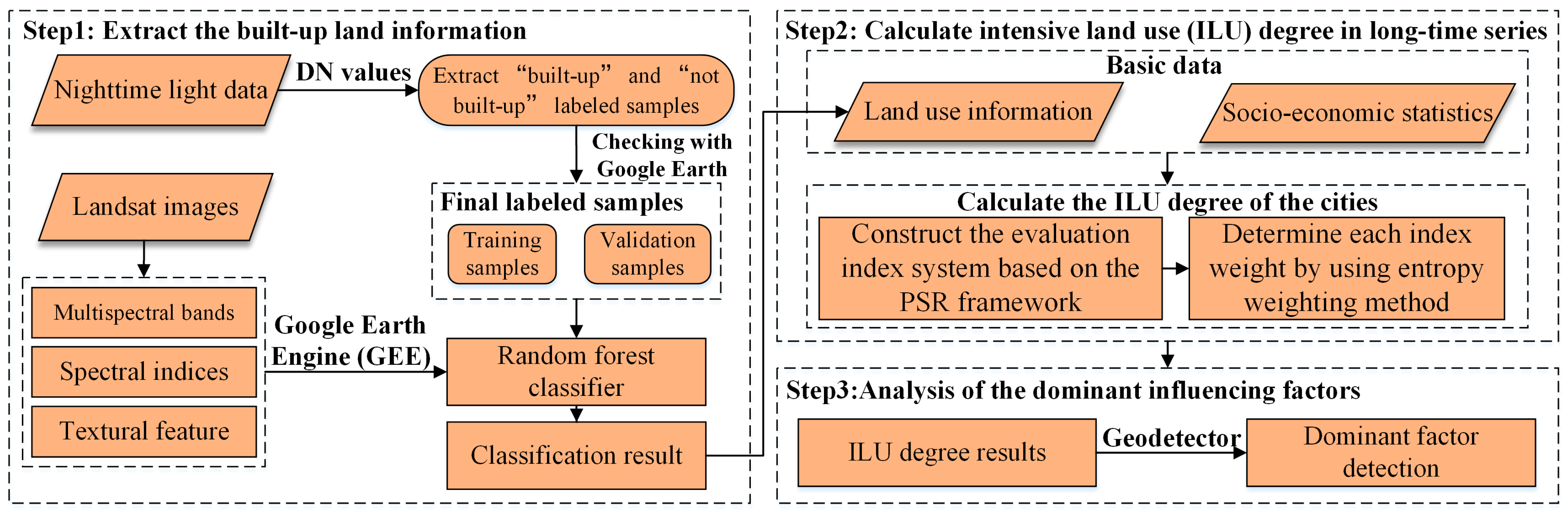
2. Materials and Methods
2.1. Study Area
2.2. Data and Preprocessing
2.3. Methods
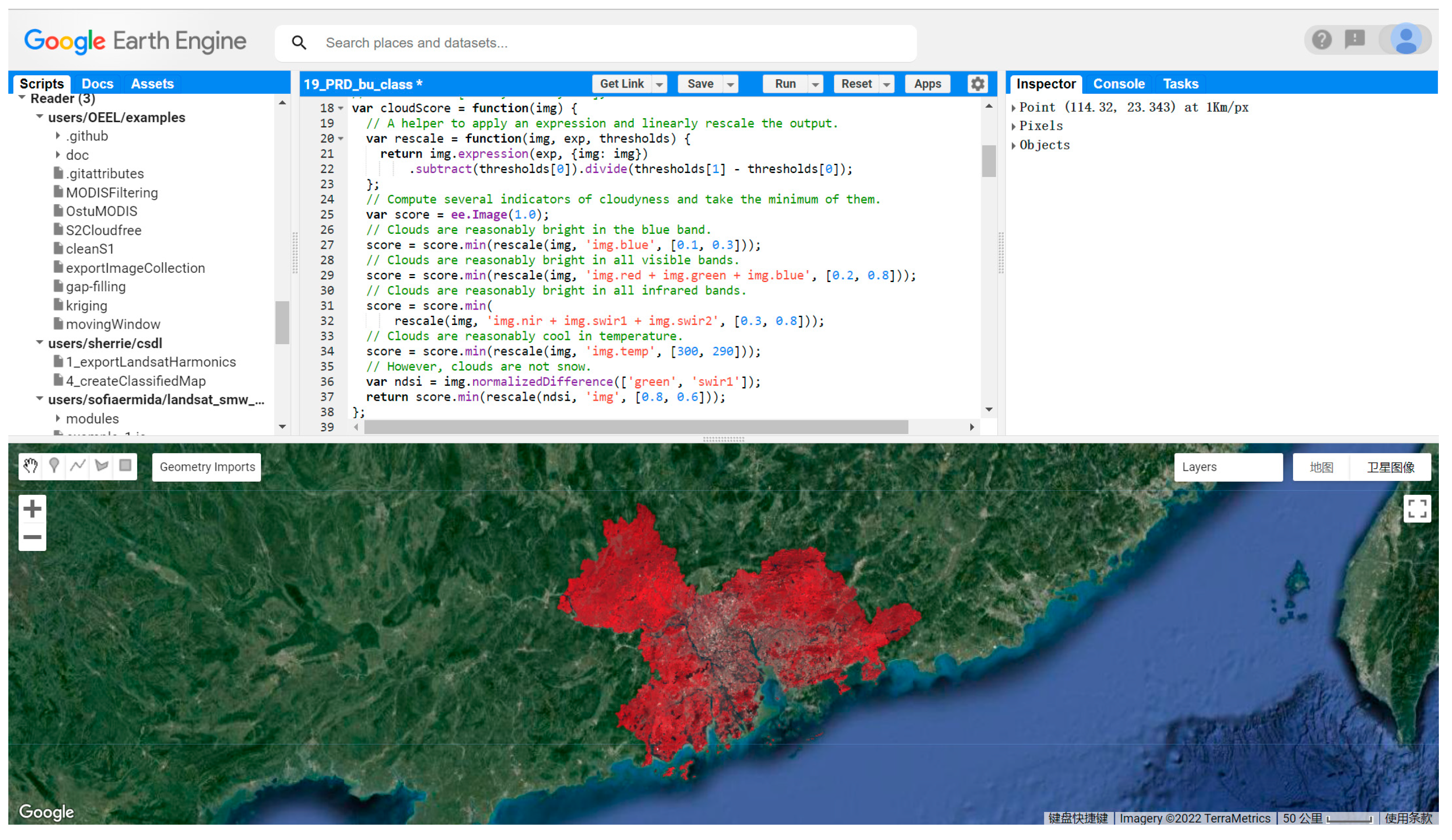
2.3.1. Google Earth Engine (GEE) Platform
2.3.2. Random Forest Classifier
2.3.3. Construction of the Evaluation Index System
2.3.4. Entropy Weighting Method
2.3.5. Dominant Factor Detection by Geodetector
3. Results
3.1. Land Use Classification Results Based on the GEE Platform
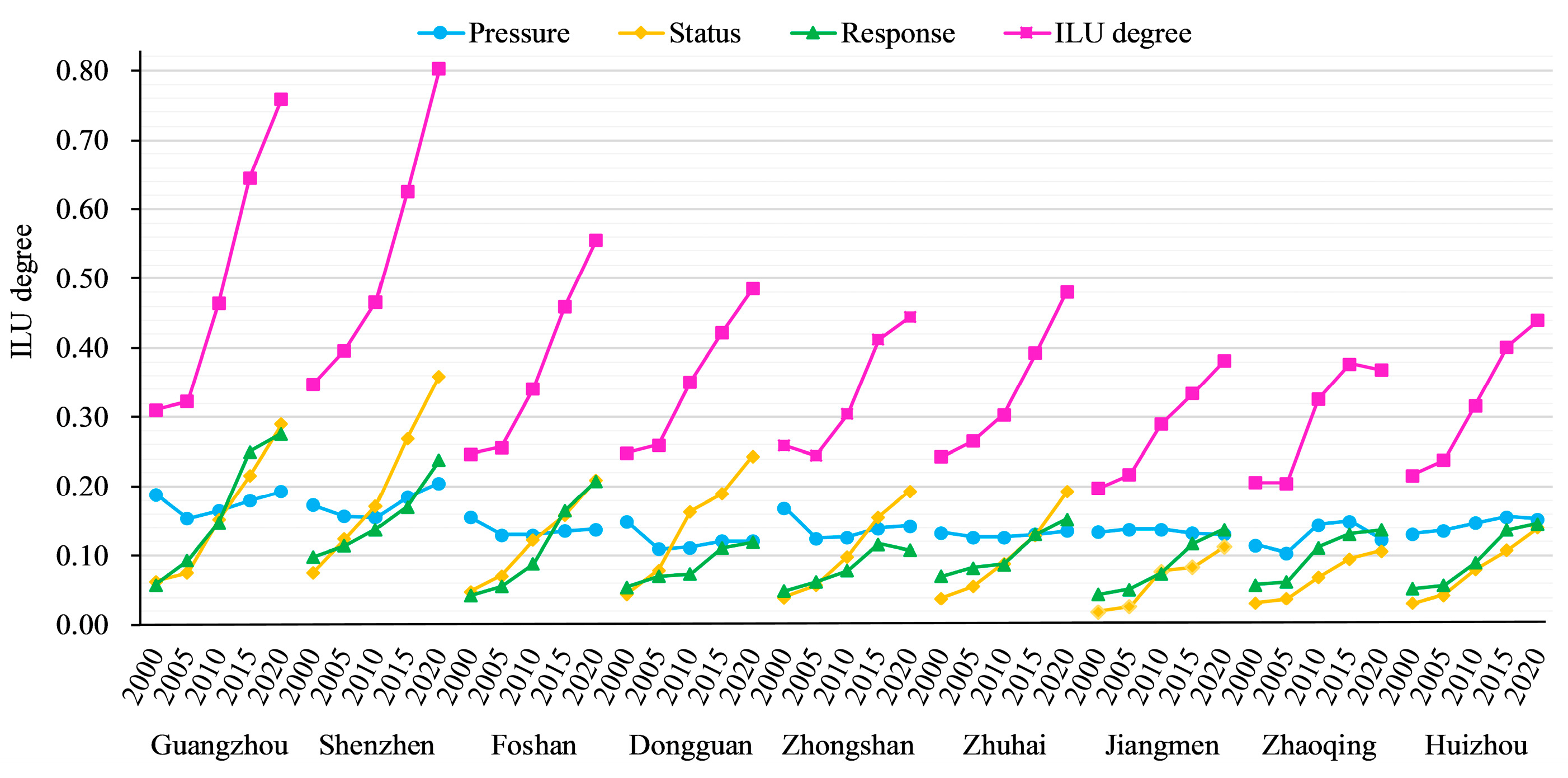
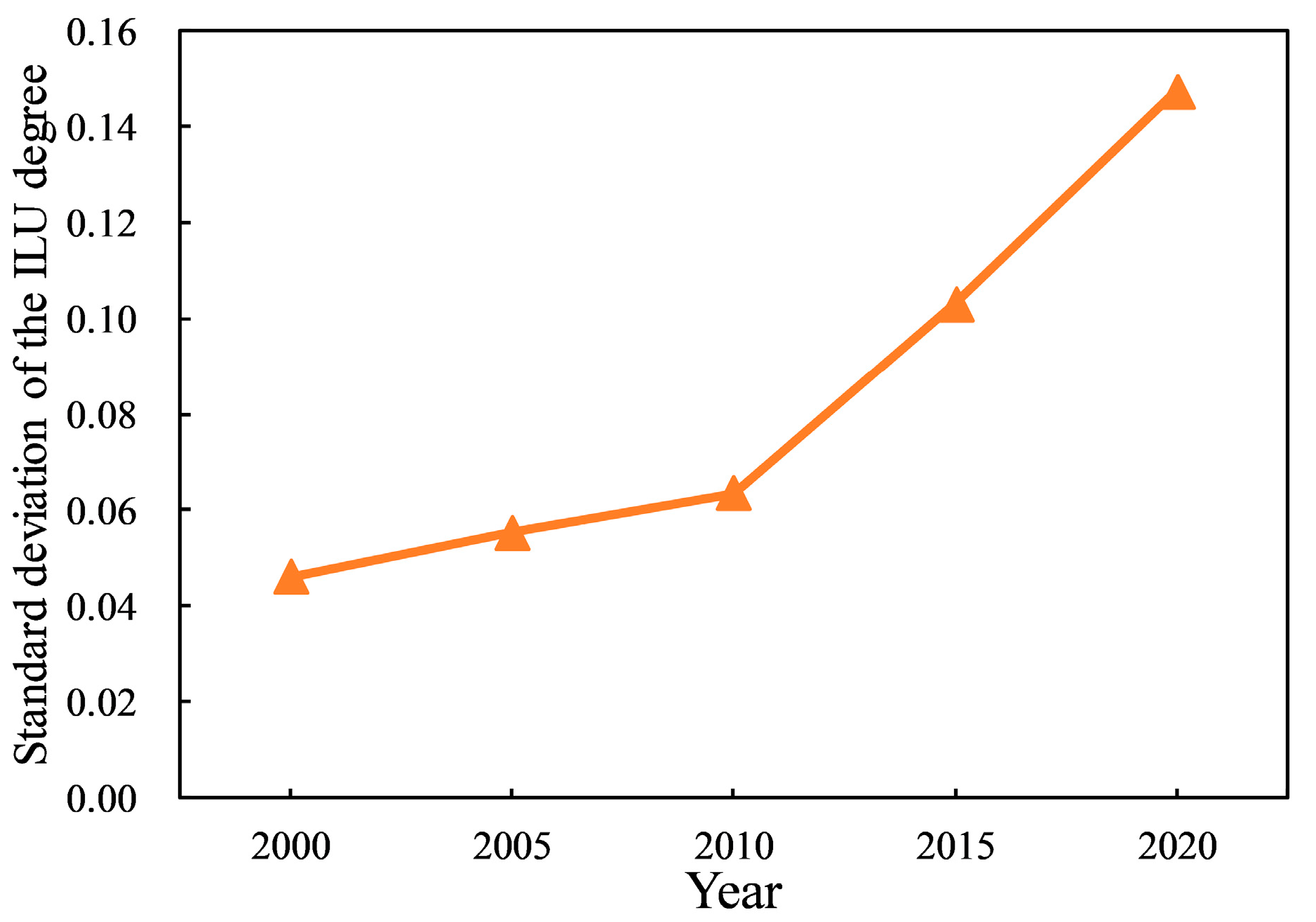
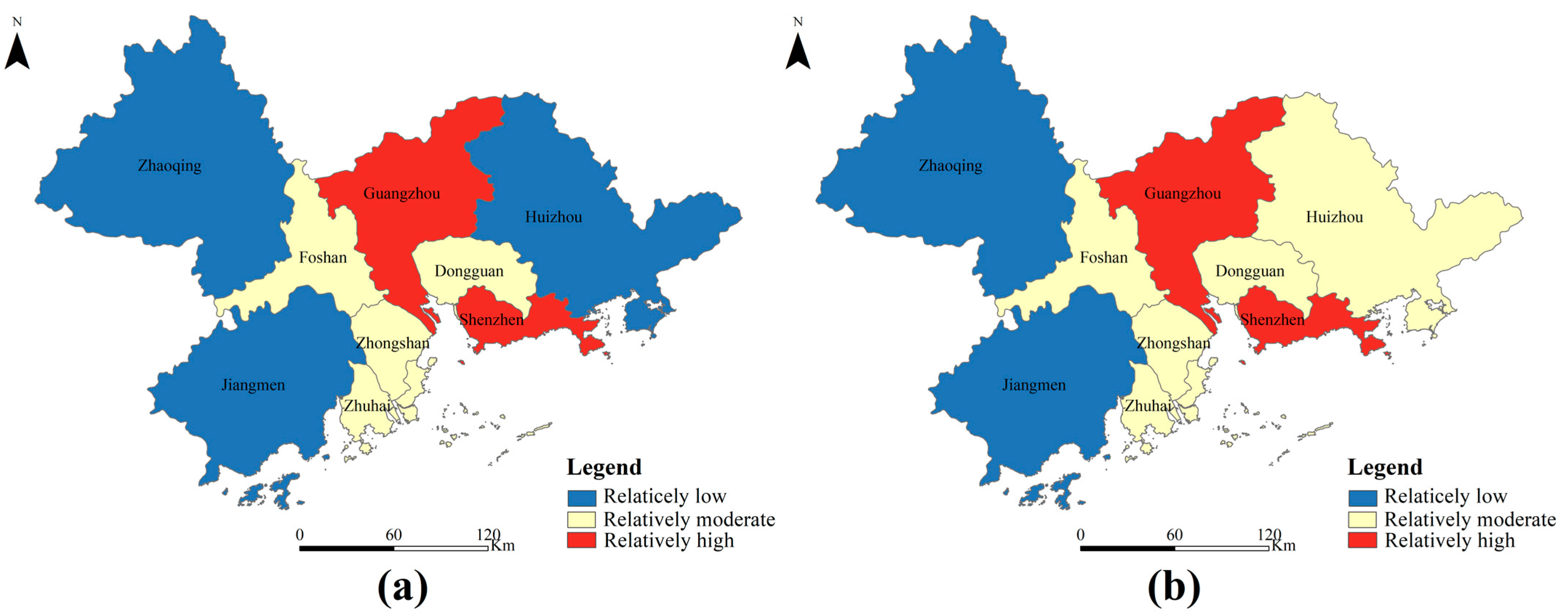
3.2. Spatial and Temporal Characteristics of ILU Changes in the Pearl River Delta
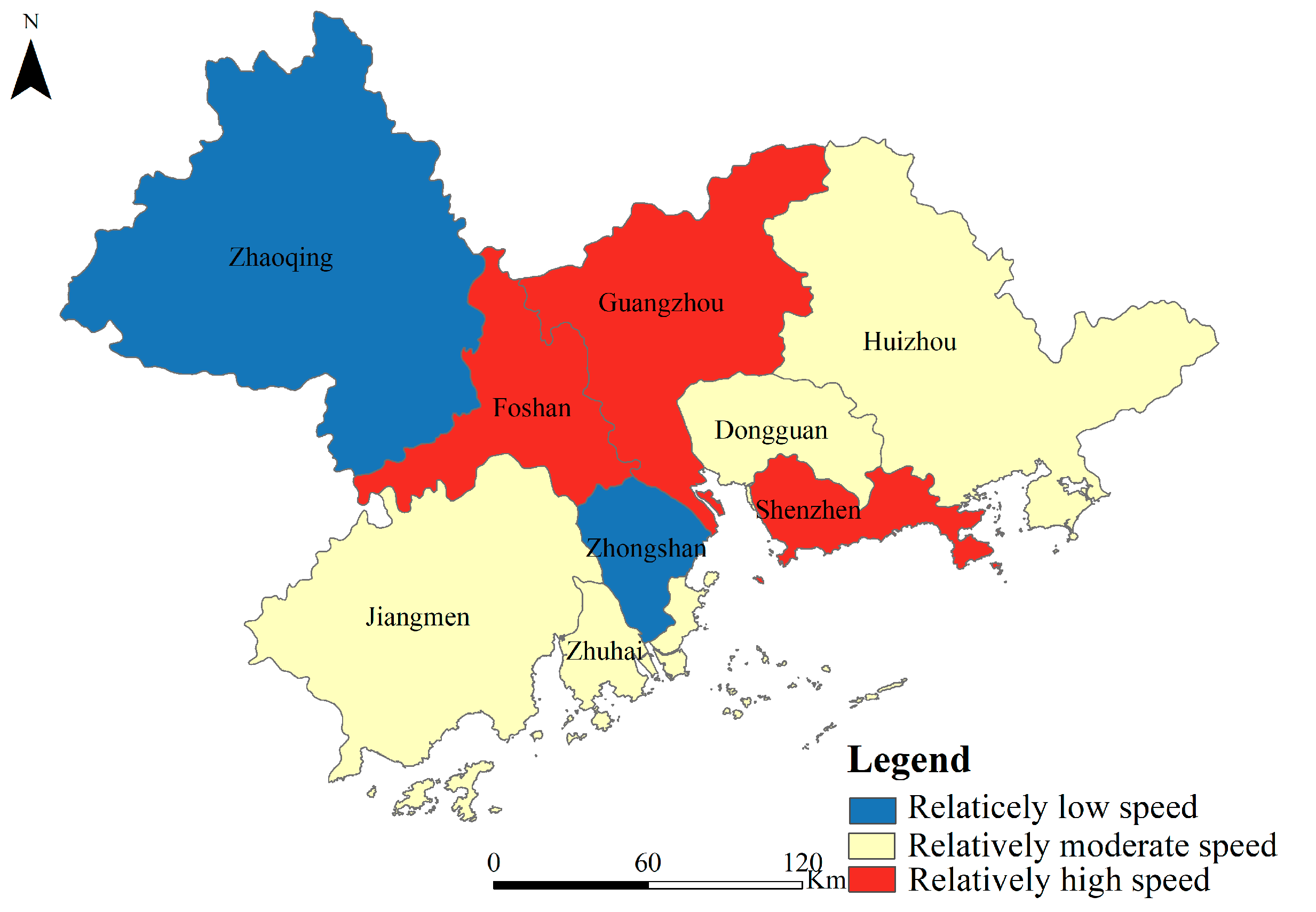
3.3. Detection Results of Geodetector
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ji, Y.; Guo, X.; Zhong, S.; Wu, L. Land Financialization, Uncoordinated Development of Population Urbanization and Land Urbanization, and Economic Growth: Evidence from China. Land 2020, 9, 481. [Google Scholar] [CrossRef]
- Peng, C.; Song, M.; Han, F. Urban economic structure, technological externalities, and intensive land use in China. J. Clean. Prod. 2017, 152, 47–62. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, B.; Yao, S. The Evaluation of Urban Land Use Intensity and its Time-Spatial Differences in Shandong Province. China Popul. Resour. Environ. 2012, 22, 109–113. [Google Scholar]
- Duan, Y.; Fan, X.; Liu, J.; Hou, Q. Operating efficiency-based data mining on intensive land use in smart city. IEEE Access 2020, 8, 17253–17262. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, C.; Hu, Z.; Li, L. Evaluation of intensive urban land use and analysis of obstacle factors in northern slope of Tianshan mountains. Trans. Chin. Soc. Agric. Eng. 2018, 34, 258–266. [Google Scholar]
- Chen, W.; Wu, Q. Evaluation of cultivated land intensive use considering land quality differences. Trans. Chin. Soc. Agric. Eng. 2013, 29, 244–253. [Google Scholar]
- Wang, J.; Sun, K.; Ni, J.; Xie, D. Evaluation and Factor Analysis of the Intensive Use of Urban Land Based on Technical Efficiency Measurement—A Case Study of 38 Districts and Counties in Chongqing, China. Sustainability 2020, 12, 8623. [Google Scholar] [CrossRef]
- Zhou, L.; Shi, Y.; Cao, X. Evaluation of Land Intensive Use in Shanghai Pilot Free Trade Zone. Land 2019, 8, 87. [Google Scholar] [CrossRef]
- Shang, Y.; Zheng, X.; Han, R.; Liu, W.; Xiao, F. Long-term evaluation on urban intensive land use in five fast-growing cities of northern China with GEE support. Sci. Rep. 2021, 11, 20734. [Google Scholar] [CrossRef]
- Qian, Q.; Liu, H.; Zheng, X. A Regional Sustainable Intensive Land Use Evaluation Based on Ecological Constraints: A Case Study in Jinan City. Sustainability 2019, 11, 1434. [Google Scholar] [CrossRef]
- He, Y.; Pang, Y.; Zhang, Q.; Jiao, Z.; Chen, Q. Comprehensive evaluation of regional clean energy development levels based on principal component analysis and rough set theory. Renew. Energy 2018, 122, 643–653. [Google Scholar] [CrossRef]
- Al Asbahi, A.A.M.H.; Gang, F.Z.; Iqbal, W.; Abass, Q.; Mohsin, M.; Iram, R. Novel approach of Principal Component Analysis method to assess the national energy performance via Energy Trilemma Index. Energy Rep. 2020, 5, 704–713. [Google Scholar] [CrossRef]
- Kazakis, N.; Kougias, I.; Patsialis, T. Assessment of flood hazard areas at a regional scale using an index-based approach and Analytical Hierarchy Process: Application in Rhodope-Evros region, Greece. Scirnce Total Environ. 2015, 538, 555–563. [Google Scholar] [CrossRef]
- Xu, G.; Yang, Y.-p.; Lu, S.-y.; Li, L.; Song, X. Comprehensive evaluation of coal-fired power plants based on grey relational analysis and analytic hierarchy process. Energy Policy 2011, 39, 2343–2351. [Google Scholar] [CrossRef]
- Zhao, D.; Li, C.; Wang, Q.; Yuan, J. Comprehensive evaluation of national electric power development based on cloud model and entropy method and TOPSIS: A case study in 11 countries. J. Clean. Prod. 2020, 277, 123190. [Google Scholar] [CrossRef]
- Jin, H.; Qian, X.; Chin, T.; Zhang, H. A Global Assessment of Sustainable Development Based on Modification of the Human Development Index via the Entropy Method. Sustainability 2020, 12, 3251. [Google Scholar] [CrossRef]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, Q.; Shao, Y.; Sun, S.; Xiao, L.; Guo, J. Ecological environment assessment based on land use simulation: A case study in the Heihe River Basin. Sci. Total Environ. 2019, 697, 133928. [Google Scholar] [CrossRef]
- Ghorbanian, A.; Kakooei, M.; Amani, M.; Mahdavi, S.; Mohammadzadeh, A.; Hasanloud, M. Improved land cover map of Iran using Sentinel imagery within Google Earth Engine and a novel automatic workflow for land cover classification using migrated training samples. ISPRS J. Photogramm. Remote Sens. 2020, 167, 276–288. [Google Scholar] [CrossRef]
- Liu, X.; Hu, G.; Chen, Y.; Li, X.; Xu, X.; Li, S.; Pei, F.; Wang, S. High-resolution multi-temporal mapping of global urban land using Landsat images based on the Google Earth Engine Platform. Remote Sens. Environ. 2018, 209, 227–239. [Google Scholar] [CrossRef]
- Stromann, O.; Nascetti, A.; Yousif, O.; Ban, Y. Dimensionality Reduction and Feature Selection for Object-Based Land Cover Classification based on Sentinel-1 and Sentinel-2 Time Series Using Google Earth Engine. Remote Sens. 2020, 12, 76. [Google Scholar] [CrossRef]
- Gong, Z.; Zhao, S.; Gu, J. Correlation analysis between vegetation coverage and climate drought conditions in North China during 2001–2013. J. Geogr. Sci. 2017, 70, 717–729. [Google Scholar] [CrossRef]
- Ferreira, A.R.L.; Fernandes, L.F.S.; Cortes, R.M.V.; Pacheco, F.A.L. Assessing anthropogenic impacts on riverine ecosystems using nested partial least squares regression. Sci. Total Environ. 2017, 583, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, B. Remote sensing and GIS-based landslide hazard analysis and cross-validation using multivariate logistic regression model on three test areas in Malaysia. Adv. Space Res. 2010, 45, 1244–1256. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, J.; Ren, Z.; Li, J.; Guo, Y. Mapping the increased minimum mortality temperatures in the context of global climate change. Nat. Commun. 2019, 10, 4640. [Google Scholar] [CrossRef]
- Zuo, S.; Dai, S.; Song, X.; Xu, C.; Liao, Y.; Chang, W.; Chen, Q.; Li, Y.; Tang, J.; Man, W.; et al. Determining the Mechanisms that Influence the Surface Temperature of Urban Forest Canopies by Combining Remote Sensing Methods, Ground Observations, and Spatial Statistical Models. Remote Sens. 2018, 10, 1814. [Google Scholar] [CrossRef]
- Shrestha, A.; Luo, W. Analysis of Groundwater Nitrate Contamination in the Central Valley: Comparison of the Geodetector Method, Principal Component Analysis and Geographically Weighted Regression. ISPRS Int. J. Geo-Inf. 2017, 6, 297. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, J.; Xu, Q.; Luo, X. Urban-rural spatial transformation process and influences from the perspective of land use: A case study of the Pearl River Delta Region. Habitat Int. 2020, 104, 102234. [Google Scholar] [CrossRef]
- Myroniuk, V.; Kutia, M.; Sarkissian, A.J.; Bilous, A.; Liu, S. Regional-Scale Forest Mapping over Fragmented Landscapes Using Global Forest Products and Landsat Time Series Classification. Remote Sens. 2020, 12, 187. [Google Scholar] [CrossRef]
- Wang, C.; Jia, M.; Chen, N.; Wang, W. Long-Term Surface Water Dynamics Analysis Based on Landsat Imagery and the Google Earth Engine Platform: A Case Study in the Middle Yangtze River Basin. Remote Sens. 2018, 10, 1635. [Google Scholar] [CrossRef]
- Goldblatt, R.; Stuhlmacher, M.F.; Tellman, B.; Clinton, N.; Hanson, G.; Georgescu, M.; Wang, C.; Serrano-Candela, F.; Khandelwal, A.K.; Cheng, W.-H.; et al. Using Landsat and nighttime lights for supervised pixel-based image classification of urban land cover. Remote Sens. Environ. 2018, 205, 253–275. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Lee, J.; Cardille, J.A.; Coe, M.T. BULC-U: Sharpening Resolution and Improving Accuracy of Land-Use/Land-Cover Classifications in Google Earth Engine. Remote Sens. 2018, 10, 1455. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Goettsche, F.-M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Gupta, V.K.; Gupta, A.; Kumar, D.; Sardana, A. Prediction of COVID-19 Confirmed, Death, and Cured Cases in India Using Random Forest Model. Big Data Min. Anal. 2022, 4, 116–123. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, J.; Guo, S.; Ye, Z.; Deng, H.; Hou, X.; Zhang, H. Urban Tree Classification Based on Object-Oriented Approach and Random Forest Algorithm Using Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2022, 14, 3885. [Google Scholar] [CrossRef]
- Al-Mukhtar, M. Random forest, support vector machine, and neural networks to modelling suspended sediment in Tigris River-Baghdad. Environ. Monit. Assess. 2019, 191, 673. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land Cover Classification using Google Earth Engine and Random Forest Classifier—The Role of Image Composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Akbari, E.; Bolooran, A.D.; Samany, N.N.; Hamzeh, S.; Soufizadeh, S.; Pignatti, S. Crop Mapping Using Random Forest and Particle Swarm Optimization based on Multi-Temporal Sentinel-2. Remote Sens. 2020, 12, 1449. [Google Scholar] [CrossRef]
- Myint, S.W. Fractal approaches in texture analysis and classification of remotely sensed data: Comparisons with spatial autocorrelation techniques and simple descriptive statistics. Int. J. Remote Sens. 2003, 24, 1925–1947. [Google Scholar] [CrossRef]
- Zheng, B.; Myint, S.W.; Thenkabail, P.S.; Aggarwal, R.M. A support vector machine to identify irrigated crop types using time-series Landsat NDVI data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 103–112. [Google Scholar] [CrossRef]
- Yang, J.; Du, X. An enhanced water index in extracting water bodies from Landsat TM imagery. Ann. GIS. 2017, 23, 141–148. [Google Scholar] [CrossRef]
- Bhatti, S.S.; Tripathi, N.K. Built-up area extraction using Landsat 8 OLI imagery. GIScience Remote Sens. 2014, 51, 445–467. [Google Scholar] [CrossRef]
- Cen, X.; Wu, C.; Xing, X.; Fang, M.; Garang, Z.; Wu, Y. Coupling Intensive Land Use and Landscape Ecological Security for Urban Sustainability: An Integrated Socioeconomic Data and Spatial Metrics Analysis in Hangzhou City. Sustainability 2015, 7, 1459–1482. [Google Scholar] [CrossRef]
- Liu, D.-j.; Li, L. Application Study of Comprehensive Forecasting Model Based on Entropy Weighting Method on Trend of PM2.5 Concentration in Guangzhou, China. Int. J. Environ. Res. Public Health 2015, 12, 7085–7099. [Google Scholar] [CrossRef]
- Wang, J.-F.; Li, X.-H.; Christakos, G.; Liao, Y.-L.; Zhang, T.; Gu, X.; Zheng, X.-Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Yin, G.; Lin, Z.; Jiang, X.; Yan, H.; Wang, X. Spatiotemporal differentiations of arable land use intensity—A comparative study of two typical grain producing regions in northern and southern China. J. Clean. Prod. 2019, 208, 1159–1170. [Google Scholar] [CrossRef]
- You, N.; Dong, J. Examining earliest identifiable timing of crops using all available Sentinel 1/2 imagery and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2020, 161, 109–123. [Google Scholar] [CrossRef]



| Type | Index | Character | Code | Calculation Formula |
|---|---|---|---|---|
| Pressure | Population density * | + | P1 | Resident population/built-up land area |
| Proportion of built-up land * | − | P2 | Built-up land area/city’s area | |
| Output value proportion of secondary and tertiary industries | + | P3 | Output value of secondary and tertiary industries/GDP | |
| State | Economic density * | + | S1 | Output value of secondary and tertiary industries/built-up land area |
| Road network density | + | S2 | Total length of urban roads/city’s area | |
| Personal disposable income | + | S3 | See statistics | |
| Employee density * | + | S4 | Number of employee in secondary and tertiary industries/built-up land area | |
| Response | Investment in fixed assets | + | R1 | See statistics |
| Public green space per capita | + | R2 | See statistics | |
| Electricity consumption per unit of GDP | − | R3 | See statistics | |
| Industrial wastewater discharge | − | R4 | See statistics |
| Year | Dominant Factors |
|---|---|
| 2000 | S1 (q = 0.912), R1 (q = 0.815), S3 (q = 0.799) |
| 2005 | R1 (q = 0.917), S3 (q = 0.904), S1 (q = 0.898) |
| 2010 | R3 (q = 0.965), S1 (q = 0.939), S3 (q = 0.780) |
| 2015 | S3 (q = 0.963), S1 (q = 0.947), R3 (q = 0.917) |
| 2020 | S1 (q = 0.922), R1 (q = 0.872), S3 (q = 0.695) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Liu, D.; Chen, Y. Evaluation of Urban Intensive Land Use Degree with GEE Support: A Case Study in the Pearl River Delta Region, China. Sustainability 2022, 14, 13284. https://doi.org/10.3390/su142013284
Shang Y, Liu D, Chen Y. Evaluation of Urban Intensive Land Use Degree with GEE Support: A Case Study in the Pearl River Delta Region, China. Sustainability. 2022; 14(20):13284. https://doi.org/10.3390/su142013284
Chicago/Turabian StyleShang, Yiqun, Dongya Liu, and Yi Chen. 2022. "Evaluation of Urban Intensive Land Use Degree with GEE Support: A Case Study in the Pearl River Delta Region, China" Sustainability 14, no. 20: 13284. https://doi.org/10.3390/su142013284
APA StyleShang, Y., Liu, D., & Chen, Y. (2022). Evaluation of Urban Intensive Land Use Degree with GEE Support: A Case Study in the Pearl River Delta Region, China. Sustainability, 14(20), 13284. https://doi.org/10.3390/su142013284







