Abstract
Storage technologies are an emerging element in the further expansion of renewable energy generation. A decentralized micro-pumped storage power plant can reduce the load on the grid and contribute to the expansion of renewable energies. This paper establishes favorable boundary conditions for the economic operation of a micro-pump storage (MPS) system. The evaluation is performed by means of a custom-built simulation model based on pump and turbine maps which are either given by the manufacturer, calculated according to rules established in studies, or extended using similarity laws. Among other criteria, the technical and economic characteristics regarding micro-pump storage using 11 pumps as turbines controlled by a frequency converter for various generation and load scenarios are evaluated. The economical concept is based on a small company (e.g., a dairy farmer) reducing its electricity consumption from the grid by storing the electricity generated by a photovoltaic system in an MPS using a pump as a turbine. The results show that due to the high specific costs incurred, systems with a nominal output in excess of around 22 kW and with heads beyond approximately 70 m are the most profitable. In the most economical case, a levelized cost of electricity (LCOE) of 29.2 €cents/kWh and total storage efficiency of 42.0% is achieved by optimizing the system for the highest profitability.
1. Introduction
Renewable energy generation is often volatile and location-dependent by nature. Its integration into power networks usually requires great flexibility and puts a strain on the grid. To reduce the load on the grid, it must either be expanded, become smarter or storage technologies must be implemented [1]. The requirements for storage technologies are manifold, and no single storage technology fulfills them all. Each energy storage technology has unique characteristics, and the optimal choice depends on the task to be fulfilled [2]. Micro-pump storage systems are one of the storage technologies used for decentralized energy storage and can therefore reduce the load on the network. The pump as turbine (PAT) technology is well-established in a number of water distribution networks for energy recovery [3,4], with a possible payback period of six years [5], by pressure reduction and reducing water loss [6] or for improving network effectiveness [7,8]. It can also be beneficial to enhance the sustainability of such networks [9]. Additionally, studies on PATs have already developed integration strategies for water distribution networks [10,11] or methodologies to select pumps from catalogues [12]. Simulation models were also developed to determine the number and optimal locations of operations as well as the optimal PATs to minimize costs [13]. For instance, a recent publication has shown that the specific decentralized installation of PATs in a water distribution network can be used to charge e-bikes or scooters by reducing the pressure in the network [14]. Something comparable could be achieved by using a PAT in a micro-pump storage (MPS) system, thus reducing the load on the power grid. A publication [15] preceding the present contribution investigated various operating strategies for an MPS system with a pump as a turbine. Therein, speed control using a frequency transformer (FUM) was identified as the best strategy in terms of economy. It has also been proven that the efficiency of pumped hydro storage can be significantly increased by varying the speed with an FUM [16]. The result of a publication on electricity costs in India shows that MPS systems can be economically viable [17]. In contrast, other publications concerned with modelling small hydropower plants [18,19,20,21,22,23] in combination with photovoltaic (PV) systems [24], wind turbines [25], or both [26], leave open the question of how such a system can be operated economically.
A pilot MPS plant using a PAT was recently implemented in Froyennes, Belgium [27], where the energy produced by a variety of PV systems and a few small wind turbines is stored in the MPS in the event of a local energy surplus and is then withdrawn at a later point in time. Attaining profitability with an MPS system is a challenge. For example, the levelized cost of electricity (LCOE) for storing and retrieving energy in Froyennes is €1.06/kWh [27], which is far above current energy prices. Throughout this paper, this pilot plant is used as an example to illustrate the general boundary conditions that are required for economical operation. For instance, the ratio of length to head (L/H) at the MPS in Froyennes is about 8. Since this ratio is usually much lower at other pumped storage power plants, there is great potential for cost reduction [27]. Depending on the filling level of the reservoir, there is only a maximum head of 11 m, which also brings the potential for improvement. The efficiency of the PAT is 72.7%, but there are now PATs with better efficiency (see Section 2.2.2), which should also lead to a better result for the LCOE. Furthermore, in Froyennes, a 30 kW motor/generator (M/G) was used for a maximum pump power of 17 kW; a better adapted M/G could reduce the investment costs. This publication is intended to identify potential for improvement and therefore focuses on how a MPS can be operated economically and what boundary conditions are necessary for achieving this goal.
In order to be able to evaluate the economic efficiency of such a system, pump and turbine maps are required as input for a simulation model. Since turbine maps, in contrast to pump maps, are usually not publicly available, turbine maps usually have to be measured or calculated. Over the years, quite a few calculation methods have been developed, e.g., by Gülich [28], Alatorre-Frenk [29], Derakhshan [30], Yang [31], and T. Lin [32], and have been compared with experimental measurements [33,34] or with other prediction methods [35]. Prediction models have also been developed, especially for multi-stage PATs [36]. The accuracy of the turbine characteristics obtained depends on the pump mode data available as a basis, and a certain degree of inaccuracy must always be taken into account. Due to the fact that a test bench is very expensive, especially when covering the full performance range considered for this paper, the calculation methods are still necessary. Based upon the given calculated turbine characteristics, a numerical model of the MPS system can be used to simulate its operation and evaluate it according to economic and technical criteria. In particular, a roadmap can be established for illustrating how an MPS system could be profitably operated, which is the major goal pursued by the present paper.
This paper is structured as follows: Section 2 describes the system calculation methods and affinity laws and is followed by a short description of the simulation model employed. In Section 3, the results of the technical and economic efficiency simulations for various generation and load profiles are presented, discussed, and used to sketch the roadmap to profitability for MPS. To cover a larger scope of load and generation scenarios, Section 4 introduces various scaling factors for the load and generation profile which are examined using the most promising pump of Section 3, the KSB 8065200.
2. Materials and Methods
The present section describes the procedure for evaluating the economic viability of an MPS. To this end, the functionality of the MPS, the basic data, the methodology of the simulation model, as well as the calculation and extension of the turbine maps are described.
2.1. Concept and Initial Data
Figure 1 presents a schematic diagram of a speed-controlled micro-pump storage plant that might be used by a small company (e.g., a dairy farmer). A centrifugal pump, which operates both as a pump and a turbine, is located between the lower and the upper reservoirs. The speed-controlled plant is connected to the power grid, to a PV system (specific yield = ) and to the consumer via an electric motor or generator (M/G) and a frequency converter.
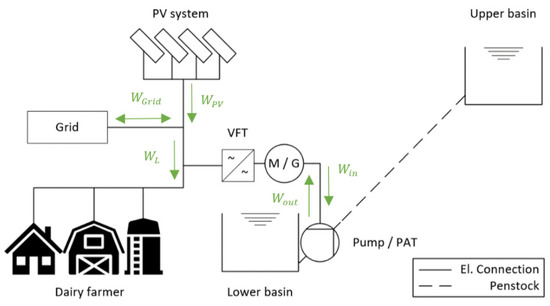
Figure 1.
Schema of the speed-controlled MPS including dairy farmer, grid, and PV system, energy demand , grid energy , total energy input , total energy output PV-energy [15].
The functionality of the MPS can be understood as follows. In pump mode, active during periods of low energy consumption and high solar power production, water is pumped into an upper basin, storing potential energy for later use. During times of high power consumption and low PV output, turbine mode is active, with water flowing back into the lower basin and powering the centrifugal pump, which now acts in turbine operation. Thus, the energy demand from the grid can be reduced, and more of the energy generated by the PV system can be used on site.
In the previous publication [15], the optimal location (i.e., optimal head and storage volume) for a given pump was identified for fixed energy production from the PV system and given energy consumption. To investigate the effects of various consumption and generation scenarios, a scaling factor for PV power and energy consumption has now been introduced. The scaling factors of 1.0 are based on the values of the previous publication, i.e., a PV power of 60 kWp, an annual energy production of MWh, and an annual energy demand of MWh. The ratio of / is therefore around 1.6. For convenience, the relation between the scaling factors and the energy production or demand is shown in Table 1.

Table 1.
Energy (per year) produced by the PV system , energy demand , scaling factor (corresponding to ) and (corresponding to ).
The penstock was assumed to have a nominal diameter of DN150, with costs of 50 €/m pipe. The slope was assumed to be 15%. One of the two basins was supposed to have already existed. The second, a snow-making style of water reservoir design, was assumed to incur construction costs of 40 €/m³ [37,38]. In this publication, due to the many different sizes of centrifugal pumps, no individual costs for the electrical installation were taken into account. Because of that, results for the KSB Etanorm 50160D174 deviate slightly from the results from the last study [15]. The investment costs of the PV system were not included in the economic efficiency calculation because this study was based on the assumption that a PV system was already available, e.g., after expiration of the subsidy by the Germany renewable energy act (EEG).
2.2. Map Calculation
The characteristic maps of various centrifugal pumps for turbine and pump operation were required in order to be able to run simulations and compare several centrifugal pumps with each other. While pump maps are provided in full for each specific pump by the respective manufacturer, turbine maps are usually not provided. For this paper, turbine maps that were not provided (or only provided in partial areas) by the manufacturer were either calculated and/or extended via similarity relationships.
2.2.1. Calculation of Turbine Characteristics at Nominal Speed
The calculation of the characteristic curves was based on empirical correlations according to J.F. Gülich [28]. The exact calculation method is explained in detail in Appendix A and briefly explained here: All values (head, flow, speed, power, and efficiency) for the BEP in pump mode are needed for determining the turbine best efficiency point (BEP). The turbine BEP values were calculated from the pump BEP. All required values for the nominal speed characteristic curve were determined from the BEP in turbine operation thus computed. The formulas were based on calculations from eight different correlations using 35 measured pumps, with a specific speed in the range between 12 and 190. Due to the small number of pumps upon which the correlations were based, considerable deviation should be expected when using these calculations, which is why and may be up to 20% different than the calculation predictions [28].
2.2.2. Extension of Turbine Maps
In order to be able to analyze speed control and to determine the optimum head, it is necessary that a certain range of the characteristic map be known. The law of similarity provides the possibility of calculating further characteristic curves for other speeds from a single measured or given speed characteristic curve. The values calculated in Section 2.2.1 for nominal speed are extended to create a wider range of the turbine map according to Gülich using similarity relationships [28]. Likewise, maps obtained from the manufacturer covering only a subrange of the full turbine operation map are extended in the same way. In order to calculate an extended turbine map, the head , the flow and the power for various speeds are calculated. The similarity laws given in formulas (1)–(3) are based on the respective rated quantities, i.e., speed and the corresponding flow , head and power , from which the turbine behavior for other speeds and operating conditions can be calculated:
One prerequisite for the affinity laws is that the flows in the channels, such as in the impellers, behave similarly kinematically and dynamically. As a consequence, the corresponding inertial and frictional forces behave similarly [28]. In addition, it is assumed that the fluid is incompressible, and no cavitation occurs. When calculating the efficiency with formula (3), there is a deviation, which results from the fact that there are losses that do not increase with the cube of the speed. Among these are the mechanical losses in the bearing and shaft sealing, as well as the disc friction loss [39].
The hydraulic power is determined for the respective speed for various points on the speed characteristic curve (formula (3) [40].
The mechanical efficiency can now be obtained with [40]:
The extended maps are now created by means of interpolation from the associated data of the extended speed curves. There is a set of two maps for the turbine mode. The first map represents the dependency of head on flow and rotational speed, while the second map, describes the power .
In order to exemplarily check the accuracy of the calculation and expansion of the turbine maps, the map of the KSB50160174 (see Table 2) was calculated from BEP pump data alone using the method described above. Comparing the calculated turbine maps with measured maps provided by the manufacturer, an efficiency deviation of only one percentage point was seen in the high rpm range. For lower speeds, the difference increased to up to four percentage points. As the pump/turbine often operates close to its nominal speed, the high-speed range is most relevant for us and, therefore, a fairly good overall accuracy can be expected.

Table 2.
The centrifugal pumps investigated, sorted by their nominal power at their best efficiency given by the manufacturer , average electrical pump efficiency , average electrical turbine efficiency , average electrical turbine efficiency , pump investment and investment for motor and frequency inverter . All results here are given for a scaling factor = = 1.0.
2.3. Simulation Model
The simulation model has also been described in detail in [15] and is reproduced for easier access in Appendix B of this work. A short description of the program sequence is provided as follows. After initiating the simulation, all of the necessary data are collected. The main task of the program is to determine the water volume in the storage reservoir. This is performed by calculating the flow rates in pump and turbine operation. To solve this numerically, the flow has to be obtained from characteristic maps which describe, respectively, the head, the efficiency, and the power as a function of the speed and the flow rate. The difference between PV power and power from the load profile results in the possible pump or turbine power depending on flow and speed, taking into account the efficiency of the electrical components. Taking pipe losses into account, the system’s characteristic curve is defined to determine the resulting head. The operating point is then determined. The flow rate and speed at the intersection point can then be read directly from the characteristic maps while also taking into account the operating limits for pump or turbine operation.
The simulation model then returns results for every point in the time of the year for all system variables. The annual electricity balance can then be obtained from these results, and a profitability calculation can be performed.
2.4. Finding the Optimal Site for Each PAT and Scaling Factor
The plant simulation model was run within a MATLAB optimizer [15] used to determine an optimal site (as defined by the geodetic head and the volume of the storage ) for each of the PATs as listed in Table 2 as well as the scaling factors provided in Table 1. By using the MATLAB 2019a simulated annealing algorithm [41,42], the economic outcome can be maximized by varying and . The results for the optimal site () for each scaling factor and are obviously specific to the PAT type chosen.
3. Results and Discussion
In this section, the investigated pumps are listed, and the results of the simulation model for the head, total efficiency, average turbine and pump efficiency, and levelized cost of energy (LCOE) are presented and discussed. At first (Section 3), the scaling factors and are set to the same value (i.e., =), while in Section 4, SPV and SL are varied independently. As will be shown later, the specific component costs play an important role, which is why they are discussed in more detail after describing the different pumps investigated.
3.1. Pumps Investigated
The following Table 2 lists 11 suitable pumps, examined with increasing nominal power . The scope of the pumps evaluated is chosen to cover the range from 5 to 50 kW, which defines micro-hydropower stations based on the classification of the Latin American Energy Organization (OKADE) [43].
In addition to the pump efficiency given by the manufacturer for the BEP, the table also shows the average efficiency for turbine () and pump () as well as the total efficiency for a scaling factor of 1.0. The values of () and () are calculated from simulation results for the optimal size and scaling factor using trapezoidal numerical integration [44] with a step size of 0.1 min using the following formulae:
The total efficiency is defined as the quotient of the total electrical energy output = and the total electrical energy input
As Table 2 shows, the highest pump efficiency at the BEP in pump mode does not indicate the highest total efficiency. Comparing the EST 65-160 pump, with high manufacturer-specified efficiency of 80.9% in pump mode, with the F080-255A-2202 H, which has only a manufacturer-specified pump efficiency of 78.4%, the total efficiency of the F080-255A-2202H exceeded that of the EST 65-160 by about 1.4 percentage points. The better efficiency is mainly based on a better average electrical efficiency in turbine operation of the F080-255A-2202H and may also be related to better efficiency in the part-load range. Comparing the efficiency of the pumps listed in Table 2 with the pump in Froyennes ( 72.7%) [27], it becomes clear that, with the exception of the F065-200A-1102H, each of the pumps listed in Table 2 has better efficiency. It should therefore be possible to use a PAT with higher efficiency for an MPS.
3.2. Specific Costs
Figure 2 shows the specific prices (€/kW rated power) of the pump including a motor (e.g., F080-255A) [45], asynchronous motor (e.g., VEM PS1R/PS2R) [46], and a frequency converter (e.g., ABB ASC 580) [47]. As expected, the specific prices decreased with the rising power. The drop is especially steep for frequency converters and pumps including motors with an output of less than 22 kW.
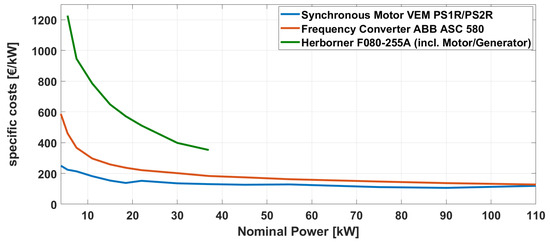
Figure 2.
Specific costs on the example of the VEM PS1R/PS2R synchronous motor, the ABB ASC 580 FUM, and the Herborner F080-255A (including motor/generator).
From a nominal output greater than approximately 22 kW, the curve flattens, and the prices per kW nominal power begin to flatten. This indicates that smaller pumped storages with outputs of below 22 kW are difficult to realize economically due to a high specific cost. To illustrate these findings, the results for centrifugal pumps with a nominal output of less than 22 kW are marked with solid lines in a subsequent part of this paper, whereas centrifugal pumps with a nominal output of greater than 22 kW are marked with dash–dot lines.
3.3. Total Efficiency
Plotting the simulated values of the total efficiencies for the various scaling factors (see Figure 3), it becomes clear that for small-scaling factors, the KSB Etanorm 50160D174 pump has the best total efficiency for an output smaller than 22 kW, and it also shows the best total efficiency for scaling factors of less than two. The excellent total efficiency of the KSB 50160D174, especially for smaller scaling factors, is also reflected in the electrical pump and turbine efficiency (see Figure 4 and Figure 5). Furthermore, a clear increase in the efficiency for factors increasing from 0.5 to 1 can be noticed and is related to the increase in the head (see Figure 6). The highest total efficiencies in all of the pumps investigated (efficiency of about 42%) were achieved by the KSB 8065200 and 50160D174, depending on the scaling factors. The KSB8065200′s pump and turbine efficiencies (see Figure 4 and Figure 5) were correspondingly rather high.
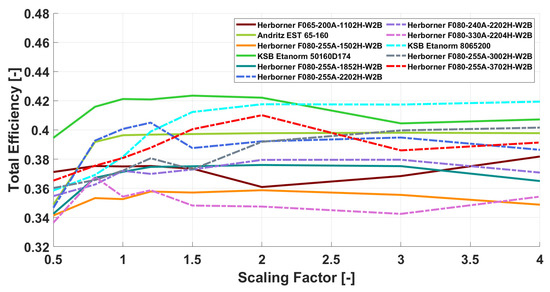
Figure 3.
Total efficiency for equal scaling factors = for various centrifugal pumps.
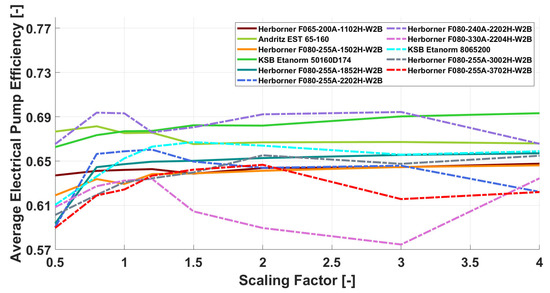
Figure 4.
Electrical pump efficiency for equal scaling factors and various centrifugal pumps.
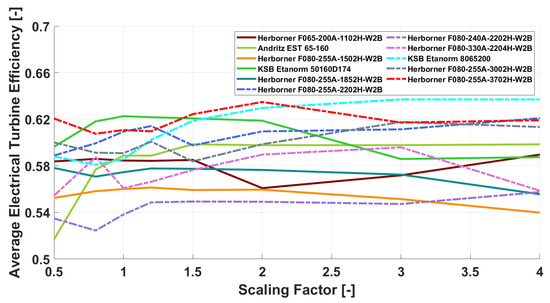
Figure 5.
Electrical turbine efficiency for equal scaling factors = for various centrifugal pumps.
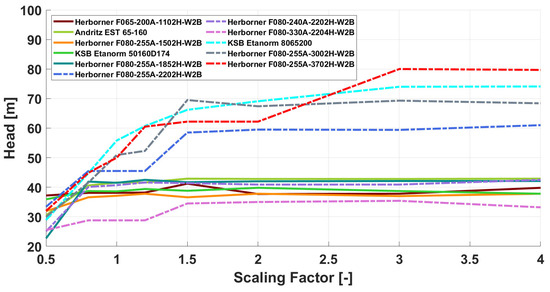
Figure 6.
Optimized head for equal scaling factors = for various centrifugal pumps.
3.4. Average Electrical Pump Efficiency
Out of the 11 investigated pumps from Table 2, the F080-240A-2202H-W2B and Andritz EST 65-160 centrifugal pumps showed the best BEP pump efficiency, with more than 80%. The results of the simulation showed a comparably good average electrical pump efficiency (see Equation (6)) of slightly below 70%. This deviation can be explained by the fact that the simulations were based on variable speed operations. As a result, the pump is not always operating at its best point and is also in the partial-load range, where the efficiency is lower than the best point efficiency. In addition, the efficiency losses due to the motor and FUM were also taken into account in calculating the averaged value. The KSB 50160D174 pump had a very good pump efficiency for pumps smaller than 22 kW. For pumps with a power greater than or equal to 22 kW, the pump efficiency showed a trend similar to that of the total efficiency (see Figure 3). The KSB 8065200 and the Herborner F080-240A-2202H showed the best efficiency in this diagram, and the optimum efficiency specified by the manufacturer was also in the upper range at over 80%.
3.5. Average Electrical Turbine Efficiency
The average electrical turbine efficiency of the pumps (see Figure 5) increased between scaling factors 0.5 and 1, which was similar to the behavior observed previously regarding pump efficiency. The pump with the best turbine efficiency varied depending on the scaling factor. Around a scaling factor of one, the KSB 50160D174 pump had an electrical turbine efficiency of 62%, but this dropped to below 60% as the factor increased. In correlation with a (high) pump efficiency, this appliance nevertheless had the best total efficiency. The second-best electrical turbine efficiency for an output smaller than 22 kW was provided by the F080-255A-2202H-W2B.
The turbine efficiencies of pumps of 22 kW and above showed significant variations. Most of the pumps exhibited high electrical turbine efficiencies, with an increasing scaling factor with a peak between 62–64%, thus higher than the turbine efficiencies for the pumps at below 22 kW. For high-scaling factors, the KSB 8065200 clearly stood out compared to the other pumps.
3.6. Head
The optimization process for the simulation model determines the optimal head for each centrifugal pump and for each scaling factor. These are shown in Figure 6. In Figure 6, an increase in the optimal head in the range of factors between 0.5 and 1 can be seen for all heads, which is due to the fact that the best possible head with optimal efficiency can often not be achieved for consumers with low energy demand and production, i.e., for small-scaling factor values. This results in the pump and/or turbine running at reduced efficiency or not at all since the available power was not enough to enter the operation range. Figure 6 thus directly shows which head would be required at the site in order to use the system optimally. For most centrifugal pumps, it can be seen that the head stagnated above a certain scaling factor. The stagnating curves can be related to the limitation of the maximum possible head of the pumps used. Each pump had a maximum head that limits its operating range.
3.7. Levelized Cost of Electricity
The LCOE for the micro-pump storage under consideration herein was calculated using the following formula [48]:
In year zero , in which the plant is established, all investment costs are considered to be and no energy is drawn from the pumped storage. For any given year t between one and the final year , the sum of costs consists of the operating and maintenance costs , the possible sale of electricity on the electricity exchange and reinvestment for replacement purchases . Since the concept considered is in this case primarily concerned with climate-friendly energy storage, reduction in the grid load and increasing the self-consumption of the produced energy from the PV system, rather than an economically profitable investment, the interest factor was set to 2%. The Federal Ministry of Finance of Germany publishes the interest rates for economic efficiency studies under document GZ II A 3-H 1012-10/07/0001. The approximate average of the interest factor from the years 2005–2020 in this document also gives a value of 2.0% [49]. The sum of costs is determined for every year and, in the final year, the residual values of the components are also taken into account and deducted from the costs:
Figure 7 shows the LCOE for all pumps as a function of the scaling factor for the optimal site. Comparing the LCOE of the EST65-160 with that of the F065-200A, which has similarly high total investment costs, the influence of the previously identified significant improvements are clearly evident. For example, the EST65-160 has slightly lower specific costs for the electrical components due to the larger nominal power of 15 kW instead of 11 kW. In addition, the overall efficiency of the EST65-160 is slightly higher (Cf. Figure 5). Altogether, this leads to an LCOE reduction of up to approximately 7 €cent/kWh.
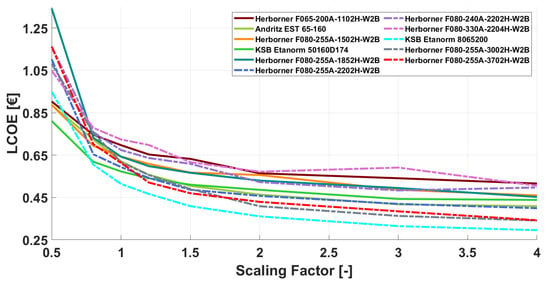
Figure 7.
LCOE for equal scaling factors and for various centrifugal pumps.
Within the scope of pumps and boundary conditions investigated, the lowest possible LCOE of slightly less than 29.2 €cents/kWh can be achieved with rising scaling factors by using the KSB 8065200. This value, though at first glance seemingly high, is very promising when compared to the LCOE of around 1.06 €/kWh for a recently built PAT storage in Froyennes, where the high values result from a small head and a long pipeline [27]. Compared to a value of 1.66 €/kWh [50] for a system with a storage tank in buildings with an open water tank on the roof, it is even more encouraging. On the other hand, for a small-scale PV system (>30 kWp) with a lithium-ion battery [51], the LCOE ranges between approximately 5.4 and 17.2 €cents/kWh. The exact value in this rather wide range depends on the irradiation and the assumed PV-battery ratio at an assumed interest rate of i = 3%. For instance, the upper value of 17.2 €cents/kWh was reached for a large battery storage size (capacity in kWh = 80% of PV system power in kW), while the 5.4 €Cent/kWh applied to a small battery storage size (capacity of 20% of the PV system power). As of 1 April 2020, commercial customers in Germany paid 23.03 €cents/kWh of electricity based on a volume-weighted average annual consumption of 50 megawatt-hours [52]. On the same date, household customers in Germany were paying an average of 33.8 €cents/kWh on the basic supply tariff with an annual electricity purchase of between 2500 and 5000 kWh [52]. Given the electricity price for household customers, the system could therefore be profitable. There still remains a gap of around 6.5 cents/kWh in order to reach the electricity prices for commercial customers, which may be closed in the future by further rising electricity prices. So far, and especially in the months of September and October, 2021 shows a sharp increase in the price of electricity on the exchange [53]. It remains to be seen how this will affect end-customer prices. Since the profitability of the pumped storage always depends on the difference between the costs of the energy obtained from the grid and the potential sales revenue on the electricity exchange, strong fluctuations in the exchange and end prices can have a significant impact—both positive and negative—on the profitability of the pumped storage.
A large contribution to the LCOE is made by (specific) investment costs for the FUM, motor, and pump (see Figure 2). As a result, the LCOE results in Figure 7 showed a behavior similar to that observed in Figure 2. As the scaling factors increased, the costs were spread over larger amounts of stored energy, and the specific costs decreased. As shown in Figure 7 of the LCOE, the three pumps (KSB 8065200, F080-255A-3002H-W2B, and F080-255A-3704H-W2B) became the most economical pumps with an increasing scaling factor. Looking at Table 1, it becomes clear that the KSB 8065200 is rather inexpensive for a 30 kW pump. In this case, the motor and pump were procured separately, which offers a cost advantage compared to the purchase of a complete system of the pump, including the motor. Figure 7 also clearly illustrates that, in most cases, pumps with a larger rated power achieve a lower LCOE. Only in areas with a scaling factor of less than one do pumps with a lower nominal power perform better. However, this sector is already rather uneconomical (see Figure 7). Combining these results for the LCOE with the corresponding results for the optimal heads, it becomes clear that these are located in the range of 70–80 m. Compared with the maximum head in Froyennes, which is about 11 m [27], the optimum head found in this study would be up to seven times higher. This is one of the main reasons for the high LCOE in Froyennes.
Finally, it should be noted that for all of the pumps investigated, a choice of geodetic heads suitable for the pump is crucial for the economic efficiency of the system.
4. Simulation Results for Various Scaling Factors Using the Example of the KSB 8065200
In order to cover a larger scope of load and PV generation scenarios, this section will now analyze the impact of various scaling factors for the load and generation profiles using the example of the KSB 8065200. This pump was selected for the extended analysis because it had the best LCOE of all simulated pumps and offered a very good total efficiency. In addition, a large part of the turbine map was provided by the manufacturer, so only a small portion had to be extended using similarity relationships. Therefore, improved accuracy of the results can be expected. The plots (as, e.g., in Figure 8) were created with the MATLAB fit function [54] using cubic interpolation between data points. In Section 3, the scaling factors for PV () and annual energy demand () varied but remained equal (i.e., ). In order to cover various load scenarios, and are then varied independently.
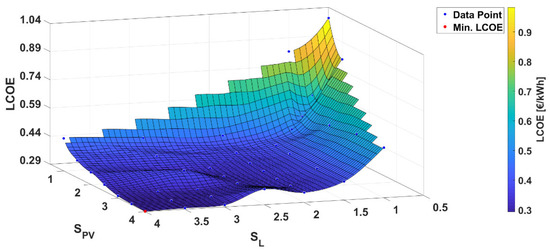
Figure 8.
LCOE for various scaling factors and for the KSB 8065200.
As can be seen clearly in Figure 8, the LCOE of the pump decreased if any of the two scaling factors rose. The lowest LCOE can be achieved if both scaling factors are large, as was already demonstrated in Figure 7 for the special case of =. Even with a relatively low PV output and high energy consumption, an acceptable LCOE of around 29.2 €cents/kWh can be achieved. Considering the LCOE and the ratio of /, the slightly better results were obtained at a ratio slightly above one. This can be understood easily given that, if the PV power is too small, the storage tank cannot be filled sufficiently. So, there is, of course, no storage content that can be discharged afterwards.
The maximum total efficiency (Figure 9) of 42.6% was reached for = 4.0 and = 4.0. In addition to the LCOE, Figure 10 and Figure 11 show the electrical pump and turbine efficiencies. Both figures show a low efficiency for scaling factors smaller than one and an increase with rising scaling factors.
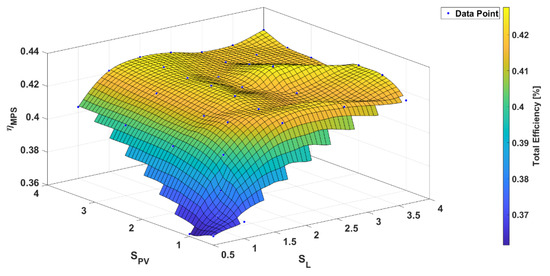
Figure 9.
Total efficiency for various scaling factors and for the KSB 8065200.
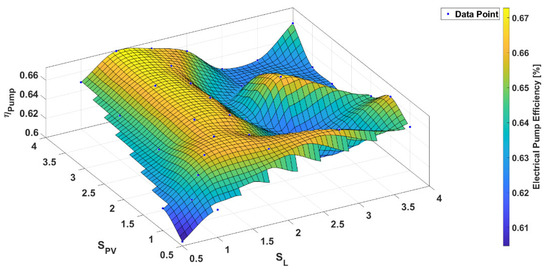
Figure 10.
Average electrical pump efficiency for various scaling factors and for the KSB 8065200.
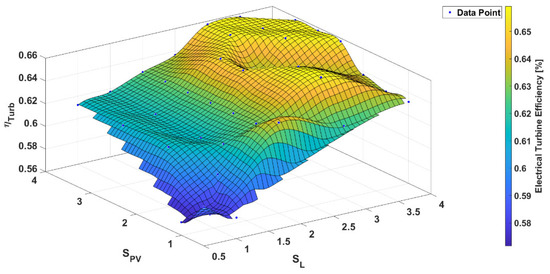
Figure 11.
Average electrical turbine efficiency for various scaling factors and for the KSB 8065200.
For = 2.0 and = 3.0, a local minimum of the electrical pump efficiency (Figure 10) is reached, whereas the electrical turbine efficiency (Figure 11) is at a local maximum. However, it should be noted that the total variation of efficiencies is only around three percentage points. For the factors = 2.0 and = 1.5, the conditions were reversed, and the turbine reached a minimum and the electrical pump efficiency a maximum.
In summary, it can be concluded that a suitable combination of high pump and turbine efficiencies is of significant importance in obtaining a high level of total efficiency. However, the trade-off is that improving the turbine efficiency often leads to a reduction in pump efficiency or vice versa.
5. Conclusions
Summarizing on the basis of the previous graphical representations of the efficiencies, it can be said that the correlation between pump and turbine efficiency plays a major role in the use of the pumps in PAT operation. Generally, it can be said that the efficiencies for small power plants (i.e., scaling factors of <1) are too low for an economical operation. Moreover, an increase in the efficiency at the scaling factors from 0.5 to 1 can also be seen. A subsequent leveling off, on the other hand, does not follow for every pump, which may be related to increasing or stagnating heads. Based on the total efficiencies (Figure 3), it can be seen that, with increasing factors, the efficiencies of the pumps below 22 kW are more dispersed, showing poorer total efficiencies. In contrast, four of the pumps with a power greater than or equal to 22 kW had a similar curve and a total efficiency of around 40% for high generation and load scenarios. It should also be noted that the PAT with the best total efficiency is not always the most economical pump. High efficiency is a basic prerequisite for profitability, but many other factors such as the head, specific costs, generation, and load scenarios, as well as the efficiency in the partial load range, play a major role. As an operating strategy, speed control using a frequency converter was shown to be the most sensible method of economical operation [15]. Basically, due to the high specific costs, no PAT with an output of less than 22 kW should be selected. As was to be expected, larger pumps were shown to lead to lower specific costs. For pumps with a nominal power of greater than 40 kW, however, the specific costs are barely reduced. Therefore, only minor savings can be expected by increasing the nominal power beyond this amount. The ratio of /, as provided in Table 1, at around 1.6, has turned out to be quite an optimal ratio, depending on the scaling factor. Qualitatively, it can be easily understood that the optimal ratio of / needs to be larger than one since smaller values indicate that the generated energy is not sufficiently larger than the energy demand which in turn leads to the fact that the storage can often not be filled sufficiently.
Even as it is important to keep in mind that the results are subject to calculation inaccuracies of the turbine maps (see Section 2.2.1), this quantitative examination nevertheless shows that pumped storage with a pump as a turbine can achieve a passable LCOE of around 29.2 €cents/kWh if the nominal power of the pump is sufficiently high and the specific costs can thus be strongly reduced. While the use of PATs in water networks may lead to short payback periods, for example, of six years, the use of a PAT in an MPS faces the challenge of achieving economic operation at all. Nevertheless, if the results obtained in this study are compared to the LCOE of the MPS from Froyennes of around 1.06 €/kWh [27], or a storage tank in buildings with a value of 1.66 €/kWh [50], an LCOE of 29.2 €cents/kWh seems very promising.
In the future, it is planned to further increase the accuracy and reliability of the results reported here by using measured instead of calculated turbine maps for the simulations. In this context, a test bench is currently being set up to measure characteristic maps and create a database that will allow new simulations to be performed. Furthermore, more accurate calculation methods recently published [55] could be used to further increase the reliability of the results.
In summary, it can be said that an MPS system with a pump as a turbine can achieve profitability in the future. However, this will require further cost savings or further increases in electricity prices. Moreover, only a few locations are suitable for the profitable use of micro-pump storage because so many conditions have to be fulfilled. A sufficiently sized PV system, a pre-existing storage basin, sufficient head (around 70 m or more), and appropriate energy consumption are all required. Taken together, this considerably limits the availability of possible locations. The PAT itself should preferably have a nominal power of 22 kW or higher, high efficiency in turbine and pump mode, which preferably extends well into the partial load range. Of course, the PAT must also be adapted to the head, the flow rates, as well as the power of the load and of the PV system. If all these conditions are fulfilled, economic viability may well be possible, but each case has to be examined individually. Based on the results presented in this article, a pre-selection of suitable PATs can be performed for a given prospective MPS site. In a second step, the simulation model can be used to evaluate the economic feasibility for these pumps at the given site in more detail.
The envisioned transition to a more sustainable future with a carbon-free and electricity-based energy system will require storage systems of all sizes and many types. For small and decentralized energy storage, concepts such as those presented in this publication could contribute to the overall solution.
Author Contributions
Conceptualization, F.J.L. and J.K.; methodology, F.J.L.; software, F.J.L. and E.G.; validation, F.J.L., J.K. and M.G.; formal analysis, F.J.L. and E.G.; investigation, F.J.L. and E.G.; resources, F.J.L.; data curation, F.J.L. and E.G.; writing—original draft preparation, F.J.L.; writing—review and editing, J.K., M.G. and E.G.; visualization, F.J.L. and E.G.; supervision, J.K. and M.G.; project administration, J.K.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bavarian State Ministry of Science. Grant number: VIII.2-F1116.WE/29/2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by IB Pfeffer, Herborner-Pumpentechnik GmbH & Co KG and KSB Aktiengesellschaft.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Nomenclature
| Symbol/Abbreviation | Interpretation |
| sum of costs | |
| nominal pipeline diameter | |
| possible energy sales proceeds | |
| Darcy friction factor | |
| gravitational acceleration | |
| head | |
| geodetic head | |
| head of the idle point | |
| arithmetic average value of the head | |
| head at nominal speed | |
| optimized head | |
| head at the best efficiency point | |
| head corresponding to the respective speed | |
| turbine head | |
| discount rate | |
| investment costs | |
| investment for motor and frequency inverter | |
| pump investment | |
| nominal power (PV) | |
| levelized cost of energy | |
| pipeline length | |
| torque | |
| rpm | |
| nominal speed | |
| specific speed | |
| operating and maintenance costs | |
| hydraulic power | |
| power demand (consumer) | |
| nominal output | |
| power at nominal speed | |
| maximum power in pump mode | |
| pump power | |
| electrical pump power | |
| PV power | |
| power corresponding to the respective speed | |
| turbine power | |
| electrical turbine power | |
| mechanical turbine power | |
| power loss | |
| PV power | |
| flow rate | |
| flow rate of the idle point | |
| arithmetic average value of the flow rate | |
| maximum flow rate | |
| minimum flow rate | |
| flow rate at nominal speed | |
| flow rate at the best efficiency point | |
| flow rate corresponding to the respective speed | |
| turbine flow rate | |
| reinvestment costs | |
| residual values | |
| scaling factor for the annual energy demand | |
| scaling factor for PV power | |
| period of time | |
| volume flow | |
| storage capacity | |
| optimized volume of the storage | |
| grid energy | |
| total energy input | |
| annual energy demand | |
| total energy output | |
| annual energy production of the PV system | |
| Greek letters | Interpretation |
| total dynamic loss coefficient of fittings | |
| efficiency | |
| electrical efficiency | |
| average electrical pump efficiency | |
| average electrical turbine efficiency | |
| best efficiency point | |
| best pump efficiency given by the manufacturer | |
| specific speed | |
| turbine efficiency | |
| total efficiency | |
| mechanical turbine efficiency | |
| density |
Appendix A
This appendix describes a possible procedure for calculating the speed characteristic according to Gülich [28]. The values given by the manufacturer for the flow rate , the head , the nominal speed , and the efficiency at the best efficiency point of pumping operation of the centrifugal pump used serve as the basic data. From this, the necessary parameters in turbine operation are calculated in the next steps, where the index stands for turbine mode and for pump mode, respectively.
The first step is the determination of , and the specific speed at the turbine BEP of operation. There are two variants for the calculation, from which an average value is then formed.
- For the first variant, the BEP in turbine operation is determined from the BEP data of the pump using the following empirical formulas:
- For the second variant, the BEP in turbine operation is also calculated from the BEP of the pump using another set of empirical formulas:
- Gülich states that both methods (Equations (A1)–(A4)) can also be used and an arithmetic mean can be formed from them. When comparing the calculations with the characteristic diagrams given by the manufacturer, the arithmetic mean of the values has proven to be the best method, which is why this is used in our calculations. The the arithmetic average value and is calculated from both variants as well as the determination of the specific speed of the turbine via the formulas:
- To determine the turbine characteristic curve at the nominal speed , the no-load characteristic curve, which at the same time represents the lower limit of the characteristic diagram. The no-load point , are calculated according to Equation (A8). For this, the specific speed of the pump is required.
Determination of the specific speed of the pump:
- Calculation of the idle point , for the nominal speed :
- For the approximation of the turbine characteristic () the characteristic curve runs as a parabola through the BEP of the turbine. The head depends on the flow and is calculated using the following formula:
- Calculation of the idle speed characteristic curve (LLK):
The characteristic curve is determined using formula (A12), where is an individual volume flow on the no-load characteristic curve. At the no-load point, the torque M is 0 Nm. The idling characteristic connects all points , which are located at different speeds for M equal to 0 Nm and thus forms a parabola through the coordinate origin.
- Calculation of the turbine efficiency for the nominal speed:
The efficiency is calculated from the quotient of the optimum efficiency and the specific speed of the pump by means of the formula:
The efficiency curve is then determined from a graph in which / is plotted as a function of the ratio of
- The turbine power can then be calculated using the following formula:
Appendix B
A detailed description of the simulation program sequence is provided as follows. Initially, all required data are gathered by the program. The relationship between the water volume in the storage reservoir to the pump and the turbine flow through the PAT ( and , respectively) is given by the following ordinary differential equation:
It should be noted that no external water inflow or evaporation is considered. To solve this numerically, and have to be obtained from characteristic maps. There is a set of two maps each for the turbine and pump operation, respectively. The map represents the dependency of head on flow and speed, while the second map (shows the power (from which the efficiency can also be obtained). Accordingly, pump operation is described by () and ().
The difference between PV power and power from the load profile results in the possible pump or turbine power depending on the flow and speed and taking into account the efficiency of the electrical components in the drive unit :
To determine the resulting head, taking pipe losses into account, the system’s characteristic curves have to be defined. The curves depend on the flow , the Darcy friction factor , the dynamic loss coefficient gravitational acceleration pipe length and diameter [56,57]:
The operating point (,n) is now determined by numerically solving the following equations:
where for turbine mode and for pump mode, respectively.
Graphically, this corresponds to the intersection of the system’s characteristic curve with the turbine or pump power isoline corresponding to the power . The flow rate and speed at the intersection point can then be read directly from the characteristic maps.
The limit values of pump or turbine operation are the lines for maximum and minimum speed , as well as the line for minimum and maximum flow. It is also important to provide hysteresis to prevent the turbine from shutting down immediately after starting due to a small drop in load request.
In total, the water volume of the storage tank is determined by numerical integration, and the states “storage tank full” and “empty” are defined. The simulation model provides results for every point in the time of year for all system variables, such as storage level, turbine and pump flow, power, and so on. The annual electricity balance can then be obtained from these results and a profitability calculation can be performed.
References
- Cebulla, F.; Haas, J.; Eichman, J.; Nowak, W.; Mancarella, P. How much electrical energy storage do we need? A synthesis for the U.S., Europe, and Germany. J. Clean. Prod. 2018, 181, 449–459. [Google Scholar] [CrossRef]
- Rohit, A.K.; Devi, K.P.; Rangnekar, S. An overview of energy storage and its importance in Indian renewable energy sector: Part I—Technologies and Comparison. J. Energy Storage 2017, 13, 10–23. [Google Scholar] [CrossRef]
- Ramos, M.H.; Dadfar, A.; Basharat, M.; Adeyeye, K. Inline pumped storage hydropower towards smart and flexible energy recovery in water networks. Water 2020, 12, 2224. [Google Scholar] [CrossRef]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy recovery in water distribution networks. Implementation of pumps as turbine in a dynamic numerical model. Procedia Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef] [Green Version]
- Spedaletti, S.; Rossi, M.; Comodi, G.; Salvi, D.; Renzi, M. Energy recovery in gravity adduction pipelines of a water supply system (WSS) for urban areas using Pumps-as-Turbines (PaTs). Sustain. Energy Technol. Assess. 2021, 45, 101040. [Google Scholar] [CrossRef]
- Muhammetoglu, A.; Karadirek, E.; Ozen, O.; Muhammetoglu, H. Full-Scale PAT Application for Energy Production and Pressure Reduction in a Water Distribution Network. J. Water Resour. Plan. Manag. 2017, 143, 04017040. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, M.H. Pump as Turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef] [Green Version]
- Fecarotta, O.; Ramos, H.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine tuning a PAT hydropower plant in a water supply network to improve system effectiveness. J. Water Resour. Plan. Manag. 2018, 144, 04018038. [Google Scholar] [CrossRef]
- Ramos, H.; McNabola, A.; Lopez-Jimenez, P.A.; Perez-Sanchez, M. Smart water management towards future water sustainable networks. Water 2020, 12, 58. [Google Scholar] [CrossRef] [Green Version]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Energy production in water distribution networks: A PAT design strategy. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef] [Green Version]
- Madeira, C.F.; Fernandes, F.P.J.; Perez-Sanchez, M.; Lopez-Jimenez, P.A.; Ramos, M.H.; Branco, P.J.C. Electro-hydraulic transient regimes in isolated pumps working as turbines with self-excited induction generators. Energies 2020, 13, 4521. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Capurso, T.; Balacco, G.; Binetti, M.; Camporeale, S.M.; Torresi, M. Selection, control and techno-economic feasibility of Pumps as Turbines in Water Distribution Networks. Renew. Energy 2020, 162, 1292–1306. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal energy management of water-energy networks via optimal placement of pumps-as-turbines and demand response through water storage tanks. Appl. Energy 2021, 283, 116335. [Google Scholar] [CrossRef]
- Balacco, G.; Binetti, M.; Caggiani, L.; Ottomanelli, M. A Novel Distributed System of e-Vehicle Charging Stations Based on Pumps as Turbine to Support Sustainable Micromobility. Sustainability 2021, 13, 1847. [Google Scholar] [CrossRef]
- Lugauer, F.J.; Kainz, J.; Gaderer, M. Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine. Energies 2021, 14, 425. [Google Scholar] [CrossRef]
- Morabito, A.; Furtado, A.; Gilton, C.; Hendrick, P. Variable speed regulation for pump as turbine in micro pumped hydro energy storage. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Anilkumar, T.T.; Simon, S.P.; Padhy, N.P. Residential electricity cost minimization model through open well-pico turbine pumped storage system. Appl. Energy 2017, 195, 23–35. [Google Scholar] [CrossRef]
- Borkowski, D. Analytical model of small hydropower plant working at variable speed. IEEE Trans. Energy Convers. 2018, 33, 1886–1894. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Predictive model estimating the performances of centrifugal pumps used as turbines. Energy 2016, 107, 103–121. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Gomathi, V.; Ekanayake, J.B.; Tiong, S.K. Modelling and simulation of variable speed pico hydel energy storage system for microgrid applications. J. Energy Storage 2019, 24, 100808. [Google Scholar]
- Mohanpurkar, M.; Ouroua, A.; Hovsepian, R.; Luo, Y.; Singh, M.; Muljadi, E.; Gevorgian, V.; Donalek, P. Real-time co-simulation of adjustable-speed pumped storage hydro for transient stability analysis. Electr. Power Syst. Res. 2018, 154, 276–286. [Google Scholar] [CrossRef]
- Schmidt, J.; Kemmetmüller, W.; Kugi, A. Modeling and static optimization of a variable speed pumped storage power plant. Renew. Energy 2017, 111, 38–51. [Google Scholar] [CrossRef]
- Stoppato, A.; Benato, A.; Destro, N.; Mirandola, A. A model for the optimal design and management of a cogenartion system with energy storage. Energy Build. 2016, 124, 241–247. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Pumped storage-based standalone photovoltaic power generation system: Modeling and techno economic optimization. Appl. Energy 2015, 137, 649–659. [Google Scholar] [CrossRef]
- Yang, W.; Yang, J. Advantage of variable-speed pumped storage plants for mitigating wind power variations: Integrated modelling and performance assessment. Appl. Energy 2019, 237, 720–732. [Google Scholar] [CrossRef]
- Simao, M.; Ramos, H. Hybrid pumped hydro storage energy solutions towards wind and PV integration: Improvement on flexibility, reliability and energy costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Morabito, A.; Hendrick, P. Pump as turbine applied to micro energy storage and smart water grids: A case study. Appl. Energy 2019, 241, 567–579. [Google Scholar] [CrossRef]
- Gülich, J.F. Kreiselpumpen; Springer: Berlin/Heidelberg, Germany, 2013; Volume 4. [Google Scholar]
- Alatorre-Frenk, C. Cost Minimization in Microhydro Systems Using Pumps-as-Turbines. Ph.D. Thesis, University of Warwick Coventry, Coventry, England, 1994; pp. 55–113. [Google Scholar]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbine in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Yang, S.; Derakhshan, S.; Kong, F. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Lin, T.; Zhu, Z.; Li, X.; Li, J.; Lin, Y. Theoretical, experimental, and numerical methods to predict the best efficiency point of centrifugal pump as turbine. Renew. Energy 2021, 168, 31–44. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps as Turbines. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S.M. Experimental investigation and performance prediction modeling of a single stage centrifugal pump operation as turbine. Energy Procedia 2017, 126, 589–596. [Google Scholar] [CrossRef]
- Renzi, M.; Nigro, A.; Rossi, M. A methodology to forecast the main non-dimensional performance parameters of pumps-as-turbines (PaTs) operating at Best Efficiency Point (BEP). Renew. Energy 2020, 160, 16–25. [Google Scholar] [CrossRef]
- Pugliese, F.; Fontana, N.; Marini, G.; Giugni, M. Experimental assessment of the impact of number of stages on vertical axis multi-stage centrifugal PATs. Renew. Energy 2021, 178, 891–903. [Google Scholar] [CrossRef]
- Beschneiungsanlage Erhält Wasserspeicher. Available online: https://bnn.de/lokales/abb/beschneiungsanlage-erhaelt-waserspeicher (accessed on 30 April 2020).
- Fahrner, H.; (Nationalpark-Hotel Schliffkopf, Schliffkopf, Germany); Lugauer, F.J.; (TUM Campus Straubing for Biotechnology and Sustanability, Weihenstephan-Triesdorf University of Applied Science, Straubing, Germany). Personal communication, 2020.
- EDUR-Pumpenfabrik Eduard Redlien GbmH & Co. KG. Die Kennlinien. Available online: www.treffpunkt-kaelte.de/wp-content/uploads/2017/komponenten/pumpen/edur/kennlinien_2.pdf (accessed on 24 August 2021).
- KSB AG Pump Affinity Laws. Available online: https://www.ksb.com/centrifugal-pump-lexicon/pump-affinity-laws/191832 (accessed on 17 August 2021).
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Mathworks. Global Optimization Toolbox: Simulated Annealing (r2019a). Available online: https://de.mathworks.com/help/gads/simulannealbnd.html (accessed on 28 January 2020).
- Nourbakhsh, A.; Derakhshan, S.; Javidpour, E.; Riasi, A. Centrifugal & axial pumps used as turbines in small hydropower stations. In Proceedings of the Hidroenergia 2010 Intenational Congress on Small Hydropower International Conference and Exhibition on Small Hydropower, Lausanne, Switzerland, 26–28 October 2009; pp. 16–19. [Google Scholar]
- Mathworks. Trapezoidal Numerical Integration (r2021a). Available online: https://de.mathworks.com/help/matlab/ref/trapz.html (accessed on 1 September 2021).
- Herborner Pumpentechnik GmbH & Co. KG. Price List 2019. Available online: https://www.herborner-pumpen.de/en/downloads/ (accessed on 20 May 2020).
- VEM GmbH. Price List 2021: Drive Technology. Available online: www.vem-group.com/fileadmin/content/pdf/Download/Kataloge/Preisliste/2021_VEM_Preisliste_Antriebstechnik.pdf (accessed on 30 June 2021).
- Ghv Vertriebs-Gmbh für Antribstechnik und Automation. Prices for Frequency Converters. Personal Communication, 2017.
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef] [Green Version]
- German Federal Ministry of Finance. Kalkulationszinssätze für Wirtschaftlichkeitsuntersuchungen GZ II A 3—H 1012-10/07/0001. 2020. Available online: https://www.bundesfinanzministerium.de/Content/DE/Standardartikel/Themen/Oeffentliche_Finanzen/Bundeshaushalt/personalkostensaetze-2020-anl.pdf (accessed on 20 November 2021).
- de Oliveira e Silva, G.; Hendrick, P. Pumped hydro energy storage in buildings. Appl. Energy 2016, 179, 1242–1250. [Google Scholar] [CrossRef]
- Kost, C. Study: Levelized Cost of Electricity-Renewable Energy Techologies. June 2021. Available online: https://www.ise.fraunhofer.de/en/publications/studies/cost-of-electricity.html (accessed on 17 August 2021).
- Bundesnetzsagentur; Bundeskartellamt. Bundesnetzagentur—Monitoringbericht 2020. 2020, pp. 269, 272, 282. Available online: https://bundesnetzagentur.de/SharedDocs/Mediathek/Berichte/2020/Monitoringbericht_Energie2020.pdf (accessed on 26 August 2021).
- Bundesnetzagentur: Market—Day-Ahead Prices. Available online: https://www.smard.de/page/home/marktdaten/78?marketDataAttributes=%7B%22resolution%22:%22day%22,%22region%22:%22DE-LU%22,%22from%22:1626300000000,%22to%22:1634248799999,%22moduleIds%22:%5B8004169%5D,%22selectedCategory%22:null,%22activeChart%22:true,%22style%22:%22color%22%7D (accessed on 20 October 2021).
- Mathworks. Fit Curve or Surface to Data (r2021a). Available online: https://de.mathworks.com/help/curvefit/fit.html (accessed on 7 September 2021).
- Macías Ávila, C.A.; Sánchez-Romero, F.-J.; López-Jiménez, P.A.; Pérez-Sánchez, M. Definition of the Operational Curves by Modification of the Affinity Laws to Improve the Simulation of PATs. Water 2021, 13, 1880. [Google Scholar] [CrossRef]
- KSB Aktiengesellscahft. Selecting Centrifugal Pumps; KSB Aktiengesellschaft: Frankenthal, Germany, 2005; Volume 4, pp. 19–31. [Google Scholar]
- Menny, K. Strömungsmaschinen; Teubner: Wiesbaden, Germany, 1985; ISBN 978-3-519-06317-9. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).