1. Introduction
Earthquakes are considered to be one of the major landslide-triggering factors [
1,
2,
3]. Earthquakes induce shear-wave propagation, causing cyclic shear stresses and strains that degrade the soil strength and generate pore-pressure build-up. This, in turn, leads to soil failure, and under some special site conditions, it can lead to soil liquefaction. Such behaviour is critical for slopes that are prone to shallow landslides. Shallow landslides are considered to have a depth of up to around five meters [
4] and are greatly affected by earthquakes and rainfall (e.g., [
5,
6]). Significant research has been conducted on the activation of shallow landslides in volcanic soil, common for regions in Japan [
7,
8,
9,
10] and Italy [
11,
12,
13,
14]. Two approaches to landslide analysis have been established: (i) a pre-failure approach and (ii) a post-failure approach. In a pre-failure approach, slopes that have potential of failure and landslide activation are analysed and are often monitored as part of early warning systems (e.g., [
15,
16,
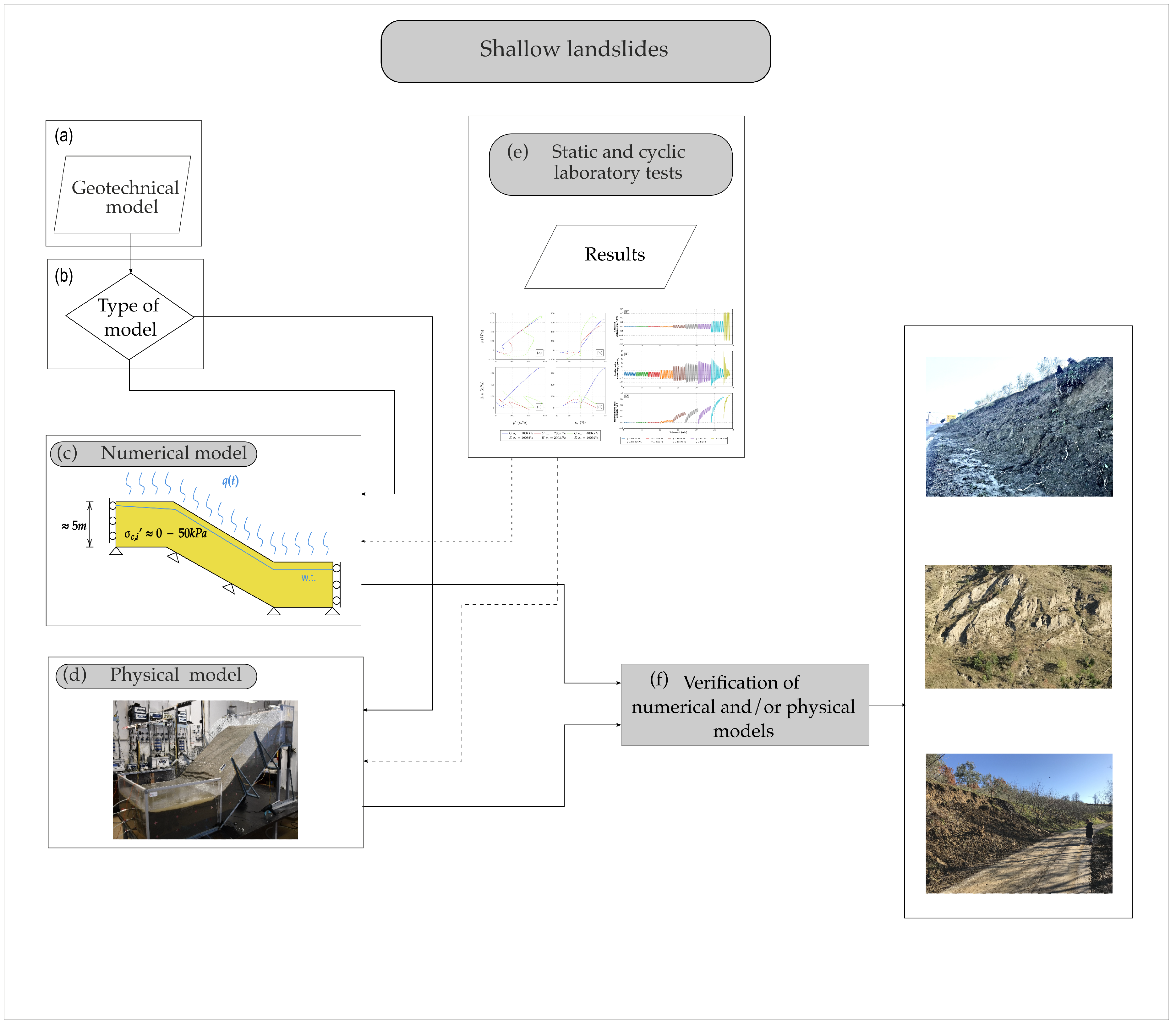
17]). For a slope that has the potential to slide, an engineering geologist can determine a geological model as the basis of a geotechnical model (
Figure 1a) from field exploration and laboratory testing. In a post-failure approach, the same procedure can be applied but with known slip-surface depth and mobilized strength parameters obtained through laboratory testing (e.g., [
18,
19,
20,
21]). It is not important which approach is used to analyse a slope; both can be used to create a numerical (
Figure 1c) or physical model (
Figure 1d) of the slope through a decision loop (
Figure 1b). Physical modelling can be divided into two categories: (i) physical models at 1g (e.g., [
22,
23,
24,
25,
26,
27,
28,
29,
30]) and (ii) physical models at ng (e.g., [
31,
32,
33,
34,
35,
36]). The first category is often simply used in laboratories where dimensions and other model elements (e.g., grain-size distribution, rain intensity, etc.) are scaled according to a decided scale factor, but the vertical acceleration is 1g. The second category requires sophisticated equipment or a geotechnical centrifuge to simulate larger values of gravitational acceleration: called ng conditions [
37]. Models used in geotechnical centrifuges usually have significantly smaller dimensions than those used at 1g. Physical modelling of small-scale landslides under 1g conditions started at the end of 1980s, when the behaviour of flowslides and liquefaction were investigated [
38]. Physical modelling under dynamic loading started in the mid 1950s [
39], while simulations of seismically induced landslides were first developed in the early 2000s. Most of the known research concerns seismic behaviour and the response of slopes and slope material (e.g., [
27,
28,
33,
40,
41]). Physical methods for assessing the stability of slopes during an earthquake were proposed by Jibson [
42] and are still used today. A common feature of both numerical and physical models is the static and/or cyclic behaviour of materials (
Figure 1e). It is necessary to determine static and/or cyclic behaviour of soil material used in models/simulations to accurately test landslide mechanisms. This is necessary for the analysis of, for example, rain infiltration, landslide run-off, erosion, degradation, and strength reduction due to cyclic loading. Results from both numerical and physical models have to be verified (
Figure 1f) in order to calibrate the numerical model, refine boundary conditions of the physical model, and select appropriate material behaviour for laboratory tests.
As part of ongoing research on landslide activation at 1g conditions, we subject slope material to dynamic loading to determine its behaviour [
22]. A slope that has the potential to become a shallow landslide (
Figure 2a) is scaled by a factor of 40 and dynamically loaded (
Figure 2b), such as would occur during an earthquake. Dynamic loading conditions are applied with a seismic platform, as explained in detail later.
Frequencies of straining amplitudes for strain-controlled cyclic triaxial tests are defined based on similarity laws for 1g conditions [
43] and small-scale landslide model dimensions (
Figure 2). The corresponding frequencies with respect to similarity law are used for dynamic loading of slope material. Sandy specimens are tested at low confining stresses that correspond to a shallow landslide forming on a prototypical slope (
Figure 2), ranging from 10 to 50 kPa. It is also assumed that the material used in the model is fully saturated, (as in post-rainfall conditions).
The behaviour of soil in shallow landslides is governed by low confining stress [
44]. Low confining stress has a significant influence on soil strength, especially if the soil’s material strength is pressure-dependent. White [
44] performed experiments in a triaxial cyclic device at low effective stresses (less than 50 kPa). All undrained cyclic tests were performed after isotropic consolidation until initial liquefaction had been reached. Such stress values correspond to a stress level in a slope at a depth less than 10 m from the soil surface. Higher confining stress values lead to a faster rise of pore pressure. The secant shear modulus,
, was found to decrease with an increasing number of cycles and with decreasing effective stress,
[
44]. Test results of an equivalent viscous ratio show significant noise in the data, especially for lower cyclic load values, which in some experiments makes it difficult to reliably estimate damping ratio [
44]. The results show that when the shear cyclic strain
is less than approximately
%, the damping of soil does not significantly increase and remains relatively the same with the increasing number of cycles. This coincides with the literature [
45,
46,
47,
48], where the cyclic volumetric shear stress threshold
is equal to
% regardless of the effective stress, compaction, and sample structure. Once this threshold is exceeded, the damping of soil changes with the change in shear cyclic deformation and the number of cycles. Kumar et al. [
3] found that samples tested at lower effective stresses (50 kPa) show a higher damping ratio compared to that of higher effective stresses (100 and 150 kPa), which was attributed to relatively higher stiffness due to sample constraints. Chakraborty and Salgado [
49] conducted triaxial compression in drained conditions, along with in-plane compression experiments (plane-strain). The sand was tested at low effective stresses to determine the dependence of dilatation and friction angle related to relative compaction and applied effective stresses. The authors concluded that sand dilatation decreases with decreasing compaction and increasing applied effective stresses. Further, it was observed that for lower effective stresses (less than 50 kPa) had larger scatter in results compared to those of higher values of effective stress (greater than 100 kPa). Shaoli et al. [
50] emphasized that clean sand has significant dilating behaviour at lower effective stresses. Therefore, clean sand is more stable at low effective stresses compared to behaviour at high effective stresses. This is usually not the case with fine sand because such sand is susceptible to static liquefaction at low effective stresses with complete loss of strength. The amplitude of the cyclic load significantly affects generated pore pressure, while the void ratio plays a dominant role in sand behaviour. Sture et al. [
51] conducted cyclic triaxial tests using a deformation control method in drained and undrained conditions. It should be emphasized that the experiments were conducted in microgravity conditions. Microgravity is a weightless state in which objects are not seemingly affected by gravitational forces [
52]. This was done because many soil characteristics such as strength, stiffness, deformation modulus, etc. are greatly influenced by interparticle forces [
51]. Therefore, it can be concluded that the behaviour of soil at low effective stresses depends on the gravitational force. High friction angles and dilatation were observed in drained tests of medium-compacted samples. In undrained tests with loosely compacted samples, a transition from the stable solid state to the viscous liquid state (liquefaction) was observed in several undrained tests. The main motivation for carrying out this research was to determine the behaviour of sandy soil to be used for small-scale physical slope modelling in 1g conditions under cyclic loading. The results of conducted undrained and drained cyclic triaxial tests on such sandy soil material under dynamic loading are presented, as well as the proposed models for pore water pressure build-up and volumetric strain behaviour. The proposed models can be used for quick determination of the pore water pressure ratio and volumetric strain behaviour of sandy soils at low confining stresses.
Although the main intention of this manuscript is not related to the use of the proposed models to develop landslide susceptibility analyses (e.g., [
53,
54,
55]), early warning systems (e.g., [
16,
17,
56]), or for other issues such are stability and run-off landslide predictions (e.g., [
57,
58]), the proposed models would be useful tools in such analyses.
To summarize, this paper presents the results of undrained and drained cyclic triaxial tests on sandy material, which is going to be used for physical modelling of a shallow landslide in 1g conditions under dynamic loading.
4. Discussion
Equivalent viscous damping,
, of uniform sand was examined in both drained and undrained conditions on dynamic triaxial equipment.
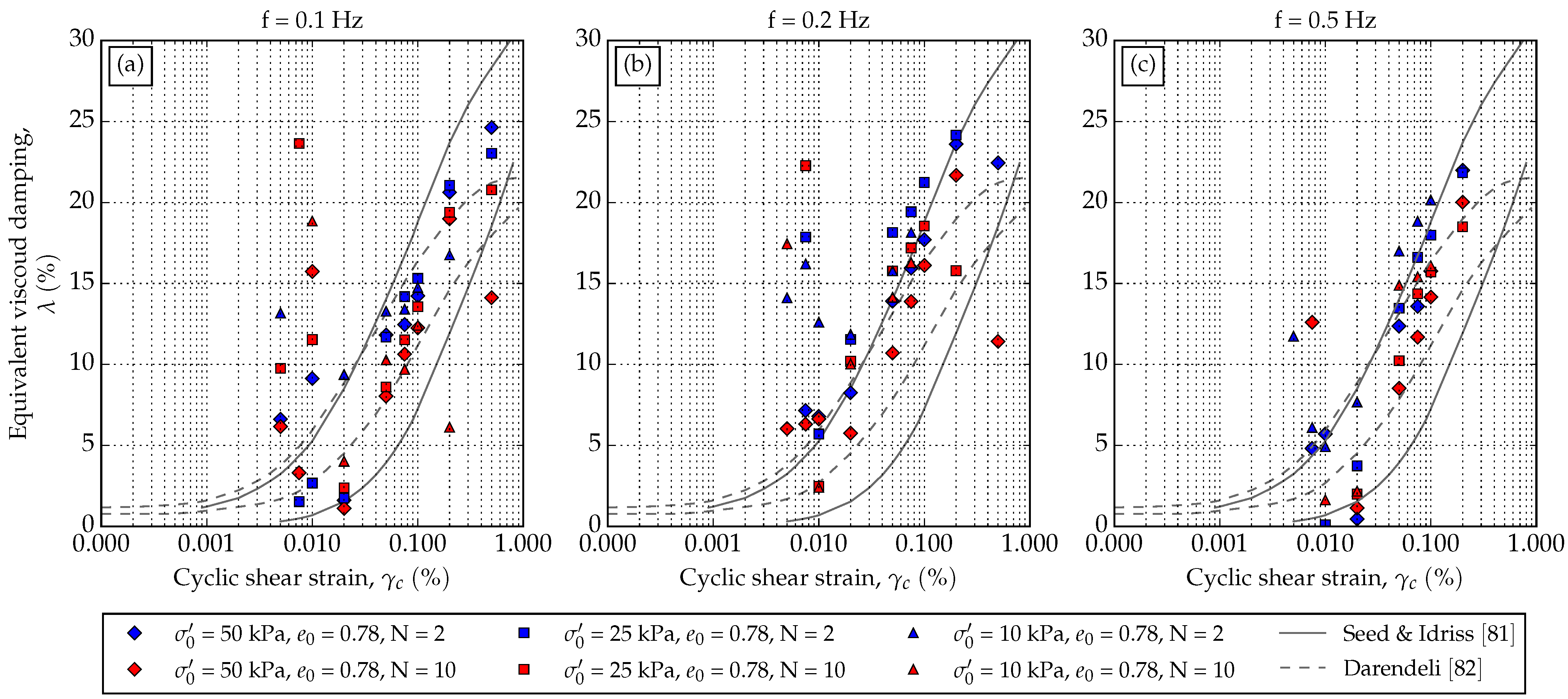
Figure 8 presents the damping ratio for low confining stresses with respect to different loading frequencies (0.1, 0.2, and 0.5 Hz). Data fit well with the regions proposed by Seed and Idris [
80] and Darendeli [
81]. There are minor discrepancies to the fit-lines, mostly for cyclic shear strainless than 0.01%. It must be noted that the regions often used in the literature, defined by Seed and Idris [
80], are for higher stress values (values higher than 80 kPa). Further, it is worth noting that the damping ratio tends to plot to the upper boundary of the Seed and Idriss regions for frequencies higher than 0.1 Hz. This scatter could also be due to the equipment used in this research. The Dynatriax system is pneumatically based and is very sensitive to system control parameters. System parameters are modified using Proportional–Integrate–Derivative (PID) [
87], which can have a small impact on the measured axial strains at values lower than 0.0075%.
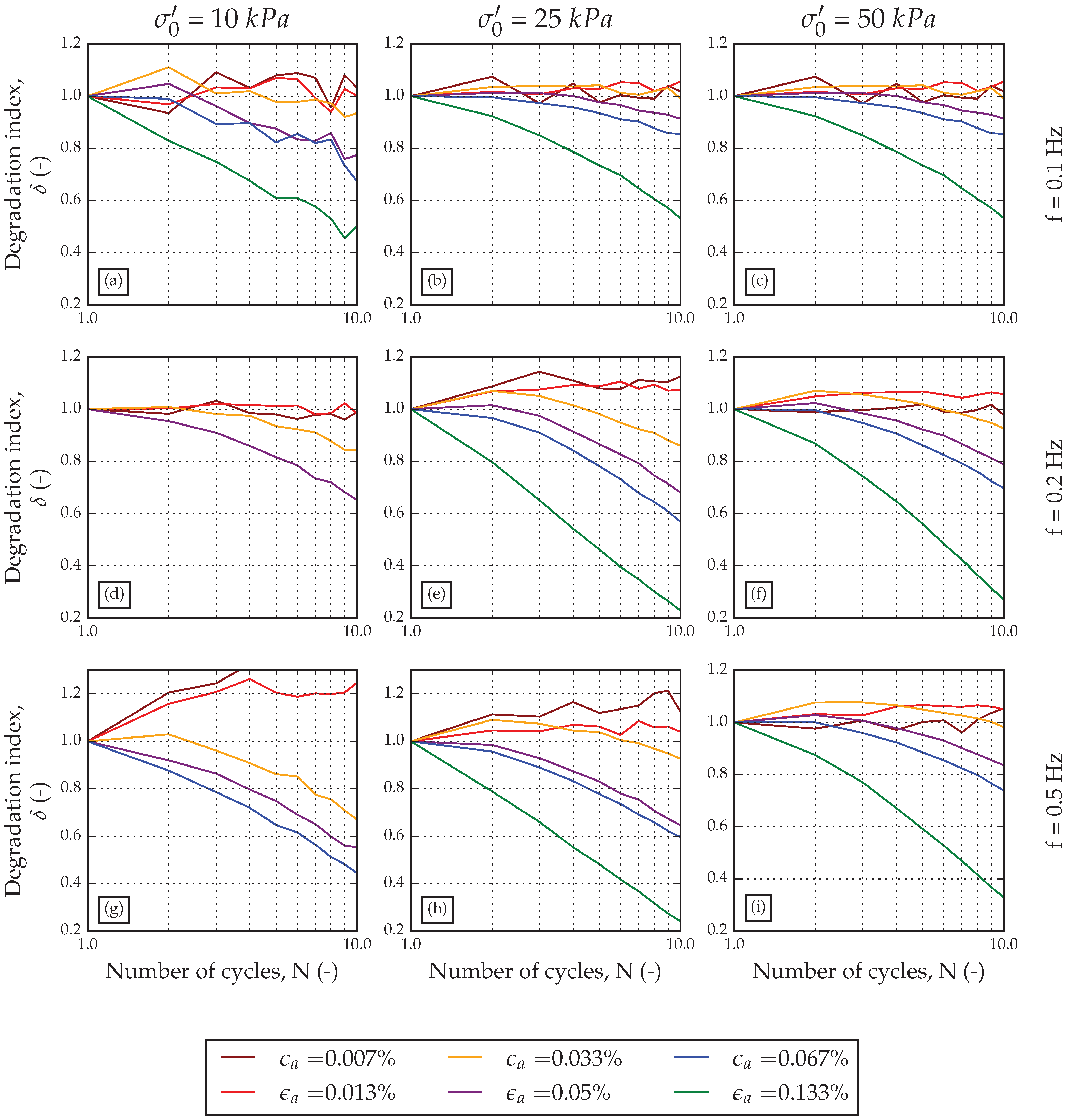
Figure 9 presents the degradation index in variation with confining stresses and frequencies for undrained tests. At 0.1 Hz (
Figure 9a–c), significant degradation occurs at the axial strain of 0.05%, which corresponds to the shear strain of 0.075%. The maximum degradation index is around 0.58 for confining stresses of 25 kPa and 50 kPa. As the frequency of loading increases, the soil tends to have larger degradation (lower values of the degradation index) that can be observed in the shape of the degradation curves. The influence of confining stress on the degradation index can easily be noticed at a loading frequency of 0.2 Hz (
Figure 9d–f). For example, the axial strain of 0.05% has a degradation index of around 0.65 at cycle
N = 10. The degradation index for confining stress of 25 kPa is around 8% higher compared to the degradation at
kPa, and around 13% lower compared to the degradation at
kPa. The degradation index shows small hardening behaviour for values of axial strain less than 0.05%. After reaching that value, degradation drops rapidly with the number of cycles. This phenomenon is well-documented behaviour for sand in cyclic simple-shear devices [
48,
82]. To examine the correlation between the degradation index and pore water pressure, the degradation index was plotted against the normalized pore water pressure ratio (
Figure 10) for various effective stresses and loading frequencies. For frequencies of 0.1 Hz and 0.2 Hz, there is rapid degradation at an effective stress of 10 kPa. For higher values of effective stress, the specimens exhibit small hardening, although the pore water pressure increases. Similar behaviour has been documented by Vucetic and Mortezaie [
48]. As the confining stress becomes higher, the normalized pore water pressure ratio value for higher loading strains is lower.
Figure 10e,f are presented as an example. At 0.2 Hz and axial shear strain of 0.1333%,
for 25 kPa confining stress is around 0.5 (
Figure 10e), while for 50 kPa effective confining stress it is 0.38 (
Figure 10f). These values are given for cycle
N = 1. The
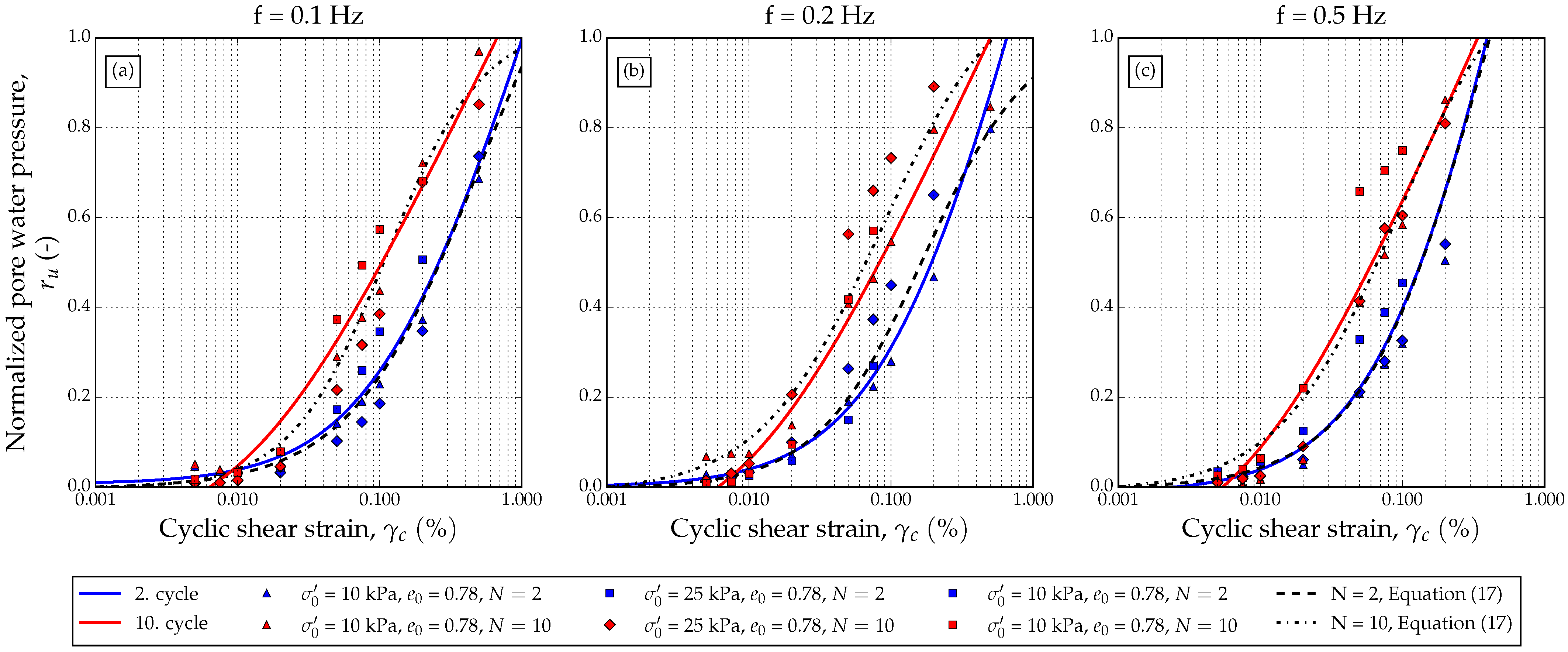
values were then plotted against the equivalent cyclic shear strain with respect to the loading frequency (
Figure 11). From the figure, it is evident that the pore water pressure threshold is somewhat lower than 0.01%. This is consistent with several findings in previous years [
48,
88]. The figure also presents the proposed simple model that takes into account the loading frequency and shearing strain. The authors suggest using Equation (
15) for fast determination of the pore water pressure ratio to quickly calculate possible soil degradation. A normalized pore water pressure model proposed by Vucetic and Dobry [
86] is also plotted in
Figure 11. Vucetic and Dobry’s model fits well at some values of cyclic shear strain.
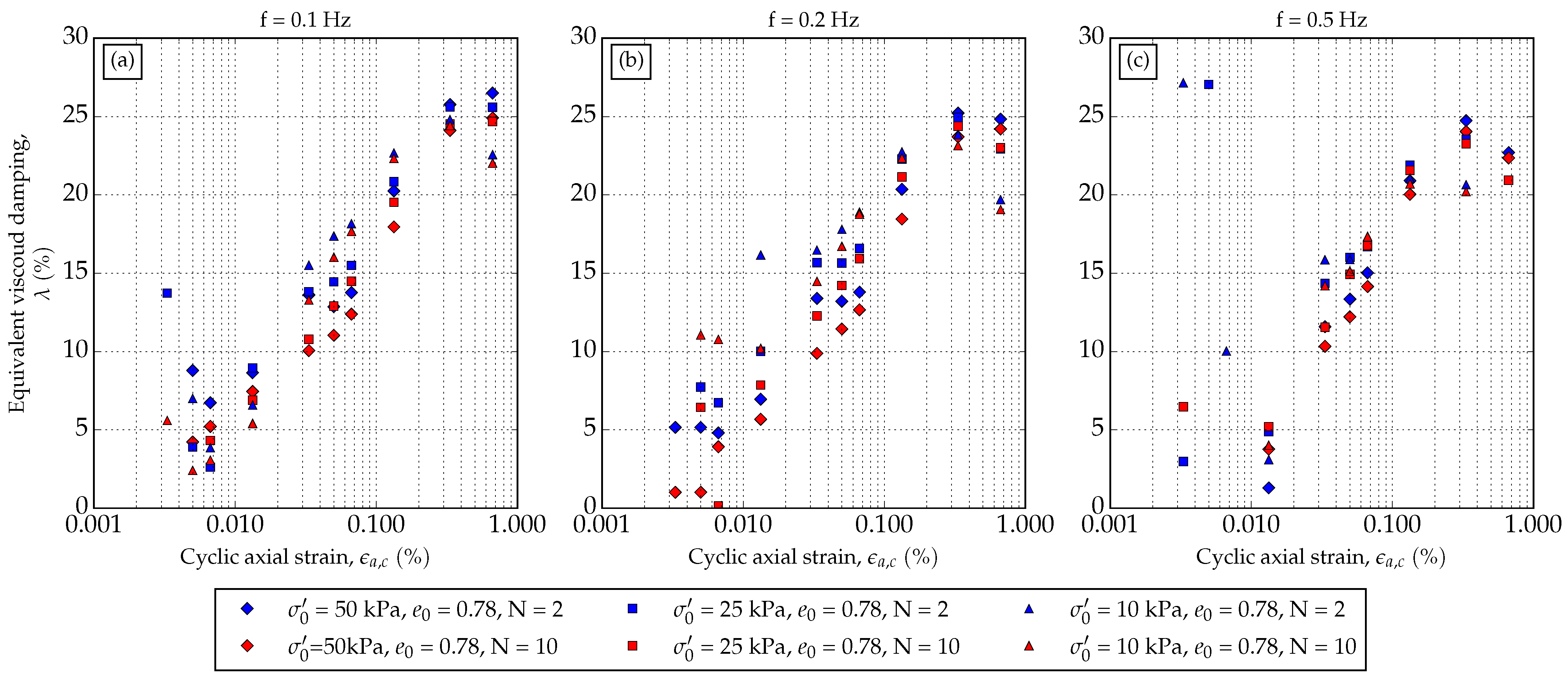
Drained tests focus on the result of the degradation index and volumetric strain. The authors also presented equivalent viscous damping ratios given for axial loading strain[s] (
Figure 12). The increase in the equivalent viscous damping ratio has a logical trend but needs to be additionally examined at higher shearing strains.
The results of the degradation index with respect to cycle number show interesting behaviour. Almost every performed test reached a loading axial strain of 0.667%, which is considered a very high loading frequency. As the confining stress rises, the degradation of the soil stops after four cycles, and in some conditions, it starts to rise. This can be interpreted to mean the soil starts to harden.
This is because in drained cyclic tests, a change in volume is allowed, and the sand densifies with the number of cycles. As the soil densifies, the average ratio of the shear modulus for a given cycle is larger than the one in the previous cycle, so the degradation index starts to rise.
This phenomenon is affected by the confining stress, as can be seen in
Figure 13b–f,h,i. At low confining stress, which corresponds to
Figure 13a,d,g, only degradation of sand is noticeable. The degradation index gets lower than 1 until it reaches constant value. Smaller hardening can be noticed at low axial strain loading due to dilatant soil behaviour at low cyclic strains.
Densification and hardening can be easily noticed in
Figure 14, where accumulated volume strain is plotted against the degradation index. The influence of confining stresses can also be noticed in these plots, as explained earlier. For lower values of axial loading strain, there is little soil hardening, especially for low confining stresses. After several loading cycles, the volumetric strain is greatly accumulated, but degradation slowly increases. This is noticeable for the loading frequency of 0.5 Hz (
Figure 14h).
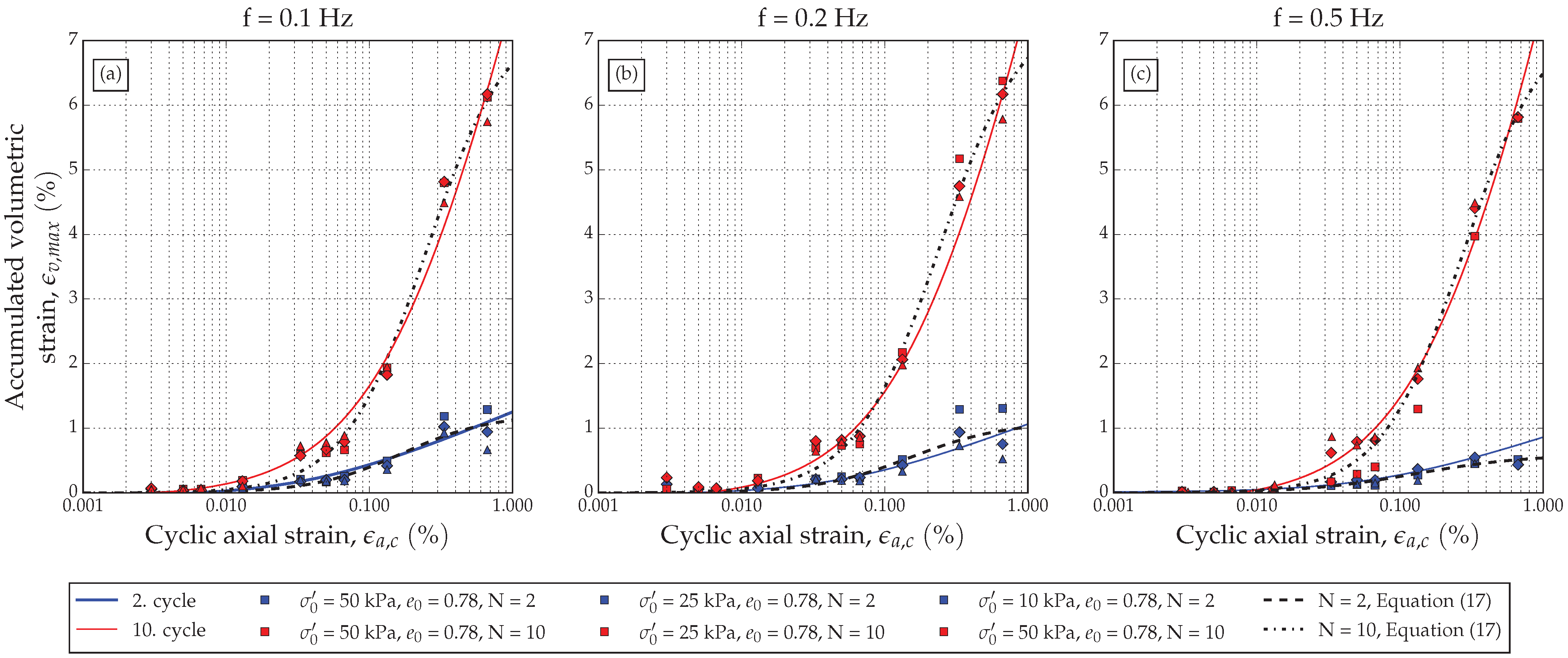
Accumulated volumetric strain is plotted against axial loading strain for cycles 2 and 10, for which simple analytical models are proposed (Equations (
18) and (
19)). A simple proposed model that takes into account loading frequency and axial loading strain, is presented in
Figure 15. From
Figure 15, it is evident that the threshold for accumulated strain is lower than 0.01% axial cyclic strain. Further worth noticing is that the accumulation of volume strain is largely affected by the number of loading cycles. This can be observed in
Figure 15 as the slope of the fit curves for cycles
N = 10 vs.
N = 2. For comparison, data of accumulated volumetric strain are also fitted with the model proposed by Vucetic and Dobry [
86], adjusted for volumetric strains and cyclic axial strains (
Figure 15). As in the example of undrained data, Vucetic and Dobry’s model fits well over some range of cyclic axial strain but cannot guarantee good calculation at larger cyclic axial strains, at least not for these test results.
5. Conclusions
Low confining stresses have a large impact on the analysis of slope stability. A combination of heavy rainfall, which can fully saturate upper soil layers, with a possible post-rainfall earthquake can cause catastrophic consequences. The ongoing research project focused on the behaviour of small-scale landslide slopes at 1g conditions subjected to dynamic loading and indicated that drainage conditions and frequency also play a significant role in slope behaviour. Similarity laws for 1g conditions were used to examine the frequency of cyclic triaxial tests on uniform sand samples equivalent to prototype slope materials. Several key parameters, such as equivalent viscous damping and strength degradation, were examined and presented in this manuscript for sand in drained and undrained conditions at low confining stresses ranging from 10–50 kPa present in small-scale slope models.
From the presented results, it can be concluded that confining stress is significant for soil damping and for the degradation index in both drained and undrained conditions. Higher frequencies cause greater damping ratios. This is in common for both drained and undrained conditions.
The degradation index of tested soil showed interesting behaviour in both drained and undrained conditions. In undrained conditions, soil degrades rapidly for axial strain values that are seven times higher than the threshold value. Between the threshold strain and strain values of around 0.075%, the material first exhibits hardening and then softening, followed by significant pore water pressure build-up. For higher values of cyclic axial strain, the material needs up to five loading cycles to achieve of 0.65, no matter what the loading frequency is. Drained conditions showed that the material first starts to degrade after hardening takes place. This is due to soil densification that occurs as the soil compacts during cyclic loading. This means that if the water can move freely through the soil skeleton, material will degrade slightly due to volume change up to a degradation index of 0.6, but it will soon start to harden. This will beadditionally tested to examine the influence of such densification on the soil skeleton and drainage.
The proposed analytical model for the normalized pore water pressure ratio,
, related to frequency and strain, and accumulation of volumetric strain
related to frequency of loading and axial strain, show very good fit to the tested results. These analytical models can help to quickly calculate the pore water pressure and/or volumetric strain for this type of material considering low confining stresses. The proposed model is compared to the model proposed by Vucetic and Dobry [
86] and can better evaluate the pore pressure and volumetric changes in conditions of low confining stress. This is important because low confining stress presents a governing factor for the behaviour of shallow landslides and for 1g conditions that exist in models areof small dimensions, such as small-scale landslide models. The proposed analytical models can simply be used to determine the pore pressure ratio values for small-scale slope models subjected to dynamic loading, such as earthquakes.
As a part of ongoing research on landslide activation at 1g conditions subjected to dynamic loading to determine slope behaviour [
22], the results presented in this manuscript show specific behaviour of sand that needs to be taken into consideration when the behaviour of a landslide in a model is analysed.
The main limitations of the study lay in limited use of proposed models to uniform, sandy soils and loading frequencies of 0.5 Hz, corresponding to maximal values used in small-scale slope testing on a shaking table. For other soil materials, especially those with higher content of fine particles, additional triaxial tests should be conducted using the procedures described in this manuscript.
To summarize:
Low confining stress plays a significant role in the dynamic properties of sand in both drained and undrained conditions.
In undrained tests, for axial strains up to , sand first hardens and then degrades. At higher values of strain, it only degrades.
In undrained tests, for axial strains up to , sand generates up to 40% , but it does not have a significant effect on degradation. At higher values of strain, rapidly rises.
In drained tests, degradation decreases after the fourth cycle for larger values of confining stress. After the fourth cycle, soil densifies due to accumulated volumetric strain.
In drained tests, degradation after the fourth cycle decreases and hardening takes place.
The proposed analytical models for and are in good correlation to the tested results and can be used to evaluate the normalized pore water pressure ratio and/or accumulated volumetric strains for cycles N = 2 or N = 10 in conditions of low confining stress.