Assessment of Urban Green Development Efficiency Based on Three-Stage DEA: A Case Study from China’s Yangtze River Delta
Abstract
1. Introduction
2. Materials and Methods
2.1. Scope of Study
2.2. Variable Selection and Description
2.3. Computation Model Description
3. Results
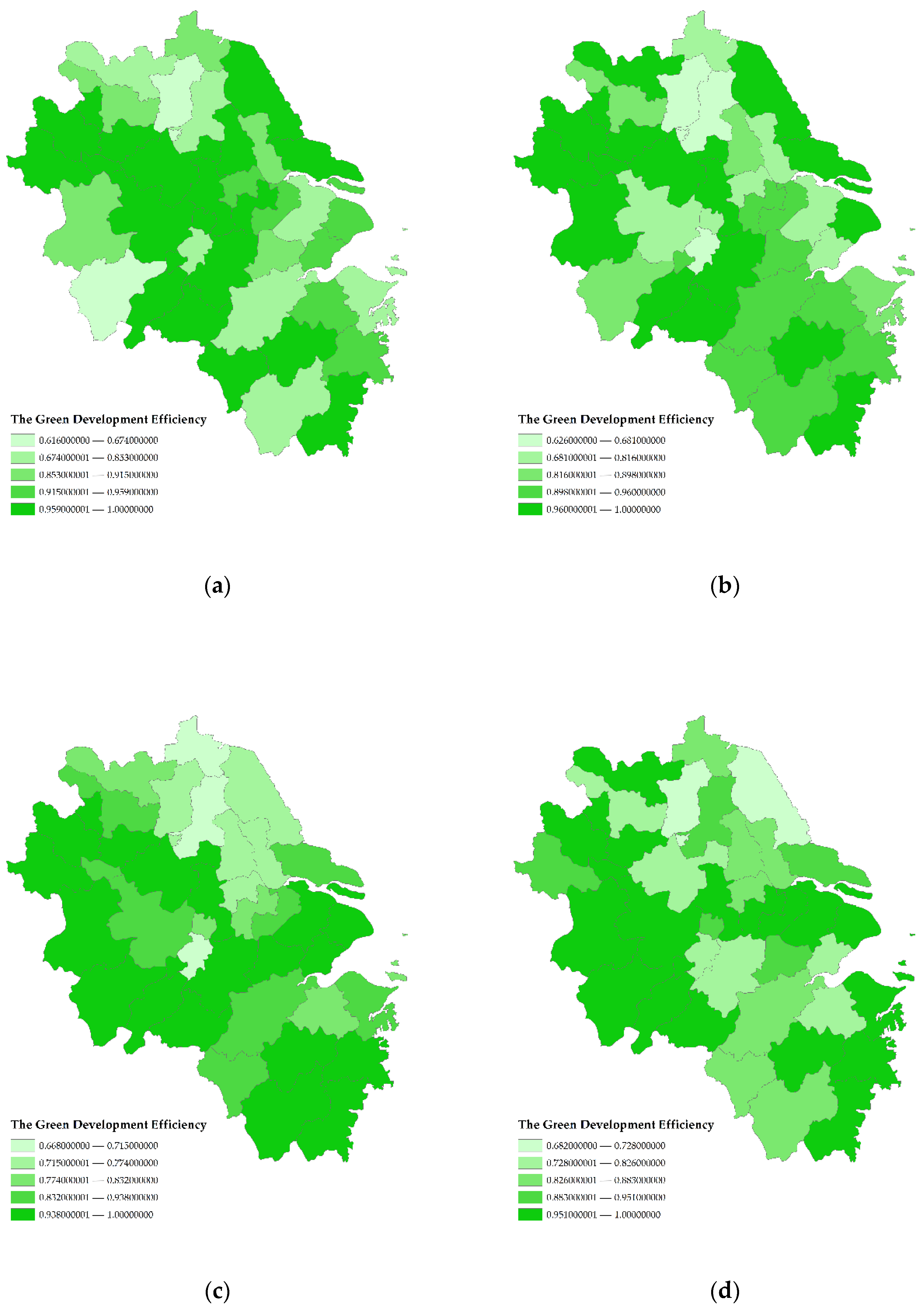
3.1. Stage I: Comprehensive Technical Efficiency from the BCC Model
3.2. Stage II: SFA Model
3.3. Stage III: Actual GDE in the YRD
4. Discussion
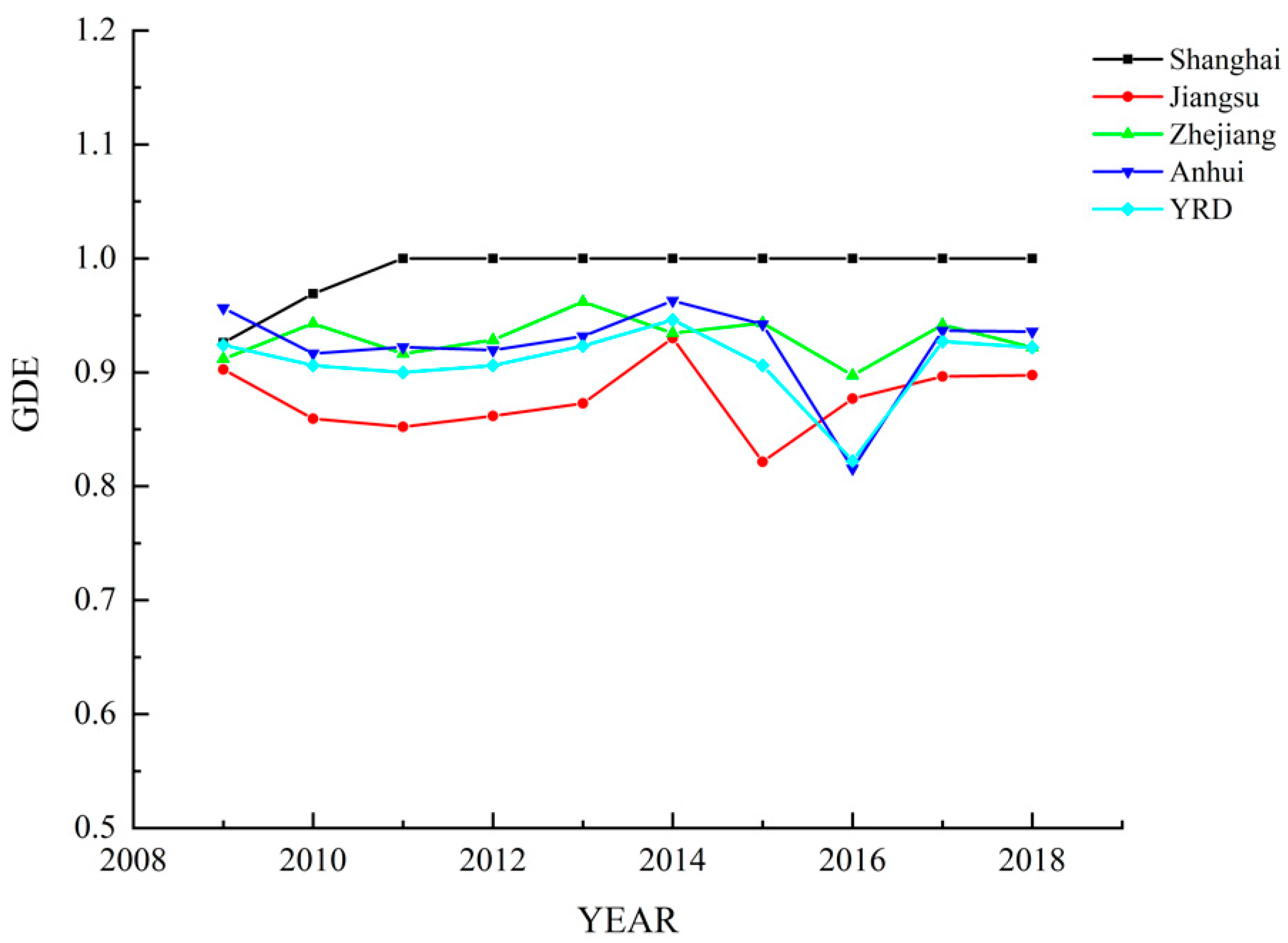
4.1. GDE Analysis in the YRD
4.2. SFA Regression Analysis
4.3. GDE Decomposition Analysis in the YRD
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruggieri, R.; Ruggeri, M.; Vinci, G. Efficient energy and electric transport in a Smart City: Evaluation of sustainability and competitivness. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–4. [Google Scholar]
- Sait, M.A.; Chigbu, U.E.; Hamiduddin, I.; De Vries, W.T. Renewable energy as an underutilised resource in cities: Germany’s ‘Energiewende’and lessons for post-brexit cities in the United Kingdom. Resources 2019, 8, 7. [Google Scholar] [CrossRef]
- Kumar, R.R.; Stauvermann, P.J.; Patel, A. Exploring the link between research and economic growth: An empirical study of China and USA. Qual. Quant. 2016, 50, 1073–1091. [Google Scholar] [CrossRef]
- Sun, C.; Tong, Y.; Zou, W. The evolution and a temporal-spatial difference analysis of green development in China. Sustain. Cities Soc. 2018, 41, 52–61. [Google Scholar] [CrossRef]
- Zhang, H.; Geng, Z.; Yin, R.; Zhang, W. Regional differences and convergence tendency of green development competitiveness in China. J. Clean. Prod. 2020, 254, 119922. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Guo, H.X.; Chen, L.F.; Liu, X.; Gu, M.Y.; Ke, X.L. Regional analysis of the green development level differences in Chinese mineral resource-based cities. Resour. Policy 2019, 61, 261–272. [Google Scholar] [CrossRef]
- Chen, L.; Jia, G. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853. [Google Scholar] [CrossRef]
- Kuosmanen, T.; Kortelainen, M. Stochastic non-smooth envelopment of data: Semi-parametric frontier estimation subject to shape constraints. J. Product. Anal. 2012, 38, 11–28. [Google Scholar] [CrossRef]
- Dyson, R.G.; Shale, E.A. Data envelopment analysis, operational research and uncertainty. J. Oper. Res. Soc. 2010, 61, 25–34. [Google Scholar] [CrossRef]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Cook, W.D.; Zhu, J. Classifying inputs and outputs in data envelopment analysis. Eur. J. Oper. Res. 2007, 180, 692–699. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Wu, J.; Lu, W.; Li, M. A DEA-based improvement of China’s green development from the perspective of resource reallocation. Sci. Total Environ. 2020, 717, 137106. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Wan, X.Z.; Ma, H.M. Assessing Green Development Efficiency of Municipalities and Provinces in China Integrating Models of Super-Efficiency DEA and Malmquist Index. Sustainability 2015, 7, 4492–4510. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, Z.; Chai, J.; Yao, L.; Wang, S.; Lev, B. Efficiency evaluation for banking systems under uncertainty: A multi-period three-stage DEA model. Omega 2019, 85, 68–82. [Google Scholar] [CrossRef]
- Fried, H.O.; Lovell, C.; Schmidt, S.S.; Yaisawarng, S. Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis. J. Product. Anal. 2002, 17, 157–174. [Google Scholar] [CrossRef]
- Lee, J.Y. Application of the three-stage DEA in measuring efficiency–an empirical evidence. Appl. Econ. Lett. 2008, 15, 49–52. [Google Scholar] [CrossRef]
- Jia, S.; Wang, C.; Li, Y.; Zhang, F.; Liu, W. The urbanization efficiency in Chengdu City: An estimation based on a three-stage DEA model. Phys. Chem. Earth Parts A/B/C 2017, 101, 59–69. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, Y.; Zhou, W.; Li, T.; Li, L. A three-stage DEA-based efficiency evaluation of social security expenditure in China. PLoS ONE 2020, 15, e0226046. [Google Scholar] [CrossRef]
- Li, H.; He, H.; Shan, J.; Cai, J. Innovation efficiency of semiconductor industry in China: A new framework based on generalized three-stage DEA analysis. Socio-Econ. Plan. Sci. 2019, 66, 136–148. [Google Scholar] [CrossRef]
- Feng, S.; Xu, L.D. Decision support for fuzzy comprehensive evaluation of urban development. Fuzzy Sets Syst. 1999, 105, 1–12. [Google Scholar] [CrossRef]
- Su, Y.; Xue, H.; Liang, H. An evaluation model for urban comprehensive carrying capacity: An empirical case from Harbin city. Int. J. Environ. Res. Public Health 2019, 16, 367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, X.; Ding, M. Energy-Consumption-Based Comprehensive Evaluation of Urban Green Development-Cases of 27 Cities in the Integrated Central Area of the Yangtze River Delta, China. IEEE Access 2021, 9, 79105–79117. [Google Scholar] [CrossRef]
- Yang, X.; Shang, G. Smallholders’ Agricultural Production Efficiency of Conservation Tillage in Jianghan Plain, China—Based on a Three-Stage DEA Model. Int. J. Environ. Res. Public Health 2020, 17, 7470. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, H.; Bressers, H.; Buchanan, K.S. Productivity growth and environmental regulations-accounting for undesirable outputs: Analysis of China’s thirty provincial regions using the Malmquist–Luenberger index. Ecol. Econ. 2011, 70, 2369–2379. [Google Scholar] [CrossRef]
- Xu, J.; Li, A.; Li, D.; Liu, Y.; Du, Y.; Pei, T.; Ma, T.; Zhou, C. Difference of urban development in China from the perspective of passenger transport around Spring Festival. Appl. Geogr. 2017, 87, 85–96. [Google Scholar] [CrossRef]
- Zhu, B.Z.; Zhang, M.F.; Zhou, Y.H.; Wang, P.; Sheng, J.C.; He, K.J.; Wei, Y.M.; Xie, R. Exploring the effect of industrial structure adjustment on interprovincial green development efficiency in China: A novel integrated approach. Energy Policy 2019, 134, 12. [Google Scholar] [CrossRef]
- Van Herzele, A.; Wiedemann, T. A monitoring tool for the provision of accessible and attractive urban green spaces. Landsc. Urban Plan. 2003, 63, 109–126. [Google Scholar] [CrossRef]
- Hailu, A. Non-parametric Productivity Analysis with Undesirable Outputs: An Application to the Canadian Pulp and Paper Industry. Am. J. Agric. Econ. 2011, 85, 1075–1077. [Google Scholar] [CrossRef]
- Dyckhoff, H.; Allen, K. Measuring ecological efficiency with data envelopment analysis (DEA). Eur. J. Oper. Res. 2001, 132, 312–325. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Jondrow, J.; Lovell, C.K.; Materov, I.S.; Schmidt, P. On the estimation of technical inefficiency in the stochastic frontier production function model. J. Econom. 1982, 19, 233–238. [Google Scholar] [CrossRef]
- Feng, M.; Li, X. Evaluating the efficiency of industrial environmental regulation in China: A three-stage data envelopment analysis approach. J. Clean. Prod. 2020, 242, 118535. [Google Scholar] [CrossRef]
- Xie, B.-C.; Duan, N.; Wang, Y.-S. Environmental efficiency and abatement cost of China’s industrial sectors based on a three-stage data envelopment analysis. J. Clean. Prod. 2017, 153, 626–636. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J. Measurement of low carbon economy efficiency with a three-stage data envelopment analysis: A comparison of the largest twenty CO2 emitting countries. Int. J. Environ. Res. Public Health 2016, 13, 1116. [Google Scholar] [CrossRef] [PubMed]
- Coelli, T.J. A Guide to Frontier Version 4.1: A Computer Program for Stochastic Frontier Production and Cost Function Estimation; CEPA Working Papers; CEPA: Armidale, Australia, 1996; Volume 7, pp. 1–33.
- Wang, Z.; Wang, X.; Liang, L. Green economic efficiency in the Yangtze River Delta: Spatiotemporal evolution and influencing factors. Ecosyst. Health Sustain. 2019, 5, 20–35. [Google Scholar] [CrossRef]
- Guo, S.; Tong, M.; Guo, J.; Han, Y. Measurement and influencing factors of inter-provincial real environmental efficiency based on three-stage DEA model. China Popul. Resour Environ. 2018, 28, 106–116. [Google Scholar]
- Deng, Q.; Qin, Y.; He, X. Recognition of the Spatio-temporal Heterogeneity Characteristics and Influencing Factors about Inclusive Green Development in the Yangtze River Economic Belt. J. Cent. South Univ. For. Technol. 2021, 15, 1–9. [Google Scholar]
- Li, D.; Shangguan, Z.; Huang, M.; Zhang, X.; Tang, L. Impacts of urban development on regional green development efficiency—A case of the Yangtze River Delta in China. Energies 2022, 15, 4785. [Google Scholar] [CrossRef]
- Dasgupta, S.; Laplante, B.; Wang, H.; Wheeler, D. Confronting the environmental Kuznets curve. J. Econ. Perspect. 2002, 16, 147–168. [Google Scholar] [CrossRef]
- Musakwa, W.; Van Niekerk, A. Monitoring sustainable urban development using built-up area indicators: A case study of Stellenbosch, South Africa. Environ. Dev. Sustain. 2015, 17, 547–566. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; He, F.; Yuan, R. Regional Green Development Level and Its Spatial Relationship under the Constraints of Haze in China. J. Clean. Prod. 2018, 210, 376–387. [Google Scholar] [CrossRef]
- Guo, Y.H.; Tong, L.J.; Mei, L. The effect of industrial agglomeration on green development efficiency in Northeast China since the revitalization. J. Clean. Prod. 2020, 258, 13. [Google Scholar] [CrossRef]
- Droste, N.; Hansjürgens, B.; Kuikman, P.; Otter, N.; Antikainen, R.; Leskinen, P.; Pitkänen, K.; Saikku, L.; Loiseau, E.; Thomsen, M. Steering innovations towards a green economy: Understanding government intervention. J. Clean. Prod. 2016, 135, 426–434. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Alinezhad, A. Window analysis using two-stage DEA in heart hospitals. In Proceedings of the 10th International Conference on Innovations in Science, Engineering, Computers and Technology (ISECT-2017), Dubai, United Arab Emirates, 17–19 October 2017; pp. 44–51. [Google Scholar]




| Variable | No. | Index | Unit |
|---|---|---|---|
| Input Variables | I1 | AEC | 10,000 kwh |
| I2 | IFA | 10,000 yuan | |
| I3 | EEST | 10,000 yuan | |
| I4 | EMWCE | person | |
| Output Variables | O1 | VIWD | 10,000 tons |
| O2 | VISDP | ton | |
| O3 | TRSCG | 10,000 yuan | |
| Environmental Variables | E1 | GRP | 10,000 yuan |
| E2 | ABD | sq. km | |
| E3 | TIP | % | |
| E4 | GCA | hectare |
| Variable | Number | Mean Value | Standard Deviation | Min. | Max. |
|---|---|---|---|---|---|
| I1 | 410 | 1,828,000 | 3,031,000 | 67,166 | 31,820,000 |
| I2 | 410 | 21,730,000 | 18,060,000 | 2,352,000 | 112,400,000 |
| I3 | 410 | 1,022,000 | 1,572,000 | 64,104 | 13,440,000 |
| I4 | 410 | 9873 | 12,761 | 455 | 93,600 |
| O1 | 410 | 11,624 | 13,123 | 486 | 80,468 |
| O2 | 410 | 43,067 | 45,387 | 1407 | 496,377 |
| O3 | 410 | 13,540,000 | 16,900,000 | 791,784 | 126,700,000 |
| E1 | 410 | 35,780,000 | 44,200,000 | 1,331,000 | 326,800,000 |
| E2 | 410 | 176.5 | 186.4 | 31 | 1238 |
| E3 | 410 | 0.42 | 0.0825 | 0.234 | 0.793 |
| E4 | 410 | 7925 | 10,934 | 1256 | 139,427 |
| City | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | 0.898 | 0.934 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.968 | 1.000 | 1.000 | 0.980 | Ⅰ |
| Nanjing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.956 | 1.000 | 1.000 | 1.000 | 0.996 | Ⅰ |
| Wuxi | 0.973 | 0.926 | 1.000 | 0.968 | 0.953 | 0.903 | 0.740 | 1.000 | 1.000 | 1.000 | 0.946 | Ⅱ |
| Xuzhou | 0.783 | 0.721 | 0.615 | 1.000 | 0.622 | 0.741 | 0.666 | 1.000 | 0.824 | 0.965 | 0.794 | Ⅲ |
| Changzhou | 1.000 | 0.956 | 0.889 | 0.938 | 0.925 | 0.923 | 0.695 | 1.000 | 1.000 | 1.000 | 0.933 | Ⅱ |
| Suzhou 1 | 0.838 | 0.819 | 0.766 | 0.759 | 0.762 | 0.808 | 0.860 | 1.000 | 1.000 | 1.000 | 0.861 | Ⅲ |
| Nantong | 1.000 | 0.951 | 0.841 | 1.000 | 0.785 | 0.778 | 0.739 | 0.935 | 0.902 | 0.943 | 0.887 | Ⅱ |
| Lian Yungang | 0.839 | 0.766 | 0.681 | 0.636 | 0.654 | 0.580 | 0.549 | 1.000 | 0.660 | 0.721 | 0.709 | Ⅳ |
| Huaian | 0.694 | 0.632 | 0.587 | 0.581 | 0.614 | 0.636 | 0.547 | 0.736 | 0.689 | 0.832 | 0.655 | Ⅳ |
| Yancheng | 0.970 | 0.952 | 0.984 | 0.987 | 1.000 | 1.000 | 0.631 | 0.792 | 0.682 | 0.634 | 0.863 | Ⅲ |
| Yangzhou | 0.966 | 0.958 | 0.888 | 0.884 | 0.867 | 0.853 | 0.585 | 0.801 | 0.765 | 0.832 | 0.840 | Ⅲ |
| Zhenjiang | 0.859 | 0.857 | 0.854 | 0.806 | 0.804 | 0.900 | 0.664 | 0.920 | 0.833 | 0.830 | 0.833 | Ⅲ |
| Taizhou 1 | 0.846 | 0.819 | 0.889 | 0.811 | 0.783 | 0.868 | 0.601 | 0.764 | 0.730 | 0.764 | 0.788 | Ⅳ |
| Suqian | 0.547 | 0.498 | 0.546 | 0.522 | 0.509 | 0.782 | 0.505 | 0.570 | 0.559 | 0.561 | 0.560 | Ⅳ |
| Hangzhou | 0.816 | 0.788 | 0.842 | 0.902 | 0.951 | 0.953 | 0.865 | 0.934 | 1.000 | 0.877 | 0.893 | Ⅱ |
| Ningbo | 0.768 | 0.768 | 0.803 | 0.813 | 0.852 | 0.858 | 0.852 | 0.869 | 0.904 | 0.886 | 0.837 | Ⅲ |
| Wenzhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Ⅰ |
| Jiaxing | 0.929 | 0.888 | 0.831 | 0.844 | 0.839 | 0.820 | 0.981 | 1.000 | 0.781 | 0.767 | 0.868 | Ⅲ |
| Huzhou | 0.886 | 0.986 | 0.972 | 1.000 | 0.995 | 0.871 | 0.918 | 1.000 | 0.925 | 0.963 | 0.952 | Ⅱ |
| Shaoxing | 0.954 | 0.976 | 0.988 | 0.947 | 0.840 | 0.789 | 0.714 | 1.000 | 0.827 | 0.773 | 0.881 | Ⅱ |
| Jinhua | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Ⅰ |
| Quzhou | 1.000 | 0.956 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.996 | Ⅰ |
| Zhoushan | 0.929 | 1.000 | 0.953 | 0.918 | 0.878 | 0.781 | 0.664 | 0.728 | 0.925 | 1.000 | 0.878 | Ⅲ |
| Taizhou 2 | 0.954 | 0.961 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | Ⅰ |
| Lishui | 0.929 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 | 1.000 | 0.992 | Ⅰ |
| Hefei | 0.948 | 0.837 | 0.750 | 0.650 | 0.690 | 0.688 | 0.708 | 0.666 | 1.000 | 0.979 | 0.792 | Ⅳ |
| Wuhu | 0.766 | 0.665 | 0.563 | 0.526 | 0.509 | 0.470 | 0.519 | 0.529 | 0.622 | 0.760 | 0.593 | Ⅳ |
| Bengbu | 0.985 | 0.881 | 0.745 | 0.756 | 0.710 | 0.711 | 0.786 | 0.597 | 0.919 | 0.880 | 0.797 | Ⅲ |
| Huainan | 1.000 | 0.954 | 0.761 | 0.852 | 0.763 | 0.929 | 0.714 | 1.000 | 0.707 | 0.766 | 0.845 | Ⅲ |
| Maanshan | 0.890 | 0.778 | 0.644 | 0.629 | 0.587 | 0.736 | 0.717 | 0.953 | 1.000 | 0.767 | 0.770 | Ⅳ |
| Huaibei | 0.939 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.994 | Ⅰ |
| Tongling | 1.000 | 1.000 | 1.000 | 0.916 | 0.896 | 0.912 | 0.791 | 0.749 | 0.821 | 1.000 | 0.909 | Ⅱ |
| Anqing | 0.625 | 0.652 | 0.650 | 0.699 | 0.706 | 0.706 | 0.865 | 0.674 | 0.840 | 0.805 | 0.722 | Ⅳ |
| Huangshan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.846 | 1.000 | 1.000 | 0.985 | Ⅰ |
| Chuzhou | 0.744 | 0.722 | 0.831 | 0.696 | 0.741 | 0.740 | 0.800 | 0.710 | 0.573 | 0.508 | 0.707 | Ⅳ |
| Fuyang | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.856 | 0.926 | 0.720 | 0.950 | Ⅱ |
| Suzhou 2 | 0.817 | 0.834 | 0.686 | 0.678 | 0.737 | 0.713 | 0.621 | 0.736 | 0.634 | 0.883 | 0.734 | Ⅳ |
| Luan | 0.767 | 0.746 | 0.691 | 0.789 | 0.726 | 1.000 | 0.725 | 0.558 | 0.750 | 0.759 | 0.751 | Ⅳ |
| Bozhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | 0.718 | 0.847 | 0.834 | 0.939 | Ⅱ |
| Chizhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 | 0.918 | 0.647 | 1.000 | 1.000 | 0.956 | Ⅰ |
| Xuancheng | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.909 | 1.000 | 0.646 | 0.668 | 0.691 | 0.891 | Ⅱ |
| YRD | 0.893 | 0.877 | 0.860 | 0.866 | 0.846 | 0.862 | 0.802 | 0.851 | 0.861 | 0.871 | 0.859 |
| Explanatory Variable | Slacks of Input Variables | |||
|---|---|---|---|---|
| AEC | IFA | EEST | EMWCE | |
| Constant term | −177,242.07 | −2,391,731.60 | −49,187.69 | −816.14 |
| −140,141.30 | −1,891,088.14 | −751.78 | −71.51 | |
| GRP | −6226.56 | −2,017,080.80 | −30,534.40 | 385.84 |
| (−511.36) *** | (−165,654.65) *** | (−319.20) *** | (1.44) * | |
| ABD | 363,134.99 | 18,522,799.00 | 499,887.82 | 7736.39 |
| (23,017.63) *** | (1,174,083.64) *** | (40,106.30) *** | (17.37) *** | |
| TIP | −55,091.87 | −1,120,127.10 | −38,150.40 | −531.48 |
| (−5258.59) *** | (−106,917.67) *** | (−234.72) *** | (−11.99) *** | |
| GCA | −328,483.35 | −15,710,684.00 | −455,881.82 | −7669.25 |
| (−21,419.04) *** | (−1,024,428.59) *** | (−19,887.36) *** | (−111.83) *** | |
| γ | 1.00 | 1.00 | 0.98 | 1.00 |
| Log likelihood function | −561.07559 | −675.04933 | −529.03493 | −357.3225 |
| LR test | 35.5 | 34.6 | 37.3 | 28.7 |
| City | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | 0.926 | 0.969 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.990 | Ⅰ |
| Nanjing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Ⅰ |
| Wuxi | 0.959 | 0.914 | 0.992 | 0.938 | 0.991 | 0.968 | 0.887 | 1.000 | 1.000 | 1.000 | 0.965 | Ⅰ |
| Xuzhou | 0.817 | 0.755 | 0.664 | 1.000 | 0.724 | 0.867 | 0.832 | 1.000 | 0.891 | 0.983 | 0.853 | Ⅳ |
| Changzhou | 1.000 | 0.923 | 0.914 | 0.935 | 0.994 | 1.000 | 0.820 | 1.000 | 1.000 | 1.000 | 0.959 | Ⅰ |
| Suzhou 1 | 0.853 | 0.833 | 0.849 | 0.772 | 0.877 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.918 | Ⅱ |
| Nantong | 1.000 | 0.961 | 0.809 | 1.000 | 0.844 | 0.843 | 0.915 | 0.997 | 0.942 | 0.951 | 0.926 | Ⅱ |
| Lian Yungang | 0.915 | 0.824 | 0.848 | 0.736 | 0.793 | 0.839 | 0.705 | 1.000 | 0.864 | 0.853 | 0.838 | Ⅳ |
| Huaian | 0.767 | 0.681 | 0.704 | 0.681 | 0.749 | 0.828 | 0.715 | 0.677 | 0.842 | 0.896 | 0.754 | Ⅳ |
| Yancheng | 1.000 | 1.000 | 0.950 | 1.000 | 1.000 | 1.000 | 0.774 | 0.864 | 0.741 | 0.682 | 0.901 | Ⅲ |
| Yangzhou | 0.997 | 0.984 | 0.877 | 0.878 | 0.950 | 0.954 | 0.743 | 0.770 | 0.867 | 0.862 | 0.888 | Ⅲ |
| Zhenjiang | 0.928 | 0.903 | 0.864 | 0.808 | 0.868 | 0.908 | 0.756 | 0.833 | 0.912 | 0.875 | 0.866 | Ⅳ |
| Taizhou 1 | 0.881 | 0.840 | 0.851 | 0.816 | 0.873 | 0.906 | 0.766 | 0.696 | 0.818 | 0.837 | 0.828 | Ⅳ |
| Suqian | 0.616 | 0.552 | 0.757 | 0.638 | 0.683 | 0.978 | 0.765 | 0.562 | 0.775 | 0.728 | 0.705 | Ⅳ |
| Hangzhou | 0.837 | 0.813 | 0.855 | 0.931 | 1.000 | 1.000 | 0.938 | 0.905 | 1.000 | 0.869 | 0.915 | Ⅲ |
| Ningbo | 0.783 | 0.801 | 0.856 | 0.880 | 0.951 | 0.787 | 0.928 | 0.913 | 1.000 | 0.975 | 0.887 | Ⅲ |
| Wenzhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Ⅰ |
| Jiaxing | 0.932 | 0.913 | 0.787 | 0.805 | 0.861 | 0.845 | 1.000 | 1.000 | 0.883 | 0.825 | 0.885 | Ⅲ |
| Huzhou | 0.913 | 0.990 | 0.927 | 0.946 | 0.989 | 0.931 | 0.990 | 0.909 | 0.902 | 0.913 | 0.941 | Ⅱ |
| Shaoxing | 0.949 | 0.999 | 0.883 | 0.943 | 0.909 | 0.844 | 0.810 | 1.000 | 0.910 | 0.826 | 0.907 | Ⅲ |
| Jinhua | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Ⅰ |
| Quzhou | 0.986 | 0.947 | 0.905 | 0.960 | 0.961 | 0.975 | 0.912 | 1.000 | 0.846 | 0.883 | 0.938 | Ⅱ |
| Zhoushan | 0.843 | 0.942 | 0.961 | 0.898 | 0.910 | 0.929 | 0.799 | 0.490 | 0.952 | 1.000 | 0.872 | Ⅳ |
| Taizhou 2 | 0.940 | 0.966 | 0.983 | 0.940 | 1.000 | 1.000 | 1.000 | 0.986 | 1.000 | 1.000 | 0.982 | Ⅰ |
| Lishui | 0.846 | 1.000 | 0.922 | 0.909 | 1.000 | 0.968 | 1.000 | 0.668 | 0.865 | 0.851 | 0.903 | Ⅲ |
| Hefei | 0.987 | 0.879 | 0.837 | 0.741 | 0.777 | 0.831 | 0.898 | 0.804 | 1.000 | 1.000 | 0.875 | Ⅲ |
| Wuhu | 0.849 | 0.755 | 0.798 | 0.626 | 0.717 | 0.890 | 0.668 | 0.588 | 0.664 | 0.787 | 0.734 | Ⅳ |
| Bengbu | 1.000 | 0.938 | 0.967 | 1.000 | 0.980 | 1.000 | 0.991 | 0.581 | 1.000 | 1.000 | 0.946 | Ⅱ |
| Huainan | 1.000 | 0.925 | 0.937 | 1.000 | 0.930 | 0.938 | 0.897 | 1.000 | 0.926 | 0.974 | 0.953 | Ⅱ |
| Maanshan | 1.000 | 0.787 | 0.818 | 0.723 | 0.811 | 0.878 | 0.793 | 0.961 | 1.000 | 0.937 | 0.871 | Ⅳ |
| Huaibei | 1.000 | 1.000 | 0.992 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 | Ⅰ |
| Tongling | 1.000 | 1.000 | 1.000 | 0.915 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 1.000 | 0.990 | Ⅰ |
| Anqing | 0.674 | 0.723 | 0.840 | 0.863 | 0.889 | 0.964 | 1.000 | 0.655 | 0.978 | 0.995 | 0.858 | Ⅳ |
| Huangshan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.422 | 0.995 | 0.993 | 0.941 | Ⅱ |
| Chuzhou | 0.984 | 0.917 | 0.867 | 0.998 | 0.990 | 0.974 | 0.988 | 0.784 | 0.822 | 0.769 | 0.909 | Ⅲ |
| Fuyang | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.882 | 0.978 | 0.905 | 0.977 | Ⅰ |
| Suzhou 2 | 0.906 | 0.918 | 0.843 | 0.870 | 0.892 | 0.936 | 0.875 | 0.654 | 0.791 | 0.812 | 0.850 | Ⅳ |
| Luan | 0.901 | 0.824 | 0.855 | 0.977 | 0.921 | 1.000 | 0.999 | 0.600 | 1.000 | 1.000 | 0.908 | Ⅲ |
| Bozhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.965 | 0.580 | 1.000 | 1.000 | 0.955 | Ⅱ |
| Chizhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 | 1.000 | 0.378 | 1.000 | 1.000 | 0.937 | Ⅱ |
| Xuancheng | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.559 | 0.849 | 0.801 | 0.921 | Ⅱ |
| YRD | 0.924 | 0.906 | 0.900 | 0.906 | 0.923 | 0.946 | 0.906 | 0.822 | 0.927 | 0.922 | 0.908 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Sun, Z.; Zhang, H. Assessment of Urban Green Development Efficiency Based on Three-Stage DEA: A Case Study from China’s Yangtze River Delta. Sustainability 2022, 14, 12076. https://doi.org/10.3390/su141912076
Yang Q, Sun Z, Zhang H. Assessment of Urban Green Development Efficiency Based on Three-Stage DEA: A Case Study from China’s Yangtze River Delta. Sustainability. 2022; 14(19):12076. https://doi.org/10.3390/su141912076
Chicago/Turabian StyleYang, Qi, Zhonggen Sun, and Hubiao Zhang. 2022. "Assessment of Urban Green Development Efficiency Based on Three-Stage DEA: A Case Study from China’s Yangtze River Delta" Sustainability 14, no. 19: 12076. https://doi.org/10.3390/su141912076
APA StyleYang, Q., Sun, Z., & Zhang, H. (2022). Assessment of Urban Green Development Efficiency Based on Three-Stage DEA: A Case Study from China’s Yangtze River Delta. Sustainability, 14(19), 12076. https://doi.org/10.3390/su141912076







