Abstract
Ground vibration induced by rock blasting is an unavoidable effect that may generate severe damages to structures and living communities. Peak particle velocity (PPV) is the key predictor for ground vibration. This study aims to develop a model to predict PPV in opencast mines. Two machine-learning techniques, including multivariate adaptive regression splines (MARS) and classification and regression tree (CART), which are easy to implement by field engineers, were investigated. The models were developed using a record of 1001 real blast-induced ground vibrations, with ten (10) corresponding blasting parameters from 34 opencast mines/quarries from India and Benin. The suitability of one technique over the other was tested by comparing the outcomes with the support vector regression (SVR) algorithm, multiple linear regression, and different empirical predictors using a Taylor diagram. The results showed that the MARS model outperformed other models in this study with lower error (RMSE = 0.227) and R2 of 0.951, followed by SVR (R2 = 0.87), CART (R2 = 0.74) and empirical predictors. Based on the large-scale cases and input variables involved, the developed models should lead to better representative models of high generalization ability. The proposed MARS model can easily be implemented by field engineers for the prediction of blasting vibration with reasonable accuracy.
1. Introduction
The assessment and prediction of ground vibration generated by blasting is one important challenge in mine management. Blast-induced ground vibration (BIGV) is an unavoidable nuisance which, at a certain level, destroys the structural integrity of the surrounding structure in the mine area and affects far-field edifices. This results in complaints from the affected dwelling residents and mine closure with collateral consequences such as job losses and stalled socio-economic development. Sometimes, high-intensity BIGV can destroy groundwater tables, existing network conduits and the ecology of surrounding living communities (fauna and flora). Studies suggested that BIGV influences vegetation development and could contribute to deforestation in the near future [1]. The vibration induced by blasting usually leads to ground/slope instability, endangering the safety of workers during loading and subsequent drilling and blasting operations.
Although a lot of advancement has been witnessed over the decades in blasting technology, the undesirable effects of BIGV cannot be completely eradicated. However, it can be predicted and controlled to meet standard levels for damage minimization. Peak particle velocity (PPV) induced by blasting is one of the best vibration indices that can effectively represent BIGV and potential damage to nearby structures [2]. The measurement of PPV using a seismograph is the only direct route, and is indubitably the most accurate measurement technique to assess the intensity of BIGV [3]. However, the method is expensive and time-consuming, and cannot predict PPV and prevent potential damages induced by blasting. Therefore, several scholars have developed indirect methods involving empirical formulas and machine-learning (ML) techniques to predict PPV [4]. The literature has revealed that several factors influence blasting PPV [5]. However, predictive empirical formulas involve only two parameters, namely maximum charge per delay and monitoring distance, and do not consider the complex interaction between PPV values and other blasting parameters, which undoubtedly leads to their low prediction capability [6]. The ML techniques have significantly improved the accuracy of PPV prediction in recent decades. ML techniques have the capability of solving complex engineering problems, and can handle more than a few effective input variables.
Studies by some researchers have applied ML techniques to predict PPV and optimize design parameters to reduce environmental, social, and economic impacts related to blasting vibration. For example, Shirani and Masoud [7] employed trial-and-error experimentation by combining gene-expression programming (GEP) and cuckoo optimization algorithm (COA) in an iron mine and achieved a significant reduction in PPV values (55.33%). Similarly, a combined method of principal component analysis (PCA) and support vector machine (SVM)-based PPV modeling was successfully used to optimize the blasting pattern in Hongtoushan Copper Mine in Vietnam [8]. Likewise, Bayat et al. [9] developed the artificial neural network (ANN) model optimized by the firefly algorithm (FA) to improve blast-design parameters. The results of their study yielded a 60% reduction in PPV which, in reality, could contribute to minimizing potential vibration impacts. Table 1 reports some studies employing ML techniques and empirical predictors in assessing PPV.
The review conducted by Dumakor-Dupey et al. [4] showed an excessive number of ML techniques applied in predicting PPV, with the common algorithms being artificial neural network (ANN), support vector machine (SVM), and the adaptive neuro-fuzzy inference system (ANFIS). The accuracy of the models depends upon the algorithm and the interaction between variables. Hybrid models have been recently introduced by combining two or more ML algorithms to enhance the accuracy of stand-alone ML techniques. However, these hybrid models result in complex mathematical expressions that are difficult to interpret and impracticable. These complex models are referred to as black-box techniques, in contrast to white-box techniques [10,11]. White-box techniques can provide interactive behavior between independent variables and the output. They are user-friendly and can be easily implemented on-site to optimize blast designs and control PPV. Therefore, this study aims to predict PPV based on two white-box ML techniques, such as classification and regression tree (CART) and multivariate adaptive regression splines (MARS), barely employed in previous studies (Table 1). In addition, different empirical methods, multiple linear regressions, and the adopted SVM algorithm, namely support vector regression (SVR), were also applied for comparison.
Although the literature shows that conventional white-box ML techniques can be easily implementable by field engineers to predict blast-induced outcomes, there are limited investigations applying CART and MARS to predict PPV. Monjezi et al. [12] reported that the generalization ability of predictive models increases with the number of input variables and datasets. Therefore, this study employed a record of 1001 sets of data from 34 different opencast mines to develop a single ML model. Each dataset involves ten blasting parameters of a wide range, including hole diameter (HDM), hole depth (HD), number of holes (NH), burden (B), spacing (S), stemming (T), charge per hole (CPH), total charge (TC), maximum charge per delay, (MCPD), and monitoring distance (D). These parameters are considered to be effective variables affecting blast-induced ground vibration (PPV) [5]. To the best of the authors’ knowledge, there is no existing investigation involving many datasets and input variables from various geo-environments to develop regression models for PPV prediction as employed in this study. Therefore, the investigation would obtain better results in representative models that could be implemented in different geo-environments for efficient prediction of PPV for safety and impact minimization. The overall study method is presented in Figure 1.
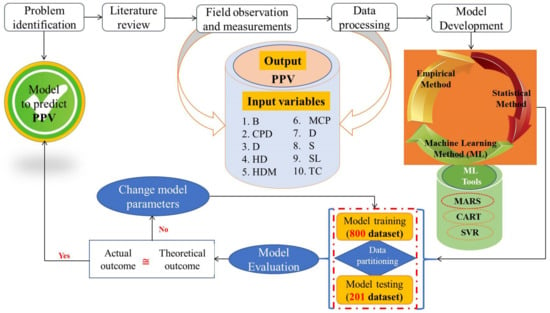
Figure 1.
Flowchart of the overall study method.
This paper is structured as follows: after the introduction, the data source and a brief description of the different techniques employed to develop the models are presented in Section 2, Section 3 and Section 4, followed by the discussion and the results. The conclusion is presented in Section 5.

Table 1.
Some studies of PPV prediction based on ML techniques.
Table 1.
Some studies of PPV prediction based on ML techniques.
| Authors | Models | Input Parameters | No. of Datasets | Best Model | Performance Indices |
|---|---|---|---|---|---|
| Ke et al. [13] | SVR, GEP, ANN-SVR, Empirical predictor | HDM, BH, HD, B, S, Hc, PF, MCPD, D | 297 | ANN-SVR | R2 = 0.887 RMSE = 1.232 |
| Nguyen and Bui [14] | HGS–ANN, GOA–ANN FA–ANN, PSO–ANN | HD, MCPD, B, PF, D, SL, S NDS, DTS | 252 | HGS– ANN | R2 = 0.922 RMSE = 1.761 |
| Singh [15] | ANN | HDM, NH, HD, B, S, SL, Hdis, Rdis | 200 | ANN | R2 = 0.83 |
| Nguyen et al. [16] | MARS, ANN, PSO–ANN, MARS-PSO–ANN, Empirical predictor | MCPD, D, HD, B, S, SL, PF | 193 | MARS-PSO–ANN | R2 = 0.902 RMSE = 1.569 |
| Singh et al. [17] | ANFIS, MVRA | MCPD, D | 192 | ANFIS | R2 = 0.98 |
| Lawal et al. [18] | ANN, BK, GEP, MLR | S/B, BH/B, B/HDM, SL/B, SD/B, UCS, ρr, MCPD, D | 191 | ANN | R2 = 0.948 RMSE = 0.0008 |
| Singh and Verma [19] | ANFIS | B, S, D, IS, TC | 187 | ANFIS | R2 = 0.77 |
| Monjezi et al. [20] | ANN | HD, T, MCPD, D | 182 | ANN | R2 = 0.949 (ANN) |
| Khandelwal and Singh [21] | ANN, MVRA | HD, S, D, E, P-wave, B, MCPD, BI, µ, VOD | 174 | ANN | R2 = 0.98 |
| Khandelwal [22] | SVM, MVRA, Empirical predictor | MCPD, D | 174 | SVM | R2 = 0.96, MAE = 0.257 |
| Khandelwal and Singh [23] | ANN | TC, D | 170 | ANN | R2 = 0.998 |
| Monjezi et al. [24] | MLPNN, RBFNN, GRNN | D, B/S, MCPD, NHPD, UCS, DPR | 169 | MLPNN | R2 = 0.954, RMSE = 0.03 |
| Yu et al. [25] | ELM, HHO–ELM, GOA–ELM, | D, HD, B/S, MCPD, PF | 166 | GOA–ELM | R2 = 0.9105 RMSE = 2.855 |
| Mohamed [26] | FS, ANN, MVRA | D, MCPD | 162 | FS | RMSE = 0.17 VAF = 87(%) |
| Bayat et al. [1] | GEP | B, S, T, D, MCPD | 154 | GEP | R2 = 0.91 RMSE = 5.78 |
| Khandelwal and Kumar [27] | ANN, Empirical predictor | MCPD, D | 150 | ANN | R2 = 0.919, RMSE = 0.352 |
| Singh et al. [28] | GA, MVRA, ANN, ANFIS, SVM | UCS, ρr, Hc, ɳ, ABS, FRC | 150 | GA | MAPE = 0.198 |
| Zhou et al. [29] | RF, ANN, XGBoost, AdaBoost, Bagging, Jaya-X-GBoost Empirical predictor | HDM, HD, CPH, S, B, CL, BI, E, D, µ, P-wave, VOD, ρe | 150 | Jaya-XGBoost | R2 = 0.957 RMSE = 4.088 |
| Mohamed [30] | ANN | P-wave, HDM, VOD, B, S, BH, HI, D, ρe, ρr, MCPD, E, TC, ɳ, UCS, | 149 | ANN | R2 = 0.94, MSE = 0.00920 |
| Rana et al. [31] | CART, ANN, MVRA, Empirical predictor | TC, TS, MCPD, NH, HDM, D, HD, CPH | 137 | CART | R2 = 0.95, RMSE = 1.56 |
| Verma and Singh [32] | SVM, ANN, MVRA | HD, B, S, T, MCPD, TC, D | 137 | SVM | MAPE = 0.001 |
| Verma and Singh [33] | GA, ANN, MVRA, Empirical predictor | HD, B, S, T, MCPD, TC | 127 | GA | R2 = 0.99, MAPE = 0.088 |
| Ghasemi et al. [34] | FS, MRA, Empirical predictor | B, S, T, NHPD | 120 | FS | R2 = 0.945, RMSE = 2.73 |
| Ghasemi et al. [35] | ANFIS-PSO, SVR | B, S, T, NH, MCPD, D | 120 | ANFIS-PSO | R2 = 0.957, RMSE = 1.83 |
| Bui et al. [36] | ANN, SVM, Tree-based ensembles, CSO–ANN Empirical predictor | MCPD, CPH, D, B, S, PF | 118 | CSO–ANN | R2 = 0.99 RMSE = 0.246 |
| Dehghani and Ataee-pour [37] | ANN, Empirical predictor, Dimensional analysis | S, B, DPR, NH, PF, D, CPD, MCPD, PLI | 116 | ANN | R2 = 0.945, RMSE = 0.0245 |
| Zhongya [38] | BPNN, MVRA, ELM- FA MIV | D, MCPD, B/S, NHPD, UCS, DPR | 108 | ELM-FA MIV | R2 = 0.96, RMSE =0.21 |
| Armaghani et al. [39] | MPMR, LSSVM, GPR PSO–ELM, AGPSO–ELM | B/S, MCPD, D, T, PF, HD | 102 | AGPSO–ELM | R2 = 0.90 RMSE = 0.08 |
| Faradonbeh et al. [40] | GEP, NLMR | T, B/S, PF, D, HD, MCPD | 102 | GEP | R2 = 0.874 |
| Mokfi et al. [41] | GMDH, GEP, NLMR | MCPD, PF, T, B/S, D, HD | 102 | GMDH | R2 = 0.874, RMSE = 0.963 |
| Ismail et al. [42] | GEP, ANFIS, SCA-ANN Empirical predictor | D, MCPD, ρr, SRH | 100 | SCA-ANN | R2 = 0.999 RMSE = 0.0094 |
| Hajihassani et al. [43] | ICA-ANN, ANN, MLR | B/S, T, MCPD, P-wave, E, D | 95 | ICA-ANN | R2 = 0.97 |
| Chen et al. [44] | FA–SVR, PSO–SVR, GA–SVR, FA–ANN, PSO–ANN, GA–ANN, MFA–SVR | B/S, T, MCPD, D, E, P-wave | 95 | MFA–SVR | R2 = 0.984 RMSE = 0.614 |
| Peng et al. [45] | ANN, ANN-PSO, ANN-GA, ANN | MCPD, D, PF, SD, RQD, B, S | 93 | ANN-PSO | R = 0.945 RMSE = 0.680 |
| Hasanipanah et al. [46] | CART, MLR, Empirical predictor | MCPD, D | 86 | CART | R2 = 0.95, RMSE = 0.17 |
| Hudaverdi and Akyildiz [47] | ANN, MLR Empirical predictor | MCPD, D, B, S | 86 | ANN | RMSE = 5.28 |
| Zhu et al. [48] | ANN, ANFIS, RANFIS CRANFIS, CRANFIS-PSO, Empirical predictor | B, S, T, PF, MCPD, D | 84 | CRANFIS-PSO | R2 = 0.997 RMSE = 0.076 |
| Shahnazar et al. [49] | PSO-ANFIS, ANFIS | D, MCPD | 81 | ANFIS-PSO | R2 = 0.984, RMSE = 0.4835 |
| Hasanipanah et al. [50] | SVM, Empirical predictor | MCPD, D | 80 | SVM | R2 = 0.96, RMSE = 0.34 |
| Abbaszadeh Shahri et al. [51] | GFFN-FA, GFFN-ICA, GFFN | B, S, TC, D, MCPD | 78 | GFFN-FMA | R2 = 0.97 RMSE = 0.187 |
| Saadat et al. [52] | ANN, Empirical predictor | MCPD, D, SL, HD | 69 | ANN | R2 = 0.95, RMSE = 8.79 |
| Álvarez-Vigil et al. [53] | ANN, MLR | RMR, BCPRA, D, HDM, S, HD, B, MCPD, VOD, TC, NH | 60 | ANN | R2 = 0.96, RMSE = 0.65 |
| Lawal et al. [3] | ANN, GEP, MFO-ANN, MLR, Empirical predictor | HD, CPD, NH, TC, D, RMR | 56 | MFO-ANN | R2 = 0.957 MSE = 0.0008 |
| Amini et al. [54] | ANN | D, ρe Ve, B, S, TC | 51 | ANN | R2 = 0.96 |
| [55] | CART, MR, Empirical predictor | MCPD, D | 51 | CART | R2 = 0.92, RMSE = 0.97 |
| Iphar et al. [56] | ANFIS, MLR | MCPD, D | 44 | ANFIS | R2 = 0.98, RMSE = 0.80 |
| Armaghani et al. [57] | BP-ANN, PSO–ANN | HDM, HD, MCPD, S, B, SL, PF, ρr, SD, NR | 44 | PSO–ANN | R2 = 0.93 |
| Lapčević et al. [58] | ANN | CPH, DT, MCPD, TC, D | 42 | ANN | R2 = 0.95 |
| Mohamadnejad et al. [59] | SVM, GRNN, Empirical predictor | MCPD, D | 37 | SVM | R2 = 0.89, RMSE = 1.62 |
| Monjezi et al. [60] | GEP, MLR, NLMR | D, MCPD | 35 | GEP | R2 = 0.918, RMSE = 2.321 |
| Li et al. [61] | SVM, Empirical predictor | MCPD, D | 32 | SVM | R2 = 0.945 |
| Ravilic et al. [62] | MCPD, D, TC | ANN, Empirical predictor | 32 | ANN | R2 = 0.9 RMSE = 0.018 |
| Monjezi et al. [12] | ANN, Empirical predictor | TC, MCPD, D | 20 | ANN | R2 = 0.924, RMSE = 0.071 |
| Ragam and Nimaje [63] | GRNN, Empirical predictor | D, MCPD | 14 | GRNN | R2 = 0.999, RMSE = 0.0001 |
2. Materials and Methods
2.1. Materials
The dataset used for this research work was gathered from 34 opencast mines. Table 2 presents the different mines/quarries along with the excavation materials. The blasting operations and the output, such as the induced vibration, flyrock and air overpressure from the different sites, are under monitoring by the rock excavation engineering division of the Central Institute of Mine and Fuel Research India (CSIR-CIMFR). In addition, the largest granite aggregate quarry, namely OKOUTA CARRIERE SA, located in Setto, Benin, was considered in this study. Thousands of blasting data were compiled and subjected to curation. After filtering, 1001 complete measured peak particle velocities with ten corresponding blast-design parameters, i.e., hole diameter (HDM), hole depth (HD), number of holes (NH), burden (B), spacing (S), stemming (SL), charge per hole (CPH), total charge (TC), maximum charge per delay, (MCPD), and monitoring distance (D), were considered to establish the models. Table 3 presents the descriptive statistics of the input and output variables. The correlation between input variables and target PPV can be seen from the Pearson correlation matrix presented in Figure 2. It can be noticed that there is no collinearity between the predictor variables and the output PPV that can significantly influence model efficiency. To further evaluate how sensitive the output response PPV is to the independent variables, sensitivity analysis was performed using cosine amplitude technique [64]. The cosine amplitude can be obtained using the following expression (Equation (1)). The value of closer to unity indicates significant influence of the input variable on the output PPV. Figure 3 shows the relative strength of all input variables to PPV. The value of ranges between 0.605 to 0.902, suggesting that all the input variable influences the response PPV. Because each variable has a relative influence ( > 0.6) on the output variable PPV, all 10 predictor variables were used to establish the models.
where and are the inputs and output, respectively.

Table 2.
List of the investigated mines/quarries for data-gathering.

Table 3.
Descriptive statistics of the input and output variables.
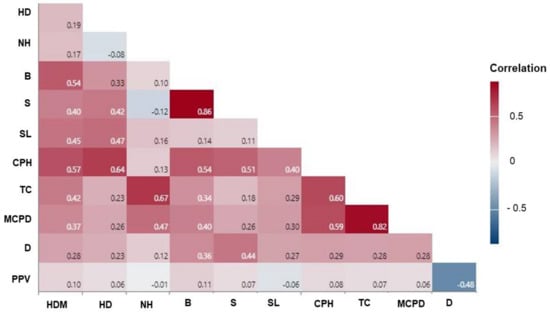
Figure 2.
Correlation matrix of PPV dataset.
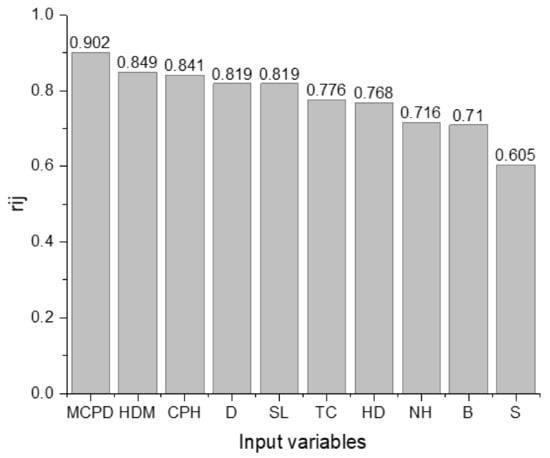
Figure 3.
Sensitivity analysis of the input variables on PPV.
2.2. Methods
This section presents a brief description of the proposed models applied in the present study. As mentioned earlier, 1001 data points were randomly split into two sets, namely training and testing. The training set comprises 800 datasets, i.e., 80% of all the data points, and was employed to calibrate the models. The remaining 20% (201 datasets) was used to test the models. Two white-box machine-learning techniques, namely CART and MARS, were developed. In addition, the traditional SVR algorithm, as well as MLR and different empirical predictors, were used for comparison.
2.2.1. Empirical Methods
Several empirical equations have been developed to predict PPV. Scaled distance-based-empirical predictors involving maximum charge per delay and distance between blasting and measuring point have been suggested for the prediction of blast-induced PPV. The performance of five commonly used empirical methods, as presented in Table 4, was evaluated on the dataset used in this research.

Table 4.
Some PPV predictive methods based on empirical equations.
The site coefficients ‘K’, ‘A’, ‘B’, and ‘n’ as presented in the equations are site-specific and can be obtained using multiple regression.
2.2.2. Multiple Linear Regression (MLR)
MLR is a statistical method used to model the relationship between two or more predictors (input variables) and one outcome variable by fitting a linear equation. Every input variable x (independent variable) is associated with a value of the response y (dependent variable). Here the blast-design parameters in Table 3 represent the predictor variables and the output response PPV. MLR assumes that the relationship between predictor variables and the output response is linear. MLR can be mathematically expressed as in Equation (2).
where stands for the output response, denotes the input variables, are the regression coefficients, and the prediction error.
2.2.3. Classification and Regression Tree (CART)
The classification and regression tree, known as CART, is one of the decision-tree algorithms that has been in use for about 40 years [65] and remains a popular machine-learning tool. CART operates using recursive partitioning of the data to break it up into smaller parts. It is a non-parametric method, with the capability of handling high-dimensional data without any prior normalisation. A CART model output is represented as an inverted tree, with a main root node and internal nodes that end up with a terminal node (Figure 4).
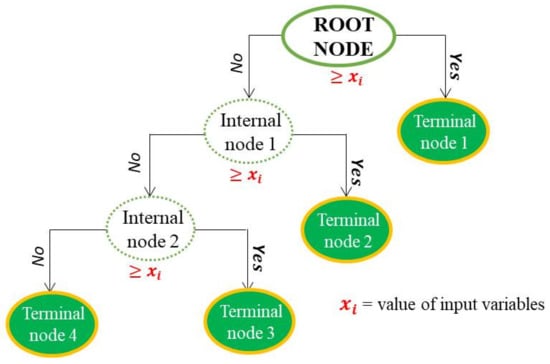
Figure 4.
Example of a simple decision tree.
The root node depicts the most influential input variable on the output. From the root node, CART evaluates all possible splits of all predictor variables, classifies them, and selects the “greatest” single split overall. The best split of the variable designated is better than the best split of any other predictor with the minimum sum of squares and placed at an internal node. The internal node has relatively more cases and is further partitioned based on the same sum-of-squares criterion until a terminal node is reached relatively homogenously. In binary partitioning, the best predictor at each internal node splits the data into two subsets using yes/no or if/then rules. The terminal node represents a prediction value of the response based on the set decision rules. The number of internal nodes depends on the complex interaction between the input variables and the output. Assuming a partition into R regions, R1, R2..., Rm and the output as a constant Cm in each region, the adaptive basis function framework of the recursive partitioning can be represented as in Equation (3) [66].
where Rm is the mth region and Cm is the mean response in a given region (scalar for regression, class probabilities for multi-class classification).
One of the challenges of CART, as with any other decision-tree algorithm, is the difficulty of obtaining the optimum tree that represents the data. A small tree is easy to interpret, but may lack information on the important structure of the data, whereas an overgrowing tree might overfit the data and be difficult to understand. There are several processes to reach the optimum tree for a given dataset, and the common approach is to grow the full tree and subject it to the pruning process [67].
2.2.4. Support Vector Regression (SVR)
Support vector regression is a regression algorithm derived from support vector machine (SVM). Initially, the algorithm was developed by Cortes and Vladimir [68] for classification purposes and later extended to solve regression problems for continuous values and designated as SVR. Unlike a simple linear regression, where the algorithm works to minimize the error rate, SVR tries to fit the error within a certain margin of tolerance (epsilon). The threshold limit is defined by two boundary lines away from the reference data which fit the maximum data points, known as the hyperplane. The epsilon is a hyperparameter used to tune the model. Figure 5 illustrates a one-dimensional SVR technique where the data points represent the predicted values along with the best fit (hyperplane). The data points, which determine the direction of the boundaries, are termed support vectors. The support vectors participate in finding a match between the data point and the hypothesis function that defines the best fit of the data (hyperplane). Assuming the hyperplane is a straight line toward the axis, the hypothesis function of the hyperplane can be expressed as presented in Figure 5, as well as the expression of the two boundary limits. SVR tries to find the maximum margin that best fits the hyperplane by constraining the errors to the acceptable threshold limit defined as the maximum error (, epsilon). On the other hand, the algorithm tends to satisfy the condition stating the fact that . The epsilon parameter is used to optimize the model by constraining the error as . The slope (learned weight vector) helps to optimize the margin by reducing the distance between the margin limits and predicted values outside the bounds. The objective function is to maximize the margin (minimizing , ≥ 0) within the acceptable error tolerance () to obtain the optimal hyperplane, and is expressed as in Equation (4).
where is the response variable, is the weight vector, and is the training input variable. is another tuning parameter that controls the error margin defined by and the weight vector .

Figure 5.
Schematic illustration of one-dimensional SVR.
For a non-linear regression, as is the case in the present study, a kernel function is used to transform the data to higher-dimensional feature space and perform linear separation. Gaussian Radial Basis Function (RBF) is widely used for non-linearity relationships between predictors and response variables, and was adopted in this study. The equation of RBF is as follows (Equation (5)).
where is the kernel RBF parameter that must be tuned during the calibration of the model.
2.2.5. Multivariate Adaptive Regression Splines (MARS)
MARS is a non-parametric ensemble machine-learning regression technique method designed for multivariate non-linear regression problems. The algorithm can split the data into several intervals (splines) depending on the variable’s pattern. Each spline represents a linear function that best characterizes the data. A MARS model can be viewed as an ensemble of linear functions referred to as splines or basis functions (BFs) as illustrated in Figure 6. The end of a spline and the beginning of another is denoted as a knot. Two general steps describe the functionality of a MARS model: a forward procedure followed by a backward procedure. In the forward stage, the algorithm splits the data into an excessive number of splines, which may lead to an overfit model. The backward step is a pruning procedure where all the splines that poorly contribute to the overall model performance are automatically deleted [69]. The generalized MARS model with appropriate knots can be expressed using the combination of the weighted BFs of all the linear splines [70] as in Equation (6).
where is the total number of splines BFs during the forward stage, , and , are the intercept and the weighting coefficients of the nth splines (BF), respectively, and are estimated using the least-squares method.
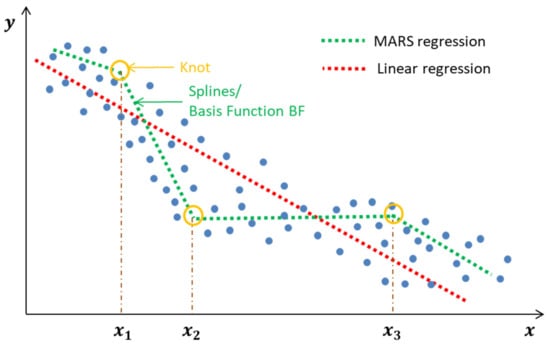
Figure 6.
Relationship between a set of predictors and an output variable .
The performance of the model in the pruning stage is evaluated using generalized cross-validation (GCV) on the training dataset. GCV error includes both residual error and model complexity [71]. A MARS model with the lowest GCV error is considered the optimal model. The GCV can be mathematically expressed as in Equation (7) [66].
where is the number of observations, is the estimated output variable by the nth piecewise linear function (BFs) (n = 1, 2,..., N), is the nth measured output variables, is an effective number of parameters, where denotes the number of independent BFs, the number of knots during the forward stage, and the penalty for adding a BF.
3. Results
The present paper adopts two statistical indices, namely co-efficient of determination () (Equation (8)) and root means square error (RMSE) (Equation (9)), to assess the optimum model and evaluate the relationship between the measured and predicted PPV value based on the proposed models.
represents the measured PPV, is the predicted PPV from the model, represents the average value of the measured PPV, and the number of samples in the training or testing stages.
All the models were developed using Python (Anaconda3) codes through a Spyder environment. Overall, 800 training datasets were used to fit the models, whereas 201 independent datasets were employed for model testing.
3.1. MLR
The multiple linear regression equation based on the training dataset is presented in Equation (10).
PPV = 1.9830 + 0.0171 × HDM + 0.2007 × HD − 0.0053 × NH + 0.0350 × B + 0.5605 × S − 0.101 × SL
− 0.01635 × CPH + 0.0003 × TC − 0.000019 × MCPD − 0.011698 × D
− 0.01635 × CPH + 0.0003 × TC − 0.000019 × MCPD − 0.011698 × D
Table 5 reports the analysis of variance (ANOVA) of the fit model. The trained model (Equation (10)) was assessed using unseen data (test data). The performance between the measured and predicted PPV values is presented in Figure 7. As it can be seen, the MLR model yielded an R2 of 0.384 and 0.4 for training and testing, respectively. This shows that MLR poorly explains the relationship between PPV and the predictor variables and confirms the non-linear interaction between variables.

Table 5.
MLR model output.
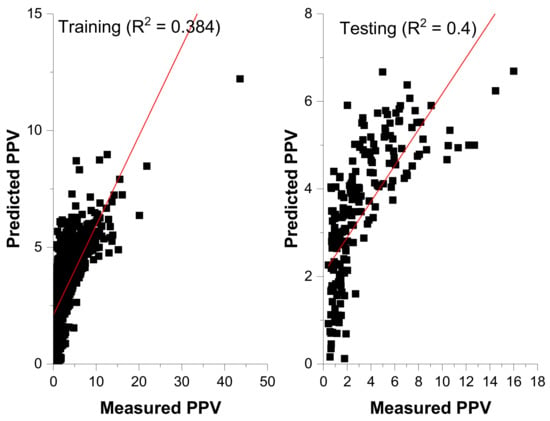
Figure 7.
Measured versus Predicted PPV by MLR.
3.2. Empirical Methods
Scaled law and several modified empirical equations based on charge quantity and distance between blasting and measuring point have been suggested for measuring blast-induced PPV. As mentioned earlier, the empirical methods involve site coefficients and 80% of all the datasets (801 datasets) termed training data was employed to determine the site constants. The remaining 20% (201 datasets) was considered to be testing for model performance evaluation. Using regression analysis, the site coefficients were obtained and reported in Table 6. The obtained coefficients were employed to predict PPV using an independent dataset (testing dataset). Figure 8a–e present the fitting curves between the measured and the predicted PPV for different empirical methods employed. The performance indices (Table 6) indicate that the Ambraseys–Hendron equation yielded the highest R2 on the testing dataset, followed by the USBM and CMRI predictor, respectively.

Table 6.
Computed site constants and performance indices from empirical predictors.
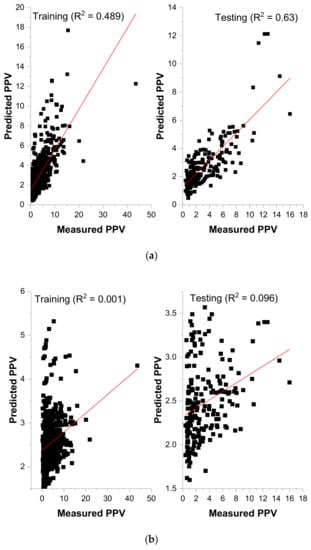
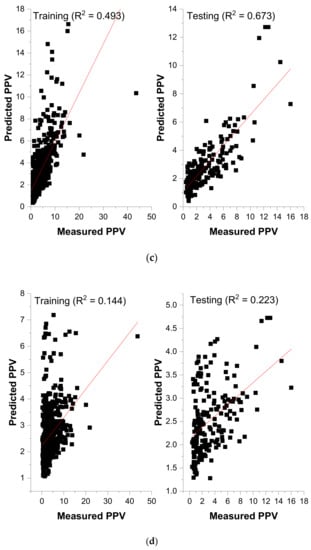
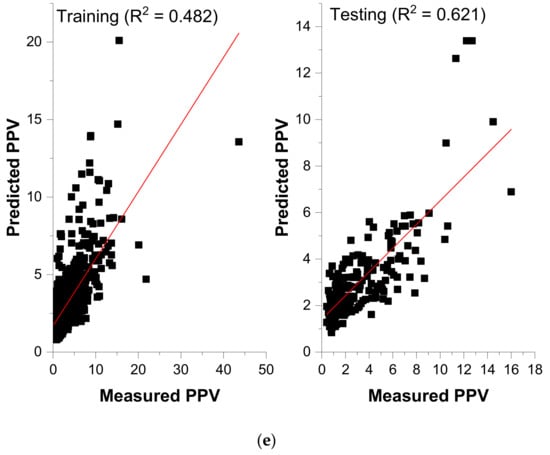
Figure 8.
(a) Measured versus Predicted PPV (USBM Method). (b) Measured versus Predicted (L–K method). (c) Measured versus Predicted (A–H). (d) Measured versus Predicted (IS method). (e) Measured versus Predicted (CMRI method).
3.3. CART Model for the Prediction of PPV
The CART model was built using the Python Scikit-learn package through the Spyder (Anaconda3) environment. Scikit-learn uses an optimized version of the CART algorithm. Initially, the default parameters were employed to grow the full tree. Cost–complexity pruning analysis is widely employed to prune regression trees. The parameters cost–complexity and pruning-alpha (ccp_alpha) were employed to prune the obtained tree. The default value of ccp_alpha is zero, corresponding to the complex initial tree to be pruned. The complexity of the tree decreases with the increase of ccp_alpha ∈ R (R ≥ 0). The optimal tree is the subtree with the largest cost–complexity and lowest error on unseen data (test data). Figure 9 presents the error (RMSE) trend on both the training and testing datasets for varying values of ccp_alpha. As can be expected, the error increases as the ccp_alpha values increase. A relatively steady level can be seen from 0.009 to 0.012 on the training error curve (Figure 9) with the lowest RMSE of 0.524 at ccp_alpha 0.01. A rational error (RMSE) of 1.139 and R2 of 0.744 was obtained on the testing dataset (Figure 9 and Table 7). Therefore, the value of 0.01 was considered the optimum ccp_alpha parameter. The performance indices for all iterations are presented in Table 7. Although the pruning stage decreases the performance of the training set, the model with ccp_alpha of 0.01 can yield efficient prediction on a new dataset and be considered the optimum CART model. The structure of the corresponding regression tree is presented in Figure 10.
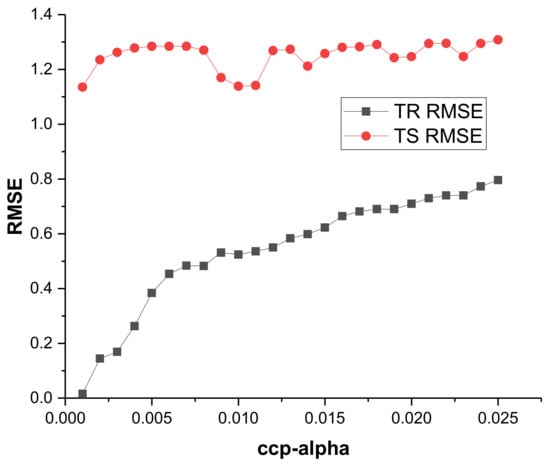
Figure 9.
RMSE performance of potential CART models under different ccp_alpha values.

Table 7.
Performance metric of CART models under different ccp_alpha values.
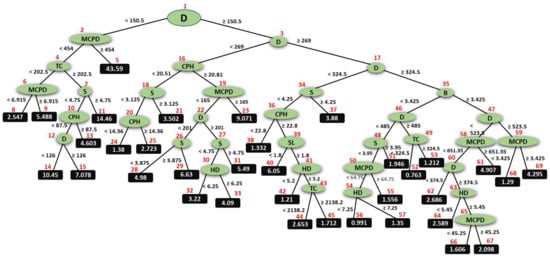
Figure 10.
Tree structure for the proposed CART model.
The relationship between the measured and predicted PPV-base CART model is presented in Figure 11 for both training and testing datasets. The proposed CART model with an R2 of 0.74 on unseen data (test dataset) outperformed the best empirical predictor (Ambraseys–Hendron equation, R2 = 0.67) and multiple linear regression (R2 = 0.4). It can be employed to estimate PPV with a prediction accuracy of over 74%.
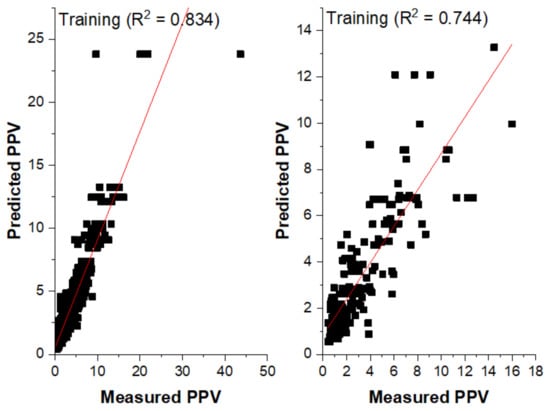
Figure 11.
Measured versus Predicted PPV (CART model).
3.4. SVR Model for the Prediction of PPV
In the SVR model, the radial basis function (RBF), which best explains the non-linearity relationship between variables, was employed to establish the model using Python numerical code. Two key hyperparameters including cost–complexity (c) and gamma (δ) govern the SVR model-based RBF kernel function. To obtain the optimum value of ‘c’, several iterations were performed as presented in Figure 12. The value for which minimum RMSE was attained on the testing dataset was considered the optimum value, which was found to be 32 at the ninth iteration. The final ‘c’ value was fixed while the other hyperparameter gamma (δ) was varied. The RMSE curve change for parameter gamma (δ) on the testing dataset as presented in Figure 13 reveals that the value of gamma (δ) for which minimum error (RMSE = 1.619) is archived is δ = 0.1 and was considered to be the optimum parameter (δ).
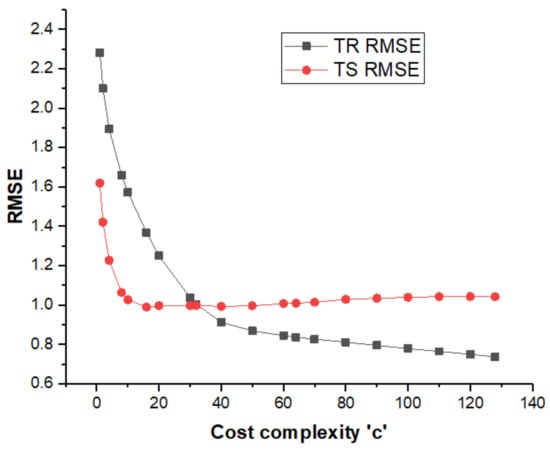
Figure 12.
RMSE change curve for cost–complexity ‘c’ parameter for SVR.
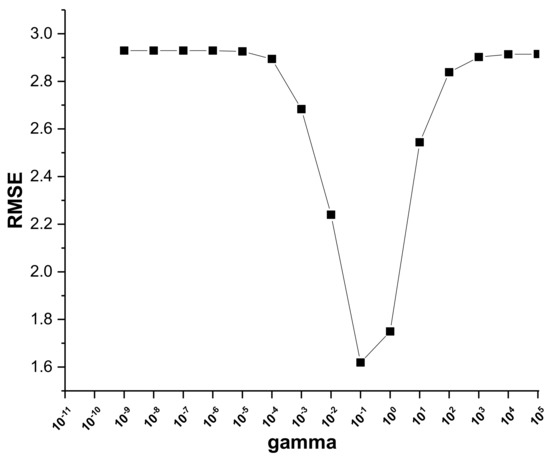
Figure 13.
RMSE change curve for gamma parameter.
A summary of the overall SVR models with varying values of ‘c’ and the optimum gamma δ = 0.1 is presented in Table 8. The proposed model with ‘c’ = 32 and δ = 0.1 yielded an R2 and RMSE of 0.9007 and 1.0047 for the training dataset and 0.876 and 0.9981 for testing datasets. The relationship between measured and predicted PPV is presented in Figure 14. The results indicate better accuracy of the SVR model as compared to MLR, empirical, and CART models.

Table 8.
Co-efficient of determination R2 change curves for endspan_alpha and minspan_alpha.
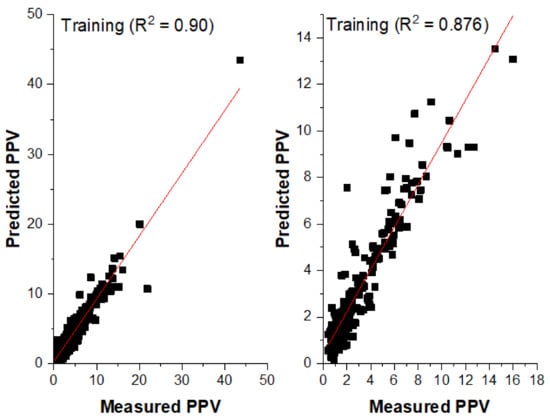
Figure 14.
Measured versus Predicted PPV (SVR model).
3.5. MARS Model for the Prediction of PPV
MARS model was trained using the py-earth Python package through the Spyder (Anaconda3) environment. The py-earth library incorporates all the parameters involved in the MARS algorithm as per Friedman [70]. In the training procedure, several iterations were performed using key hyperparameters such as penalty parameter, endspan_alpha, and minspan_alpha. The performance of the developed model during training stage with varying values of the hyperparameters are presented in Figure 15 and Figure 16 for penalty and endspan/minspan_alpha, respectively. From Figure 15, it can be seen that the minimum error (RMSE = 0.227) during the testing stage was obtained at the penalty value of 3.0 and considered the optimum. Then, the parameters endspan_alpha and minspan_alpha were varied consecutively (Table 9), keeping the optimum penalty value constant at 3.0. The value of 0.05 for both parameters yielded the highest performance (R2 = 0.951) on training and testing datasets (Figure 16). The optimum hyperparameter values yielded a total of 55 candidate BFs, as shown in Figure 17. It is worth noting that the generalized cross-validation (GCV) method is applied to remove insignificant BFs during the backward stage. Figure 17 indicates 32 prominent numbers of terms with the highest general co-efficient of determination (R2). The remaining terms (BFs) does not influence the model performance as the R2 remains relatively unalterable with further BFs (Figure 17). Therefore, the insignificant BFs were removed (pruned) and the final MARS model involves 32 imperative BFs. A similar methodology was employed by Abdulelah Al-Sudani et al. [72] and Chen et al. [73] in previous research to identify the optimum MARS model. The elected 32 BFs and their corresponding coefficients are presented in Table 10 alongside the general regression equation. The application of this equation consists of summing the regression equations of each spline (BF). The obtained value represents the target response PPV based on the proposed MARS model. From Table 9, it can be seen that the performance of both training and testing data are similar, suggesting a good generalization ability of the proposed MARS model.
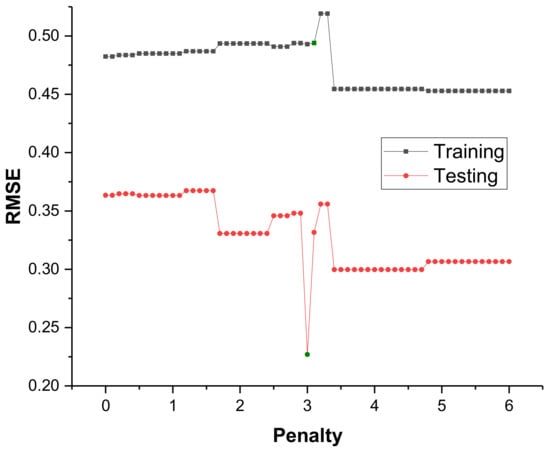
Figure 15.
RMSE change curve for penalty parameter.
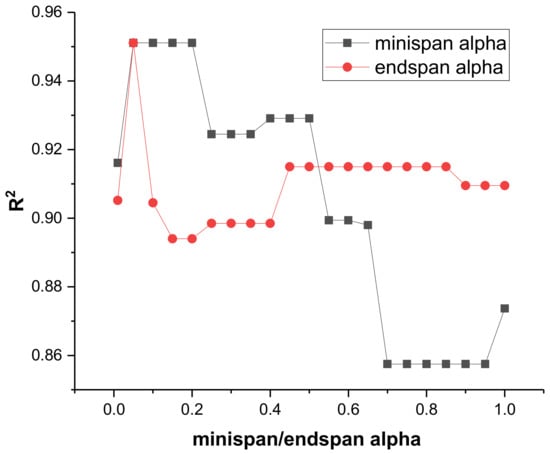
Figure 16.
R2 change curve for minispan alpha and endspan alpha parameter.

Table 9.
Performance metrics of different MARS models with varying values of minispan alpha and endspan of alpha.
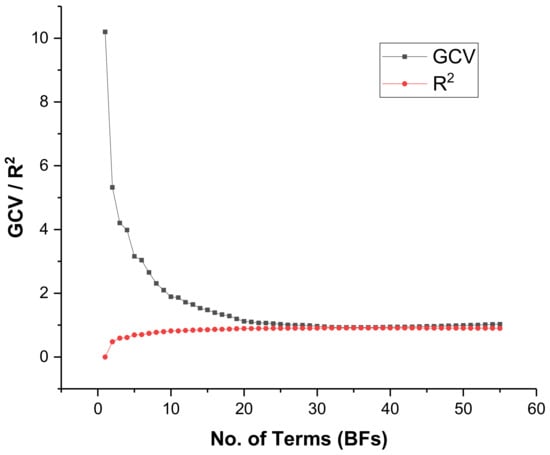
Figure 17.
Pruning stage and model selection.

Table 10.
Effective BFs and the corresponding coefficients.
Further analysis is performed to evaluate the importance of the input variables for the MARS model. Figure 18 shows the relative importance of the input parameters expressed as percentages. It can be seen that the monitoring distance (D) and maximum charge per delay (MCPD) are the critical predictors, whereas the number of holes (NH) has the least influence on PPV. This is in line with the results of previous investigations, stating the strong relationship between scaled distance and PPV [74]. The relationship between the predicted and measured PPV based on the proposed MARS model is shown in Figure 19.
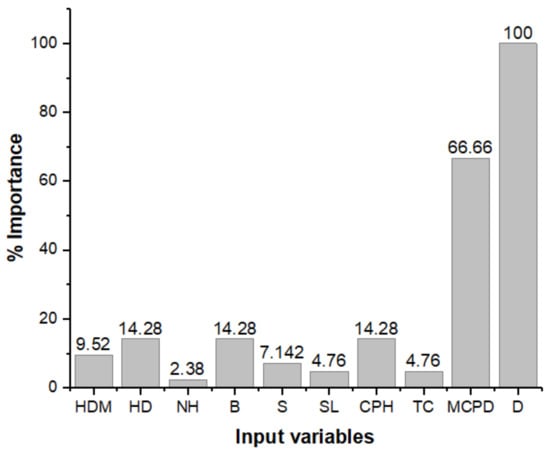
Figure 18.
Predictor importance analysis for MARS model.
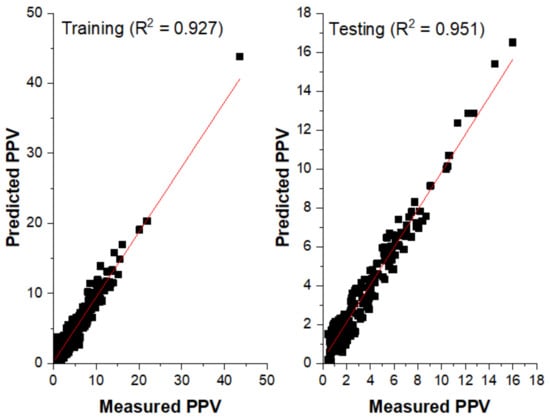
Figure 19.
Measured versus Predicted PPV (MARS model).
4. Discussion
Predicting PPV is one technique to minimize the damage induced by rock-blasting vibration in mines. PPV is influenced by various blasting parameters. The ability to identify the most influential factors is key to building a good predictive model. This study uses cosine amplitude and observes the influence of rock-blasting parameters on the induced PPV. These include hole diameter, hole depth, number of holes, burden, spacing, stemming length, charge per hole, total charge, maximum charge per delay, and monitoring distance. These parameters diversely influence PPV and have been used by various researchers to develop PPV predictive models based on machine-learning technique [9,42,75]. Machine learning is extensively used to solve several prediction problems because of its accuracy as compared to empirical and statistical methods. The prediction accuracy depends upon the techniques employed and inter-correlation between input and output variables. It has been observed that a model generalization ability increases with the input variables and the number of datasets. Recently, hybrid models have been introduced to increase prediction accuracy. However, these models are difficult to interpret and implement by practitioners in the field. White-box ML techniques such as MARS and CART can provide reasonable prediction accuracy and are easily implementable. This study develops a simple ML model that can be easily used by field practitioners to predict PPV. Many datasets from various geo-environments have been involved to develop conventional ML models to increase generalization ability. The models were well trained based on a trial-and-error approach to obtain the best fitting with minimum error for PPV prediction. Three ML techniques, including MARS, CART and SVR, were employed in this study, and the results were compared to conventional statistical methods and empirical predictors. The performance of all developed models for both training and testing sets is reported in Table 11. As can be seen, the best performances were obtained through machine-learning techniques. This confirms that the relationships between the influential parameters and the PPV are non-linear.

Table 11.
Performance indices of the proposed models for predicting PPV.
For a more convenient comparison and model performance assessment, a Taylor diagram was established, as shown in Figure 20. From Figure 20, it can be seen that ML models are the nearest to the reference point. This indicates that these models agree well with the actual observation [76]. According to the presented result (Figure 20), the MARS model indisputably agrees best with the observations, as it yielded the lowest centered root-mean-square difference (RMS) and highest correlation co-efficient. This observation compared well with the results presented in Table 11, which showed that the proposed MARS model discloses superior performance in this study. The model can be adopted in predicting PPV resulting from blasting in opencast mines. A similar method was employed to compare and assess the best machine-learning model in predicting blast-induced air overpressure [77].
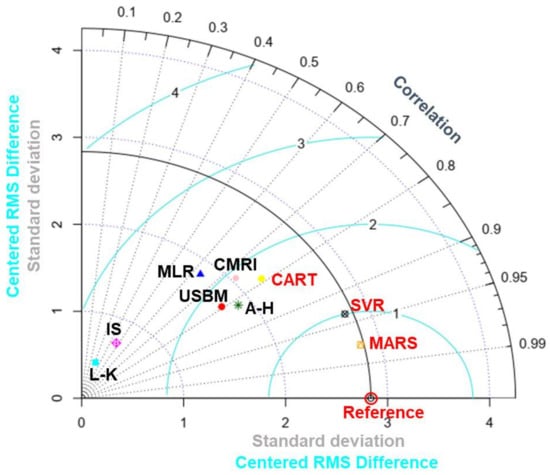
Figure 20.
Comparison of the proposed model performances using a Taylor diagram.
The MARS model outperformed all other developed models. It is reported that the performance of a model on unseen data (test data) with respect to the training dataset is an indicator to evaluate model generalization ability. As shown in Table 11, the performance of the proposed MARS model on the training set and the testing set do not differ significantly, and the prediction error (RMSE) was the lowest. This indicates the strong generalization ability of the MARS model as compared to SVR and CART. Furthermore, the MARS model provides the interactive behavior between variables. The input variables (basis function (BFs)) with their corresponding co-efficient from the MARS model led to the general equation for the prediction of PPV (Table 10). Although the SVR model outperformed the CART model (Table 11), the latter has the advantage of easy interpretability. The tree generated by the CART model can be used as a benchmark for the optimization process based on trial-and-error experimentation. It is worth noting that except for the MARS model, the accuracy of the proposed models underperformed some models available in the literature (Table 1). This might be attributed to the high number of input variables and datasets, which increases the complexity of the models [8]. However, it is reported that many datasets and input variables enhance the generalization ability of regression models [12]. To the best knowledge of the authors, there are no existing models involving many blasting events and input variables as in the case of the present study. It suggests that the proposed models will better estimate PPV in practical engineering with reasonable accuracy than other existing models developed with fewer variables and datasets. The proposed model involved only blast-design parameters, and has the advantage of applying it in areas where rock (mass) properties are difficult to obtain. However, further investigations should be carried out involving both blasting parameters and rock (mass) properties with large datasets to ensure the generalization ability of the models.
5. Conclusions
Ground vibration is one of the inevitable adverse effects induced by rock blasting. Peak particle velocity (PPV) is the universally used parameter to assess blast-induced damages. Predicting PPV is the only way to prevent and reduce the damages induced by blasting vibration. This study applied machine-learning techniques to develop a generalized and interpretable model for PPV estimation. CART and MARS, as white-box ML techniques, have the advantage of easy interpretability and application and were employed in this study. Furthermore, a black-box SVR algorithm, as well as multiple linear regression and conventional empirical predictors, were applied and compared to CART and MARS models. Several conclusions from the presented study can be drawn as follows:
- ▪
- Based on 1001 datasets, the effective parameters on PPV were assessed using sensitivity analysis. PPV depends upon various blast-design parameters such as hole diameter, hole depth, number of holes, burden, spacing, stemming length, charge per hole, total charge, maximum charge per delay, and monitoring distance.
- ▪
- Machine-learning techniques outperformed traditional prediction techniques including empirical and statistical methods and better explain the non-linear interaction between input variables and the response PPV.
- ▪
- A comprehensive quantitative interaction between input variables and the response PPV is obtained from CART and MARS models, and can be easily employed to predict PPV with reasonable accuracy.
- ▪
- Despite using many datasets and input variables, the study shows that the MARS model can be easily employed to estimate PPV with high prediction accuracy (R2 = 0.951; RMSE = 0.227) compared to CART and SVR.
Author Contributions
Conceptualization, A.R. and G.C.K.; Data curation, G.J.; Formal analysis, A.R.; Funding acquisition, P.A.O.; Methodology, G.C.K.; Project administration, C.S.; Resources, P.A.O.; Software, G.C.K. and G.J.; Supervision, A.R. and V.A.; Validation, L.A.G., V.A., A.R. and C.S.; Visualization, A.R.; Writing—original draft, G.C.K.; Writing—review & editing, A.R., L.A.G., V.A. and P.A.O.; Materials, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Council of Scientific and Industrial Research-Central Institute of Mining and Fuel Research (CSIR-CIMFR), Dhanbad, India. And supported by CSIR-The World Academy of Science (TWAS) and the Partnership for skills in Applied Sciences, Engineering and Technology (PASET).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ABS | Absorption | MCPD | Maximum charge per delay |
| AGPSO | Autonomous groups particles swarm optimization | MFA | Modified firefly algorithm |
| A–H | Ambraseys–Hendron predictors | MFA | Modified firefly algorithm |
| ANFIS | Adaptive neuro-fuzzy inference system | MFO | Moth-flame optimization algorithm |
| ANN | Artificial neural network | MIV | Mean impact value |
| B | Burden | ML | Machine learning |
| BCPRA | Blast-control point relative angle | MLPNN | Multilayer perceptrons neural network |
| BF | Basis function | MLR | Multiple linear regression; |
| BI | Blasting index | MPMR | Minimax probability machine regression |
| BIGV | Blast-induced ground vibration | MR | Multiple regression; |
| BK | Buckingham π (pi) theorem | MVRA | Multivariate regression analysis |
| BP | Backpropagation | NDS | Number of blasting groups |
| BPNN | Backpropagation neural network | NH | Number of holes |
| CART | Classification and regression tree | NHPD | Number of holes per delay |
| CL | Average charge length | NLMR | Non-linear multiple regression |
| CMRI | Central Mining Research Institute predictor | NR | Number of rows |
| CPH | Average explosive charge per hole | PF | Powder factor |
| CRANFIS | Chaos recurrent adaptive neuro-fuzzy inference system | PLI | Point load index |
| CSO | Cuckoo search optimization | PPV | Peak particle velocity |
| D | Distance | PSO | Particle swarm optimization |
| DPR | Delay per row | P-wave | P-wave velocity |
| DTS | Time delay for each group, | R2 | Co-efficient of determination |
| E | Young’s modulus | RANFIS | Recurrent adaptive neuro-fuzzy inference system |
| ELM | Extreme learning machine | RBFNN | Radial basis function neural network |
| FA | Firefly algorithm | Rdis | Radial distances |
| FRC | Fracture roughness co-efficient | RF | Random forest |
| FS | Fuzzy system | RMR | Rock mass rating |
| GA | Genetic algorithm | RMSE | Root-mean-square error |
| GCV | Generalized cross-validation | RQD | Rock quality designation |
| GEP | Gene-expression programming | S | Spacing |
| GFFN | Generalized feed-forward neural network | SCA | Sine cosine algorithm |
| G–D | Ghosh–Daemen empirical predictor | SD | Sub-drilling; |
| GMDH | Group method of data handling | SL | Steaming length |
| GOA | Grasshopper optimization algorithm | SRH | Schmidt rebound hardness value |
| GPR | Gaussian process regression | SVM | Support vector machine |
| GRNN | General regression neural network | SVR | Support vector regression |
| H | Bench height | TC | Total charge |
| Hc | Hardness co-efficient | TS | Tunnel cross-section |
| HD | Hole depth | UCS | Uniaxial compressive strength |
| Hdis | Horizontal distances | USBM | United states bureau of mines |
| HDM | Hole diameter | Ve | Volume of extracted block |
| HGS | Hunger games search | VOD | Velocity of detonation |
| HHO | Harris hawks optimization | XGBoost | Extreme gradient boosting |
| ICA | Imperialist competitive algorithm | ρe | Explosive density |
| IS | Indian standard predictor | ρr | Rock density |
| L–K | Langefors–Kihlstrom predictor | ɳ | Porosity |
| LSSVM | Least-squares support vector machine | µ | Poisson ratio |
| MARS | Multivariate adaptive regression splines |
References
- Bayat, P.; Monjezi, M.; Mehrdanesh, A.; Khandelwal, M. Blasting pattern optimization using gene expression programming and grasshopper optimization algorithm to minimise blast-induced ground vibrations. Eng. Comput. 2021, 38, 3341–3350. [Google Scholar] [CrossRef]
- Siskind, D.E.; Strachura, V.J.; Stagg, M.S.; Kopp, J.W. Structure Response and Damage Produced by Airblast from Surface Mining; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1980. [Google Scholar]
- Lawal, A.I.; Kwon, S.; Kim, G.Y. Prediction of the blast-induced ground vibration in tunnel blasting using ANN, moth-flame optimized ANN, and gene expression programming. Acta Geophys. 2021, 69, 161–174. [Google Scholar] [CrossRef]
- Dumakor-Dupey, N.; Arya, S.; Jha, A. Advances in Blast-Induced Impact Prediction—A Review of Machine Learning Applications. Minerals 2021, 11, 601. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, X.; Fei, H. Review of predicting the blast-induced ground vibrations to reduce impacts on ambient urban communities. J. Clean. Prod. 2020, 260, 121135. [Google Scholar] [CrossRef]
- Ghoraba, S.; Monjezi, M.; Talebi, N.; Armaghani, D.J.; Moghaddam, M.R. Estimation of ground vibration produced by blasting operations through intelligent and empirical models. Environ. Earth Sci. 2016, 75, 1137. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Monjezi, M. Prediction and minimization of blast-induced ground vibration using two robust meta-heuristic algorithms. Eng. Comput. 2017, 33, 835–851. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Liu, J.; Zhang, F. Optimization of blasting parameters for an underground mine through prediction of blasting vibration. J. Vib. Control 2019, 25, 1585–1595. [Google Scholar] [CrossRef]
- Bayat, P.; Monjezi, M.; Rezakhah, M.; Armaghani, D.J. Artificial Neural Network and Firefly Algorithm for Estimation and Minimization of Ground Vibration Induced by Blasting in a Mine. Nat. Resour. Res. 2020, 29, 4121–4132. [Google Scholar] [CrossRef]
- Giustolisi, O. Using genetic programming to determine Chezy resistance coefficient in corrugated channels. J. Hydroinform. 2004, 6, 157–173. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Monjezi, M.; Hasanipanah, M.; Khandelwal, M. Evaluation and prediction of blast-induced ground vibration at Shur River Dam, Iran, by artificial neural network. Neural Comput. Appl. 2013, 22, 1637–1643. [Google Scholar] [CrossRef]
- Ke, B.; Nguyen, H.; Bui, X.-N.; Costache, R. Estimation of Ground Vibration Intensity Induced by Mine Blasting using a State-of-the-Art Hybrid Autoencoder Neural Network and Support Vector Regression Model. Nat. Resour. Res. 2021, 30, 3853–3864. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N. A Novel Hunger Games Search Optimization-Based Artificial Neural Network for Predicting Ground Vibration Intensity Induced by Mine Blasting. Nat. Resour. Res. 2021, 30, 3865–3880. [Google Scholar] [CrossRef]
- Singh, T. Artificial neural network approach for prediction and control of ground vibrations in mines. Min. Technol. 2004, 113, 251–256. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Nguyen, H.A.; Nguyen, D.-A.; Hoa, L.T.T.; Le, Q.-T. Prediction of ground vibration intensity in mine blasting using the novel hybrid MARS–PSO–MLP model. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Singh, T.N.; Dontha, L.K.; Bhardwaj, V. Study into blast vibration and frequency using ANFIS and MVRA. Min. Technol. 2008, 117, 116–121. [Google Scholar] [CrossRef]
- Lawal, A.I.; Olajuyi, S.I.; Kwon, S.; Onifade, M. A comparative application of the Buckingham π (pi) theorem, white-box ANN, gene expression programming, and multilinear regression approaches for blast-induced ground vibration prediction. Arab. J. Geosci. 2021, 14, 1073. [Google Scholar] [CrossRef]
- Singh, T.N.; Verma, A.K. Sensitivity of total charge and maximum charge per delay on ground vibration. Geomat. Nat. Hazards Risk 2010, 1, 259–272. [Google Scholar] [CrossRef]
- Monjezi, M.; Ghafurikalajahi, M.; Bahrami, A. Prediction of blast-induced ground vibration using artificial neural networks. Tunn. Undergr. Space Technol. 2011, 26, 46–50. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T. Prediction of blast-induced ground vibration using artificial neural network. Int. J. Rock Mech. Min. Sci. 2009, 46, 1214–1222. [Google Scholar] [CrossRef]
- Khandelwal, M. Evaluation and prediction of blast-induced ground vibration using support vector machine. Int. J. Rock Mech. Min. Sci. 2010, 47, 509–516. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T. Evaluation of blast-induced ground vibration predictors. Soil Dyn. Earthq. Eng. 2007, 27, 116–125. [Google Scholar] [CrossRef]
- Monjezi, M.; Ahmadi, M.; Sheikhan, M.; Bahrami, A.; Salimi, A. Predicting blast-induced ground vibration using various types of neural networks. Soil Dyn. Earthq. Eng. 2010, 30, 1233–1236. [Google Scholar] [CrossRef]
- Yu, C.; Koopialipoor, M.; Murlidhar, B.R.; Mohammed, A.S.; Armaghani, D.J.; Mohamad, E.T.; Wang, Z. Optimal ELM–Harris Hawks Optimization and ELM–Grasshopper Optimization Models to Forecast Peak Particle Velocity Resulting from Mine Blasting. Nat. Resour. Res. 2021, 30, 2647–2662. [Google Scholar] [CrossRef]
- Mohamed, M.T. Performance of fuzzy logic and artificial neural network in prediction of ground and air vibrations. Int. J. Rock Mech. Min. Sci. 2011, 48, 845–851. [Google Scholar] [CrossRef]
- Khandelwal, M.; Kumar, D.L.; Yellishetty, M. Application of soft computing to predict blast-induced ground vibration. Eng. Comput. 2011, 27, 117–125. [Google Scholar] [CrossRef]
- Singh, J.; Verma, A.K.; Banka, H.; Singh, T.N.; Maheshwar, S. A study of soft computing models for prediction of longitudinal wave velocity. Arab. J. Geosci. 2016, 9, 224. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Khandelwal, M.; Zhu, S.; Zhang, X. Developing a hybrid model of Jaya algorithm-based extreme gradient boosting machine to estimate blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 2021, 145, 104856. [Google Scholar] [CrossRef]
- Mohamed, M.T. Artificial neural network for prediction and control of blasting vibrations in Assiut (Egypt) limestone quarry. Int. J. Rock Mech. Min. Sci. 2009, 46, 426–431. [Google Scholar] [CrossRef]
- Rana, A.; Bhagat, N.K.; Jadaun, G.P.; Rukhaiyar, S.; Pain, A.; Singh, P.K. Predicting Blast-Induced Ground Vibrations in Some Indian Tunnels: A Comparison of Decision Tree, Artificial Neural Network and Multivariate Regression Methods. Min. Met. Explor. 2020, 37, 1039–1053. [Google Scholar] [CrossRef]
- Verma, A.; Singh, T.N. Comparative study of cognitive systems for ground vibration measurements. Neural Comput. Appl. 2013, 22, 341–350. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, T.N. Intelligent systems for ground vibration measurement: A comparative study. Eng. Comput. 2011, 27, 225–233. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M.; Hashemolhosseini, H. Development of a fuzzy model for predicting ground vibration caused by rock blasting in surface mining. J. Vib. Control 2013, 19, 755–770. [Google Scholar] [CrossRef]
- Ghasemi, E.; Kalhori, H.; Bagherpour, R. A new hybrid ANFIS–PSO model for prediction of peak particle velocity due to bench blasting. Eng. Comput. 2016, 32, 607–614. [Google Scholar] [CrossRef]
- Bui, X.-N.; Nguyen, H.; Tran, Q.-H.; Nguyen, D.-A.; Bui, H.-B. Predicting Ground Vibrations Due to Mine Blasting Using a Novel Artificial Neural Network-Based Cuckoo Search Optimization. Nat. Resour. Res. 2021, 30, 2663–2685. [Google Scholar] [CrossRef]
- Dehghani, H.; Ataee-Pour, M. Development of a model to predict peak particle velocity in a blasting operation. Int. J. Rock Mech. Min. Sci. 2011, 48, 51–58. [Google Scholar] [CrossRef]
- Zhongya, Z.; Xiaoguang, J. Prediction of Peak Velocity of Blasting Vibration Based on Artificial Neural Network Optimized by Dimensionality Reduction of FA-MIV. Math. Probl. Eng. 2018, 2018, 8473547. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Kumar, D.; Samui, P.; Hasanipanah, M.; Roy, B. A novel approach for forecasting of ground vibrations resulting from blasting: Modified particle swarm optimization coupled extreme learning machine. Eng. Comput. 2021, 37, 3221–3235. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Armaghani, D.J.; Monjezi, M.; Mohamad, E.T. Genetic programming and gene expression programming for flyrock assessment due to mine blasting. Int. J. Rock Mech. Min. Sci. 2016, 88, 254–264. [Google Scholar] [CrossRef]
- Mokfi, T.; Shahnazar, A.; Bakhshayeshi, I.; Derakhsh, A.M.; Tabrizi, O. Proposing of a new soft computing-based model to predict peak particle velocity induced by blasting. Eng. Comput. 2018, 34, 881–888. [Google Scholar] [CrossRef]
- Lawal, A.I.; Kwon, S.; Hammed, O.S.; Idris, M.A. Blast-induced ground vibration prediction in granite quarries: An application of gene expression programming, ANFIS, and sine cosine algorithm optimized ANN. Int. J. Min. Sci. Technol. 2021, 31, 265–277. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Vibrations au sol prédiction dans quarry dynamitage à travers un réseau neural artificiel optimisé par une concurrence impérialiste algorithme. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Chen, W.; Hasanipanah, M.; Rad, H.N.; Armaghani, D.J.; Tahir, M.M. A new design of evolutionary hybrid optimization of SVR model in predicting the blast-induced ground vibration. Eng. Comput. 2021, 37, 1455–1471. [Google Scholar] [CrossRef]
- Peng, K.; Zeng, J.; Armaghani, D.J.; Hasanipanah, M.; Chen, Q. A Novel Combination of Gradient Boosted Tree and Optimized ANN Models for Forecasting Ground Vibration Due to Quarry Blasting. Nat. Resour. Res. 2021, 30, 4657–4671. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Faradonbeh, R.S.; Amnieh, H.B.; Armaghani, D.J.; Monjezi, M. Forecasting blast-induced ground vibration developing a CART model. Eng. Comput. 2016, 33, 307–316. [Google Scholar] [CrossRef]
- Hudaverdi, T.; Akyildiz, O. Prediction and evaluation of blast-induced ground vibrations for structural damage and human response. Arab. J. Geosci. 2021, 14, 378. [Google Scholar] [CrossRef]
- Zhu, W.; Rad, H.N.; Hasanipanah, M. A chaos recurrent ANFIS optimized by PSO to predict ground vibration generated in rock blasting. Appl. Soft Comput. 2021, 108, 107434. [Google Scholar] [CrossRef]
- Shahnazar, A.; Rad, H.N.; Hasanipanah, M.; Tahir, M.M.; Jahed Armaghani, D.; Ghoroqi, M. A new developed approach for the prediction of ground vibration using a hybrid PSO-optimized ANFIS-based model. Environ. Earth Sci. 2017, 76, 527. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Jahed Armaghani, D.; Farazmand, A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Meas. J. Int. Meas. Confed. 2015, 75, 289–297. [Google Scholar] [CrossRef]
- Shahri, A.A.; Pashamohammadi, F.; Asheghi, R.; Shahri, H.A. Automated intelligent hybrid computing schemes to predict blasting induced ground vibration. Eng. Comput. 2021, 1–5. [Google Scholar] [CrossRef]
- Saadat, M.; Khandelwal, M.; Monjezi, M. An ANN-based approach to predict blast-induced ground vibration of Gol-E-Gohar iron ore mine, Iran. J. Rock Mech. Geotech. Eng. 2014, 6, 67–76. [Google Scholar] [CrossRef]
- Álvarez-Vigil, A.E.; González-Nicieza, C.; López Gayarre, F.; Álvarez-Fernández, M.I. Predicting blasting propagation velocity and vibration frequency using artificial neural networks. Int. J. Rock Mech. Min. Sci. 2012, 55, 108–116. [Google Scholar] [CrossRef]
- Amini, H.; Gholami, R.; Monjezi, M.; Torabi, S.R.; Zadhesh, J. Evaluation of flyrock phenomenon due to blasting operation by support vector machine. Neural Comput. Appl. 2012, 21, 2077–2085. [Google Scholar] [CrossRef]
- Khandelwal, M.; Armaghani, D.J.; Faradonbeh, R.S.; Yellishetty, M.; Majid, M.Z.A.; Monjezi, M. Classification and regression tree technique in estimating peak particle velocity caused by blasting. Eng. Comput. 2017, 33, 45–53. [Google Scholar] [CrossRef]
- Iphar, M.; Yavuz, M.; Ak, H. Prediction of ground vibrations resulting from the blasting operations in an open-pit mine by adaptive neuro-fuzzy inference system. Environ. Earth Sci. 2008, 56, 97–107. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hajihassani, M.; Mohamad, E.T.; Marto, A.; Noorani, S.A. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab. J. Geosci. 2013, 7, 5383–5396. [Google Scholar] [CrossRef]
- Lapčević, R.; Kostić, S.; Pantović, R.; Vasović, N. Prediction of blast-induced ground motion in a copper mine. Int. J. Rock Mech. Min. Sci. 2014, 69, 19–25. [Google Scholar] [CrossRef]
- Mohamadnejad, M.; Gholami, R.; Ataei, M. Comparison of intelligence science techniques and empirical methods for prediction of blasting vibrations. Tunn. Undergr. Space Technol. 2012, 28, 238–244. [Google Scholar] [CrossRef]
- Monjezi, M.; Baghestani, M.; Faradonbeh, R.S.; Saghand, M.P.; Armaghani, D.J. Modification and prediction of blast-induced ground vibrations based on both empirical and computational techniques. Eng. Comput. 2016, 32, 717–728. [Google Scholar] [CrossRef]
- Li, D.T.; Yan, J.L.; Zhang, L. Prediction of Blast-Induced Ground Vibration Using Support Vector Machine by Tunnel Excavation. Appl. Mech. Mater. 2012, 170–173, 1414–1418. [Google Scholar] [CrossRef]
- Vasović, D.; Kostić, S.; Ravilić, M.; Trajković, S. Environmental impact of blasting at Drenovac limestone quarry (Serbia). Environ. Earth Sci. 2014, 72, 3915–3928. [Google Scholar] [CrossRef]
- Ragam, P.; Nimaje, D.S. Assessment of blast-induced ground vibration using different predictor approaches—A comparison. Chem. Eng. Trans. 2018, 66, 487–492. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Q. A hierarchical analysis for rock engineering using artificial neural networks. Rock Mech. Rock Eng. 1997, 30, 207–222. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 1984. [Google Scholar]
- Hastie, T.; Jerome, F.; Tibshirani, R. The Elements of Statistical Learning Data Mining, Inference, and Prediction, 2nd ed.; Springer: Stanford, CA, USA, 2008. [Google Scholar]
- Ramesh Murlidhar, B.; Yazdani Bejarbaneh, B.; Jahed Armaghani, D.; Mohammed, A.S.; Tonnizam Mohamad, E. Application of tree-based predictive models to forecast air overpressure induced by mine blasting. Nat. Resources Res. 2021, 30, 1865–1887. [Google Scholar] [CrossRef]
- Cortes, C.; Vladimir, V. Support-vector networks. Machine learning. IEEE Expert Syst. Appl. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A. Multivariate adaptive regression splines for analysis of geotechnical engineering systems. Comput. Geotech. 2013, 48, 82–95. [Google Scholar] [CrossRef]
- Friedman, J.H.T. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Application of the Multi-Adaptive Regression Splines to Integrate Sea Level Data from Altimetry and Tide Gauges for Monitoring Extreme Sea Level Events. Mar. Geod. 2015, 38, 261–276. [Google Scholar] [CrossRef]
- Al-Sudani, Z.A.; Salih, S.Q.; Sharafati, A.; Yaseen, Z.M. Development of multivariate adaptive regression spline integrated with differential evolution model for streamflow simulation. J. Hydrol. 2019, 573, 1–12. [Google Scholar] [CrossRef]
- Chen, Z.; Li, H.; Goh, A.; Wu, C.; Zhang, W. Soil Liquefaction Assessment Using Soft Computing Approaches Based on Capacity Energy Concept. Geosciences 2020, 10, 330. [Google Scholar] [CrossRef]
- Jimeno, C.L.; Jimeno, E.L.; Carcedo, F.J.A.; De Ramiro, Y.V. Drilling and Blasting of Rocks; Routledge: London, UK, 2017. [Google Scholar]
- Choi, Y.-H.; Lee, S.S. Predictive Modelling for Blasting-Induced Vibrations from Open-Pit Excavations. Appl. Sci. 2021, 11, 7487. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- He, Z.; Armaghani, D.J.; Masoumnezhad, M.; Khandelwal, M.; Zhou, J.; Murlidhar, B.R. A Combination of Expert-Based System and Advanced Decision-Tree Algorithms to Predict Air-Overpressure Resulting from Quarry Blasting. Nat. Resour. Res. 2021, 30, 1889–1903. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).