1.2. Literature Review
Unit commitment determines when a particular unit should be started so that, at a given time when the power is needed, it can be provided because each unit needs time to startup and shutdown. These startups and shutdowns have an economic impact in terms of fuel, manpower, apparatus, and other related costs [
4,
5]. On the other hand, the economic dispatch of the generating units determine how much power each unit produces at a certain time to cope with the load and overcome losses due to the transmission network. Ultimately, to minimize the cost of the generating units, scheduling of the generating units is performed based on the load profile data, whether it is one day ahead or one hour [
6]. The problem of economic dispatch and UC becomes more complex when there is an intermittent and uncertain renewable energy source, i.e., solar PV.
For better approximations and more reliable results, more historical data is needed to access the true distribution of the data, i.e., the normal distribution, mean, variance, standard deviation, and probabilities of specific events that behave periodically [
7]. Similarly, high penetration of renewable sources means more and more historical data is needed to deal with the uncertain profile of those renewable sources [
8,
9,
10]. Handling this data distribution is performed in [
11] using a method proposed to adjust the parameter of the distribution in distributionally robust optimization. Unit commitment and energy management/economic dispatch in [
12,
13] use distributionally robust optimization with chance constrained. A method proposed in this system uses mean and variance for the distribution set to handle uncertainty in renewable energy sources for the micro-grid and performs the energy dispatch by not considering unit commitment as constrained to reduce the start-up/shut-down cost.
The uncertainty of wind and solar power needs to be modeled to use for the current power generation system [
13,
14]. There are many models proposed to deal with the uncertainty of wind power generation so that the UC of all the generating units becomes possible. From the numerous uncertainty models proposed for UC over the last decade, stochastic programming [
15,
16] is being extensively explored to improve the scheduling of UC decisions under wind farm uncertainty [
17,
18]. The method proposed in [
19] uses an alternative scenario selection method to check consistency with the moments of a wind time series and to explicitly specify the modelers that are believed to significantly influence the performance of the unit commitment schedule. Nevertheless, stochastic programming performs a lot of computations pertaining to various scenarios to outline and formulate the expected results. This leads to undesirable computational time and space as well as requiring a bigger processing unit. To address a large number of scenarios for a given problem, some advanced scenario selection algorithms [
18] and decomposition techniques have been developed, i.e., at the first stage, mixed-integer programming provides the results and modeling approaches for deterministic UC, i.e., priority listing, Lagrangian relaxation, and dynamic programming; later on, stochastic programming changes the conventional way of solving such UC problems [
20,
21]. Then, combined stochastic UC and robust UC formulations are introduced for unit commitment decisions to overcome problem solving time required due to the larger set of scenarios in stochastic optimization and the conservativeness of the robust optimization; the weights of the events for the robust and stochastic parts in the objective function are adjusted by the system operator to obtain optimal and time-saving results [
22]. However, a feasible and effective realization requires an optimal compromise between the degree of accuracy and computational time.
Besides the aforementioned methods above, a comprehensive formulation of security-constrained unit commitment with compressed air energy storage and wind generation is developed in [
23]. Simultaneous optimization of energy and ancillary services with storage is proposed and justified with case studies and results. With the help of case studies, the impact of compressed air energy storage on both economical and technical aspects is reported. Pumped hydro energy storage is also an option for storing the energy in a dynamic economic dispatch problem where unit commitment is a major part of reducing the cost of power produced by thermal generators. This type of energy storage is being used in [
24], where deterministic unit commitment and interval unit commitment formulations are modeled that co-optimize the UC and pumped hydro energy storage decisions considering hydraulic limits constraining the pumped hydro energy storage. The study is performed on the system for day-ahead decisions and the results are reported. It employs the stochastic unit commitment model to solve the small-scale (available) wind power.
The optimal sizing of BESS in a system that includes renewable resources is discussed in many papers due to the uncertainties of the renewable resources that could be overcome with the integration of the BESS. Reference [
25] suggested a method to find the optimal size of BESS integrated with wind turbines and considered wind and load uncertainties. Two parts of the operational strategy are proposed in [
26] for distribution companies. Those two parts are day-ahead and real-time, where, in day-ahead, the load, wind, solar, and prices should be forecasted and in real-time, the gap between the forecasted and real value is considered. The objective here is to locate BESS in the network to minimize the cost and the loss by developing a highly nonlinear model for the network and BESS. Stochastic planning formulation for BESS in a micro-grid using Monte Carlo simulations (MCS) is proposed in [
27]. Although uncertainties in wind generation are considered, the network constraints are neglected. Reference [
28] used a similar Stochastic approach but with a Radial IEEE distribution system nonlinear model to simulate the line and voltage limits. A deterministic approach to optimize the battery sizing and location in the distribution network is proposed in [
29]. The effects of uncertainty in wind power resources using the point estimate method (PEM) are enlisted in [
30], where the naturally inspired PSO is combined with the tabu search (TS) to solve the problem. For the optimum size and location of the storage system, the stochastic mixed integer linear programming (MILP) technique is used in the distribution system to minimize the costs of investment and operation [
31]. In [
32], two levels of the profit-maximizing strategy were introduced, including planning and control. For optimal BESS planning and control in the primary control market, a framework has been developed to achieve the goal. This developed framework provides the balance between the capital cost and the operating cost considering the energy capacity factor. BESS degradation was considered here as a weighting factor that depends on the BESS lifetime.
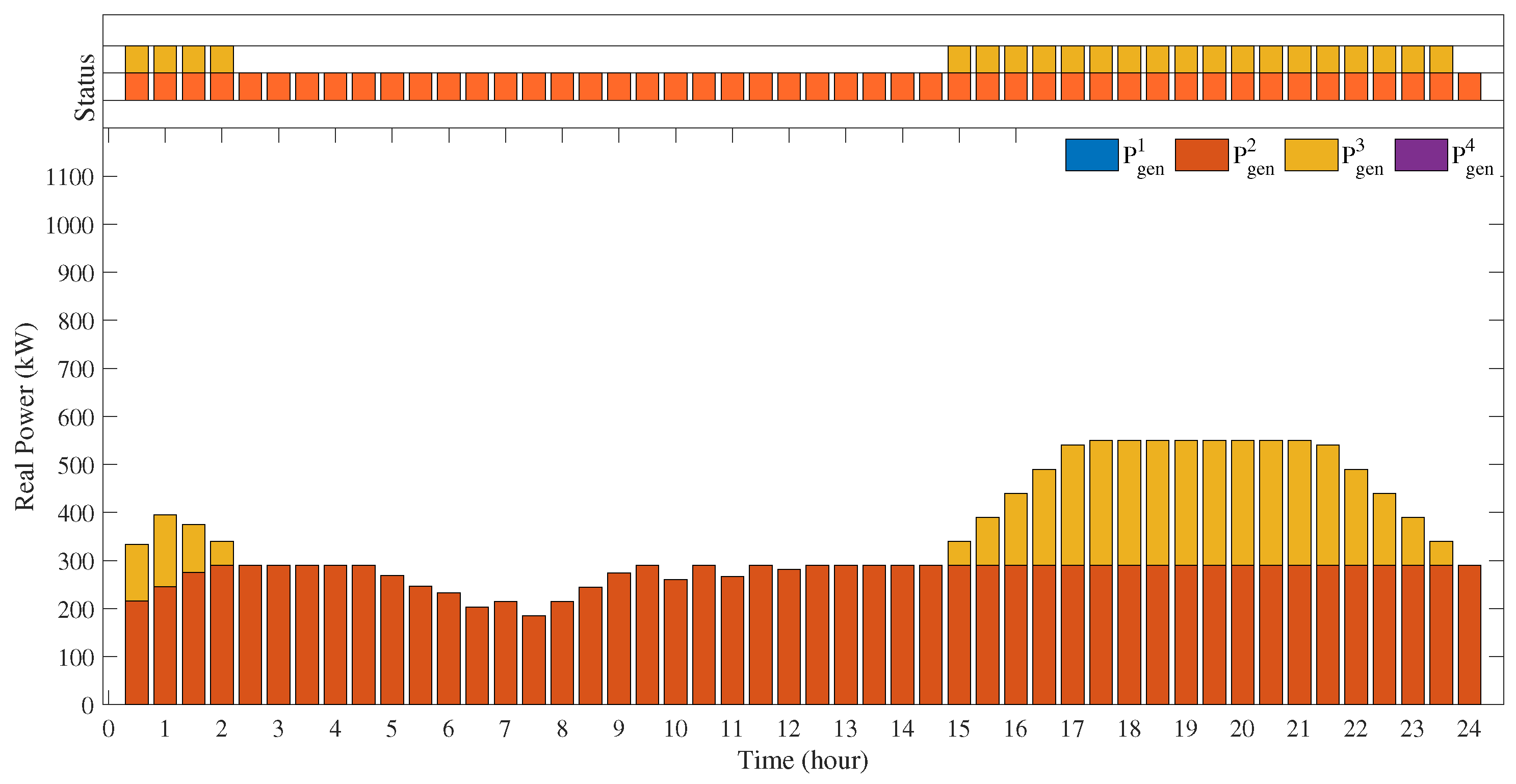
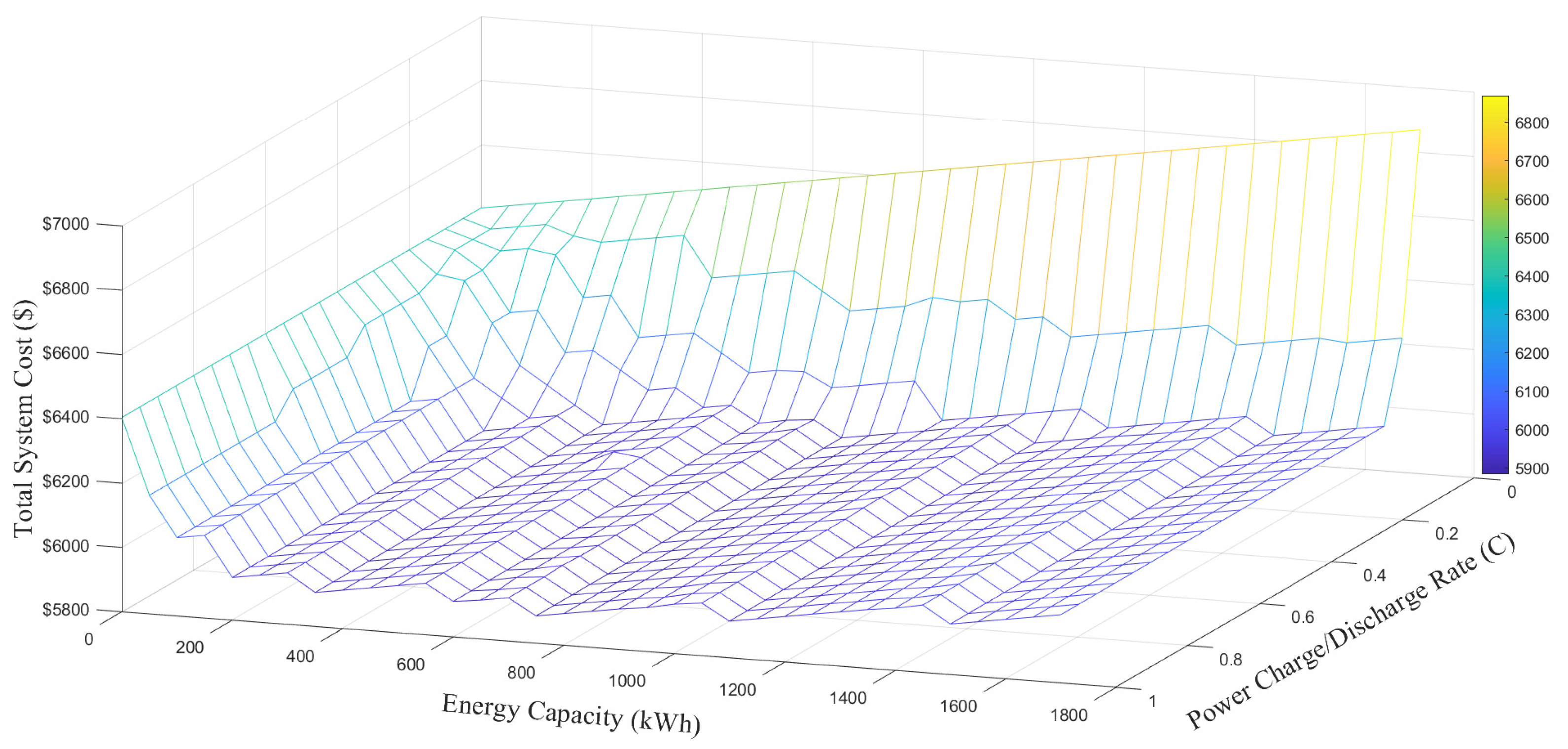
The charging and discharging rate (C), or the rate at which the power is provided by the battery at any instant, is directly related to battery size. For the better operation of energy storage, an optimum value of the charging and discharging rates of the battery play a major role [
33,
34]. By using a smaller battery size but larger power requirement, the battery will discharge more quickly than its rated power discharge, which will not only reduce the battery life but also damage the battery cell by increasing the temperature of the battery due to higher power losses inside the battery [
35,
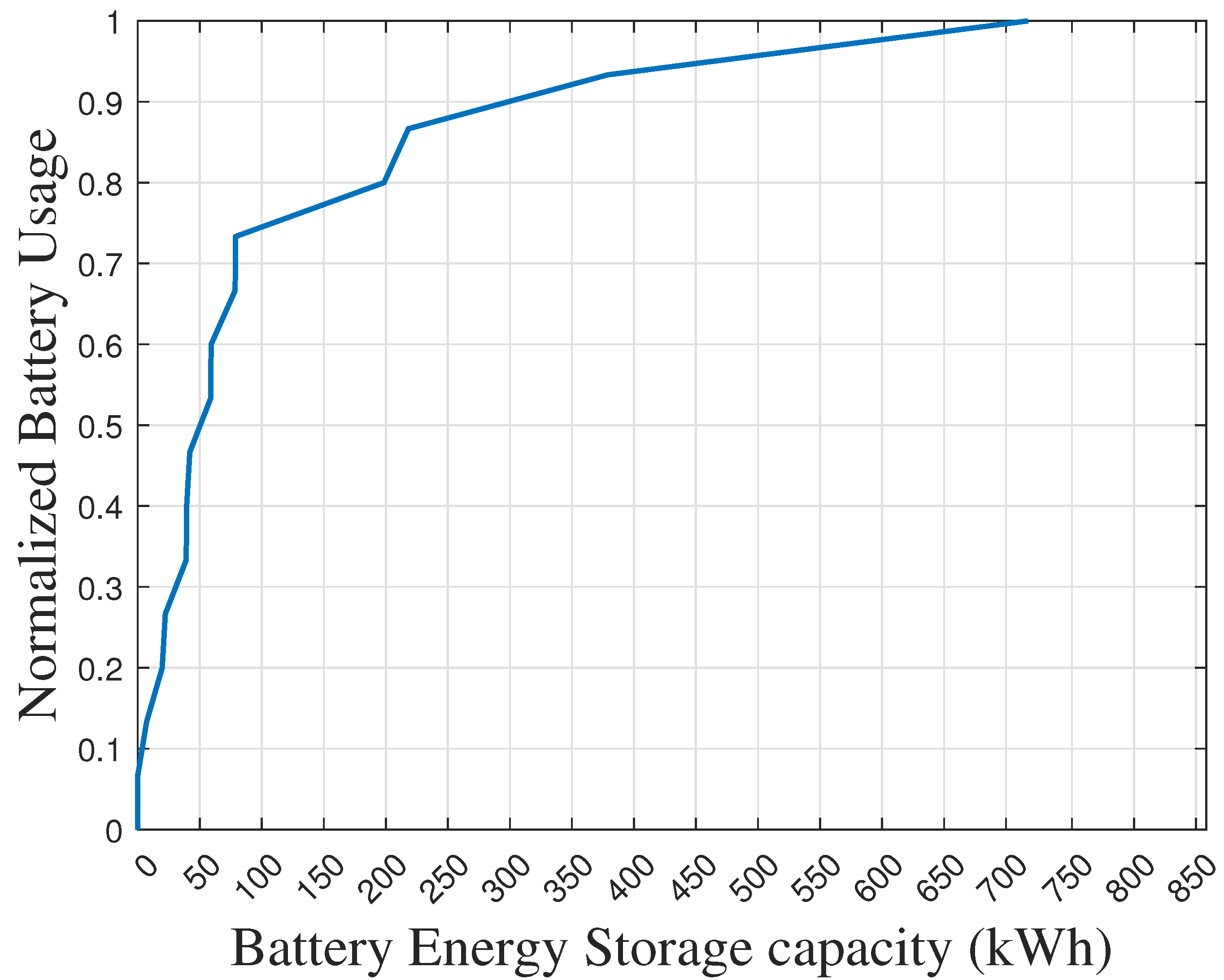
36]. With a small storage capacity and lesser charging and discharging rates, the battery will not be fully charged/discharged as compared to the bigger storage size for the same power requirement.
For a high penetration of renewable energy sources, more historical data will be required for distribution to be more contracted and to achieve true distribution (i.e., normal distribution) for any uncertain parameter, which makes the optimization model more complex in terms of solving techniques, i.e., the quantization of the normal distribution curve for each event generated by the CPLEX compiler [
8]. To deal with the distribution, ref. [
11] proposed a method to address economic dispatch and energy management, using distributionally robust optimization with chance constrained, which uses only mean and variance for the distribution set to forecast wind for the micro-grid, and performs the energy dispatch, but unit commitment constraints are not considered for units scheduling. In [
12], UC is performed with DRO using chance constrained for wind-farm uncertainty, but the impact of BESS on unit scheduling is not studied. According to the model solved through chance constrained, the total cost of the system increases with a higher confidence bound due to an uncertainty error. Due to rapid change in the total system cost using DRO and chance constrained, this model creates the research gap for improvements in terms of handling the distribution curve. In addition, the chance-constrained transformation increases the optimization complexity if the distribution is precisely modeled over a set of linear values for random numbers [
37]. In addition, with higher uncertainties, chance constraint becomes more computationally complex for random numbers [
38]. An ambiguity set method was developed in [
39] which was based on historical data. In fact, more historical data gives more ambiguous sets and, consequently, a less conservative solution. The case study conducted in this paper shows that the more information and maximum confidence bound in uncertainty an error is, the lower will be the system total cost. A model discussed in [
40] describes the estimated and real energy consumption by an energy storage system. The proposed model estimates the energy consumption by electric vehicles with traffic flow theory and mechanics of locomotion. The author focuses on the percentage usage of ESS in terms of estimated and actual usage of ESS by using floating cara data (FCD) with available data provided by information and communications technology (ICT) devices.
As discussed above, the impact of ESS on UC with uncertainties of RES is not discussed with the help of distributionally robust optimization. Some topics in the literature are near to the topic discussed in this research work. A robust optimization approach for designing an off-grid solar-powered charging station is proposed to provide electric vehicles (EVs) with electricity and hydrogen vehicles (HV) with hydrogen using deterministic mixed-integer linear programming (MILP) and robust optimization in [
41]. Therein, a robust optimization approach was employed to design the charging station based on the different levels of system robustness against the uncertainties. This stochastic approach provides worst-case solutions for the uncertainties, i.e., either the smallest or the largest outcome for the uncertainty to minimize or maximize the objective function. Due to worst-case outcomes, this model gives a robust solution. The sizing and siting of the RES for the local distribution system having solar PV uncertainty are designed using DRO and cone relaxation techniques. By using the cone relaxation technique, the DRO becomes mixed-integer second-order cone programming (MISOCP) [
42]. The second-order cone programming (SOCP) makes the system more complex, and the solution time also increases as compared to the linear decision rule where nonlinear functions (equations) are linearized by finding their respective linear coefficients for their cumulative linear function (equation).