Decision Models for a Dual-Recycling Channel Reverse Supply Chain with Consumer Strategic Behavior
Abstract
:1. Introduction
2. Literature Review
3. Analytical Models
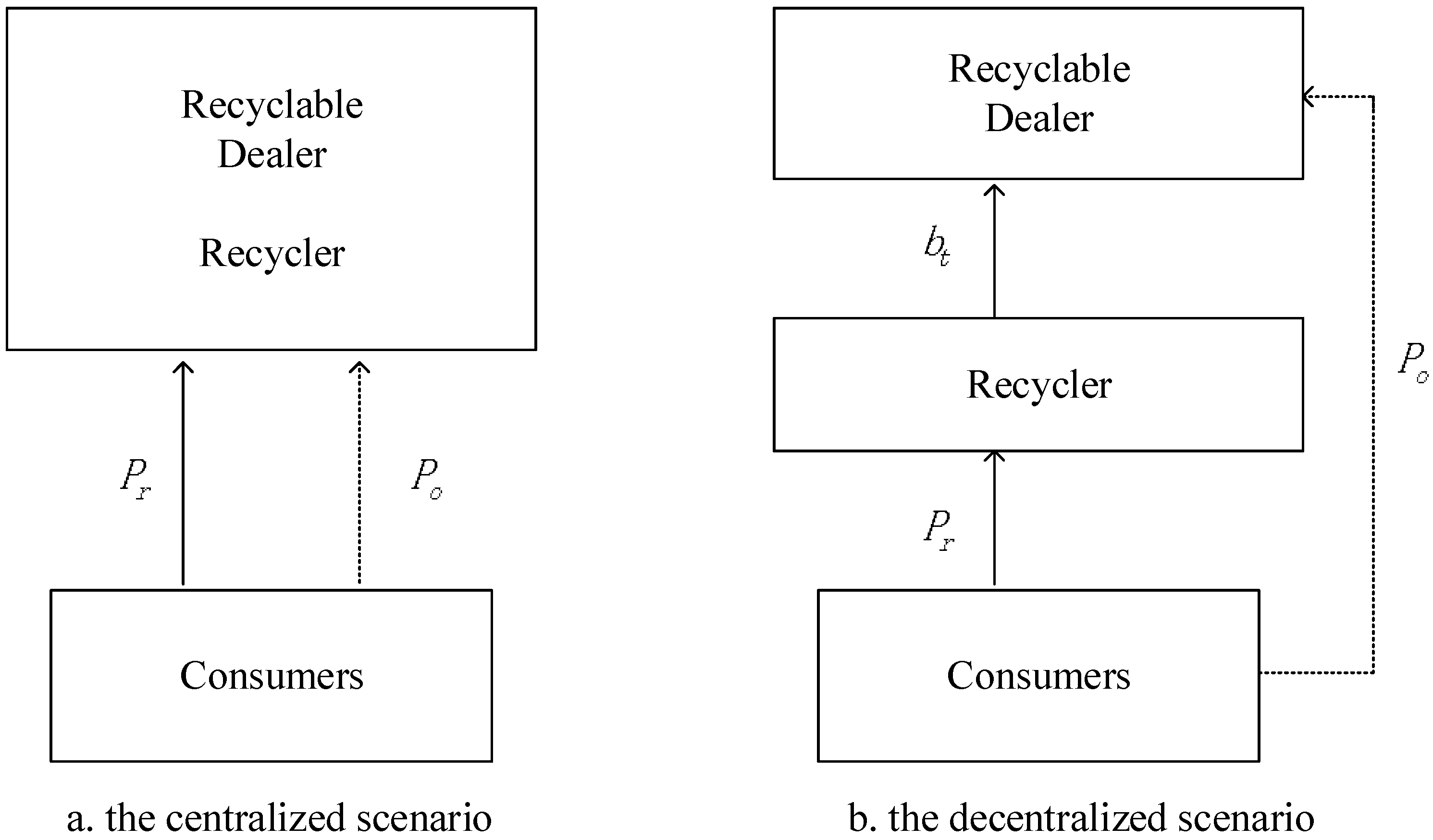
3.1. Problem Description
3.2. Basic Assumption
4. Optimization Problems
4.1. The Benchmark Case
4.2. The Model of Reverse Supply Chain with Dual-Channel in Decentralized Case (SG Model)
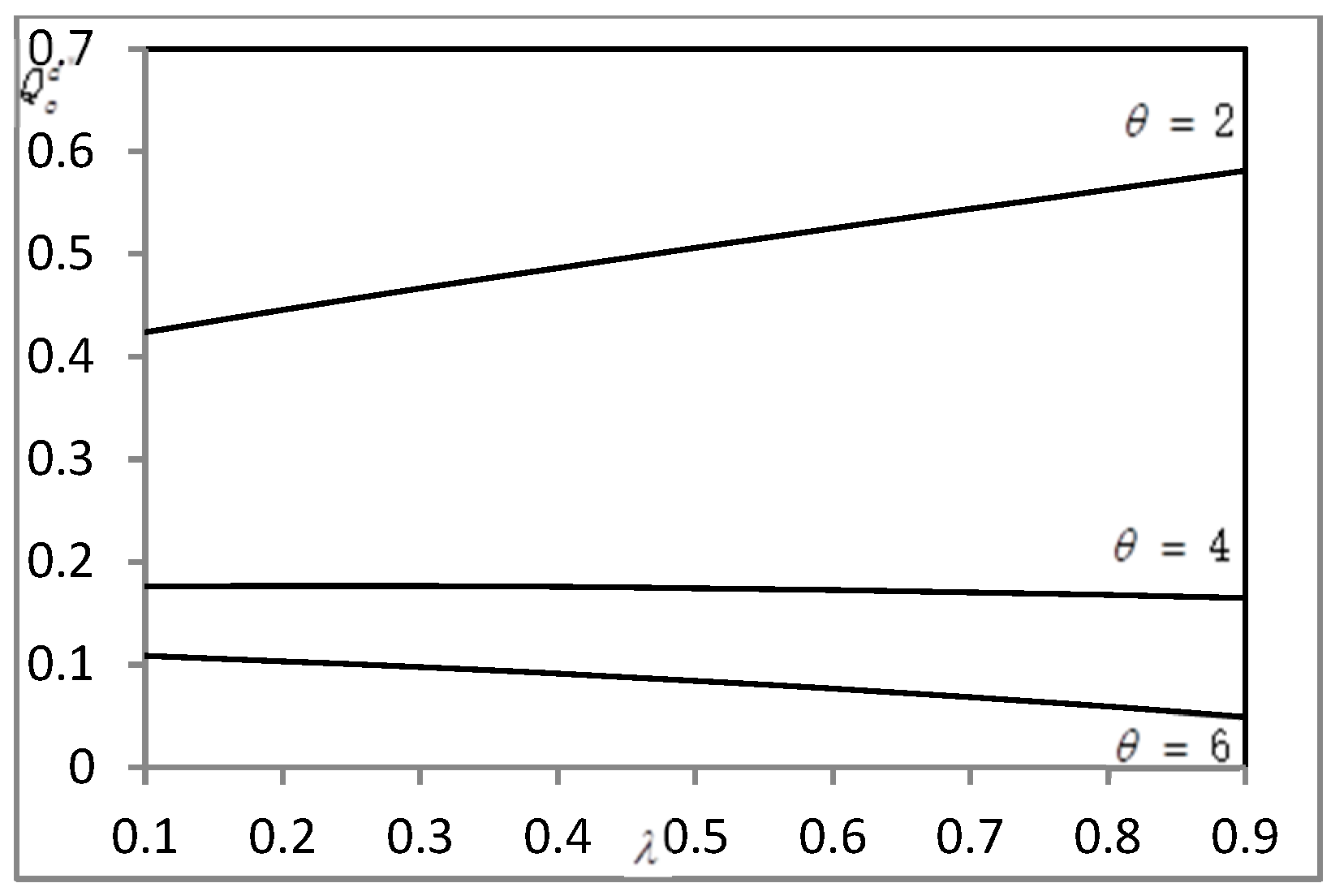
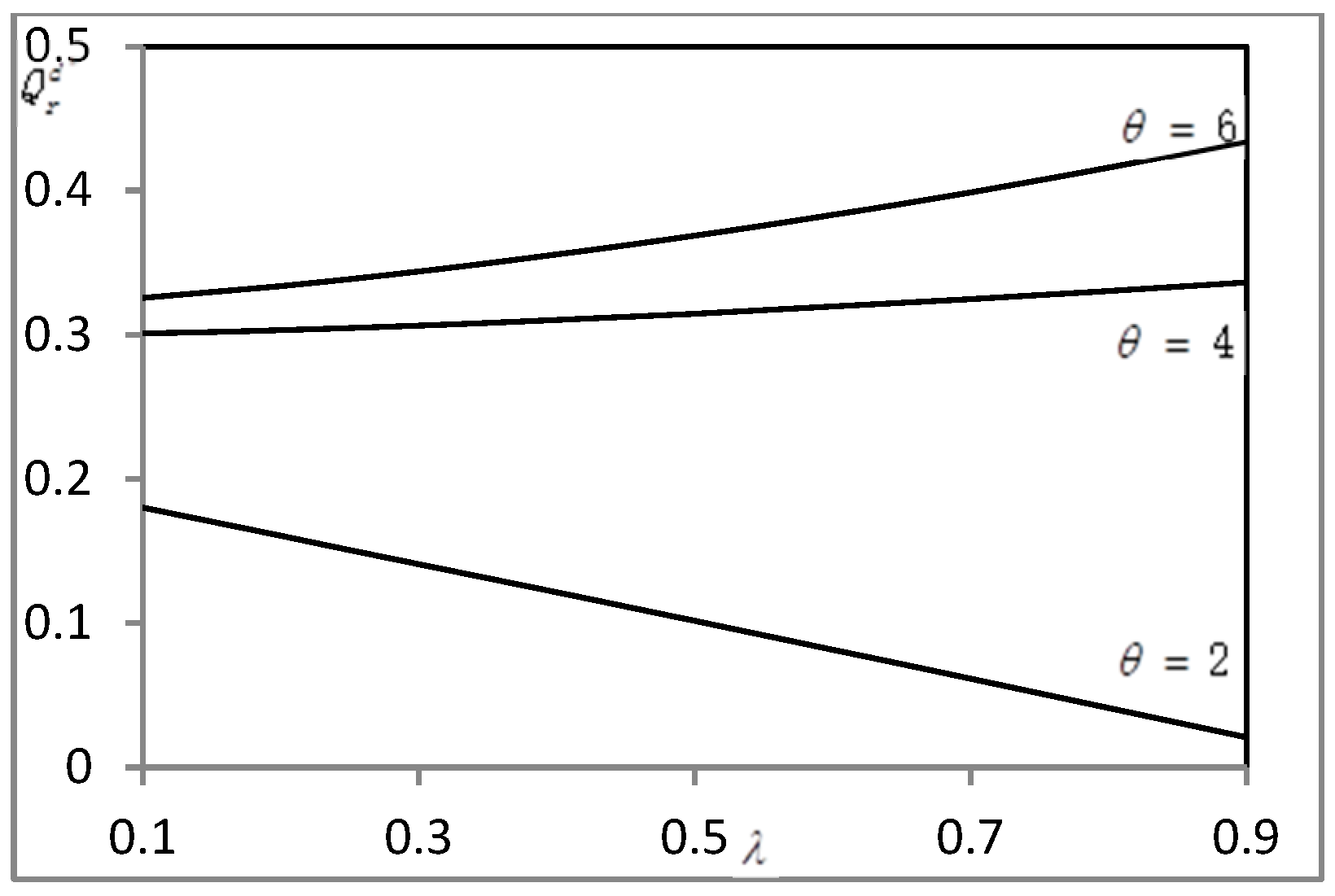
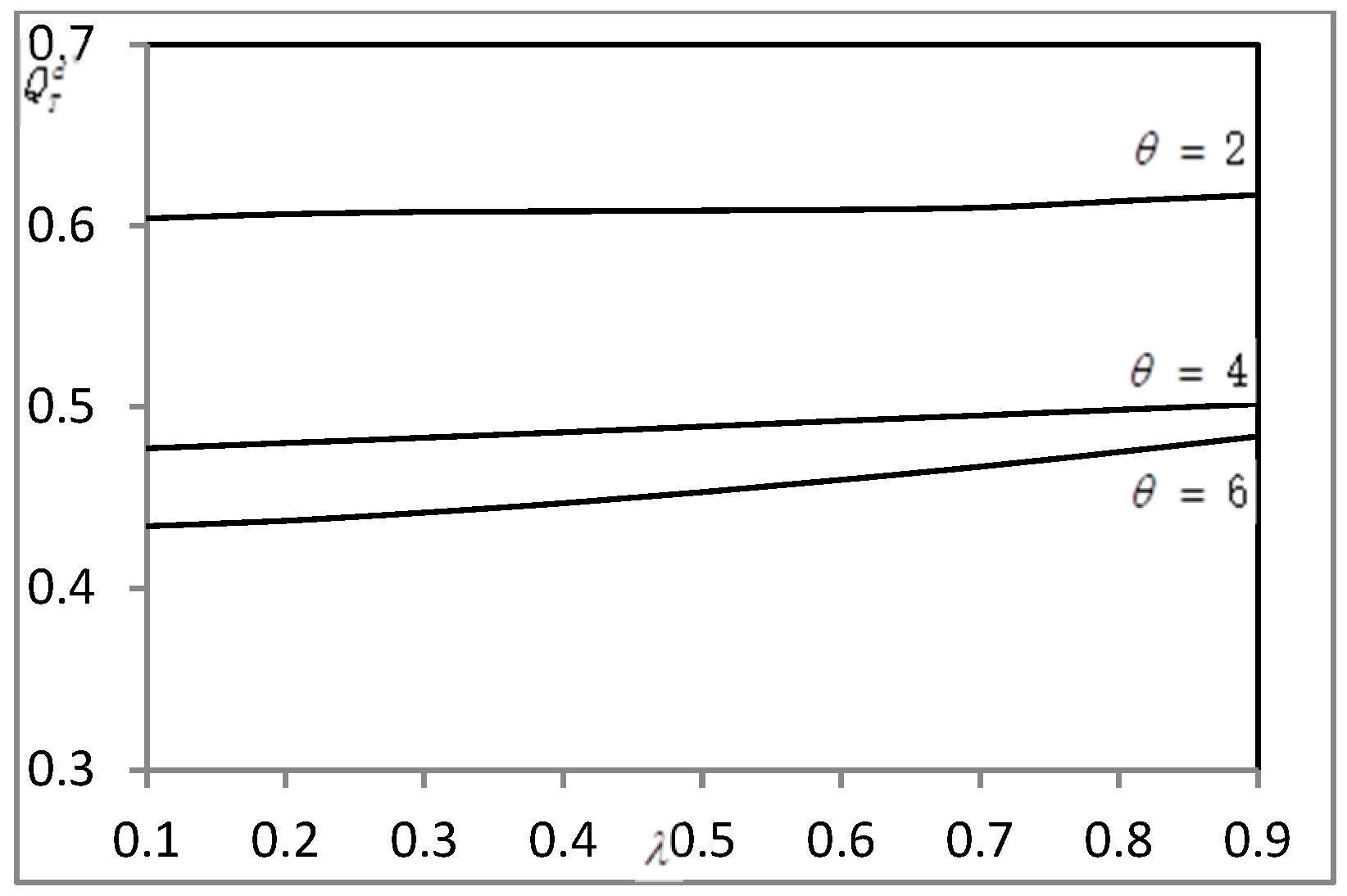
4.3. A Numerical Example
5. Coordination
5.1. Coordination via Revenue Cost-Sharing Contracts
5.2. Coordination via a Two-Part Tariff Contract
- (1)
- , ;
- (2)
- ;
- (3)
- , , .
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Appolloni, A.; D’Adamo, I.; Gastaldi, M.; Santibanez-Gonzalez, D.R.E.; Settembre-Blundo, D. Growing e-waste management risk awareness points towards new recycling scenarios: The view of the Big Four’s youngest consultants. Environ. Technol. Innov. 2021, 23, 101716. [Google Scholar] [CrossRef]
- Ali Qazi, A.; Appolloni, A. Systematic review on barriers and enablers toward circular procurement management. Sustain. Prod. Consum. 2022, 33, 343–359. [Google Scholar] [CrossRef]
- Mathiyazhagan, K.; Bharathi, U.; Appolloni, A. Pathways towards reverse logistics adoption in Indian educational institutes: A challenging factors analysis. Opsearch 2021, 58, 661–689. [Google Scholar] [CrossRef]
- Balasubramaruan, S. Mailversus Mall: A Strategic analysis of competition between direct marketers and conventional retailers. Mark. Sci. 1998, 17, 181–195. [Google Scholar] [CrossRef]
- Wang, B.; Ren, C.; Dong, X.; Zhang, B.; Wang, Z. Determinants shaping willingness towards on-line recycling behaviour: An empirical study of household e-waste recycling in China. Resour. Conserv. Recycl. 2019, 143, 218–225. [Google Scholar] [CrossRef]
- .Savaskan, R.C.; Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Atasu, A.; Toktay, L.B.; Van Wassenhove, L.N. How collection cost structure drives a manufacture’s reverse channel choice. Prod. Oper. Manag. 2013, 22, 1089–1102. [Google Scholar]
- Savaskan, R.C.; Bhattacharya, B.; Wassenhove, L.N. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, C.X.; Zhao, Y. Closed-loop supply chain Models for a High-tech product under alternative reverse channel and collection cost Structures. Int. J. Prod. Econ. 2014, 156, 108–123. [Google Scholar] [CrossRef]
- Jena, S.K.; Sarmah, S.P. Price competition and co-operation in a duopoly closed-loop supply chain. Int. J. Prod. Econ. 2014, 156, 346–360. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Deng, H.; Leong, G.K.; Huang, T. A dual channel, quality-based price competition model for the WEEE recycling market with government subsidy. Omega 2016, 59, 290–302. [Google Scholar] [CrossRef]
- Zu-Jun, M.; Zhang, N.; Dai, Y.; Hu, S. Managing channel profits of different cooperative models in closed-loop supply chains. Omega 2016, 59, 251–262. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhao, Q.; Zhou, Y. Manufacturer-remanufacturing vs supplier-remanufacturing in a closed-loop supply chain. Int. J. Prod. Econ. 2016, 176, 21–28. [Google Scholar] [CrossRef]
- Govindan, K.; Popiuc, M.N. Reverse supply chain coordination by revenue sharing contract: A case for the personal computers industry. Eur. J. Oper. Res. 2014, 233, 326–336. [Google Scholar] [CrossRef]
- Xiong, Y.; Yan, W. Implications of channel structure for marketing remanufactured products. Eur. J. Ind. Eng. 2016, 10, 126–144. [Google Scholar] [CrossRef]
- Souza, G.C. Closed-loop supply chains: A critical review, and future research. Decis. Sci. 2013, 44, 7–38. [Google Scholar] [CrossRef]
- Atasu, A.; Wassenhove, L.N.V. An operations perspective on product take-back legislation for e-waste: Theory, practice, and research needs. Prod. Oper. Manag. 2012, 21, 407–422. [Google Scholar] [CrossRef]
- Govindan, K.; Soleimani, H.; Kannan, D. Reverse logistics and closed-loop supply chain: A comprehensive review to explore the future. Eur. J. Oper. Res. 2015, 240, 603–626. [Google Scholar] [CrossRef]
- Cai, X.; Lai, M.; Li, X.; Li, Y.; Wu, X. Optimal acquisition and production policy in a hybrid manufacturing/remanufacturing system with core acquisition at different quality levels. Eur. J. Oper. Res. 2014, 233, 374–382. [Google Scholar] [CrossRef]
- Hong, I.H.; Lee, Y.T.; Chang, P.Y. Socially optimal and fund-balanced advanced recycling fees and subsidies in a competitive forward and reverse supply chain. Resour. Conserv. Recycl. 2014, 82, 75–85. [Google Scholar] [CrossRef]
- Choi, T.M.; Li, Y.J.; Xu, L. Channel leadership, performance and coordination in closed loop supply chains. Int. J. Prod. Econ. 2013, 146, 371–380. [Google Scholar] [CrossRef]
- Zuo, L.; Wang, C.; Sun, Q. Sustaining WEEE collection business in China: The case of online to offline (O2O) development strategies. Waste Manag. 2020, 101, 222–230. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Feng, L.; Luo, S. Strategic introduction of an online recycling channel in the reverse supply chain with a random demand. J. Clean. Prod. 2019, 236, 117683. [Google Scholar] [CrossRef]
- Wu, D.; Chen, J.; Li, P.; Zhang, R. Contract coordination of dual channel reverse supply chain considering service level. J. Clean. Prod. 2020, 260, 121071. [Google Scholar] [CrossRef]
- Wu, D.; Chen, J.; Yan, R.; Zhang, R. Pricing strategies in dual-channel reverse supply chains considering fairness concern. Int. J. Environ. Res. Public Health 2019, 16, 1657. [Google Scholar] [CrossRef]
- Chen, D.; Ignatius, J.; Sun, D.; Zhan, S.; Zhou, C.; Marra, M.; Demirbag, M. Reverse logistics pricing strategy for a green supply chain: A view of customers’ environmental awareness. Int. J. Prod. Econ. 2019, 217, 197–210. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Liu, Y.; Lu, R. Optimal environmental quality and price with consumer environmental awareness and retailer’s fairness concerns in supply chain. J. Clean. Prod. 2019, 213, 1063–1079. [Google Scholar] [CrossRef]
- Ren, M.; Liu, J.; Feng, S.; Yang, A. Pricing and return strategy of online retailers based on return insurance. J. Retail. Consum. Serv. 2021, 59, 102350. [Google Scholar] [CrossRef]
- Ismail, L.B.; Alawamleh, M.; Aladwan, K.; Alragheb, A.A. The relationship between green SCM practices and organisational performance: Evidence from Jordanian pharmaceutical manufacturers. Int. J. Logist. Syst. Manag. 2019, 34, 172–192. [Google Scholar] [CrossRef]
- Atasu, A.; Subramanian, R. Extended producer responsibility for e-waste: Individual or collective producer responsibility? Prod. Oper. Manag. 2012, 21, 1042–1059. [Google Scholar] [CrossRef]
- Hong, X.; Wang, Z.; Wang, D.; Zhang, H. Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection. Int. J. Adv. Manuf. Technol. 2013, 68, 1851–1865. [Google Scholar] [CrossRef]
- Örsdemir, A.; Kemahlıoğlu-Ziya, E.; Parlaktürk, A.K. Competitive quality choice and remanufacturing. Prod. Oper. Manag. 2014, 23, 48–64. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, P.R. Trade-in remanufacturing, strategic customer behavior, and government subsidies. Customer Behavior 2015, and Government Subsidies. 14 September 2015. Available online: https://web.archive.org/web/20160626201810id_/http://apps.olin.wustl.edu:80/faculty/zhang/Zhang-Journal/Remanufacturing.pdf (accessed on 16 July 2022).
- Ferguson, M.; Guide VD, R.; Souza, G.C. Supply chain coordination for false failure returns. Manuf. Serv. Oper. Manag. 2006, 8, 376–393. [Google Scholar] [CrossRef]
- Zeng, A.Z. Coordination mechanisms for a three-stage reverse supply chain to increase profitable returns. Nav. Res. Logist. 2013, 60, 31–45. [Google Scholar] [CrossRef]
- Xu, G.Y.; Dan, B.; Zhang, X.M.; Liu, C. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract. Int. J. Prod. Econ. 2014, 147, 171–179. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Sun, Y. Implementing coordination contracts in a manufacturer Stackelberg dual-channel supply chain. Omega 2012, 40, 571–580. [Google Scholar] [CrossRef]
- Cao, E.B.; Ma, Y.J.; Wan, C.; Lai, M.Y. Contracting with asymmetric cost information in a dual-channel supply chain. Oper. Res. Lett. 2013, 41, 410–414. [Google Scholar] [CrossRef]
- Cai, G.G. Channel selection and coordination in dual-channel supply chain. J. Retail. 2010, 86, 22–36. [Google Scholar] [CrossRef]
- Tridib, M.; Raj, S.R.; Indrajit, S. Reference price research: Review and propositions. J. Mark. 2005, 69, 84–102. [Google Scholar]
- Winer, R.S. A reference price model of demand for frequently purchased products. J. Consum. Res. 1986, 13, 250–256. [Google Scholar] [CrossRef]
- Zhang, J.U.; Gou, Q.L.; Zhang, J.; Liang, L. Supply chain pricing decisions with price reduction during the selling season. Int. J. Prod. Res. 2014, 52, 165–187. [Google Scholar] [CrossRef]
- Rajendran, K.N.; Tellis, G.J. Contextual and temporal components of reference price. J. Marking 1994, 58, 22–34. [Google Scholar] [CrossRef]
- Chandrashekaran, R.; Grewal, D. Assimilation of advertised reference prices: The moderating of involvemen. J. Retail. 2003, 79, 53–62. [Google Scholar] [CrossRef]
- Martin-Herran, G.; Taboubi, S. Price coordination in distribution channels: A dynamic perspective. Eur. J. Oper. Res. 2015, 240, 401–414. [Google Scholar] [CrossRef]
- Zhang, J.; Kevin, W.Y.; Liang, L. Strategic pricing with reference effects in a competitive supply chain. Omega 2014, 44, 126–135. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, Q.L.; Liang, L.; Huang, Z. Supply chain coordination through cooperative advertising with reference price effect. Omega 2013, 41, 345–353. [Google Scholar] [CrossRef]
- Geng, Q.; Wu, C.Q.; Li, K.P. Pricing and promotion frequency in the presence of reference price effects in supply chains. Calif. J. Oper. Manag. 2010, 8, 74–82. [Google Scholar]
- Qian, L.; Song, Z. Price and quality competition in a duopoly with reference-dependent preferences. In Proceedings of the 7th International Conference on Service Systems and Service Management(ICSSM), IEEE, Tokyo, Japan, 28–30 June 2010; pp. 1–4. [Google Scholar]
- Feng, L.; Govindan, K.; Li, C. Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. Eur. J. Oper. Res. 2017, 260, 601–612. [Google Scholar] [CrossRef]
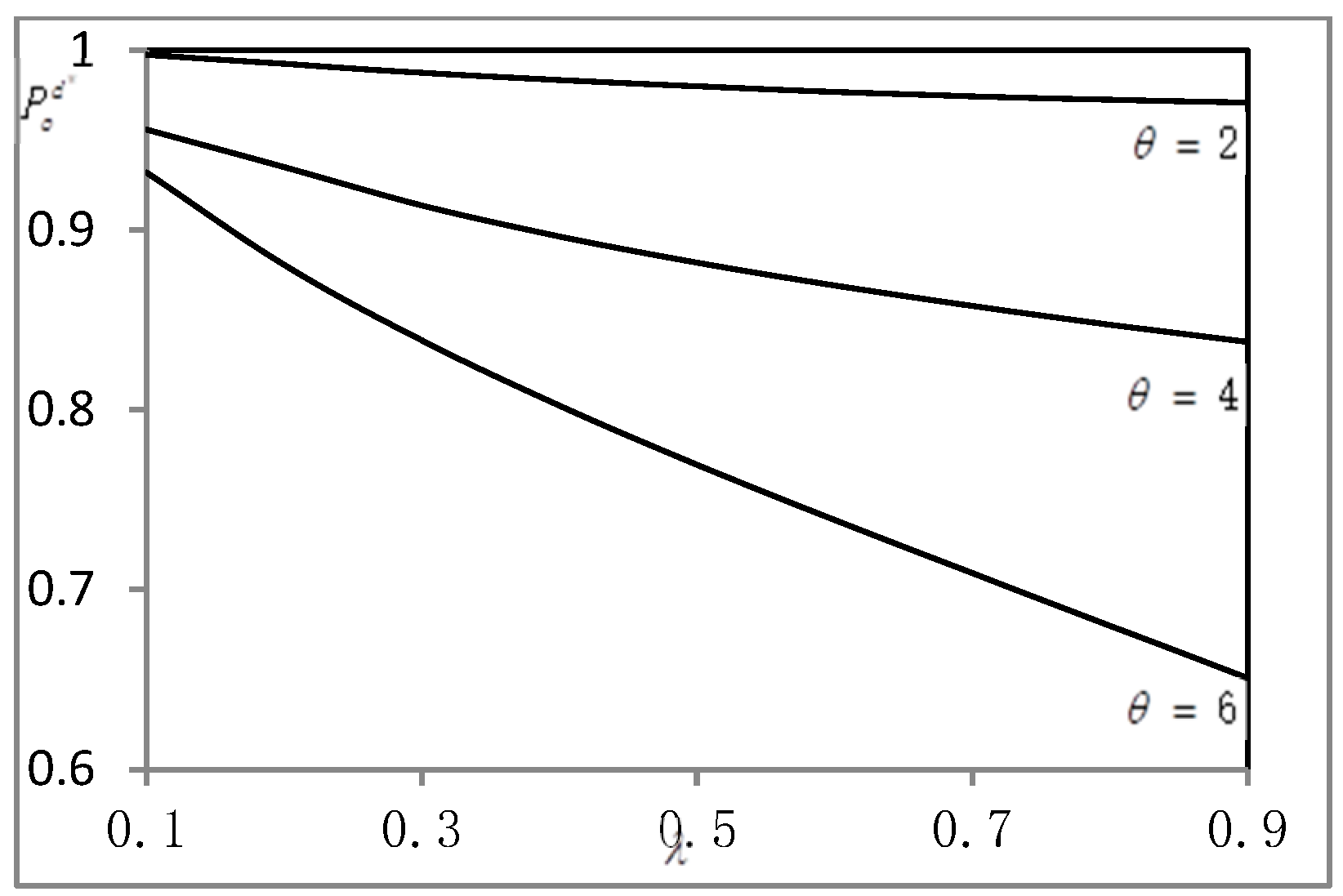
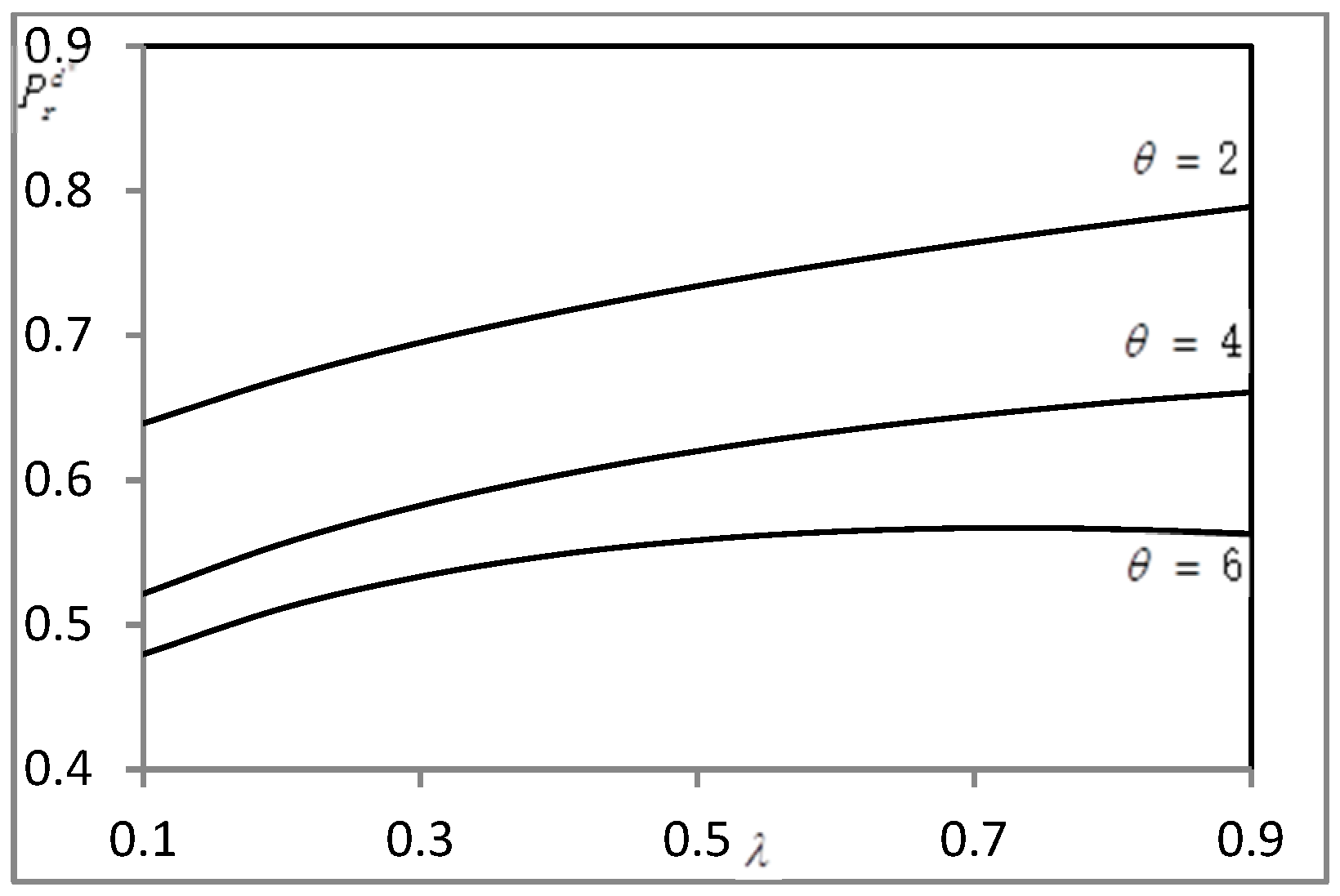
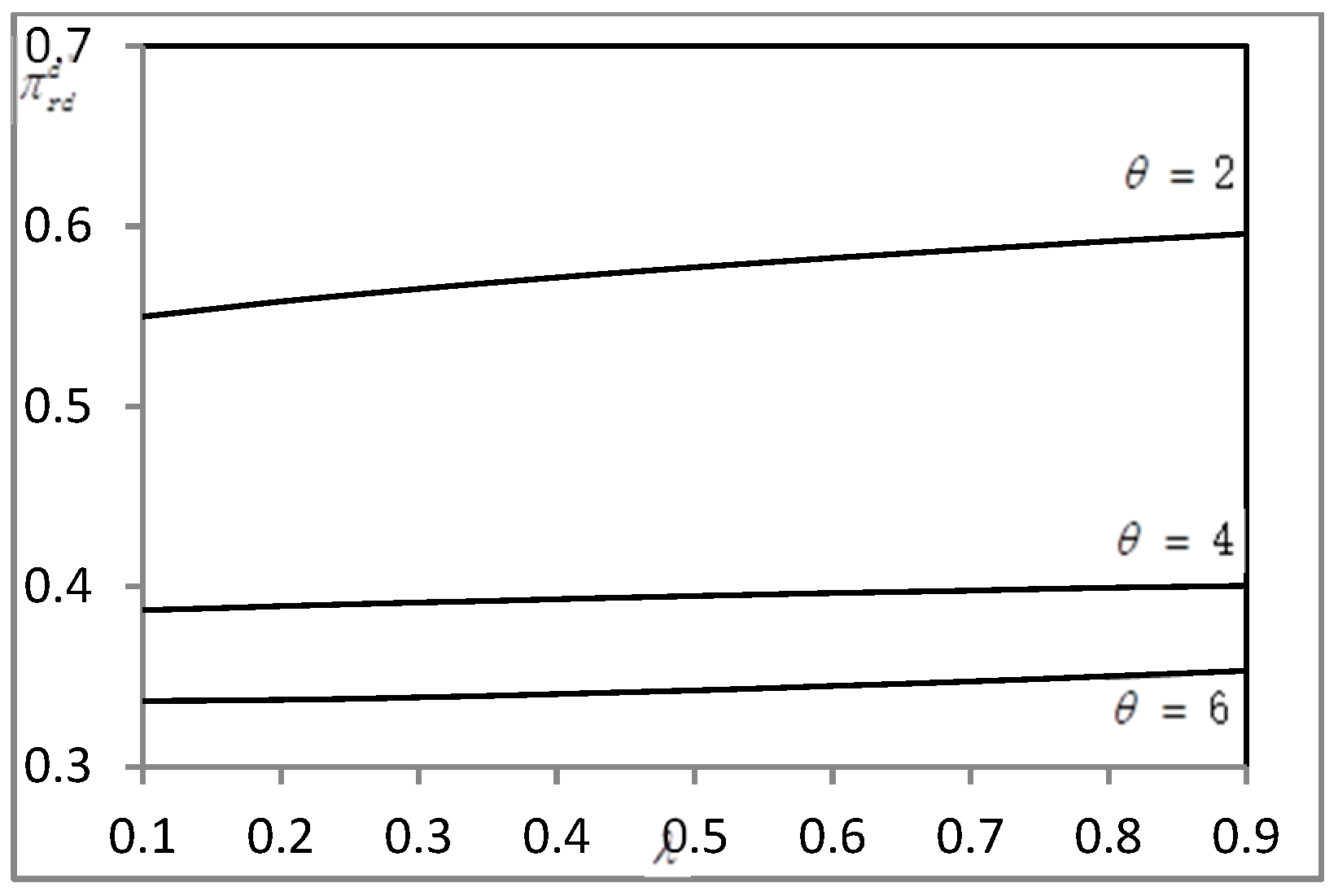
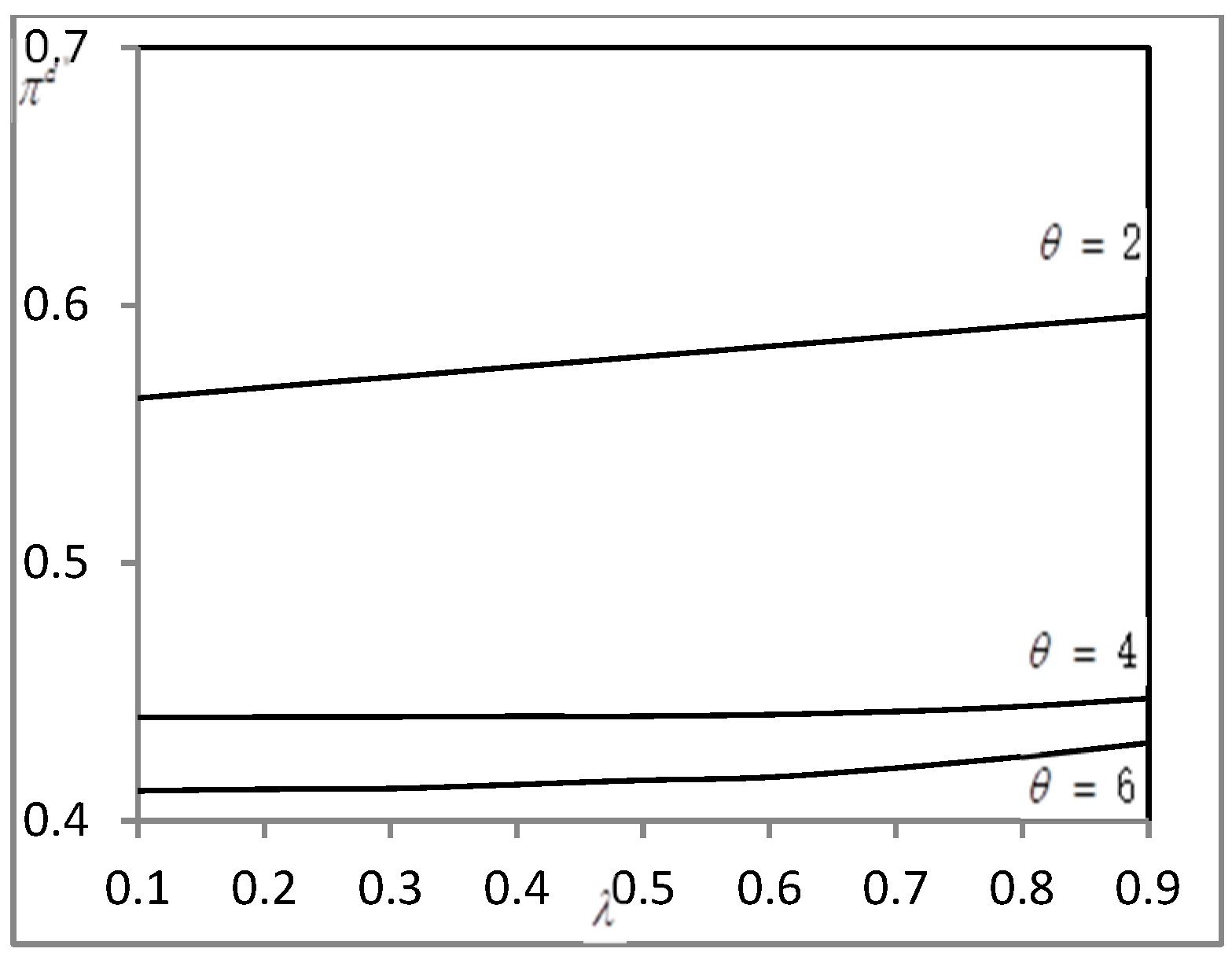
| Model Parameters | Definition |
|---|---|
| Recycling price of the offline channel | |
| Recycling price of the online channel | |
| The consumer popularity of online recycling methods | |
| The expected revenue from the disposal of one unit of scrap product | |
| The willingness of the consumer to return one unit of scrap | |
| Reference-price effect degree | |
| The cost of recycling one unit of scrap product by a recycler | |
| The disposal cost of one unit of scrap product by the RD | |
| The internal transfer price paid by the RD to the recycler | |
| The function of the amount of recycling scrap product in offline and online recycling channel, where takes and | |
| The profit function of recycling scrap products in offline recycling and online recycling channels in case ; subscript takes and |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wang, N. Decision Models for a Dual-Recycling Channel Reverse Supply Chain with Consumer Strategic Behavior. Sustainability 2022, 14, 10870. https://doi.org/10.3390/su141710870
Wang B, Wang N. Decision Models for a Dual-Recycling Channel Reverse Supply Chain with Consumer Strategic Behavior. Sustainability. 2022; 14(17):10870. https://doi.org/10.3390/su141710870
Chicago/Turabian StyleWang, Bo, and Ning Wang. 2022. "Decision Models for a Dual-Recycling Channel Reverse Supply Chain with Consumer Strategic Behavior" Sustainability 14, no. 17: 10870. https://doi.org/10.3390/su141710870
APA StyleWang, B., & Wang, N. (2022). Decision Models for a Dual-Recycling Channel Reverse Supply Chain with Consumer Strategic Behavior. Sustainability, 14(17), 10870. https://doi.org/10.3390/su141710870





