Abstract
In this paper, we propose a novel simultaneous localization and mapping algorithm, R-LIO, which combines rotating multi-line lidar and inertial measurement unit. R-LIO can achieve real-time and high-precision pose estimation and map-building. R-LIO is mainly composed of four sequential modules, namely nonlinear motion distortion compensation module, frame-to-frame point cloud matching module based on normal distribution transformation by self-adaptive grid, frame-to-submap point cloud matching module based on line and surface feature, and loop closure detection module based on submap-to-submap point cloud matching. R-LIO is tested on public datasets and private datasets, and it is compared quantitatively and qualitatively to the four well-known methods. The test results show that R-LIO has a comparable localization accuracy to well-known algorithms as LIO-SAM, FAST-LIO2, and Faster-LIO in non-rotating lidar data. The standard algorithms cannot function normally with rotating lidar data. Compared with non-rotating lidar data, R-LIO can improve localization and mapping accuracy in rotating lidar data.
1. Introduction
Accurate state estimation and building map of the surrounding environment are essential for intelligent mobile robots in environments without GNSS (Global Navigation Satellite System) localization signal. SLAM (Simultaneous Localization and Mapping), as a sensing technology in mobile robots, can help with localization, pose information, and motion control. The created map can help mobile robots plan routes and avoid obstacles by providing environment information.
According to the classification of sensors, SLAM can be separated into two categories: vision-based and lidar-based. Compared with the vision-based SLAM [1,2], the lidar-based SLAM is not affected by illumination change or camera motion blur and can directly collect the accurate information in 3D space. At the same time, lidar hardware is getting lighter and cheaper, for example, the DJI livox [3] and Velodyne puck lite [4]. Therefore, the lidar-based SLAM has been studied widely.
Many SLAM methods based on 3D lidar have been proposed in the last 20 years, including pure lidar SLAM scheme [5], lidar-inertial sensor fusion SLAM scheme [6,7,8,9,10,11,12,13,14], and lidar-vision-inertial sensor fusion SLAM scheme [15,16,17,18,19,20,21,22].
As the most popular lidar SLAM framework, LOAM [6], proposed in 2014, has been extensively studied. The LOAM scheme uses a horizontal lidar and inertial sensor to achieve effective localization and mapping performance. Subsequently, many scholars have proposed improvement schemes based on the LOAM framework, such as Lego LOAM [7] and LIO-SAM [8] methods. Although the LOAM scheme is very successful, there are still some limitations.
First, the localization and mapping accuracy in the actual test process is not high due to the lack of loop closure detection module. Second, the algorithm is based on the uniform motion model. The localization and mapping will fail under the carrier’s vigorous motion and the robustness is insufficient.
In order to solve the above problems, we propose a simultaneous localization and mapping framework which is coupled by rotating lidar and inertial measurement unit.
Firstly, the lidar on the mechanical device is rotated to capture more environment feature points which will be used to participate in the matching process.
Secondly, a nonlinear motion distortion compensation method based on rotating lidar is proposed by fusing low-frequency lidar and high-frequency inertial data.
Thirdly, the laser point cloud matching effect evaluation module and the loop closure detection module for sub-map to sub-map matching based on the key-frame strategy are added, and the loop closure detection module includes the double judgment candidate loop-frame strategy.
2. Related Work
The existing 3D lidar SLAM is usually improved based on the LOAM framework [6], which consists of three main modules: feature extraction, laser odometry, and laser mapping. To save the computational effort, feature points are extracted based on local smoothness, such as edge feature points and plane feature points. Then, the laser odometry module matches the feature points of two consecutive laser frames to obtain a rough but real-time laser odometry (10 Hz). Multiple laser frames are combined into one set using laser odometry, and then they are registered and merged into the global map. The laser mapping process is usually time-consuming and performed at a relatively low frequency (1–2 Hz). Inertial data have two functions, one is to provide initial registration parameters for point cloud matching, and the other is to compensate the motion distortion of each frame of laser point cloud data. Many other lidar-based SLAM methods maintain a framework similar to LOAM. For example, ALOAM [5] only retains lidar sensors, and uses Ceres-Solver library and Eigen library to reconstruct and optimize LOAM code. Lego-LOAM [7] improves LOAM in light weight, extracts ground feature points to participate in point cloud matching, performs L-M optimization based on line and surface feature points in two steps, and introduces a loop closure detection module based on European distance to reduce accumulated drift. LIO-SAM [8] uses 9-axis inertial data to participate in system initialization and front-end laser odometry, and the back-end integrates GPS factor and loop closure factor to improve the accuracy of localization and mapping. F-LOAM [9] uses a two-step procedure to correct the motion distortion of the original point cloud. In the process of nonlinear optimization, the idea of parallel processing of laser odometry and laser mapping in LOAM is dropped in favor of a weighted feature point constraint.
LOAM livox [10] applies LOAM framework to the emerging solid-state lidar. The lidar frame is directly matched with the global map because of the small field angle and non-repetitive scanning characteristics, which reduces the feature points overlap rate of two consecutive frames of data. The accuracy of the odometry is increased by this direct lidar frame to map matching, but at the expense of more computation being required to build a kd-tree in the updated map at each step.
Due to the time-consuming construction of kd-tree for point cloud data, especially in the point cloud data of a large-scale scene, some research has been put forward in recent years to improve the operation efficiency of the algorithm. For example, FAST-LIO [11] and FAST-LIO2 [12] use incremental kd-tree (ikd-tree) in the front end and iterative error state Kalman Filter in the back end, which has the characteristics of a short process and fast calculation. Faster-LIO [13] improved based on FAST-LIO2, replaced ikd tree with incremental voxels (ivox), achieved similar localization and mapping accuracy, and realized faster lidar-inertial odometry.
Because the geometric features are not obvious in some scenes, such as underground mines, tunnels, highways, and other environments, algorithms similar to the LOAM framework may produce low mapping accuracy or even mapping failure. Some scholars use all laser points to participate in the point cloud matching processes, such as FAST-LIO2 and Faster-LIO algorithms. Zhao et al. [14] integrate the 3D NDT [23,24] point cloud matching algorithm into the laser odometry and laser mapping module. It realizes the localization and mapping in the highway environment. LION [19] implemented the generalized iterative closest point cloud matching algorithm [20] for all laser points and realized high-precision laser odometry in the underground mine environment.
Multi-sensor data fusion frameworks are usually divided into two categories: loose coupling framework and tight coupling framework. For example, inertial data in LOAM and Lego-LOAM algorithms do not participate in the laser mapping process and do not feedback useful information to their respective sensors, so they are regarded as loose coupling framework. In recent years, many scholars believed that the tight coupling framework can provide more accurate pose estimation. LINS [21] introduced a tightly coupled iterated Kalman filter and robocentric formula into the LiDAR pose optimization in the odometry. Using the ideas of LOAM and Vins-mono for reference, LIOM [22] jointly optimized the measurement of lidar and inertial data.
The lidar used in the above 3D lidar SLAM method is all placed horizontally. Due to the small field angle of the lidar, it is unable to capture all the laser point cloud data in the environment, resulting in incompetence for applications that want to obtain dense laser point cloud data with full coverage, such as exploration of a tunnel in an underground mine. Therefore, this paper rotates the lidar in the mechanical device to make more laser points participate in the state estimation process, and a localization and mapping framework of rotating lidar-inertial sensors is proposed.
3. Rotating Lidar Inertial Odometry and Mapping
3.1. A System Overview
We propose a novel simultaneous localization and mapping algorithm, R-LIO, which is coupled with a rotating multi-line lidar and inertial measurement unit. R-LIO can achieve real-time and high-precision pose estimation and map-building. In R-LIO, there are four sequential modules: the nonlinear motion distortion compensation module, the frame-to-frame point cloud matching module based on normal distribution transformation by a self-adaptive grid, the frame-to-submap point cloud matching module based on line and surface feature, and the loop closure detection module based on submap-to-submap point cloud matching. Figure 1 displays the R-LIO system framework.
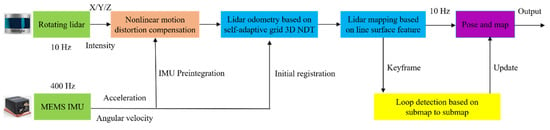
Figure 1.
System overview of R-LIO.
3.2. B Motion Distortion Compensation
The laser point cloud data collected by multi-line lidar will be severely distorted due to carrier movement and motor rotation. The direct use of distorted laser point cloud data will lead to the reduction of state estimation accuracy or even fail. The essence of erasing the motion distortion of laser point cloud is to restore each point state before distortion in a laser frame. In this paper, the time before distortion is defined as the starting time of a frame of laser point cloud. The following are the steps in compensating for motion distortion.
Step 1: The system timestamp is applied to the data collected by the multi-line lidar and the inertial measurement unit in accordance with the acquisition time, ensuring that each laser frame point cloud data point and inertial data point is consistent with the system time stamp. The time stamp of the lidar is obtained according to the period of the point cloud and the horizontal resolution of the current laser beam.
where represents timestamp of current laser point, represents start scanning time of laser scan, represents the scanning period of laser scan, represents rotation angle is relative to the start point at current scanning time of laser scan, represents rotation angle is relative to the start point at end scanning time of laser scan.
Step 2: According to the angular velocity information in the inertial data, calculate the inertial attitude variation between timestamps n and n + 1, as shown in Equation (2), distribution of laser frame timestamp and inertial data timestamp as illustrated in Figure 2, and then obtain the attitude of each frame of inertial data relative to the world coordinate system, as shown in Equation (3). The world coordinate system is defined as the inertial coordinate system at the starting time.
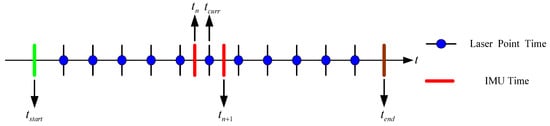
Figure 2.
Distribution of laser frame timestamp and inertial data timestamp.
Step 3: Find the inertial data of two consecutive frames closest to the timestamp of the current laser point, and .
Step 4: According to the timestamp of the current laser point, use the time scale factor and to linearly interpolate the attitude information (illustrated in Figure 3) in the two frames of inertial data based on the high-frequency inertial data. This is equivalent to obtaining the attitude of the inertial data at the current time in the world coordinate system.
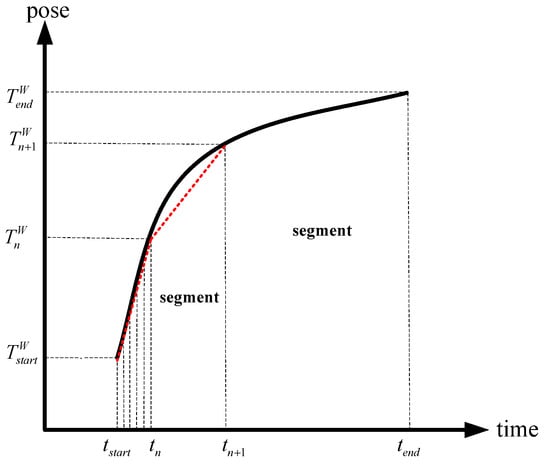
Figure 3.
Schematic diagram of attitude linear interpolation method.
Step 5: Combination with the attitude of the inertial data in the world coordinate system at the start time of the laser frame, calculate the attitude variation of inertial data at the current time relative to the start time of the laser frame, , which is the attitude of the inertial data corresponding to the start time of the laser frame in the world coordinate system.
Step 6: According to the external parameter relationship between the lidar and the inertial sensor , convert the attitude variation to the lidar coordinate system, and calculate the attitude variation of the lidar at the current time relative to the starting time of the laser frame.
Step 7: Multiply the original coordinates of all laser points in the current frame by the above rotation change to complete the motion distortion removal of a frame of the laser point cloud.
3.3. C Self-Adaptive Gird Divide
The distribution of laser frame point cloud data shows that the near point cloud is dense and the far point cloud data are sparse. The uniform grid will cause to the problem that the point cloud data of the internal grid cannot reflect the real distribution. To effectively solve this problem, self-adaptive grid division of laser frame point cloud data is carried out in this paper. The specific steps are as follows:
(1) Get main direction: The corresponding axes of laser frames collected by multi-line lidar are X axis, Y axis, and Z axis. However, the laser frame data do not show a gradual distribution along the axis from dense to sparse. Therefore, Principal Component Analysis (illustrated in Figure 4) is used to identify a set of orthogonal bases to project the laser frame point cloud data onto the plane defined by the orthogonal basis. The largest variance between the data result from the largest distance between the data. If the variance of data after projection on each orthogonal basis is the largest, the orthogonal basis with the largest projection distance and the largest eigenvalue of laser frame point cloud data is the main direction of laser frame.
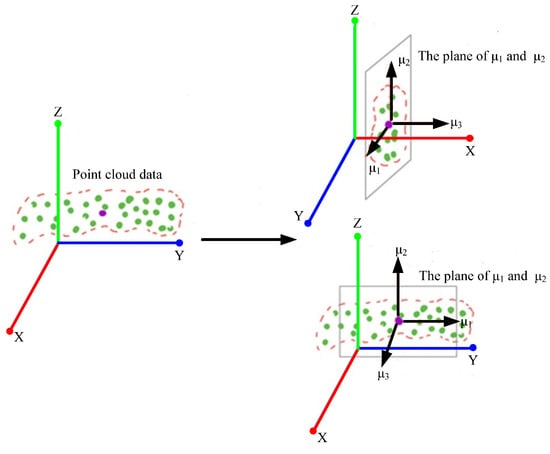
Figure 4.
Principal Component Analysis diagram.
(2) Compute grid size: After determining the main direction of the laser frame point cloud data, the laser frame point cloud data can be divided into grids. According to the characteristics of the laser frame point cloud data, small cubic grids are used to divide the area close to the multi-line lidar, and large grids are used to divide the area far from the multi-line lidar (illustrated in Figure 5). Firstly, the minimum grid side length is determined as , and the intersection point of a line segment in the opposite direction of Z axis is drawn with the origin of coordinates as the starting point. Then, a line segment is drawn with the direction of X axis as the starting point , and the intersection point is . One point is taken on the line segment to make its length equal to , and the Angle is . Then, the edge length of all grids along the main direction of the laser frame point cloud data are determined. The origin of coordinates is set as the center point, and the rays R rotate along the segment around the origin of coordinates. Each increasing angle is , and the intersection points of rays and line segments are respectively ,…. Finally, all the edge lengths of the self-adaptive grid are determined by segment , … . Similar to this procedure, the bounding box is divided along the Y axis and Z axis with the origin as the starting point and the length as the side.
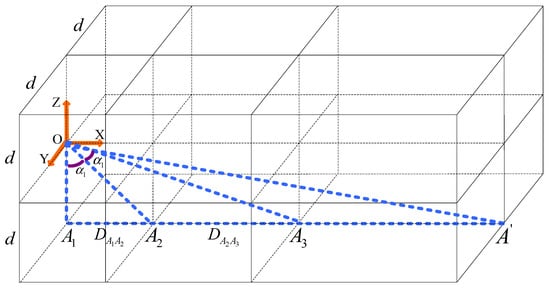
Figure 5.
Self-adaptive gird division diagram.
3.4. D Lidar Inertial Odometry
In the laser odometry module, our algorithm differs from LOAM algorithm in that we use the improved 3D NDT point cloud matching algorithm instead of the feature-based approach. The 3D NDT point cloud matching method is superior to the feature-based point cloud matching method in the robustness.
The serial number of the laser frame of the matched point is , the serial number of the grid of the point to be matched is , the number of point cloud in the grid is , and the coordinate of the point cloud in a grid of the matched laser point cloud data is . The serial number of source laser frame is , the serial number of source laser frame grid is , the number of point cloud in the grid is , and the coordinate of point cloud in a grid of source laser frame is . The pose transformation matrix of the source laser frame point cloud data and the laser frame point cloud data to be matched is . The rotation axis corresponding to the quaternion is , and the corresponding rotation angle is , where , , . Coordinate rotation function of the two frames’ laser point cloud data is . In order to achieve accurate matching of the two frames’ laser point cloud data, the corresponding objective function established is:
where: ,
The corresponding maximum likelihood estimation function is:
The maximum likelihood estimation function can be rewritten as:
where: .
In order to obtain the rotation transformation of the two frames laser point cloud data, the logarithmic function needs to be minimized as . According to the formula of Newton method of multivariate function, the following can be obtained:
where: , , , , , .
3.5. E Lidar Mapping
In order to further improve the accuracy of pose estimation and mapping, we use real-time lidar frames and a submap to match features, and we evaluate the point cloud matching effect. The feature extraction principle adopts a strategy like the LOAM algorithm. The algorithm flow of laser mapping is as follows:
First, the local point cloud map in the world coordinate system is rasterized. Then, the lidar frame point cloud in the lidar odometry coordinate system is transformed into the world coordinate system according to the initial registration parameters. The line feature point set and plane feature point set nearest to the laser frame are extracted from the local point cloud map, the point line distance constraint and point plane distance constraint are constructed, and the pose is iteratively solved. Finally, the pose, local point cloud map, and initial registration parameters in the world coordinate system are updated.
In the process of optimizing the pose, we innovatively proposed the point cloud matching effect evaluation mechanism. The current lidar frame feature points will find the nearest matched linear feature point set or planar feature point set in the local point cloud map. For the linear feature point set, the covariance matrix is calculated to judge whether the direction vector meets the requirements, and for the planar feature point set, the normal vector meets the requirements. The current lidar frame is counted and the line feature points and plane feature points are found to meet the above requirements in the local point cloud map. To assess the effect of point cloud matching of the current frame, the ratio of the number of line feature points that meet the requirements of the current frame to the number of all line feature points of the current frame, and the ratio of the number of plane feature points that meet the requirements of the current frame to the number of all plane feature points of the current frame are taken as the threshold of map matching quality. To decrease the likelihood of incorrect map matching, the lidar frame whose proportion calculated from the data of the next frame is below a certain threshold does not participate in the process of updating pose and map.
3.6. F Loop Closure Detection
The loop closure detection module adopts the matching strategy of submap-to-submap based on key frames, and it takes two steps to select the loop lidar frame. Loop closure constraints are added to the factor graph optimization framework to optimize the pose and map. The specific algorithm flow is as follows:
Step 1: Key frames are extracted from all lidar frames based on attitude difference and position difference;
Step 2: Based on the time and distance threshold, search the key frame which will be used to loop;
Step 3: The feature point set of the current nearest 5 key frames constitutes the source sub-map, the feature point set of the 5 key frames around the key frame to be looped constitutes the target sub-map, and the source sub-map and the target sub-map are registered with iterative closest point matching algorithm (ICP);
Step 4: The point cloud matching score with ICP algorithm is assessed and the constraint to the factor graph optimization framework [25] is added according to the score. The point cloud whose score is below the threshold is evaluated for the second time;
Step 5: Filter the error constraints that fall into local optimization through point cloud similarity calculation. Traverse the feature points in the target submap, locate the nearest point in the source submap, and verify whether the distance between the points is less than the threshold. After traversing all the points in the target submap, we divide the number of points less than the threshold by the total number of feature points in the target submap to obtain the similarity index. If the similarity index is greater than threshold, the loop closure constraint is qualified;
Step 6: Optimize the pose and map.
4. Experiments
We now describe a series of experiments to qualitatively and quantitatively analyze our proposed framework R-LIO. Eleven test datasets were employed, including two KITTI public datasets, four other public datasets, and five private datasets. Four other public datasets were provided by the authors of LIO-SAM and LVI-SAM. In the public datasets, there was no excessive rotation of lidar and inertial sensors. Five private datasets were collected based on the handheld 3D laser scanning system, As shown in Figure 6, the sensor kit used by the system includes Velodyne puck lite 16-line lidar, xsens-630 inertial measurement unit, and rotating motor with adjustable speed. The scanning field angle of the rotating 3D laser scanning system is 330° × 360°.

Figure 6.
Handheld 3D laser scanning system.
The five private datasets are named corridor, garage, mine, tunnel, and forest. The details of these data are shown in Table 1.

Table 1.
Basic information of dataset.
We compare the proposed R-LIO framework with LOAM in KITTI public datasets, then compare the proposed R-LIO framework with ALOAM, LIO-SAM, FAST-LIO2, and Faster-LIO in other public datasets and private datasets. The test environment for all methods runs on Intel i9-11900H CPU notebook, using the Ubuntu robot operating system. For the convenience of subsequent statements, the algorithm name is unified, R-LIO refers to the mapping algorithm with loop closure detection, and R-LIO-odom refers to the mapping algorithm with loop closure detection disabled.
4.1. KITTI Public Dataset
We verify the accuracy of our proposed algorithm in the KITTI public datasets and select the LOAM algorithm that performs well in the KITTI datasets for comparison. Since the loop detection module is not included in the LOAM algorithm, in order to test the fairness, we select the R-LIO-odom algorithm with the loop detection module disabled. The accumulative drift of the positioning errors of different algorithms is shown in Table 2, and the comparison of the pose trajectories of different algorithms with the laser odometry evaluation tool EVO [26] is shown in Figure 7. It can be seen that the R-LIO-odom algorithm has smaller localization error. The laser point cloud map constructed by R-LIO-odom algorithm is shown in Figure 8, and the point cloud map has good consistency.

Table 2.
Quantitative comparison of KITII datasets using various methods.
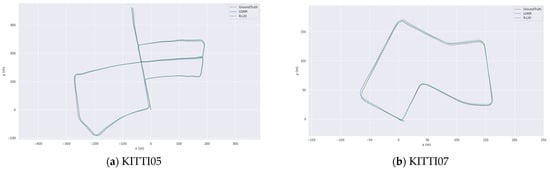
Figure 7.
The comparison of estimated trajectories after applying R-LIO-odom and LOAM algorithms on KITTI dataset.

Figure 8.
Mapping results of R-LIO-odom algorithm in KITTI dataset.
4.2. Other Public Dataset
The four other public datasets contain GPS information. We use the GPS information as the ground truth, and quantitatively compare the laser odometry accuracy of different algorithms. The accuracy evaluation index is the absolute pose error, and the root mean square value of the absolute pose error is taken as the statistical error. In order to improve the accuracy of the experiment results, each algorithm is tested three times for each scene. Here, only the laser odometry accuracy of different algorithms is compared. Therefore, the loop closure detection and GPS optimization module of LIO-SAM is prohibited, and it is named LIO-SAM-odom.
4.2.1. Park
These data were collected by UGV trolley on the forest covered a hiking path. We compared various algorithms and displayed their localization trajectories, as shown in Figure 9. The root mean square values of absolute pose errors of various algorithms are shown in Table 3. It can be seen that ALOAM has a large drift in the trajectory due to the lack of inertial data for motion distortion compensation and participation in the point cloud matching process. The accuracy of R-LIO-odom laser odometry is better than FAST-LIO2 and Faster-LIO, and the performance is equivalent to that of LIO-SAM-odom. The global mapping results of Park data by R-LIO-odom method are shown in the Figure 10a.
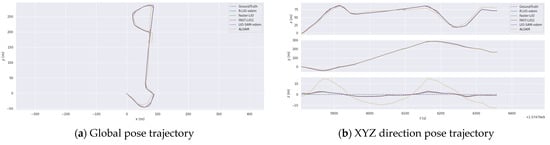
Figure 9.
Pose trajectory comparison of different algorithms in park data.

Table 3.
Quantitative comparison of various datasets using various methods.

Figure 10.
Public dataset global mapping results through R-LIO-odom method.
4.2.2. Campus
These data were collected by handheld devices on the MIT campus. We compared various algorithms and displayed their pose trajectories, as shown in Figure 11. The root mean square values of absolute pose errors of various algorithms are shown in Table 2. LIO-SAM-odom achieves the lowest absolute pose error and R-LIO-odom has the same performance as LIO-SAM-odom, FAST-LIO2, and Faster-LIO algorithms. The global mapping results of the campus data by R-LIO-odom method are shown in the Figure 10b.
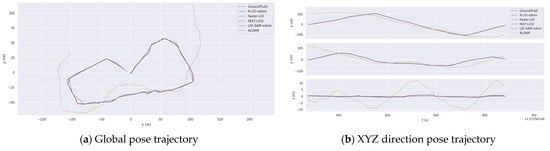
Figure 11.
Pose trajectory comparison of different algorithms in campus data.
4.2.3. Handheld
Handheld data were collected by handheld devices. The majority of the survey area is made up of grassland and ground. It lacks obvious structural characteristics and belongs to a structural degradation scene. We compare various algorithms and show their pose trajectories in Figure 12. The root mean square values of absolute pose errors for various algorithms are shown in Table 3. R-LIO-odom has the lowest absolute trajectory error. FAST-LIO2 produces serious mapping errors in this dataset, so it is not shown here. The global mapping results of Handheld data by R-LIO-odom method are shown in the Figure 10c.
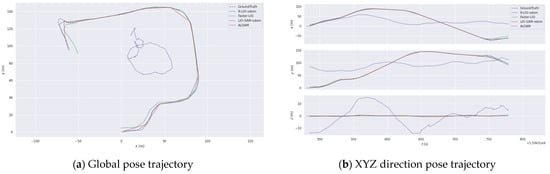
Figure 12.
Pose trajectory comparison of different algorithms in handheld data.
4.2.4. Jackal
Jackal data were collected by unmanned ground vehicles. The survey region has a variety of vegetation, roads, and structured characteristic environment. We compare various algorithms and show their pose trajectories in Figure 13. The root mean square values of absolute pose errors for various algorithms are shown in Table 3. Fast-LIO2 achieves the lowest absolute pose error. R-LIO-odom outperforms LIO-SAM-odom and Faster-LIO algorithms while offering the same performance as FAST-LIO2. The global mapping results of Jackal data by R-LIO-odom method are shown in the Figure 10d.
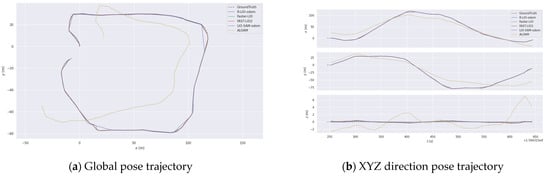
Figure 13.
Pose trajectory comparison of different algorithms in Jackal data.
4.3. Private Dataset
In the private dataset, we hand-held a three-dimensional laser scanning system to collect data, as shown in Figure 6. In order to verify the end-to-end error of different algorithms and the loop closure detection effect of R-LIO algorithm, the equipment will be returned to the starting position after data collection. Two groups of forest data were separately collected by the motor rotation and by the motor non rotation along the same walking route. When the rotation data were collected, the rotation speed of the motor was 360 °/s.
4.3.1. Corridor
The test scenario is a closed long and narrow corridor with few features. It belongs to a geometric structure degradation scenario, which is challenging. The real environment [27,28,29] diagram is shown in Figure 14a. In this scenario, the motor speed is set to 0 m/s, and the local point cloud maps of different algorithms at the start and end positions are shown in Figure 15. ALOAM, FAST-LIO2, and Faster-LIO methods all produce different drift. R-LIO-odom and LIO-SAM-odom have good consistency. The end-to-end translation error results of different algorithms are shown in Table 4.

Figure 14.
Test environment.

Figure 15.
Local mapping results of different algorithms in corridor dataset at the beginning and end positions.

Table 4.
Quantitative comparison of private datasets using various methods.
4.3.2. Garage
This test scenario is an indoor parking lot with rich environmental characteristics, and there are occasionally dynamic pedestrians and vehicles. The real environment diagram is shown in Figure 14b. In this scenario, the motor speed is set to 0 m/s, and the global point cloud map of different algorithms is shown in Figure 16. The ALOAM method has a large drift at the start and end positions, and the mapping performance of R-LIO-odom is equivalent to that of FAST-LIO2, Faster-LIO, and LIO-SAM-odom algorithms. Good consistency of construction drawings shall be maintained. The end-to-end translation error results of different algorithms are shown in Table 4.
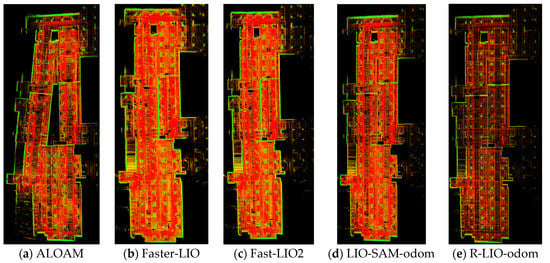
Figure 16.
Global mapping results of different algorithms in the garage dataset.
4.3.3. Mine
In order to verify the positioning accuracy and mapping effect of different algorithms in the structural degradation scene, the open-pit mine scene is selected. The scene is relatively empty and the environment has no significant landmarks. The real environment is shown in Figure 14c. In this scenario, the equipment starts from the marked position and returns to the original position after a period of time. The local laser point cloud maps constructed by different algorithms are shown in Figure 17. The point cloud maps constructed by ALOAM, FAST-LIO2, and Faster-LIO are fuzzy. The point cloud maps constructed by R-LIO-odom and LIO-SAM-odom are clear. The rock mass structure can be clearly identified in the point cloud maps output by R-LIO-odom. The end-to-end translation errors of different algorithms are shown in Table 4. The R-LIO-odom algorithm has the best accuracy.

Figure 17.
Local mapping results of different algorithms in the mine dataset.
4.3.4. Tunnel
In order to verify the mapping effect of different algorithms under large rotational motion and the loop closure detection ability of LIO-SAM and R-LIO algorithms, the above-ground and underground linkage scenes are selected. The underground part belongs to the artificial tunnel and there are few landmarks. The real environment is shown in Figure 14d. In this scene, the rotation speed of the motor was 360 °/s, and the loop closure position is located on the left side of the underground environment. The global laser point cloud map constructed by different algorithms is shown in Figure 18. ALOAM, FAST-LIO2, and Faster-LIO algorithms cannot work normally, resulting in serious drift. R-LIO and LIO-SAM algorithms can perform normally. R-LIO algorithm has better loop closure detection ability and better map consistency. Although LIO-SAM algorithm triggers loop closure detection, loop closure precision is not enough, and laser point cloud has a ghost phenomenon at loop closure position.

Figure 18.
Global mapping results of different algorithms in tunnel dataset.
4.3.5. Forest
The test scenario is a forest park, which includes buildings, grasslands, trees, and cement roads. The surrounding environment is rich in characteristics, with occasional dynamic pedestrians and slight fluctuations in elevation. The real environment diagram is shown in Figure 15e. This test scenario verifies the performance of different algorithms in non-rotating lidar data and rotating lidar data and the loop closure detection effect of LIO-SAM and R-LIO algorithms.
In the non-rotating lidar data, the local point cloud map of different algorithms at the begin and end positions are shown in Figure 19. The mapping of ALOAM method in this environment is seriously disordered, and the deviation at the start and end positions is large, resulting in meaningless data. Therefore, the results of ALOAM are not shown here. FAST-LIO2, Faster-LIO, LIO-SAM-odom, and R-LIO-odom all generate cumulative drift to varying degrees, of which the drift generated by R-LIO-odom algorithm is the smallest. The end-to-end translation error results of different algorithms are shown in Table 5.

Figure 19.
Local mapping results of different algorithms in forest dataset at the beginning and end positions. (Left: Plane direction error, Right: Elevation direction error).

Table 5.
Quantitative comparison of forest datasets using various methods.
The loop closure detection effects of LIO-SAM and R-LIO are shown in Figure 20. Although the loop closure detection is triggered by the LIO-SAM algorithm, and the end-to-end error is significantly reduced, the overall point cloud map is greatly misaligned after the loop detection is triggered, which is inconsistent with the actual environment.

Figure 20.
R-LIO and LIO-SAM loop closure result comparison.
In rotating lidar data, ALOAM, FAST-LIO2, Faster-LIO, LIO-SAM-odom, and LIO-SAM algorithms cannot work normally because the motor rotates too fast. The effect of R-LIO-odom algorithm in the mapping of rotating lidar data is shown in Figure 19e and the global mapping is shown in Figure 19f. This is because the rotating lidar mode will capture more feature information in the environment, increasing the number of features participating in the SLAM process. It is clear that rotating lidar mapping has obvious advantages and can achieve the effect of loop closure detection in the non-rotating lidar mode.
5. Conclusions
In this paper, we propose R-LIO, a novel simultaneous localization and mapping algorithm, which is coupled by rotating multi-line lidar and inertial measurement unit. R-LIO can achieve real-time and high-precision pose estimation and map-building. The experiment results demonstrate that R-LIO has competitive localization accuracy as compared to well-known algorithms such as LOAM, LIO-SAM, FAST-LIO2, and Faster-LIO in non-rotating lidar data. The common algorithms cannot function normally with rotating lidar data. Compared with non-rotating lidar data, R-LIO can improve localization and mapping accuracy in rotating lidar data. To further improve the robustness of the algorithm, we will attempt to establish sensor fusion employing laser, camera, and IMU.
Author Contributions
Conceptualization, K.C.; methodology, K.C.; software, F.P.; validation, K.C., K.Z. and F.P.; formal analysis, K.C.; investigation, X.Y.; data curation, D.Z.; writing—original draft preparation, K.C.; writing—review and editing, F.P.; project administration, K.Z.; funding acquisition, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by National Key Research and Development Program of China (grant no. 2020YFE0202800, 020YFC1909602, 2018YFE0121000) and Youth Technology and Innovation Fund of Bgrimm (grant no 04-2203).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodr´ıguez, J.J.G.; Montiel, J.M.; Tardos, J.D. Orb-SLAM3: An accurate open-source library for visual, visual–inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Avia. Available online: https://www.livoxtech.com/avia (accessed on 12 May 2022).
- Velodyne Puck Lite. Available online: https://velodynelidar.com/products/puck-lite (accessed on 8 May 2022).
- ALOAM. Available online: https://github.com/HKUST-Aerial-Robotics/A-LOAM (accessed on 1 May 2022).
- Zhang, J.; Singh, S. Loam: Lidar odometry and mapping in realtime. In Proceedings of the Robotics: Science and Systems 2014, Berkeley, USA, 12–16 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Shan, T.; Englot, B. Lego-loam: Lightweight and groundoptimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 5135–5142. [Google Scholar]
- Wang, H.; Wang, C.; Chen, C.L.; Xie, L. F-LOAM: Fast LiDAR Odometry and Mapping. arXiv 2021, arXiv:2107.00822. [Google Scholar]
- Lin, J.; Zhang, F. Loam livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–August 2020; pp. 3126–3131. [Google Scholar]
- Xu, W.; Zhang, F. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. Fast-lio2: Fast direct lidar-inertial odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight Tightly Coupled Lidar-Inertial Odometry Using Parallel Sparse Incremental Voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- Zhao, S.; Fang, Z.; Li, H.; Scherer, S. A robust laser-inertial odometry and mapping method for large-scale highway environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1285–1292. [Google Scholar]
- Lin, J.; Zheng, C.; Xu, W.; Zhang, F. R2live: A robust, realtime, lidar-inertial-visual tightly-coupled state estimator and mapping. arXiv 2021, arXiv:2102.12400. [Google Scholar]
- Lin, J.; Zhang, F. R3LIVE: A Robust, Real-time, RGB-colored, LiDAR-Inertial-Visual tightly-coupled state Estimation and mapping package. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. Lvi-sam: Tightly-coupled lidar-visual-inertial odometry via smoothing and mapping. arXiv 2021, arXiv:2104.10831. [Google Scholar]
- FAST-LIVO: Fast and Tightly-Coupled Sparse-Direct LiDAR-Inertial-Visual Odometry. Available online: https://arxiv.org/abs/2203.00893v1 (accessed on 20 May 2022).
- Tagliabue, A.; Tordesillas, J.; Cai, X.; Santamaria-Navarro, A.; How, J.P.; Carlone, L.; Agha-mohammadi, A.A. Lion: Lidar-inertial observability-aware navigator for vision-denied environments. arXiv 2021, arXiv:2102.03443. [Google Scholar]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. In Proceedings of the Robotics: Science and Systems, Seattle, DC, USA, 28 June–1 July 2009. [Google Scholar]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. Lins: A lidar-inertial state estimator for robust and efficient navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2020; pp. 8899–8906. [Google Scholar]
- Ye, H.; Chen, Y.; Liu, M. Tightly coupled 3d lidar inertial odometry and mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QU, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection. Ph.D. Thesis, Orebro Universitet, Örebro, Sweden, 2009. [Google Scholar]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- EVO. Available online: https://github.com/MichaelGrupp/evo (accessed on 7 May 2022).
- Sun, Y.; Bi, R.; Sun, J.; Zhang, J.; Taherdangkoo, R.; Huang, J.; Li, G. Stability of roadway along hard roof goaf by stress relief technique in deep mines: A theoretical, numerical and field study. Geomech. Geophys. Geo Energy Geo Resour. 2022, 8, 45. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Huang, J. Rockburst intensity evaluation by a novel systematic and evolved approach: Machine learning booster and application. Bull. Eng. Geol. Environ. 2021, 80, 8385–8395. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Sun, J.; Huang, J.; Taherdangkoo, R. New insights of grouting in coal mass: From small-scale experiments to microstructures. Sustainability 2021, 13, 9315. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).