Abstract
The route recommendation system helps the driver find the best route between origin and destination. A recommendation system often suggests its decision without considering some criteria. This paper proposes a multicriteria decision-making method, namely Fuzzy—Analytic Hierarchy Process—Express (F-AHP-Express) for recommending a personal travel route from several alternative routes. It is calculated based on the driving preferences of a driver and road conditions for each road segment. We compare the F-AHP-Express to others; Fuzzy—Analytic Hierarchy Process (F-AHP) and Fuzzy—Analytic Hierarchy Process—Technique for Others Preference by Similarity to Ideal Solution (F-AHP-TOPSIS), for its recommendation results, time processing, agility, and complexity. Our experiments show that F-AHP-Express could deliver similar recommendation results compared to other methods, and it is additionally the fastest method. F-AHP-Express is 45% and 23% faster than F-AHP and F-AHP-TOPSIS, respectively. F-AHP-Express not only has the fastest time processing among the others but also has the least judgments in agility testing. It needs 37.5% and 16.67% fewer judgments from F-AHP and F-AHP-TOPSIS, respectively. Moreover, AHP-Express has a complexity of O(n), meanwhile, the others have O(n2) for their complexity. Thus, the results show that F-AHP-Express is the best method for recommending a personal route.
1. Introduction
All roads lead to Rome. This is the most suitable expression to describe the process to reach a goal, it can be carried out in many ways. It is similar in the area of transportation; to reach a destination, there will be lots of choices of travel routes that can be passed. It means we can choose one of the paths that have the best values for us.
The choice of travel route by a driver can be measured based on several aspects, such as traffic conditions, heterogeneity, weather conditions, etc. Based on these several aspects, the driver could choose which one is prioritized first. Next, they could choose one route that is the most suitable to their preferences. As an example, a driver looks for an alternative route in order to avoid the traffic on the main route, even if it has a longer distance. Furthermore, there is a driver who prioritized the travel time between other road criteria, or for a motorcycle driver, a route with good weather (e.g., sunny, cloudy, or clear sky) is preferred over a route with a possibility of bad weather.
In selecting the travel route, there is a probability that a driver makes mistake in their choices. It is common that the chosen route is not good as their expectation. Based on this condition, we proposed a personal route recommendation system that has the capability to consider the driver’s preferences. By using multicriteria decision making (MCDM), the best route for drivers is determined.
MCDM is a common method that is used for deciding a decision based on several alternatives, e.g., choosing the best way to fill a dam based on costs, capacity, construction difficulty, and other criteria [1]; or an Optimal Route Selection in a Highway which considering travel time, fee, comfort, and safety [2]. Da Silva et al., state that the most common method in MCDM is Analytic Hierarchy Process (AHP) and the Technique for Others Preference by Similarity to Ideal Solution (TOPSIS) [3]. These methods are the top-5 methods from 2000 to 2019 [4,5].
AHP was developed by Saaty in 1980 [6,7] and in its development, there are many modifications of AHP. One of the modifications is the implementation of the Fuzzy method in calculating the criteria weights (F-AHP) [8,9]. The purpose of this modification is to simplify the judgment of decision-makers when deciding the importance level between criteria. In 2020, Leal et al. simplified this method and it makes AHP works faster than before, called AHP-Express [10]. They claimed that AHP-Express is faster than classic AHP since it reduces the number comparison from to for n criteria.
Meanwhile, TOPSIS which is created in 1981, also has several modifications due to its needs, such as Fuzzy-TOPSIS [11,12], Alternatives-Weight TOPSIS [13], Weight-modification TOPSIS [14], and other modifications [15,16].
This paper discussed the development and modification of AHP-Express in order to recommend a personalized travel route based on the preferences of drivers. The modification of AHP-Express lies in the weight calculation process, which is implemented by using F-AHP. The addition of F-AHP as criteria weight calculation in AHP-Express simplified the judgment (importance level of criteria) of drivers.
The implementation of Fuzzy logic in the measurement of criteria weight helps humans to decide the importance of criteria in order to determine the travel route. It is because, in the Fuzzy logic concept, the value is in the linguistic form. This type of value is lots easier to understand than the crisp value which is used in Saaty’s AHP. The comparison in classic AHP needs 19 choices of important levels, meanwhile, by using Fuzzy-AHP, we only need 11 choices that spread into 5 linguistic values. It covers three crisp values as classical AHP did. By using the geometric mean, the criteria weight in F-AHP is measured.
By the time this paper is written, there is no research that combines the Fuzzy-AHP and AHP-Express as a method for calculating criteria’s weight and decision-making for recommending a personalized travel route. In order to confirm that it is the best method for deciding the personal route, we compared it with other methods (Fuzzy-AHP and Fuzzy-AHP-TOPSIS).
2. Literature Review
2.1. Road Network
The road network illustrates the connection between several intersections (nodes) and road segments (edges), with the arrangement of direction, as in the directed graph [17,18,19,20]. To reach a destination in the road network, vehicles need to pass several nodes whether directly connected or not by its edges. Generally, the notation of connectivity in the road segment is described by [21]. On the other hand, the road network element is not limited to nodes and edges. According to George and Kim, the road network is also influenced by weight (w) in every road segment [22].
The definition of weight in road networks could be as wide as the system requirements. Ge et.al., considering road infrastructure as a criterion that must be calculated in road networks [23]. Meanwhile, based on Ferreira et al., time travel is also a criterion considered by drivers in order to reach their destination. So, they tried to calculate these two criteria for their road network [24]. Other criteria that could be used as a weight in road networks are implemented are traffic condition [25], weather [26,27], travel time [24,28,29,30], etc. [31]. Nasution et al., create a new point of view in calculating the road network’s weight by using Road Capacity Value (RCV) [32].
Road Capacity Value (RCV)
RCV is a compilation of several criteria in road networks, and it is processed in such a way in order to calculate the weight of the road. RCV also calculates the suitability between the road size and the width of the vehicle that will be passing through.
RCV in road networks can be used as a basis for determining the travel route. The advantage of RCV is not only the compatibility value that can compare the size of the road and vehicles, but also considering the driving preferences of a driver. Driving preference is another criterion that must be taken into consideration [26,28,32,33,34,35]. There is no point to recommends the best route if the drivers refuse to pass it.
The creation of RCV needs driver preferences. The driver preferences in Nasution et al. are manually determined by using priority order [32]. This paper discussed the procedure of determining the preferences of the driver, so later it could be used as the basis of personalized route recommendations.
2.2. Multicriteria Decision Making
Multicriteria decision-making (MCDM) is a common method that is used to define a solution based on several alternatives. Forming any possible alternatives, required several criteria. As an example, whenever there is recruitment for academic staff in a university, the employer will review each candidate and consider their education, age, language skill, etc. [36].
Based on the criteria for defining the alternatives, decision-makers set the importance of each criterion (priority). The process of determining the priority for each criterion is called weight calculation [37,38]. When each criterion has its priority, the process of decision-making continues [38]. Figure 1 shows the workflow of multicriteria decision-making.
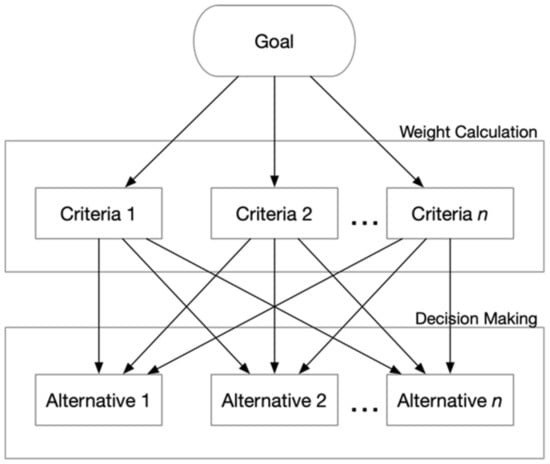
Figure 1.
Multicriteria Decision Making.
There are a lot of MCDM methods. Based on da Silva et al., top-5 MCDM methods from 2005 until 2019 are Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), Analytic Network Process (ANP), VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE), etc. [3].
Even though Mardani et al. also state that AHP is the top common method in MCDM. It is followed by Hybrid MCDM, Aggregate Methods, TOPSIS, and The Elimination et Choix Traduisant la Realité (Electre) as the next top common methods after AHP before 2014 [4,5]. Contrary to da Silva et al., who state AHP is the most common method in decision making, Eltarabishi et al., state differently, state Hybrid MCDM is the most common method from 2015 until 2019, followed by AHP, and other methods [5]. Table 1 shows the list of common methods based on the previous research.

Table 1.
Common MCDM Methods.
The hybrid MCDM method is a combination of several methods used in the process of weight calculation and decision making. The combination of AHP as a weight calculation method and TOPSIS as a decision-making method is commonly implemented by several researchers [39,40,41,42,43,44].
In the route recommendation system proposed in this paper, the criteria that are used to define the best route for each driver are route length, traffic condition, heterogeneity, travel time, and weather condition. In order to calculate the criteria weight, the driving preferences are collected using a questionnaire. In the workflow of MCDM, whenever the criteria weight is gathered, the process of decision-making is begun.
2.2.1. Weight Calculation
The criteria priority measurement can be carried out by implementing various weighting methods. Commonly, the criteria weight is defined based on the simulation result. Based on those data, the impact of each criterion on the simulation result illustrates its priority. Thus, it will be used as criteria weight in the next process.
The calculation of criteria weight in this paper is slightly different from the common measurement. In order to create a personalized recommendation, the criteria weight collection is carried out by using a questionnaire to several drivers (motorcycles and cars). In this case, these drivers are the decision makers for deciding their own best travel route. The driving preferences (criteria weight) are specifically designated for each driver.
Weight calculation in this paper is using the AHP approach which compared each criterion based on the decision-makers [6,7]. Soon after the comparison of criteria is complete, the criteria weight is calculated using Additive Normalization Method [6,7,45].
Weight calculation in AHP needs a comparison value between criteria. For every compared criterion, there will be a reciprocal value of its results. This process applies to each criterion used in defining the alternatives. Later, every compared value between criteria is arranged in the form of a pairwise comparison matrix (PCM).
If the criteria comparison process is finished, its value will be used to calculate the consistency ratio (CR). The usage of consistency ratio is to control the comparison between each criterion is consistent. If the consistency ratio is greater than the threshold determined, the driving preferences must be tuned until its ratio comes under the threshold. Figure 2 illustrates the process of the criteria weight measurement.
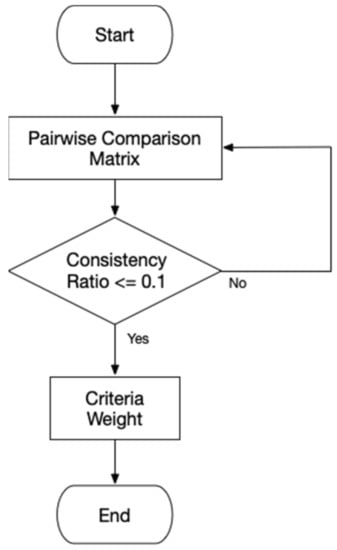
Figure 2.
The Calculation of Criteria Weight.
Fuzzy Analytic Hierarchy Process (F-AHP)
A comparison of criteria in Classic AHP defines the importance level between two criteria. As shown in Table 2, the importance level is defined using this rule [45]. As an example, if criterion A is moderately more important than criterion B, then criterion A compared to criterion B is 1 to 3, otherwise, the comparison between criterion B and A is 3 to 1, as shown in Equation (1). The importance level of the same criteria (A:A) is always equal (1). This comparison applied to all criteria used in the MCDM methods.

Table 2.
AHP Importance Level.
This step seems simple when implemented in a system. However, when it is implemented by humans as decision makers, it gives confusion to them. Human prefers linguistic value to crisp value. The solution to this problem is implementing the Fuzzy Logic into the calculation of criteria weight. Chou and Yu claimed this method simplified the process of criteria comparison by humans [46].
As mentioned before, humans as decision-makers do not need detailed (crisp) value. By using Fuzzy Logic, the importance level is simplified into linguistic value, so it makes it easier to humans to input their preferences [47]. The common Fuzzy Logic method is Triangular Fuzzy Numbers (TFN) [47,48,49,50].
Linguistic value in TFN covers three (3) crisp values (lower, middle, upper), which describe the range of Fuzzy membership values, as shown in Equation (2). F-AHP makes small cluster based on several categories, such as: “Equally” and “Moderately” covers (1, 1, 1) and (2, 3, 4), ”Strongly”, “Very Strongly”, and “Extremely” takes in (4, 5, 6), (6, 7, 8), and (9, 9, 9) [48].
The membership function is easily customized based on requirements. Kwong and Bai set their membership function to cover only two crisp values, as (1, 2) is given for “Equally”, (2, 4) for “Moderately”, etc. [48]. On the other hand, Khorramrouz et al. takes the middle value between two values. They use (1, , 2) as “Moderately”, (, 2, ) for the next category, and so on [51].
Compared to classic AHP, there is a difference when creating the reciprocal value using F-AHP. In F-AHP, the calculation of reciprocal value is using Equation (3). It swaps the lower and upper values from the original form of Fuzzy membership in Equation (2).
PCM in F-AHP will be filled up with these two methods: Fuzzy Membership Function (TFN) and its reciprocal value. Soon after the criteria comparison process is completed, the consistency of preferences is measured. As aforementioned, the consistency ratio checks the criteria comparison of decision makers [52]. Since in F-AHP there are several values (l, m, u), the calculation of the consistency ratio will use only the middle value [9].
The consistency ratio needs the value of the index of consistency (CI) and ratio index (RI). The consistency index is calculated by finding the maximum eigenvalue, using Equation (4). By using Equation (5), the consistency index is measured. n is the number of criteria in the calculation. On the other hand, the ratio index is a constant. As shown in Table 3, the ratio index is determined.

Table 3.
Ratio Index.
The value of RI is chosen based on the number of criteria in the measurement. Whenever CI and RI are calculated, the measurement of the consistency ratio begins. By using Equation (6), the CR is defined by dividing the CI and RI.
Validation of criteria comparison is needed in order to verify the preferences are consistent. There will be adjustment in criteria comparison if the value of CR is more than 0.1 (. The adjustment stops when CR is less than equal to 0.1 (). By the time the value of CR is already less than equal to 0.1, the lower and upper value from F-AHP is returned to the pairwise comparison according to the TFN rule.
In general, the calculation of criteria weight in F-AHP is almost similar to classic AHP. However, in the step of averaging the Fuzzy membership, it will be carried out by using Geometric Mean [8,53], as shown in Equation (7). Meanwhile, Equation (8) is used to define the criteria weight in the form of a Fuzzy membership function.
The next step in calculating the criteria weight using F-AHP is finding the Center of Area (COA). It will do the defuzzification step to the previous criteria weight and it is carried out by using Equation (9). Before its result can be used in the decision-making process, the criteria weight must be normalized using Equation (10) first. Whenever the criteria weight is normalized, its ready to be used in decision making.
2.2.2. Decision Making
Criteria weight that calculated in the previous step is used in decision making. The alternatives will be calculated by using simulation or other methods for each criterion. Figure 3 shows the step of decision-making. The final decision comes after the decision-making process is completely carried out. It is common for the result comes from the highest comparison score of all alternatives.
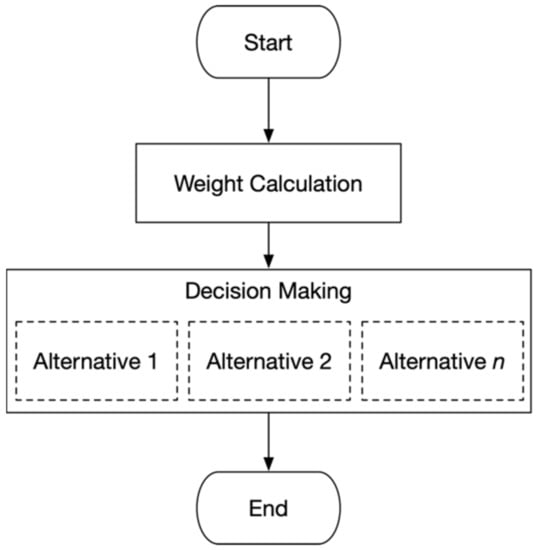
Figure 3.
The Process of Decision Making.
In this paper, we implement several decision-making methods, namely Analytic Hierarchy Process (AHP) [7], Analytic Hierarchy Process (AHP-Express) [10], and the Technique for Others Preference by Similarity to Ideal Solution (TOPSIS) [54].
Analytics Hierarchy Process
In AHP, the process of decision-making needs to compare each alternative based on criteria. The amount of alternative comparison is for each criterion [55]. Comparing the alternatives uses a similar method when calculating the criteria weight. However, there will be iterations as much as the number of criteria that are used, so the result of the comparison will have a point of view from each criterion.
In order to calculate the average value of alternative comparison, there is a collaboration between its results based on each criterion. The final output of this calculation is the priority of each alternative. The highest priority defines the result of decision-making using AHP.
Alternatives can be collected by using simulation or other methods. All information of each alternative will be converted into numerical values within range 1–9 (as AHP requirement). Equations (11) and (12) try to find the maximum and minimum value for each criterion. This value will be used as the upper bound (UB) and lower bound (LB) of the simulation result. Meanwhile, in Equation (13), the range level (RL) of each alternative in a criterion is measured. The level of number in RL is 9, this number is taken due to complying with the importance level in AHP. In the end, Equation (14) calculates the importance level (IV) of alternatives for each criterion.
This process converts raw information from the simulation into the importance level in AHP. The decision-making process continues by using these values and measures as criteria weight calculation.
Analytics Hierarchy Process Express
Since AHP needs for each comparison, the method proposed by Saaty in 1980 is claimed to be slow. Leal, et al., proposed a simpler AHP that only needs comparison, called AHP-Express [10]. This method reduces the number of alternative comparisons based on the criteria.
The biggest difference between these methods is in AHP-Express only needs one (1) alternative comparison for each criterion. Based on this situation, AHP-Express is faster than classic AHP. The steps of decision-making in AHP-Express are: (1) a single comparison of alternatives (for each criterion), (2) calculating the reciprocal value and its summation, and (3) normalization. Every comparison value is combined into one matrix and later the decision-making process works as classic AHP should.
Technique for Others Preference by Similarity to Ideal Solution (TOPSIS)
TOPSIS is one of the common methods used for finding a decision based on several alternatives [56]. This method is proposed by Hwang and Yoon in 1981 with considering the ideal solution to a problem [57]. The calculation of the ideal solution comes from the distance between positive and negative solutions. A positive ideal solution measures the values of alternatives in their best condition. On the other hand, the negative ideal solution takes the worst values in every alternative.
There is no comparison between alternatives as AHP does. TOPSIS looks at the best and worst conditions in each alternative. In this method, there are categorizations for its criterion, namely, benefit and cost. The benefit category takes the maximum value for its positive ideal solution in each criterion. However, in the cost category, the maximum value is used as a negative ideal solution and the minimum value from each criterion is set to its positive ideal solution [1].
The process of decision-making using TOPSIS begins with normalization using Equation (15). It continues with the step of finding the ideal value (positive and negative) based on the criterion category. Right after the ideal value was determined, the process advanced to the calculation of the distance of alternatives with its ideal value, using Euclidian Distance. Equation (16) determines the distance of the positive ideal solution and Equation (17) tries to calculate its negative ideal solution distance .
Based on the distance values, the performance index (P) is determined for each alternative, using Equation (18). The highest performance index will be set as the final decision in this method.
3. Proposed System
In our proposed system, there are five (5) criteria in order to find the route that has minimum RCV and its alternatives. The criteria in this paper covered the route length, traffic condition, heterogeneity, travel time, and the condition of weather. Figure 4 shows the proposed framework that is used to define the best route for a driver based on the driving preferences.
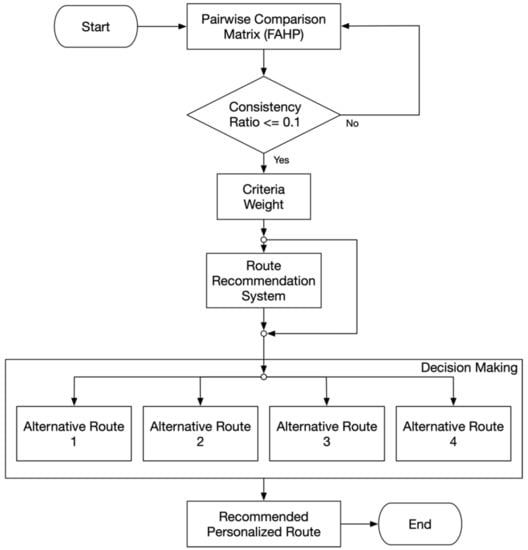
Figure 4.
Proposed Framework.
3.1. Calculation of Criteria Weight
Before recommending a travel route to drivers, the driving preferences are needed. There will be a questionnaire for seven (7) taxi bikes and seven (7) taxi drivers who will participate to inform their driving preferences. Its results are processed using F-AHP as mentioned in the previous section. Figure 5 shows the driving preferences questionnaire.
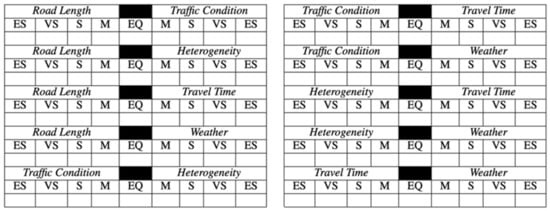
Figure 5.
Driving Preferences Questionnaire.
The importance level in this paper is divided into five (5) linguistic values, namely “Equal” (EQ), “Moderate” (M), “Strong” (S), “Very Strong” (VS), and “Extremely Strong” (ES). Every linguistic value covers three (3) crisp values. EQ and ES cover the top and bottom value of importance levels. It covers (1, 1, 1) and (9, 9, 9). Meanwhile, the rest covers (2, 3, 4), (4, 5, 6), (6, 7, 8) for M, S, and VS, respectively. The reciprocal value will convert the crisp value into (1, 1, 1) and ( for and . The reciprocal value of M, S, and VS cover (, ( and , respectively. It is determined by using Equation (3) mentioned earlier in the previous section.
F-AHP reduces the preference selection by the drivers from 19 (AHP) to 11 choices. It also makes them easier to choose their preferences. Every choice of driving preferences converted from linguistic into crisp value. Figure 6 shows the Fuzzy membership function in this paper. According to Ball and Korukoglu, F-AHP is the most suitable approach for evaluating multiple criteria and alternatives in an uncertain conditions [58].
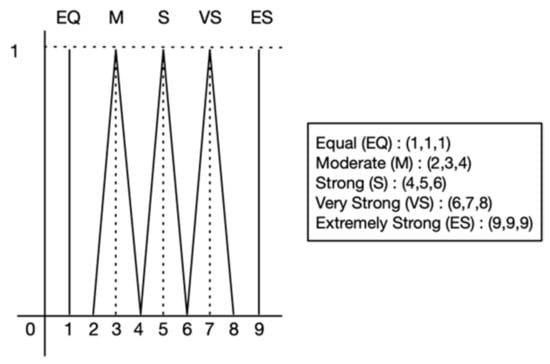
Figure 6.
Fuzzy Membership Function.
To maintain consistency, the driving preferences will be evaluated before being used in decision-making. According to the threshold of consistency ratio, the driving preferences must have a ratio less than 0.1. If it is greater than this value, the driving preferences must be an adjustment until the ratio is below the threshold. Whenever the driving preferences are already below the threshold, they can be used in other processes.
3.2. Route Recommendation System
According to Nasution et al., driving preferences is not only used for RCV determination but also used in calculating the best route among its alternatives. The recommended route is calculated by using Dijkstra shortest path algorithm [59,60]. Nasution et al. only provides one route which comes from the least of RCV summation from an origin to a destination. Figure 7 illustrates how the route recommendation system is based on minimum RCV.
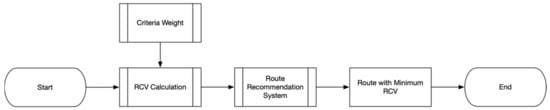
Figure 7.
Route Recommendation System using Minimum RCV.
In this paper, we proposed an adjustment in the RCV calculation of each road segment. Its calculation will be using the consistent driving preferences as the criteria weight. Moreover, by using a similar method to define the shortest path from its origin and destination, this paper provides several alternatives route in order to reach the destination. Figure 8 shows the proposed improvement from previous research. Somehow, the route with minimum RCV may not be appropriate for the preferences of the driver.
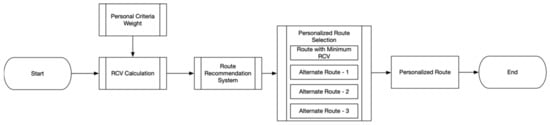
Figure 8.
Improvement of Route Recommendation System.
3.3. Decision-Making
Right after the calculation of RCV, there is a comparison between alternative routes. In order to define the best routes for each driver, this paper combines weight calculation and various decision-making methods, namely (1) F-AHP, (2) F-AHP-Express, and (3) Hybrid Method (F-AHP-TOPSIS). This paper also compares the results of personalized route recommendations using MCDM methods.
F-AHP is a common method that is used in decision-making, such as deciding the best location for an international logistic warehouse [46], failure in the business plan [51], university rank [9], etc. [50,61,62]. Meanwhile, the F-AHP-TOPSIS is a hybrid method that combines several MDCM methods. This method is implemented in several kinds of research with various purposes, such as: deciding the best waterway for filling a dam [1], operating system in a company’s computer [58], the high-class taxpayer [63], etc. [40,41,42]. On the other hand, AHP-Express is a new method proposed by Leal et al. [10]. In this paper, we proposed F-AHP-Express as a method for suggesting a personal route. We improved the AHP-Express with F-AHP as a weight calculation method.
4. Results and Discussion
As mentioned in the previous section, Nasution et.al. provides only the best route by using the minimum RCV [32]. However, this paper provides the route with minimum RCV along with its alternatives. The alternative routes come from the next minimum RCV on the simulation. It gathers its information and compares the RCV of all routes. The four (4) routes with minimum RCV are selected. Figure 9 shows the alternative route provided in this paper. Since its simulation uses real-time information, these routes could be varied over time.

Figure 9.
Alternative Routes.
Based on these alternative routes, the recommendation system finds which routes have the most suitability with the preferences of a driver. Since every driver has their preferences, the route that recommends could be different from others.
4.1. Weight Calculation
In the process of calculating criteria weight, there are several criteria that are used in this system, namely: (1) road length (RL), (2) traffic condition (TC), (3) Heterogeneity (H), (4) travel time (TT), and weather condition (W). Drivers give their responses with the importance level between two (2) criteria. Figure 10 shows the questionnaire result of a driver.
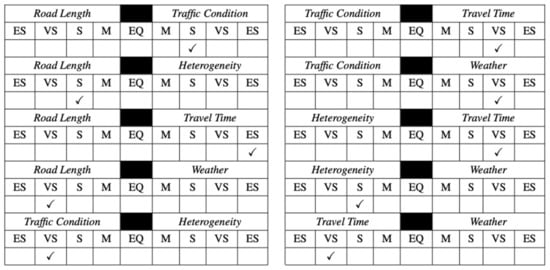
Figure 10.
Driver (1) Questionnaire Result.
The preference of the driver is converted into PCM. As seen in the following matrix, at first, the driving preferences are converted into a linguistic PCM. Based on the Fuzzy membership function that is used in this paper, the PCM with linguistic value will change into three (3) crisp values, as seen in the matrix on the right side.
| RL | TC | H | TT | W | RL | TC | H | TT | W | |||
| RL | EQ | S | VS | RL | (1, 1, 1) | (4, 5, 6) | (6, 7, 8) | |||||
| TC | S | EQ | VS | TC | (4, 5, 6) | (1, 1, 1) | (6, 7, 8) | |||||
| H | EQ | S | => | H | (1, 1, 1) | (4, 5, 6) | ||||||
| TT | ES | VS | VS | EQ | VS | TT | (9, 9, 9) | (6, 7, 8) | (6, 7, 8) | (1, 1, 1) | (6, 7, 8) | |
| W | VS | EQ | W | (6, 7, 8) | (1, 1, 1) |
As seen in the conversion matrix, the reciprocal value is also converted based on the following rule of F-AHP. The reciprocal value of “Moderate” ( covers (, , and ), the reciprocal value of “Strong” ( is used to define the value of (, , and ), and so on. By using the middle value in Fuzzy, the consistency ratio is calculated.
Consistency Ratio Validation for Driver’s Preferences
The following PCMs (left side) contain the middle value in Fuzzy membership based on the criteria comparison. The normalization process begins by summing up each criterion in the same column and dividing each criterion value with the summation results. As seen on the right side of the following PCMs, it shows the result of normalization PCM. In the end, for every column in the same row, these values will be calculated as its average value.
The average value illustrates the initiation of criteria weight in classic AHP. If the consistency ratio fit the threshold, criteria weight could be used in RCV calculation and personalized route recommendation. Otherwise, there must be an adjustment in PCW. Overall, the measurement of the consistency ratio begins based on this value.
| RL | TC | H | TT | W | RL | TC | H | TT | W | Average | |||
| RL | 1 | 0.2 | 5 | 0.11 | 7 | RL | 0.07 | 0.01 | 0.25 | 0.07 | 0.35 | 0.15 | |
| TC | 5 | 1 | 7 | 0.14 | 0.14 | TC | 0.33 | 0.07 | 0.35 | 0.09 | 0.01 | 0.17 | |
| H | 0.2 | 0.14 | 1 | 0.14 | 5 | => | H | 0.01 | 0.01 | 0.05 | 0.09 | 0.25 | 0.08 |
| TT | 9 | 7 | 7 | 1 | 7 | TT | 0.59 | 0.46 | 0.35 | 0.65 | 0.35 | 0.48 | |
| W | 0.14 | 7 | 0.2 | 0.14 | 1 | W | 0.01 | 0.46 | 0.01 | 0.09 | 0.05 | 0.12 | |
| Sum | 15.34 | 15.34 | 20.20 | 1.54 | 20.14 |
Furthermore, the following matrix is the product between the middle value of Fuzzy membership and the average value from the previous calculation. This step must be carried out in order to calculate the maximum eigenvalue from PCW and criteria weight.
| RL | TC | H | TT | W | Sum (x’) | |
| RL | 0.15 | 0.03 | 0.41 | 0.05 | 0.87 | 1.51 |
| TC | 0.75 | 0.17 | 0.58 | 0.07 | 0.02 | 1.58 |
| H | 0.03 | 0.02 | 0.08 | 0.07 | 0.62 | 0.82 |
| TT | 1.34 | 1.17 | 0.58 | 0.48 | 0.87 | 4.43 |
| W | 0.02 | 1.17 | 0.02 | 0.07 | 0.12 | 1.40 |
The eigenvalue calculates by dividing the x′ by x. In this case, x′ is the row summation in the previous matrix, and x is the average value (initial criteria weight) that was calculated before. By using Equation (3), the eigenvalue of each criterion is calculated. Meanwhile, is the average eigenvalue from every criterion.
According to Equation (4), the determination of consistency index (CI) needs the maximum eigenvalue and the number of criteria. As mentioned in the previous section, the ratio index (RI) is a constant. Since this research is using five (5) criteria, the value of RI is 1.12. Table 4 shows the measurement results of maximum eigenvalue, consistency index, and consistency ratio. It shows 1.12 as the consistency ratio, and it means the initial PCM must be adjusted.

Table 4.
Ratio Index.
The adjustment of PCM must be carried out by changing the middle value (based on the Fuzzy membership function). This process must be carried out continuously until .
| RL | TC | H | TT | W | RL | TC | H | TT | W | |||
| RL | 1 | 0.2 | 5 | 0.11 | 7 | RL | 1 | 0.33 | 0.33 | 0.14 | 0.33 | |
| TC | 5 | 1 | 7 | 0.14 | 0.14 | TC | 3 | 1 | 0.33 | 0.14 | 0.33 | |
| H | 0.2 | 0.14 | 1 | 0.14 | 5 | => | H | 3 | 3 | 1 | 0.20 | 3 |
| TT | 9 | 7 | 7 | 1 | 7 | TT | 7 | 7 | 5 | 1 | 7 | |
| W | 0.14 | 7 | 0.2 | 0.14 | 1 | W | 3 | 3 | 0.33 | 0.14 | 1 |
The matrices above show the adjustment in order to reach consistency in driving preferences. On the left side, it shows the original PCM from a driver, and on the other side, it shows the results of adjustment in PCM. The ratio in the right-side matrix is 0.1. At the time the consistency is in the threshold, the PCM is returned into the Fuzzy form PCM, as shown in the matrix below. Every comparison of criteria has lower, middle, and upper values.
| RL | TC | H | TT | W | |
| RL | (1, 1, 1) | (4, 5, 6) | (6, 7, 8) | ||
| TC | (4, 5, 6) | (1, 1, 1) | (6, 7, 8) | ||
| H | (1, 1, 1) | (4, 5, 6) | |||
| TT | (9, 9, 9) | (6, 7, 8) | (6, 7, 8) | (1,1,1) | (6, 7, 8) |
| W | (6, 7, 8) | (1, 1, 1) |
This final PCM is used to find the criteria weight. By using the Geometric Mean as shown in Equations (6)–(9), the criteria weight in F-AHP is concluded. Figure 11 shows the proportion of each criterion priority for a driver. It shows that “Travel Time” is the most important criterion for this driver, which dominates another criterion. The rest of the criteria’s priorities are “Heterogeneity”, “Weather”, “Traffic Condition”, and “Route Length”.
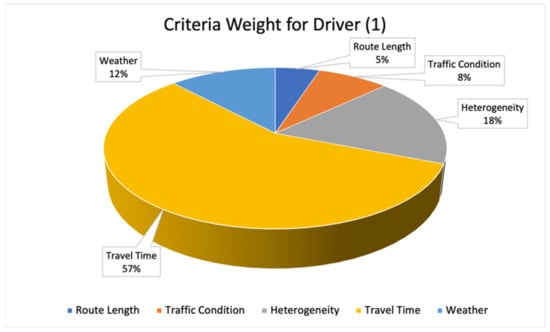
Figure 11.
Criteria Weight for Driver (1).
4.2. Decision Making
The decision-making process begins when criteria weight and alternative routes are calculated. Alternative routes generate based on the minimum RCV. The observation area in this research covers 265 road segments in R.E Martadinata Street, Bandung, Indonesia. In the simulation, the pair of origin and destination is given to a specific intersection, namely “Juanda” and “Laswi” nodes, respectively.
Based on the calculation of RCV, several routes are generated from the origin to its destination. Table 5 shows the routes for drivers for whom criteria weight is calculated. These routes have the minimum RCV among other route possibilities.

Table 5.
Alternate Routes based on Minimum RCV.
Meanwhile, Table 6 shows the value for every criterion of alternative routes. The route length is measured by meters and travel time is measured by seconds. Another criterion has its own scale, as traffic condition is described by 0–3 which illustrates from free flow to heavy traffic. Heterogeneity illustrates the various kind of vehicles on the road, higher value describes that there is a lot of variances of vehicles on the road. This condition also applies to the weather condition. The value range in this criterion is 0–1, which 1 illustrates the worst condition.

Table 6.
Criteria Value of Alternative Routes.
The best route is determined based on these alternative routes. The process of decision-making is measured by using MCDM methods: Analytic Hierarchy Process (AHP), Analytic Hierarchy Process—Express (AHP-Express), and Technique for Others Preference by Similarity to Ideal Solution (TOPSIS).
4.2.1. Analytic Hierarchy Process (AHP)
AHP needs to compare every alternative based on the criterion. In this route recommendation, every alternative will be compared to each other based on its route length, traffic condition, heterogeneity, travel time, and weather condition. AHP compared the alternatives based on their importance level. It means the simulation results in Table 6, must be converted to the scale of AHP’s importance level (1–9).
The result of conversion and comparison of alternatives based on the criterion is shown in Table 7. The normalization process for every comparison matrix is a must. It is normalized by counting the summation of every row in the same column, and each value in the comparison of alternatives. Later, by calculating the average of a row in alternative to the comparison, the priority of each alternative based on the criterion is determined.

Table 7.
Comparison of Alternatives based on Criterion—AHP.
Matrices below show the compilation of alternative priorities based on the criterion (left side), the criteria weight (center), and the final alternative priority (right side). The alternative priority based on the criteria is determined by normalization and averaging the comparison of alternatives.
The product between the alternative priority (for each criterion) and criteria weight is the final priority of each alternative. The highest priority determines the result of the decision-making process. In this case, the best route for the driver (1) is Route 2.
| RL | TC | H | TT | W | Criteria Weight | Alternative Priority | |||||
| Route-1 | 0.318 | 0.32 | 0.060 | 0.328 | 0.25 | . | RL | 0.049 | Route-1 | 0.269 | |
| Route-2 | 0.534 | 0.04 | 0.151 | 0.540 | 0.25 | TC | 0.082 | Route-2 | 0.393 | ||
| Route-3 | 0.093 | 0.32 | 0.638 | 0.069 | 0.25 | H | 0.182 | = | Route-3 | 0.216 | |
| Route-4 | 0.055 | 0.32 | 0.151 | 0.064 | 0.25 | TT | 0.566 | Route-4 | 0.123 | ||
| W | 0.121 |
4.2.2. Analytic Hierarchy Process—Express (AHP-Express)
AHP-Express is claimed faster in deciding classic AHP. This is caused by the number of alternative comparisons in AHP-Express is not much as classic AHP. AHP-Express only compares one alternative among others for each criterion.
It could choose randomly the alternative which will be compared. As shown in Table 8, compares route-4 to other alternatives in the route length and travel time. Route-2, route-1, and route-3 are compared to others in the criteria of traffic condition, heterogeneity, and weather condition, respectively.

Table 8.
Comparison of Alternatives based on Criterion—AHP-Express.
The alternative priority of each criterion is measured by determining the reciprocal value and normalization. Matrices below are the alternative priority of each criterion (left side) which is formed based on the normalization value in Table 8, the criteria weight (center) that was calculated earlier, and the final result of the priority of each alternative (right side). The determination of the best route for the driver (1) is based on the highest priority among the alternatives. For driver (1), the AHP-Express recommends Route-2 to be passed.
| RL | TC | H | TT | W | Criteria Weight | Alternative Priority | |||||
| Route-1 | 0.353 | 0.32 | 0.045 | 0.375 | 0.25 | . | RL | 0.049 | Route-1 | 0.294 | |
| Route-2 | 0.471 | 0.04 | 0.136 | 0.5 | 0.25 | TC | 0.082 | Route-2 | 0.364 | ||
| Route-3 | 0.118 | 0.32 | 0.682 | 0.062 | 0.25 | H | 0.182 | = | Route-3 | 0.221 | |
| Route-4 | 0.059 | 0.32 | 0.136 | 0.062 | 0.25 | TT | 0.566 | Route-4 | 0.119 | ||
| W | 0.121 |
4.2.3. Technique for Others Preference by Similarity to Ideal Solution (TOPSIS)
In TOPSIS, there is no conversion of criteria values and comparison between criteria. The decision-making process uses the result of simulation directly. It begins with normalization using Equation (14). The left side of the matrices below shows the result of the calculation using this formula. Meanwhile, the right side shows the normalization of alternative values.
| Alternatives | RL | TC | H | TT | W | Alternatives | RL | TC | H | TT | W | |
| 1 | 8,225,424 | 3.61 | 9 | 140,379.108 | 0.25 | 1 | 0.483 | 0.455 | 0.525 | 0.477 | 0.5 | |
| 2 | 7,177,041 | 6.25 | 8.41 | 110,598.814 | 0.25 | 2 | 0.451 | 0.598 | 0.508 | 0.423 | 0.5 | |
| 3 | 9,603,801 | 3.61 | 6.76 | 181,038.336 | 0.25 | => | 3 | 0.522 | 0.455 | 0.455 | 0.541 | 0.5 |
| 4 | 10,240,000 | 4 | 8.463 | 185,813.586 | 0.25 | 4 | 0.539 | 0.479 | 0.509 | 0.548 | 0.5 | |
| Sum | 35,246,266 | 17.47 | 32.633 | 617,829.844 | 1 |
The normalized value will be processed with the criteria weight, and it delivers the weighted normalization matrix, as shown in the matrix below. According to this result, the value of the ideal solution (positive and negative) is defined.
| Alternatives | RL | TC | H | TT | W |
| 1 | 0.024 | 0.037 | 0.096 | 0.270 | 0.61 |
| 2 | 0.022 | 0.059 | 0.092 | 0.239 | 0.61 |
| 3 | 0.026 | 0.037 | 0.083 | 0.306 | 0.61 |
| 4 | 0.026 | 0.039 | 0.093 | 0.310 | 0.61 |
All criterion in this research is cost criterion since the lower value is expected in order to find the best route. Based on this condition, the positive ideal solution is the smallest value among the alternatives based on each criterion, and the highest value will be the negative ideal solution. Table 9 shows the positive and negative ideal solutions from the weighted normalization matrix.

Table 9.
Positive and Negative Ideal Solution.
Using these ideal values, the distance between each value in weighted normalization and its ideal solution is determined. Table 10 and Table 11 show the distance between positive () and negative () ideal solutions to the criteria value in the weighted normalization matrix.

Table 10.
Positive Ideal Distance.

Table 11.
Negative Ideal Distance.
The distance of the ideal value (positive and negative) is important due to finding the decision using TOPSIS. These values are used in calculating the performance index () for each alternative. The final decision is determined based on the highest performance index among the alternatives. According to the calculation of the performance index, the recommended route for driver (1) is Route-2, as shown in Table 12.

Table 12.
Performance Index.
4.3. Personal Route Recommendation Analysis
4.3.1. Driver’s Criteria Weight
The validation for each driver who participated in the questionnaires is processed. Several driving preferences of drivers need to be adjusted in order to have consistent preferences. For every driving preference that is already consistent, the process of weight calculation begins using F-AHP. Table 13 shows the criteria weight for drivers that participated in this research.

Table 13.
Criteria Weight for Drivers.
As seen in Figure 12a,b, the distribution of criteria weight for motorcycle and car drivers is shown. For motorcycle drivers, there are two drivers who prioritize the travel time among the other criteria. Meanwhile, the other motorcycle drivers choose traffic conditions as the top-prioritized criteria between others. Slightly different from the previous type of vehicle, several car drivers prioritize the route length and weather conditions only. There are three (3) drivers who set the travel time as the priority of their driving preferences. There is a driver has two priorities, namely traffic condition and travel time. The other driver has almost similar priority in traffic conditions, route length, and weather conditions.
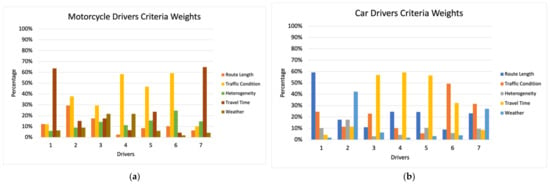
Figure 12.
Distribution of Driving Preferences (Criteria Weight) for Drivers: (a) Motorcycle; (b) Car.
4.3.2. Personal Route Recommendation
The origin and destination in the simulation are already designated namely the “Juanda” and “Laswi” intersection. Based on the diversity in driving preferences of each driver, the recommended route could be varied. In order to decide the recommended route that is appropriate to the driver’s preference, there will be an alternative route calculation. As mentioned in the previous section, in this paper the alternative routes come from the next minimum of RCV. The system will have four (4) alternatives as inputs of personalized route recommendations. Table 14 shows the result of the alternative route calculation for motorcycle driver 1.

Table 14.
Alternative Routes for Motorcycle Driver 1.
Based on its alternatives, there will be a selection of the best route for each driver according to their preferences. By using AHP, AHP-Express, and TOPSIS as decision-making methods, the personalized route is measured. Table 15 shows the route comparison between decision-making methods. As result, the three (3) decision-making methods draw the same personal route for drivers.

Table 15.
Route Recommendation based on Decision-Making Methods.
In addition to the route comparison between decision-making methods, there is also time processing comparison using these methods. When calculating the best route using AHP, it needs 0.000120367 to 0.000150967 s to deliver the recommended route. Slightly faster than AHP, TOPSIS needs up to 0.000194667 s to decide which route to recommend to the driver. Meanwhile, by using AHP-Express the time needed for finding the best route is only not more than 0.000262633 s for every driver.
Overall, AHP-Express not only decides the route 45% faster than AHP but also 23 % faster than TOPSIS. Figure 13 shows the time that takes in order to calculate the best route for each driver.
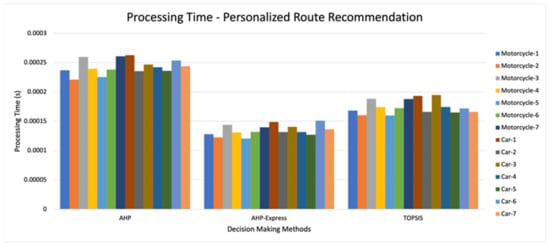
Figure 13.
Processing Time Comparison between Decision-Making Methods.
Since the recommendation system delivers the same personal route for various methods, Table 16 shows the route complete with its road segments that are suggested to be passed. In this simulation, the recommended route covers two routes, such: (1) Juanda-Trunojoyo-RuasTrunojoyo-Halmahera-Banda-Cimanuk 1-Lombok-Cihapit-Pramuka-Anggrek 0-Laswi, and (2) Juanda-Merdeka-Seram 0-Saparua 2-Saparua 0-LombokSelatan 1-Aceh 2-Aceh 1-Pramuka-Anggrek 0-Laswi. The calculation of these routes is determined based on the criteria weight of the drivers.

Table 16.
Variances of Route Recommendation for Each Driver.
The recommendation system suggests route group 1 (red colored line) to the driver who has travel time as their main driving preference. Meanwhile, the second group (blue colored line) can be used by the other driver with other criteria as their preferences. Figure 14 shows the variance of route recommendations. This result shows that the proposed system could recommend the personal route based on driving preferences.
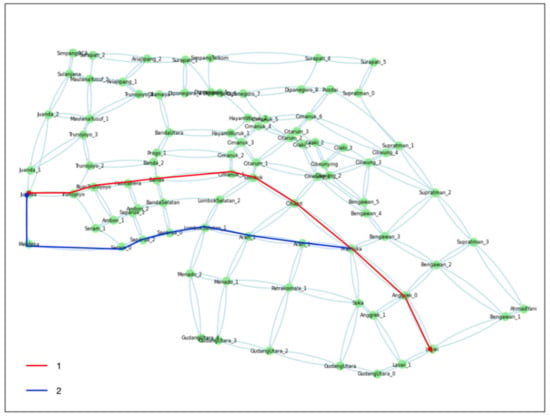
Figure 14.
Variances of Route Recommendation.
4.3.3. Agility Comparison
Agility is a method for validating multicriteria decision-making [55]. This method evaluates the requirement of judgments that comes from humans or systems. In this paper, the agility of decision-making methods that will be compared is limited to the AHP, AHP-Express, and TOPSIS. However, in the weight calculation, the measurement of agility is only for F-AHP. In the end, the comparison of agility MCDM covers F-AHP, F-AHP-Express, and Hybrid Methods (F-AHP-TOPSIS).
Overall, the final measurement of judgment (J) is a compilation of the weight calculation () and decision-making () methods. Equation (19) is used to measure the final judgment.
The calculation of criteria weight using AHP needs comparison from decision makers. The number in comparison is the judgment that is needed in this method. AHP requires comparison of criteria or alternatives (Leal, 2020). The number of criteria comparisons is influenced by the number of criteria (c). Based on the F-AHP workflow, its judgment needs a similar number to classic AHP judgment. Equation (20) shows the judgment of weight calculation using F-AHP.
Decision-making using classic AHP requires the number of comparisons as much as the weight calculation method, but in decision-making, it compares the alternatives (a) despite the criteria (c). In the process of making a decision using this method, it needs a comparison between alternatives based on each criterion. More criteria need more comparison in making a decision. Equation (21) shows the judgment in decision-making using AHP.
AHP-Express is developed in order to reduce the number of comparisons from classic AHP. It successfully reduces the total comparison from to , because it only compares one alternative among others. However, the required judgment for AHP-Express still needs the comparison of alternatives based on criteria. The judgment of decision-making using AHP-Express is shown in Equation (22).
Decision-making using TOPSIS needs judgments from the system, and it needs simpler judgments compared to classic AHP. Judgment is needed in order to calculate the weighted normalized matrix. It makes TOPSIS requirements for judgments are alternatives (a) and criteria (), as shown in Equation (23).
Table 17 shows all judgments that are needed in each MCDM method. The route recommendation system in this paper uses five (5) criteria, namely: route length; traffic condition; heterogeneity; travel time; weather condition, and four (4) alternatives. According to the number of criteria and alternatives in this research, the agility of each method is compared.

Table 17.
Total Judgment for MCDM Methods.
According to the agility calculation of each method, F-AHP and F-AHP-TOPSIS requires 40 and 30 judgments, respectively. On the other hand, F-AHP-Express needs only 25 judgments. Based on this comparison, F-AHP-Express needs the least judgments among others. It means F-AHP-Express has the best agility since it needs minimum judgment than F-AHP and F-AHP-TOPSIS. This comparison of agility between these three methods is shown in Figure 15.
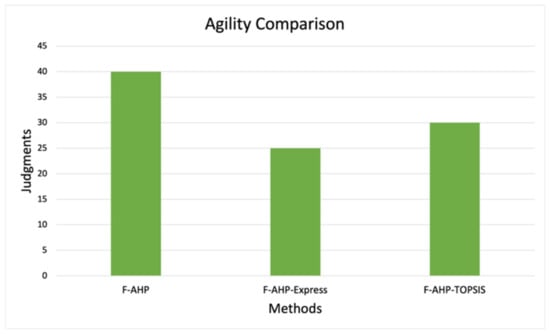
Figure 15.
Agility Comparison between MCDM Methods.
4.3.4. Decision-Making Complexity
There will be an explanation for each process in the decision-making methods in order to determine its complexity. The complexity measurement is only applied to the decision-making methods. The measurement complexity takes the highest notation and removes the smaller notation. If it is applied to whole methods, there will be no differences between the methods. Table 18 shows the steps in the decision-making methods used in this paper.

Table 18.
The Steps of Decision-Making Methods.
AHP needs several steps to decide its decision, namely: (1) comparison of alternatives based on criteria; (2) row summation; (3) normalization of alternative comparison matrix; (4) averaging the value; (5) calculation of alternative priority.
Even though AHP-Express works almost similar to classical AHP, the detailed step in making a decision using AHP-Express is completely different from classical AHP. It needs (1) alternative comparison (one alternative for each criterion); (2) creating the reciprocal value; (3) normalization; and (4) decision making.
On the other hand, TOPSIS needs lots of steps to determine a decision. It consists of (1) row summation; (2) normalization of the simulation results; (3) calculation of weighted normalization matrix; (4) positive and negative ideal value calculation; (5) distance measurement of positive and negative ideal solution; (6) decision-making.
The measurement of complexity takes only the highest notation in the whole process. It removes the lower notation and the constant. As shown in the complexity calculation below, AHP, AHP-Express, and TOPSIS have , , and , respectively. AHP-Express has the lowest complexity among others.
Overall, the result of the experiments concludes that F-AHP-Express is the most suitable MCDM method for recommending the personal route for a driver. This method is not only having the fastest processing time but also requires the least judgments from decision makers. Meanwhile, the AHP-Express has the lowest complexity if compared to other decision-making methods. The final comparison between various MCDM methods is shown in Table 19.

Table 19.
Compilation of MCDM Methods Comparison.
5. Conclusions
This proposed system recommends a personalized route, which means that the route is suggested only to a specified driver based on the driving preferences. By using multicriteria decision making the best route is suggested to drivers according to their own preferences. MCDM methods that used in this paper consists of two (2) main process: weight calculation using F-AHP, and decision-making with various methods (AHP, AHP-Express, and TOPSIS).
F-AHP is a modified AHP that uses Fuzzy logic to simplify the process of comparison between criteria or alternatives in AHP. Fuzzy logic uses linguistic value which is easier to understand by humans than crisp value. In this paper, we reduce 19 options (as AHP needed) in criteria comparison to 11 options using the linguistic value in Fuzzy logic.
In the calculation of criteria weight, the validation of driving preferences is needed. It aimed at the consistency of preferences chosen by the drivers. In order to reach the suggested consistency ratio (less than 0.1), the adjustment of driving preferences is needed. It is carried out by changing the value of the driving preference continuously until the ratio is suitable for the threshold.
Based on the analysis, F-AHP-Express is the best combination between weight calculation and decision-making methods. F-AHP-Express has the smallest agility among others. It needs 37.5% and 16.67% fewer judgments from F-AHP and F-AHP-TOPSIS, respectively. As in the decision-making methods, AHP-Express works 45% faster than classical AHP and 23% faster than TOPSIS. Not only has the fastest processing time, but this method also has as its complexity, it is the lowest complexity compared to other methods (AHP and TOPSIS).
The observation area in this paper is in Jl. R.E. Martadinata, Bandung, Indonesia. The length of the road for each node in the observation area is categorized as a short distance road. The recommendation result may differ when there are several long-distance roads in the area.
For further research, the additional criteria can be considered as driving preferences, such as traffic lights or road closures. It makes the road networks change dynamically so the system will recommend more route variances. The automation of adjustment in defining the criteria weight is also possible to develop in the next research.
Author Contributions
Conceptualization, S.M.N., E.H. and K.K.; methodology, S.M.N., E.H. and K.K.; software, S.M.N.; validation, S.M.N. and R.Y.; formal analysis, S.M.N., E.H. and K.K.; investigation, S.M.N.; resources, S.M.N.; data curation, S.M.N.; writing—original draft preparation, S.M.N.; writing—review and editing, S.M.N.; visualization, S.M.N.; supervision, E.H. and K.K.; project administration, S.M.N.; funding acquisition, E.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to permission from owner.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Balioti, V.; Tzimopoulos, C.; Evangelides, C. Multi Criteria Decision Making Using TOPSIS Method Under Fuzzy Environment. Application in Spillway Selection. Proceedings 2018, 2, 637. [Google Scholar]
- Xiang, Q.J.; Ma, Y.F.; Lu, J. Optimal Route Selection in Highway Network Based on Travel Decision Making. In Proceedings of the 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007; pp. 1266–1270. [Google Scholar] [CrossRef]
- da Silva, R.F.; Bellinello, M.M.; de Souza, G.F.M.; Antomarioni, S.; Bevilacqua, M.; Ciarapica, F.E. Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants. Energies 2021, 14, 8281. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.M.D.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple Criteria Decision-Making Techniques and Their Applications—A Review of The Literature from 2000 to 2014. Econ. Res. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Eltarabishi, F.; Omar, O.H.; Alsyouf, I.; Bettayeb, M. Multi-Criteria Decision Making Methods and Their Applications—A Literature Review. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Detroit, MI, USA, 10–12 March 2020. [Google Scholar]
- Saaty, T.L. Fundamentals of the Analytic Hierarchy Process. In The Analytic Hierarchy Process in Natural Resource and Environmental Decision Making; Springer: Dordrecht, The Netherlands, 2001; pp. 15–35. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with The Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Helmy, S.E.; Eladl, G.H.; Eisa, M. Fuzzy Analytical Hierarchy Process (FAHP) Using Geometric Mean Method to Select Best Processing Framework Adequate to Big Data. J. Theor. Appl. Inf. Technol. 2021, 99, 20. [Google Scholar]
- Aliyev, R.; Temizkan, H.; Aliyev, R. Fuzzy Analytic Hierarchy Process-Based Multi-Criteria Decision Making for Universities Ranking. Symmetry 2020, 12, 1351. [Google Scholar] [CrossRef]
- Leal, J.E. AHP-Express: A Simplified Version of The Analytical Hierarchy Process Method. MethodX 2020, 7, 100748. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria Decision Making in Energy Planning Using a Modified Fuzzy TOPSIS Methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Vinodh, S.; Mulanjur, G.; Thiagarajan, A. Sustainable Concept Selection Using Modified Fuzzy TOPSIS: A Case Study. Int. J. Sustain. Eng. 2013, 6, 109–116. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A Comparative Analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Alhabo, M.; Zhang, L. Multi-Criteria Handover Using Modified Weighted TOPSIS Methods for Heterogeneous Networks. IEEE Access 2018, 6, 40547–40558. [Google Scholar] [CrossRef]
- Kuo, T. A Modified TOPSIS with a Different Ranking Index. Eur. J. Oper. Res. 2017, 260, 152–160. [Google Scholar] [CrossRef]
- García-Cascales, M.S.; Lamata, M.T. On Rank Reversal and TOPSIS Method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Hendawi, A.M.; Rustum, A.; Ahmadain, A.A.; Hazel, D.; Teredesai, A.; Oliver, D.; Ali, M.; Stankovic, J.A. Smart Personalized Routing for Smart Cities. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 1295–1306. [Google Scholar] [CrossRef]
- Chang, G.; Wang, S.; Xiao, X. Review of Spatio-Temporal Models for Short-Term Traffic Forecasting. In Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Engineering (ICITE 2016), Singapore, 20–22 August 2016; pp. 8–12. [Google Scholar] [CrossRef]
- Dauwels, J.; Aslam, A.; Asif, M.T.; Zhao, X.; Mitrovic, N.; Cichocki, A.; Jaillet, P. Predicting Traffic Speed in Urban Transportation Subnetworks for Multiple Horizons. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014. [Google Scholar]
- Nasution, S.M.; Husni, E. Kuspriyanto the Effect of Heterogeneous Traffic Flow on the Transportation System. In Proceedings of the 2018 International Conference on Electrical Engineering, Computing Science, Mexico City, Mexico, 12–14 November 2008; Volume 1. [Google Scholar]
- Kponyo, J.; Kung, Y.; Zhang, E. Dynamic Travel Path Optimization System Using Ant Colony Optimization. In Proceedings of the 2014 UKSim—AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 142–147. [Google Scholar] [CrossRef]
- George, B.; Kim, S. Spatio-Temporal Networks Modeling and Algorithms; Briefs in Computer Science; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ge, Y.; Li, H.; Tuzhilin, A. Route Recommendations for Intelligent Transportation Services. IEEE Trans. Knowl. Data Eng. 2021, 33, 1169–1182. [Google Scholar] [CrossRef]
- Ferreira, H.; Rodrigues, C.M.; Pinho, C. Impact of Road Geometry on Vehicle Energy Consumption and CO2 Emissions: An Energy-Efficiency Rating Methodology. Energies 2019, 13, 119. [Google Scholar] [CrossRef]
- Namoun, A.; Tufail, A.; Mehandjiev, N.; Alrehaili, A.; Akhlaghinia, J.; Peytchev, E. An Eco-Friendly Multimodal Route Guidance System for Urban Areas Using Multi-Agent Technology. Appl. Sci. 2021, 11, 2057. [Google Scholar] [CrossRef]
- Paiva, S.; Pañeda, X.G.; Corcoba, V.; García, R.; Morán, P.; Pozueco, L.; Valdés, M.; Del Camino, C. User Preferences in the Design of Advanced Driver Assistance Systems. Sustainability 2021, 13, 3932. [Google Scholar] [CrossRef]
- Litzinger, P.; Navratil, G.; Sivertun, Å.; Knorr, D. Using Weather Information to Improve Route Planning. In Bridging the Geographic Information Sciences. Lecture Notes in Geoinformation and Cartography; Gensel, J., Josselin, D., Vandenbroucke, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 199–214. [Google Scholar] [CrossRef]
- Bin, C.; Gu, T.; Sun, Y.; Chang, L.; Sun, L. A Travel Route Recommendation System Based on Smart Phones and IoT Environment. Wirel. Commun. Mob. Comput. 2019, 2019, 7038259. [Google Scholar] [CrossRef]
- Das, P.; Ribas-Xirgo, L. Parameter Estimation for Optimal Path Planning in Internal Transportation. arXiv 2018, arXiv:1808.00522. [Google Scholar]
- Kazhaev, A.; Almetova, Z.; Shepelev, V.; Shubenkova, K. Modelling Urban Route Transport Network Parameters with Traffic, Demand and Infrastructural Limitations Being Considered. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 177. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Mahmoodian, V.; Bojović, N. Dynamic Inventory Routing and Pricing Problem with a Mixed Fleet of Electric and Conventional Urban Freight Vehicles. Sustainability 2021, 13, 6703. [Google Scholar] [CrossRef]
- Nasution, S.M.; Husni, E.; Kuspriyanto, K.; Yusuf, R.; Yahya, B.N. Contextual Route Recommendation System in Heterogeneous Traffic Flow. Sustainability 2021, 13, 13191. [Google Scholar] [CrossRef]
- Jung, J.; Park, S.; Kim, Y.; Park, S. Route Recommendation with Dynamic User Preference on Road Networks. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing (BigComp), Kyoto, Japan, 27 February 2019–2 March 2019; pp. 1–7. [Google Scholar]
- Shenpei, Z.; Xinping, Y. Driver’s Route Choice Model Based on Traffic Signal Control. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 2331–2334. [Google Scholar] [CrossRef]
- He, Z.; Chen, K.; Chen, X. A Collaborative Method for Route Discovery Using Taxi Drivers’ Experience and Preferences. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2505–2514. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Erkan, T.E. Selection of Academic Staff Using The Fuzzy Analytic Hierarchy Process (FAHP): A Pilot Study. Teh. Vjesn. 2012, 19, 923–929. [Google Scholar]
- Odu, G. Weighting Methods for Multi Criteria Decision Making Technique. J. Appl. Sci. Environ. Manag. 2019, 23, 1449. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Ozcan, E.C.; Unlusoy, S.; Eren, T. A Combined Goal Programming—AHP Approach Supported with TOPSIS for Maintenance Strategy Selection in Hydroelectric Power Plants. Renew. Sustain. Energy Rev. 2017, 78, 1410–1423. [Google Scholar] [CrossRef]
- He, C.; Zhang, Q.; Ren, J.; Li, Z. Combined Cooling Heating and Power Systems: Sustainability Assessment Under Uncertainties. Energy 2017, 139, 755–766. [Google Scholar] [CrossRef]
- Rajak, M.; Shaw, K. Evaluation and Selection of Mobile Health (MHealth) Applications Using AHP and Fuzzy TOPSIS. Technol. Soc. 2019, 59, 923–929. [Google Scholar] [CrossRef]
- Abdel-Malak, F.F.; H. Issa, U.; H.Miky, Y.; Osman, E.A. Applying Decision-Making Techniques to Civil Engineering Projects. Beni-Suef Univ. J. Basic Appl. Sci. 2017, 6, 326–331. [Google Scholar]
- Parezanovic, T.; Tarle, S.P.; Petrovic, N. A Multi-Criteria Decision Making Approach for Evaluating Sustainable City Logistics Measures. In Proceedings of the 5th International Conference Transport and Logistics, Hammamet, Tunisia, 1–3 May 2014. [Google Scholar]
- Kumar, R.R.; Mishra, S.; Kumar, C. Prioritizing The Solution of Cloud Service Selection Using Integrated MCDM Methods Under Fuzzy Environment. J. Supercomput. 2017, 73, 4652–4682. [Google Scholar] [CrossRef]
- Kou, G.; Lin, C. A Cosine Maximization Method for the Priority Vector Derivation in AHP. Eur. J. Oper. Res. 2014, 235, 225–232. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Lo, W.T.; Sheu, R.K. An AHP-Based Recommendation System for Exclusive or Specialty Stores. In Proceedings of the 2011 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Beijing, China, 10–12 October 2011; pp. 16–23. [Google Scholar] [CrossRef]
- Chou, C.-C.; Yu, K.-W. Application of a New Hybrid Fuzzy AHP Model to the Location Choice. Math. Probl. Eng. 2013, 2013, 12. [Google Scholar] [CrossRef]
- Putra, M.S.D.; Andryana, S.; Fauziah; Gunaryati, A. Fuzzy Analytical Hierarchy Process Method to Determine the Quality of Gemstones. Adv. Fuzzy Syst. 2018, 2018, 6. [Google Scholar]
- Kwong, C.K.; Bai, H. A Fuzzy AHP Approach to The Determination of Importance Weights of Customer Requirements in Quality Function Deployment. J. Intell. Manuf. 2002, 13, 367–377. [Google Scholar] [CrossRef]
- Aggarwal, A.G. Aakash An Innovative B2C E-Commerce Websites Selection Using the ME-OWA and Fuzzy AHP. In Proceedings of the First International Conference on Information Technology and Knowledge Management, Turin, Italy, 22–26 October 2018; Volume 14, pp. 13–19. [Google Scholar]
- Khorramrouz, F.; Kajabadi, N.P.; Galankashi, M.R.; Rafiei, F.M. Application of Fuzzy Analytic Hierarchy Process (FAHP) in Failure Investigation of KnowledgeBased Business Plans. Appl. Sci. 2019, 1, 1386. [Google Scholar]
- Chandak, M.M.A.; Borkar, P. Review on Optimal Route Guidance Using Analytical Hierarchy Process. In Proceedings of the 2015 IEEE 9th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, Indiam, 9–10 January 2015; Volume 9. [Google Scholar]
- Buckley, J.J. Fuzzy Hierarchical Analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Zlaugotne, B.; Zihare, L.; Balode, L.; Kalnbalkite, A.; Khabdullin, A.; Blumberga, D. Multi Criteria Decision Analysis Methods Comparison. Environ. Clim. Technol. 2020, 24, 454–471. [Google Scholar] [CrossRef]
- Ghaleb, A.M.; Kaid, H.; Alsamhan, A.; Mian, S.H.; Hidri, L. Assessment and Comparison of Various MCDM Approaches in the Selection of Manufacturing Process. Adv. Mater. Sci. Eng. 2020, 2020, 4039253. [Google Scholar] [CrossRef]
- Nadaban, S.; Dzitac, S.; Dzitac, I. Fuzzy TOPSIS: A General View. Procedia Comput. Sci. 2016, 91, 823–831. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications A State-of-the-Art Survey. In Lecture Notes in Economics and Mathematical Systems; Springer: New York, NY, USA, 1981. [Google Scholar]
- Ball, S.; Korukoglu, S. Operating System Selection Using Fuzzy AHP and TOPSIS Methods. Math. Comput. Appl. 2009, 14, 119–130. [Google Scholar] [CrossRef]
- Shafiq, M. Dynamic Route Optimization for Heterogeneous Agent Envisaging Topographic of Maps. EPiC Ser. Eng. 2018, 2, 206–217. [Google Scholar]
- Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. Engineering and Augmenting Route Planning Algorithms. Algorithm. Large Complex Netw. 2009, 5515, 117–139. [Google Scholar]
- Elmahmoudi, F.; El Kheir Abra, O.; Raihani, A.; Serrar, O.; Bahatti, L. GIS Based Fuzzy Analytic Hierarchy Process for Wind Energy Sites Selection in Tarfaya Morocco. In Proceedings of the 2020 IEEE International conference of Moroccan Geomatics (Morgeo), Casablanca, Morocco, 11–13 May 2020. [Google Scholar]
- Meng, W.; Kai, L.; Songhui, Z. Evaluation of Electric Vehicle Charging Station Sitting Based on Fuzzy Analytic Hierarchy Process. In Proceedings of the 2013 Fourth International Conference on Digital Manufacturing & Automation, Shinan, China, 29–30 June 2013. [Google Scholar]
- Jupri, M.; Sarno, R. Data Mining, Fuzzy AHP and TOPSIS for Optimizing Taxpayer Supervision. Indones. J. Electr. Eng. Comput. Sci. 2020, 18, 75–87. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).