Abstract
The paper firstly proposes a deterministic deep feedforward neural network model aimed at predicting the city bus velocity profile over receding time horizon based on the following inputs: actual vehicle position, actual velocity or short-term history of vehicle velocities, time of day and day of week. A systematic analysis of the influence of different input subsets, history interval length and prediction horizon length is carried out to find an optimal configuration of NN model inputs and hyperparameters. Secondly, a stochastic version of neural network prediction model is proposed, which predicts expectations and standard deviations of velocity patterns over the receding time horizon. The stochastic model prediction accuracy is verified against the recorded test dataset features, as well as by comparing the predicted velocity expectation with the deterministic model prediction and correlating the predicted velocity standard deviation with deterministic model prediction uncertainty metrics. The verification results indicate that: (i) the deterministic model velocity prediction accuracy is characterized by the R2 score greater than 0.8 for the prediction horizon length of 10 s and remains to be solid (greater than 0.6) for the horizon lengths up to 25 s; (ii) the actual vehicle position and the velocity history are the most significant input features, where the optimal value of history interval length lies in the range from 30 to 50 s; (iii) the stochastic model have only slightly lower accuracy of predicting the velocity expectation along the receding horizon when compared to the deterministic model (the root mean square error is higher by 2.2%), and it outputs consistent standard deviation prediction.
1. Introduction
The design of an optimal energy management strategy of a plug-in hybrid electric vehicle (PHEV) is aimed at minimizing the fuel/energy consumption, while providing a high level of driving comfort and long battery life [1,2]. As such, it can benefit from knowing oncoming driving cycle time profiles, including those of vehicle velocity, road slope, ambient conditions, and similar. For instance, global optimization of PHEV control trajectories, used to establish performance benchmark, requires knowledge of the entire driving cycle in advance [3]. In online control strategies, the control trajectory is carried out over a receding time horizon, typically through Model Predictive Control (MPC) [4]. The main driving cycle-related feature relates to velocity time profile [5] because it directly translates into the power requirements for a particular vehicle. There are strong inherent uncertainties in predicting the vehicle velocity, which are associated with the stochasticity of traffic environment (due to traffic congestion, traffic lights and signs, pedestrians crossing the road, etc.), and which make the formulation and execution of prediction task challenging [6,7,8]. To summarize, recent research efforts in the field of PHEVs, and in general intelligent vehicles, have been focused on the development of advanced predictive vehicle control strategies, which require accurate and at least short-term predictions of future vehicle velocity profiles [9].
1.1. Literature Review
Due to the stochastic nature of driving cycles, it is difficult to perform accurate vehicle velocity prediction using traditional time series prediction approaches based on the linear regression models, such as ARIMA model [9]. Therefore, more sophisticated models have commonly been used in literature to predict the vehicle velocity, with emphasis on Markov chains and artificial neural networks (NN) [10]. In [8], the authors use the vehicle geographical coordinates, velocity, departure date and time, and historical data from a traffic database as inputs to a long short-term memory (LSTM) NN that predicts velocity on a particular road segment. Despite a rich set of input variables, a relatively rough prediction accuracy was obtained due to the insufficient amount of data used for prediction model training. A somewhat different approach is employed in [11], where an advanced Evolutionary Least Learning Machine (E-LLM) tool is proposed to predict the velocity sequence over a given time horizon, and where an exceptional prediction accuracy is reported, but for a very limited set of test-driving cycles. In [12], the authors systematically compare the performance of different prediction models divided in two main categories: (i) deterministic models that predict velocity expectation, and (ii) stochastic models that predict the entire velocity distribution. Numerous input data are used therein to parameterize prediction models, including vehicle internal data (CAN bus data) and external data, such as traffic light positions and stop signs and upcoming bends (on-board radar and traffic database). In [13], different designs of multivariate Markov chains for vehicle velocity prediction are systematically compared, and an approach based on multiple transition probability matrices (TPM) is proposed, where each serves to predict the vehicle velocity steps away in the future. The main advantage of the NN approach is the ability to automatically learn complex underlying patterns, i.e., non-linear relationships between input features, from the available data [9]. In addition, the NN approach has no limit on the number of input features as opposed to the alternative models based on Markov chains, where the TPM size increases exponentially with the number of input features.
In some studies, vehicle velocity prediction is performed in the position domain [14,15], since uncertainties related to road geometry (bends), traffic lights, bus stops, etc., are directly associated with position rather than time domain. In these approaches, different prediction models are typically combined for better prediction accuracy. For example, in [14] a Markov chain is combined with a NN model, and it is claimed that the combined model improves the prediction accuracy by approximately 25% on average when compared to the individual prediction models. In [15], the velocity profiles are predicted by using a stochastic Markov chain-based model, with vehicle velocity limits determined by applying statistical methods to recorded driving data along the considered route. The main disadvantage of position domain prediction comes from the fact that MPC systems require time profiles of predicted velocity, whereby the process of transforming profiles from the position domain to the time domain is not ambiguous, especially at the zero-velocity singularity point.
The velocity prediction models are typically tested in terms of prediction accuracy, execution time, and predictive control performance [9,10]. For example, in [16] the PHEV fuel consumption reduction performance is assessed for the following three cases: (i) full driving cycle knowledge, (ii) perfect velocity predictions on a receding horizon of 10 s, and (iii) actual velocity predictions on a receding horizon of 10 s obtained by applying LSTM NN model. The common metrics, such as root mean square error (RMSE), mean absolute error (MAE), and a coefficient of determination, i.e., R2 score between the actual and predicted velocity profiles are commonly used as prediction accuracy indicators.
1.2. Problem Statement
The design of PHEV powertrain configuration and associated control strategy can be more effective if the driving cycles utilized are more realistic and/or if the driving route is known in advance and/or if the statistical features of driving cycles are known from historical traffic data [17,18]. A priori knowledge of driving route and a rich set of historical data are regularly available in delivery and public transport systems due to known and often repeating driving schedules [19]. This makes the delivery and public transport vehicles suitable for the application of predictive control strategies [20]. To make the control strategy effective and viable, the velocity prediction models should be accurate, robust, and computationally efficient [21].
In the authors’ recent conference publication [22], a NN-based static stochastic model (labelled as NN-STC; see Figure 1a) has been proposed for predicting vehicle velocity distribution along a regular city bus route. The NN-STC relies on the vehicle position (i.e., the travelled distance from the departure station) as the only input feature and is capable of predicting the velocity probability distribution at different positions, , based on historical city bus tracking data. Although the analysis of NN-STC prediction accuracy have pointed to solid model performance in terms of capturing the recorded velocity distribution expectation and deviation (Figure 1b), it is evident that the single-input model is not capable to accurately predict individual, actual, and future velocity values. As such, the NN-STC model is not suitable for MPC applications. To overcome this weakness, the model should be extended with richer traffic information in terms of taking into account a wider set of model inputs and history of inputs, and formulating the output as a deterministic or stochastic velocity time profile over receding horizon, which is the main topic of this paper.
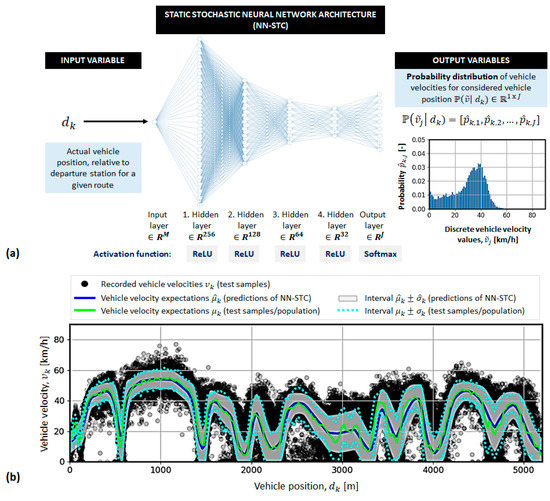
Figure 1.
Illustration of previously proposed static stochastic neural network (NN-STC) model [22] for predicting city bus velocity distribution along route (a), including related testing results (b).
1.3. Research Aim and Contributions
Based on the above state-of-the-art review, it may be concluded that the existing approaches to vehicle velocity prediction typically demands a multitude of input data, such as on-board radar data and traffic database [9,12], which are often unavailable in vehicles. Additionally, despite a rich set of input features used, the testing results of prediction models are mostly given only for a very limited set of test-driving cycles [8,11]. Finally, the prediction models are typically designed for the case of a generic route, thus relying only on the vehicle velocity and acceleration states as the main driving cycle-related input features [10,13]. As such, they do not consider the vehicle position state as an additional input feature that may significantly contribute to the vehicle velocity prediction accuracy [15], particularly for the vehicles operating over prescribed routes (such as city buses considered herein).
To this end, the paper proposes and systematically tests deterministic and stochastic NN models for predicting city bus velocity time profiles on receding horizon based on readily available vehicle data, which include actual vehicle position, actual vehicle velocity or velocity history sequence, time of the day, and day of the week, while the outputs contain sequence of vehicle velocities over the receding time horizon, including the velocity standard deviation in the case of a stochastic model.
The main contributions of this paper include: (i) design and comprehensive assessment of deterministic and stochastic variants of data-driven model for predicting vehicle velocity on receding time horizon, which is suitable for application in various intelligent transport systems based on the vehicle data only; and (ii) approach to in-depth analysis of the proposed models’ prediction accuracy aimed at finding the most suitable model configurations and hyperparameters in terms of selecting relevant input features and setting the velocity history interval and prediction horizon lengths.
The remaining part of the paper is organized as follows. Section 2 describes the overall procedure of city bus driving cycle recording and pre-processing for the need of training, validation, and testing of the proposed vehicle velocity prediction models. Section 3 presents the deterministic velocity prediction model, including a comprehensive analysis of prediction accuracy with respect to different sets of model hyperparameters. Section 4 introduces the stochastic velocity prediction model and presents a comparative analysis of its expectation prediction accuracy with respect to deterministic model. Concluding remarks are given in Section 5.
2. Description of the Recorded Dataset
2.1. Recorded Driving Cycles
The driving cycles have been collected on a set of 10 city buses of the same type (MAN Lion’s City NL 323) operating in the city of Dubrovnik [23]. Data recording was performed continuously for a period of six months by using a commercial GPS/GPRS vehicle tracking device installed on selected buses. The sampling time was set to one second to ensure sufficient data density with respect to the dynamics of vehicle velocity change. The relevant GPS recorded data include:
- Bus garage number;
- Timestamp;
- Bus geographical coordinates;
- Bus longitudinal velocity;
- Cumulative distance travelled (from odometer).
The data related to circular route Babin kuk–Pile–Babin kuk are considered herein, because this route has a relatively long length and stretches over different parts of the city. The recorded driving data have been segmented into driving cycles, where each driving cycle is defined by a time series of vehicle velocity and distance travelled between the two end stations, here Babin kuk and Pile. The driving cycles were filtered primarily to select those that do not include GPS signal losses or outliers. The criteria that a driving cycle needed to meet to be declared valid included:
- (1)
- The driving cycle follows the reference route trajectory, i.e., no detours are acceptable;
- (2)
- The time difference between each pair of consecutive driving cycle samples is equal to the nominal sampling time, i.e., 1 s;
- (3)
- The initial and final velocity of the driving cycle is equal to zero;
- (4)
- The vehicle acceleration values are within the interval of [–3, 3] m/s2;
- (5)
- The total number of numerically undetermined values (NaN) is zero;
- (6)
- The proportion of the dwell time samples to the total number of samples is less than 75%.
This filtration procedure has resulted in the total number of 2313 (91.6%) valid recorded driving cycles.
Figure 2 shows ten randomly selected valid driving cycles in the time and vehicle position domains. The variability of velocity time profiles is due to variations in traffic conditions along the day (Figure 2a). The velocity profiles are more predictable when expressed in the vehicle position domain (Figure 2b) because characteristic road features (e.g., traffic light, bus stops, open road segments, etc.) are spatially determined.
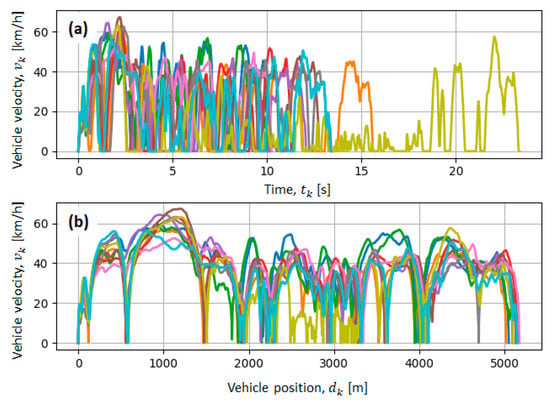
Figure 2.
Examples of ten randomly selected valid recorded driving cycles for the direction Babin kuk–Pile: velocity vs. time (a) and velocity vs. travelled distance (b) profiles.
2.2. Preparation of Training, Validation, and Test Datasets
The full set of 2313 valid driving cycles consists of a total set of 1,908,209 recorded data samples/points. Due to the complexity of the prediction task, learning the NN model on such a wide set of recorded data (2 million samples) can be a computationally demanding in terms of NN training time. Therefore, the following method of isolating a reduced set of data samples has been applied [22]: by passing through every 5th consecutive recorded time step for every -th recorded driving cycle, a single sample is randomly selected from each consecutive time interval and stored in the set . As shown in Figure 3, each selected time sample represents the reference point from which the history and future discrete velocity values are taken with the original sampling time of 1 s (vectors and , respectively), including the data on vehicle position , time of day , and day of week .
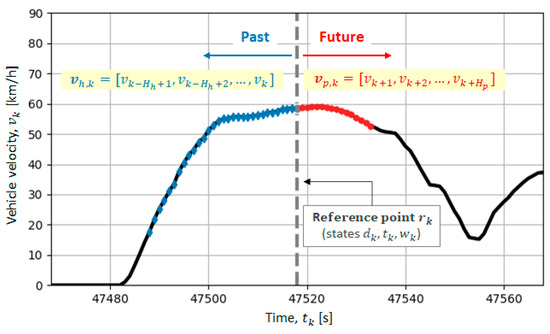
Figure 3.
Illustration of the process of generating input-output datasets and , necessary for training, validation, and testing of NN-based velocity prediction models.
The above pre-processing procedure results in the final/reduced set of 382,553 data samples, which forms NN input dataset and target values . The datasets and . are scaled to the interval [0, 1] according to the principle of min–max normalization and randomly divided into sets for NN model training (70% of samples), validation (15% of samples), and testing (15% of samples). The training dataset is used for the initial training/parameterization of the proposed models. The validation dataset is used for tuning the model’s hyperparameters and preventing of model overfitting. The test dataset is used to provide an unbiased evaluation of the final model on the previously unseen data.
3. Deterministic Vehicle Velocity Prediction Model
3.1. Modelling of Deep Neural Network with Deterministic Output
The deterministic velocity prediction model, hereinafter referred to as NN-DET, is based on the deep feedforward NN, whose architecture is shown in Figure 4. Inputs to the NN-DET model include data on the current vehicle position (), the current vehicle speed (or velocity history , as an alternative), the time of day , and the day of week . The output from the NN-DET model is the vector of predicted vehicle velocities , on the receding time horizon of length , where the index denotes the discrete time step of the input state (see Section 2). The NN-DET model consists of an input layer that receives input variables/features, four fully connected hidden layers containing 256, 128, 64, and 32 hidden neurons, and an output layer of elements. Note that if the vehicle velocity history vector , is used as the second input to NN-DET instead of the current velocity , then the number of inputs of NN-DET model increases by , which, consequently, increases the model complexity in terms of total number of adjustable model parameters. The hidden layers use the ReLU activation function, while the output layer contains the linear activation function [24]. The discrete time window lengths and represent hyperparameters, whose optimal values need to be determined through separate analysis.
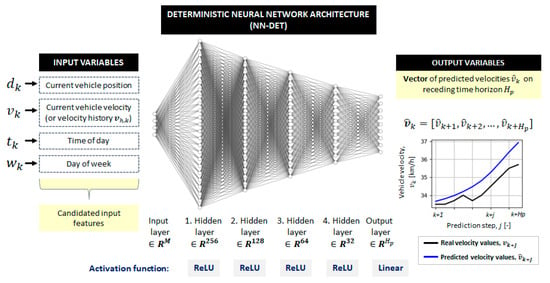
Figure 4.
Proposed architecture of deterministic deep feedforward neural network (NN-DET) for predicting vehicle velocity profile on receding time horizon .
To solve the regression problem, the mean squared error (MSE) between predicted ) and actual/recorded velocity vectors on the discrete time horizon has been chosen as the loss function to be minimized [24]:
where denotes the total number of samples used to train the NN-DET model (here 382,553; see Section 2). For better generalization of the NN-DET model, each hidden layer is regularized by regularization method (also known as ridge regression) [24], which adds the “squared magnitude” of the NN coefficients/weights, , as the penalty term to the loss function , with the regularization factor set to .
The realization of the NN-DET model from Figure 4 is performed within the Python programming environment by using the Keras [25] module with the Tensorflow [26] module as the backend. The built-in ADAM optimization algorithm with default settings is used to train the NN-DET model, since it has proven to be particularly suitable for training of deep NNs [27]. The number of samples from which the gradient is calculated (i.e., batch size) is set to 16, while the number of training epochs is set to 150.
3.2. Analysis of Deterministic Model Prediction Accuracy
3.2.1. Influence of Input Features
The main goal of this analysis is to determine the relevant input features for further consideration of NN-DET model. It is of particular interest to assess the benefits of including the current city bus position as an additional input in addition to velocity data that are typically used in the literature (see, e.g., [9]). To this end, the following combinations of input features are considered:
- (1)
- Current vehicle position ;
- (2)
- Current vehicle position and current vehicle velocity ;
- (3)
- Vehicle velocity history ;
- (4)
- Current vehicle position and vehicle velocity history ;
- (5)
- Current vehicle position , vehicle velocity history , and time of day ;
- (6)
- Current vehicle position , vehicle velocity history , time of day , and day of week .
For each of the above combinations of input features, training of separate NN-DET models is performed, which are denoted as NN-DET-In, where denotes the ordinal number of the input combination as listed above. Note that the fixed prediction horizon length s (and the fixed velocity history interval length s, when applicable) are applied to each model to make the comparative analysis consistent.
The NN-DET prediction accuracy is evaluated based on the root value of the loss function defined by Equation (1) and calculated for the case of validation dataset:
is given in km/h, thus providing better interpretability of results than that is given in km2/h2.
Figure 5 shows the loss values for each NN-DET-In model, which are also given in Table 1 along the number of adjustable NN parameters. The vehicle velocity profile prediction accuracy saturates in the case of NN-DET-I4 model ( km/h), which clearly indicates that both time of day and day of week have a negligible influence on the model prediction accuracy. The worst prediction accuracy is obtained for the NN-DET-I1 model ( km/h), which relies on the current vehicle position as the only input feature. The reason for this is the insufficient conditionality of the model with respect to the input data, as previously confirmed when predicting individual vehicle velocity values in the case of NN-STC model (Figure 1, [22]). By adding the current velocity next to the vehicle position (NN-DET-I2 model), a significant but still insufficient drop in from 11.84 km/h to 7.28 km/h (≈40%) is achieved. Despite using the vehicle velocity history as only input, the NN-DET-I3 model achieves the prediction accuracy close to the NN-DET-I4 model (km/h vs. km/h), which additionally uses the vehicle position input. It is important to note that none of the input feature combinations result in model overfitting, as evidenced by the absence of a gap between training and validation losses (Figure 5). Good model generalization properties are additionally confirmed through the closeness of the testing and validation losses (Table 1).
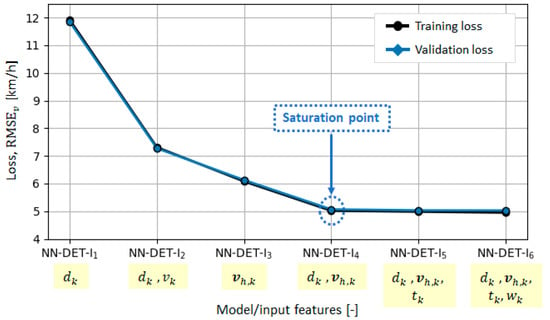
Figure 5.
RMSEv loss values obtained for each NN-DET-In model (defined by characteristic input feature sets) by using training and validation datasets.

Table 1.
Training, validation, and testing results for each NN-DET-In models (defined by characteristic input feature sets), including the number of adjustable model parameters.
3.2.2. Influence of Vehicle Velocity History Interval Length
To determine the optimal value of the vehicle velocity history interval length , the prediction accuracy of the NN-DET model is examined for the lengths {3, 7, 10, 15, 20, 30, 40, 50, 100, 200} s. The resulting models are referred to as NN-DET-Hh,T, where denotes the history interval length in seconds. Again, the loss values, defined by Equation (2) and calculated for the case of the validation dataset, are used to evaluate the prediction accuracy of the NN-DET-Hh,T model. When training each of the NN-DET-Hh,T models, the full set of candidate input features (, , , and ) is used along the fixed prediction horizon length s.
Figure 6 shows the values for each NN-DET-Hh,T model, with the numerical values contained in Table 2. These results point out that the validation loss is locally saturated at s, where equals 4.85 km/h, while in the case of longer velocity history ( s) increases to 4.96 km/h. The reason for this is that the NN-DET-Hh,200 model is overly conditioned by the input data, which leads to model overfitting, i.e., poorer model generalization properties. This is reflected in the increasing gap between the training and validation loss plots in Figure 6, while the validation and testing loss values are close to each other (Table 2). The values of in the range of 30 to 50 s represent an optimal selection, as they provide minimal loss on validation (and test) dataset and reduce the complexity of NN-DET model.
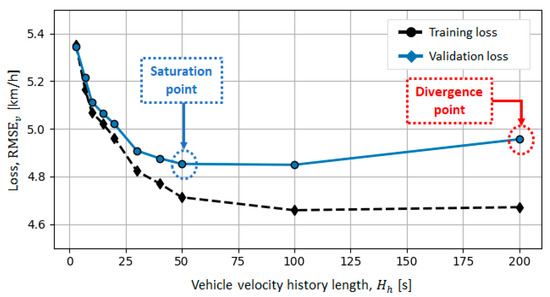
Figure 6.
RMSEv loss values obtained for different velocity history interval lengths Hh of NN-DET model by using training and validation datasets.

Table 2.
Training, validation, and testing results of NN-DET models with different history interval length [s], including the number of adjustable model parameters.
3.2.3. Influence of Vehicle Velocity Prediction Horizon Length
The prediction accuracy of the individual vehicle velocity profiles is evaluated for the following receding horizon lengths {3, 7, 10, 15, 20, 50, 100, 200} s. The prediction models are designated as NN-DET-Hp,T, where T denotes the receding horizon length in seconds. Each model is trained separately for the following input sets:
- Full set of candidate features (, , i );
- Vehicle velocity history only (),
With a fixed velocity history interval length s. Evaluation of the NN-DET-Hp,T model prediction accuracy is performed based on the following indicators calculated for the validation dataset:
- The loss value defined by Equation (2);
- The score value, calculated for each th discrete step of the prediction horizon length :
Figure 7 and Table 3 show the loss values for the various prediction horizon lengths , where the indices a and b correspond to the above-defined model input sets. These results indicate that the validation loss assumes almost linear upward trend until s for both input set cases, and then begin to saturate to the levels km/h in the case of NN-DET-Hp,a model (full set of inputs) and km/h in the case of NN-DET-Hp,b model (only the velocity history input), which are reached at s. The loss is higher by 23% on average for NN-DET-Hp,b model when compared to full model NN-DET-Hp,a, reaffirming the importance of including the current city bus position as an additional input feature of the model.
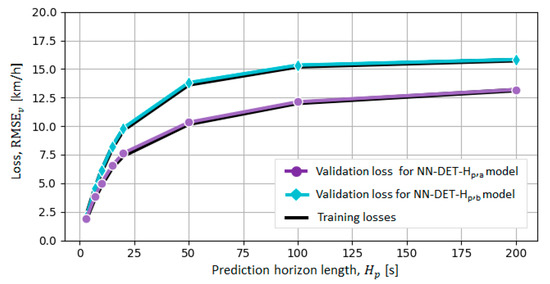
Figure 7.
RMSEv loss values obtained for different prediction horizon lengths Hp of NN-DET-Hp,a and NN-DET-Hp,b models by using training and validation datasets.

Table 3.
Training, validation, and testing results of NN-DET models with different prediction horizon length [s], including the number of adjustable model parameters.
According to the score results shown in Figure 8, the full, NN-DET-Hp,a,200 model maintains a satisfactory prediction accuracy (, for all , ) which is not the case with the NN-DET-H200,b model, thus confirming once again the importance of including the current vehicle position in the input feature set. The prediction accuracy is very good () for the first 10 prediction steps () and remains to be solid () up to first 25 prediction steps ().
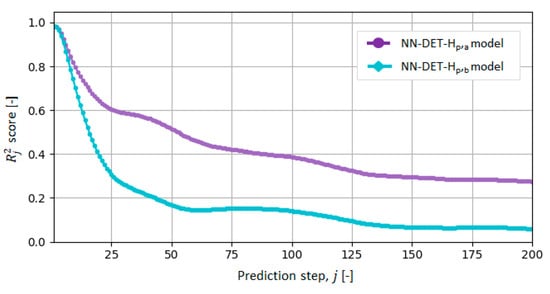
Figure 8.
score values corresponding to jth discrete step of prediction horizon with length Hp = 200 s and calculated for validation data set (note that for given sampling time of 1 s, the prediction in-terval of, e.g., j = 200 steps correspond to the length of 200 s).
4. Stochastic Vehicle Velocity Prediction Model
To combine characteristics of the previously discussed NN-STC and NN-DET vehicle velocity prediction models, a dynamic stochastic prediction model is proposed as an ultimate solution (hereinafter referred to as NN-DSTC model). The model represents an extension of the NN-DET model with a stochastic component, which represents prediction uncertainty for each discrete time step along the prediction horizon.
4.1. Modelling of Deep Neural Network with Stochastic Output
The architecture of NN-DSTC model is also based on the deep feedforward NN, and it is shown in Figure 9. The model outputs are assumed to be the expectation and the standard deviation of normal (Gaussian) velocity distributions , while the inputs to the model remain the same as in the case of NN-DET model (cf. Figure 4). In this way, the discrete velocity distributions of NN-STC model (Figure 1a) are approximated with normal distributions, thus reducing the output dimension per prediction step from to , i.e., there are only two parameters per each prediction step along the prediction horizon. The essential difference between NN-DSTC model and NN-STC model is that the former provides prediction of vehicle velocity along the prediction horizon. On the other hand, the NN-DSTC model extends upon the NN-DET model in terms of outputting the entire (normal) velocity distribution for each prediction step in addition to providing the velocity expectation.
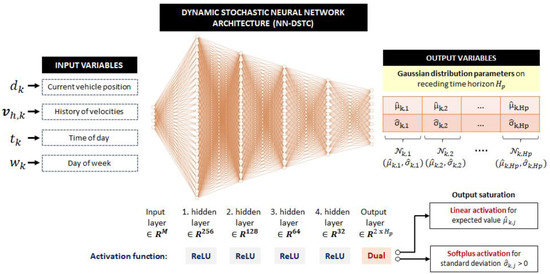
Figure 9.
Proposed architecture of dynamic stochastic deep feedforward neural network (NN-DSTC) for predicting parameters of normal vehicle velocity distribution along receding time horizon of length .
The hidden layers of the NN-DSTC model again contain the ReLU activation function, while the output layer includes a dual activation function, i.e., linear one for prediction of the expectation and softplus one for prediction of the standard deviation . The latter is motivated by the need to saturate the parameter to values greater than or equal to zero [24]:
One of the main challenges of training the NN-DSTC model relates to structuring the loss function, which is defined herein as the mean of negative log-likelihoods (NLL) [24] of predicted normal distributions for each prediction step :
The NN-DSTC model is again realized by using the Python libraries Keras and Tensorflow, with the same settings as in the case of the NN-DET model. For the purpose of training, validation, and testing of the NN-DSTC model, the prediction horizon length is set to 10 s, while the velocity history interval length is set to 20 s.
Figure 10 shows the progress of NN-DSTC model training and validation loss defined by Equation (5). The validation response of exhibit somewhat stronger oscillatory behaviour and spikes compared to the NN-STC model (cf. Figure 8 in [22]). This effect can be explained by the complexity of loss function. Nevertheless, the absence of a notable gap between the training and validation loss curves indicates that the NN-DSTC model possesses good generalization properties. The minimum validation loss of 2.593 is reached in the 128th epoch, and the weighting coefficients obtained in that epoch are adopted as the final parameters of NN-DSTC model. The final NN-DSTC model testing loss is found to be equal to 2.598, which further confirms the good generalization properties of the model on unseen data.
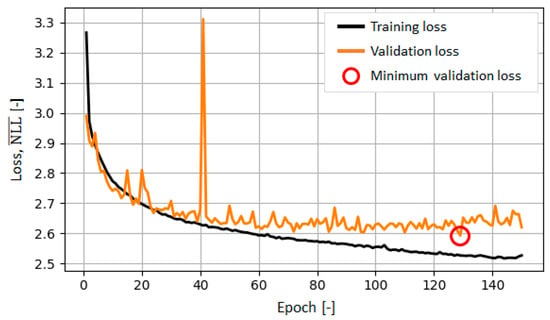
Figure 10.
Progress of NN-DSTC model training and validation loss .
4.2. Comparative Analysis of Prediction Accuracies of Stochastic and Deterministic Models
4.2.1. Considered Metrics
A comprehensive validation of the NN-DSTC model cannot be performed unambiguously in relation to the recorded data due to the stochastic nature of the model. More specifically, validation of such a model would require knowledge of the exact values of the original vehicle velocity distribution parameters for each combination of input data, for which a virtually infinite set of recorded data would be necessary. Therefore, the validation is narrowed in this subsection to comparison of the velocity expectation prediction of NN-DSTC model with the prediction of NN-DET model, based on the test dataset and the following metrics:
- Loss function defined by Equation (2);
- score defined by Equation (3), calculated for each th discrete step along the prediction horizon (), as applied in Section 3;
- Mean value of , also calculated for each th discrete step along the prediction horizon:
- Mean prediction RMSE along the prediction horizon and for the given time step along the driving cycle:where, in the case of the NN-DSTC model, the predicted velocity expectations are used instead of predicted velocity .
4.2.2. Analysis of Prediction Accuracy along the Prediction Horizon
The value of indicator , obtained for NN-DSTC model and test dataset, is equal to 5.12 km/h, which is only 2.2% higher when compared to NN-DET model of the same configuration ( km/h; see Table 1). The certain performance degradation is illustrated in Figure 11, which shows comparative plots of the individual recorded () vs. predicted velocity values ( for NN-DET and for NN-DSTC) for the two models. The reason for the somewhat higher prediction error of NN-DSTC model compared to NN-DET model is more complex model structure providing richer, stochastic velocity prediction (cf. Figure 4 and Figure 9). Nevertheless, the resulting, modest increase in the prediction error of NN-DSTC model can readily be justified by the structural advantage of this model in terms of providing the extra output ( describing the prediction uncertainty.
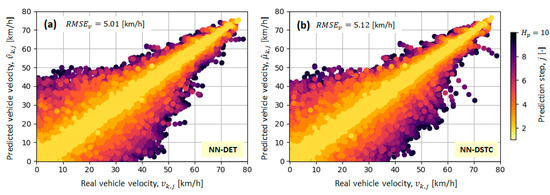
Figure 11.
Predicted velocity and velocity expectation in relation to real velocity values for NN-DET model (a) and NN-DSTC model (b), respectively, where predictions for each jth time step along the prediction horizon Hp are marked in different colours.
Figure 11 clearly illustrates that the prediction accuracy deteriorates along the prediction horizon, i.e., the prediction error grows as the prediction step increases towards the horizon length . Additionally, the prediction error is higher at lower vehicle velocities, which is explained by more rapid vehicle accelerations in the low-speed (i.e., low-gear) range, resulting in a wider spread of velocity values to be predicted.
Figure 12 shows the score and values determined at different steps along the prediction horizon. These results confirm that the prediction accuracy lowers as the prediction steps grows towards the end of prediction horizon. They also indicate that the prediction accuracy along the prediction horizon is mostly somewhat higher for NN-DET model than NN-DSTC model. The relative differences of the medians of considered metrics for the two models equals 0.24% for and 1.53% for , which is close to the corresponding difference of 2.2% related to metric discussed above.
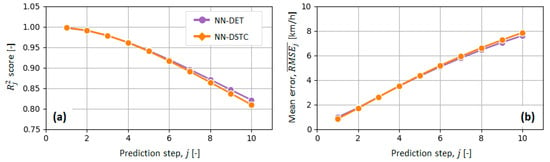
Figure 12.
Comparative plots of prediction performance of NN-DET and NN-DSTC models, expressed in terms of (a) and (b) metrics, determined for different prediction steps j along prediction horizon Hp.
Figure 13 shows time responses of the velocity predictions provided by NN-DET and NN-DSTC models for one of the test-driving cycles. These responses confirm that the velocity prediction accuracy of NN-DSTC model is close, although generally lower than that of NN-DET model, and that the accuracy deteriorates towards the end of prediction horizon. Additionally, the prediction accuracy is higher in the case of less uncertain traffic conditions, i.e., when the predicted confidence interval is narrower. This points to consistent estimation of predicted velocity distribution parameter Finally, Figure 13 indicates that the uncertainty of vehicle velocity prediction expectedly increases as the prediction is conducted farther in future (i.e., as the prediction step grows toward ). This is clearly illustrated in Figure 14 by the box plot of the predicted velocity uncertainty parameter , which shows that the mean and median values of uncertainty parameter grow approximately linearly with the prediction step . The same, approximately linear trend is recognized in the and plots of NN-DET model (purple curves in Figure 12). Indeed, Figure 15 illustrates that the mean values of NN-DTSC model (orange triangles in Figure 14) are highly correlated with and values of NN-DET model, which further confirms the accuracy of confidence interval prediction of NN-DSTC model.
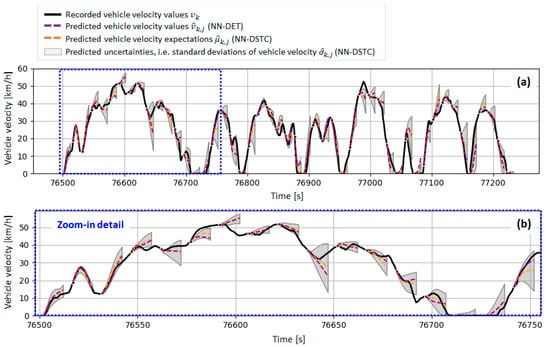
Figure 13.
Comparative time response of vehicle velocity predictions provided by NN-DET and NN-DSTC models for one of driving cycles from test data set (a) and characteristic response zoom-in detail (b).
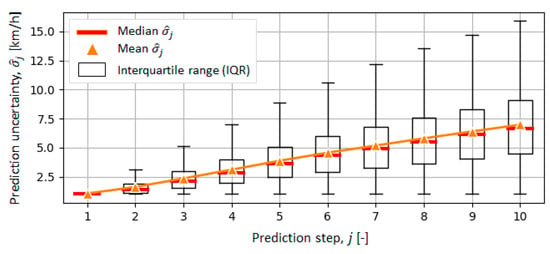
Figure 14.
Boxplot of NN-DSTC model-predicted uncertainty parameter (i.e., standard deviation ) of vehicle velocity prediction along steps of prediction horizon.
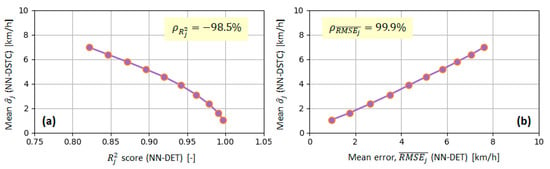
Figure 15.
Dependence of NN-DET model velocity prediction accuracy metrics (a) and (b) on mean of NN-DTSC model-predicted standard deviation , where represents the corresponding Pearson correlation index value (100% means full correlation, and −100% denotes full anti-correlation).
4.2.3. Analysis of Prediction Accuracy along the Route
Figure 16a shows the individual RMS prediction errors along the route (the indicator defined by Equation (7)) for NN-DET and NN-DSTC models (purple and orange circles, respectively). These values are higher on road sections that have greater uncertainty of traffic conditions, i.e., on those sections for which the standard deviation of recorded test samples/population gets higher. These sections evidently correspond to the congested traffic area, characterized with low expectation of recorded test samples and zero values of confidence interval lower border . The two models are characterized by almost identical scattering of individual prediction errors, as well as their mean values (solid lines in Figure 16a). This again confirms the ability of more general and complex NN-DTSC model to predict velocity expectation that is close to NN-DET model velocity prediction. Figure 16b,c shows the distributions of individual RMS prediction errors for the two models. The mean value and standard deviation of distributions are around 3.7 km/h and 3.4 km/h, respectively, for both models.
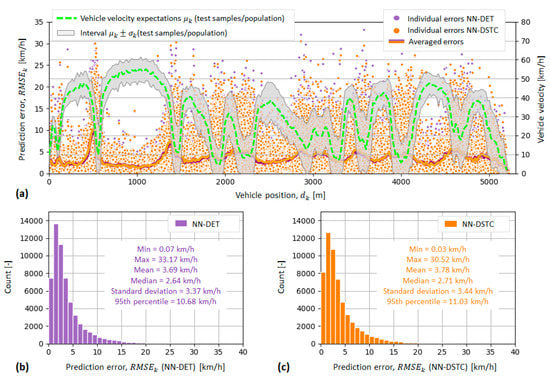
Figure 16.
Scattering of NN-DET and NN-DSTC models individual RMS velocity prediction errors along the selected bus route (a), including the corresponding distributions given separately for NN-DET (b) and NN-DSTC models (c).
5. Conclusions
Deterministic and stochastic versions of deep neural network-based vehicle velocity prediction model have been proposed. The deterministic (NN-DET) model predicts the velocity expectation along the receding prediction horizon, while the stochastic (NN-DSTC) one additionally predicts the velocity distribution standard deviation. The proposed models have been parameterized and tested based on GPS-based tracking data recorded on several city buses during six-month period of their regular operation on a selected route.
Analysis of the influence of different model input features on the NN-DET model prediction accuracy has pointed out that the current vehicle position and short-term velocity history are the most significant input features, while the time of day and day of week information have a negligible impact (the root mean square error, , drops from 5.07 to 5.03 km/h). In addition, vehicle velocity history interval length has found to have optimal value in the range from 30 to 50 s from the standpoint of high prediction accuracy on the validation/test dataset and limited model complexity. For the full-input-set NN-DET model and the prediction horizon length s, the score, calculated individually for each prediction step on the validation dataset, monotonically falls with and reaches the value of approximately 0.25 for , thus indicating solid accuracy throughout relatively long prediction horizons. The accuracy is significantly improved for shallow prediction sub-horizons, e.g., for and for . The accuracy is considerably lower when only the velocity history input is concerned: for , for , and for This confirms the importance of including the current vehicle position as the model input, particularly for the particular city bus application where driving cycles are related to fixed routes.
The NN-DSTC model has been found to have only slightly lower accuracy of predicting the velocity expectation along the receding horizon when compared to the NN-DET model of the same configuration (the root mean square error, , is higher by 2.2%), while offering a significant advantage of including prediction uncertainty along the horizon. The velocity expectation prediction accuracy is lower when conducted farther in future and in the case of less uncertain traffic conditions (i.e., for km/h), which occur typically at lower vehicle velocity expectation, i.e., for congested traffic and frequent vehicle stops. The accuracy of NN-DSTC model-predicted standard deviation of velocity normal distribution has been examined indirectly, i.e., through confirming that (i) the predicted standard deviation grows with the prediction step , (ii) the velocity expectation accuracy is higher when the predicted standard deviation is lower, and (iii) the correlation between the mean predicted standard deviation and the NN-DET model’s velocity prediction accuracy metrics along the prediction horizon expectation is higher than 98%.
The main foreseen limitation of the presented velocity prediction models and related assessment analysis is that they have been designed based on the data related to specific, although still very relevant transport system with repeating routes (city bus transport, herein). Additionally, the work is limited to feedforward NNs, while more advanced NNs may generally be more suitable for dynamic system response prediction. The future work can be directed to the following activities:
- (a)
- Applying and examining the proposed vehicle prediction models within vehicle deterministic or stochastic model predictive control strategies (e.g., energy management strategy of a PHEV aimed at minimizing the vehicle fuel and electricity consumption for a wide range of driving cycles);
- (b)
- Considering other types of NNs, such as recurrent NNs, which can be more suitable for the task of dynamic system behaviour prediction and potentially bring further gains in model prediction accuracy;
- (c)
- Considering Markov chain-based stochastic velocity prediction method, which, in addition to the vehicle velocity (and acceleration), would also take information about the vehicle position when defining the Markov states;
- (d)
- Examining the proposed prediction models for other transport systems that are not characterized by fixed/repeating routes (unlike the city bus transport system considered herein), including different types of vehicles, as well;
- (e)
- Adding more relevant inputs to the model such as accelerator pedal opening and traffic related inputs (not available in the presented study) for potentially improved prediction performance;
- (f)
- Comparing the various developed prediction models to each other, as well as with respect to existing models.
Author Contributions
Conceptualization, J.T., B.Š. and J.D.; methodology, J.T. and B.Š.; software, J.T.; validation, J.T., B.Š. and J.D.; writing—original draft preparation, J.T.; writing—review and editing, J.D. and B.Š.; visualization, J.T.; supervision, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
It is gratefully acknowledged that this work has been done within the project ACHIEVE (“Adaptive and Predictive Control of Plug-in Hybrid Electric Vehicles”; website: http://achieve.fsb.hr/ (accessed on 15 July 2022)), supported by the Croatian Science Foundation under the Grant agreement No. IP-2018-01-8323.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are not publicly available due to privacy restrictions of related transport company.
Acknowledgments
The authors are grateful to the company Libertas d.o.o., Dubrovnik, Croatia, for providing the city bus tracking data and related technical support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ADAM | Adaptive Moment Estimation (optimization algorithm used for training of neural networks) |
| CAN | Controller Area Network |
| GPRS | General Packet Radio Service |
| GPS | Global Positioning System |
| MPC | Model Predictive Control |
| MSE | Mean Squared Error |
| NLL | Negative Log-Likelihood |
| NN | Neural Network |
| NN-DET | Deterministic Neural Network (model) |
| NN-DSTC | Dynamic Stochastic Neural Network (model) |
| NN-STC | Static Stochastic Neural Network (model) |
| PHEV | Plug-in Hybrid Electric Vehicle |
| RMSE | Root Mean Squared Error |
| TPM | Transition Probability Matrix |
| Table of Symbols | |
| Mean squared error of predicted vs. recorded vehicle velocities (used as loss function for NN-DSTC model) | |
| Mean of negative log-likelihoods of predicted normal distributions of vehicle velocity for each prediction step (used as loss function for NN-DET model) | |
| j | Discrete step of prediction horizon, |
| k | kth discrete time instant (i.e., data sample) of given recorded driving cycle |
| N | Total number of data samples used to train NN-DET and NN-DSTC models |
| Vehicle velocity history interval length | |
| Prediction horizon length | |
| Mean prediction RMSE calculated along the full prediction horizon for the kth time instant | |
| Mean prediction RMSE calculated for jth discrete step of prediction horizon | |
| Coefficient of determination value calculated for jth discrete step of prediction horizon | |
| Vehicle position (i.e., distance travelled from reference route departure station) for kth time instant of given recorded driving cycle | |
| Time of day for kth time instant of given recorded driving cycle | |
| Vehicle velocity for kth time instant of given recorded driving cycle | |
| Day of week for kth time instant of given recorded driving cycle | |
| Vector of historical vehicle velocities of length | |
| Vehicle velocity standard deviation calculated from test samples/population | |
| Vehicle velocity predicted by NN-DET model | |
| Vehicle velocity expectation predicted by NN-STC/NN-DSTC model | |
| Vehicle velocity standard deviation predicted by NN-STC/NN-DSTC model | |
| Set of input (training) values | |
| Set of output (target) values related to inputs |
References
- Arata, J.; Leamy, M.; Cunefare, K. Power-split HEV control strategy development with refined engine transients. SAE Int. J. Altern. Powertrains 2012, 1, 119–133. [Google Scholar] [CrossRef]
- Jauch, C.; Tamilarasan, S.; Bovee, K.; Güvenc, L.; Rizzoni, G. Modeling for drivability and drivability improving control of HEV. Control Eng. Pract. 2018, 70, 50–62. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems: Introduction to Modeling and Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 243–276. [Google Scholar]
- Hrovat, D.; Cairano, S.D.; Tseng, H.E.; Kolmanovsky, I.V. The development of Model Predictive Control in automotive industry: A survey. In Proceedings of the IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 295–302. [Google Scholar]
- Rajamani, R. Longitudinal Vehicle Dynamics. In Vehicle Dynamics and Control, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 87–111. [Google Scholar]
- Karbowski, D.; Kim, N.; Rousseau, A. Route-based online energy management of a PHEV and sensitivity to trip prediction. In Proceeding of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Lemieux, J.; Ma, Y. Vehicle Speed Prediction Using Deep Learning. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Zhou, Y.; Ravey, A.; Marion-Pera, M.C. A survey on driving prediction techniques for predictive energy management of plug-in hybrid electric vehicles. J. Power Sources 2019, 412, 480–495. [Google Scholar] [CrossRef]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity Predictors for Predictive Energy Management in Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Mozaffari, L.; Mozaffari, A.; Azad, N.L. Vehicle speed prediction via a sliding-window time series analysis and an evolutionary least learning machine: A case study on San Francisco urban roads. Eng. Sci. Technol. Int. J. 2015, 18, 150–162. [Google Scholar] [CrossRef]
- Liu, K.; Asher, Z.; Gong, X.; Huang, M.; Kolmanovsky, I. Vehicle Velocity Prediction and Energy Management Strategy Part 1: Deterministic and Stochastic Vehicle Velocity Prediction Using Machine Learning; SAE Technical Paper, No. 2019-01-1051; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Li, Y.; Peng, J.; He, H.; Xie, S. The Study on Multi-scale Prediction of Future Driving Cycle Based on Markov Chain. Energy Procedia 2017, 105, 3219–3224. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, W.; Qi, B. Combined Prediction for Vehicle Speed with Fixed Route. Chin. J. Mech. Eng. 2020, 33, 60. [Google Scholar] [CrossRef]
- Shin, J.; Sunwoo, M. Vehicle Speed Prediction Using a Markov Chain With Speed Constraints. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3201–3211. [Google Scholar] [CrossRef]
- Gaikwad, T.D.; Asher, Z.; Liu, K.; Huang, M.; Kolmanovsky, I. Vehicle Velocity Prediction and Energy Management Strategy Part 2: Integration of Machine Learning Vehicle Velocity Prediction with Optimal Energy Management to Improve Fuel Economy; SAE Technical Paper, No. 2019-01-1212; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Rezaei, A.; Burl, J.B. Effects of Time Horizon on Model Predictive Control for Hybrid Electric Vehicles. IFAC-Pap. 2015, 48, 252–256. [Google Scholar] [CrossRef]
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef] [Green Version]
- Van Duin, J.H.R.; Tavasszy, L.A.; Quak, H.J. Towards E(lectric)-Urban Freight: First Promising Steps in the Electric Vehicle Revolution. Eur. Transp. Trasp. Eur. 2013, 54, 9. [Google Scholar]
- Sirmatel, I.I.; Geroliminis, N. Dynamical Modeling and Predictive Control of Bus Transport Systems: A Hybrid Systems Approach. IFAC-PapersOnLine 2017, 50, 7499–7504. [Google Scholar] [CrossRef]
- Hyeon, E.; Kim, Y.; Prakash, N.; Stefanopoulou, A.G. Influence of Speed Forecasting on the Performance of Ecological Adaptive Cruise Control. In Proceedings of the ASME 2019 Dynamic Systems and Control Conference, Park City, UT, USA, 8–11 October 2019; pp. 1–8. [Google Scholar]
- Topić, J.; Škugor, B.; Deur, J. Static Stochastic Model-Based Prediction of City Bus Velocity. In Proceedings of the 5th International Conference on Smart Systems and Technologies, Osijek, Croatia, 19–21 October 2022. [Google Scholar]
- Topić, J.; Škugor, B.; Deur, J. Synthesis and Feature Selection-Supported Validation of Multidimensional Driving Cycles. Sustainability 2021, 13, 4704. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 18 July 2022).
- Tensorflow. Available online: https://tensorflow.org (accessed on 18 July 2022).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).