Research on the Dynamic Response of a Continuous Steel Box Girder Bridge Based on the ANSYS Platform
Abstract
:1. Introduction
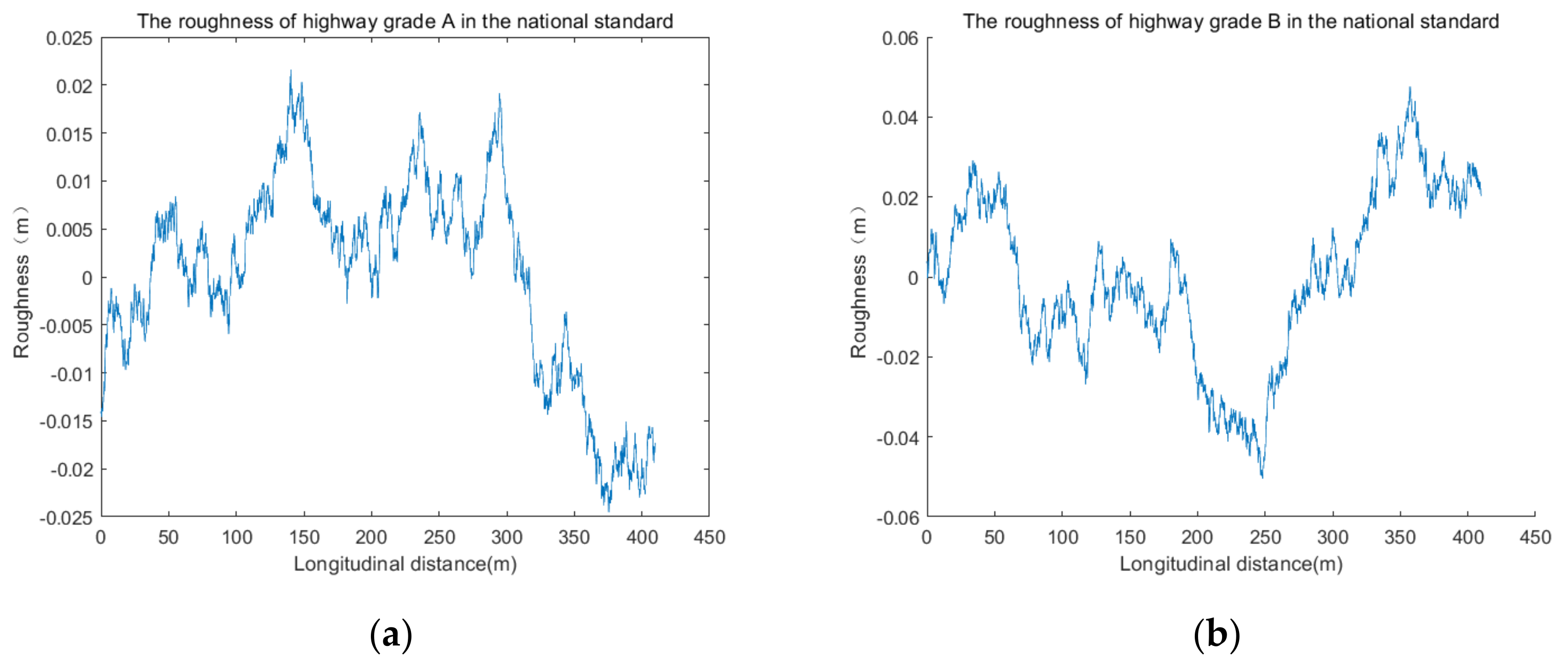
2. Road Surface Irregularities Sample
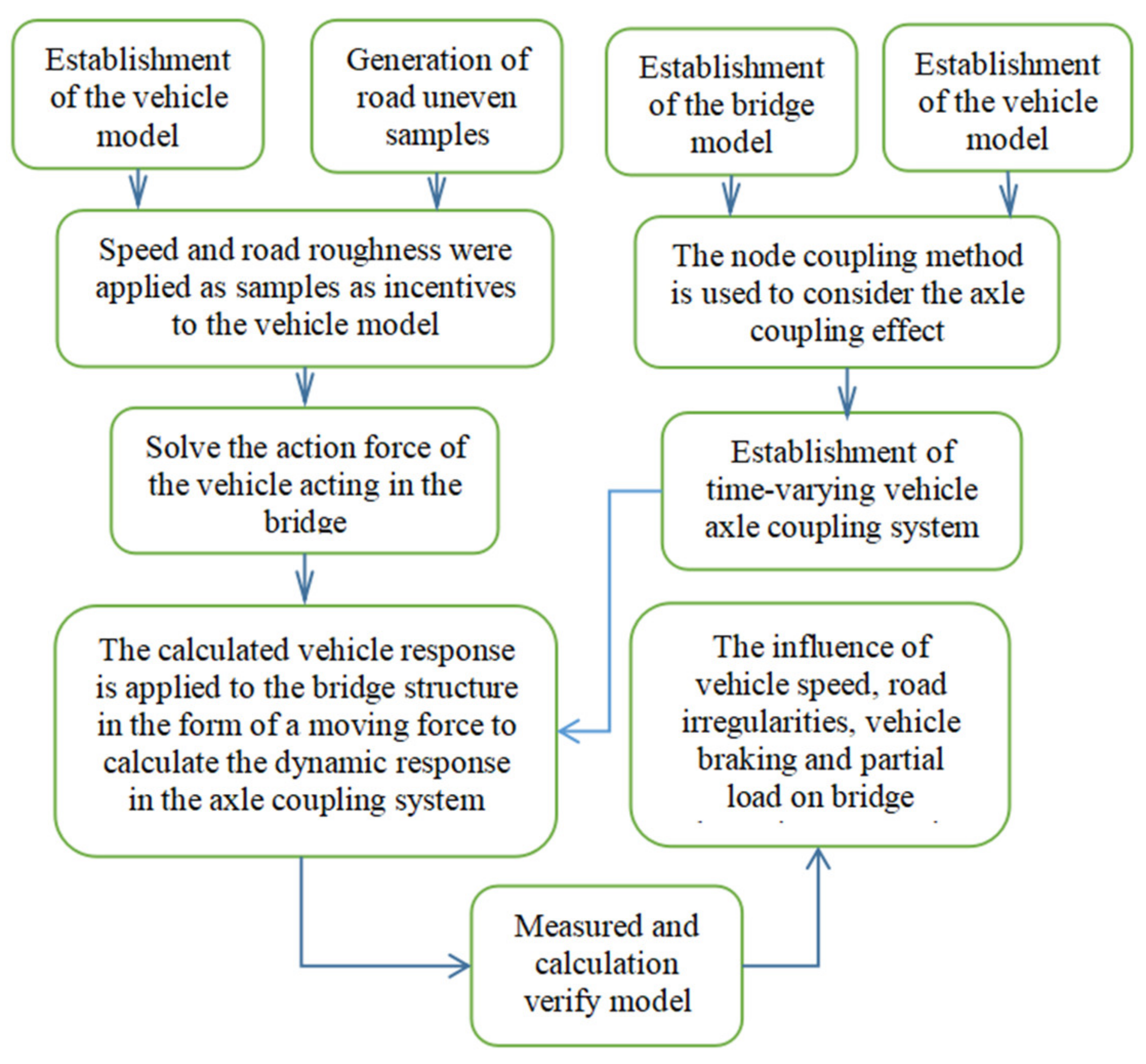
3. Decomposition of Vehicle Force and Steps of the Vehicle Axle Coupling Calculation
3.1. Vehicle Force Decomposition
- (1)
- The vehicle force is caused by gravity, which is a constant moving force that changes with the vehicle’s position. This force has nothing to do with the bridge vibration, which can be defined as the gravity effect of vehicle force;
- (2)
- The vehicle force is caused by the road roughness. This force is the moving variable force that changes with the vehicle’s position on the bridge. Because the road roughness is random, this variable force is random. Assuming that the force has nothing to do with the vibration of the bridge, it is advisable to define the variable force as the random effect of vehicle force. If the road surface is smooth, the force is zero. For the convenience of calculation, the force is considered as the external force;
- (3)
- Applying the gravity effect of vehicle force and the random effect of vehicle force to the vehicle bridge coupling system will inevitably cause bridge vibration. The vibration of the bridge will cause vehicle vibration. Because the force generated by the coupling movement of the vehicle and the bridge (which may be defined as the coupling effect of vehicle force) is closely related to the bridge’s vibration, it is necessary to solve the force in axle coupling system.
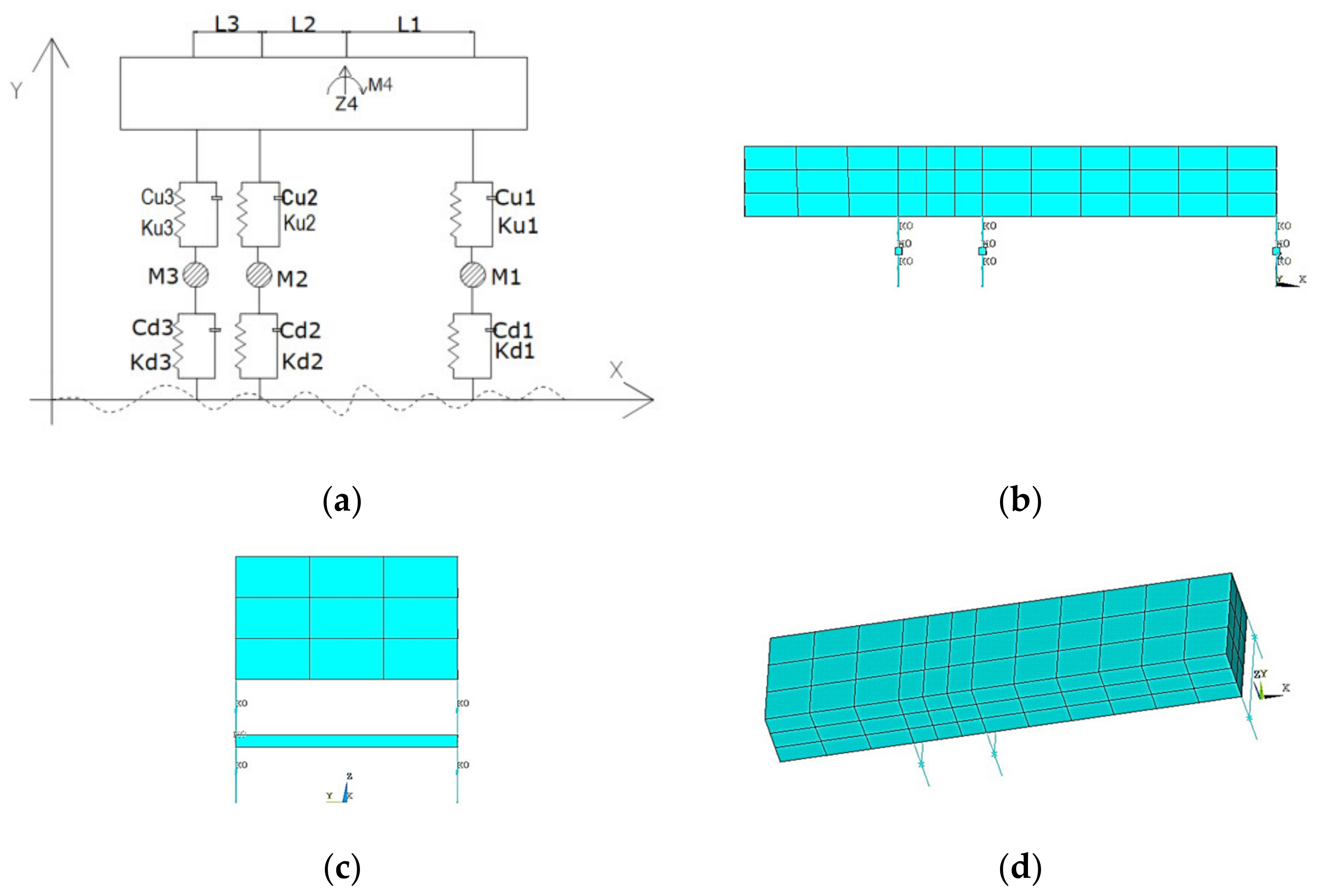
3.2. Establishment of the Vehicle Model
3.3. The Acting Force of the Vehicle Acting on the Bridge
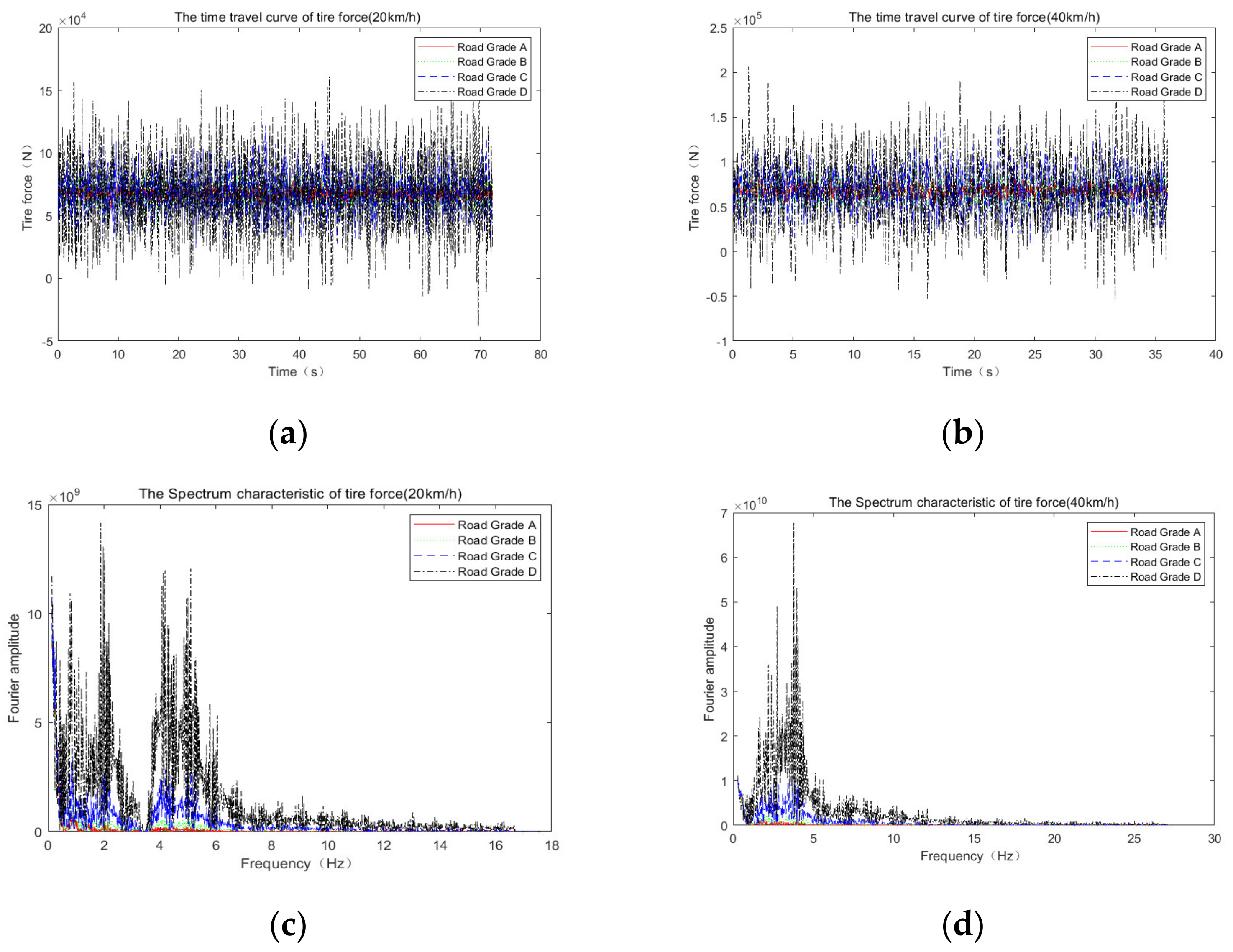
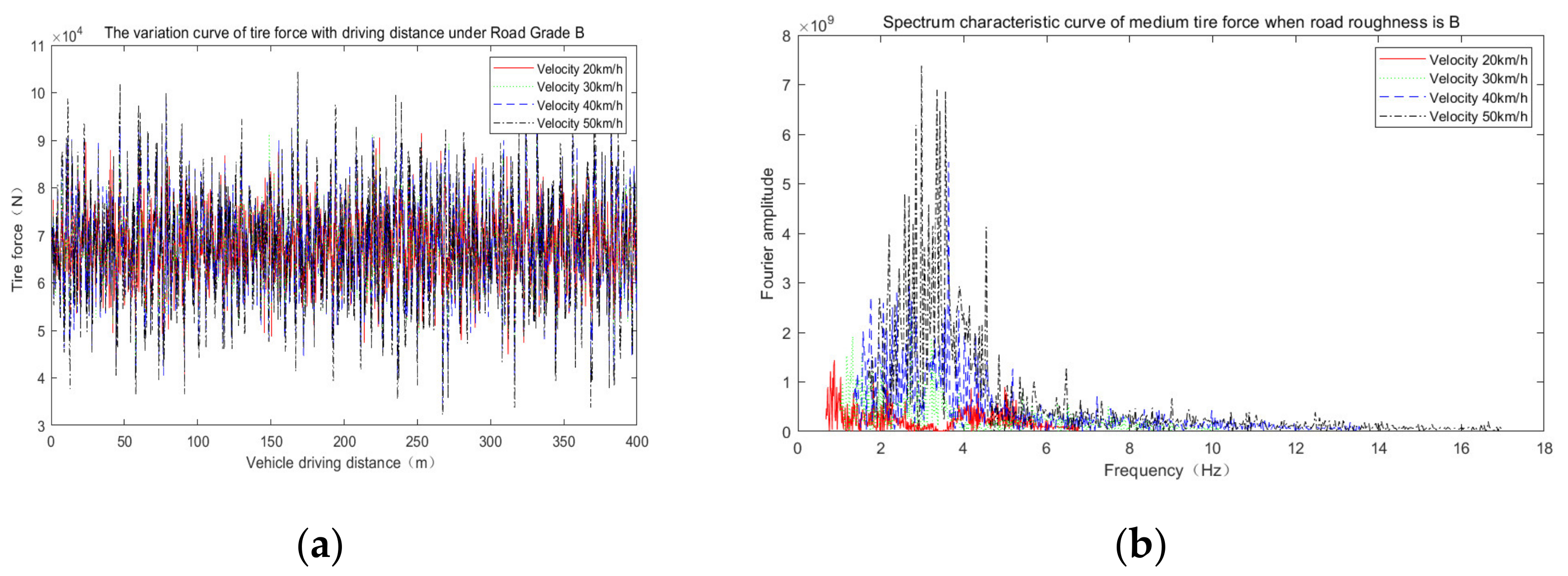
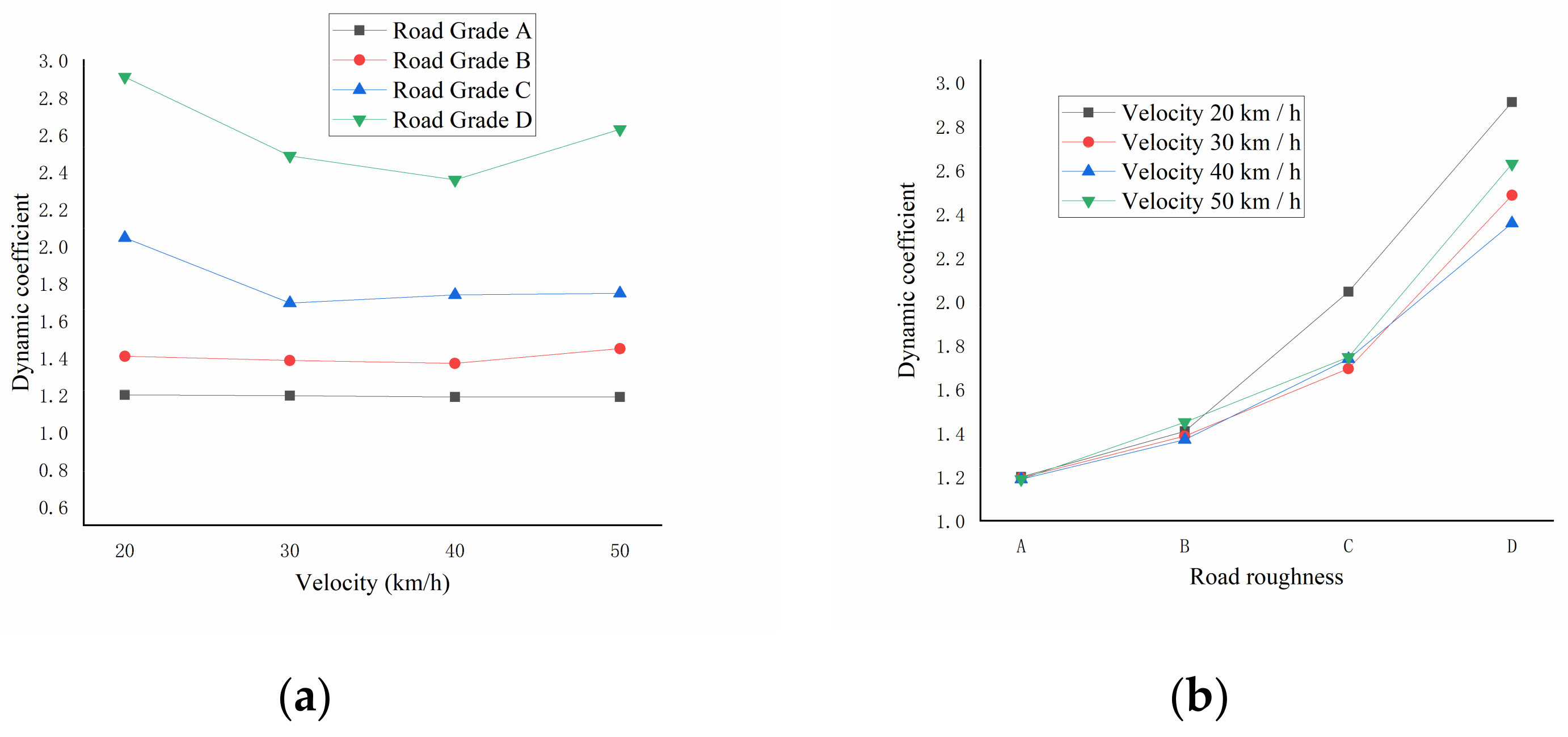
4. Force Characteristics of Vehicle Tires
4.1. Influence of Irregularities and Speed on the Vehicle Tire Force
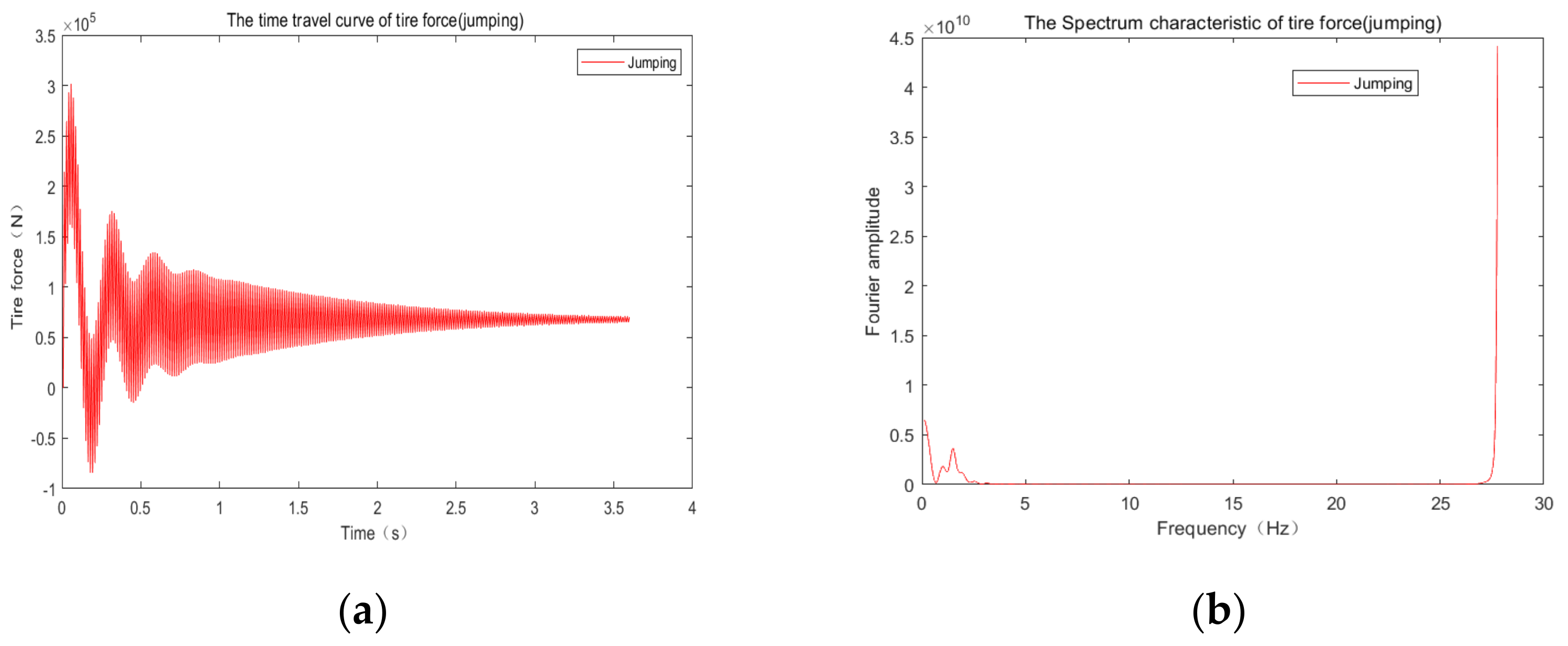
4.2. Influence of Braking and Jumping on Vehicle Force
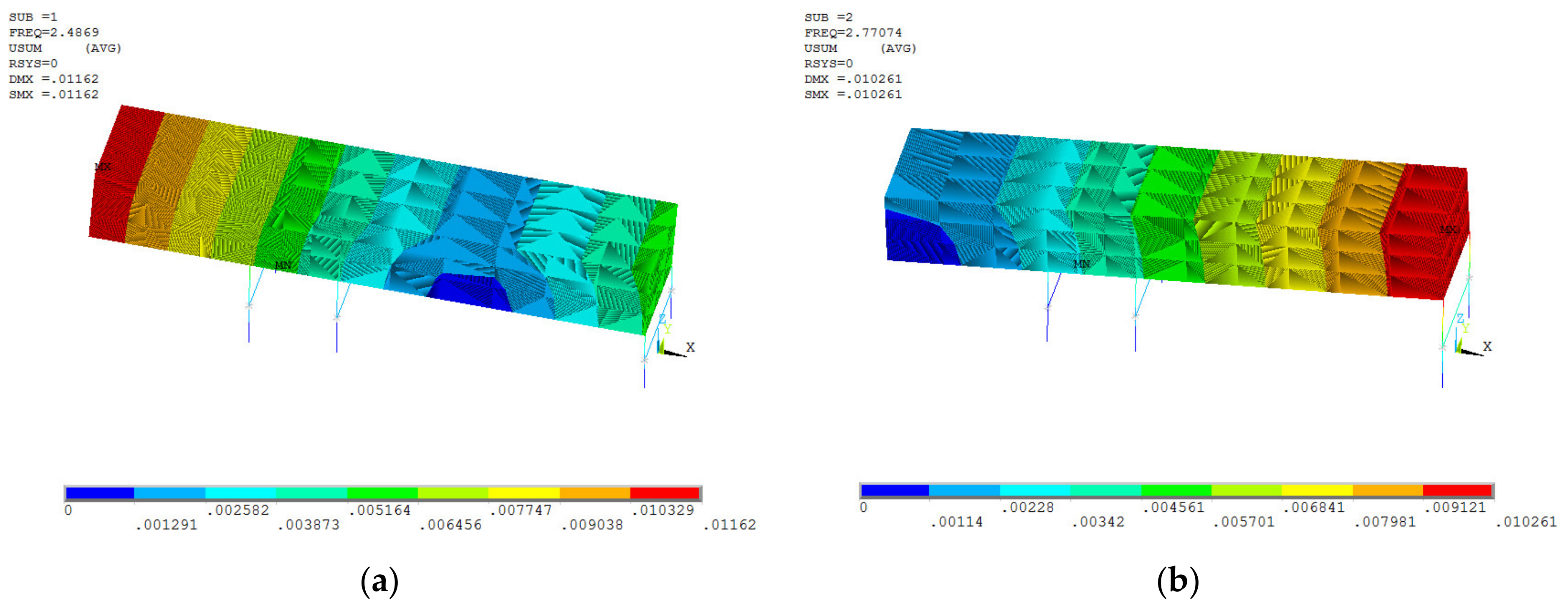
5. Establishment and Verification of the Vehicle Axle Coupling Model
5.1. Establishment of the Bridge Coupling Model
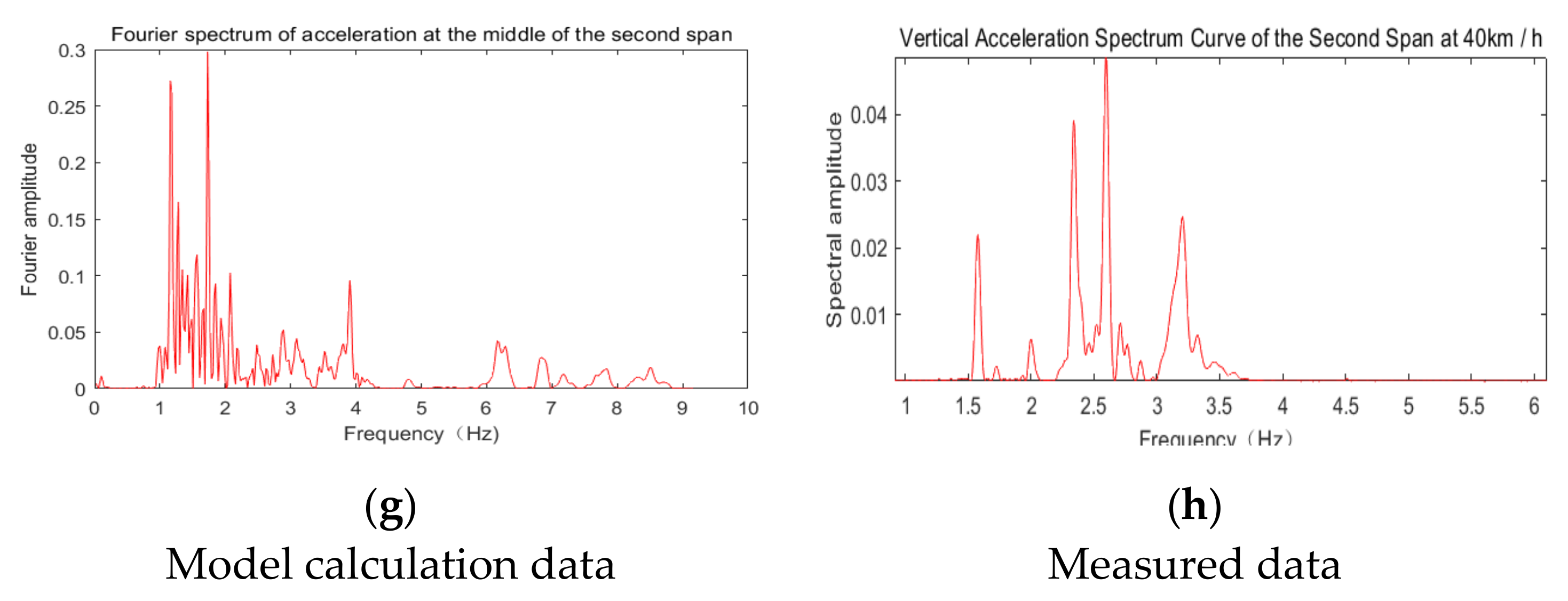
5.2. Model Test Validation
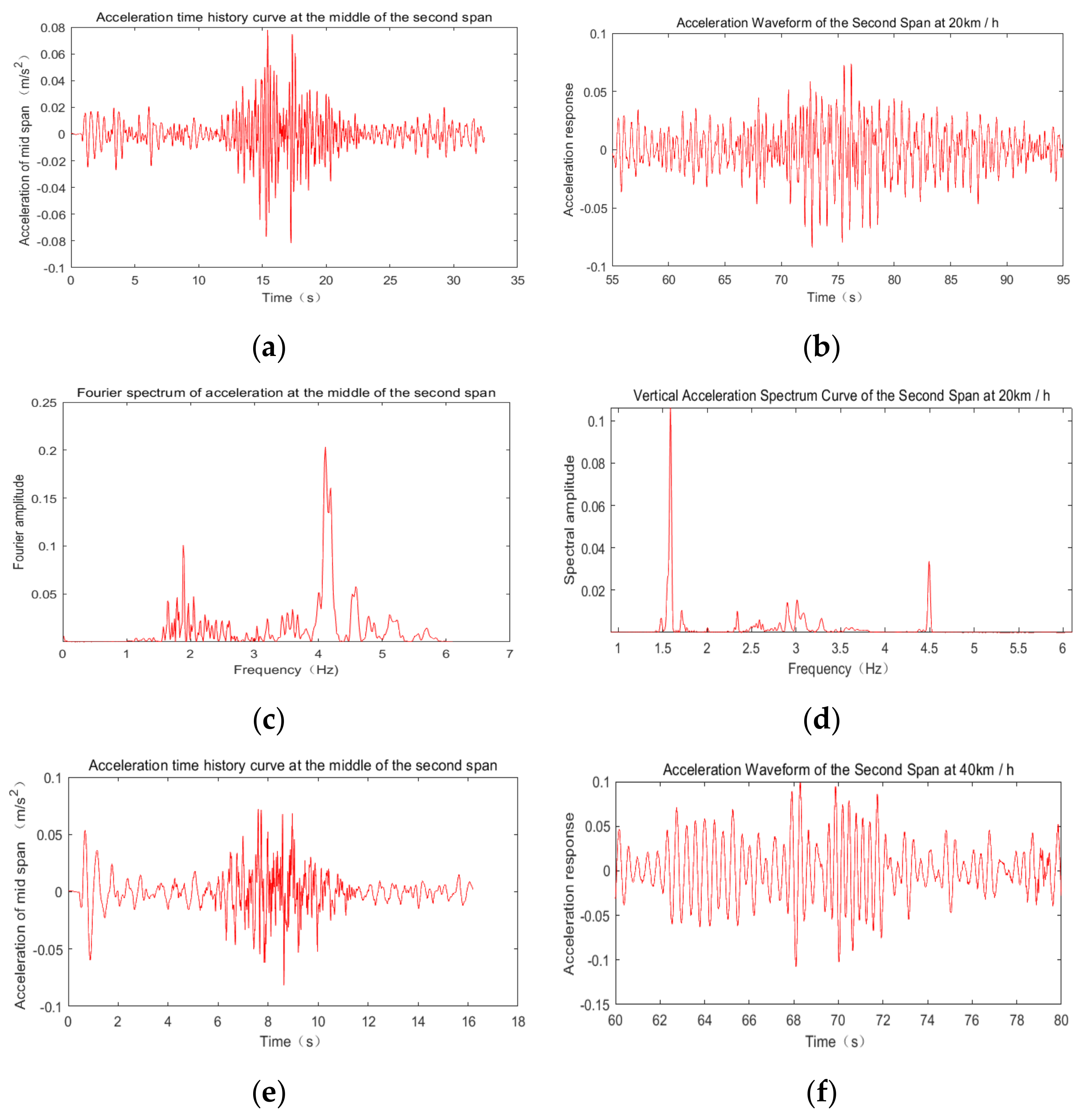
5.3. Comparison of the Bridge Dynamic Response Calculation and the Test
6. Dynamic Response of the Bridge Structure
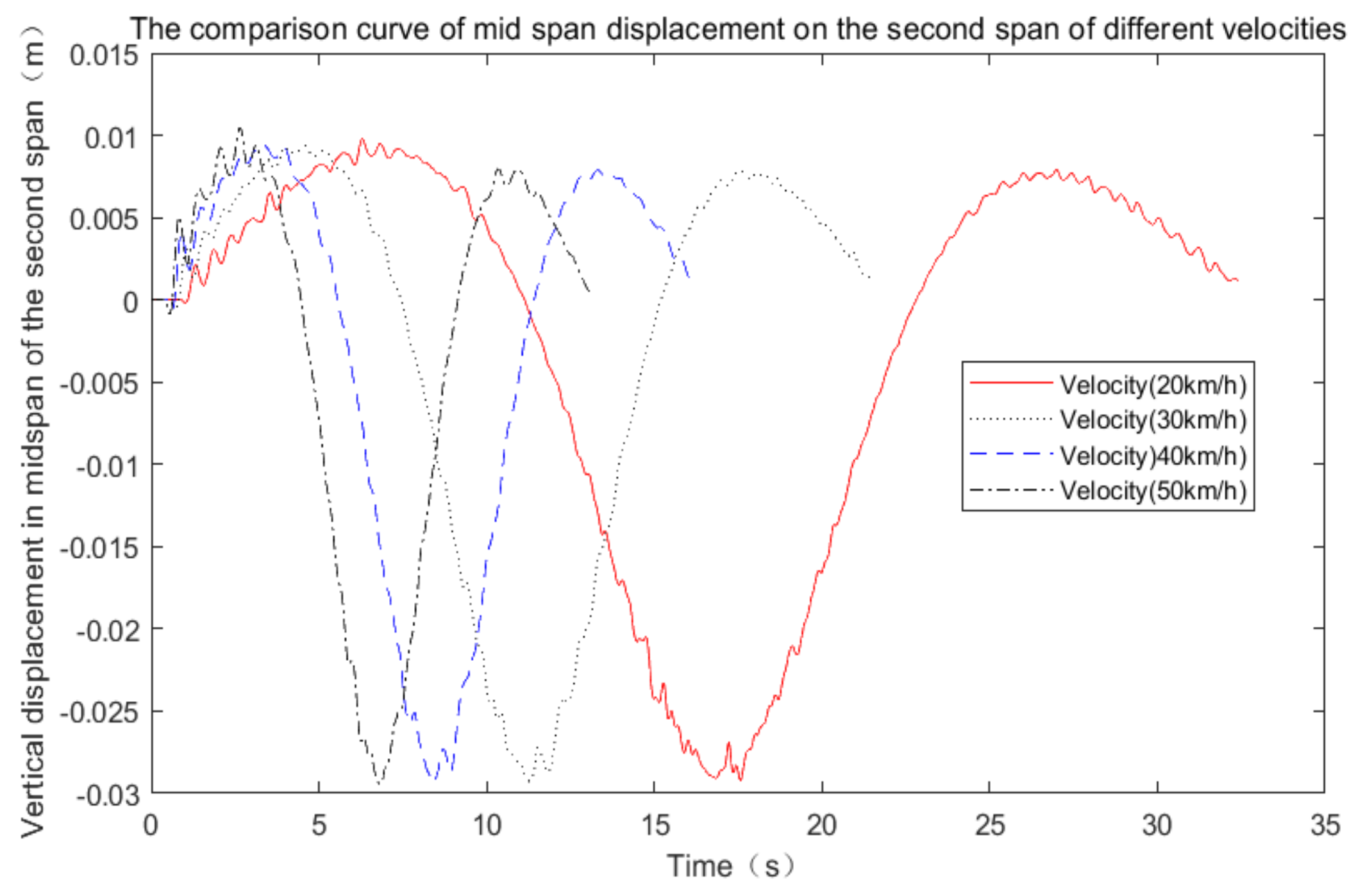
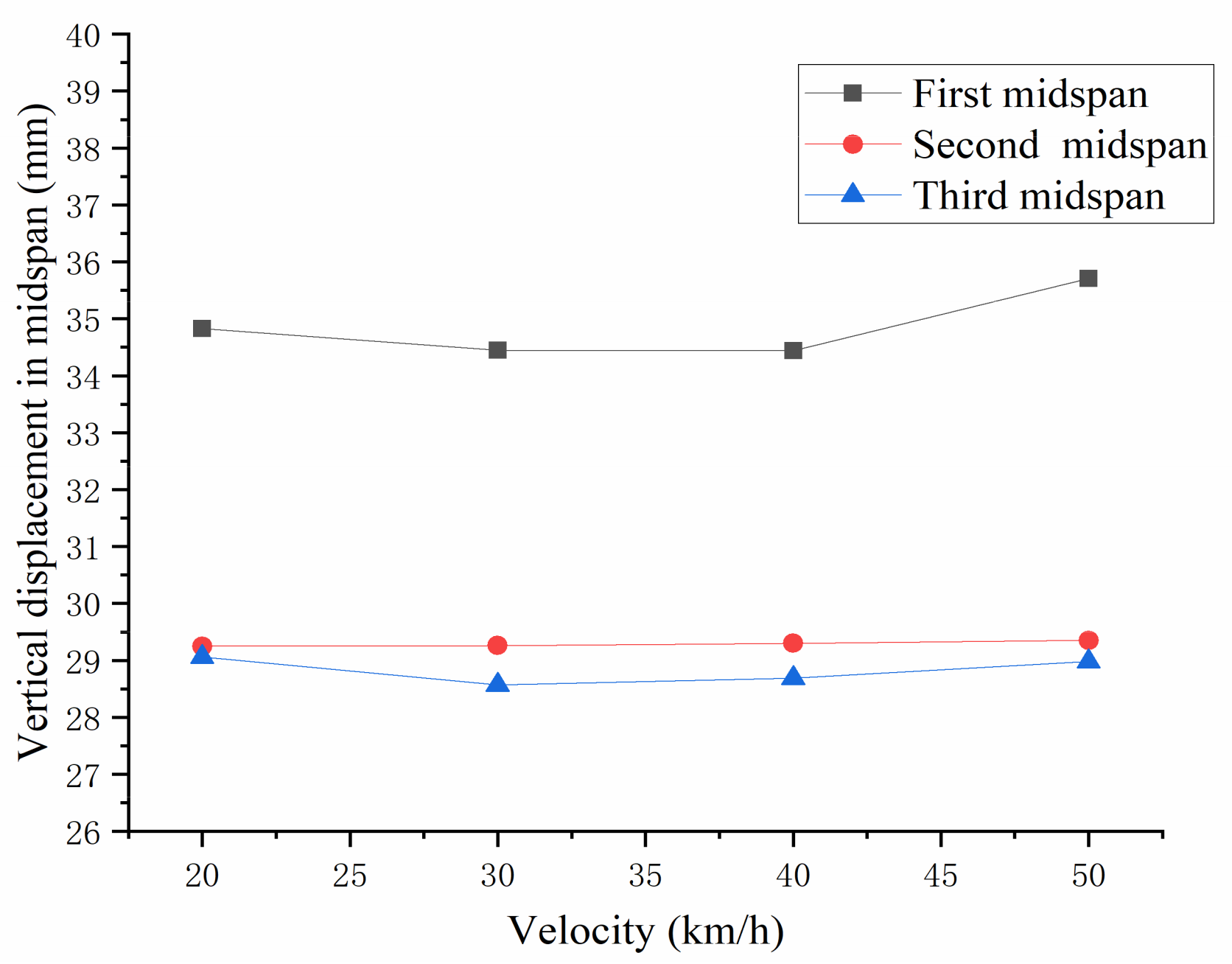
6.1. Influence of the Vehicle Driving Speed
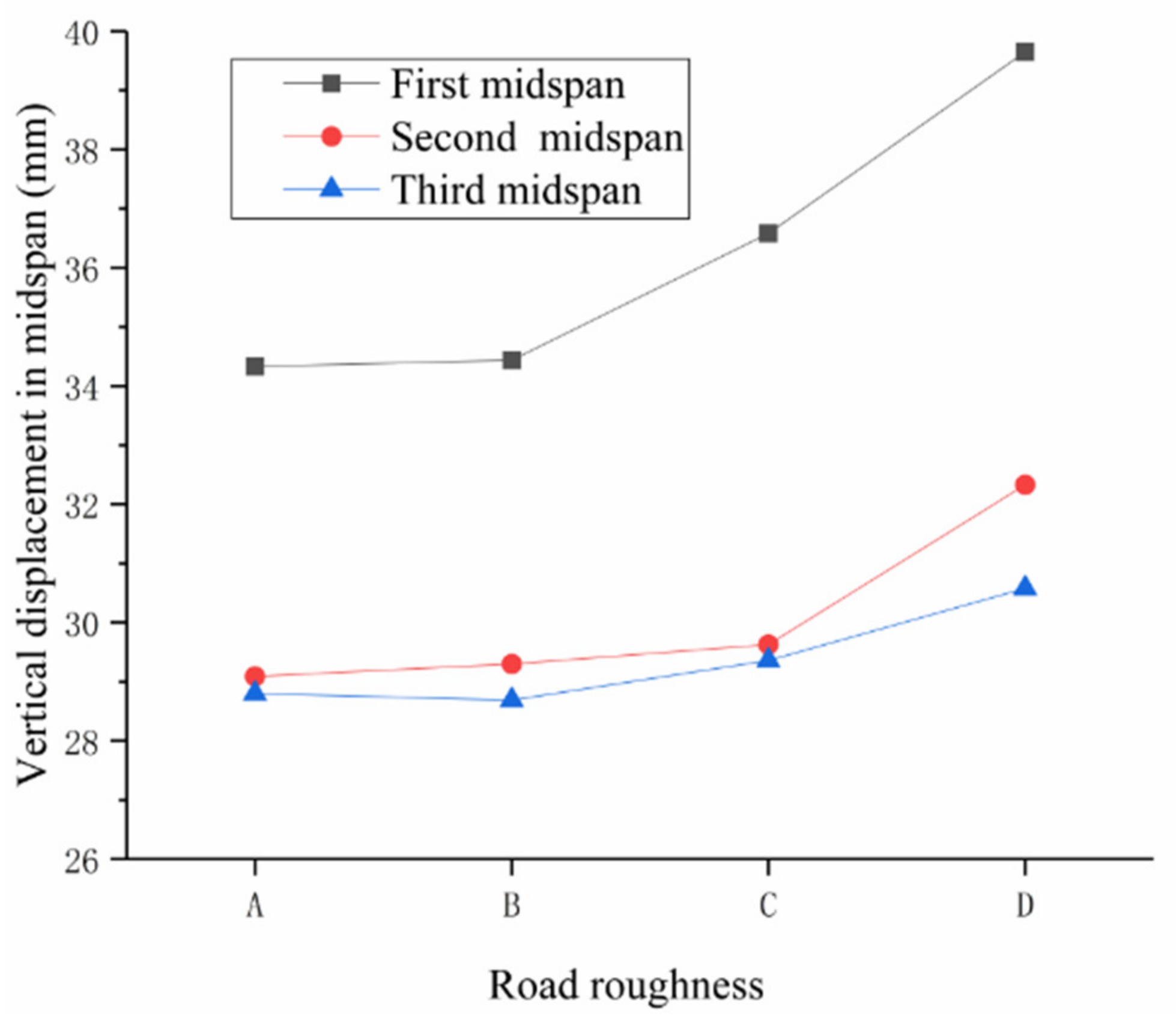
6.2. Influence of Deck Roughness on the Dynamic Response of the Bridge Span Structure
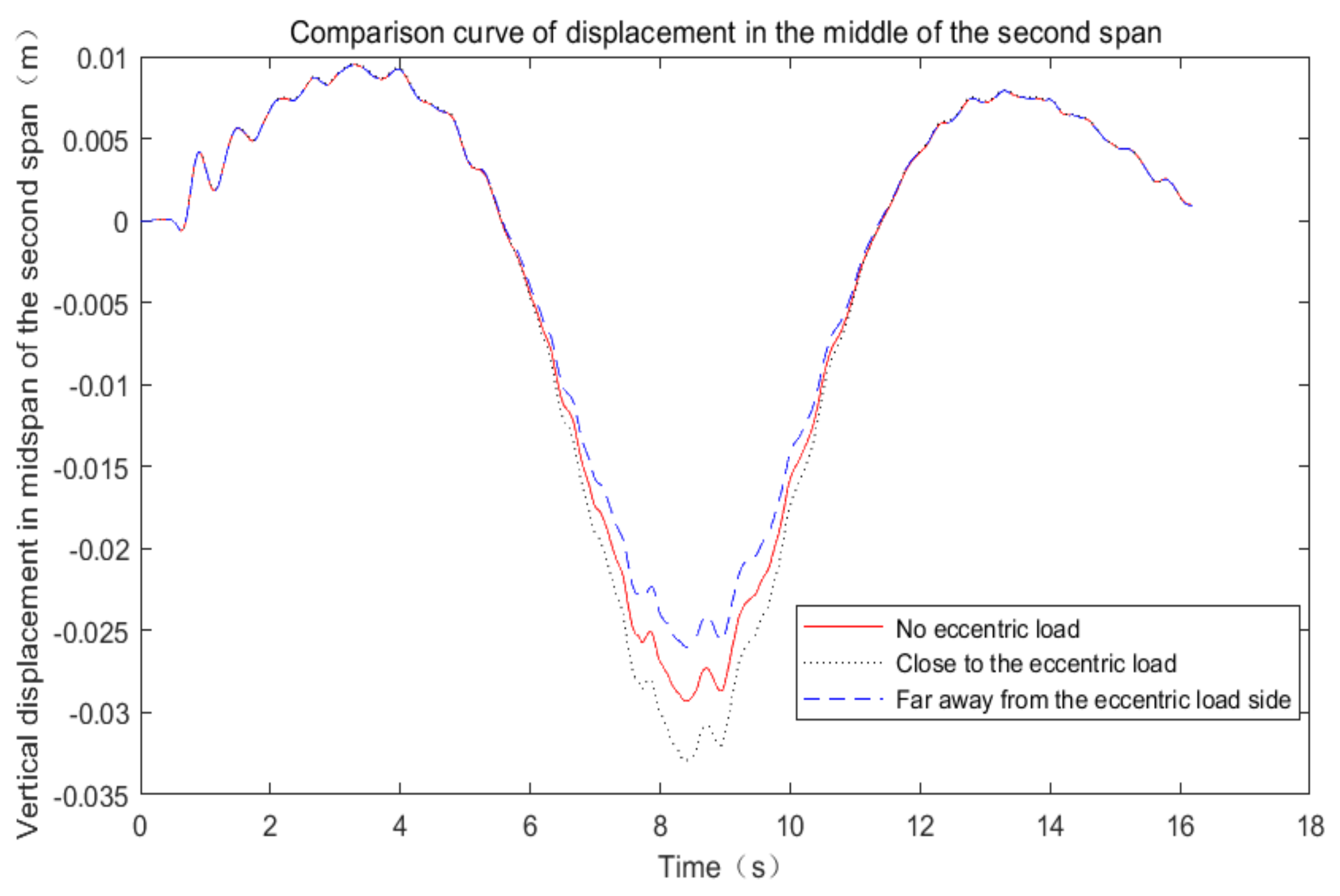
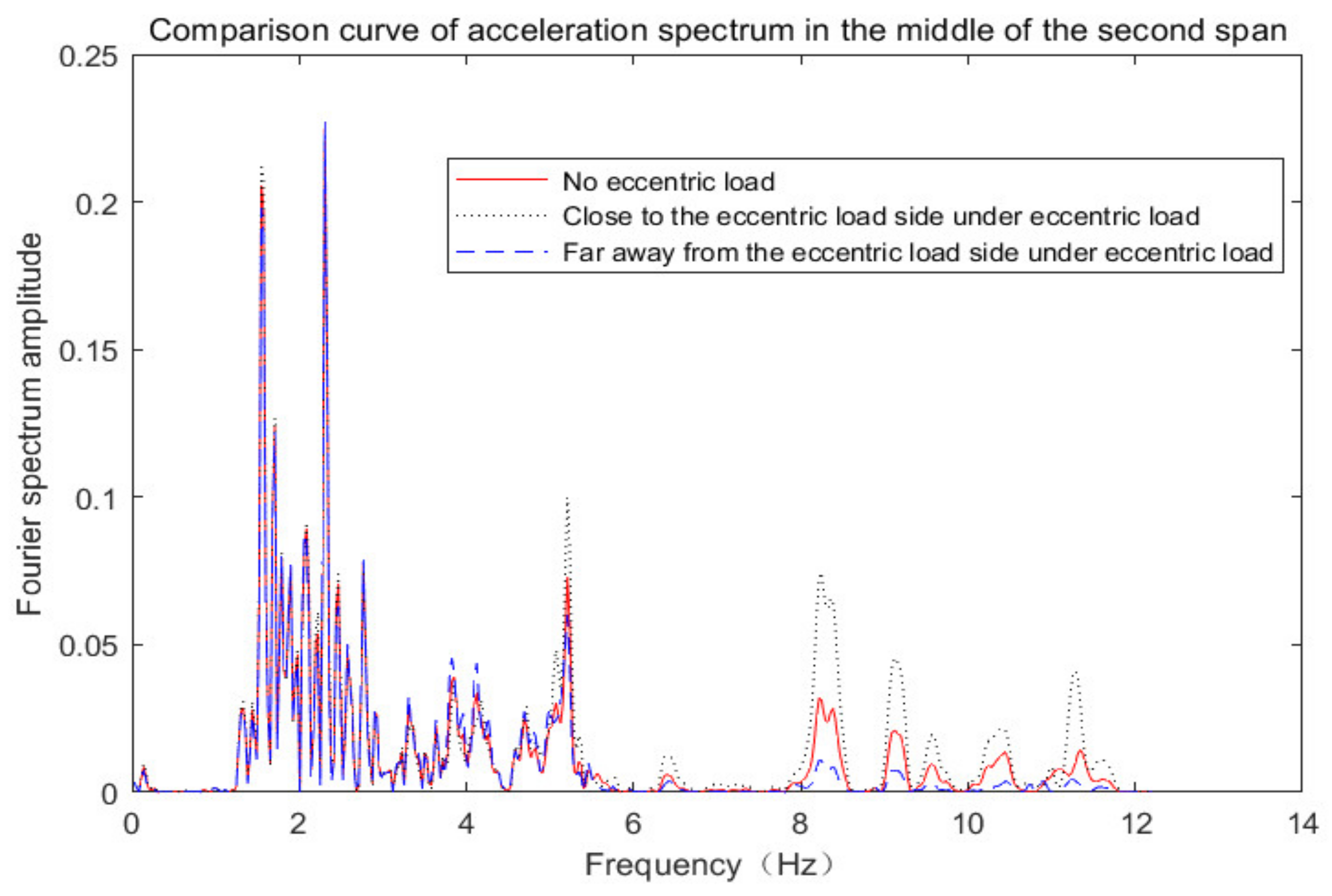
6.3. Influence of the Vehicle Eccentric Load on the Dynamic Response of Bridge Span Structure
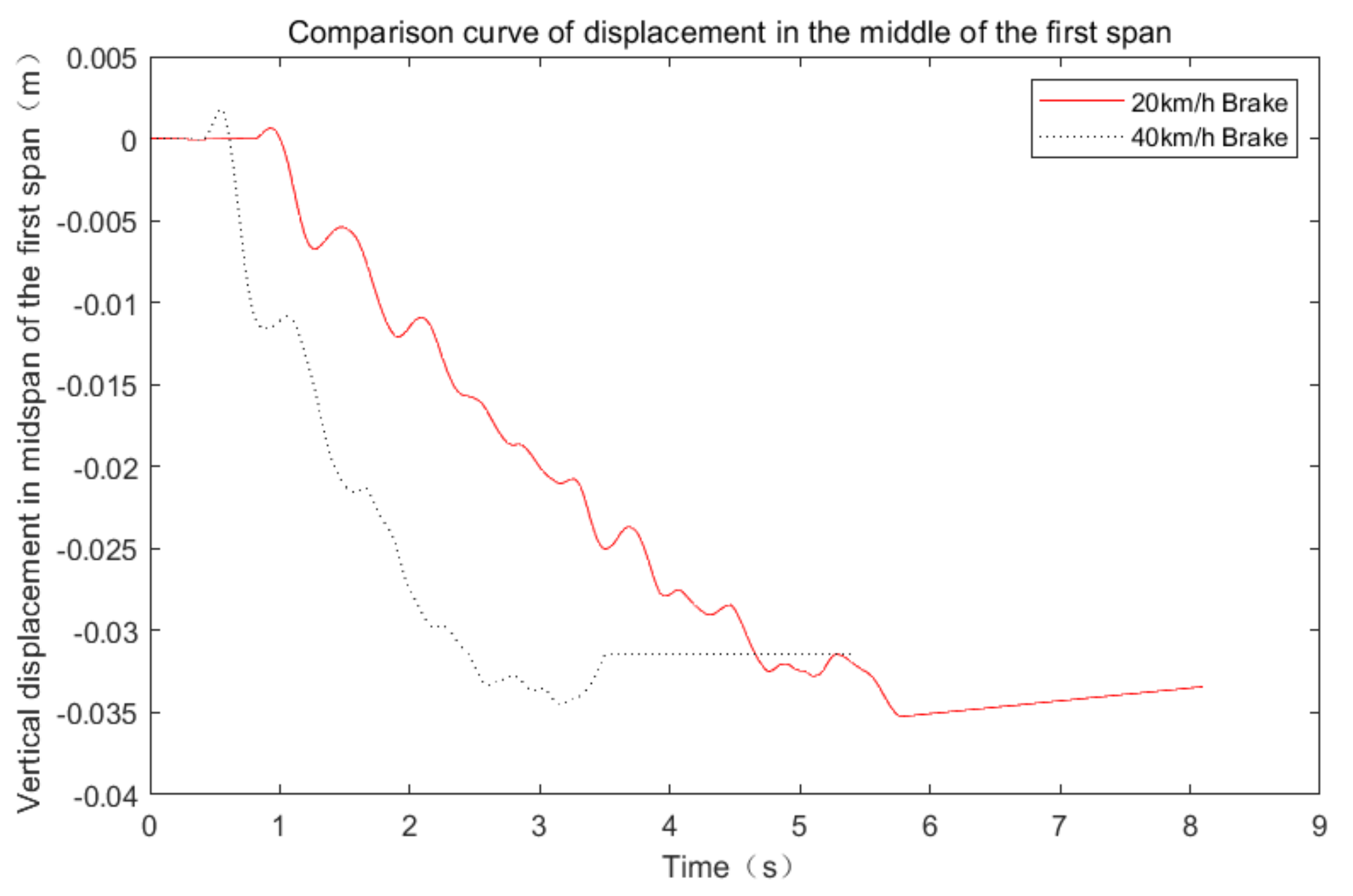
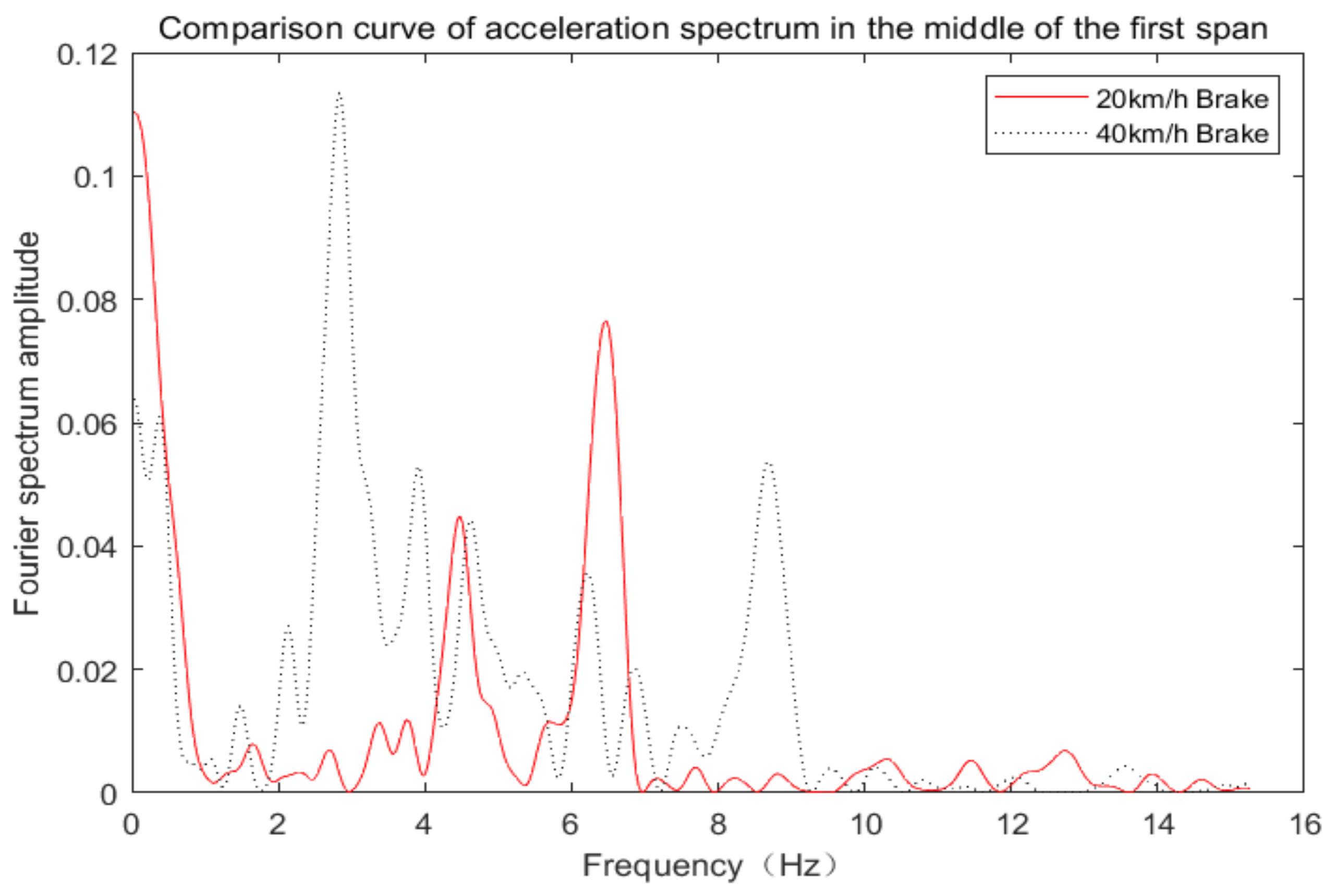
6.4. Influence of Vehicle Braking
7. Conclusions
- (1)
- The vehicle speed had no significant influence on the displacement time-history and the force of the middle wheel of the vehicle at a specific driving position. A particular fluctuation phenomenon may be related to the speed’s change of the excitation characteristics. With the speed increase, the spectrum curve did not change in a specific direction, and the peak value appeared between 1~7 Hz, although the speed changed the influence of the force of the vehicle tire. However, due to the influence of the natural frequency characteristics of the bridge and the complex vehicle bridge coupling, we did not find the law of the influence of speed change on the spectrum characteristics.
- (2)
- The pavement grade significantly influenced the bridge’s displacement time-history and acceleration spectrum. With the deterioration of road conditions, the peak force of the vehicles gradually increased, the amplitude of the frequency spectrum also gradually increased, the peak displacement of the bridge increased significantly, the fluctuation of vertical displacement waveform at the midspan position increased significantly, and the frequency at the peak of vertical acceleration spectrum curve at the midspan position did not change significantly. The corresponding amplitude of the frequency band above 5 Hz increased significantly.
- (3)
- In the case of an eccentric vehicle load, the peak displacement of the flange near the vehicle position was significantly greater than that without an eccentric load, while the peak displacement of the flange away from the vehicle position was less than that without an eccentric load. The spectrum characteristics of the mid-span vertical acceleration spectrum curve did not change significantly, but the frequency amplitude above 5 Hz increased significantly.
- (4)
- Different braking speeds had no impact on the vertical displacement. The acceleration spectrum pattern was distributed more at high speeds in the high-frequency bands.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Pan, J.; Zhang, X. Nonlinear analysis of cable bridge bridge coupling vibration. Appl. Mech. 2008, 25, 524–528. [Google Scholar]
- Wei, X.; Li, X.Z.; Li, J.; Qiang, S.Z. Research on the dynamic performance of railway large-span continuous rigid structure bridge. Vib. Impact 2009, 28, 118–121. [Google Scholar]
- Timoshenko, S.P. CV. On the forced vibrations of bridges. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 1018–1019. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Forced Vibration of Prismatics; Izvestiya Kievskogo Politekhnivheskogo Institute: Kiev, Ukraine, 1908. [Google Scholar]
- Inglis, C.E. A Mathematical Treatise on Vibrations in Railway Bridges; Cambridge University Press: Cambridge, UK, 1934. [Google Scholar]
- Mise, K.; Kunii, S. A theory for the forced vibrations of a railway bridge under the action of moving loads. Q. J. Mech. Appl. Math. 1956, 9, 195–206. [Google Scholar] [CrossRef]
- Chen, Y.J. The Evolution of Bridge Vibration Theory under Vehicle Load. Bridge Constr. 1975, 2, 21–36. [Google Scholar]
- Huang, X.Y. Dynamic Response Study of Concrete Continuous Curve Beam Bridge under Vehicle Load; Harbin Institute of Technology: Harbin, China, 2008. [Google Scholar]
- Ge, C.; Tan, C.A.; Lin, K.; Wang, L. On the efficacy and accuracy of freezing technique for the response analysis of time-varying vehicle-bridge interaction systems. J. Sound Vib. 2021, 514, 116453. [Google Scholar]
- Stoura, C.D.; Dimitrakopoulos, E.G. A Modified Bridge System method to characterize and decouple vehicle–bridge interaction. Acta Mech. 2020, 231, 3825–3845. [Google Scholar] [CrossRef]
- Zeng, Q.; Stoura, C.D.; Dimitrakopoulos, E.G. A localized lagrange multipliers approach for the problem of vehicle-bridge-interaction. Eng. Struct. 2018, 168, 82–92. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; De Roeck, G. Dynamic analysis of high speed railway bridge under articulated trains. Comput. Struct. 2003, 81, 2467–2478. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; Guo, W. Dynamic Interaction of Train-Bridge Systems in High-Speed Railways; Beijing Jiaotong University Press: Beijing, China, 2018. [Google Scholar]
- Neves, S.; Azevedo, A.; Calçada, R. A direct method for analyzing the vertical vehicle–structure interaction. Eng. Struct. 2012, 34, 414–420. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Y.; Shen, W.; Kong, F. A stochastic analysis method of transient responses using harmonic wavelets, Part 1: Time-invariant structural systems. Mech. Syst. Signal Process. 2021, 160, 107870. [Google Scholar] [CrossRef]
- Shamsi, M.; Zakerinejad, M.; Vakili, A.H. Seismic analysis of soil-pile-bridge-train interaction for isolated monorail and railway bridges under coupled lateral-vertical ground motions. Eng. Struct. 2021, 248, 113258. [Google Scholar] [CrossRef]
- Bucinskas, P.; Andersen, L.V. Dynamic response of vehicle–bridge–soil system using lumped-parameter models for structure–soil interaction. Comput. Struct. 2020, 238, 106270. [Google Scholar] [CrossRef]
- Camara, A. Vehicle–bridge interaction and driving accident risks under skew winds. J. Wind Eng. Ind. Aerodyn. 2021, 214, 104672. [Google Scholar] [CrossRef]
- GB/T7031-2005; Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data. Standards Press of China: Beijing, China, 2005.
- Kim, C.W.; Kawatani, M.; Kim, K.B. Three-dimensional dynamic analysis for bridge–vehicle interaction with roadway roughness. Comput. Struct. 2005, 83, 1627–1645. [Google Scholar] [CrossRef]
- Gupta, R.K.; Traill-Nash, R.W. Vehicle braking on highway bridges. J. Eng. Mech. Div. 1980, 106, 641–658. [Google Scholar] [CrossRef]
- Han, G.; Zhou, Y.; Liu, R.; Tang, Q.; Wang, X.; Song, L. Infuence of surface roughness on shear behaviors of rock joints under constant normal load and stifness boundary conditions. Nat. Hazards 2022, 2, 367–385. [Google Scholar] [CrossRef]


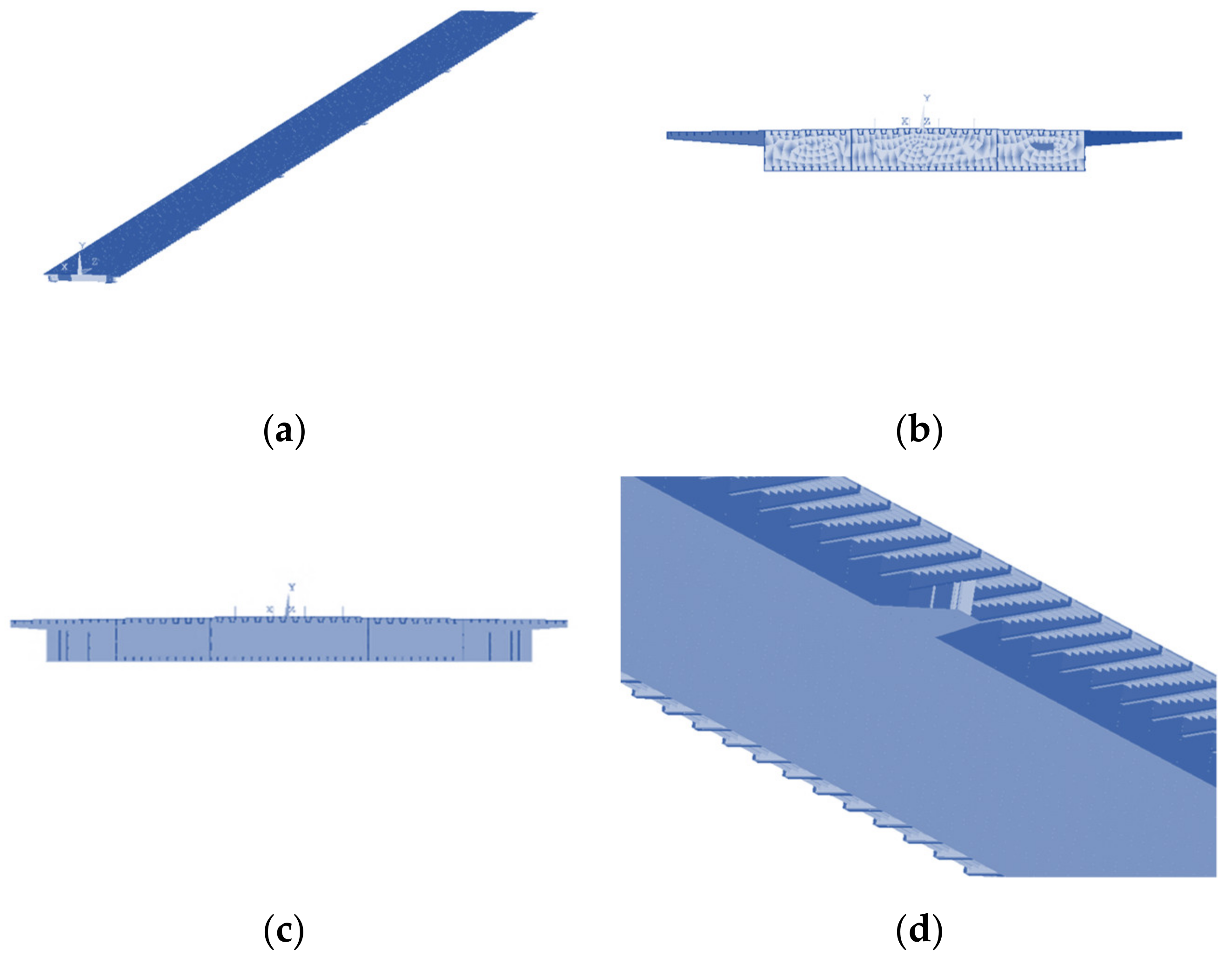





| Parameter Name | Physical Meanings | Numerical Size | Unit |
|---|---|---|---|
| M1 | Front-wheel and suspension mass | 500 | kg |
| M3 | Medium wheel and suspension mass | 1450 | kg |
| M3 | Rear-wheel and suspension mass | 1450 | kg |
| M4 | Body mass | 28,500 | kg |
| Ku1 | Front-wheel suspension elasticity coefficient | 1,577,000 | N/m |
| Ku2 | Medium-wheel suspension elasticity coefficient | 4,724,000 | N/m |
| Ku3 | Rear-wheel suspension elastic coefficient | 4,724,000 | N/m |
| Cu1 | Front-wheel suspension damping factor | 112,000 | kg/s |
| Cu2 | Mid-wheel suspension damping coefficient | 334,200 | kg/s |
| Cu3 | Rear-wheel suspension damping coefficient | 334,200 | kg/s |
| Kd1 | Front-wheel tire elasticity coefficient | 3,146,000 | N/m |
| Kd2 | Medium-wheel tire elasticity coefficient | 4,724,000 | N/m |
| Kd3 | Rear-wheel tire elasticity coefficient | 4,724,000 | N/m |
| Cd1 | Front-wheel tire damping coefficient | 13,300 | kg/s |
| Cd2 | Mid-wheel tire damping coefficient | 10,000 | kg/s |
| Cd3 | Rear-wheel tire damping coefficient | 10,000 | kg/s |
| L2 | Distance between the front wheel and the center | 3.8 | m |
| L1 | The distance between the middle wheel and the center | 0.4 | m |
| L3 | Distance between the middle and rear wheels | 1.2 | m |
| L0 | Left and right wheel distance of the vehicle | 1.8 | m |
| Mode Order | Modality | Vibration Characteristics |
|---|---|---|
| 1 | 2.49 | Car-body nodded |
| 2 | 2.77 | Car-body swing |
| 3 | 3.11 | Car-body twist |
| 4 | 11.05 | Suspension vibration |
| 5 | 11.06 | Suspension vibration |
| Road Grade | Vehicle Speed (km/h) | Middle-Wheel Acting Force (N) | Static Load (N) | Dynamic Coefficient |
|---|---|---|---|---|
| grade A | 20 | 84,643 | 70,525 | 1.200 |
| 30 | 84,380 | 70,525 | 1.196 | |
| 40 | 83,880 | 70,525 | 1.189 | |
| 50 | 83,857 | 70,525 | 1.189 | |
| grade B | 20 | 99,333 | 70,525 | 1.408 |
| 30 | 97,724 | 70,525 | 1.386 | |
| 40 | 96,620 | 70,525 | 1.370 | |
| 50 | 102,211 | 70,525 | 1.449 | |
| grade C | 20 | 144,205 | 70,525 | 2.045 |
| 30 | 119,480 | 70,525 | 1.694 | |
| 40 | 122,578 | 70,525 | 1.738 | |
| 50 | 123,242 | 70,525 | 1.747 | |
| grade D | 20 | 205,249 | 70,525 | 2.910 |
| 30 | 175,250 | 70,525 | 2.485 | |
| 40 | 166,237 | 70,525 | 2.357 | |
| 50 | 185,361 | 70,525 | 2.628 |
| Vehicle Speed (km/h) | Road Grade | Middle-Wheel Acting Force (N) | Static Force Value | Dynamic Coefficient |
|---|---|---|---|---|
| 20 | grade A | 84,643 | 70,525 | 1.200 |
| grade B | 99,333 | 70,525 | 1.408 | |
| grade C | 144,205 | 70,525 | 2.045 | |
| grade D | 205,249 | 70,525 | 2.910 | |
| 30 | grade A | 84,380 | 70,525 | 1.196 |
| grade B | 97,724 | 70,525 | 1.386 | |
| grade C | 119,480 | 70,525 | 1.694 | |
| grade D | 175,250 | 70,525 | 2.485 | |
| 40 | grade A | 83,880 | 70,525 | 1.189 |
| grade B | 96,620 | 70,525 | 1.370 | |
| grade C | 122,578 | 70,525 | 1.738 | |
| grade D | 166,237 | 70,525 | 2.357 | |
| 50 | grade A | 83,857 | 70,525 | 1.189 |
| grade B | 102,211 | 70,525 | 1.449 | |
| grade C | 123,242 | 70,525 | 1.747 | |
| grade D | 185,361 | 70,525 | 2.628 |
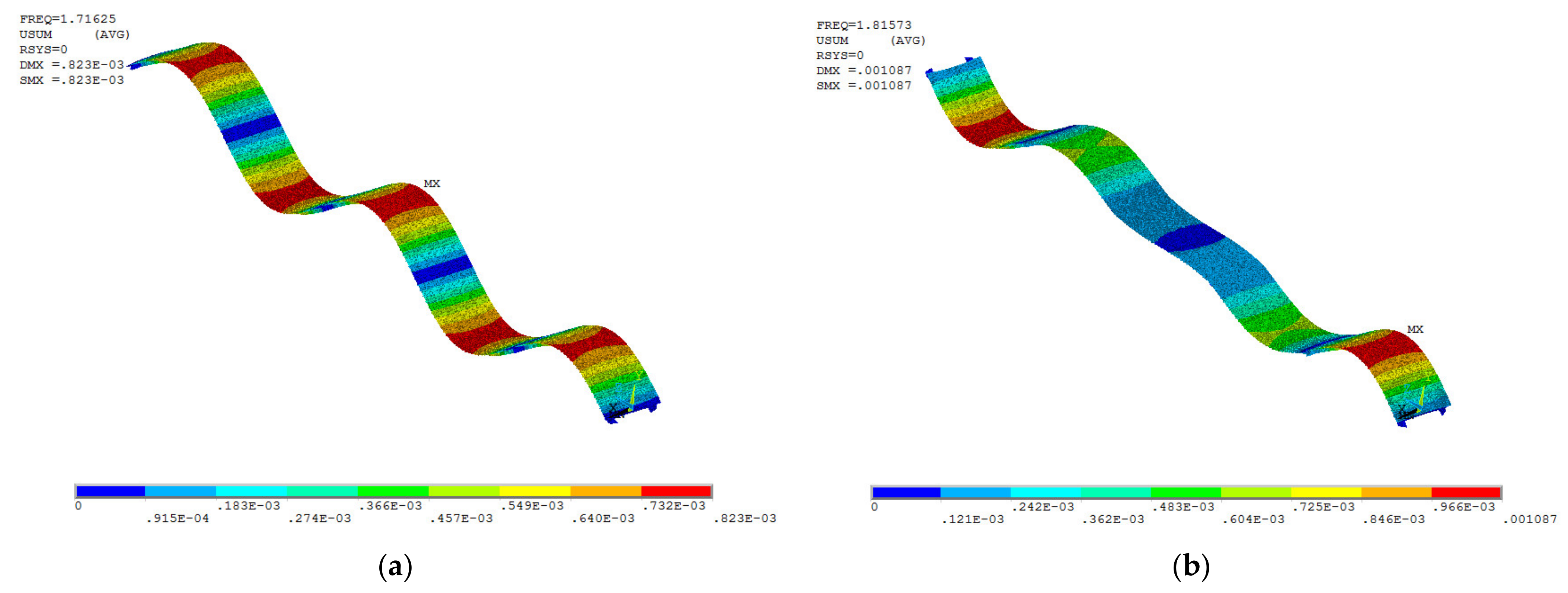
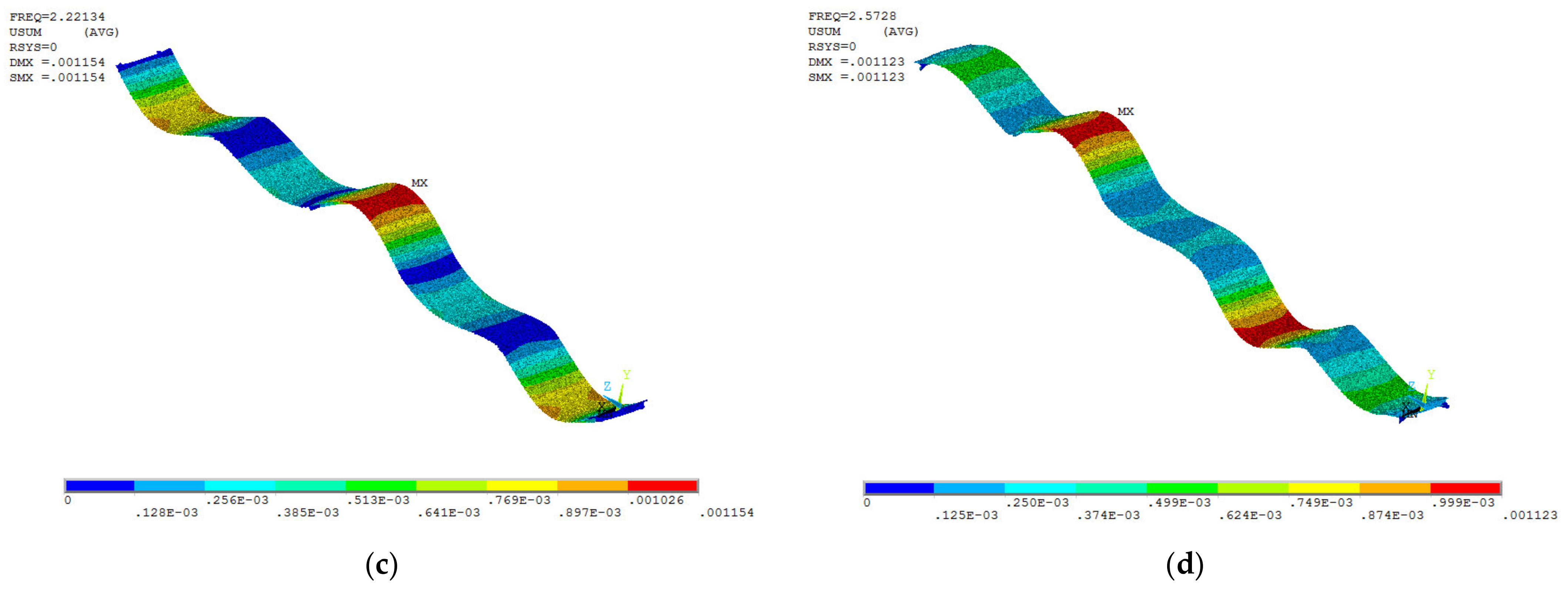
| Order | Natural Frequency Of Vibration (Hz) | Natural Vibration Period (s) | Measured Frequency (Hz) | Error ((Self-Vibration Frequency-Measured) /Measured) | Vibration Description |
|---|---|---|---|---|---|
| 1 | 1.72 | 0.582 | 1.65 | 4.24% | First-order vertical symmetric bending vibration |
| 2 | 1.82 | 0.550 | 1.75 | 3.94% | First-order vertical antisymmetric bending vibration |
| 3 | 2.22 | 0.449 | 2.15 | 3.49% | Second-order vertical symmetric bending vibration |
| 4 | 2.57 | 0.388 | 2.45 | 5.14% | Third-order vertical antisymmetric bending vibration |
| 5 | 2.92 | 0.343 | 2.76 | 5.65% | Fourth-order vertical antisymmetric bending vibration |
| 6 | 2.98 | 0.336 | 2.78 | 7.01% | Third-order vertical symmetric bending vibration |
| 7 | 4.94 | 0.203 | 4.51 | 9.49% | First-order bending and torsion are coupled to the vibration |
| 8 | 4.94 | 0.202 | 4.62 | 6.90% | Second-order twisted-coupled vibration |
| Location | The Measurement of the Second Span (A) | The Calculation of the Second Span (B) | Error |(A−B)/A| | The Measurement of the First Span (A) | The Calculation of the First Span (B) | Error |(A−B)/A| | |
|---|---|---|---|---|---|---|---|
| Test Type | |||||||
| 20 km/h | 0.076 | 0.078 | 2.63% | 0.073 | 0.075 | 2.74% | |
| 30 km/h | 0.124 | 0.101 | 18.55% | 0.062 | 0.069 | 11.29% | |
| 40 km/h | 0.096 | 0.084 | 12.50% | 0.078 | 0.089 | 14.10% | |
| Jumping | 0.122 | 0.142 | 16.39% | ||||
| Speed | 20 km/h | 30 km/h | 40 km/h | 50 km/h | Maximum Static Displacement | |
|---|---|---|---|---|---|---|
| Position | ||||||
| The first span | 34.83 | 34.45 | 34.44 | 35.71 | 26.59 | |
| The second pan | 29.25 | 29.26 | 29.30 | 29.35 | 21.28 | |
| The third span | 29.06 | 28.57 | 28.69 | 28.98 | 20.99 | |
| Grade | Grade A | Grade B | Grade C | Grade D | Maximum Static Position Move | |
|---|---|---|---|---|---|---|
| Location | ||||||
| The first span | 34.33 | 34.44 | 36.58 | 39.65 | 26.59 | |
| The second span | 29.09 | 29.30 | 29.63 | 32.33 | 21.28 | |
| The third span | 28.80 | 28.69 | 29.36 | 30.58 | 20.99 | |
| Condition | Without Eccentric Load | Close to the Load | Away from the Load | |
|---|---|---|---|---|
| Location | ||||
| The first span | 34.44 | 38.20 | 31.25 | |
| The second span | 29.30 | 32.96 | 25.99 | |
| The third span | 28.69 | 32.42 | 25.39 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Jia, Y.; Zhao, H.; Wang, S.; Jin, Z.; Yang, J. Research on the Dynamic Response of a Continuous Steel Box Girder Bridge Based on the ANSYS Platform. Sustainability 2022, 14, 10638. https://doi.org/10.3390/su141710638
Wang B, Jia Y, Zhao H, Wang S, Jin Z, Yang J. Research on the Dynamic Response of a Continuous Steel Box Girder Bridge Based on the ANSYS Platform. Sustainability. 2022; 14(17):10638. https://doi.org/10.3390/su141710638
Chicago/Turabian StyleWang, Baitian, Yudong Jia, Hongjuan Zhao, Simeng Wang, Zhengchuang Jin, and Jinfeng Yang. 2022. "Research on the Dynamic Response of a Continuous Steel Box Girder Bridge Based on the ANSYS Platform" Sustainability 14, no. 17: 10638. https://doi.org/10.3390/su141710638
APA StyleWang, B., Jia, Y., Zhao, H., Wang, S., Jin, Z., & Yang, J. (2022). Research on the Dynamic Response of a Continuous Steel Box Girder Bridge Based on the ANSYS Platform. Sustainability, 14(17), 10638. https://doi.org/10.3390/su141710638








