Encoder–Decoder-Based Velocity Prediction Modelling for Passenger Vehicles Coupled with Driving Pattern Recognition
Abstract
1. Introduction
2. Driving Pattern Recognition
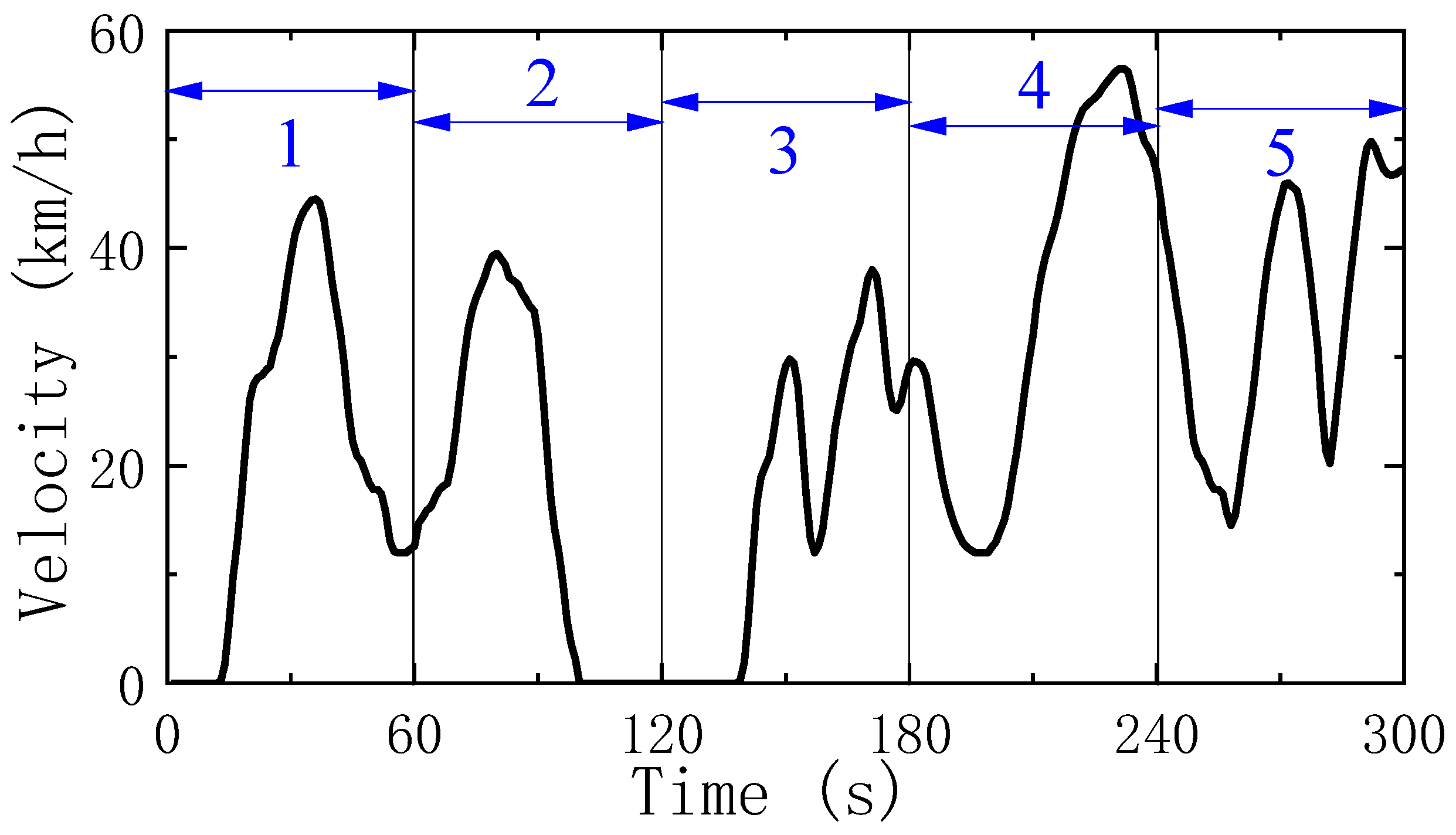
2.1. Dataset and Characteristics
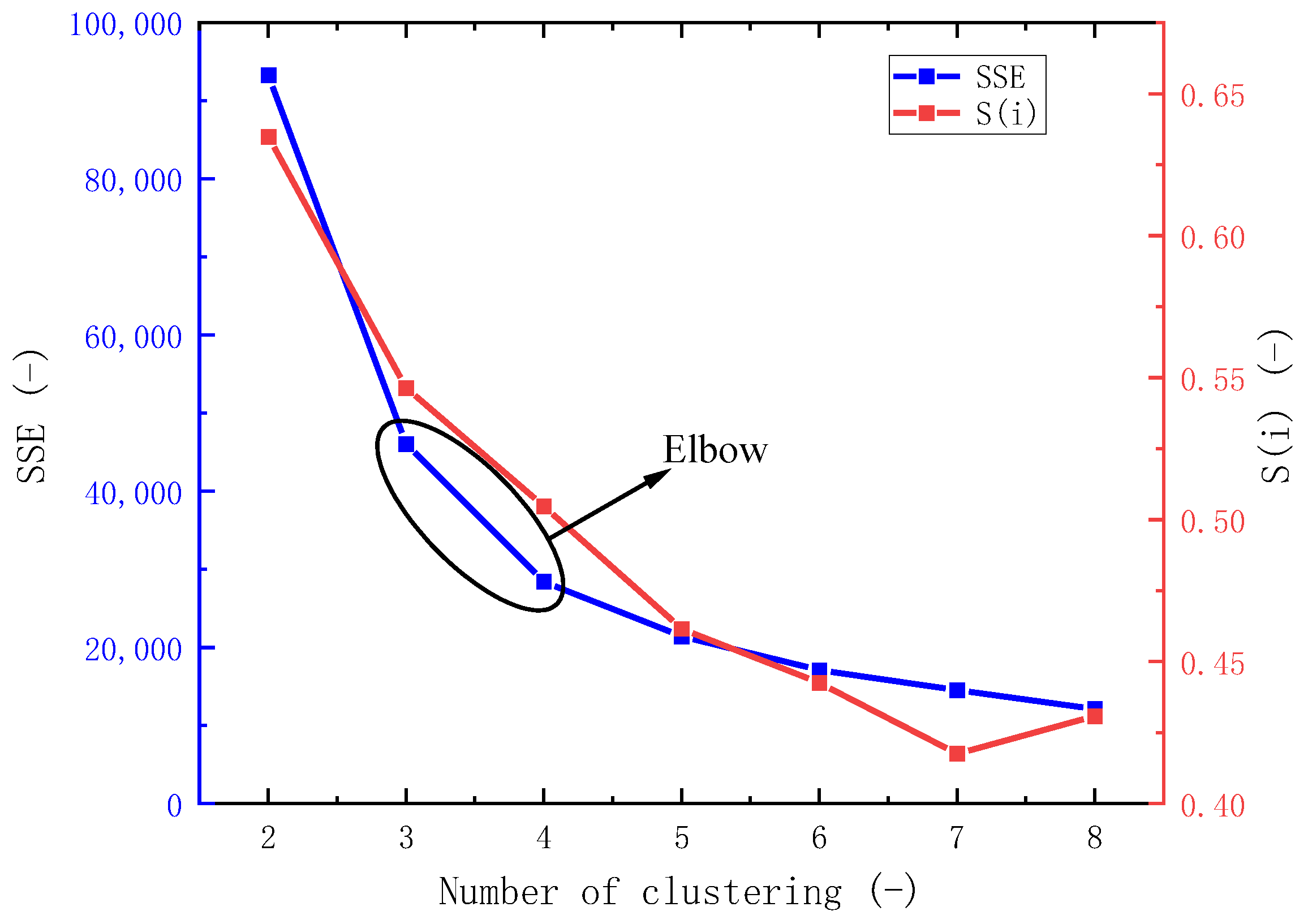
2.2. K-Means Cluster Analysis
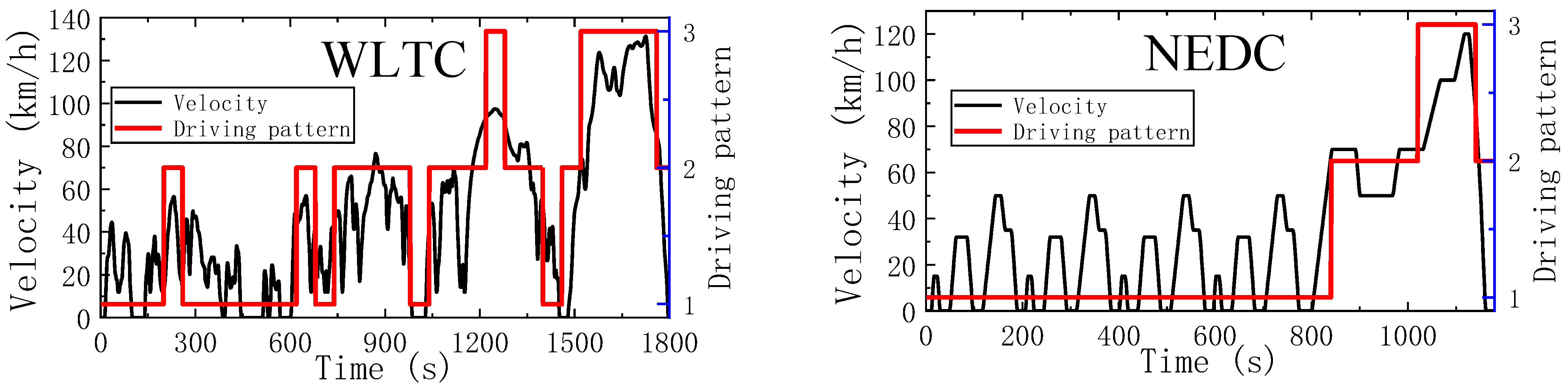
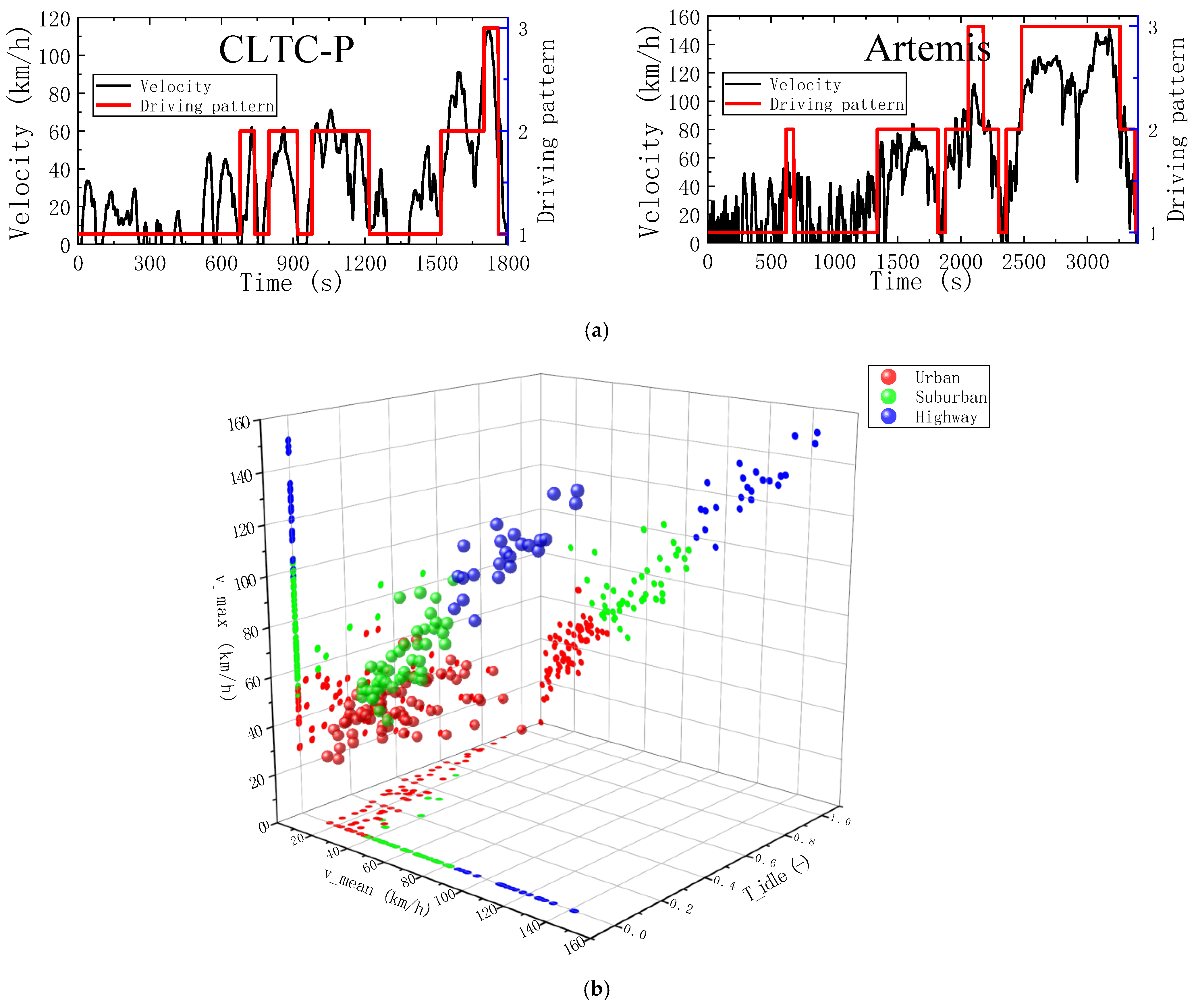
2.3. Driving Pattern Recognition
3. Velocity Prediction Based on the Encoder–Decoder Model
3.1. Basic Conception of LSTM
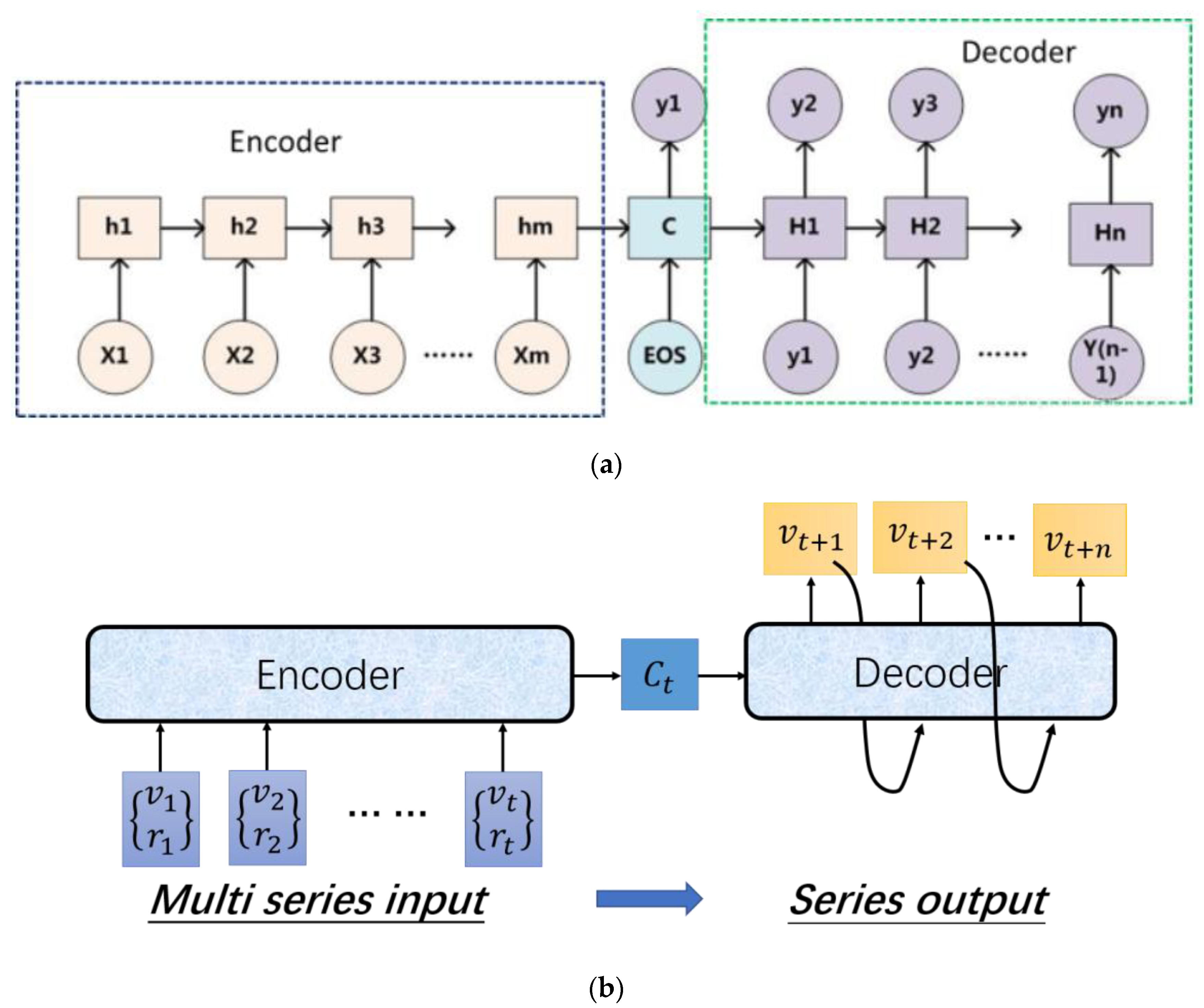
3.2. An Encoder–Decoder Structure Coupled with Driving Pattern Recognition
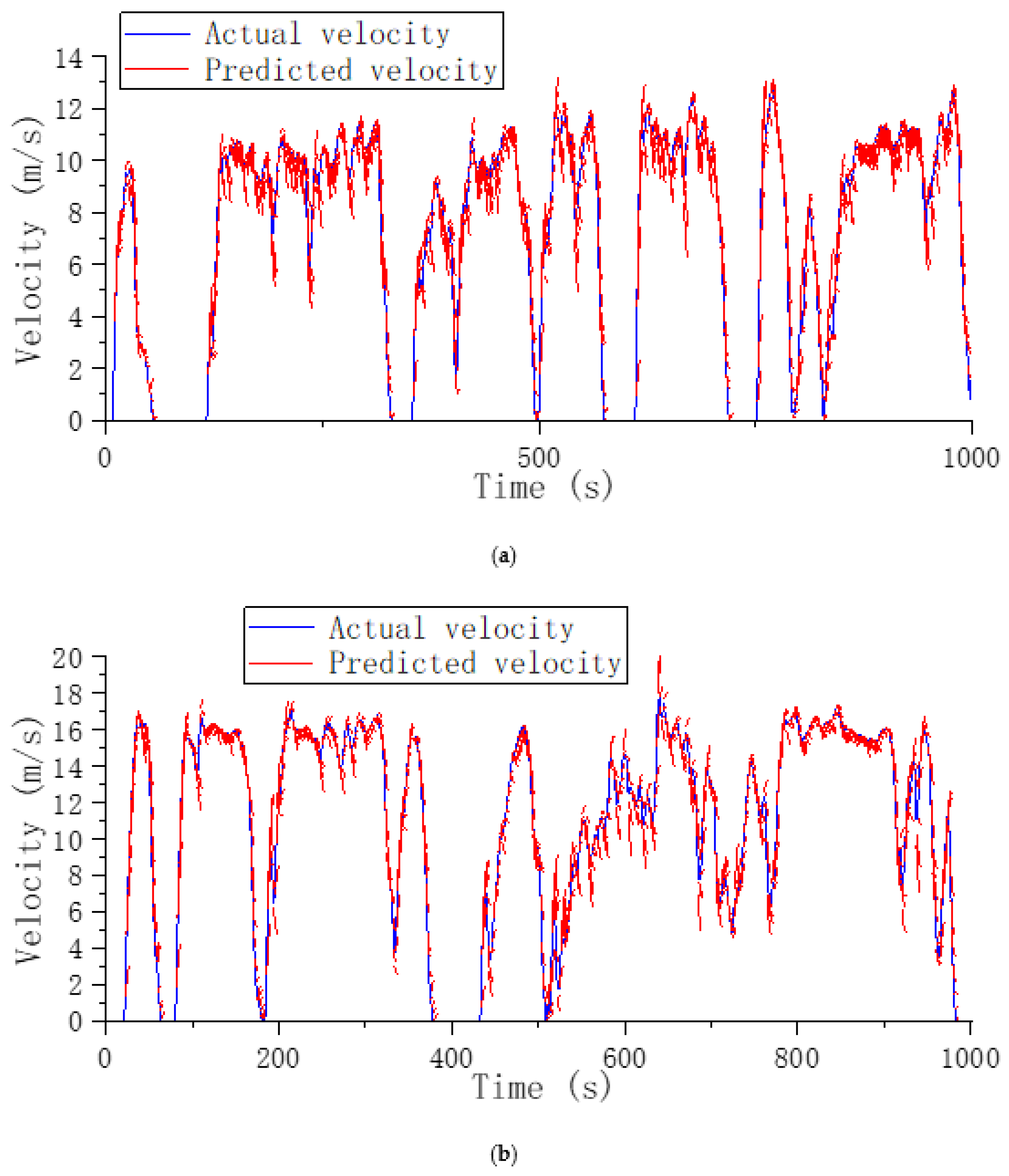
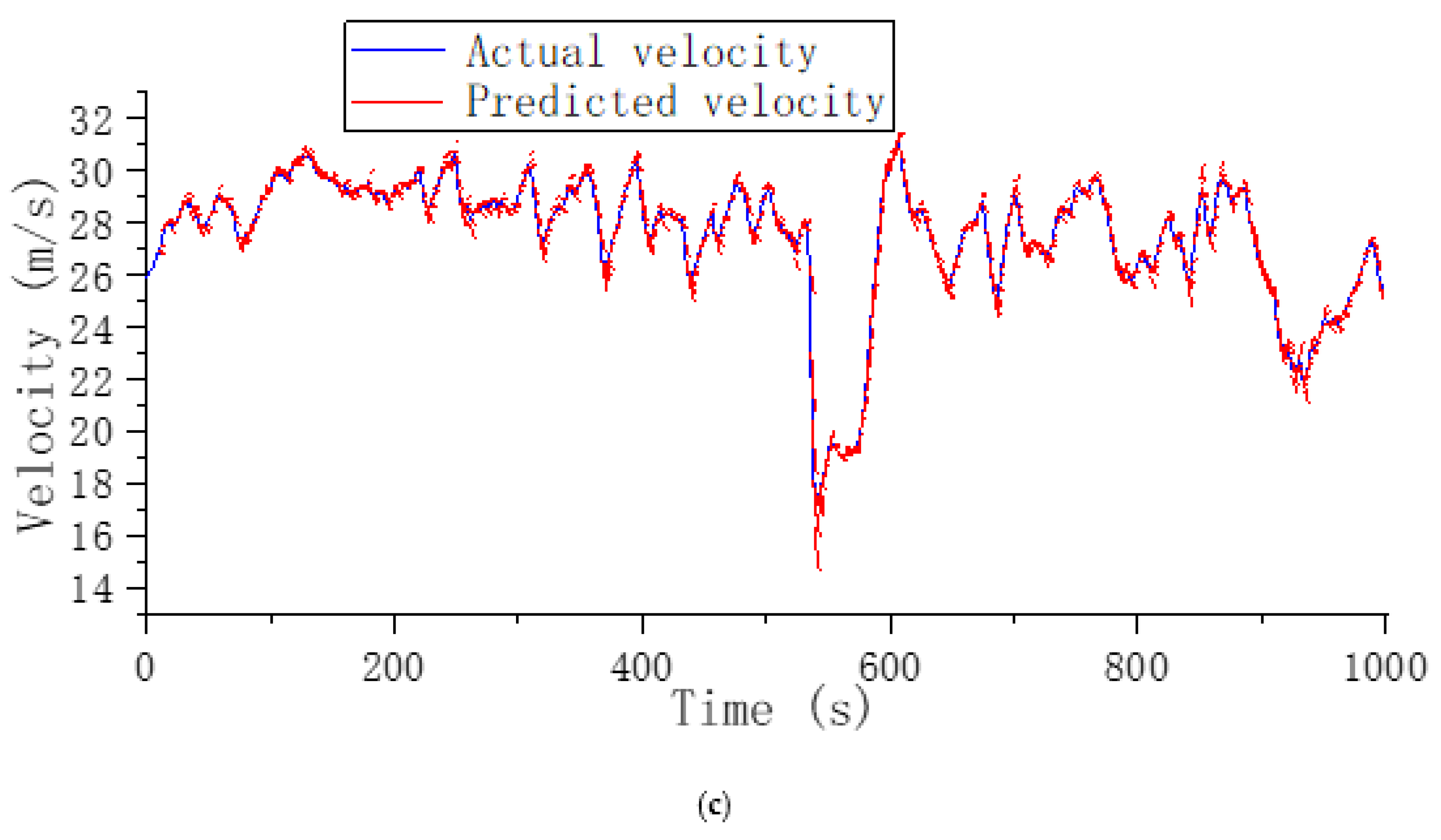
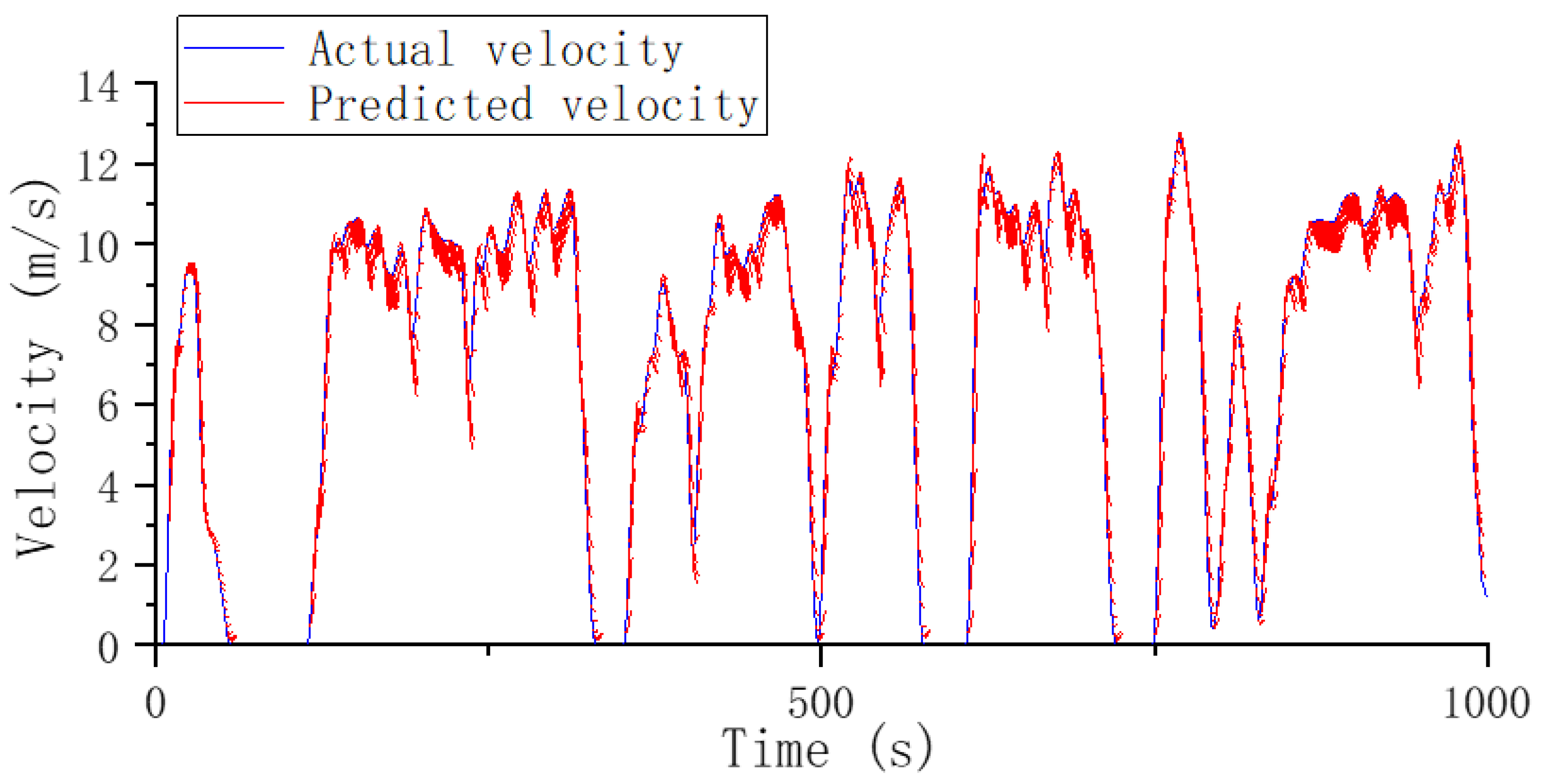
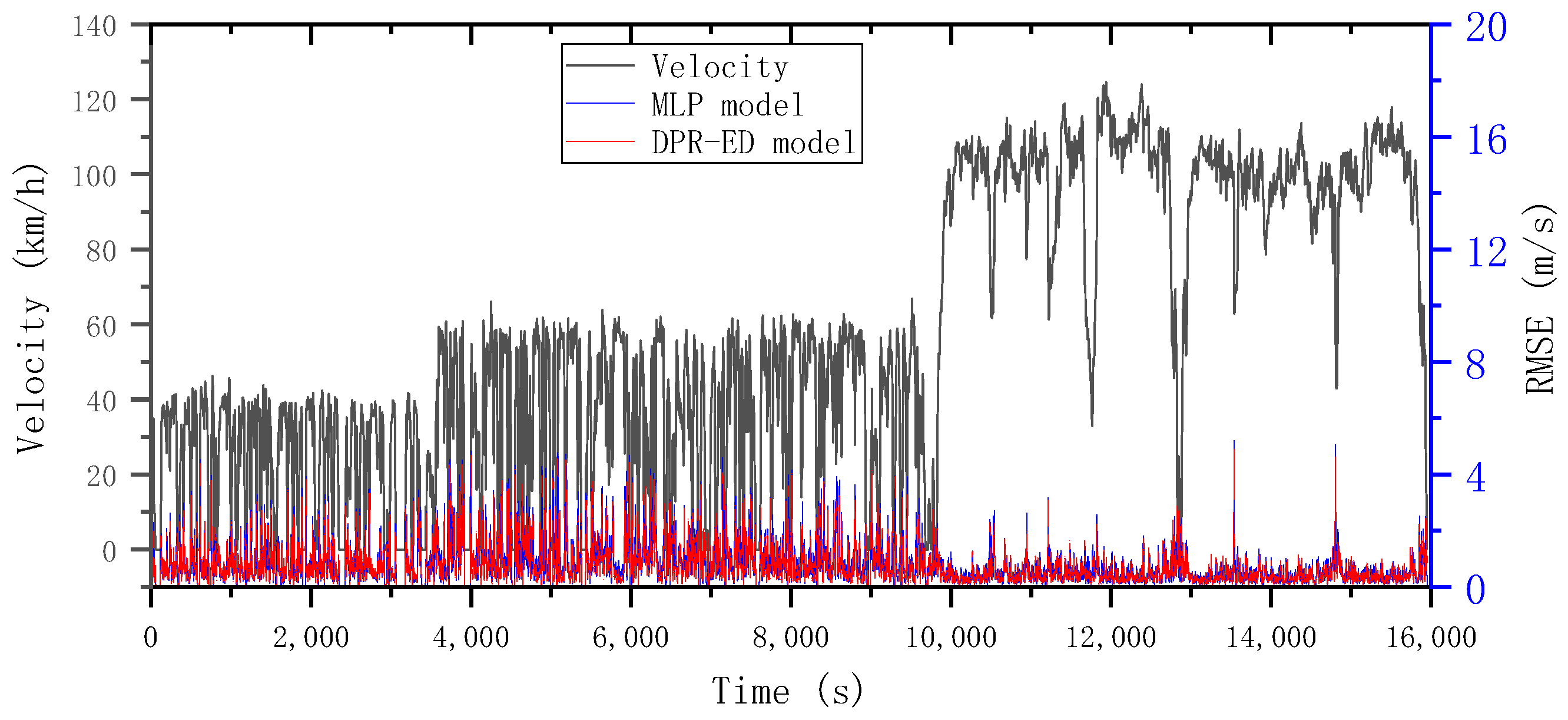
4. Results and Discussion
5. Conclusions
- (1)
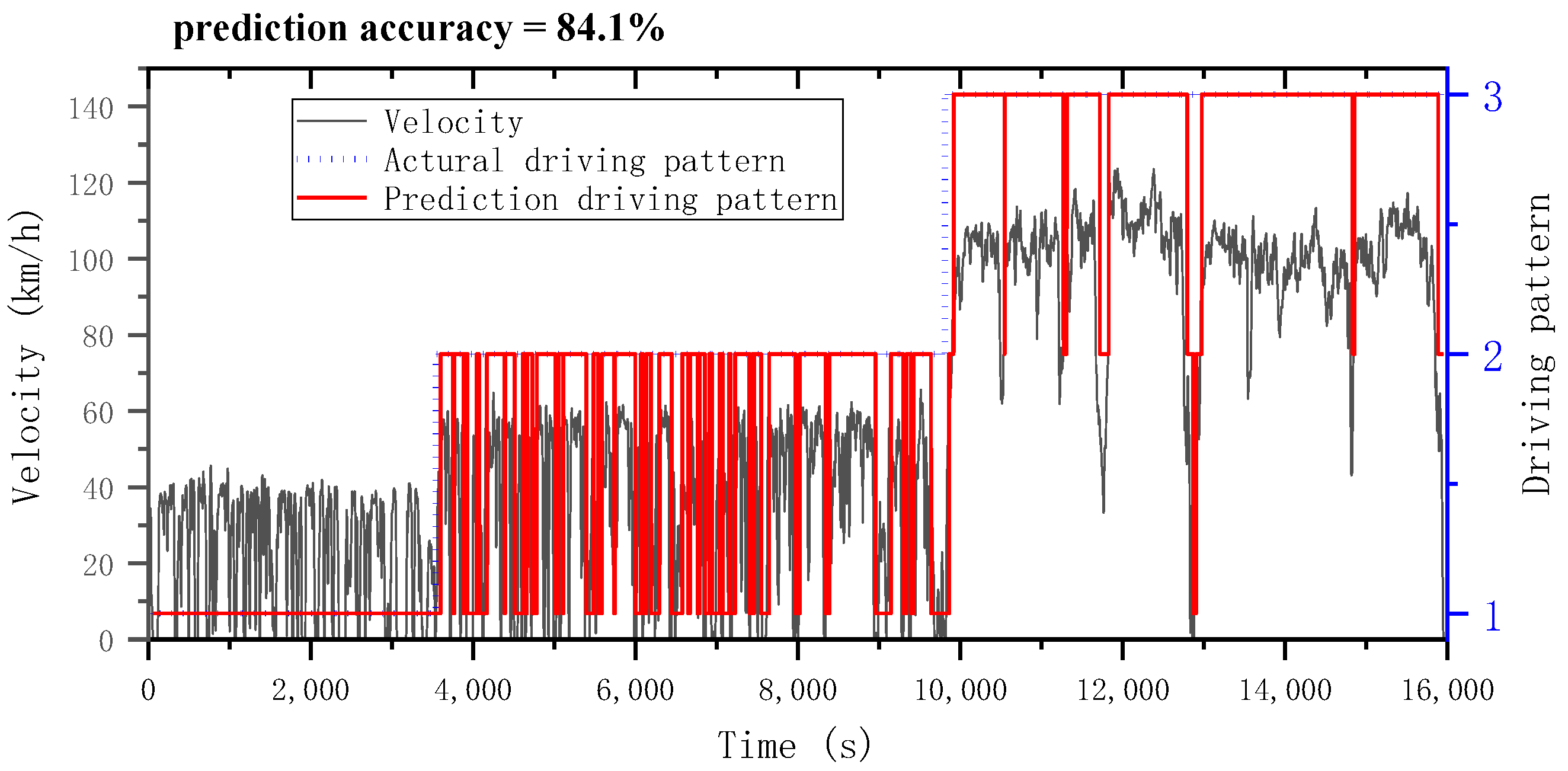
- The driving-pattern-recognition model was established by a K-means clustering algorithm and validated based on the test data; the driving patterns were identified as urban, suburban, and highway patterns. The model achieved a satisfactory recognition accuracy of 84.1% on the total length of 16,000 s of real road spectrum data, achieving results that can be used as the basis for subsequent studies.
- (2)
- The MLP, basic ED, and DPR-ED models, trained using the early stopping method, were developed. The effect of different numbers of neurons on the prediction accuracy and stability of each model was investigated and the optimization of the models was completed. The results show that the DPR-ED model with 30 LSTM hidden neurons can achieve the optimal overall performance for velocity prediction, which obtains an average RMSE of 0.000862 and a standard deviation of 0.000032 after the dataset’s normalization.
- (3)
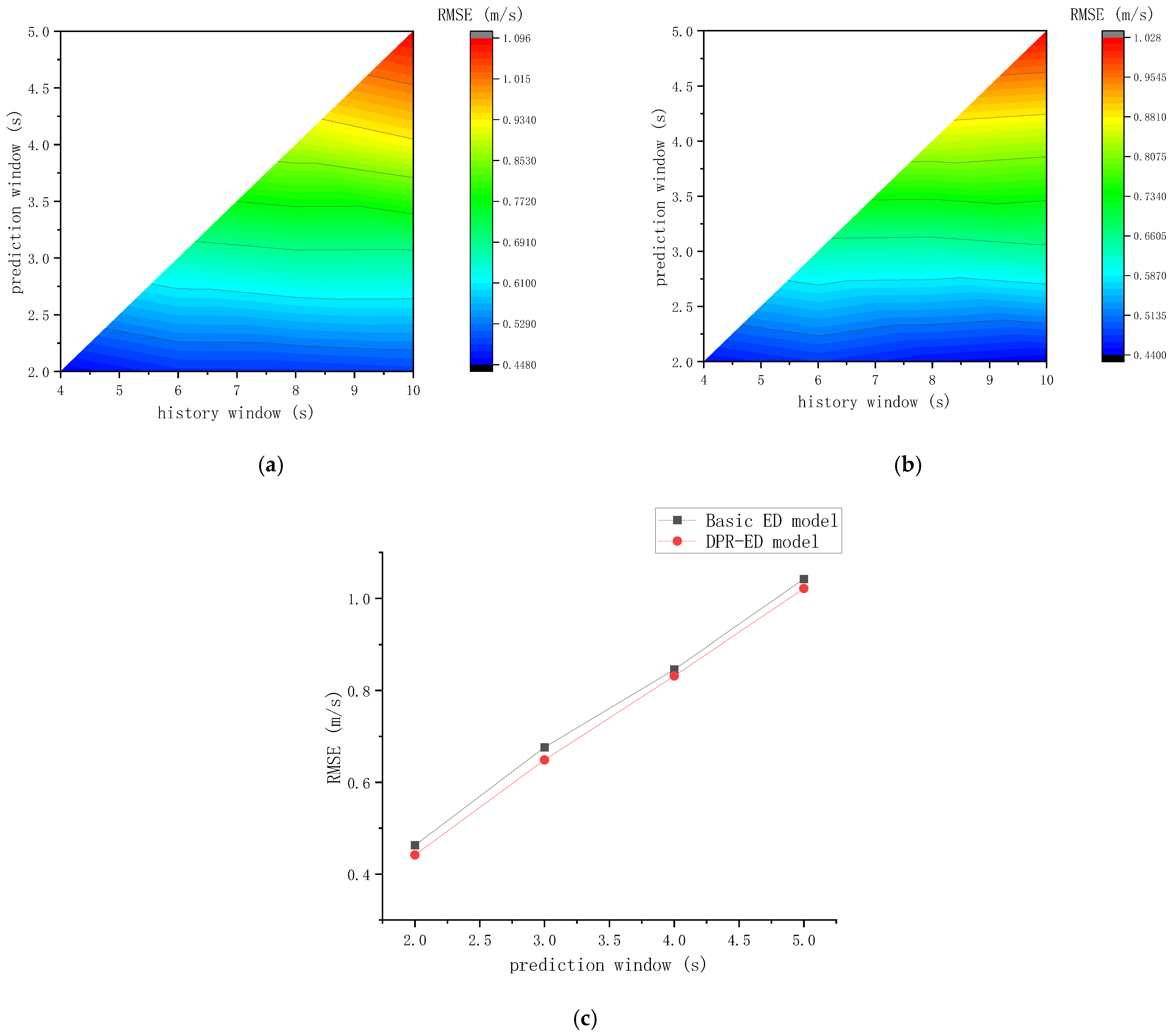
- Compared with the MLP model, the DPR-ED model is designed to improve the performance by implementing multidimensional inputs and applying time series analysis. In the long-time prediction series case, the DPR-ED model shows a significant advantage over the MLP model: the RMSE of the DPR-ED model applied to the validation set was 1.028 m/s, while the RMSE of the MLP model was 1.096 m/s, with a 6.6% deterioration in performance compared to the former. When the two models were applied to 16,000 s road spectrum data for testing, the proportion with a low error of 0.1~0.3 m/s was improved by 4% and a larger error proportion was filtered for the results predicted by the DPR-ED model. The DPR-ED model performed 5.2% better than the MLP model with respect to the average prediction accuracy. Meanwhile, the variance was decreased by 15.6%. This novel framework enables the processing of long-time sequences with multiple input dimensions, which improves the prediction accuracy under complicated driving patterns and enhances the generalization performance and robustness of the model.
Author Contributions
Funding
Conflicts of Interest
Definitions/Abbreviations
| v_mean | Average velocity |
| v_max | Maximum velocity |
| T_idle | idle ratio |
| WLTC | World Light-duty vehicle Test Cycle |
| NEDC | New European Driving Cycle |
| CLTC-P | China Light-duty vehicle Test Cycle-Passenger |
| SSE | sum of squared errors |
| SC | Silhouette coefficient |
| DPR | Driving pattern recognition |
| LSTM | Long short-term memory |
| ED | Encoder–decoder |
| MLP | Multilayer perceptron |
| RMSE | Root mean square error |
References
- Wang, Y.; Lou, D.; Xu, N.; Fang, L.; Tan, P. Energy management and emission control for range extended electric vehicles. Energy 2021, 236, 121370. [Google Scholar] [CrossRef]
- Karbaschian, M.A.; Söffker, D. Review and Comparison of Power Management Approaches for Hybrid Vehicles with Focus on Hydraulic Drives. Energies 2014, 7, 3512–3536. [Google Scholar] [CrossRef]
- Biswas, A.; Emadi, A. Energy management systems for electrified powertrains: State-of-the-art review and future trends. IEEE Trans. Veh. Technol. 2019, 68, 6453–6467. [Google Scholar] [CrossRef]
- Rizzoni, G.; Onori, S. Energy Management of Hybrid Electric Vehicles: 15 years of development at the Ohio State University. Oil Gas Sci. Technol. Rev. D’Ifp Energ. Nouv. 2014, 70, 41–54. [Google Scholar] [CrossRef]
- Tran, D.D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Wu, J.; Zhangc, H.; Cuin, X. Fuzzy energy management strategy for a hybrid electric vehicle based on driving cycle recognition. Int. J. Automot. Technol. 2012, 13, 1159–1167. [Google Scholar] [CrossRef]
- Chen, B.C.; Guan, J.C.; Li, J.H. Adaptive Power Management Control of Range Extended Electric Vehicle. Energy Procedia 2014, 61, 67–70. [Google Scholar] [CrossRef][Green Version]
- Skugor, B.; Deur, J. Instantaneous Optimization-based Energy Management Control Strategy for Extended Range Electric Vehicle. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Rezaei, A.; Burl, J.B.; Zhou, B.; Rezaei, M. A New Real-Time Optimal Energy Management Strategy for Parallel Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2019, 27, 830–837. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.; Kou, G.; Gao, W.; Qin, D. Energy Management for Plug-In Hybrid Electric Vehicle Based on Adaptive Simplified-ECMS. Sustainability 2018, 10, 2060. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Xi, L.; Zhang, X.; Sun, C.; Wang, Z.; Hou, X.; Zhang, J. Intelligent Energy Management Control for Extended Range Electric Vehicles Based on Dynamic Programming and Neural Network. Energies 2017, 10, 1871. [Google Scholar] [CrossRef]
- Zhang, P.; Yan, F.; Du, C. A comprehensive analysis of energy management strategies for hybrid electric vehicles based on bibliometrics. Renew. Sustain. Energy Rev. 2015, 48, 88–104. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Khajepour, A.; Wang, H.; Peng, J. Energy management for a power-split hybrid electric bus via deep reinforcement learning with terrain information. Appl. Energy 2019, 255, 113762.1–113762.13. [Google Scholar] [CrossRef]
- Li, G.; Görges, D. Energy management strategy for parallel hybrid electric vehicles based on approximate dynamic programming and velocity forecast. J. Frankl. Inst. 2019, 356, 9502–9523. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Peng, J.; Zhang, H. Power management for a plug-in hybrid electric vehicle based on reinforcement learning with continuous state and action spaces. Energy Procedia 2017, 142, 2270–2275. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, H.; Peng, J.; Jiang, Z.; Wu, Y. Energy management of hybrid electric bus based on deep reinforcement learning in continuous state and action space. Energy Convers. Manag. 2019, 195, 548–560. [Google Scholar] [CrossRef]
- Olia, K.; Shahverdi, M.; Mazzola, M.; Sherif, A. Developing a Model Predictive Control-Based Algorithm for Energy Management System of the Catenary-Based Electric Truck; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Zhang, S.; Xiong, R.; Sun, F. Model predictive control for power management in a plug-in hybrid electric vehicle with a hybrid energy storage system. Appl. Energy 2017, 185, 1654–1662. [Google Scholar] [CrossRef]
- Rezaei, A.; Burl, J.B. Prediction of Vehicle Velocity for Model Predictive Control. IFAC-Paper 2015, 48, 257–262. [Google Scholar] [CrossRef]
- Liu, K.; Asher, Z.; Gong, X.; Huang, M.; Kolmanovsky, I. Vehicle Velocity Prediction and Energy Management Strategy Part 1: Deterministic and Stochastic Vehicle Velocity Prediction Using Machine Learning; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Shin, J.; Sunwoo, M. Vehicle Speed Prediction Using a Markov Chain with Speed Constraints. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3201–3211. [Google Scholar] [CrossRef]
- Wang, F.; Luo, Y.T. A Research on Power Splitting Strategy for Hybrid Energy Storage System Based on Driving Condition Prediction. Automot. Eng. 2019, 41, 1251–1258, 1264. [Google Scholar]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity Predictors for Predictive Energy Management in Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Guo, J.; He, H.; Sun, C. ARIMA-Based Road Gradient and Vehicle Velocity Prediction for Hybrid Electric Vehicle Energy Management. IEEE Trans. Veh. Technol. 2019, 68, 5309–5320. [Google Scholar] [CrossRef]
- Jing, J.; Filev, D.; Kurt, A.; Özatay, E.; Michelini, J.; Özgüner, Ü. Vehicle speed prediction using a cooperative method of fuzzy Markov model and auto-regressive model. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 881–886. [Google Scholar]
- Rosolia, U.; Zhang, X.; Borrelli, F. Data-Driven Predictive Control for Autonomous Systems. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 259–286. [Google Scholar] [CrossRef]
- Fengqi, Z.; Xiaosong, H.; Kanghui, X.; Xiaolin, T.; Yahui, C. Current Status and Prospects for Model Predictive Energy Management in Hybrid Electric Vehicles. J. Mech. Eng. 2019, 55, 86–108. [Google Scholar]
- Choudhury, A.; Shanmugavadivelu, S.; Velpuri, B. Real Time Speed Trend Analysis and Hours of Service Forecasting Using LSTM Network. In Proceedings of the 2019 IEEE 5th International Conference for Convergence in Technology (I2CT), Bombay, India, 29–31 March 2019; pp. 1–6. [Google Scholar]
- Shi, F.; Wang, Y.; Chen, J.; Wang, J.; Hao, Y.; He, Y. Short-term Vehicle Speed Prediction by Time Series Neural Network in High Altitude Areas. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 032072. [Google Scholar] [CrossRef]
- Wang, Y.Q. Traffic Flow Prediction Based on Combined Model of ARIMA and RBF Neural Network. In Proceedings of the 2017 2nd International Conference on Machinery, Electronics and Control Simulation (Mecs 2017), Taiyuan, China, 24–25 June 2017; Volume 138, pp. 82–86. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Sun, C.; Moura, S.J.; Hu, X.; Hedrick, J.K.; Sun, F. Dynamic traffic feedback data enabled energy management in plug-in hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2014, 23, 1075–1086. [Google Scholar]
- Liu, G.C. Study of Energy Management Strategy of Range-Extended Electric Vehicle; Shanghai Jiao Tong University: Shanghai, China, 2017. [Google Scholar]
- Hu, J.; Liu, D.; Du, C.; Yan, F.; Lv, C. Intelligent energy management strategy of hybrid energy storage system for electric vehicle based on driving pattern recognition—ScienceDirect. Energy 2020, 198, 17298. [Google Scholar] [CrossRef]
- Rousseeuw, P. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1999, 20, 53–65. [Google Scholar] [CrossRef]
- Cao, M.; Xu, Q.; Bian, H.; Yuan, X.; Du, P. Research on configuration strategy for regional energy storage system based on three typical filtering methods. IET Gener. Transm. Distrib. 2016, 10, 2360–2366. [Google Scholar] [CrossRef]
- Li, M.; Lu, F.; Zhang, H.; Chen, J. Predicting Future Locations of Moving Objects with Deep Fuzzy-LSTM Networks. Transp. A Transp. Sci. 2020, 16, 119–136. [Google Scholar] [CrossRef]
- Xiang, C.; Ding, F.; Wang, W.; He, W. Energy management of a dual-mode power-split hybrid electric vehicle based on velocity prediction and nonlinear model predictive control. Appl. Energy 2017, 189, 640–653. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Y.; Li, G.; Shen, J.; Chen, Z.; Liu, Y. A predictive energy management strategy for multi-mode plug-in hybrid electric vehicles based on multi neural networks. Energy 2020, 208, 118366. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Z.; Ji, C.; Li, X.; Di, L.; Wu, Z. Potential improvement in combustion and pollutant emissions of a hydrogen-enriched rotary engine by using novel recess configuration. Chemosphere 2022, 299, 134491. [Google Scholar] [CrossRef] [PubMed]





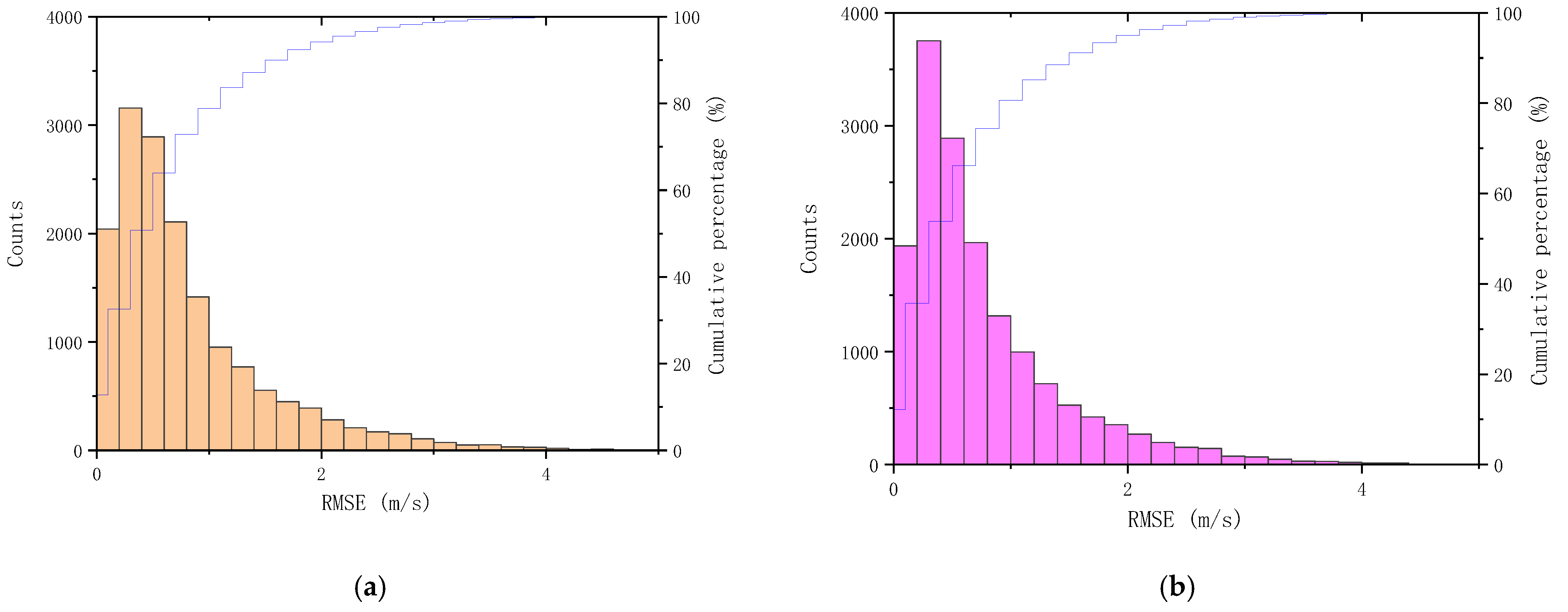
| RMSE Segment (m/s) | Proportion (MLP Model) | Proportion (DPR-ED Model) |
|---|---|---|
| 0~0.1 | 12.81% | 12.15% |
| 0.1~0.3 | 19.81% | 23.55% |
| 0.3~0.5 | 18.15% | 18.13% |
| 0.5~0.7 | 13.22% | 12.34% |
| 0.7~1.1 | 14.85% | 14.5% |
| 1.1~2.1 | 15.35% | 14.37% |
| >2.1 | 5.81% | 4.96% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, D.; Zhao, Y.; Fang, L.; Tang, Y.; Zhuang, C. Encoder–Decoder-Based Velocity Prediction Modelling for Passenger Vehicles Coupled with Driving Pattern Recognition. Sustainability 2022, 14, 10629. https://doi.org/10.3390/su141710629
Lou D, Zhao Y, Fang L, Tang Y, Zhuang C. Encoder–Decoder-Based Velocity Prediction Modelling for Passenger Vehicles Coupled with Driving Pattern Recognition. Sustainability. 2022; 14(17):10629. https://doi.org/10.3390/su141710629
Chicago/Turabian StyleLou, Diming, Yinghua Zhao, Liang Fang, Yuanzhi Tang, and Caihua Zhuang. 2022. "Encoder–Decoder-Based Velocity Prediction Modelling for Passenger Vehicles Coupled with Driving Pattern Recognition" Sustainability 14, no. 17: 10629. https://doi.org/10.3390/su141710629
APA StyleLou, D., Zhao, Y., Fang, L., Tang, Y., & Zhuang, C. (2022). Encoder–Decoder-Based Velocity Prediction Modelling for Passenger Vehicles Coupled with Driving Pattern Recognition. Sustainability, 14(17), 10629. https://doi.org/10.3390/su141710629






