Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses
Abstract
1. Introduction
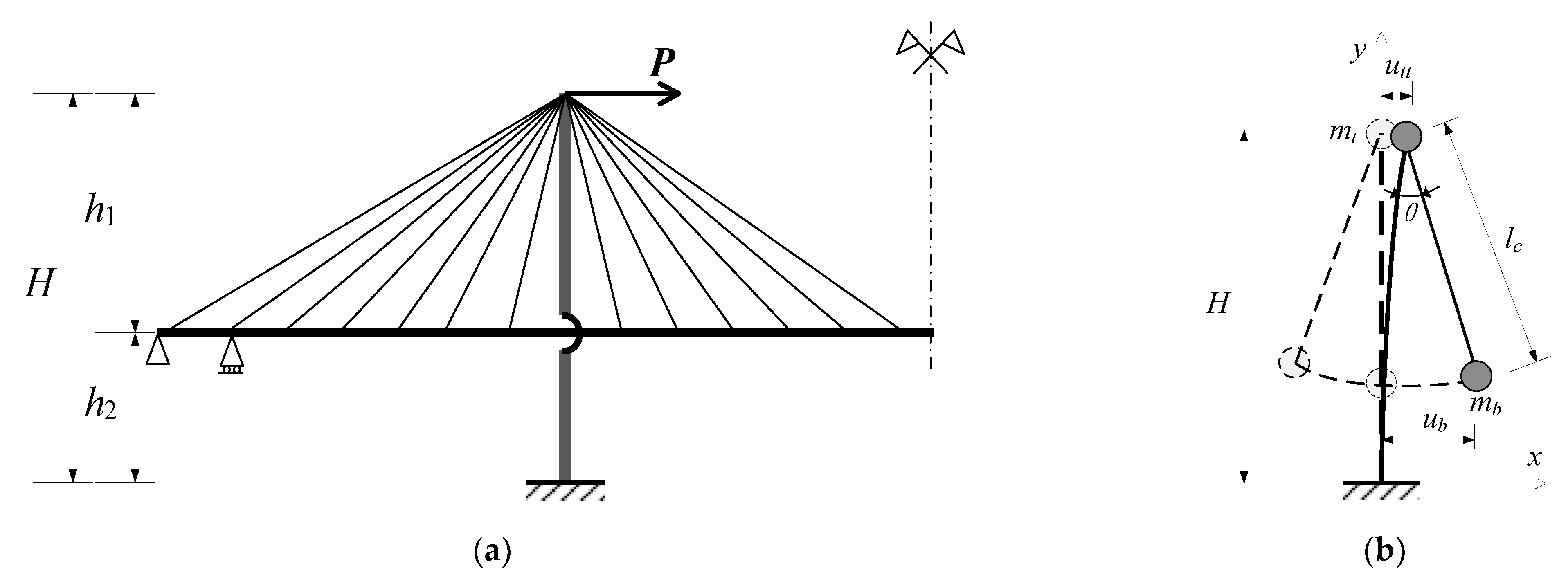
2. Simplified Calculation of the Fundamental Period of Cable-Stayed Bridge
2.1. The Floating Cable-Stayed Bridge
2.2. The Longitudinal Hinged Cable-Stayed Bridge
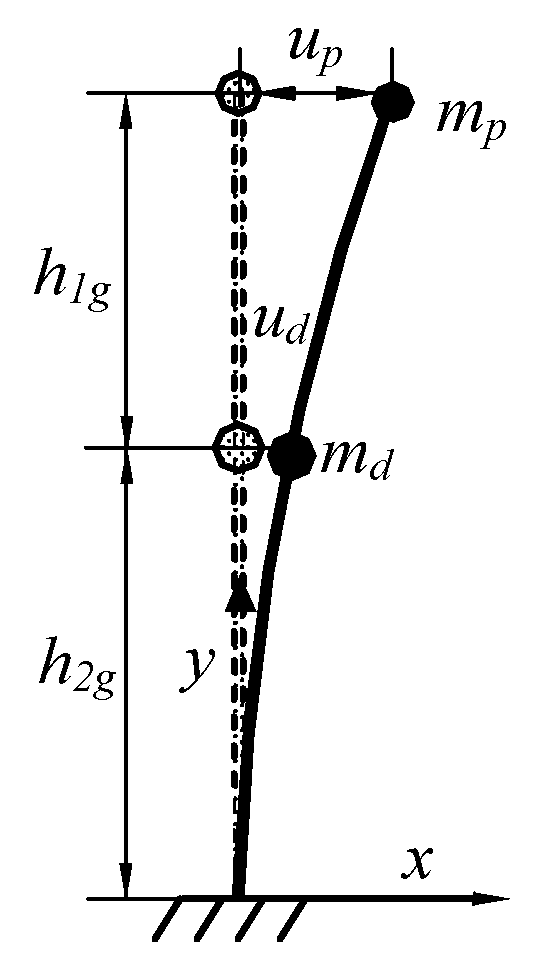
3. Criterion of Low Gravity Center Cable-Stayed Bridge
3.1. Simplified Calculation of Tower Bottom Moment
3.2. Criterion of Low Gravity Center Cable-Stayed Bridge
3.3. Comparison with Numerical Results
- (1)
- For the 10 floating cable-stayed bridges, according to the comparison of the bottom bending moment calculated by Equation (9) and that from the finite element method (FEM) with the 10 floating cable-stayed bridges, the maximum relative error was −12.56%, the minimum relative error was only −0.83%, and the average relative error was 1.36%. This indicates that the simplified calculation formula of Equation (9) could very well predict the bottom bending moment of the floating cable-stayed bridge.
- (2)
- For the 10 longitudinal hinged cable-stayed bridges, the maximum relative error between the bottom bending moment calculated by Equation (11) and that of the FEM was 11.55%, the minimum relative error was only −2.17%, and the average relative error was 4.65%. This showed that the simplified calculation formula of the bottom bending moment of the longitudinal hinged cable-stayed bridge was reasonable.
- (3)
- The standard deviations of relative error of the bending moment calculated by the simplified formulae and FEM of the floating cable-stayed bridge and the longitudinal hinged cable-stayed bridge were 9.2% and 4.5%, respectively, which showed that the simplified formulae had good stability.
- (4)
- The conclusion given by the criterion formula of Equation (12) of a low gravity center cable-stayed bridge was in good agreement with that from the FEM, which showed that the criterion formula of a low gravity center cable-stayed bridge was reliable and was helpful for the reasonable structural system selection in the preliminary design of the cable-stayed bridge.
4. Conclusions
- (1)
- Based on the simplified formula of the longitudinal fundamental period of cable-stayed bridges and combined with the response spectrum analysis method, the criterion formula of a low gravity center cable-stayed bridge was developed.
- (2)
- The conclusion given by the criterion formula of a low gravity center cable-stayed bridge was in good agreement with that from the FEM and tests, which revealed that the criterion formula of a low gravity center cable-stayed bridge is reasonable and can provide references for the preliminary design and the scheme selection of the cable-stayed bridge.
- (3)
- The seismic response characteristics of cable-stayed bridges are related to the structural system and the seismic characteristics. Therefore, whether a cable-stayed bridge is a low center of gravity cable-stayed bridge is also related to the structural characteristics of the cable-stayed bridge itself and the ground motion characteristics of its site.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Zhou, Q.-X. Structural behaviors of cable-stayed bridge with high piers. In Proceedings of the International Conference on Energy Development and Environmental Protection (EDEP 2017), Guilin, China, 18–20 August 2017. [Google Scholar]
- Camara, A.; Astiz, M.A. Analysis and control of cable-stayed bridges subject to seismic action. Struct. Eng. Int. 2014, 24, 27–36. [Google Scholar] [CrossRef]
- Su, X.; Kang, H.; Guo, T.; Cong, Y. Modeling and parametric analysis of in-plane free vibration of a floating cable-stayed bridge with transfer matrix method. Int. J. Struct. Stab. Dyn. 2019, 20, 2050004. [Google Scholar] [CrossRef]
- Kim, T.; Kwon, O.-S.; Song, J. Seismic performance of a long-span cable-stayed bridge under spatially varying bidirectional spectrum-compatible ground motions. J. Struct. Eng. 2021, 147, 04021015. [Google Scholar] [CrossRef]
- Li, X.; Fu, P.; Xu, L.; Xin, L. Assessing time-dependent damage to a cable-stayed bridge through multi-directional ground motions based on material strain measures. Eng. Struct. 2021, 227, 111417. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, J.-B.; Jia, H.-Y.; Lai, Z.-C.; Li, X.; Wang, P.-G. Influence of near-fault ground motion characteristics on the seismic response of cable-stayed bridges. Bull. Earthq. Eng. 2020, 18, 6375–6403. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, J.; Zhou, Z.; Yan, X.; Xu, L.; Lin, J. Lateral seismic fragility assessment of cable-stayed bridge with diamond-shaped concrete pylons. Shock Vib. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Zhang, C.; Wen, J.; Han, Q.; Du, X.; Lai, Z.; Fu, G. Transverse seismic response of diamond-shaped pylon in cable-stayed bridge: Experiment and analysis. Eng. Struct. 2022, 250, 113414. [Google Scholar] [CrossRef]
- Nazmy, A.S.; Abdel-Ghaffar, A.M. Non-linear earthquake-response analysis of long-span cable-stayed bridges: Applications. Earthq. Eng. Struct. Dyn. 1990, 19, 63–76. [Google Scholar] [CrossRef]
- Ren, W.-X.; Peng, X.-L.; Lin, Y.-Q. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge. Eng. Struct. 2005, 27, 535–548. [Google Scholar] [CrossRef]
- Soneji, B.B.; Jangid, R.S. Passive hybrid systems for earthquake protection of cable-stayed bridge. Eng. Struct. 2007, 29, 57–70. [Google Scholar] [CrossRef]
- Zhang, W.X.; Li, J.Z.; Li, H.F. Study of seismic response characteristics of low gravity center cable-stayed bridge. Bridge Constr. 2007, 5, 21–23. (In Chinese) [Google Scholar]
- Guo, W.; Li, J.; Guan, Z. Shake table test on a long-span cable-stayed bridge with viscous dampers considering wave passage effects. J. Bridge Eng. 2021, 26, 04020118. [Google Scholar] [CrossRef]
- Liang, X.; Li, B.; Liu, X.; Liang, L. Optimisation of longitudinal seismic energy dissipation system for straddle-type monorail-cum-road long-span cable-stayed bridge. Shock Vib. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, C.; Li, J. Simplified calculation method for supplemental viscous dampers of cable-stayed bridges under near-fault ground motions. J. Earthq. Eng. 2018, 25, 65–81. [Google Scholar] [CrossRef]
- Zhang, W.X.; Li, C.H.; Yang, J.B. Earthquake Resistance of Cable-stayed Bridge with One Tower of Low Gravity Center. J. Shijiazhuang Tiedao Univ. Nat. Sci. Ed. 2010, 23, 88–93. (In Chinese) [Google Scholar]
- Zhang, W.; Lu, P.; Wu, H.; Li, Q. Study on the damping reduction of the safe-belt constraint system of low Gravity Center cable-stayed bridge. Vibroeng. Procedia 2017, 14, 184–191. [Google Scholar] [CrossRef][Green Version]
- Camara, A.; Efthymiou, E. Deck–tower interaction in the transverse seismic response of cable-stayed bridges and optimum configurations. Eng. Struct. 2016, 124, 494–506. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Fang, R.; Zhao, H. Dynamic model testing of low-gravity-center cable-stayed bridges with different girder-to-tower connections. J. Bridge Eng. 2021, 26, 04020112. [Google Scholar] [CrossRef]
- Xie, W.; Sun, L.; Lou, M. Wave-passage effects on seismic responses of pile–soil–cable-stayed bridge model under longitudinal non-uniform excitation: Shaking table tests and numerical simulations. Bull. Earthq. Eng. 2020, 18, 5221–5246. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Ye, A. Shake table test on transverse steel damper seismic system for long span cable-stayed bridges. Eng. Struct. 2019, 179, 106–119. [Google Scholar] [CrossRef]
- Sun, L.; Xie, W. Evaluation of pile-soil-structure interaction effects on the seismic responses of a super long-span cable-stayed bridge in the transverse direction: A shaking table investigation. Soil Dyn. Earthq. Eng. 2019, 125, 105755. [Google Scholar] [CrossRef]
- Luo, X.; Li, X.; Fu, X.; Gu, L. Research on bridge structural health assessment based on Finite Element Analysis. Tehnički Vjesnik 2020, 27, 96–105. [Google Scholar]
- Dong, F.-H. Virtual reality research on vibration characteristics of long-span bridges with considering vehicle and wind loads based on neural networks and finite element method. Neural Comput. Appl. 2017, 29, 1303–1309. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Y.; Kou, W.; Du, X. Simplified calculation method for the fundamental period of floating cable-stayed bridge. Arch. Appl. Mech. 2017, 88, 329–339. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Y.; Huang, J.; Li, Y. Simplified calculation method for transverse seismic response of aqueducts considering fluid-structure interaction. J. Vibroeng. 2017, 19, 6135–6151. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- China Construction Industry Press. Code for Design of the Municipal Bridge; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2011. [Google Scholar]
- China Merchants Chongqing Transportation Scientific Research Institute Co., Ltd. Specifications for Seismic Design of Highway Bridge; Ministry of Transport of the People’s Republic of China: Beijing, China, 2020. [Google Scholar]
- Yuan, W.; Yan, D. Simplified calculation method for longitudinal drift frequency of cable-stayed bridge. J. Tongji Univ. Nat. Sci. Ed. 2005, 11, 5–9. (In Chinese) [Google Scholar]
- Liu, C. The Design Analyses of the Displacement Constraint and the Seismic Mitigation for Elastic-Plastic Seismic Isolator of Railway Bridges. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2019. (In Chinese). [Google Scholar]
- Yang, H.; Li, J. Simplified calculation of the concept of longitudinal drift frequency of cable-stayed bridges and discussion of influencing factors. Build. Struct. 2015, 45, 93–96. (In Chinese) [Google Scholar]
- Zhang, W.; Kou, W.; Chen, Y.; Wang, Z. Calculation of first-order natural vibration period of longitudinal first-order cable-stayed bridge based on double-particle model. Bridge Constr. 2016, 46, 98–102. (In Chinese) [Google Scholar]
- Zhang, W.; Liang, K.; Chen, Y. Relationship between the vibration acceleration and stability of a continuous girder bridge during horizontal rotation. Sustainability 2022, 14, 5853. [Google Scholar] [CrossRef]
- Su, Q.; Zhai, H.; Wu, C. Model Test Study of Horizontal Load-Bearing Behavior of Anchorage Zone in Cable Pylon of the 3rd Ji’ nan Huanghe River Bridge. Bridge Constr. 2008, 3, 12–14. (In Chinese) [Google Scholar]
- Li, L.; Li, L.; Wang, X. Design of Main Bridge of North Bridge of Qidu Bridge. Bridge Constr. 2016, 46, 4. (In Chinese) [Google Scholar]


| Site Type | Single-Tower Cable-Stayed Bridge (Ji’nan No.3 Bridge) | Dual-Tower Cable-Stayed Bridge (Qidu Bridge) | |||||
|---|---|---|---|---|---|---|---|
| I | 1/10 | 8.86 | 9.80 | 1.23 | 5.45 | 6.34 | 1.19 |
| 2/10 | 9.04 | 10.1 | 1.37 | 8.28 | 8.65 | 1.09 | |
| 3/10 | 11.52 | 12.93 | 1.47 | 13.66 | 13.29 | 1.06 | |
| 4/10 | 13.35 | 14.28 | 1.49 | 19.33 | 18.57 | 1.01 | |
| 5/10 | 15.65 | 17.33 | 1.52 | 26.42 | 25.02 | 1.05 | |
| II | 1/10 | 13.12 | 14.52 | 1.25 | 8.07 | 9.26 | 1.18 |
| 2/10 | 13.39 | 14.97 | 1.37 | 12.27 | 12.74 | 1.09 | |
| 3/10 | 17.06 | 19.15 | 1.47 | 20.24 | 19.7 | 1.06 | |
| 4/10 | 19.78 | 21.16 | 1.49 | 28.64 | 27.52 | 1.06 | |
| 5/10 | 23.18 | 25.67 | 1.52 | 39.14 | 37.07 | 1.09 | |
| III | 1/10 | 18.04 | 19.96 | 1.23 | 11.09 | 12.76 | 1.18 |
| 2/10 | 18.41 | 20.58 | 1.39 | 16.87 | 17.39 | 1.09 | |
| 3/10 | 23.46 | 26.34 | 1.47 | 27.84 | 27.1 | 1.06 | |
| 4/10 | 27.2 | 29.10 | 1.49 | 39.38 | 37.86 | 1.10 | |
| 5/10 | 31.87 | 35.30 | 1.52 | 53.81 | 50.96 | 1.11 | |
| IV | 1/10 | 22.14 | 24.50 | 1.25 | 13.62 | 15.57 | 1.18 |
| 2/10 | 22.6 | 25.27 | 1.39 | 8.28 | 8.65 | 1.08 | |
| 3/10 | 28.79 | 32.35 | 1.47 | 34.16 | 33.24 | 1.05 | |
| 4/10 | 33.38 | 35.72 | 1.49 | 48.33 | 46.48 | 1.11 | |
| 5/10 | 39.11 | 43.32 | 1.52 | 66.04 | 62.56 | 1.12 | |
| average | - | - | 1.42 | - | - | 1.10 | |
| Bridge | The Floating Cable-Stayed Bridge | The Longitudinal Hinged Cable-Stayed Bridge | Criterion | |||||
|---|---|---|---|---|---|---|---|---|
| Jinan No.3 | 18.41 | 20.58 | 10.55 | 16.87 | 17.39 | 3.03 | 0.92 | 0.84 |
| Songhuajiang | 15.36 | 14.31 | −7.33 | 10.49 | 10.27 | −2.17 | 0.68 | 0.72 |
| Songyuan | 14.58 | 13.20 | −10.45 | 24.14 | 26.43 | 8.66 | 1.66 | 2.00 |
| Nanye Road | 12.88 | 12.23 | −5.30 | 16.59 | 16.06 | −3.29 | 1.29 | 1.31 |
| Haihe | 16.01 | 17.08 | 6.26 | 18.73 | 19.81 | 5.44 | 1.17 | 1.16 |
| Feiyunjiang | 7.51 | 8.44 | 11.02 | 9.53 | 10.03 | 4.99 | 1.27 | 1.19 |
| Jintang | 15.07 | 13.39 | −12.56 | 20.43 | 22.56 | 9.47 | 1.36 | 1.68 |
| Qidu | 8.02 | 9.01 | 10.98 | 10.47 | 10.74 | 2.51 | 1.31 | 1.19 |
| Taizhouwan | 10.06 | 9.98 | −0.83 | 10.18 | 10.86 | 6.28 | 1.01 | 1.09 |
| Sutong | 48.15 | 54.25 | 11.24 | 48.51 | 54.85 | 11.55 | 1.01 | 1.01 |
| Standard Deviation | / | / | 9.2% | / | / | 4.5% | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, Y.; Zhang, W.; Liang, K.; Du, X. Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses. Sustainability 2022, 14, 10570. https://doi.org/10.3390/su141710570
Chen Y, Wang Y, Zhang W, Liang K, Du X. Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses. Sustainability. 2022; 14(17):10570. https://doi.org/10.3390/su141710570
Chicago/Turabian StyleChen, Ying, Yonghuan Wang, Wenxue Zhang, Kun Liang, and Xiuli Du. 2022. "Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses" Sustainability 14, no. 17: 10570. https://doi.org/10.3390/su141710570
APA StyleChen, Y., Wang, Y., Zhang, W., Liang, K., & Du, X. (2022). Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses. Sustainability, 14(17), 10570. https://doi.org/10.3390/su141710570





