Study on Stability of Anchored Slope under Static Load with Weak Interlayer
Abstract
1. Introduction
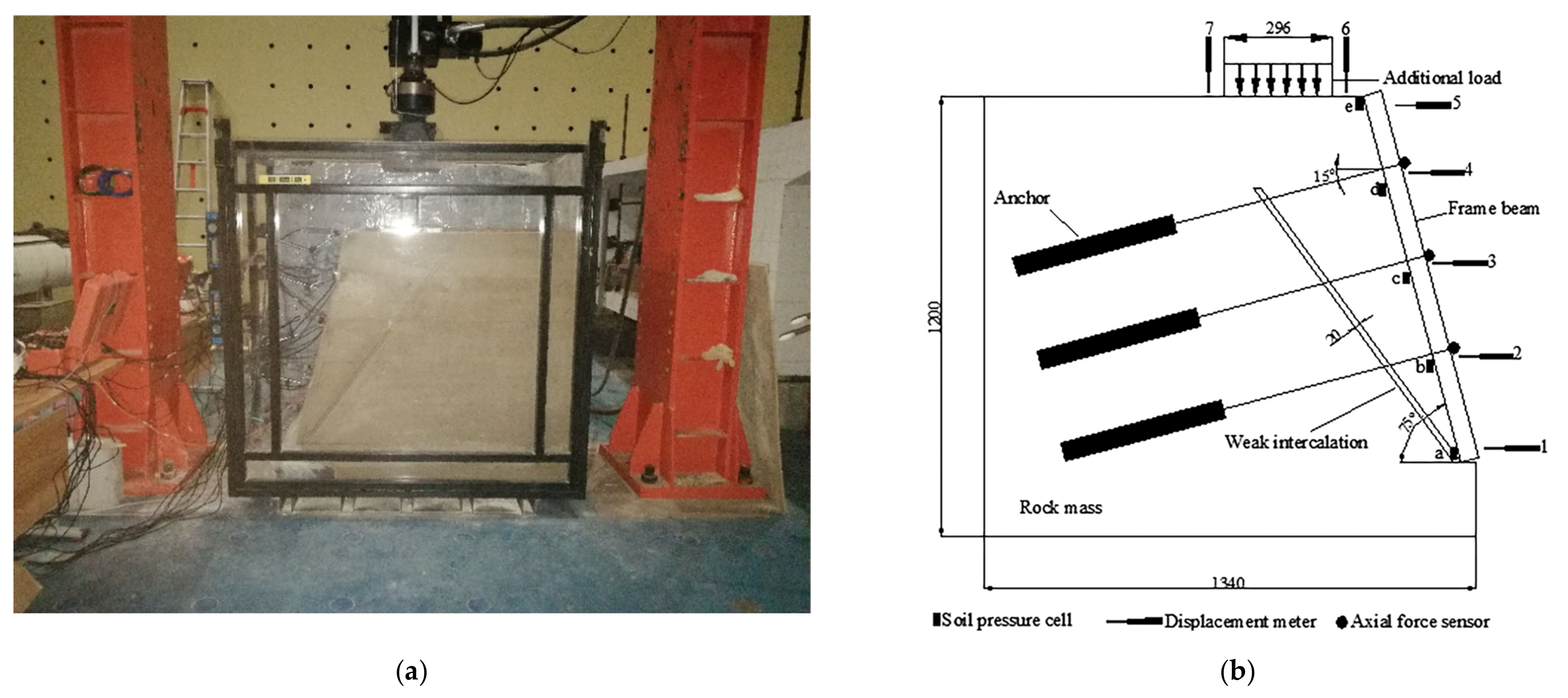
2. The Model Test
2.1. Basic Test Conditions
2.2. Similarity Design and Model-Making Procedure
2.3. Layout of Monitoring Points and Loading Conditions
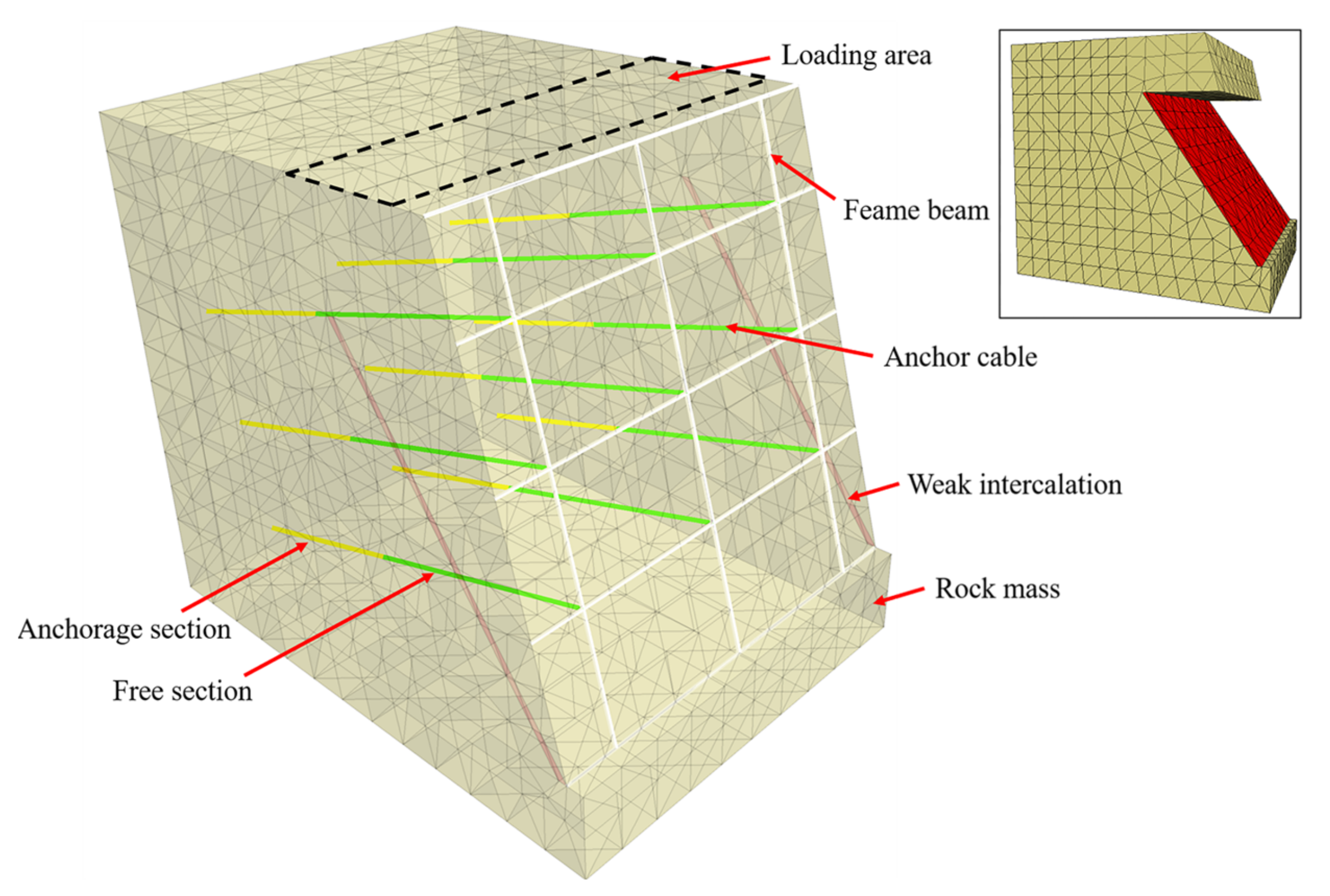
3. Numerical Simulation
4. Numerical Model Verification
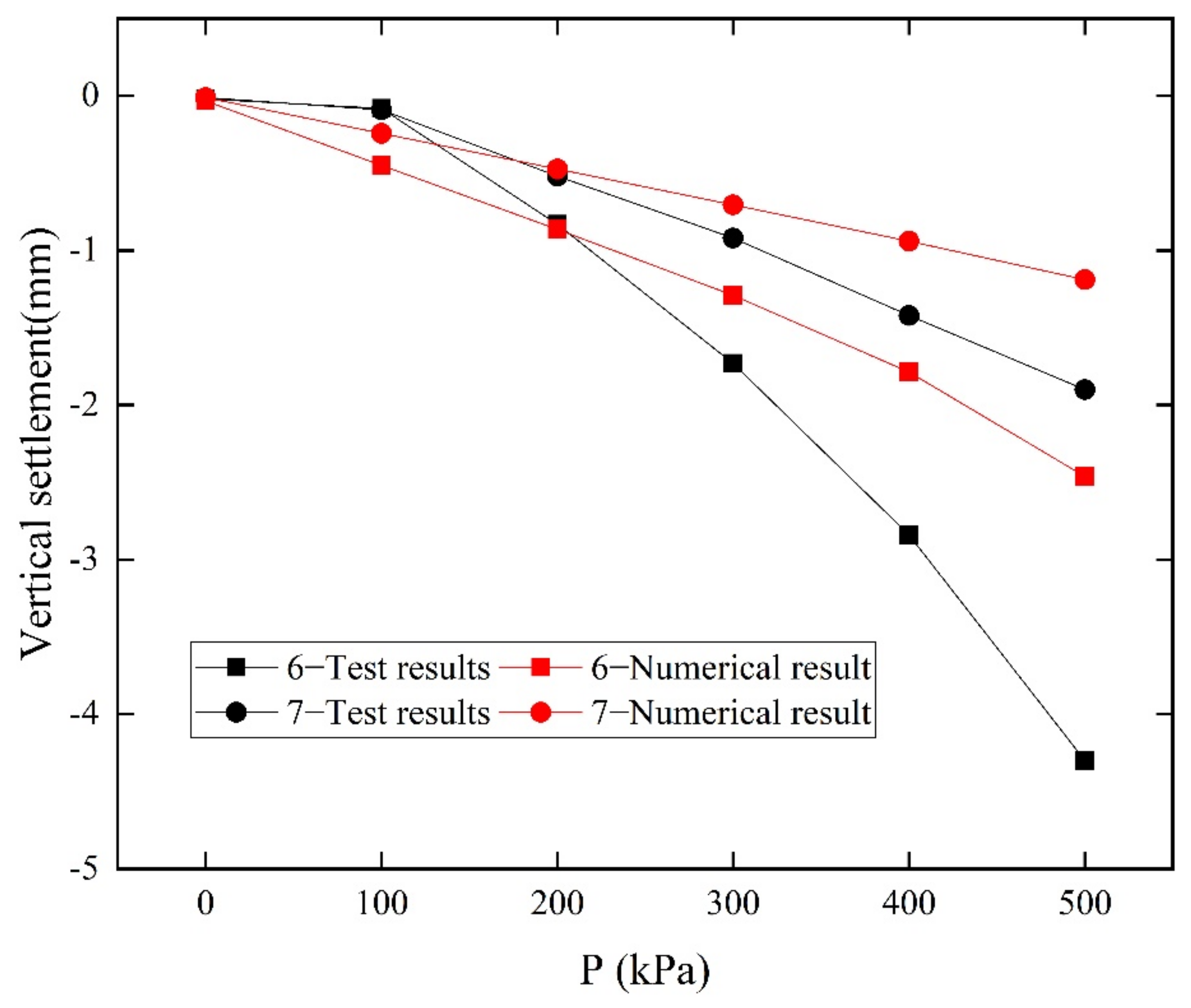
4.1. Horizontal Displacement
4.2. Vertical Settlement
5. Results and Discussion
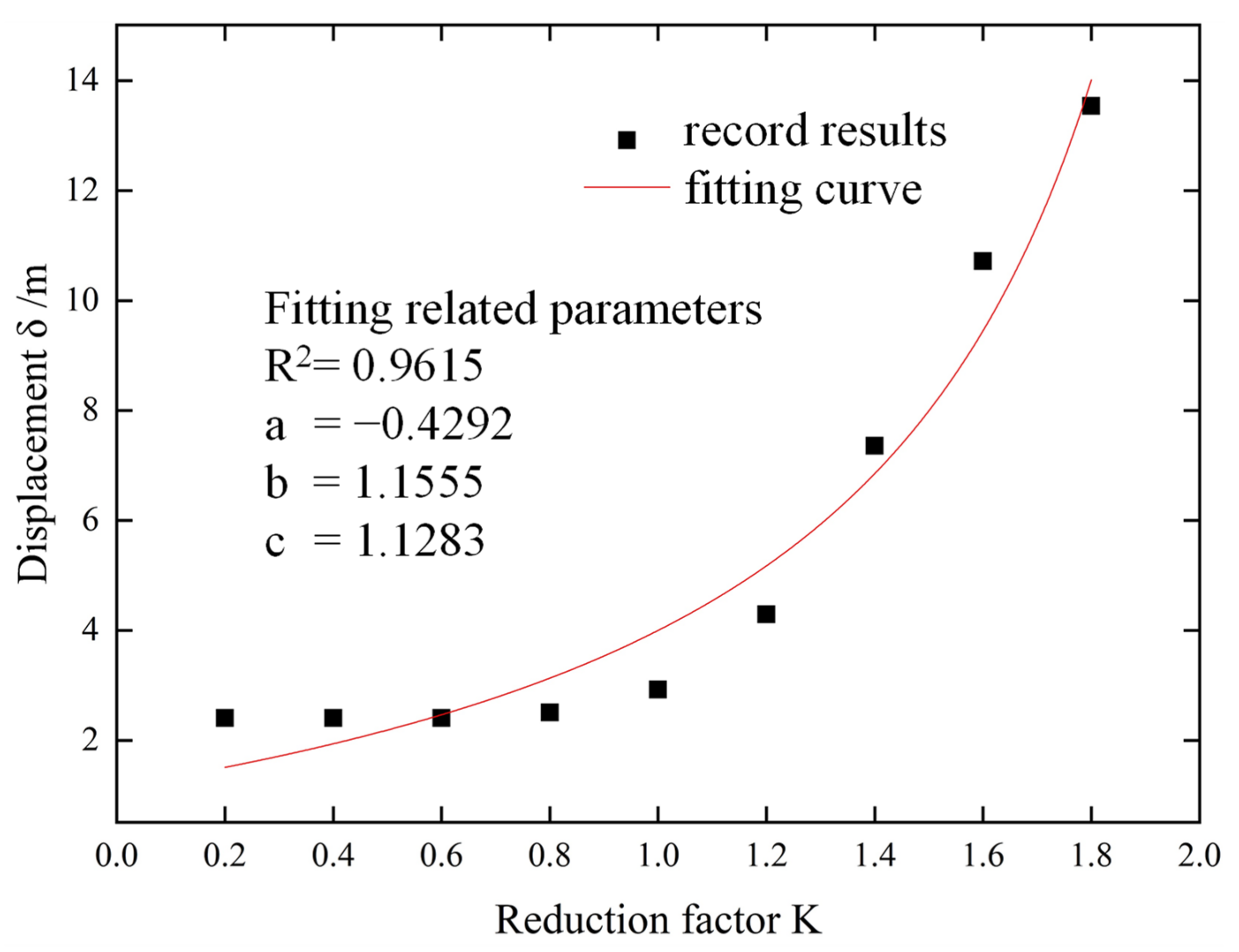
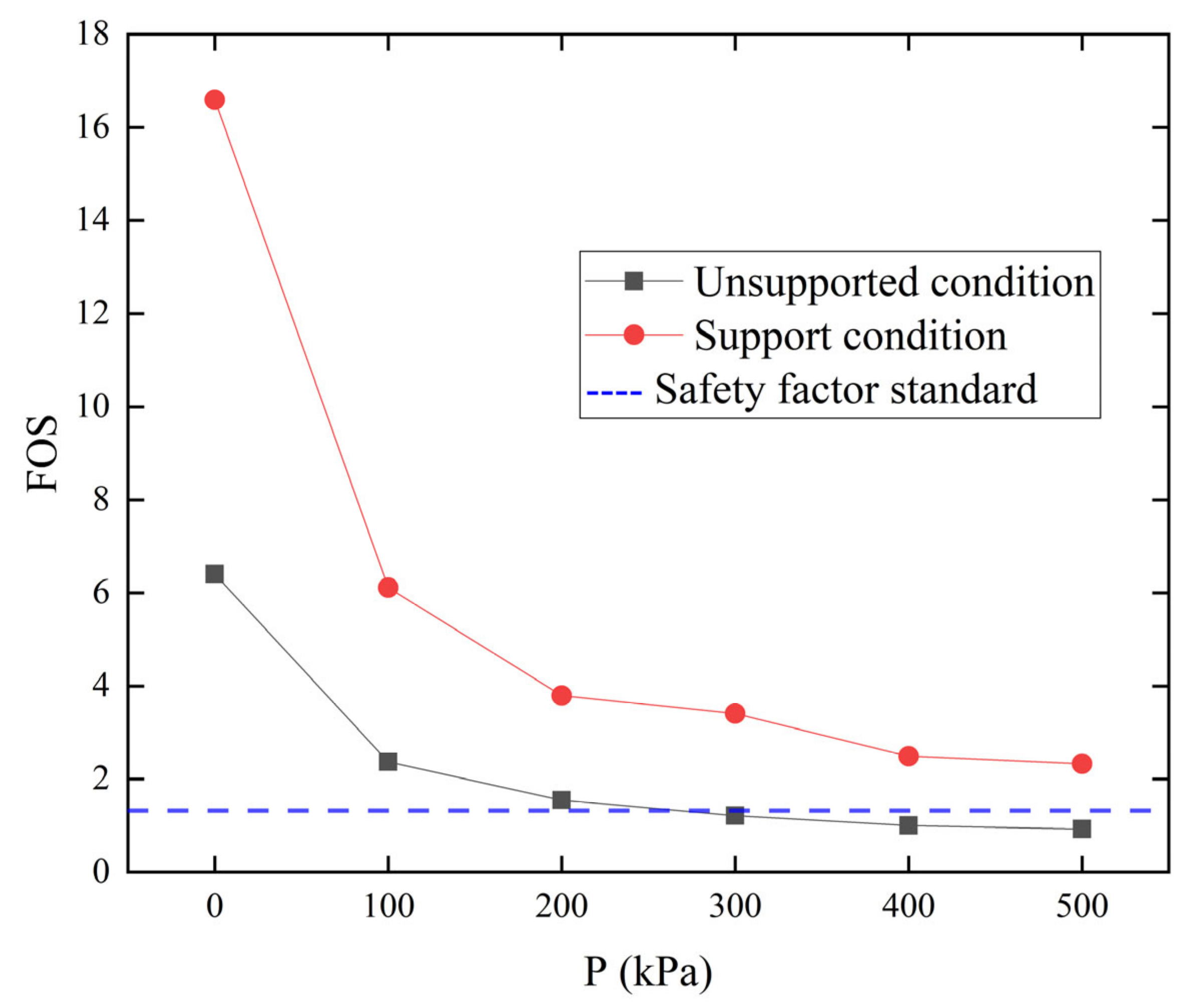
5.1. Factor of Safety
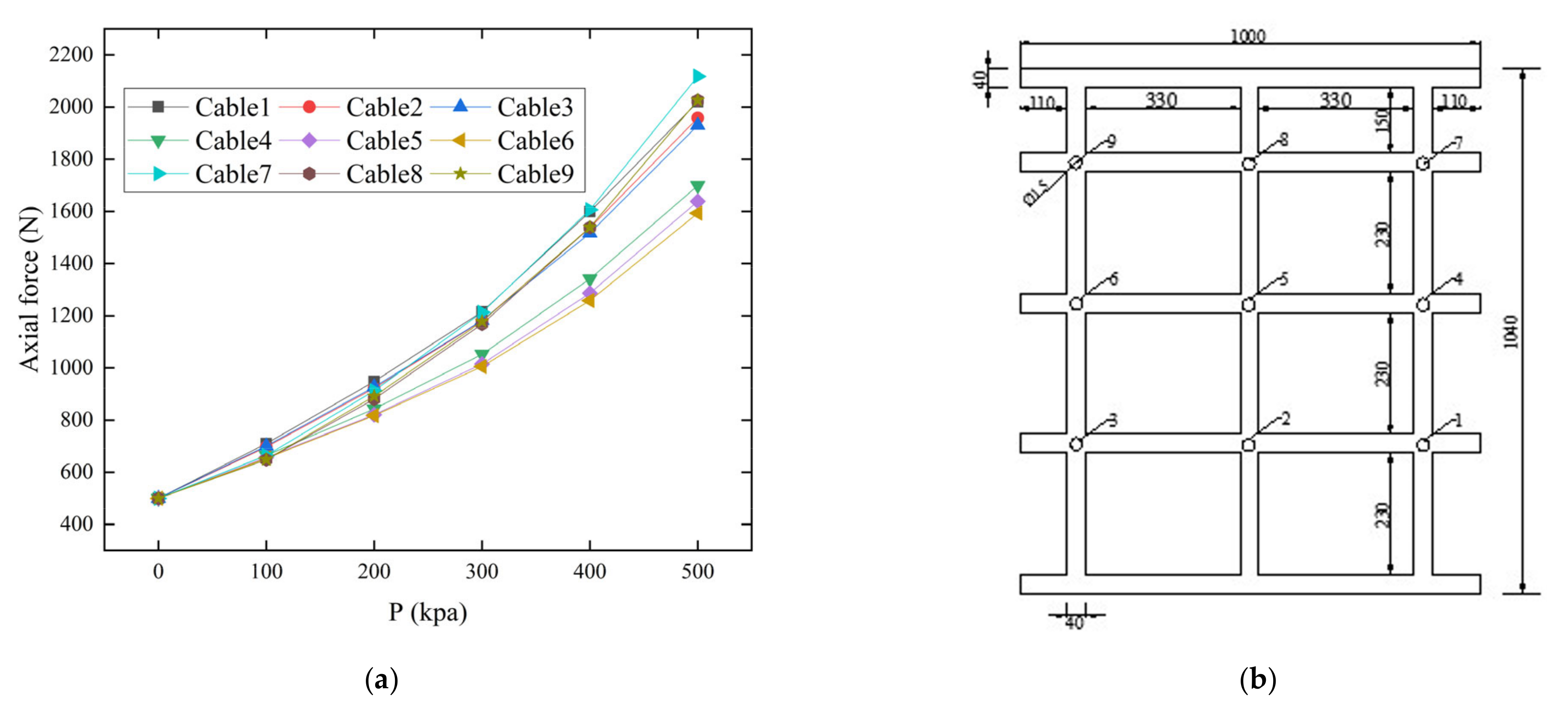
5.2. Anchor Axial Force
5.3. Slope Deformation
5.4. Earth Pressure
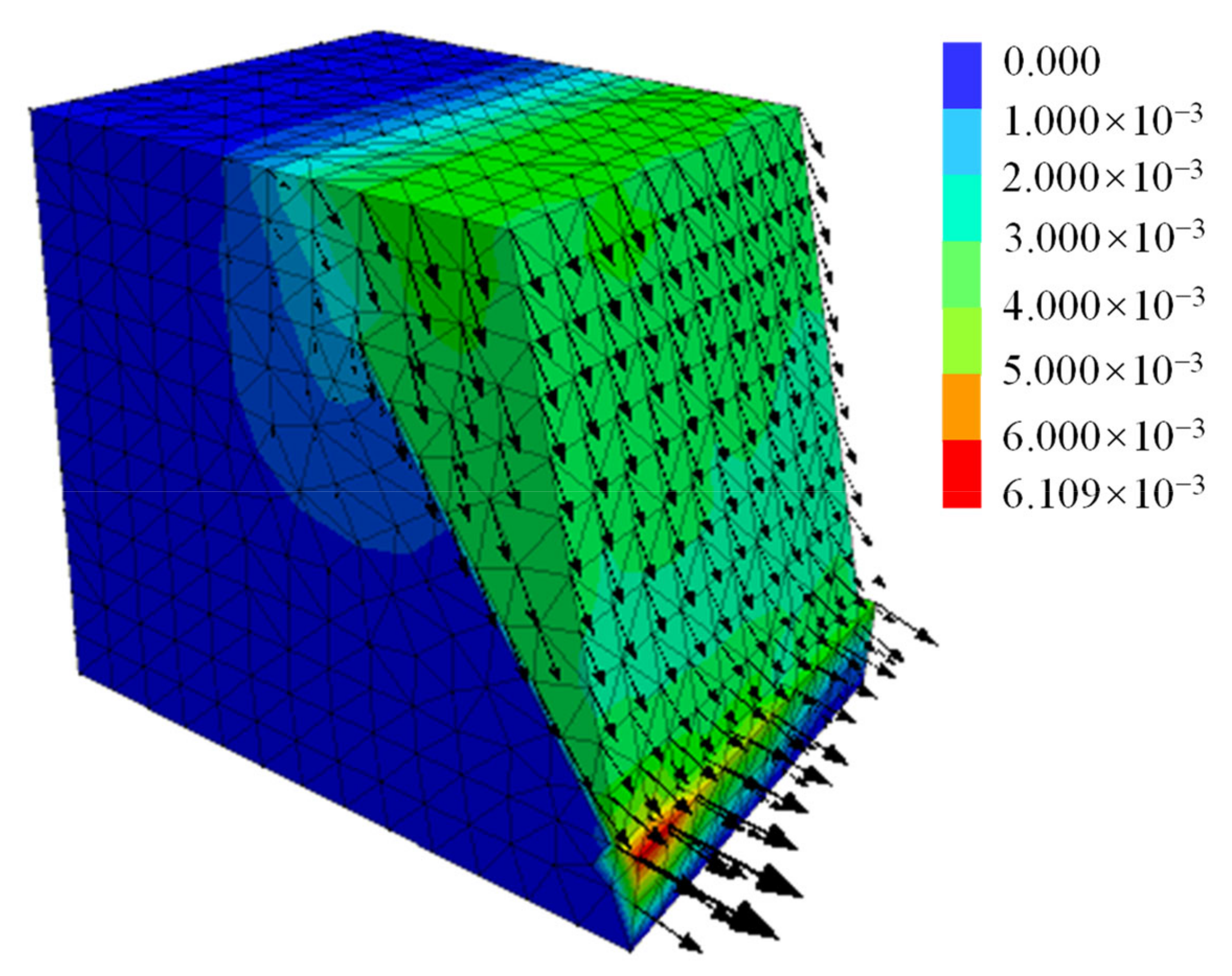
5.5. Maximum Shear Strain Increment
6. Conclusions
- (1)
- The load on the top of the slope has a great influence on the safety factor of the slope. The increase of the load on the top of the slope made the safety factor of the slope decrease differently. The safety factor was highly sensitive to the load less than 300 kPa, but when the load on the top of the slope was large, the influence on the safety factor of the slope was small.
- (2)
- Under the action of graded additional load on the top of the slope, the lateral deformation mode of the slope was called wedge failure. The maximum deformation occurred at the top of the slope and the position of the slope toe, and the middle deformation was small. The overall deformation showed a trend of small, middle, and large at two ends. The vertical deformation of the slope mainly occurred in the upper part of the slope. The vertical deformation of the slope mainly occurred below the loading area and above the weak interlayer. The overall deformation trend developed along the direction of weak interlayer, and slope collapse occurred when the load reaches its peak value.
- (3)
- Weak interlayer was a potential slip surface. Under the action of slope vertical load, the maximum shear strain increment of the weak interlayer was obviously different from that of the weak rock mass. The velocity vector and displacement vector also developed along the direction of the weak interlayer, and were cut out near the slope toe. There is basically no flow trend behind the weak interlayer.
- (4)
- The axial force of the anchor cable increased with the increase of the peak load, and the force was divided into different sizes. The force of the upper anchor cable of the rock mass was the largest, followed by the bottom anchor cable and the middle anchor cable. The effect of frame anchor cable controlled the failure process of the slope, and the failure still moved along the weak interlayer without tilting, indicating that the reinforcement effect of frame anchor cable effectively delays the failure rate of the slope.
- (5)
- In the actual project with weak interlayer slope protection, attention should be paid to the impact of overloading on the upper side. The frame anchor support adopts a progressive design, and appropriately increases the axial force of the upper anchor cables to avoid the collapse of the upper side. At the same time, the slope foot strengthens the strength of the frame anchor and improves the sliding resistance. The anchorage cable arrangement in the area with weak interlayer increases the prestress and weakens the tendency of the weak interlayer to develop into a slope sliding surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cambio, D.; Hicks, D.D.; Moffitt, K.; Yetisir, M.; Carvalho, J.L. Back-Analysis of the Bingham Canyon South Wall: A Quasi-static Complex Slope Movement Mechanism. Rock Mech. Rock Eng. 2019, 52, 4953–4977. [Google Scholar] [CrossRef]
- Hibert, C.; Ekstroem, G.; Stark, C.P. Dynamics of the Bingham Canyon Mine landslides from seismic signal analysis. Geophys. Res. Lett. 2014, 41, 4535–4541. [Google Scholar] [CrossRef]
- Mccoll, S.T. Paraglacial rock-slope stability. Geomorphology 2012, 153, 1–16. [Google Scholar] [CrossRef]
- Lee, D.-H.; Yang, Y.-E.; Lin, H.-M. Assessing slope protection methods for weak rock slopes in Southwestern Taiwan. Eng. Geol. 2007, 91, 100–116. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, J.; Fu, X.; Zhou, L. Dynamic failure mode and energy-based identification method for a counter-bedding rock slope with weak intercalated layers. J. Mt. Sci. 2016, 13, 2111–2123. [Google Scholar] [CrossRef]
- Ding, S.; Jing, H.; Chen, K.; Xu, G.; Meng, B. Stress evolution and support mechanism of a bolt anchored in a rock mass with a weak interlayer. Int. J. Min. Sci. Technol. 2017, 27, 573–580. [Google Scholar] [CrossRef]
- Rawat, S.; Gupta, A.K. Analysis of a Nailed Soil Slope Using Limit Equilibrium and Finite Element Methods. Int. J. Geosynth. Ground Eng. 2016, 2, 34. [Google Scholar] [CrossRef][Green Version]
- Rawat, S.; Gupta, A.K. Testing and Modelling of Screw Nailed Soil Slopes. Indian Geotech. J. 2018, 48, 52–71. [Google Scholar] [CrossRef]
- Luo, G.; Zhong, Y.; Yang, Y. Failure Mechanism and Mitigation Measures of the G1002 Electricity Pylon Landslide at the Jinping I Hydropower Station. Adv. Civ. Eng. 2020, 2020, 8820315. [Google Scholar] [CrossRef]
- Lin, P.; Liu, X.; Zhou, W.; Wang, R.; Wang, S. Cracking, stability and slope reinforcement analysis relating to the Jinping dam based on a geomechanical model test. Arab. J. Geosci. 2015, 8, 4393–4410. [Google Scholar] [CrossRef]
- Brown, E.T. Rock engineering design of post-tensioned anchors for dams—A review. J. Rock Mech. Geotech. Eng. 2015, 7, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Yu, F.; Jiang, L. Reinforcement Mechanism and Optimisation of Reinforcement Approach of a High and Steep Slope Using Prestressed Anchor Cables. Appl. Sci. 2020, 10, 266. [Google Scholar] [CrossRef]
- Xu, Y.; Wei, F.; Yan, R.; Li, J. Study on Slope Stability Effected by Creep Characteristics of Weak Interlayer in Clastic Rock Slope in Guangxi. In Proceedings of GeoShanghai 2018 International Conference: Geoenvironment and Geohazard; Springer: Singapore, 2018. [Google Scholar]
- Li, J.; Zhang, B.; Sui, B. Stability Analysis of Rock Slope with Multilayer Weak Interlayer. Adv. Civ. Eng. 2021, 2021, 1409240. [Google Scholar] [CrossRef]
- Zhang, S.L.; Zhu, Z.H.; Qi, S.C.; Hu, Y.X.; Du, Q.; Zhou, J.W. Deformation process and mechanism analyses for a planar sliding in the Mayanpo massive bedding rock slope at the Xiangjiaba Hydropower Station. Landslides 2018, 15, 2061–2073. [Google Scholar] [CrossRef]
- Lin, Y.L.; Cheng, X.M.; Yang, G.L.; Li, Y. Seismic response of a sheet-pile wall with anchoring frame beam by numerical simulation and shaking table test. Soil Dyn. Earthq. Eng. 2018, 115, 352–364. [Google Scholar] [CrossRef]
- Zhang, J.J.; Niu, J.Y.; Fu, X.; Cao, L.C.; Yan, S.J. Failure modes of slope stabilized by frame beam with prestressed anchors. Eur. J. Environ. Civ. Eng. 2022, 26, 2120–2142. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, J.; Cheng, Q.; Wu, J.; Wang, Z.; Tian, H. Earthquake loading response of a slope with an inclined weak intercalated layer using centrifuge modeling. Bull. Eng. Geol. Environ. 2019, 78, 4439–4450. [Google Scholar] [CrossRef]
- Wu, L.Z.; Huang, R.Q. Calculation of the Internal Forces and Numerical Simulation of the Anchor Frame Beam Strengthening Expansive Soil Slope. Geotech. Geol. Eng. 2008, 26, 493–502. [Google Scholar] [CrossRef]
- Yang, G.; Zhong, Z.; Zhang, Y.; Fu, X. Optimal design of anchor cables for slope reinforcement based on stress and displacement fields. J. Rock Mech. Geotech. Eng. 2015, 7, 411–420. [Google Scholar] [CrossRef]
- Yan, M.; Xia, Y.; Liu, T.; Bowa, V.M. Limit analysis under seismic conditions of a slope reinforced with prestressed anchor cables. Comput. Geotech. 2019, 108, 226–233. [Google Scholar] [CrossRef]
- Cui, L.; Sheng, Q.; Dong, Y.K.; Xie, M.X. Unified elasto-plastic analysis of rock mass supported with fully grouted bolts for deep tunnels. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 247–271. [Google Scholar] [CrossRef]
- Cui, L.; Sheng, Q.; Dong, Y.; Ruan, B.; Xu, D.D. A quantitative analysis of the effect of end plate of fully-grouted bolts on the global stability of tunnel. Tunn. Undergr. Space Technol. 2021, 114, 104010. [Google Scholar] [CrossRef]
- Krahn, J. The 2001 R.M. Hardy Lecture: The limits of limit equilibrium analyses. Can. Geotech. J. 2003, 40, 643–660. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Discussion: Associated and non-associated visco-plasticity and plasticity in soil mechanics. Geotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]





| Physical Quantity | Size | Weight | Strain | Stress | Displacement | Poisson | Friction | Cohesion | Young |
|---|---|---|---|---|---|---|---|---|---|
| Similarity ratio | 1/8 | 1 | 1 | 1/8 | 1/8 | 1 | 1 | 1/8 | 1/8 |
| Material | Density (kg/m3) | Young (MPa) | Poisson | Cohesion (kPa) | Friction (°) |
|---|---|---|---|---|---|
| Rock mass | 2100 | 140 | 0.25 | 252.6 | 36 |
| Weak intercalation | 2000 | 0.6 | 0.25 | 8.7 | 23 |
| Mechanical Parameters of the Anchor | The Parameters of the Frame Beam | ||
|---|---|---|---|
| Density(kg/m3) | 8400 | Density(kg/m3) | 2500 |
| Young (GPa) | 70 | Young (GPa) | 9 |
| Grout-cohesion (kPa) | 100 | Poisson ratio | 0.3 |
| Grout-friction (°) | 30 | ||
| Grout-stiffness (MPa) | 1000 | ||
| Grout-Perimeter (m) | 0.157 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Gao, H.; Zhao, Q.; Chang, Z.; Miao, C. Study on Stability of Anchored Slope under Static Load with Weak Interlayer. Sustainability 2022, 14, 10542. https://doi.org/10.3390/su141710542
Gao M, Gao H, Zhao Q, Chang Z, Miao C. Study on Stability of Anchored Slope under Static Load with Weak Interlayer. Sustainability. 2022; 14(17):10542. https://doi.org/10.3390/su141710542
Chicago/Turabian StyleGao, Mengliang, Haifeng Gao, Qiang Zhao, Zhihuan Chang, and Chenxi Miao. 2022. "Study on Stability of Anchored Slope under Static Load with Weak Interlayer" Sustainability 14, no. 17: 10542. https://doi.org/10.3390/su141710542
APA StyleGao, M., Gao, H., Zhao, Q., Chang, Z., & Miao, C. (2022). Study on Stability of Anchored Slope under Static Load with Weak Interlayer. Sustainability, 14(17), 10542. https://doi.org/10.3390/su141710542






