Application of Machine Learning and Multivariate Statistics to Predict Uniaxial Compressive Strength and Static Young’s Modulus Using Physical Properties under Different Thermal Conditions
Abstract
:1. Introduction
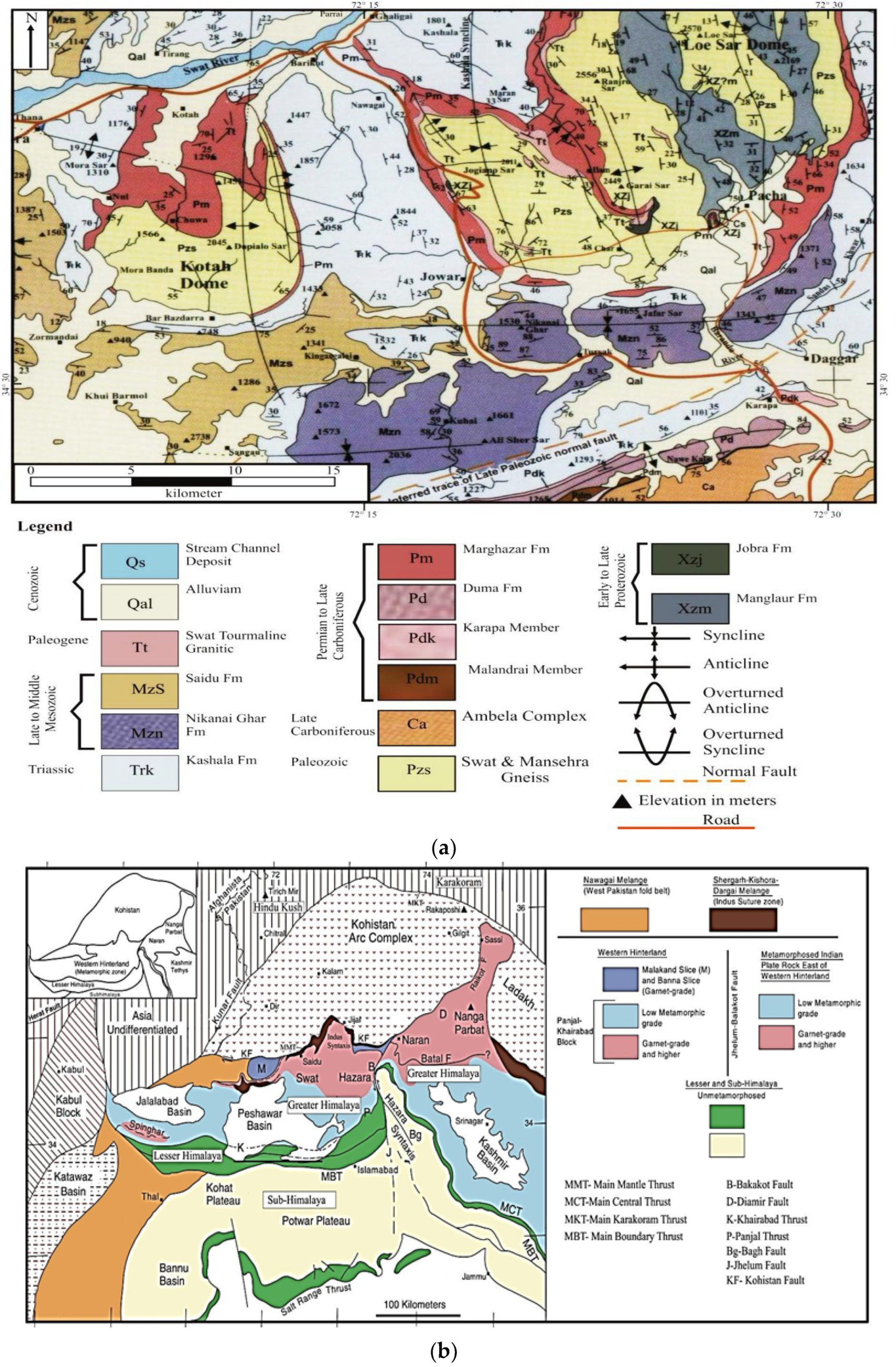
2. Regional Geological Setting
3. Experimental Design
3.1. Rock Specimen
3.2. Heating Procedure
3.3. Samples Characterization
3.4. Ultrasonic Test
3.5. Universal Testing Machine (UTM)
3.6. Intelligent Models
3.6.1. Multiple Linear Regression (MLR) Model
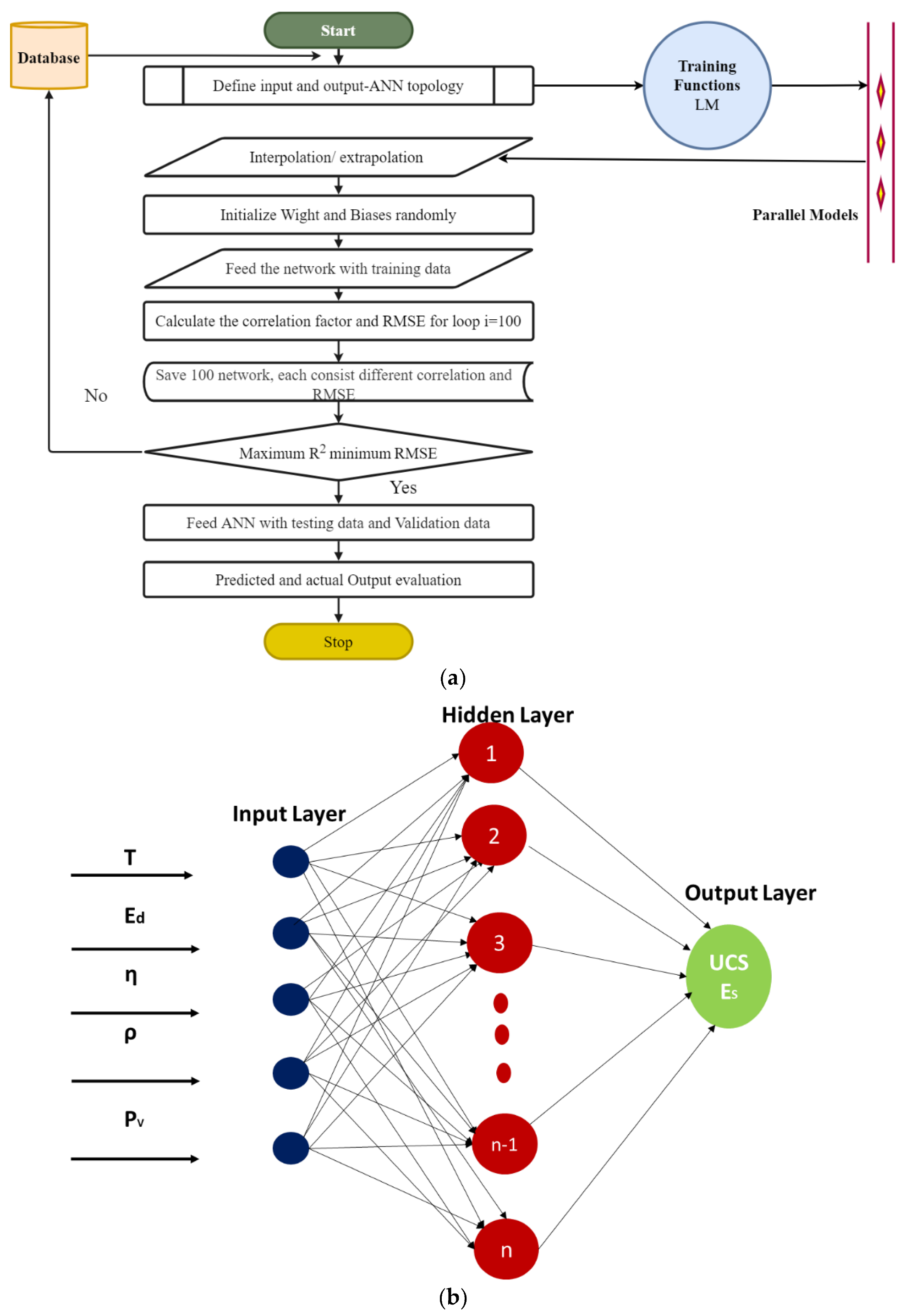
3.6.2. Artificial Neural Network (ANN) Model
ANN Code Compilation in MATLAB
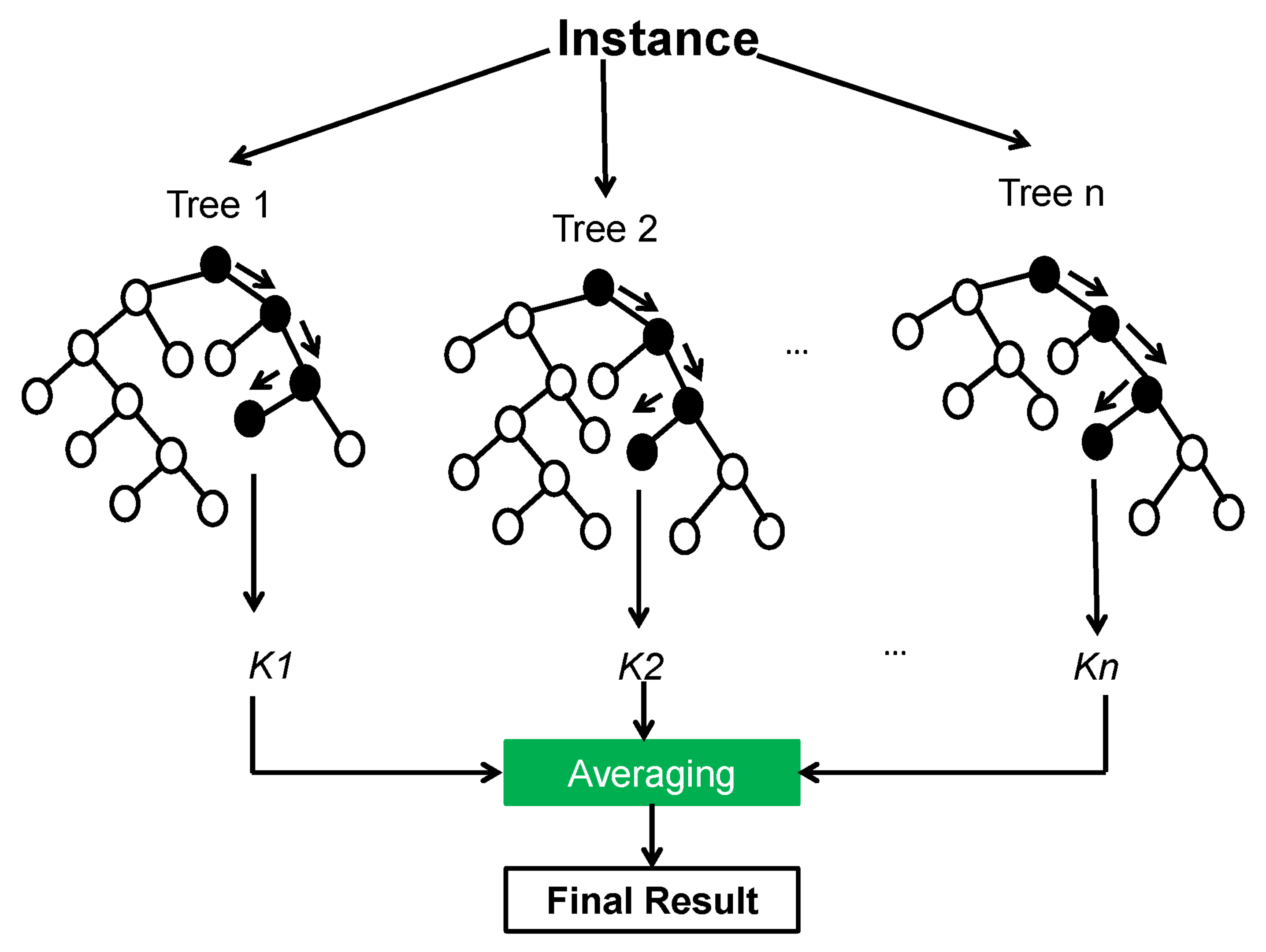
3.6.3. Random Forest Regression
3.6.4. k-Nearest Neighbor
- It is straightforward to grasp and put into practice.
- When it is employed for classification and regression, it can learn non-linear decision boundaries, and it can also invent a highly flexible choice limit by adjusting the value of K. Both of these capabilities are available when it is applied.
- The KNN architecture does not have a step that is specifically dedicated to training.
- Since there is only one hyperparameter, which is denoted by the letter K, adjusting the other hyperparameters is quite simple.
4. Experimental Results
4.1. Physical Properties
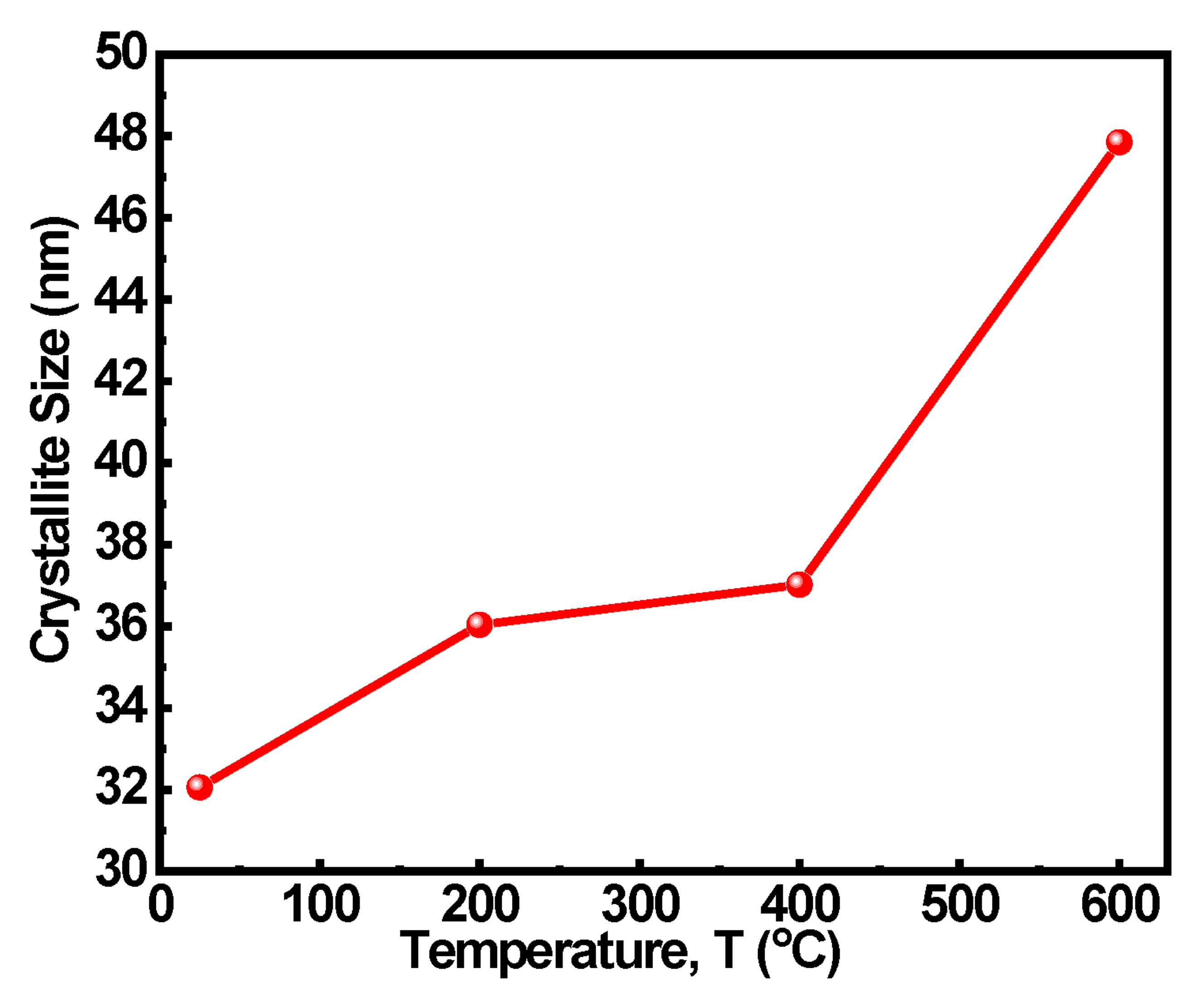
4.2. Micro Crack Analysis
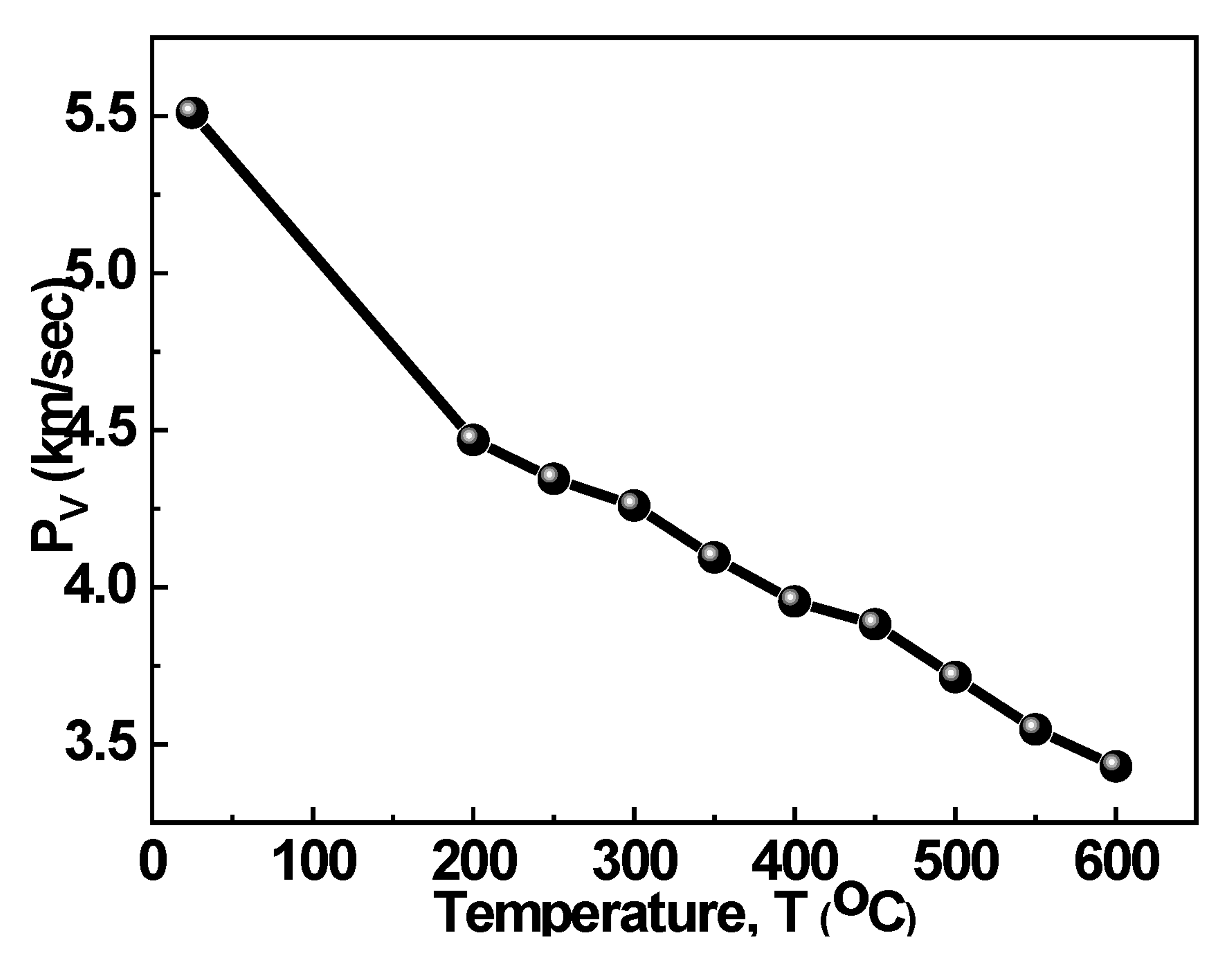
4.3. P-Wave Analysis
4.4. Effect of Temperature on Stress–Strain Curve
5. Prediction Models of UCS and ES
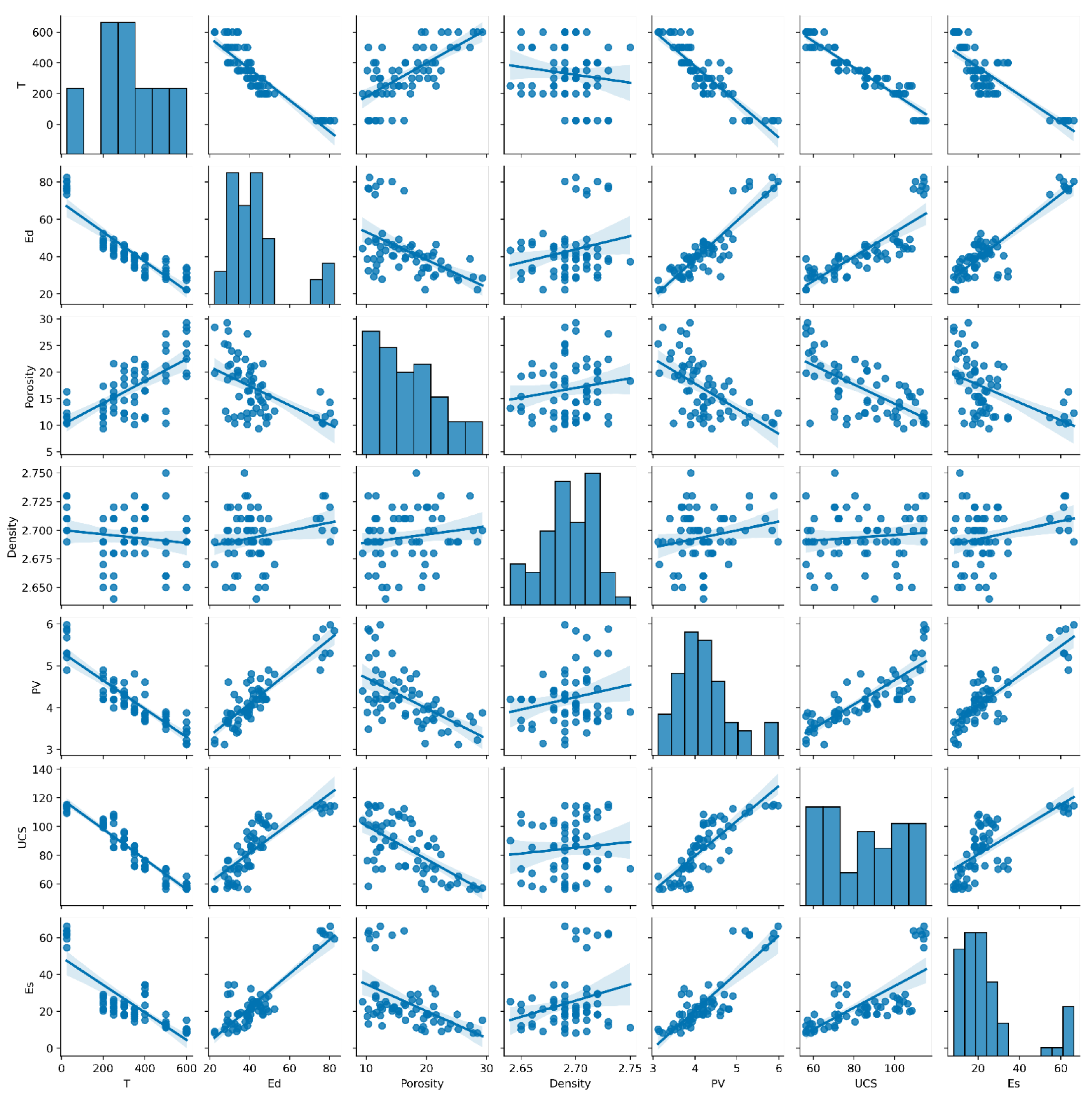
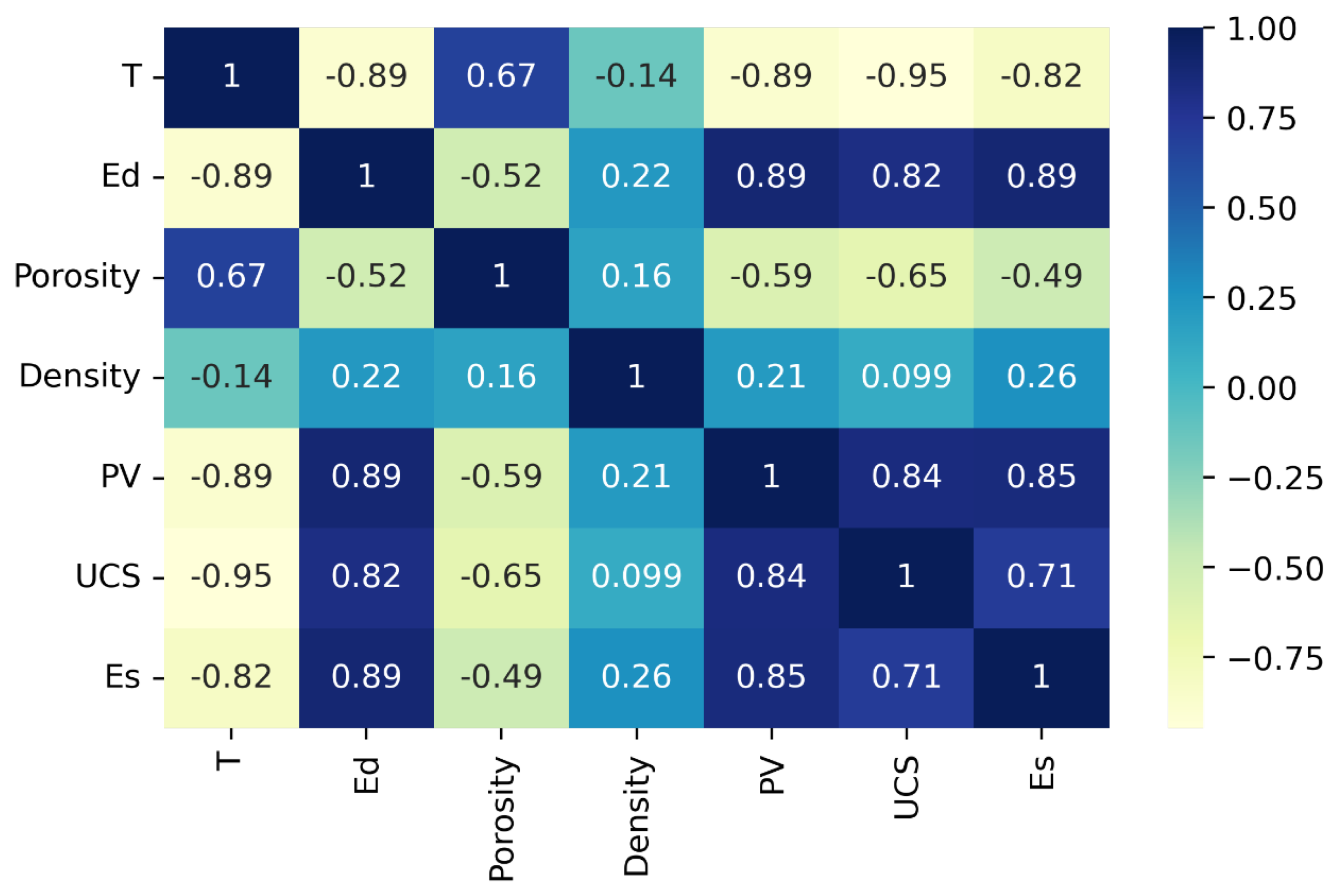
5.1. Preliminary Data Analysis
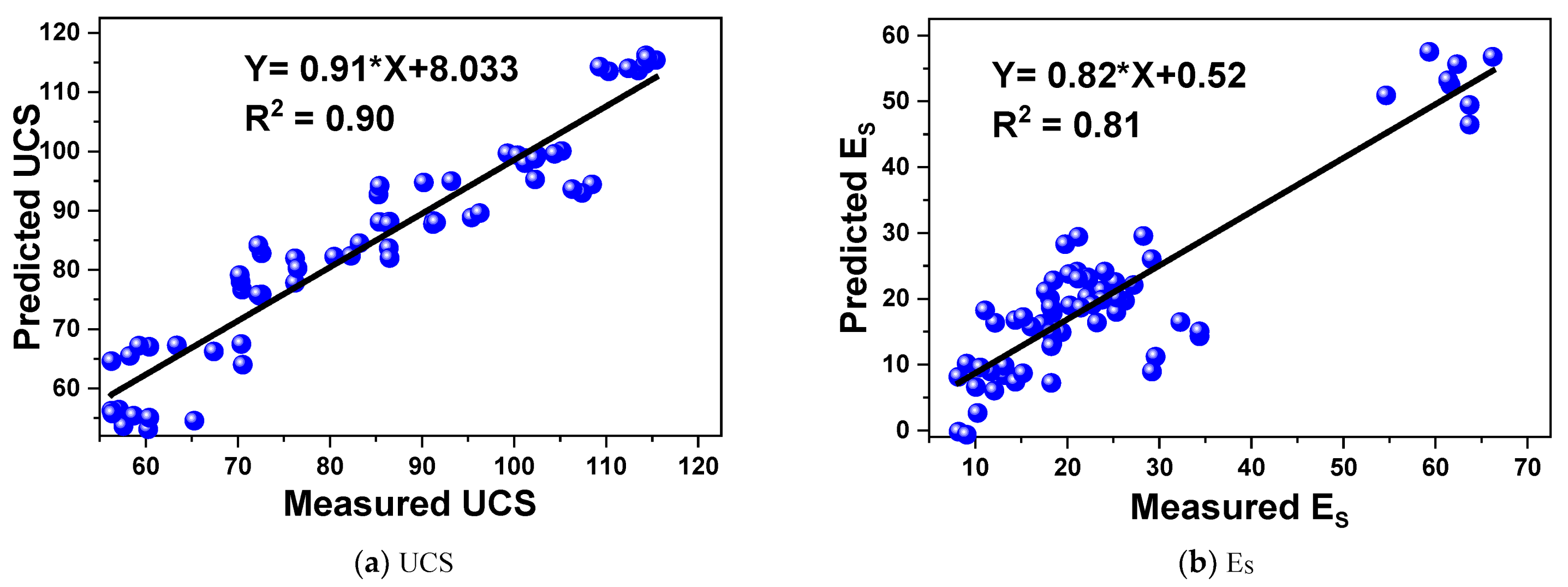
5.2. MLR Prediction Models
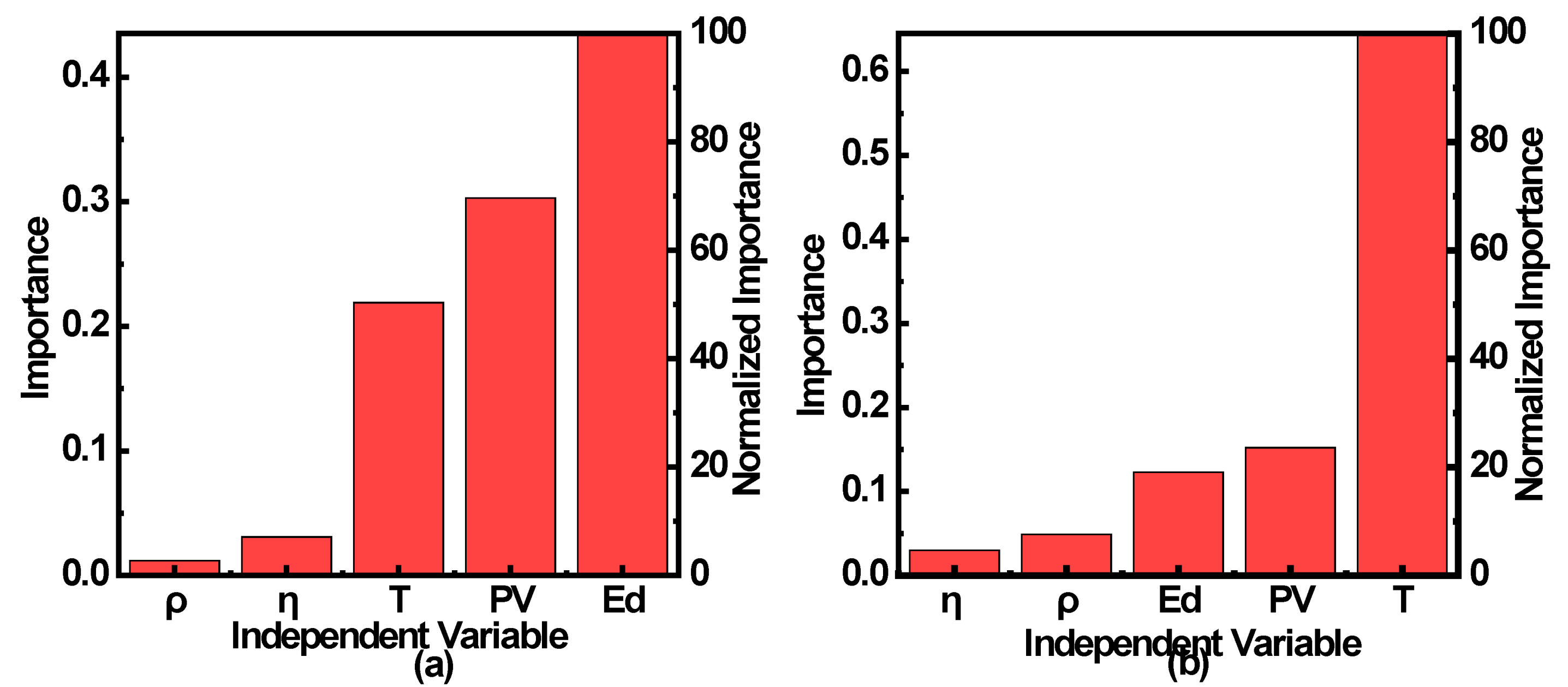
Importance of Variable in MLR Models
5.3. Network Phases and Regression Model
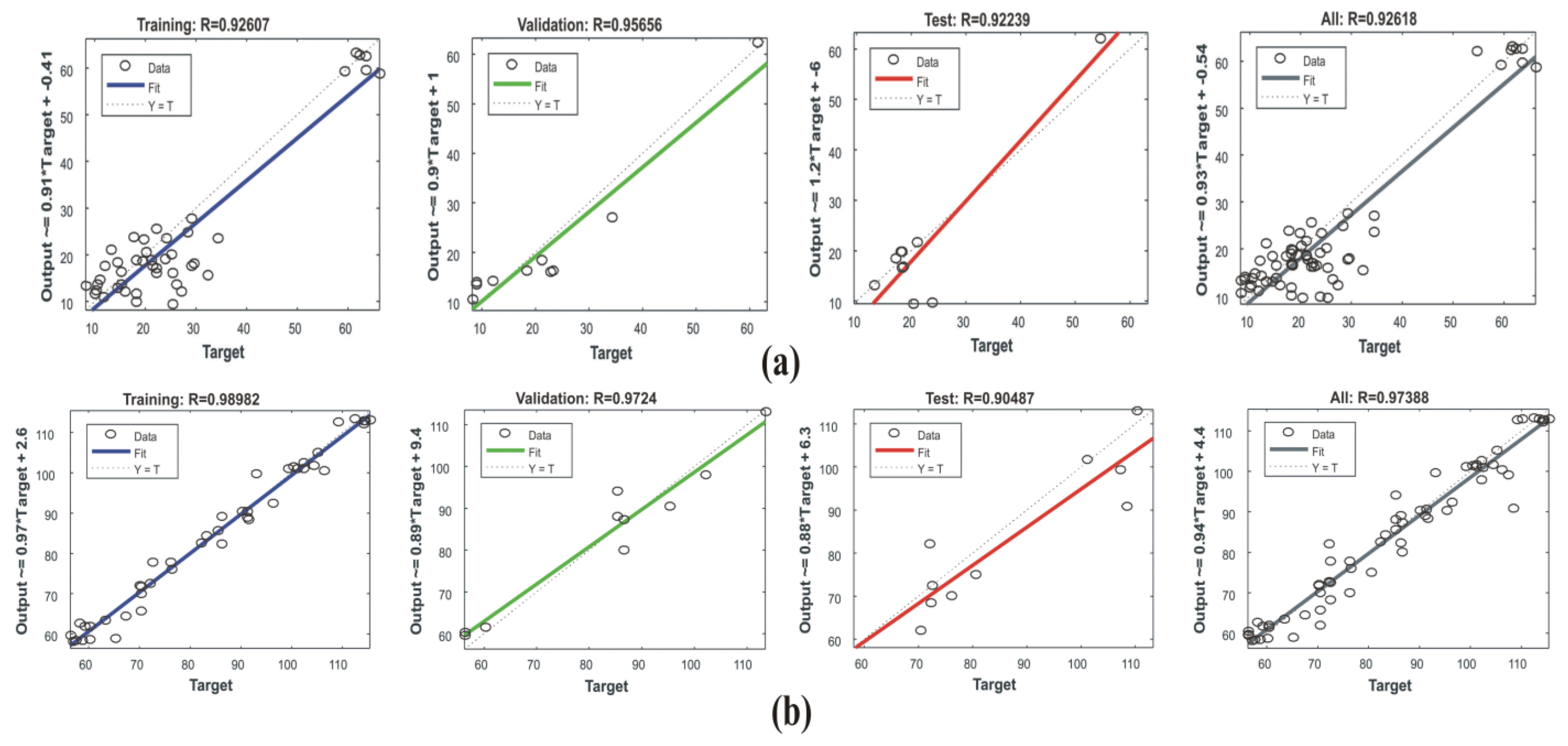
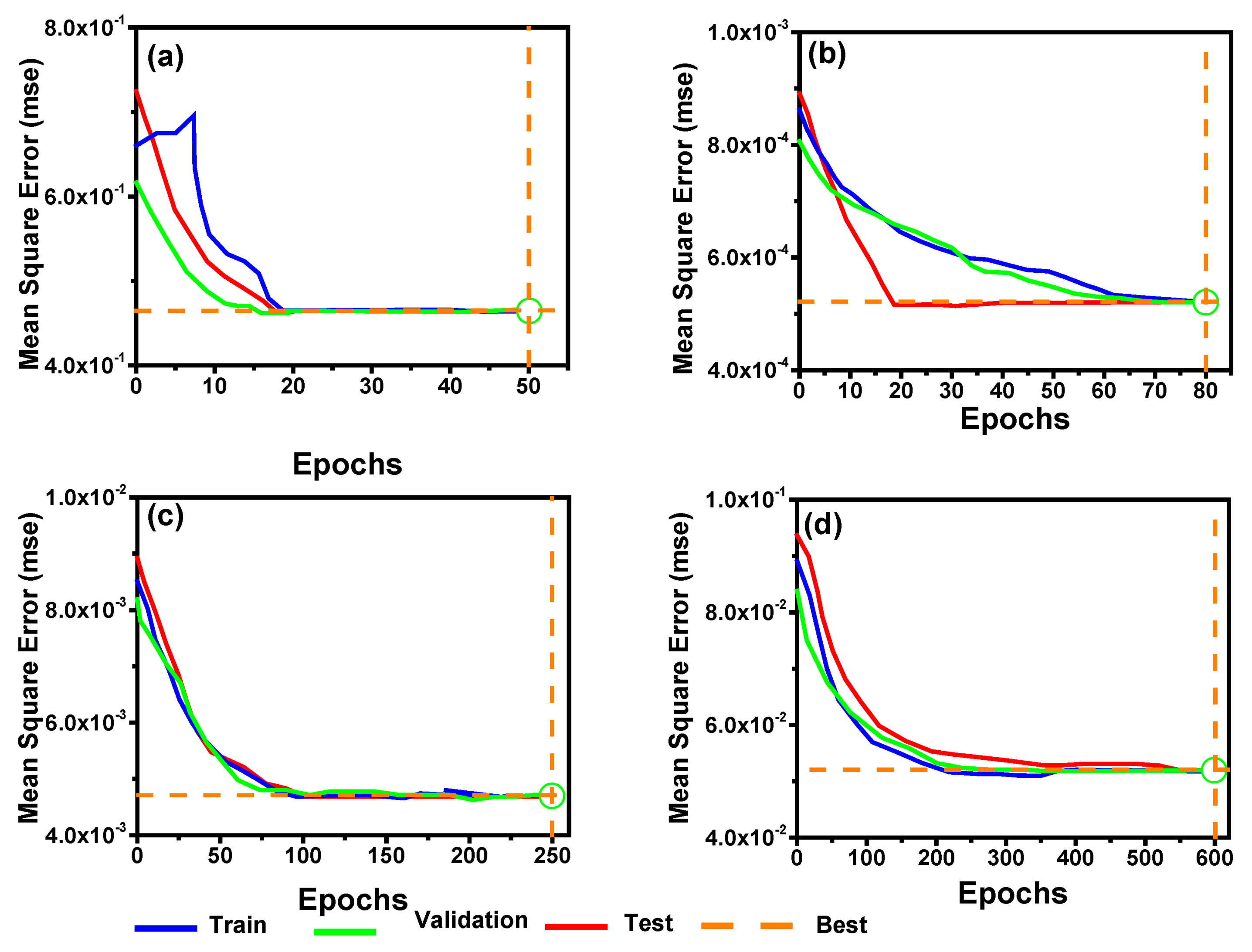
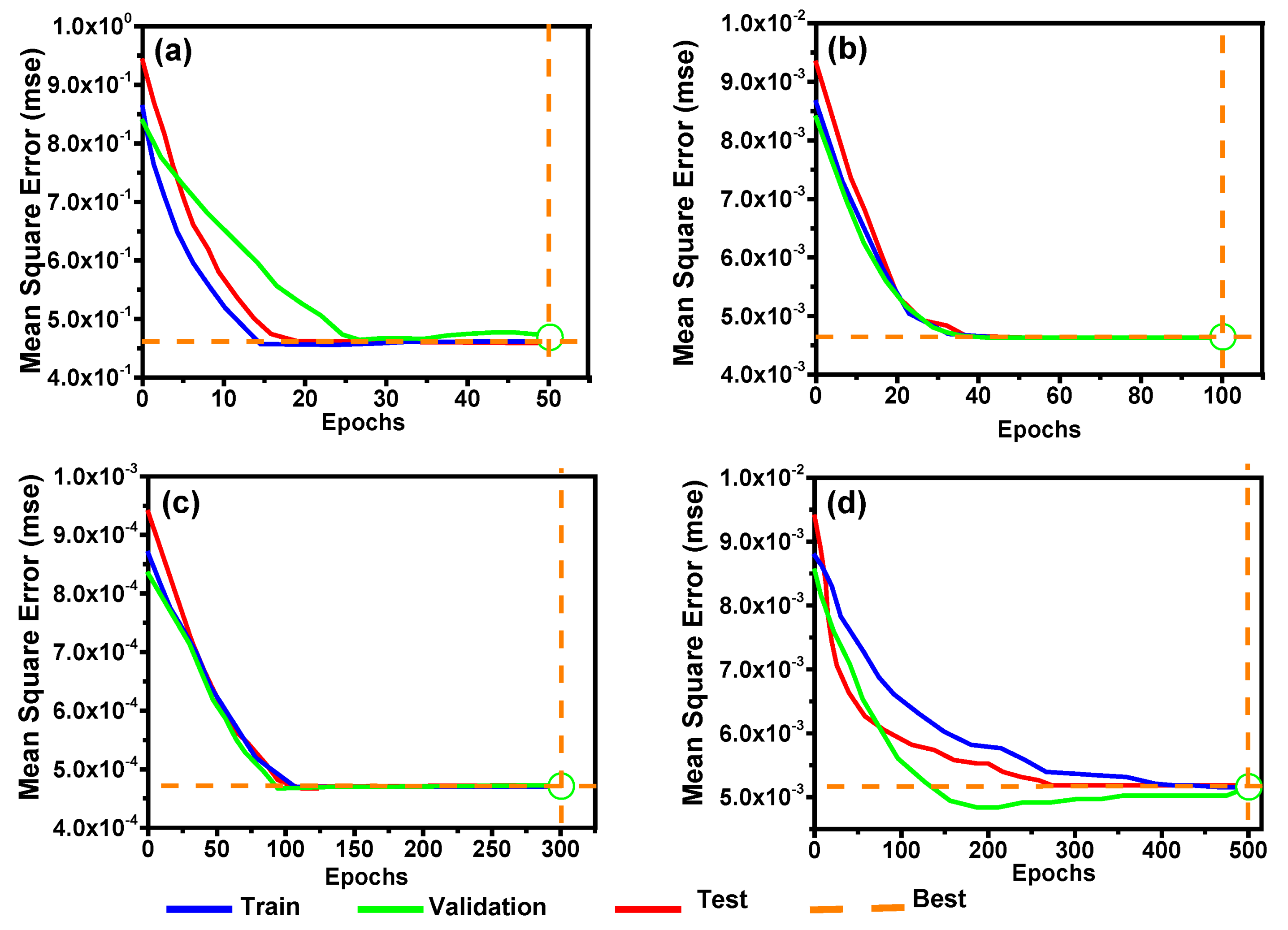
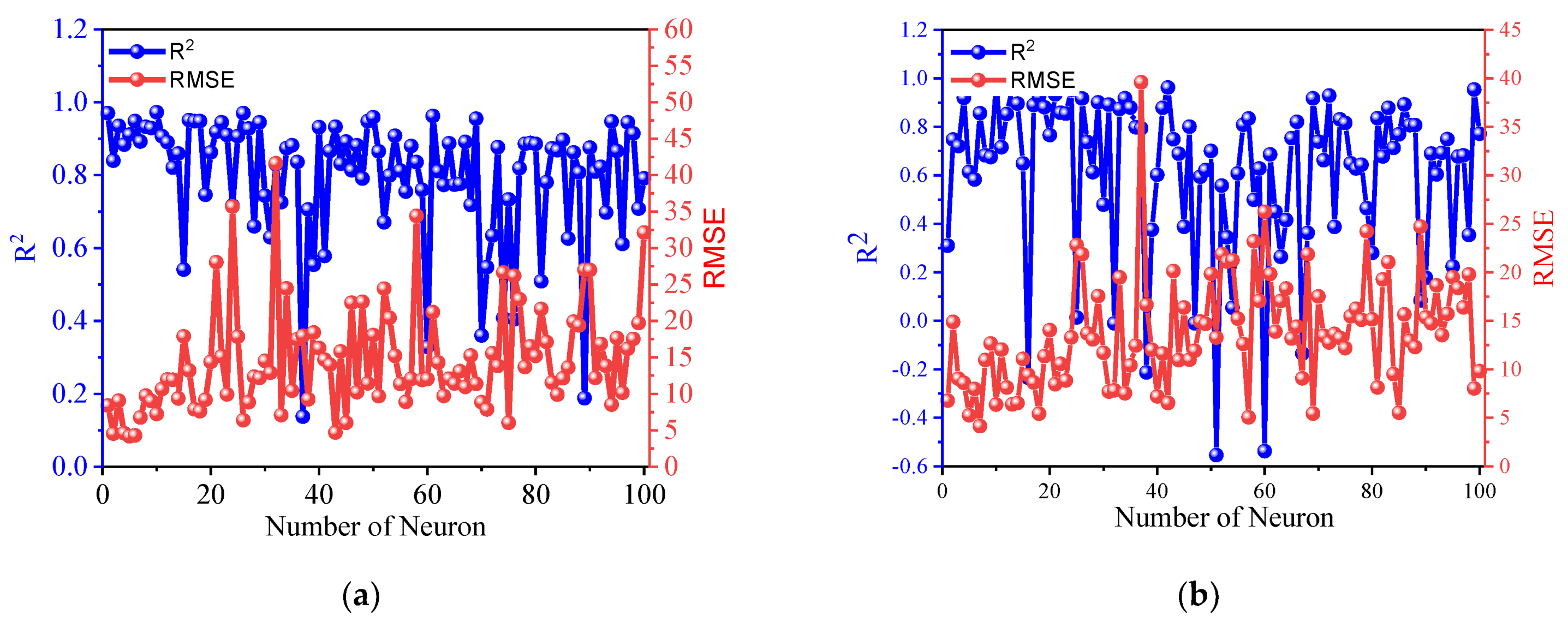
5.3.1. Network Performance and Accuracy
5.3.2. Importance of Variable in ANN Models
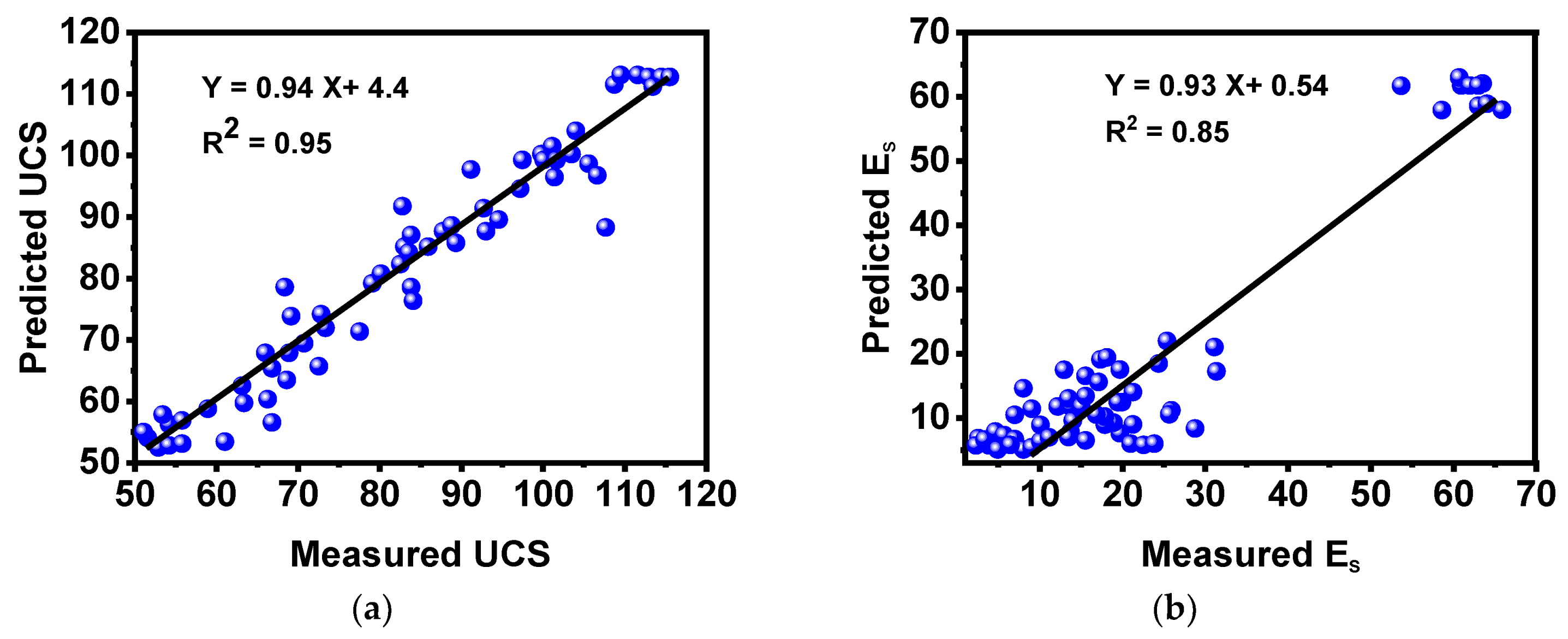
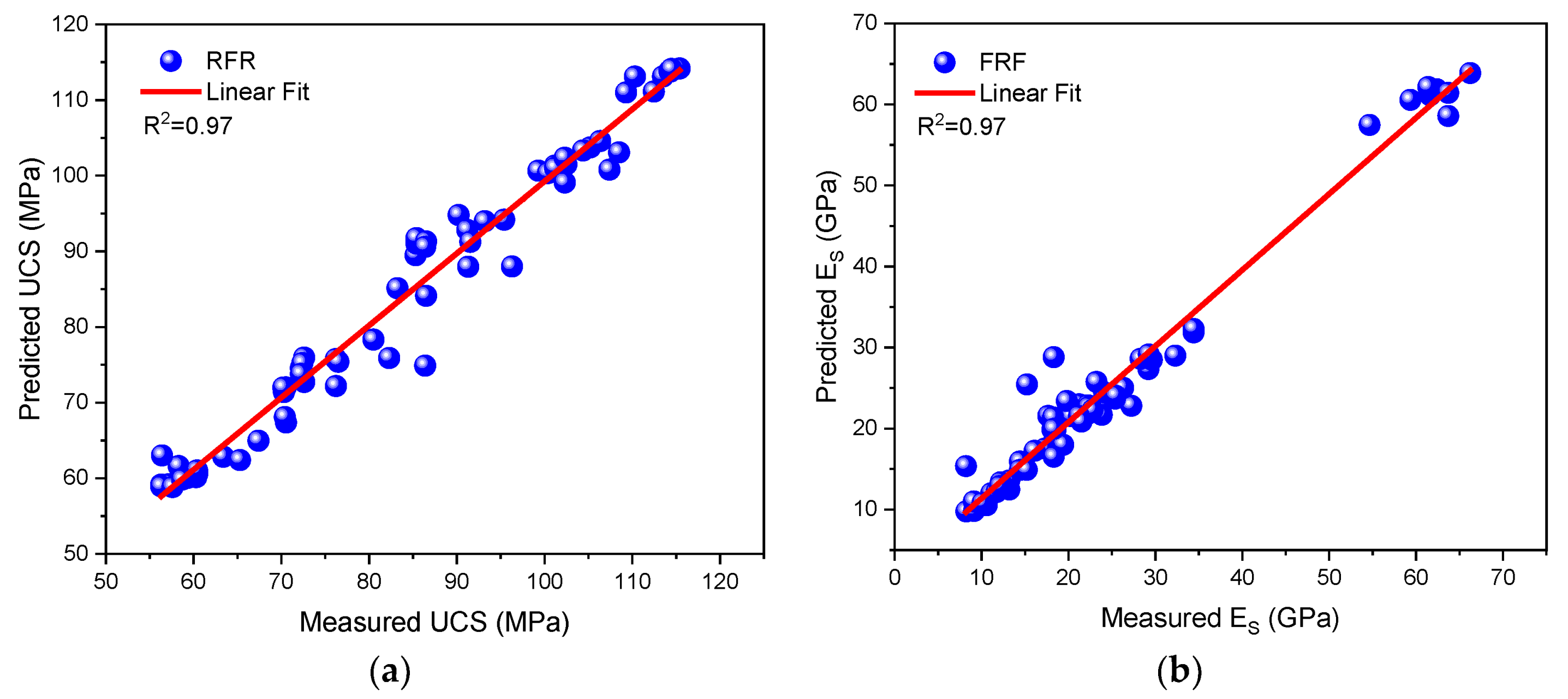
5.4. Random Forest
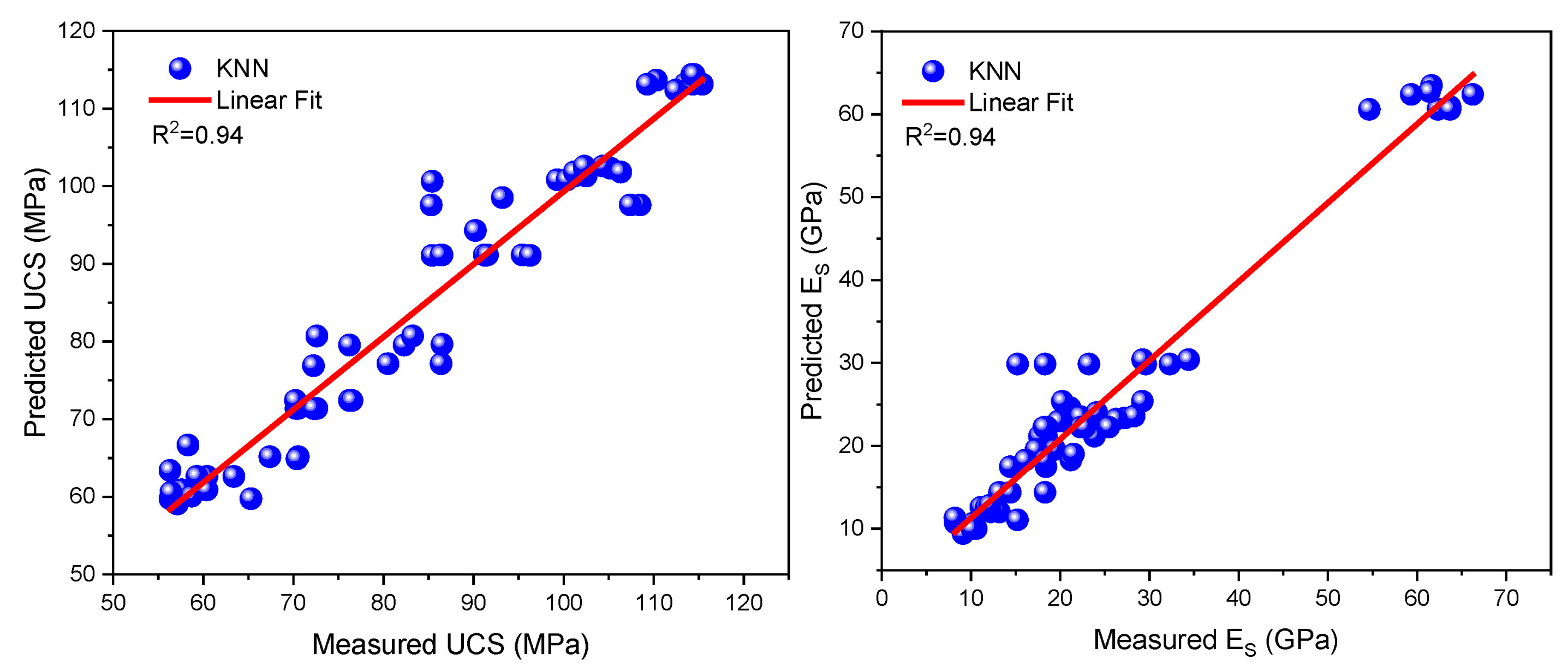
5.5. k-Nearest Neighbor
6. A Comparative Evaluation of Statistics and Intelligent Techniques
7. Discussion
8. Conclusions
- The physical and mechanical properties are greatly affected by the increase in temperature from 200–600 °C due to the generation and propagation of micro-cracks. The porosity is increased, while PV is decreased with the increase in temperature. The strength properties i.e., UCS and ES, of rock also decrease with the increasing temperature;
- The behavior of the stress–strain curve is changed from brittle to ductile when the temperature is increased;
- The MLR predictive models for UCS and ES give a performance coefficient of 0.90% and 0.81%, respectively. The intelligent models i.e., ANN, RFR, and KNN for UCS and ES give a performance coefficient, revealing that the model for UCS is (5–7%) and ES is (4–16%) better than the statistical model (MRL models).
- The model’s important feature revealed that the temperature and PV have a significant role in prediction models;
- Based on comparative analysis of MLR, ANN, RFR, and KNN, it has been proposed that RFR model is suitable for use in the prediction of UCS and ES under thermal treatment.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qin, Y.; Tian, H.; Xu, N.-X.; Chen, Y. Physical and mechanical properties of granite after high-temperature treatment. Rock Mech. Rock Eng. 2020, 53, 305–322. [Google Scholar] [CrossRef]
- Vagnon, F.; Colombero, C.; Colombo, F.; Comina, C.; Ferrero, A.M.; Mandrone, G.; Vinciguerra, S.C. Effects of thermal treatment on physical and mechanical properties of Valdieri Marble-NW Italy. Int. J. Rock Mech. Min. Sci. 2019, 116, 75–86. [Google Scholar] [CrossRef]
- Gautam, P.; Verma, A.; Jha, M.; Sharma, P.; Singh, T.N. Effect of high temperature on physical and mechanical properties of Jalore granite. J. Appl. Geophys. 2018, 159, 460–474. [Google Scholar] [CrossRef]
- Lin, K.; Huang, W.; Finkelman, R.B.; Chen, J.; Yi, S.; Cui, X.; Wang, Y.J. Distribution, modes of occurrence, and main factors influencing lead enrichment in Chinese coals. Int. J. Coal Sci. Technol. 2020, 7, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Tan, F.; Huo, T.; Tang, S.; Zhao, W.; Chao, H.J. Origin of the hydrate bound gases in the Juhugeng Sag, Muli Basin, Tibetan Plateau. Int. J. Coal Sci. Technol. 2020, 7, 43–57. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Mao, X.; Wu, P. Effect of High Temperature and Inclination Angle on Mechanical Properties and Fracture Behavior of Granite at Low Strain Rate. Sustainability 2020, 12, 1255. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, T.; Zhang, D.; Tang, J.; Xu, P.; Duan, X. A Comprehensive Set of Cooling Measures for the Overall Control and Reduction of High Temperature-Induced Thermal Damage in Oversize Deep Mines: A Case Study. Sustainability 2020, 12, 2489. [Google Scholar] [CrossRef] [Green Version]
- Gomah, M.E.; Li, G.; Sun, C.; Xu, J.; Yang, S.; Li, J. On the Physical and Mechanical Responses of Egyptian Granodiorite after High-Temperature Treatments. Sustainability 2022, 14, 4632. [Google Scholar] [CrossRef]
- Meng, Q.-B.; Wang, C.-K.; Liu, J.-F.; Zhang, M.-W.; Lu, M.-M.; Wu, Y. Physical and micro-structural characteristics of limestone after high temperature exposure. Bull. Eng. Geol. Environ. 2020, 79, 1259–1274. [Google Scholar] [CrossRef]
- Lian, X.; Hu, H.; Li, T.; Hu, D. Main geological and mining factors affecting ground cracks induced by underground coal mining in Shanxi Province, China. Int. J. Coal Sci. Technol. 2020, 7, 362–370. [Google Scholar] [CrossRef] [Green Version]
- Zuo, J.; Wang, J.; Jiang, Y. Macro/meso failure behavior of surrounding rock in deep roadway and its control technology. Int. J. Coal Sci. Technol. 2019, 6, 301–319. [Google Scholar] [CrossRef] [Green Version]
- Barla, G. Comprehensive study including testing, monitoring and thermo-hydro modelling for design and implementation of a geothermal system in Torino (Italy). Geomech. Geophys. Geo-Energy Geo-Resour. 2017, 3, 175–188. [Google Scholar] [CrossRef]
- Breede, K.; Dzebisashvili, K.; Liu, X.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geotherm. Energy 2013, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Homand-Etienne, F.; Houpert, R. Thermally induced microcracking in granites: Characterization and analysis. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 125–134. [Google Scholar] [CrossRef]
- Peng, J.; Rong, G.; Cai, M.; Yao, M.-D.; Zhou, C.-B. Physical and mechanical behaviors of a thermal-damaged coarse marble under uniaxial compression. Eng. Geol. 2016, 200, 88–93. [Google Scholar] [CrossRef]
- Ferreira, A.P.G.; Farage, M.C.; Barbosa, F.S.; Noumowé, A.; Renault, N. Thermo-hydric analysis of concrete–rock bilayers under fire conditions. Eng. Struct. 2014, 59, 765–775. [Google Scholar] [CrossRef]
- Tang, Z.C.; Sun, M.; Peng, J. Influence of high temperature duration on physical, thermal and mechanical properties of a fine-grained marble. Appl. Therm. Eng. 2019, 156, 34–50. [Google Scholar] [CrossRef]
- Jansen, D.P.; Carlson, S.R.; Young, R.P.; Hutchins, D.A. Ultrasonic imaging and acoustic emission monitoring of thermally induced microcracks in Lac du Bonnet granite. J. Geophys. Res. Solid Earth 1993, 98, 22231–22243. [Google Scholar] [CrossRef]
- Dwivedi, R.D.; Goel, R.K.; Prasad, V.V.R.; Sinha, A. Thermo-mechanical properties of Indian and other granites. Int. J. Rock Mech. Min. Sci. 2008, 45, 303–315. [Google Scholar] [CrossRef]
- Zhao, Y.; Wan, Z.; Feng, Z.; Yang, D.; Zhang, Y.; Qu, F. Triaxial compression system for rock testing under high temperature and high pressure. Int. J. Rock Mech. Min. Sci. 2012, 52, 132–138. [Google Scholar] [CrossRef]
- Wong, T.-F. Effects of temperature and pressure on failure and post-failure behavior of Westerly granite. Mech. Mater. 1982, 1, 3–17. [Google Scholar] [CrossRef]
- Chaki, S.; Takarli, M.; Agbodjan, W.P. Influence of thermal damage on physical properties of a granite rock: Porosity, permeability and ultrasonic wave evolutions. Constr. Build. Mater. 2008, 22, 1456–1461. [Google Scholar] [CrossRef]
- Lion, M.; Skoczylas, F.; Ledésert, B. Effects of heating on the hydraulic and poroelastic properties of bourgogne limestone. Int. J. Rock Mech. Min. Sci. 2005, 42, 508–520. [Google Scholar] [CrossRef]
- Malaga-Starzec, K.; Åkesson, U.; Lindqvist, J.E.; Schouenborg, B. Microscopic and macroscopic characterization of the porosity of marble as a function of temperature and impregnation. Constr. Build. Mater. 2006, 20, 939–947. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Ni, J.; Shao, W.; Azzam, R. Experimental study on the influence of temperature on the mechanical properties of granite under uni-axial compression and fatigue loading. Int. J. Rock Mech. Min. Sci. 2012, 56, 62–66. [Google Scholar] [CrossRef]
- Torabi-Kaveh, M.; Naseri, F.; Saneie, S.; Sarshari, B. Application of artificial neural networks and multivariate statistics to predict UCS and E using physical properties of Asmari limestones. Arab. J. Geosci. 2015, 8, 2889–2897. [Google Scholar] [CrossRef]
- Heidari, M.; Khanlari, G.; Momeni, A. Prediction of Elastic Modulus of Intact Rocks Using Artificial Neural Networks and non-Linear Regression Methods. Aust. J. Basic Appl. Sci. 2010, 4, 5869–5879. [Google Scholar]
- Abdi, Y.; Garavand, A.T.; Sahamieh, R.Z. Prediction of strength parameters of sedimentary rocks using artificial neural networks and regression analysis. Arab. J. Geosci. 2018, 11, 587. [Google Scholar] [CrossRef]
- Tariq, Z.; Elkatatny, S.; Mahmoud, M.; Ali, A.Z.; Abdulraheem, A. A new approach to predict failure parameters of carbonate rocks using artificial intelligence tools. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar]
- Manouchehrian, A.; Sharifzadeh, M.; Moghadam, R. Application of artificial neural networks and multivariate statistics to estimate UCS using textural characteristics. Int. J. Min. Sci. Technol. 2012, 22, 229–236. [Google Scholar] [CrossRef]
- Dehghan, S.; Sattari, G.; Chehreh Chelgani, S.; Aliabadi, M.A. Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using regression and artificial neural networks. Min. Sci. Technol. 2010, 20, 41–46. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Aslani, F.; Nener, B.J. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
- Matin, S.; Farahzadi, L.; Makaremi, S.; Chelgani, S.C.; Sattari, G. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest. Appl. Soft Comput. 2018, 70, 980–987. [Google Scholar] [CrossRef]
- Suthar, M. Applying several machine learning approaches for prediction of unconfined compressive strength of stabilized pond ashes. Neural Comput. Appl. 2020, 32, 9019–9028. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W.; Zhao, Y. Prediction of the uniaxial compressive strength of rocks from simple index tests using a random forest predictive model. Comptes Rendus Mec. 2020, 348, 3–32. [Google Scholar] [CrossRef]
- Ren, Q.; Wang, G.; Li, M.; Han, S. Prediction of rock compressive strength using machine learning algorithms based on spectrum analysis of geological hammer. Geotech. Geol. Eng. 2019, 37, 475–489. [Google Scholar] [CrossRef]
- Ghasemi, E.; Kalhori, H.; Bagherpour, R.; Yagiz, S. Model tree approach for predicting uniaxial compressive strength and Young’s modulus of carbonate rocks. Bull. Eng. Geol. Environ. 2018, 77, 331–343. [Google Scholar] [CrossRef]
- Saedi, B.; Mohammadi, S.D.; Shahbazi, H. Prediction of uniaxial compressive strength and elastic modulus of migmatites using various modeling techniques. Arab. J. Geosci. 2018, 11, 574. [Google Scholar] [CrossRef]
- Shahani, N.M.; Zheng, X.; Liu, C.; Hassan, F.U.; Li, P. Developing an XGBoost Regression Model for Predicting Young’s Modulus of Intact Sedimentary Rocks for the Stability of Surface and Subsurface Structures. Front. Earth Sci. 2021, 9, 761990. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Tonnizam Mohamad, E.; Momeni, E.; Monjezi, M.; Sundaram Narayanasamy, M. Prediction of the strength and elasticity modulus of granite through an expert artificial neural network. Arab. J. Geosci. 2016, 9, 48. [Google Scholar] [CrossRef]
- Larson, K.P.; Ali, A.; Shrestha, S.; Soret, M.; Cottle, J.M.; Ahmad, R. Timing of metamorphism and deformation in the Swat valley, northern Pakistan: Insight into garnet-monazite HREE partitioning. Geosci. Front. 2019, 10, 849–861. [Google Scholar] [CrossRef]
- Fahad, M.; Iqbal, Y.; Riaz, M.; Ubic, R.; Abrar, M. Geo-mechanical properties of marble deposits from the Nikani Ghar and Nowshera formations of the Lesser Himalayas, Northern Pakistan—A review Himal. Himal. Geol. 2016, 37, 17–27. [Google Scholar]
- DiPietro, J.A.; Ahmad, I.; Hussain, A. Cenozoic kinematic history of the Kohistan fault in the Pakistan Himalaya. Geol. Soc. Am. Bull. 2008, 120, 1428–1440. [Google Scholar] [CrossRef]
- Hussain, A.; Dipietro, J.; Pogue, K.; Ahmed, I. Geologic Map of 43-B Degree Sheet of NWFP, Pakistan; Geological Map Series; Geological Survey of Pakistan: Peshawar, Pakistan, 2004. [Google Scholar]
- Hatheway, A.W. The complete ISRM suggested methods for rock characterization, testing and monitoring; 1974–2006. Environ. Eng. Geosci. 2009, 15, 47–48. [Google Scholar] [CrossRef]
- Fairhurst, C.; Hudson, J. Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Garson, G.D. Multiple Regression; Statistical Associates Publishers: Fargo, ND, USA, 2014. [Google Scholar]
- Cohen, J.; Cohen, P.; West, S.S.; Aiken, L. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: New York, NY, USA, 2002. [Google Scholar]
- Roy, M.; Singh, P. Application of artificial neural network in mining industry. Indian Min. Eng. J. 2004, 43, 19–23. [Google Scholar]
- Lawal, A.I.; Aladejare, A.E.; Onifade, M.; Bada, S.; Idris, M.A. Predictions of elemental composition of coal and biomass from their proximate analyses using ANFIS, ANN and MLR. Int. J. Coal Sci. Technol. 2021, 8, 124–140. [Google Scholar] [CrossRef]
- Aboutaleb, S.; Behnia, M.; Bagherpour, R.; Bluekian, B. Using non-destructive tests for estimating uniaxial compressive strength and static Young’s modulus of carbonate rocks via some modeling techniques. Bull. Eng. Geol. Environ. 2018, 77, 1717–1728. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Lee, S.; Ha, J.; Zokhirova, M.; Moon, H.; Lee, J. Background Information of Deep Learning for Structural Engineering. Arch. Comput. Methods Eng. 2018, 25, 121–129. [Google Scholar] [CrossRef]
- Facchini, L.; Betti, M.; Biagini, P. Neural network based modal identification of structural systems through output-only measurement. Comput. Struct. 2014, 138, 183–194. [Google Scholar] [CrossRef]
- Ham, F.K.I. Principles of Neurocomputing for Science and Engineering; McGraw-Hill Education Europe: London, UK, 2001; p. 642. [Google Scholar]
- Sonmez, H.; Gokceoglu, C.; Nefeslioglu, H.A.; Kayabasi, A. Estimation of rock modulus: For intact rocks with an artificial neural network and for rock masses with a new empirical equation. Int. J. Rock Mech. Min. Sci. 2006, 43, 224–235. [Google Scholar] [CrossRef]
- Ceryan, N.; Okkan, U.; Kesimal, A. Prediction of unconfined compressive strength of carbonate rocks using artificial neural networks. Environ. Earth Sci. 2013, 68, 807–819. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, I.; AlSalman, H.; Islam, S.; Asif Zahoor Raja, M.; Shoaib, M.; Gumaei, A.; Fiza, M.; Ullah, K.; Mizanur Rahman, S.M.; et al. Levenberg–Marquardt Backpropagation for Numerical Treatment of Micropolar Flow in a Porous Channel with Mass Injection. Complexity 2021, 2021, 5337589. [Google Scholar] [CrossRef]
- Rao, A.R.; Kumar, B. Neural Modeling of Square Surface Aerators. J. Environ. Eng. 2007, 133, 411–418. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of open stope hangingwall stability using random forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Ma, G.; Tang, X.; Du, X. Comparative study of hybrid artificial intelligence approaches for predicting hangingwall stability. J. Comput. Civ. Eng. 2018, 32, 04017086. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Akbulut, Y.; Sengur, A.; Guo, Y.; Smarandache, F. NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier. Symmetry 2017, 9, 179. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing Machine Learning Classifiers for Object-Based Land Cover Classification Using Very High Resolution Imagery. Remote Sens. 2015, 7, 153–168. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Ranjith, P.; Jing, H.-W.; Tian, W.-L.; Ju, Y. An experimental investigation on thermal damage and failure mechanical behavior of granite after exposure to different high temperature treatments. Geothermics 2017, 65, 180–197. [Google Scholar] [CrossRef]
- Heap, M.; Lavallée, Y.; Laumann, A.; Hess, K.-U.; Meredith, P.; Dingwell, D. How tough is tuff in the event of fire? Geology 2012, 40, 311–314. [Google Scholar] [CrossRef]
- Brotons, V.; Tomás, R.; Ivorra, S.; Alarcón, J. Temperature influence on the physical and mechanical properties of a porous rock: San Julian’s calcarenite. Eng. Geol. 2013, 167, 117–127. [Google Scholar] [CrossRef]
- Entwisle, D.; Hobbs, P.; Jones, L.; Gunn, D.; Raines, M. The relationships between effective porosity, uniaxial compressive strength and sonic velocity of intact Borrowdale Volcanic Group core samples from Sellafield. Geotech. Geol. Eng. 2005, 23, 793–809. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Minimum | Maximum | Mean | Std. Deviation | Mean Std. Error |
|---|---|---|---|---|---|
| T | 25 | 600 | 328.12 | 168.77 | 21.09 |
| Ed | 22 | 82 | 43.08 | 14.91 | 1.86 |
| N | 9 | 29 | 16.80 | 5.21 | 0.65 |
| Ρ | 3 | 3 | 2.69 | 0.02 | 0.01 |
| PV | 3 | 6 | 4.22 | 0.65 | 0.08 |
| UCS | 63 | 115 | 84.72 | 18.72 | 2.34 |
| Es | 8 | 66 | 24.77 | 15.41 | 1.93 |
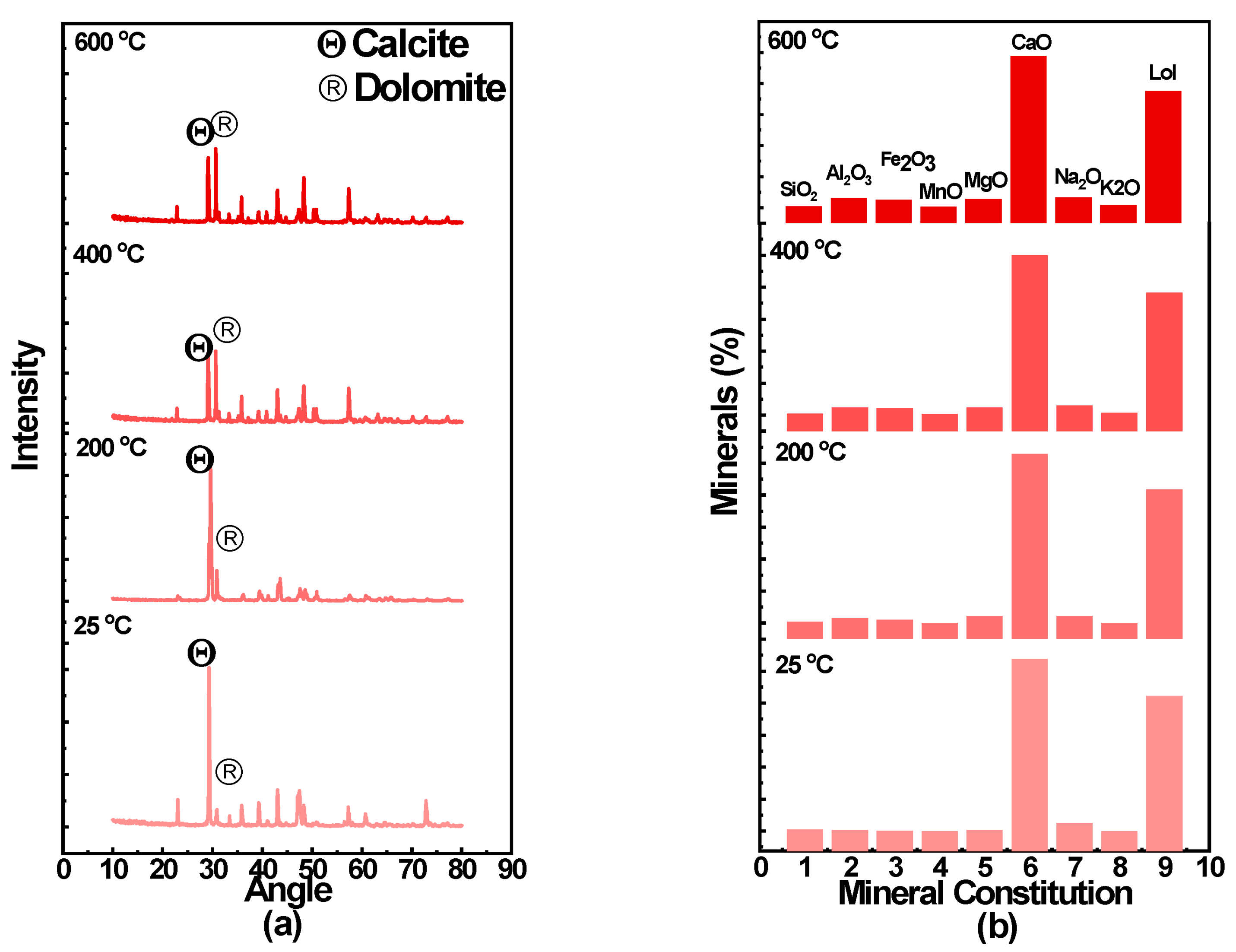
| Temperature (°C) | SiO2 (%) | TiO2 (%) | Al2O3 (%) | Fe2O3 (%) | MnO (%) | MgO (%) | CaO (%) | Na2O (%) | K2O (%) | P2O5 (%) | LoI (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 0.405 | 0 | 0.352 | 0.121 | 0.012 | 0.373 | 53.892 | 2.552 | 0.012 | 0.000 | 42.28 |
| 200 | 0.404 | 0 | 1.5 | 1 | 0.014 | 2.17 | 52.89 | 2.2 | 0.012 | 0.000 | 41.81 |
| 400 | 0.5 | 0 | 2.45 | 2.3 | 0.34 | 2.37 | 50 | 3.1 | 0.71 | 0.000 | 38.23 |
| 600 | 0.51 | 0 | 3.1 | 2.6 | 0.4 | 2.80 | 48.9 | 3.3 | 0.82 | 0.000 | 37.58 |
| S. No | T (°C) | PV (km/s) | ρ (gr/cm3) | n (%) | Dynamic Moduli | Static Moduli | Strain | UCS (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ed (GPa) | Kd (GPa) | Gd (GPa) | Es (GPa) | Ks (GPa) | Gs (GPa) | ԑp (10−3) | |||||||
| 1 | 25 | 5.49 | 2.711 | 12.15 | 77.83 | 48.304 | 35.086 | 61.62 | 42.792 | 24.453 | 1.83 | 113 | |
| 2 | 200 | 5.03 | 2.707 | 12.56 | 47.73 | 28.393 | 19.577 | 24.5 | 17.229 | 9.699 | 4.16 | 105 | |
| 3 | 250 | 4.98 | 2.698 | 15.79 | 44.32 | 27.403 | 18.018 | 22.32 | 15.966 | 8.808 | 4.25 | 107 | |
| 4 | 300 | 4.87 | 2.695 | 16.02 | 41.90 | 26.642 | 16.932 | 20.9 | 15.145 | 8.228 | 4.30 | 109 | |
| 5 | 350 | 4.78 | 2.689 | 16.51 | 41.37 | 25.370 | 15.041 | 18.32 | 13.754 | 7.167 | 4.36 | 80 | |
| 6 | 400 | 4.67 | 2.685 | 17.09 | 40.75 | 24.287 | 13.524 | 16.32 | 12.477 | 6.365 | 4.47 | 73 | |
| 7 | 500 | 4.48 | 2.681 | 19.78 | 40.00 | 23.682 | 12.744 | 15.34 | 12.117 | 5.950 | 4.75 | 69 | |
| 8 | 600 | 4.35 | 2.68 | 24.49 | 39.13 | 22.404 | 11.091 | 13.24 | 10.712 | 5.116 | 5.80 | 63 | |
| Model | Variables | Coefficient | Std. Error | T | p-Value | R2 |
|---|---|---|---|---|---|---|
| UCS | C | 186.017 | 95.212 | 1.954 | 0.056 | 0.905 |
| T(°C) | −0.116 | 0.013 | −9.053 | 0.038 | ||
| Ed (GPa) | −0.232 | 0.133 | −1.747 | 0.086 | ||
| η (%) | 0.078 | 0.216 | 0.359 | 0.721 | ||
| ρ (gr/cm3) | −24.410 | 36.162 | −0.675 | 0.502 | ||
| PV (km/sec) | 2.694 | 2.898 | 0.930 | 0.356 | ||
| ES | C | −164.932 | 108.981 | −1.513 | 0.136 | 0.817 |
| T(°C) | 0.003 | 0.015 | 0.235 | 0.036 | ||
| Ed (GPa) | 0.657 | 0.152 | 4.325 | 0.000 | ||
| η (%) | −0.098 | 0.248 | −0.397 | 0.693 | ||
| ρ (gr/cm3) | 49.318 | 41.391 | 1.192 | 0.238 | ||
| PV (km/sec) | 6.890 | 3.317 | 2.078 | 0.042 |
| Parameters | Values | Details |
|---|---|---|
| n_estimators | 100 | Number of trees in RFR |
| max_depth | 12 | Maximum depth of tree |
| random_state | 32 | Random state |
| Parameters | Values | Descriptions |
|---|---|---|
| n_neighbors | 5 | Number neighbors |
| Metric | Minkowski | The distance metric to use |
| Predicted Paramter | Models | R2 | MSE | MAPE (%) | VAF (%) |
|---|---|---|---|---|---|
| UCS | MLR | 0.90 | 23.15 | 31.53 | 90.23 |
| ANN | 0.94 | 0.14 | 1.18 | 94.23 | |
| RFR | 0.97 | 2.04 | 0.25 | 97.22 | |
| KNN | 0.94 | 3.02 | 0.94 | 94.01 | |
| ES | MLR | 0.81 | 27.15 | 34.53 | 81.02 |
| ANN | 0.86 | 0.54 | 2.18 | 86.03 | |
| RFR | 0.97 | 2.04 | 0.25 | 97.22 | |
| KNN | 0.94 | 3.02 | 0.94 | 94.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.M.; Cao, K.; Yuan, Q.; Bin Mohd Hashim, M.H.; Rehman, H.; Hussain, S.; Emad, M.Z.; Ullah, B.; Shah, K.S.; Khan, S. Application of Machine Learning and Multivariate Statistics to Predict Uniaxial Compressive Strength and Static Young’s Modulus Using Physical Properties under Different Thermal Conditions. Sustainability 2022, 14, 9901. https://doi.org/10.3390/su14169901
Khan NM, Cao K, Yuan Q, Bin Mohd Hashim MH, Rehman H, Hussain S, Emad MZ, Ullah B, Shah KS, Khan S. Application of Machine Learning and Multivariate Statistics to Predict Uniaxial Compressive Strength and Static Young’s Modulus Using Physical Properties under Different Thermal Conditions. Sustainability. 2022; 14(16):9901. https://doi.org/10.3390/su14169901
Chicago/Turabian StyleKhan, Naseer Muhammad, Kewang Cao, Qiupeng Yuan, Mohd Hazizan Bin Mohd Hashim, Hafeezur Rehman, Sajjad Hussain, Muhammad Zaka Emad, Barkat Ullah, Kausar Sultan Shah, and Sajid Khan. 2022. "Application of Machine Learning and Multivariate Statistics to Predict Uniaxial Compressive Strength and Static Young’s Modulus Using Physical Properties under Different Thermal Conditions" Sustainability 14, no. 16: 9901. https://doi.org/10.3390/su14169901
APA StyleKhan, N. M., Cao, K., Yuan, Q., Bin Mohd Hashim, M. H., Rehman, H., Hussain, S., Emad, M. Z., Ullah, B., Shah, K. S., & Khan, S. (2022). Application of Machine Learning and Multivariate Statistics to Predict Uniaxial Compressive Strength and Static Young’s Modulus Using Physical Properties under Different Thermal Conditions. Sustainability, 14(16), 9901. https://doi.org/10.3390/su14169901







