Vehicle Routing Problem for the Simultaneous Pickup and Delivery of Lithium Batteries of Small Power Vehicles under Charging and Swapping Mode

Abstract

Due to the national policy of encouraging the development of power exchange modes, the reasonable planning of vehicle distribution paths to meet the demand of lithium battery power exchange points has become a topic of considerable research interest. In this study, we propose the “centralized charging + unified distribution” power exchange mode for optimizing the charging and transporting of lithium batteries. Considering lithium batteries are dangerous goods, the vehicle path problem of simultaneous pickup and delivery of lithium batteries with vehicle load and soft time window constraints is studied. The model objective is to minimize the transportation risk and total cost of delivery. By performing crossover and mutation operations on the initial solutions generated by the ant colony algorithm, a hybrid ant colony genetic algorithm (ACO-GA) is designed to solve the model. The results of ACO-GA are compared with the GA, ACO, and SAA methods using the Solomon dataset; the results show that the optimized ant colony algorithm can achieve a smaller total cost in solving the model. Finally, taking a lithium battery leasing business in Company A, we determine the optimal path under different preferences by setting different weights for distribution cost and transportation risk in the model transformation, which provides a reference for the company to select the distribution route. Thus, the model provides a reference for companies that intend to develop power exchange businesses.

1. Introduction

With the strengthening of the concept of healthy travel and the further improvement and supplementation of urban infrastructure, the urban micro-travel tools market has continued to expand, and micro-travel tools such as electric bicycles have become common, safe, and reliable means of transportation. In 2020, the ownership of electric bicycles in China was approximately 320 million units [1]. Electric bicycle batteries are mainly run on lead-acid batteries and lithium batteries. Driven by factors such as product technology advancement and environmental protection requirements for green travel, the sales of lithium batteries for two-wheeled electric vehicles have increased significantly from 5.4% in 2016 to 23.4% in 2021 [2]. Lithium batteries offer many advantages, such as long life, being light weight, and having a high energy density. To ensure the safe and standardized usage of electric vehicles, the New National Standard stipulates that the weight of electric bicycles should not exceed 55 kg [3]. The capacity of the battery is limited by the weight of the vehicle, making the farthest travel distance with a single battery limited to less than 60 km, which requires frequent charging operations of the battery during use, subsequently increasing the demand for power exchange [4].

By the end of 2020, 1500 highway service areas (including parking areas) in 31 provinces in China had been replaced by charging and replacement facilities [5]. New infrastructure such as charging piles and replacement stations are also under active construction. With the continuous development of the urban express service industry, the demand for lithium battery leasing and replacement from takeaway, express, and other groups has gradually increased. However, this increase in usage of green energy is not without risks. In 2021, nearly 18,000 fires and 57 deaths were caused by electric bicycles and their battery failures [6]. The high incidence of accidents is mainly concentrated in self-built houses, residences, and stores along the streets, with overcharging and wire short-circuiting being the root causes of the fires. As a result of policy and market demand, the electric vehicle power exchange model is once again being promoted and developed. There are two main types of power exchange modes: the centralized charging mode and the battery swap mode [7]. The centralized charging mode refers to the use of charging stations to store and charge a large number of batteries in a centralized manner; then, unified distribution is provided to each demand point as well as damaged battery replacement services. The battery swap mode refers to the use of the exchange station as a carrier to provide users with battery charging and battery replacement services. Both of these two modes require the construction of a large number of charging stations (piles) as carriers and need to solve a series of problems such as voltage and land. As a result, the “centralized charging + unified distribution” mode was created, that is, using centralized charging stations to store and charge a large number of batteries centrally, and then arranging vehicles to collect the fully charged batteries for distribution. In this mode, we can choose to build large-scale centralized charging stations in the suburbs, and then carry out unified distribution, which can alleviate the power and land pressure caused by the construction of a large number of urban exchange stations [7].

Taking a lithium battery leasing business in Company A, we propose the “centralized charging + unified distribution” power exchange mode (see Figure 1) for optimizing the charging and transporting of lithium batteries. Since lithium batteries belong to the ninth category of dangerous goods in the “United Nations Model Regulations on the Transport of Dangerous Goods”, we add the consideration of transportation risks to the objective function; the vehicle path problem of simultaneous pickup and delivery of lithium batteries with vehicle load and soft time window constraints is studied; the model objective is to minimize the transportation risk and total cost of delivery. This model is intended to help companies optimize delivery routes while taking into account safety and cost, reducing delivery costs and transportation risks. At the same time, the battery swap mode of “centralized charging + unified distribution” will be developed to improve the mileage anxiety of small power vehicles.

The main contributions of this study are as follows:

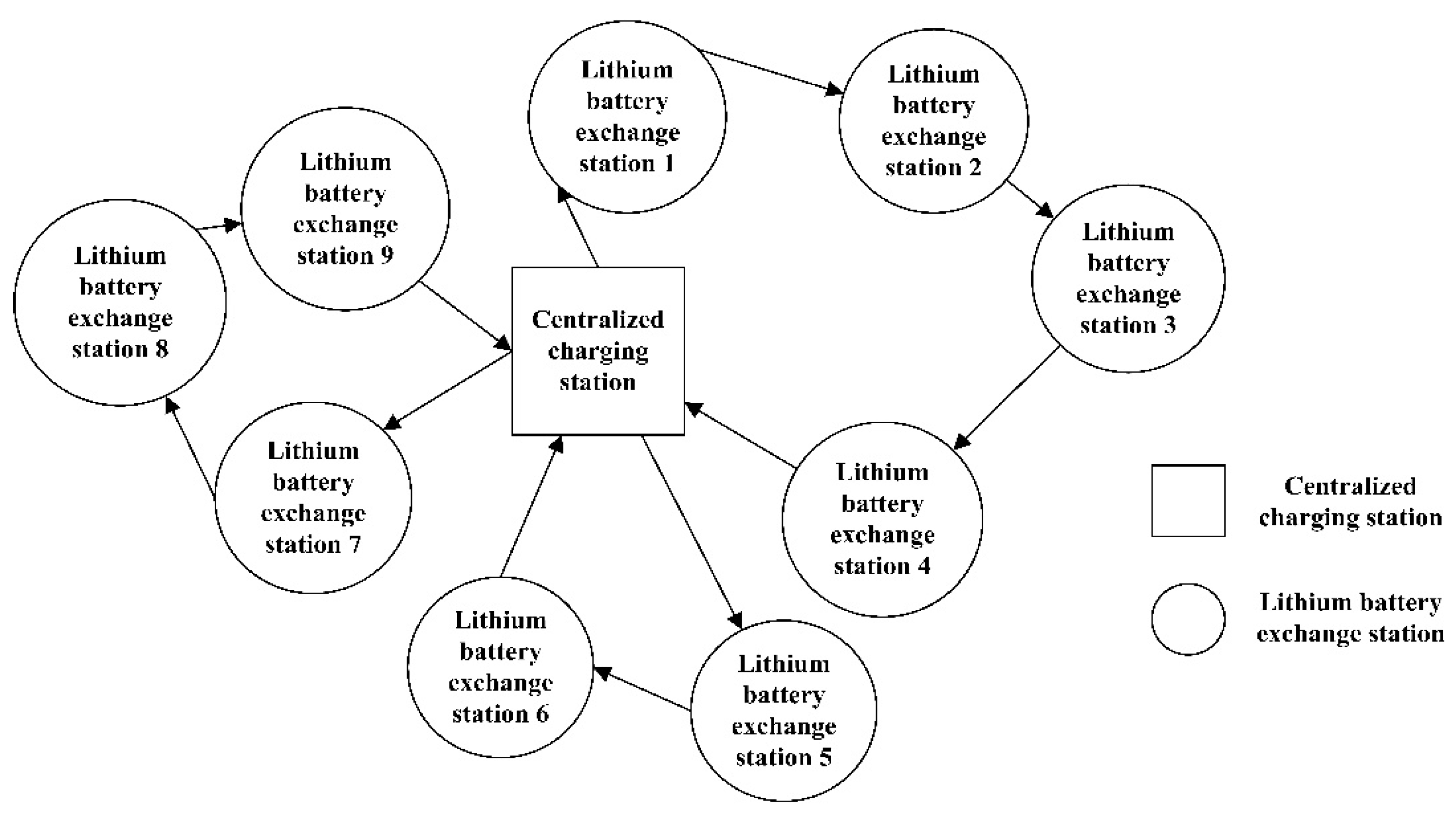
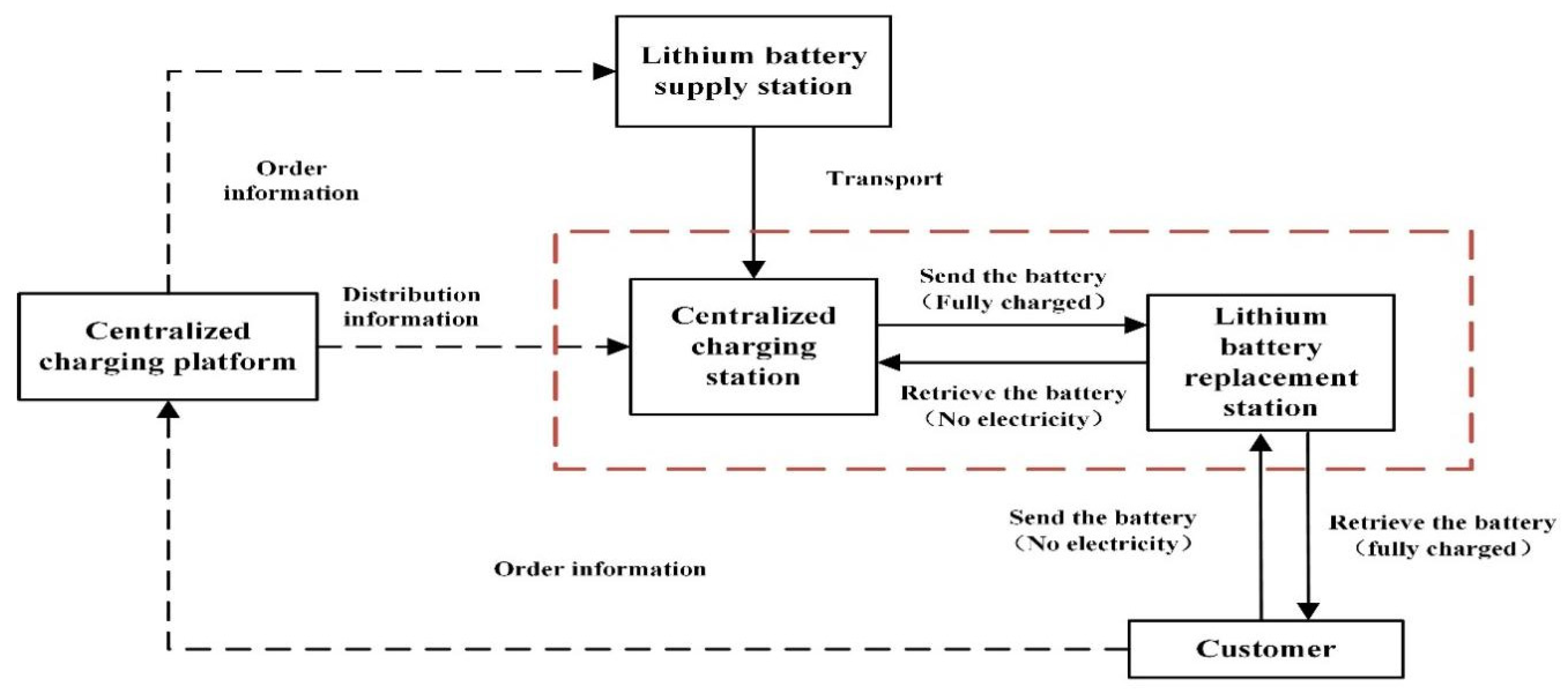
• We first recommend a “centralized charging + unified distribution” power exchange mode, which can help companies take into account safety and cost, optimize their distribution routes, and reduce distribution costs and transportation risks.
• We proposed a dual-objective model to minimize delivery cost and transportation risk, and study a time-windowed vehicle routing problem for simultaneous pickup and delivery of dangerous goods.
• We improved the traditional ant colony algorithm and added the crossover and mutation operations of the genetic algorithm. Based on the R-type data in the Solomon dataset, the effectiveness of the proposed algorithm is verified by comparing the effects of the improved algorithm with the ant colony algorithm, genetic algorithm, and simulated annealing algorithm.
• Change the dual-objective model to a single-objective model by giving different weights to distribution cost and transportation risk. We also explore the optimal distribution paths under different weight combinations to provide decision-making reference for companies with different risk preferences.

2. Literature Review

In 1959, Dantzig and Ramser [8] first proposed the Vehicle Routing Problem (VRP) for logistics distribution. The problem states that a certain number of customers require picking up and delivering goods; the distribution center provides goods to customers and arranges a fleet to provide pickup and delivery services for these customers. The distribution center needs to arrange appropriate driving routes in advance that can meet the needs of customers under certain constraints and achieve goals such as the lowest vehicle mileage, lowest total cost, and smallest number of vehicles used. The VRP is an NP-hard problem, and the solution algorithm contains exact and approximate algorithms. The exact algorithms include [9]: branch and bound (BB), cutting plane method (CPM), dynamic programming (DP), and more. Approximation algorithms can be divided into metaheuristic-based algorithms such as [10]: tabu search algorithms (TSA), simulated annealing algorithm (SAA), genetic algorithm (GA), population intelligence-based algorithms, ant colony algorithm (ACO), glowworm swarm optimization (GSO), particle swarm optimization (PSO), and more. When the size of the problem is small, the exact algorithm can find the optimal solution in an acceptable time. When the problem size is large, heuristic algorithms are more suitable.

(1)

VRP with Time Windows

The vehicle path problem with time windows (VRPTW) is an extension of the classical path problem, which was reviewed and expanded in detail by Solomon et al. [11]. VRPTW generally refers to vehicles with weight constraints that provide delivery or pickup services within a time specified by the customer [9]. Common time window path planning problems consist of: the vehicle routing problem with hard time windows (VRPHTW), the vehicle routing problem with soft time windows (VRPSTW) and the vehicle routing problem with mixed time windows (VRPMTW). As early as 1992, Koskosidis et al. [12], in their study of VRPTW, regarded the time window constraint as a soft constraint that can violate the cost. The research problem in this study also belongs to the soft time window problem. If the goods are delivered within the time interval requested by the customer, then no penalty cost is incurred, and if they are delivered earlier or later than the time interval requested by the customer, then a penalty is imposed depending on the length of the delay (or early arrival). Soft time windows can effectively reduce the delivery cost without significantly reducing customer satisfaction, which is more realistic [13]. Existing studies on VRPTW are shown in

Table 1. Existing studies on VRPTW.

Literature	Problem	Algorithm	Objective
Bae et al. [14]	Multi-depot vehicle routing problem with time windows (MDVRPTW)	Heuristic algorithm and a hybrid genetic algorithm	Minimize the total relevant costs
Ye et al. [15]	VRPTW	Wolf pack algorithm	Minimum total transportation cost
Sun et al. [16]	Multi-depot open vehicle routing problem with soft time windows (MDOVRPTW)	Improved glowworm swarm optimization (GSO)	Minimum total cost
Wu et al. [17]	VRPSTW	Optimized ACO	Minimum total transportation cost
He et al. [18]	VRPSTW	Optimized ACO	Minimize delivery costs
Yu et al. [19]	Heterogeneous fleet green vehicle routing problem with time windows (HFGVRPTW)	Multi-vehicle approximate dynamic programming (MVADP)	The branches and computational time
Wang et al. [20]	Multi-depot VRPTW (MDVRPTW)	Two-stage multi-objective evolutionary algorithm	Minimize the number of vehicles, total travel distance, makespan, total waiting time, and total delay time
Song et al. [21]	VRPTW in cold chain logistics	Improved artificial fish swarm (IAFS)	Minimize the fixed cost and the energy consumptions

.

The vehicle path problem with time window constraints has been studied in different application scenarios, expanding it to HFGVRPTW, MDOVRPTW, etc. Most of the literature takes cost minimization as the objective function. In terms of solution algorithms, most of them are heuristic-based and improve the existing heuristic algorithms for specific problems to obtain faster convergence and smaller cost.

(2)

VRP with simultaneous pickup and delivery

The vehicle path problem with simultaneous pickup and delivery (VRPSPD) belongs to the vehicle path problem with backhaul pick (VRPB) [22]. In 1989, Min [23] first proposed the VRPSPD problem and defined it as follows: all demand points are set to have pickup and delivery demands, the vehicles are loaded in the warehouse and arrive at each demand point in order from the warehouse, but finally return to the warehouse after satisfying the pickup and delivery demands of each demand point. When studying VRPSPD, Reil et al. [24] considered the three-dimensional loading constraints, aimed at minimizing the total driving distance, based on the principle of first packing and then routing, and considered the influence of unloading and reloading as appropriate, and finally used the TSA to find the most optimal path.

By reviewing the literature, we found (see

Table 2. Existing studies on VRPSPD.

Literature	Application Scenarios	Algorithm	Objective
Goksal et al. [28]	VRPSPD	Optimized PSO	Extend the algorithm for solving VRPSPD
Avci et al. [29,30]	VRPSD with multiple vehicle models	Hybrid Local Search Algorithm	Extend the algorithm for solving VRPSPD
Ni et al. [31]	Multiple courier companies jointly deliver	Optimized ACO	Minimize total delivery costs
Chen et al. [32]	Dual-objective VRPSPD model considering both vehicle capacity and distance constraints	Optimized ACO	Minimize the maximum length difference routes and minimize transportation cost
Ma et al. [33]	Uncertain simultaneous pickup and delivery vehicle routing problem	Optimized PSO	Lowest operating costs and highest customer satisfaction
Ren et al. [34]	The problem of picking up and delivering orders in the same city	Optimized GA	Minimize total cost

) that algorithms are most often used to solve the VRPSPD problem [25]. Some scholars also combine the metaheuristic algorithm with the variable neighborhood search (VNS) [26,27] or the variable neighborhood descent algorithm (VND) [28] to obtain a hybrid metaheuristic algorithm for optimizing the capability of local search.

(3)

Vehicle routing problem with simultaneous pickup and delivery with time window constraints (VRPSPDTW)

In actual logistic services, time window and pickup and delivery services are realistic requirements that need to be met; hence the vehicle routing problem with simultaneous pickup and delivery with time window constraints (VRPSPDTW) has received increasing attention [35]. Existing studies on VRPSPDTW are shown in

Table 3. Existing studies on VRPSPDTW.

Literature	Algorithm	Objective
Wang et al. [36]	Simulated annealing (SA) algorithm	Minimize the routing cost
Zhang, Q.H et al. [37]	Memetic algorithm	Minimum the number of vehicles and shortest vehicle travel path
Zhang, S.Z et al. [38]	Optimized TSA	Minimize the total cost including time penalty cost
Hornstra et al. [39]	Adaptive large neighborhood search (ALNS)	Minimize the total processing cost
Yan et al. [40]	K-means-ACO	Minimize the total travel cost during return and delivery service
Ahkamiraad et al. [41]	A hybrid of the genetic algorithm and particle swarm optimization (HGP)	Minimize the transportation and fixed costs
Lagos et al. [42]	PSO	Minimize the total distance of the paths and serving customers’ demands

.

In analyzing the existing literature, it can be seen that in VRPSPDTW, the most basic constraint is the vehicle load constraint or the distance constraint. The objective function is mainly the multi-objective function, and total cost minimization is the main goal of optimization. The cost includes distribution, time window, and distance cost. In terms of solving algorithms, heuristic algorithms are often used to solve the model. This study researches the vehicle path planning problem from the centralized charging station to the lithium battery exchange stations under the “centralized charging + unified distribution” mode. It is necessary to consider the time window requirements of each site, and the simultaneous pickup and delivery requirements, so it is a VRPSPDSTW problem.

(4)

Research on the path problem of dangerous goods distribution and the solution method

The dangerous goods distribution problem refers to the organization of a suitable transportation route (e.g., minimum risk to personnel, shortest distance, lowest cost, minimum time, etc.) for a series of loading and unloading points for dangerous goods, so that the vehicles transporting these goods can pass through in an orderly manner and achieve certain optimal goals under certain constraints (such as transportation volume, speed, cycle time, and acceptable risk criteria) [43].

Due to the flammable and explosive nature of hazardous materials, accidents during the transportation of these materials can be extremely dangerous. Therefore, in the actual transportation process, it is necessary to increase the consideration of risks when transporting dangerous goods in order to ensure transportation safety. Erkut et al. [44] summarized eight common methods to measure transport risk: traditional risk, population coverage, accident rate, perceived risk, expectation-variance risk, minimum-maximum risk, negative utility risk, and conditional risk. Also studied was the vehicle route optimization problem of hazardous materials transportation. The research on the hazardous materials path problem advanced from a single-objective problem to a multi-objective hazardous materials vehicle path problem, especially in recent years. The research objectives now encompass transportation cost, transportation risk, transportation distance, transportation time, accident rate, and transportation loss [45]. Kara et al. [46] first proposed a bi-optimal objective model considering both transportation risk and transportation cost and converted the bi-objective model into a single-objective model using Kuhn–Tucker conditions and complementary slackness conditions. Zografos et al. [47] proposed a two-objective hazardous materials transportation model and gave a simplified transportation risk formula, which measured transportation risk in terms of conventional risk. The proposed bi-objective model was later converted into a single-objective model using a linear weighting approach. Androutsopoulos et al. [48] considered time constraints and used an improved insertion method to solve the model with the objective of minimizing transportation costs and risks when transporting chemical supplies. Chai et al. [49] first simplified the process of quantifying the risk factors of vehicles passing through densely populated areas, and used the small number of vehicles, the total transport distance, and the shortest driving distance through densely populated areas as the objective function in constructing the model and solved it using an improved genetic algorithm. Zhang et al. [50] established a route optimization model for dangerous goods transportation vehicles that simultaneously minimizes the maximum accident consequences and transportation costs and designed the exact algorithm for solving the model based on the ε-constraint method. Li et al. [51] constructed a mathematical model with the objectives of minimizing transportation cost and transportation risk, and the transportation risk was measured by the number of people affected by the accident, after which the improved NSGA-II algorithm was applied to solve the model.

In general, research on the vehicle path problem focuses on two aspects: model construction and solution algorithms. In terms of model construction, scholars have studied the vehicle path problem from two aspects: adding constraints or increasing the number of objective functions. The constraints mainly focus on time constraints and vehicle volume constraints, and the objective functions can be divided into single-objective and multi-objective, of which the main objective is the minimization of total cost. In terms of solution algorithms, most scholars use heuristic algorithms, among which ant colony algorithms have been widely used. However, studies on the simultaneous pickup and delivery vehicle routing problem ignore the inherent dangers of transporting goods. Combining the characteristics of lithium battery dangerous goods and the service time constraints of the power exchange point, this study adds the consideration of “transportation risk” when building the model and studies the routing problem of vehicles for simultaneous pickup and delivery of dangerous goods with on-board capacity and time window constraints in detail.

3. Basic Model

3.1. Problem Description and Model Assumptions

In view of the current battery exchange mode, this study proposes a “centralized charging + unified distribution” battery exchange mode, with a specific operation flow as seen in Figure 2. In other words, there is a centralized charging station and multiple lithium battery exchange stations in a particular area, and the centralized charging station provides a battery replacement service by centralized storage, centralized charging, and unified distribution for a large number of batteries.

The problem can be specifically described as follows: there exists a centralized charging station and multiple lithium battery exchange stations in a certain area, and the centralized charging station is responsible for providing pickup and delivery services of lithium batteries from the lithium battery exchange stations in the area. The locations of the centralized charging station and the battery exchange stations are determined each time a distribution vehicle with a certain load capacity departs from the centralized charging station, delivers the fully charged batteries to each lithium battery exchange station during the service time, and then transports the lithium batteries that need to be charged back to the centralized charging station for charging. If the delivery vehicle does not deliver the lithium battery within the service time required by the lithium battery exchange station, a corresponding penalty cost will be paid. In this case, the following factors are known: the location and number of centralized charging stations and each lithium battery exchange station, the demand for lithium batteries the day before delivery, the service time limit, the number of vehicles, the vehicle travel speed, and information related to transportation risk. The objective of the problem is to reasonably arrange vehicles as well as driving routes under certain constraints to satisfy the demand for all lithium battery exchange stations while minimizing distribution costs and transportation risks. The following assumptions are made to facilitate the study.

• The “centralized charging + unified distribution” mode of power exchange has been applied on a large scale in a certain area, and the number of batteries can meet the demand of all lithium battery exchange stations.
• There is a centralized charging station (24 h charging service) in the region, the number of vehicles is certain, and the starting and ending points of vehicle distribution are centralized charging stations.
• The location of each lithium battery exchange station and the demand for picking up and delivering lithium batteries are known before the vehicle departs.
• The distance between the centralized charging station and each lithium battery exchange station, the service time, the accident probability of each road section, the accident impact radius, the population density, and the number of people affected are known.
• Each vehicle has the same specification and maximum load capacity. Assume that the number of vehicles is three, and the driving speed is constant at 60 km/h.
• Each lithium battery exchange station is delivered and picked up by only one vehicle and the pickup and delivery demand is met at one time.
• The lithium batteries can be mixed and delivered with the same specifications, and the actual loading capacity of each vehicle cannot exceed the maximum loading capacity of the vehicle.
• Each lithium battery exchange station has a designated service window, and the distribution vehicle needs to provide service within this timeframe.
• The service time of the distribution vehicle at the lithium battery exchange station is not related to the distribution volume.
• The distribution cost only considers variable cost (proportional to the number of miles driven by the vehicle) and time window penalty cost. Fixed costs (constants, including driver’s salary, vehicle insurance, etc.) are not considered for the time being.

3.2. Model Constraint

For the lithium battery distribution business of Company A, the path planning model is constructed with the objective of minimizing distribution costs and transportation risks. The multi-objective hazardous material vehicle path problem can reflect the trade-off between cost as well as risk and is closer to the actual research situation. The mathematical notations used in this study are listed in

Table A1. Table of notations.

Sets and Parameters
$O$	Centralized charging station
$N=\{i|i=1,2,\dots ,\overline{N}\}$	The number of lithium battery exchange stations
$K=\{k|k=1,2,\dots ,\overline{K}\}$	The number of delivery vehicles at centralized charging stations
$d_{ij}$	$\mathrm{The} \mathrm{distance} \mathrm{from} \mathrm{station} i$$\mathrm{to} j$ for lithium battery exchange
$t_{ij}$	$\mathrm{Delivery} \mathrm{time} \mathrm{for} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{to} j$
$s_{ik}$	$\mathrm{Service} \mathrm{hours} \mathrm{of} \mathrm{delivery} \mathrm{vehicles} k$$\mathrm{at} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$v_i$	$\mathrm{Lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$ delivery volume
$p_i$	$\mathrm{Pickup} \mathrm{volume} \mathrm{at} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$[E{T}_i,L{T}_i]$	$\mathrm{The} \mathrm{best} \mathrm{service} \mathrm{time} \mathrm{range} \mathrm{required} \mathrm{by} \mathrm{the} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$C_1$	Delivery vehicle unit distance transportation cost
$C_2$	Unit penalty cost for early arrival
$C_3$	Unit penalty cost for being late
$L$	Maximum load capacity of the vehicles.
$R_{ij}$	$\mathrm{Personnel} \mathrm{risk} \mathrm{from} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{to} j$
$p_{ij}$	$\mathrm{Accident} \mathrm{probability} \mathrm{from} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{to} j$
$P_{ij}$	$\mathrm{The} \mathrm{number} \mathrm{of} \mathrm{people} \mathrm{affected} \mathrm{from} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{to} j$
$\lambda$	The radius of influence of the accident
${\rho }_{ij}$	$\mathrm{Population} \mathrm{density} \mathrm{of} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{to} j$
${\omega }_1$	Weighting factor for delivery cost
${\omega }_2$	Weighting factor for transportation risk
$T_{ik}$	$\mathrm{The} \mathrm{time} \mathrm{the} \mathrm{delivery} \mathrm{vehicle} k$$\mathrm{arrives} \mathrm{at} \mathrm{the} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$f_{wagon}^{ik}$	$\mathrm{The} \mathrm{load} \mathrm{of} \mathrm{the} \mathrm{delivery} \mathrm{vehicle} k \mathrm{when} \mathrm{it} \mathrm{arrives} \mathrm{at} \mathrm{the} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$x_{ijk}=\{0,1\}$	$\mathrm{delivery} \mathrm{vehicle} k$$\mathrm{heading} \mathrm{to} j$$\mathrm{from} \mathrm{the} \mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$
$y_{ik}=\{0,1\}$	$\mathrm{lithium} \mathrm{battery} \mathrm{exchange} \mathrm{station} i$$\mathrm{is} \mathrm{serviced} \mathrm{by} \mathrm{the} \mathrm{vehicle} k$

. The specific constraints are explained and taken as follows:

(1)

Distribution cost

The distribution cost includes variable cost and time window penalty cost, where the variable cost includes the fuel cost and maintenance cost of each operating vehicle. The variable cost is related to the unit transportation cost of the vehicle and the transportation distance; the longer the distance the vehicle travels, the higher the fuel cost required. Assuming there are $\overline{K}$ vehicles serving all lithium battery exchange stations, the variable cost of one of the vehicles in the distribution process can be expressed as $f_1$:

$$f_1=C_1{{\displaystyle \sum }}_{i\in N}{{\displaystyle \sum }}_{j\in N}{{\displaystyle \sum }}_{k\in K}{x}_{ijk}{d}_{ij} \forall i\in N,k\in K$$

(1)

where $C_1$ denotes the transportation cost per unit of distance of the distribution vehicle, $d_{ij}$ denotes the distance from lithium battery exchange station $i$ to $j$, and $x_{ijk}$ denotes whether the distribution vehicle k drives from lithium battery exchange station $i$ to $j$.

In the actual process of distributing lithium batteries, different lithium battery exchange stations have different requirements for the delivery service time. If the vehicle completes the delivery within the expected time of the lithium battery exchange station, the penalty cost is 0. If the vehicle arrives earlier than the expected service time of the lithium battery exchange station, the vehicle must wait at the lithium battery exchange station and has to pay an additional waiting cost. If it arrives later than the desired delivery time of the lithium battery exchange station, the exchange station imposes a penalty cost to encourage the delivery vehicle to complete the service within the desired service time. In this study, a soft time window constraint was applied to the penalty cost incurred by the delivery vehicle k arriving at the lithium battery exchange station j, as shown in Equation (2).

$$f_2=\{\begin{array}{ll}{C}_2(E{T}_j-T_{jk}),& T_{jk}<E{T}_j\\ 0,& E{T}_j<T_{jk}<L{T}_j\\ C_3(T_{jk}-L{T}_j),& L{T}_j< T_{jk}\end{array}$$

(2)

where $[E{T}_j,L{T}_j]$ denotes the best service time range required by the lithium battery replacement station $j$. $T_{jk}$ denotes the moment the delivery vehicle $k$ arrives at the lithium battery swap station$j$. $\left(E{T}_j-T_{jk}\right)$ denotes the length of time that the vehicle$k$arrives early at the lithium battery exchange station $j$. $C_2$denotes the unit penalty cost incurred for arriving earlier than the optimal service time required by the lithium battery exchange station$j$. $(T_{jk}-L{T}_j)$denotes the delayed arrival of vehicle$k$ at the lithium battery exchange station j for the length of time. $C_3$ denotes the unit penalty cost incurred for arriving later than the optimal service time required by the lithium battery exchange station$j$.

In summary, the distribution cost of the distribution vehicle is shown in Equation (3).

$$f_3=f_1+f_2$$

(3)

(2)

Transportation risk

Transportation risk, i.e., the impact of possible accidents during transportation on people, property, and the environment, depends on the rate of transportation accidents and the consequences of the impact of accidents [52]. In the vehicle path problem of hazardous materials transportation, the risk factors are mostly random and uncertain, which makes the process of quantification complicated, and no unified evaluation model has emerged to address this so far. Measuring transportation risk by personnel risk is still a widely used method by scholars [53]. The equation is: Personnel risk = Probability of accident $\times$ Number of people affected within a given distance [54], defined as Equation (4).

$$R_{ij}=p_{ij}{P}_{ij}$$

(4)

where $R_{ij}$denotes the risk of people in the section of road from the lithium battery exchange stations $i$ to $j$. $p_{ij}$denotes the probability of an accident from lithium battery exchange stations$i$ to $j$. $P_{ij}$denotes the number of people that can be affected in the area in case of an accident in the section of road from lithium battery exchange stations $i$ to$j$. The specific definition is given in Equation (5).

$$P_{ij}=2d_{ij}\lambda {\rho }_{ij}$$

(5)

where $d_{ij}$denotes the distance from lithium battery exchange stations $i$ to$j$. λ denotes the radius of the area that can be affected in case of an accident in the section of road from lithium battery exchange stations $i$ to$j$. ${\rho }_{ij}$ denotes the population density from the lithium battery exchange stations i to j. The values of $p_{ij}$ and ${\rho }_{ij}$ are randomly generated similarly as in [43].$p_{ij}$is taken in the range [1, 2], ${\rho }_{ij}$is taken in the range [300, 600] (in people), and the value of λ is 0.1 km.

3.3. Multi-Objective Model

The objective of this study is to minimize distribution cost and transportation risk, which is part of the multi-objective model. The solution methods for multi-objective problems mainly include the weighting method, hierarchical solution method, and multi-objective evolutionary method (e.g., NSGA-II). Referring to the literature [48], in this study, distribution cost and transportation risk are transformed into a single-objective function using a weighting method. The problem of setting the weighting coefficients of it can be determined based on the importance of distribution cost and transportation risk of company A (the weighting coefficients of both need to satisfy the summation equal to 1).

Target model:

$$\begin{array}{ll}minZ=& {\omega }_1{C}_1{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{\displaystyle \sum }_{k\in K}{x}_{ijk}{d}_{ij}\\ & +{\omega }_1[C_2{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{\displaystyle \sum }_{k\in K}{x}_{ijk}max\{\left(E{T}_j-T_{jk}\right),0\}\\ & +C_3{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{\displaystyle \sum }_{k\in K}{x}_{ijk}max\{\left(T_{jk}-L{T}_j\right),0\}]\\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\omega }_2{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{R}_{ij}\end{array}$$

(6)

$${\omega }_1+{\omega }_2=1$$

(7)

Load capacity constraint:

$$f_{wagon}^{ik}+{{\displaystyle \sum }}_{j\in N}{x}_{ijk}\left(p_i-v_i\right)\le L,i,j\in N,k\in K$$

(8)

Vehicle number constraints:

$${{\displaystyle \sum }}_{i\in N}{{\displaystyle \sum }}_{k\in K}{x}_{Oik}\le K$$

(9)

$${{\displaystyle \sum }}_{i\in N}{{\displaystyle \sum }}_{k\in K}{x}_{\mathrm{O}ik}={{\displaystyle \sum }}_{j\in N}{{\displaystyle \sum }}_{k\in K}{x}_{j\mathrm{O}k}$$

(10)

Demand non-splittable constraints:

$${{\displaystyle \sum }}_{i=1}^{\overline{N}}{x}_{ijk}=y_{jk},\forall j\in N,k\in K$$

(11)

$${{\displaystyle \sum }}_{j=1}^{\overline{N}}{x}_{ijk}=y_{ik},\forall i\in N,k\in K$$

(12)

Delivery time continuity constraint:

$$T_{jk}=T_{ik}+t_{ij}+s_{ik},\forall i,j\in N,k\in K$$

(13)

Variable Constraints:

$$x_{ijk}\in \{0,1\},\forall i,j,k$$

(14)

$$y_{ik}\in \{0,1\},\forall i,k$$

(15)

Sub-tour elimination constraint:

$${{\displaystyle \sum }}_{i\in N}{{\displaystyle \sum }}_{j\in N}{{\displaystyle \sum }}_{k\in K}{x}_{ijk}\le \left|S\right|-1,S\subset \{1,2,\dots ,\overline{N}+1\},2\le \left|S\right|\le \overline{N}$$

(16)

Constraint (6) indicates that the total distribution cost and transportation risk are minimized, and consists of three items, which are the distribution cost, the penalty cost for early or late delivery time, and the transportation risk. The second term of max (x, 0) indicates that the penalty cost is 0 if the vehicle arrives within the best service time required by the lithium battery exchange station, otherwise, either early or late arrival will incur the corresponding penalty cost. Constraint (7) indicates the weight relationship, and the sum of the two equals 1. Constraint (8) indicates that the actual weight of the vehicle k after completing the task of delivering or picking up lithium batteries at each lithium battery exchange station cannot exceed the maximum weight of that vehicle. Constraint (9) ensures that the number of vehicles departing from the centralized charging station does not exceed the maximum number of vehicles. Constraint (10) ensures that the vehicle departs from and eventually returns the centralized charging station, and the number of departure vehicles is equal to the number of return vehicles. Constraints (11) and (12) indicate that each lithium battery exchange station has and can only be delivered by one vehicle, and there must be a path connected to it when the demand is not split and the lithium battery exchange station is served by the same vehicle. Constraint (13) ensures continuity in the distribution process. Constraints (14) and (15) represent variable constraints. Constraint (16) means that the vehicle only visits each lithium battery exchange station once.

4. Ant Colony Genetic Hybrid Algorithm Design and Verification

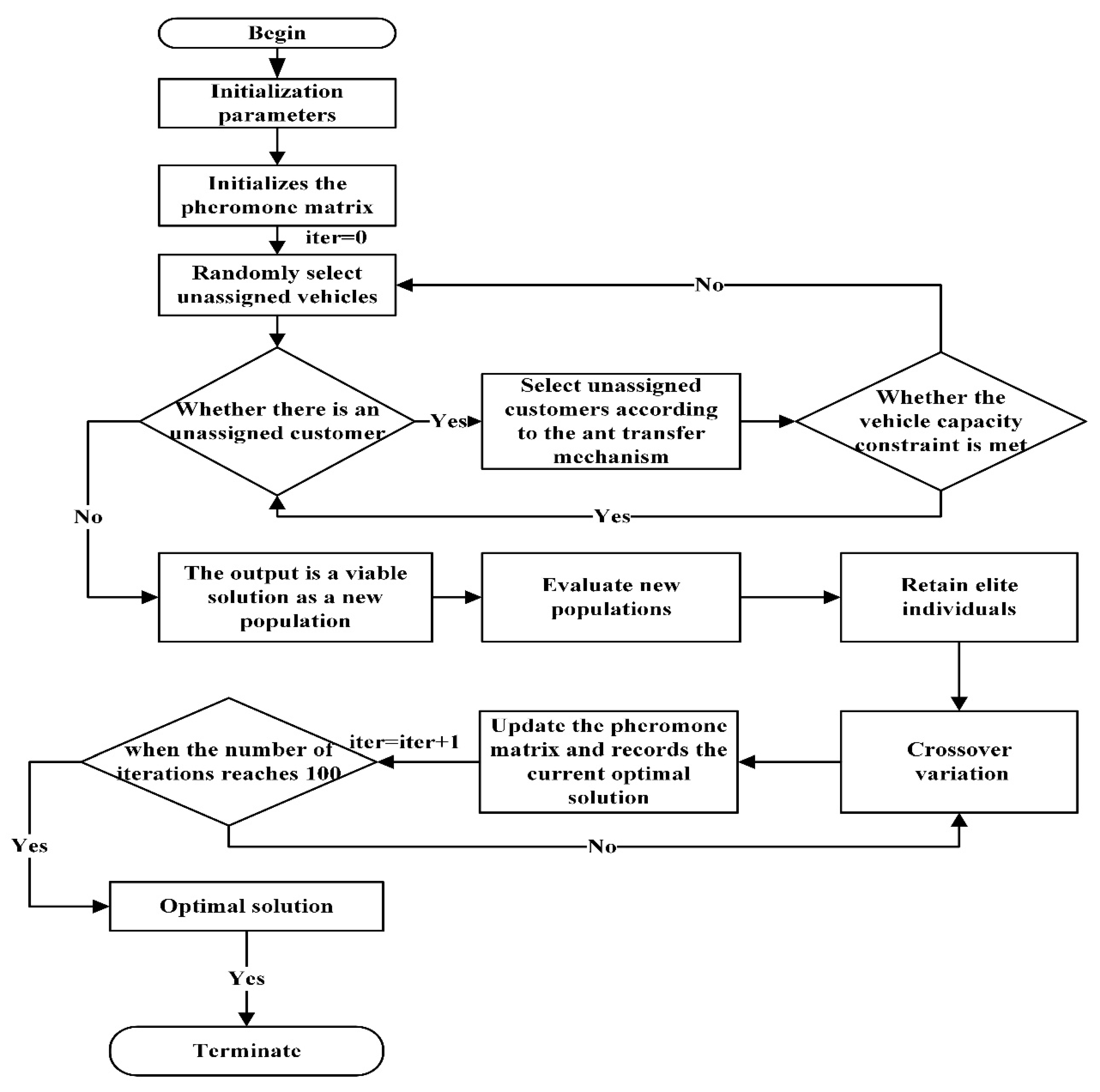
4.1. Algorithm Design

To address the problems of traditional heuristics such as failure to converge and the tendency to fall into local optimality, optimizing a single heuristic algorithm or combining multiple heuristics into a hybrid metaheuristic algorithm can improve the solving ability. From reviewing the literature, it can be seen that the two algorithms, ant colony and genetic, have a wide research base and have relative advantages in solving vehicle path optimization problems. The ant colony algorithm can produce good quality solutions with a small number of iterations, while the genetic algorithm has a good global search capability, which can effectively solve the problems faced by the ant colony algorithm in the local optimization problem. Therefore, this study proposes the ant colony genetic algorithm to solve the model.

The basic design idea is shown in Figure 3; the ant colony algorithm is used as the main body, and the feasible solution is first output as a new population by the algorithm. Then, the fitness function is used to evaluate the new population; that is, the objective function is used to judge the quality of the individuals in the population. Since the objective function in this study is to minimize the delivery cost and risk, the inverse of the objective function is taken as the value of the fitness function. The solution corresponding to the minimum value of the objective function is chosen. Then, the solution is inserted into the genetic algorithm; the crossover and variation operators of the genetic algorithm are used to further optimize the better solution obtained by the ant colony algorithm, so as to expand the search space. In the case of satisfying the termination condition, the convergence speed of the algorithm is accelerated to improve the quality of the solution.

These are some explanations for the specific steps:

(1)

Initialization parameters. Set the initial value of the iteration number iter = 1 and the maximum iteration number iter_max = 100. The definitions and values of other parameters ($\mathrm{m},\partial ,\beta ,\rho ,Q,P_c,P_m$) are shown in

Table 4. Algorithm parameter settings.

Parameters	Parameter Meaning	Parameter Value
$m$	Population size	10
$\partial$	Information heuristic factor	1
$\beta$	Expectation heuristic factor	5
$\rho$	Information volatility factor	0.75
$Q$	Total pheromone release	10
$P_c$	Crossover probability	0.5
$P_m$	Mutation probability	0.1
$C_1$	Delivery vehicle unit distance transportation cost	3 CNY/km
$C_2$	Unit penalty cost for early arrival	20 CNY/h
$C_3$	Unit penalty cost for being late	$30$ CNY/h
$\lambda$	The radius of influence of the accident	0.1 km

.

(2)

Pheromone updating. Set the initial pheromone of all locations to 1, so that the ants have the same probability of crawling to each location. Calculate the length path traversed by the ants, record the current optimal solution, and update the pheromone.

(3)

Transfer of ants. When choosing the next place to visit, the ants will use the pheromone concentration on each connection path as a reference. $P_{ij}^k\left(t\right)$ denotes the probability that ant k moves from point i to j at time t.

$$P_{ij}^k\left(t\right)=\{\begin{array}{ll}\frac{{[{\tau }_{ij}\left(t\right)]}^{\alpha }·{[{\eta }_{ij}\left(t\right)]}^{\beta }}{{\sum }_{s\in {\mathrm{allow}}_k}{[{\tau }_{is}\left(t\right)]}^{\alpha }·{[{\eta }_{is}\left(t\right)]}^{\beta }},& s\in {\mathrm{allow}}_k\\ 0,& s\notin {\mathrm{allow}}_k\end{array}$$

(17)

${\eta }_{ij}\left(t\right)$denotes the heuristic function, the value is the reciprocal of the distance between points i and j, which represents the expected degree of ants $i$transferring from point i to j. ${\mathrm{allow}}_k\left(k=1,2,\dots ,m\right)$ denotes the set of all locations except the departure location of ant k, including (n − 1) elements. It can be seen from Equation (18) that after the ants release the pheromone, the pheromone concentration between the sites decreases with time.

$$\{\begin{array}{l}{\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\mathsf{\Delta }{\tau }_{ij}\\ \mathsf{\Delta }{\tau }_{ij}={{\displaystyle \sum }}_{k=1}^n\mathsf{\Delta }{\tau }_{ij}^k\end{array},0<\rho <1$$

(18)

$\mathsf{\Delta }{t}_{ij}$ denotes the sum of the pheromone concentrations released by all ants on the way from point i to j. The pheromone released by ants was studied through the ant density system, the concentration of pheromone released in this model was a constant value Q.

(4)

Load capacity check of the visiting location: if the load constraints are met, continue to visit, otherwise re-select the next place to be visited. The sites visited by the ants are added to the taboo list until the ants have visited all the sites.

(5)

Evaluate the new population: In this study, the fitness function was used to evaluate the new population judging the quality of individuals in the group through the objective function. Since the objective function in this study is to minimize the delivery cost and transportation risk, the inverse of the objective function is used as the value of the fitness function.

(6)

Crossover and mutation: according to the crossover probability $P_c$, some genes on the chromosomes corresponding to the two individuals are crossed to generate a new individual. Then, according to the mutation probability $P_m$, the gene on the chromosome is mutated. Through crossover and mutation, new individuals can be generated to increase population diversity.

4.2. Validity Verification

Based on the Solomon arithmetic example set, 15 rows of the dataset from the R class test set were selected to validate the model as well as the algorithm effectiveness. The original data is improved by borrowing the data generation of pickups and deliveries from the literature [55]. In this case, the basic data in the example are kept unchanged, and the data of delivery quantity $d_i$ and pickup quantity $p_i$ are generated according to the following rules: let the demand of customer i in the original example be$G_i$, the coordinates of station i are ($x_i$, $y_i$), and let $r_i$ = min($x_i$/$y_i$, $y_i$/$x_i$), then $d_i$=$G_i{r}_i$, $p_i$ =$G_i$(1 − $r_i$). The details of the coordinate system, coordinate position, delivery volume, pickup volume, time window, and service time corresponding to each station are shown in

Table 5. Detailed information table for each location.

Serial Number	Customer Coordinates	Delivery Quantity (Pieces)	Pickup Quantity (Pieces)	Time Window (min)	Service Time (min)
0	(35, 35)
1	(41, 49)	8	2	[161, 171]	10
2	(35, 17)	3	4	[50, 60]	10
3	(55, 45)	11	2	[116, 126]	10
4	(55, 20)	7	12	[149, 159]	10
5	(15, 30)	13	13	[34, 44]	10
6	(25, 30)	3	0	[99, 109]	10
7	(20, 50)	2	3	[81, 91]	10
8	(10, 43)	2	7	[95, 105]	10
9	(55, 60)	15	1	[97, 107]	10
10	(30, 60)	8	8	[124, 134]	10
11	(20, 65)	4	8	[67, 77]	10
12	(50, 35)	13	6	[63, 73]	10
13	(30, 25)	19	4	[159, 169]	10
14	(15, 10)	13	7	[32, 42]	10
15	(30, 5)	1	7	[61, 71]	10

. The specific calculation of personnel risk refers to Equations (4) and (5). Referring to the method in [43], relevant information such as the accident rate between points, the radius of the affected area when the accident occurs, and the population density, are generated. The accident rate between points is randomly generated in the range [1, 2], the population density between points is randomly generated in the range [300, 600] (in people) (for specific values, see

Table A2. Annual transport accident rate of road section.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	1.13	1.76	1.44	1.51	1.45	1.84	1.22	1.64	1.06	1.48	1.90	1.43	1.27	1.01	1.39
1	1.13	0	1.28	1.33	1.79	1.33	1.35	1.90	1.54	1.21	1.80	1.56	1.87	1.02	1.48	1.14
2	1.76	1.28	0	1.50	1.36	1.81	1.26	1.37	1.08	1.59	1.31	1.29	1.01	1.67	1.17	1.91
3	1.44	1.33	1.50	0	1.56	1.28	1.75	1.09	1.37	1.61	1.35	1.93	1.26	1.43	1.61	1.69
4	1.51	1.79	1.36	1.56	0	1.25	1.31	1.45	1.81	1.44	1.56	1.27	1.02	1.42	1.63	1.43
5	1.45	1.33	1.81	1.28	1.25	0	1.30	1.81	1.47	1.39	1.93	1.46	1.38	1.40	1.04	1.49
6	1.84	1.35	1.26	1.75	1.31	1.30	0	1.21	1.08	1.32	1.69	1.64	1.50	1.83	1.05	1.73
7	1.22	1.90	1.37	1.09	1.45	1.81	1.21	0	1.87	1.21	1.10	1.34	1.68	1.35	1.45	1.88
8	1.64	1.54	1.08	1.37	1.81	1.47	1.08	1.87	0	1.39	1.05	1.49	1.33	1.40	1.35	1.08
9	1.06	1.21	1.59	1.61	1.44	1.39	1.32	1.21	1.39	0	1.33	1.47	1.45	1.05	1.46	1.39
10	1.48	1.80	1.31	1.35	1.56	1.93	1.69	1.10	1.05	1.33	0	1.01	1.59	1.39	1.04	1.30
11	1.90	1.56	1.29	1.93	1.27	1.46	1.64	1.34	1.49	1.47	1.01	0	1.38	1.29	1.90	1.07
12	1.43	1.87	1.01	1.26	1.02	1.38	1.50	1.68	1.33	1.45	1.59	1.38	0	1.28	1.42	1.47
13	1.27	1.02	1.67	1.43	1.42	1.40	1.83	1.35	1.40	1.05	1.39	1.29	1.28	0	1.17	1.03
14	1.01	1.48	1.17	1.61	1.63	1.04	1.05	1.45	1.35	1.46	1.04	1.90	1.42	1.17	0	1.29
15	1.39	1.14	1.91	1.69	1.43	1.49	1.73	1.88	1.08	1.39	1.30	1.07	1.47	1.03	1.29	0

and

Table A3. Average density of people affected by transport sections (people/km).

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	572	338	574	490	329	383	464	588	590	347	592	588	446	540	342
1	572	0	538	588	497	310	555	581	504	528	523	418	497	351	512	309
2	338	538	0	547	509	395	586	310	432	414	530	539	356	447	434	494
3	574	588	547	0	497	348	335	450	588	402	476	367	526	376	452	510
4	490	497	509	497	0	377	553	376	545	373	579	405	359	375	485	442
5	329	310	395	348	377	0	527	526	414	470	322	316	459	534	581	339
6	383	555	586	335	553	527	0	459	349	481	379	496	507	525	435	325
7	464	581	310	450	376	526	459	0	332	589	300	533	546	561	325	420
8	588	504	432	588	545	414	349	332	0	474	465	343	556	487	405	454
9	590	528	414	402	373	470	481	589	474	0	447	589	556	487	405	454
10	347	523	530	476	579	322	379	300	465	447	0	406	547	304	312	350
11	592	418	539	367	405	316	496	533	343	589	406	0	534	324	579	533
12	588	497	356	526	359	459	507	546	556	556	547	534	0	582	563	465
13	446	351	447	376	375	534	525	561	487	487	304	324	582	0	429	355
14	540	512	434	452	485	581	435	325	405	405	312	579	563	429	0	452
15	342	309	494	510	442	339	325	420	454	454	350	533	465	355	452	0

in Appendix A). Referring to the analysis of parameters in [56], the settings of other parameters required are shown in Table 5.

In order to compare the results in a more stable and scientific manner, each algorithm is run ten times, and the average value of the weighted function value is output (see

Table 6. Algorithm result comparison.

Algorithm	${\mathit{\omega }}_1-{\mathit{\omega }}_2$					Number of Iterations
	0.8–0.2	0.6–0.4	0.5–0.5	0.4–0.6	0.2–0.8
ACO-GA	1008.23	889.22	789.14	708.29	556.42	35
ACO	1015.13	865.88	801.90	725.51	560.19	45
GA	1471.99	1232.84	1200.59	1007.75	767.58	68
SAA	1547.08	1377.72	1202.06	983.86	728.12	89

). The platform for running the algorithm is a laptop with an Intel(R) Core(TM) i7-8565U CPU.

As can be seen from Table 6, when the weights are combined as (0.8, 0.2), (0.5, 0.5), (0.4, 0.6), and (0.8, 0.2), the average value of the ten-run results of the improved ant colony algorithm (ACO-GA) is the smallest. When the weight combination is (0.6, 0.4), the weighting function value of ACO-GA is the second smallest. It can be seen that the ACO-GA proposed in this paper can obtain better objective function values than the benchmark algorithm in most cases.

5. Empirical Analysis

5.1. Case Introduction and Preprocessing

Company A is a lithium battery sales and operation and R&D company, and its location is in Beijing. Company A’s stores are located in several districts in Beijing; nine stores plus one warehouse of Company A were selected for this study. There are three vehicles in the warehouse, which are used to provide the delivery service for each store. Figure 4 shows the locations of Company A’s warehouses and stores. Location 0 is the warehouse of Company A, and locations 1–9 are the stores. The specific latitude and longitude information is given in

Table A4. Coordinates of distribution center and store locations.

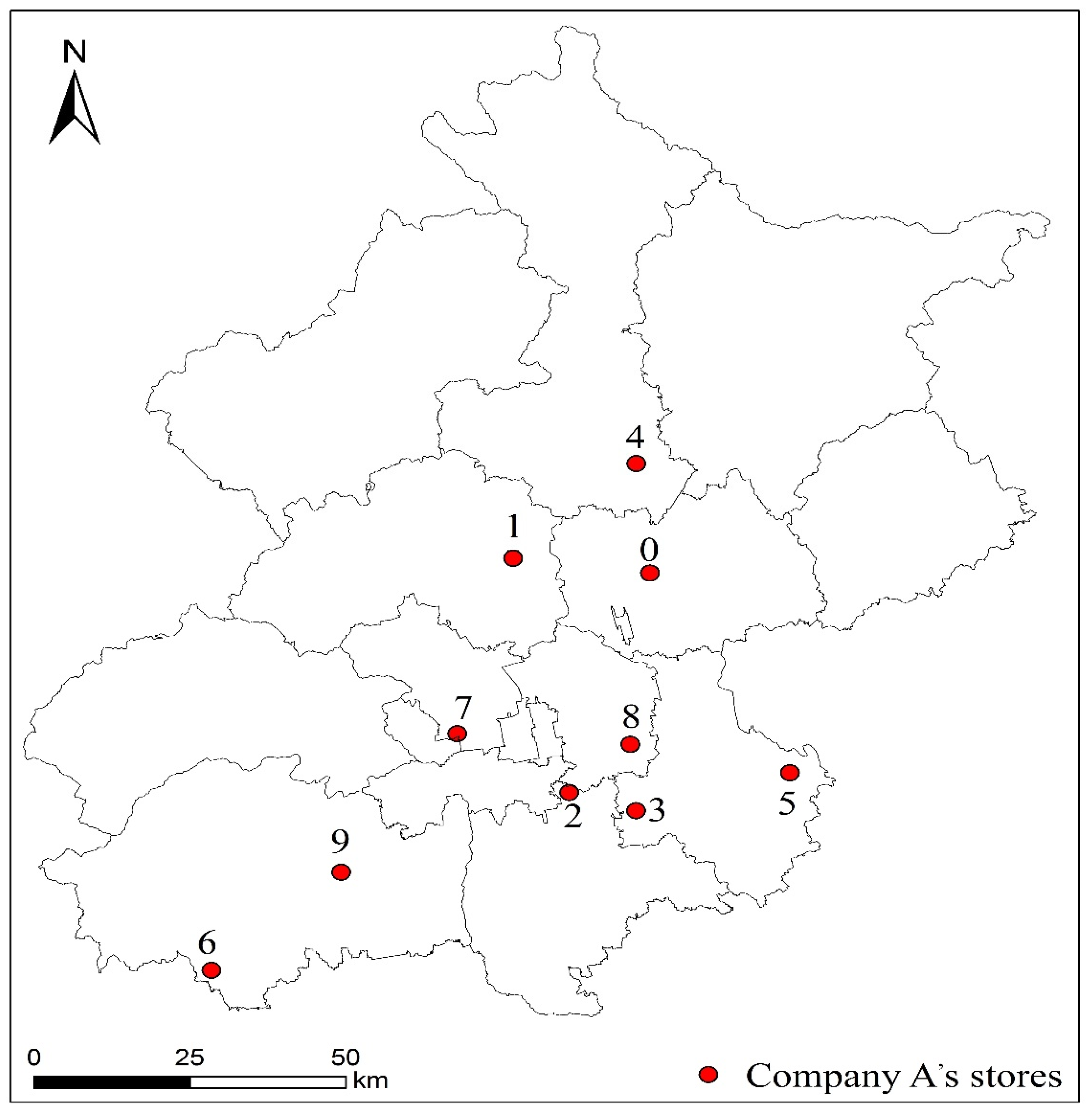
Number	Store Name	Longitude	Latitude
0	Company A warehouse	116.650873	40.154191
1	Store 1	116.394265	40.200878
2	Store 2	116.441387	39.810124
3	Store 3	116.563345	39.769598
4	Store 4	116.653201	40.334977
5	Store 5	116.864538	39.805573
6	Store 6	115.721256	39.577671
7	Store 7	116.244193	39.923892
8	Store 8	116.569297	39.878586
9	Store 9	115.990276	39.71676

.

Since the distance data between each store are required for the calculation of the distribution cost and transportation risk, the latitude and longitude between two points needs to be transformed into the actual distance. According to Equation (17) [57], the transformed distance matrix is shown in

Table 7. Distance matrix between stores of Company A (kilometers).

Stores No.	0	1	2	3	4	5	6	7	8	9
0	0	22.4	42.2	43.4	20.1	42.8	102.3	43.0	31.4	72.3
1		0	43.6	50.1	26.5	59.4	89.2	33.3	38.8	63.8
2			0	11.4	61.1	36.1	66.7	21.1	13.3	39.9
3				0	63.3	26.1	75.3	32.2	12.1	49.3
4					0	61.5	11.5	57.4	51.2	88.8
5						0	100.9	54.6	26.5	75.3
6							0	59.1	80.0	27.8
7								0	28.2	31.6
8									0	52.6
9										0

, where it is assumed that B2 denotes the latitude of Store 1, C2 denotes the longitude of Store 1, D2 denotes the latitude of Store 2, E4 denotes the longitude of Store 2, F2 denotes the actual distance between Store 1 and Store 2, and R = 6371.373 (km) denotes the radius of the Earth.

$$\mathrm{F}2=\mathrm{R}·\mathrm{arcos}[\cos \left(\mathrm{B}2\right)·\cos \mathrm{D}2·\cos \left(\mathrm{C}2-\mathrm{E}4\right)+\sin \left(\mathrm{B}2\right)·\sin \left(\mathrm{D}2\right)]$$

(19)

Company A’s delivery vehicle has a maximum loading capacity of 50 pieces, and the vehicle travels at a constant speed of 60 km/h. The warehouse provides services 24 h a day, and the pickup requirements, service hours and time windows of each store are shown in

Table 8. Detailed information table of each store.

Serial	Store Name	Delivery	Pickup	Time	Service Time
Number		Quantity (Pieces)	Quantity (Pieces)	Window (min)	(min)
0	Company A warehouse
1	Store 1	10	2	[7:30–7:45]	8
2	Store 2	7	10	[7:45–8:00]	10
3	Store 3	6	3	[8:10–8:35]	5
4	Store 4	5	6	[7:05–7:20]	5
5	Store 5	4	14	[8:15–8:25]	10
6	Store 6	14	7	[8:30–9:00]	10
7	Store 7	11	6	[7:55–8:10]	9
8	Store 8	6	3	[7:50–8:15]	6
9	Store 9	14	2	[8:00–8:30]	7

.

5.2. Parameter Combination Analysis

Determining the appropriate parameter values not only reduces the program running time, but also finds the optimal value of the objective function. Since the algorithm in this study is a hybrid algorithm, it is necessary to perform sensitivity analysis on the main parameters of the ant colony algorithm and the genetic algorithm to determine the optimal parameter combination. Parameters such as α, β, and ρ in the ant colony algorithm have great impact on the performance of the algorithm. Regarding the parameter settings of the ant colony algorithm, it is generally believed that the larger the values of α and β, the larger the computational effort and the longer the program run time. In the case that satisfactory solutions can be obtained, it is recommended that α and β be relatively small values. Generally, values of α between 1 and 2, β between 1 and 5, and ρ between 0 and 1 will achieve a solution with better results.

The initial values of the parameters were set as follows: population size m = 10, information heuristic factor α = 1, expectation heuristic factor β = 5, information volatility factor ρ = 0.75, total pheromone release Q = 10 (constant, the total amount of pheromone released by ants in one cycle), $P_c$ = 0.5, and $P_m$ = 0.1. Under the condition that other parameter values remain unchanged, only one parameter value is changed for analysis. If some optimal parameters have been determined in the previous step, we proceed to the sensitivity analysis of the next parameter based on the existing optimal combination. In this section, we set the weights as: ${\omega }_1={\omega }_2=0.5$; indicating that the company places equal emphasis on delivery costs and transportation risks. After ten repeated tests, objective function values and iteration times of different combinations are compared, and a more appropriate parameter combination is finally selected.

(1)

Information heuristic factor α and the expectation heuristic factor β

From

Table 9. Results of the effect of α value on the ant colony genetic hybrid algorithm.

α	β	Average Cost (CNY)	Average Risk	Weighted Objective Function Value (CNY)	Number of Iterations to Reach Convergence	Time (s)
0	5	32.30	5.78	19.04	89	11.70
0.5	5	37.84	5.76	21.80	32	12.91
1	5	34.91	5.99	20.45	79	12.57
2	5	21.37	5.41	13.88	7	11.73

and

Table 10. Results of the effect of β value on the ant colony genetic hybrid algorithm.

α	β	Average Cost (CNY)	Average Risk	Weighted Objective Function Value	Number of Iterations to Reach Convergence	Time (s)
2	0	41.65	8.68	24.90	20	13.83
2	2	33.08	6.25	19.66	38	17.60
2	4	34.33	5.66	20.00	6	16.20
2	5	32.89	5.87	19.38	5	11.86

, it can be seen that while keeping other parameters constant, the larger the values of α and β, the faster the algorithm converges. The results are that the optimal values of α and β are 2 and 5, respectively, at which time the weighted objective function value and the number of iterations to achieve convergence are minimal.

(2)

Information volatility factor ρ

As can be seen from

Table 11. Results of information volatility factor ρ on hybrid ant colony genetic algorithm.

ρ	Average Cost (CNY)	Average Risk	Weighted Objective Function Value	Number of Iterations to Reach Convergence	Time (s)
0.2	36.11	5.69	20.90	52	13.78
0.4	33.88	5.67	19.78	42	12.03
0.6	38.17	5.94	22.06	57	12.10
0.8	32.36	5.90	19.13	36	13.29

, when ρ is relatively small, the pheromone volatilizes slowly, and the algorithm has strong global search ability, but requires a larger number of iterations to achieve convergence. When ρ is relatively large, the pheromone volatilizes quickly, the convergence speed is fast, and the global search ability of the algorithm is weak, making it is easy to fall into the local optimum. After comprehensive consideration, the value of ρ was chosen to be 0.8 in this study. At this time, the value of the weighted objective function value is minimal and convergence can be achieved in 36 iterations.

(3)

Crossover operator $P_c$ and variational operator $P_m$

It can be seen from

Table 12. Results of $P_c$ on the ant colony genetic algorithm.

${\mathit{P}}_{\mathit{c}}$	${\mathit{P}}_{\mathit{m}}$	Average Cost (CNY)	Average Risk	Weighted Objective Function Value	Number of Iterations to Reach Convergence	Time (s)
0.2	1	28.11	5.85	16.98	23	16.11
0.4	1	29.53	5.98	17.75	56	13.06
0.6	1	28.29	5.77	17.03	71	14.64
0.8	1	29.64	5.92	17.78	95	12.35

that while keeping the value of the variational operator $P_m$constant, $P_c$ is taken as 0.2, the weighted objective function value and the number of iterations to reach convergence are minimal.

It can be seen from

Table 13. Results of $P_m$ on the ant colony genetic hybrid algorithm.

${\mathit{P}}_{\mathit{c}}$	${\mathit{P}}_{\mathit{m}}$	Average Cost (CNY)	Average Risk	Weighted Objective Function Value	Number of Iterations to Reach Convergence	Time (s)
1	0.2	33.75	5.89	19.82	88	13.23
1	0.4	30.69	5.46	18.08	31	13.76
1	0.6	28.85	5.79	17.32	14	14.32
1	0.8	28.98	5.85	17.42	17	12.75

that while keeping the value of the crossover operator $P_c$ constant, and $P_m$ is taken as 0.6, the weighted objective function value and the number of iterations to reach convergence are minimal. Although, the transportation risk and running time of the model are not minimal when $P_c$ = 0.6. But, based on the total cost (weighted value of the objective function), we determine the optimal $P_c$ = 0.6.

Therefore, the algorithm parameters in this study will be taken as follows: m = 10, α = 2, β = 5, ρ = 0.8, Q = 10, $P_c$ = 0.2,$P_m$ = 0.6.

5.3. Path Preference Analysis

In order to explore how to choose the best route solution under different preferences, different weights are set for distribution cost and transportation risk for total cost accounting, where the size of the weights represent the importance of the decision makers, and a larger weight indicates that the decision makers want the goal to be smaller. Since the cost and risk have different orders of magnitude and units, they are standardized to ensure the uniformity of the scale in the weighting process. When setting weights for distribution cost and transportation risk, the principle that the sum of the two weights is equal to 1 is observed. By setting different weights for distribution cost and transportation risk, indicating different transportation preferences of enterprises, the optimal path is shown in Table 10, and the route planning schematic is shown in Figure 5.

According to

Table 14. Path selection preference results with different weights.

Strategy	Weights		Optimal Path
	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	Vehicle 1	Vehicle 2	Vehicle 3	Normalized Objective Function Value	Distribution Cost	Shipping Risks	Programs Preference
A	0.2	0.8	0→4→1 →2→3→8→5→0	0→7→9 →6→0		0.76	60.14	5.40	Very concerned about risk
B	0.4	0.6	0→1→4 →8→2→7→0	0→3→5 →6→0	0→5→3 →2→0	0.47	29.34	8.67	More concerned about risk
C	0.5	0.5	0→4→1 →7→0	0→8→3 →2→9→0	0→5→6 →0	0.83	55.17	8.08	Intentional risk and cost
D	0.6	0.4	0→4→1 →7→2→8→0	0→5→3 →9→0	0→6→0	0.42	29.88	7.85	More concerned about cost
E	0.8	0.2	0→4→1 →7→2→8→0	0→3→5 →9→0	0→6→0	0.80	28.40	8.51	Very concerned about cost

, companies will have five different options when setting different weights on distribution costs and transportation risks. When an enterprise is facing the decision of both distribution cost and transportation risk, the more the enterprise cares, the greater the corresponding weight value, and the resulting value of this part will be small. The smaller the weight value, the lower the degree of concern of the enterprise, and the resulting value of this part will be larger.

6. Conclusions

In view of the practical problems of unsafe home charging, insufficient number of charging piles, high purchase cost of lithium batteries, and difficulty in charging distribution vehicles, this paper proposes a battery replacement mode of “centralized charging + unified distribution” for small electric vehicles based on the lithium battery leasing and distribution business of company A.

The proposed dual-objective model and improved ant colony algorithm (ACO-GA) can provide an optimal path that takes into account the distribution cost and transportation risk when solving the transportation path problem of hazardous goods such as lithium batteries. This can also provide reference for other enterprises that intend to develop power exchange businesses. When verifying the effectiveness of the improved algorithm, different weight combinations are used to verify the effectiveness of ACO-GA on the R-type dataset in the Solomon test set, which make the results more stable. After determining the optimal parameter combination through sensitivity analysis, we set different weight coefficients when calculating the weighted objective function value, which meet the distribution needs of enterprises with different risk preferences.

The study also has several limitations, which we plan to improve in our future work. Firstly, in terms of algorithm improvement, it can be combined with more intelligent algorithms suitable for VRPSPDSTW to carry out a variety of algorithm variants. Secondly, on the scale of the calculation example, a larger-scale data set can be further selected for experiments. Finally, in the comparison of algorithms, comparisons with other deep learning and reinforcement learning-based algorithms can be added in the future.