Compensation Strategy of PMSM Predictive Control with Reduced Parameter Disturbance

Abstract

This paper proposes a double closed-loop predictive control scheme for a permanent-magnet synchronous motor system, which consists of a speed loop model predictive control and a current loop deadbeat predictive control, current loop and speed loop adopt different predictive control methods, compensate the unstable switching frequency, and reduce the amount of calculation. Considering the influence of parameter mismatch on the control performance, a parameter disturbance sliding mode observer and a parameter disturbance internal mode observer are designed to compare the compensation ability of the two observers for current tracking errors, which improves the disturbance rejection ability and robustness of the system, and the compensation ability of the internal mode observer is better. The simulated and experimental results show that the improved strategy and predictive control method proposed in this paper can obtain better speed tracking performance compared with traditional control, which verify the effectiveness and feasibility of the proposed control scheme on a servo control system.

1. Introduction

The traditional control strategy of permanent magnet synchronous motor (PMSM) is proportional integral differential (PID) control, but PMSM has interferences such as load torque fluctuations and motor parameter changes under actual working conditions. Since the traditional PID control strategy has the poor ability of disturbance rejection, it is difficult to guarantee a good steady-state performance [1,2,3,4]. Therefore, many improved measurements have been carried out to solve the above problems. In [5], an intelligent algorithm based on an evolutionary algorithm is proposed to automatically adjust the parameters of the fuzzy PID controller, which improves the anti-load torque disturbance performance on PMSM. In [6], an adaptive nonlinear fractional-order PID sliding mode controller is designed using an extended state observer to improve the dynamic and steady-state performance and robustness of the system. In [7], an adaptive PID speed control scheme is proposed based on the gradient descent method, whose controller gain can be adjusted online. Compared with the traditional PID control method, the adaptive PID speed control scheme can improve the control performance of the system under uncertain parameters. These improvements to PID controllers are effective, but at the same time they also make the controller design more complicated, which is not conducive to being put into practical applications.

In addition to the improvement of PID controllers, in recent years, many researchers have proposed various advanced control strategies, such as fuzzy control, nonlinear optimal control (NOC), sliding mode control (SMC) and adaptive control. In [8], in order to solve the problem of controller model parameter mismatch, a current predictive control based on fuzzy algorithm is proposed. In [9], a NOC and observer based on the θ-D approximation method is proposed, which improves the robustness of PMSM under load disturbances and parameter changes. In [10], a sliding mode speed control method combined with an extended state observer is introduced to reduce the jitter of the system and improve the dynamic performance of the system. In [11], an adaptive speed control method considering parameter changes and load fluctuations is proposed.

In addition, combining intelligent algorithms such as particle swarm algorithm and genetic algorithm with other basic control methods is also a common control strategy [12,13], such as using particle swarm algorithm to optimize controller parameters [14], [15]. Although the control strategy does not heavily rely on manual adjustment compared with the shortcomings of those basic control methods, it is not mature enough in practical applications, and has disadvantages such as huge calculation burden, complex design process, and low stability, which makes it difficult to ensure the stability of the system.

The application of predictive control in PMSM control system is mature, and the more common predictive control methods include model predictive control (MPC) and the deadbeat predictive control [16]. MPC has almost no requirement on the form of mathematical model, and the control system has good robustness and stability. By adopting the method of rolling optimization, the control system is little affected by external disturbances, and the dynamic response performance is good [17]. The deadbeat predictive control (DPC) is to accurately calculate the dq-axes voltage vector required for the next control cycle, according to the given value of the dq-axes current, the three-phase current sampling value and the electrical angular velocity value at each sampling moment. Then, the switching signal is obtained, which is required by the inverter through space vector modulation to ensure that after the voltage vector is applied, the actual current value of the motor can track the given current reference value. Compared with traditional control methods, this control strategy requires less calculation and can obtain better dynamic and steady-state performance. Therefore, DPC is increasingly used in motor servo control systems [18,19]. However, it heavily relies on the precise mathematical model of the motor. When the motor parameters change, the control performance of the system is easily affected. Many methods have been proposed to solve this problem [20,21]. The identification methods of resistance inductance and flux parameters have been proposed in [22,23]. However, on-line identification is difficult and the computational burden is increased. Model-free deadbeat predictive current control was applied to get rid of the dependence on motor parameters [24,25], but this method a is complex and heavy computational burden. Meanwhile, the disturbance observer is proposed to compensate for the parametric dependence of DPC. A sliding mode disturbance observer is proposed to optimize current control performance of PMSM with model parameter mismatch [20]. In [21], a robust predictive current control with parallel compensation terms is proposed for the influence of motor parameter mismatch on system stability and current tracking error. In [24], a combination of parameter-free Luenberger disturbance observer and DPC is proposed to improve robustness.

However, according to the characteristics of the speed loop and current loop, previous studies seldom use different predictive control methods. In view of the dependence of DPC on the model, only a single observer control method is used to compensate, and different observers are not compared.

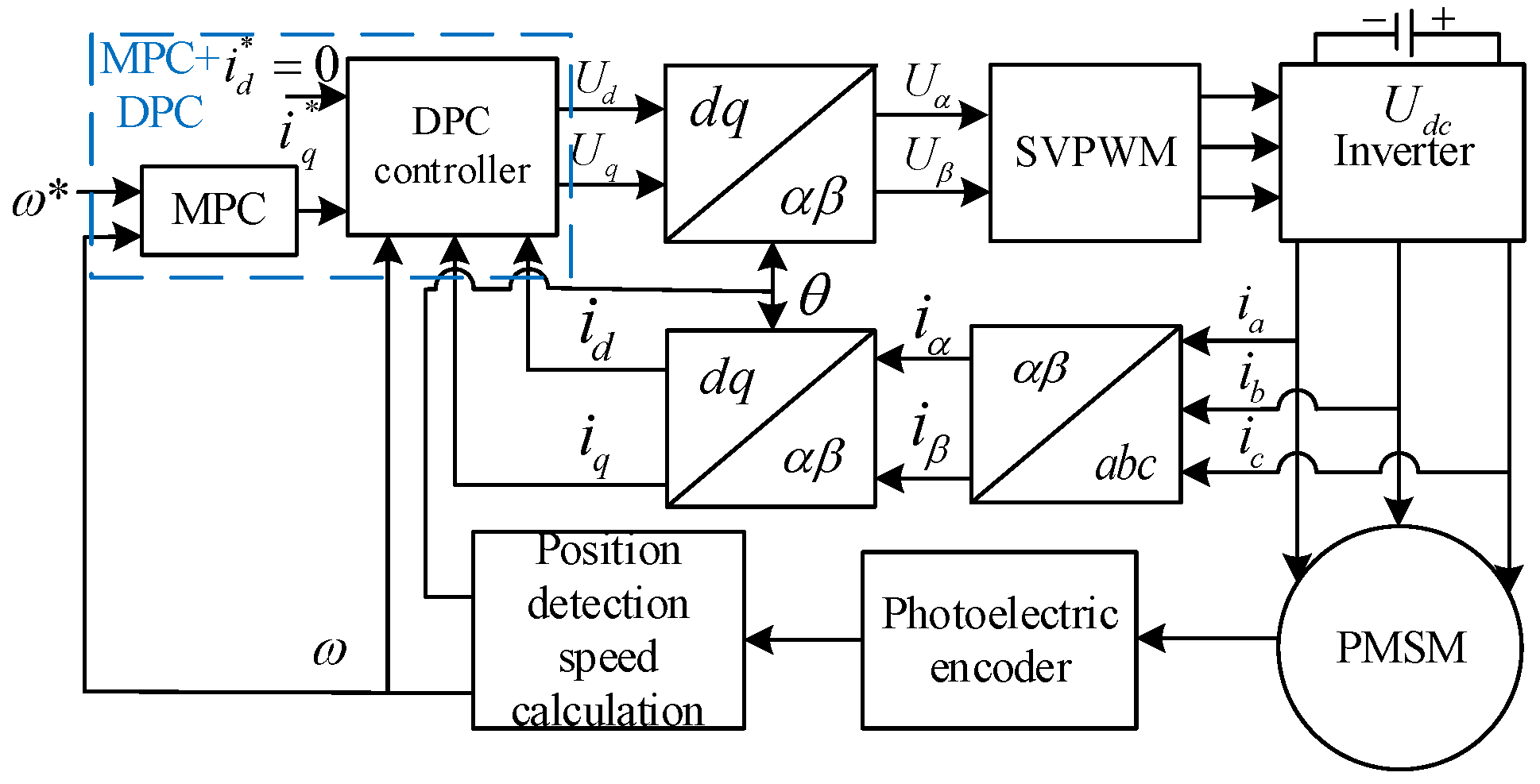
The main contribution of this paper lies in the proposal of double-loop predictive control considering disturbance compensation of PMSM servo system. The novelty of this paper can be summarized as:

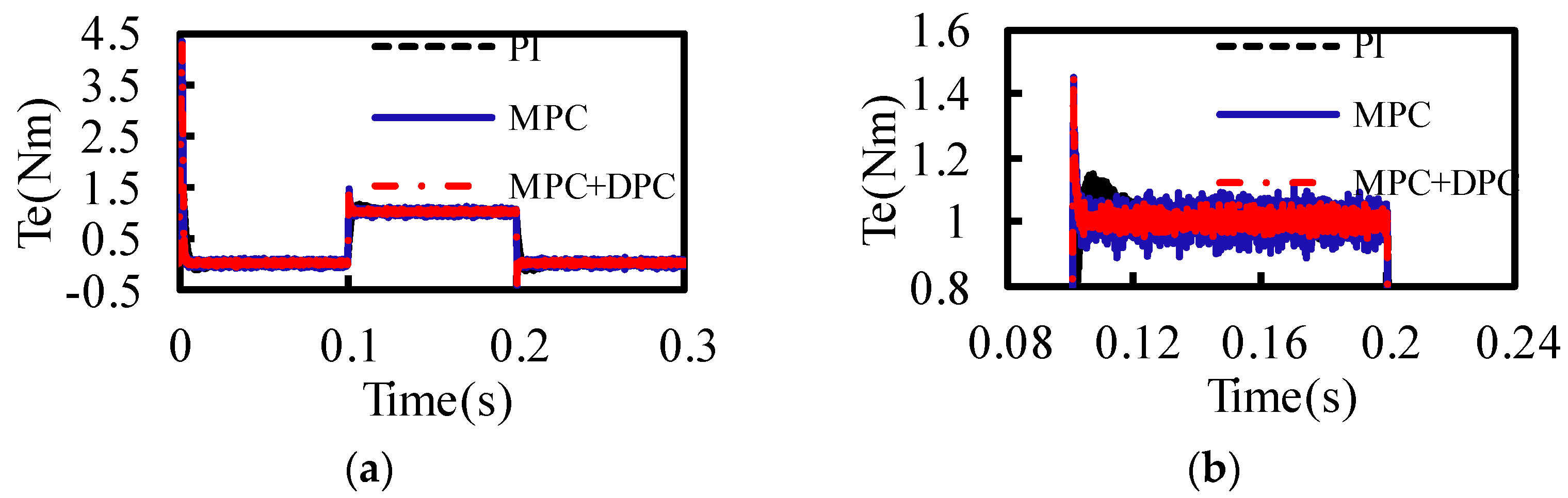
• The speed loop model predictive control and the current loop deadbeat predictive control are designed to form a cascaded double closed-loop predictive control system.
• The influence of parameter mismatch on DPC current loop is analyzed.
• The sliding mode disturbance observer and internal mode disturbance observer are proposed to compensate the parameter dependence of the DPC current loop.

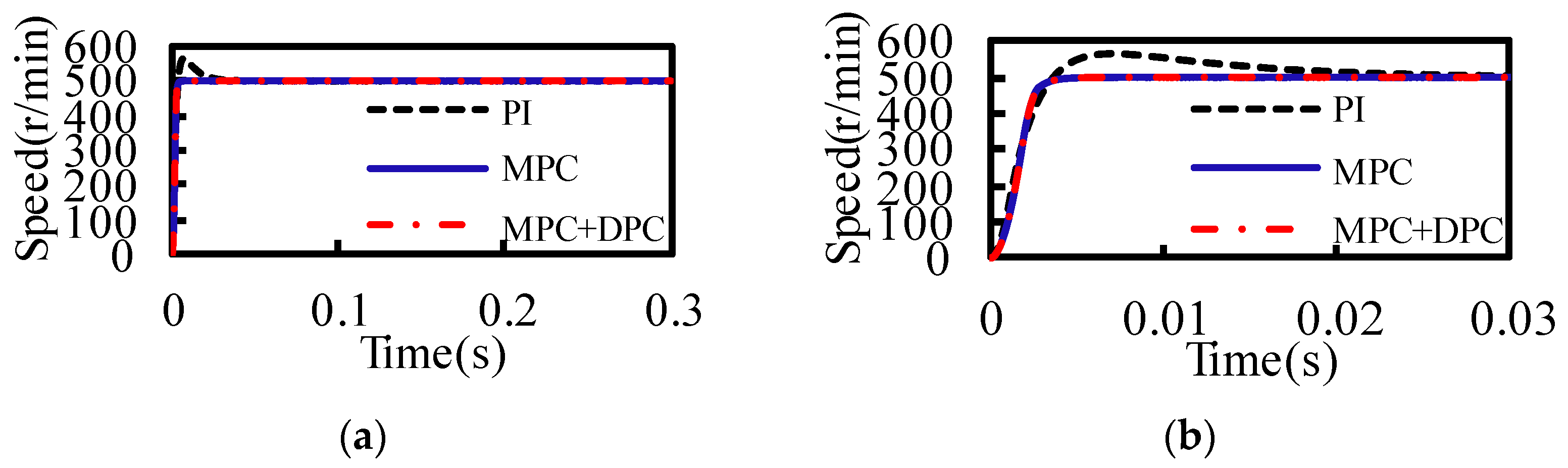
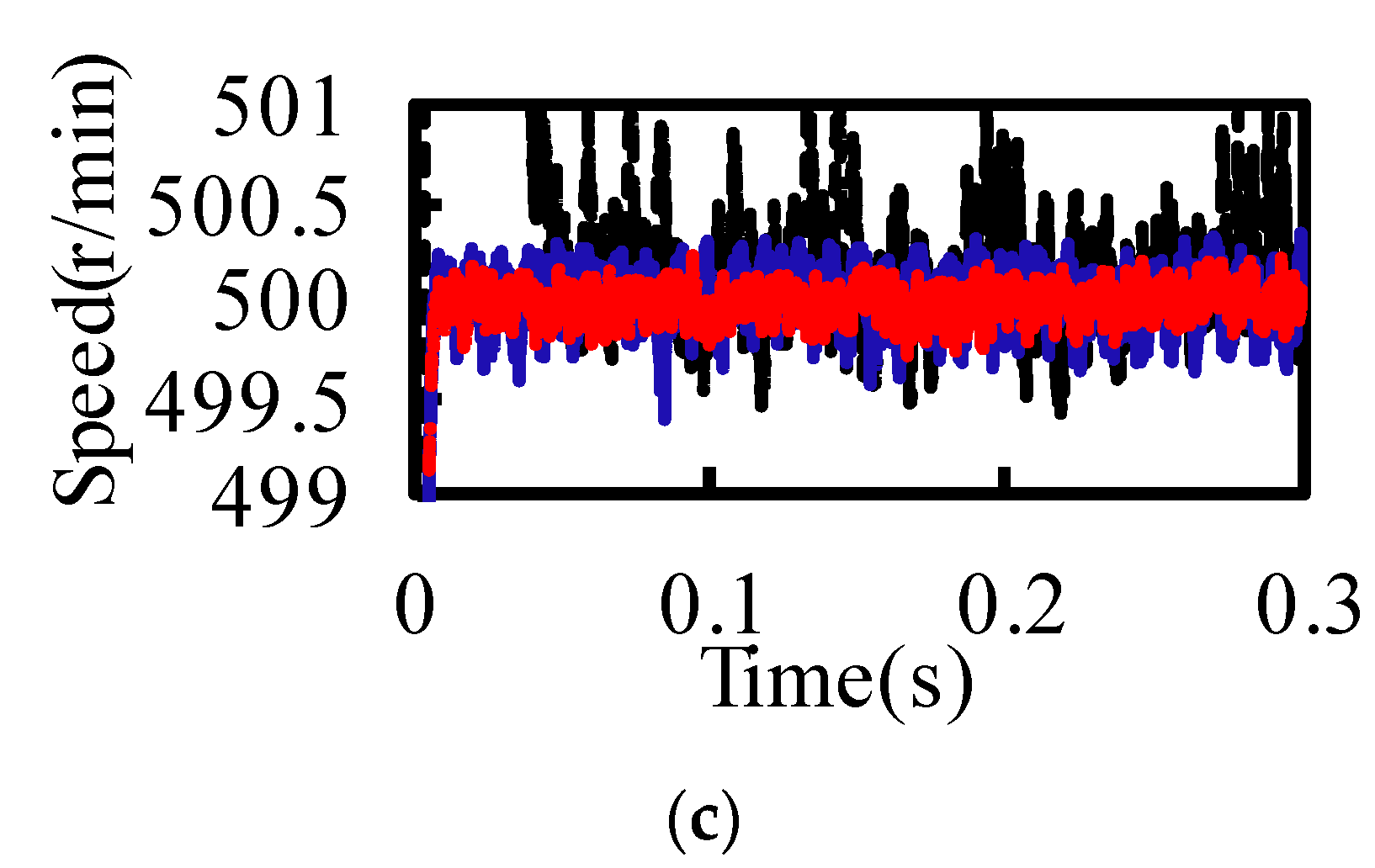
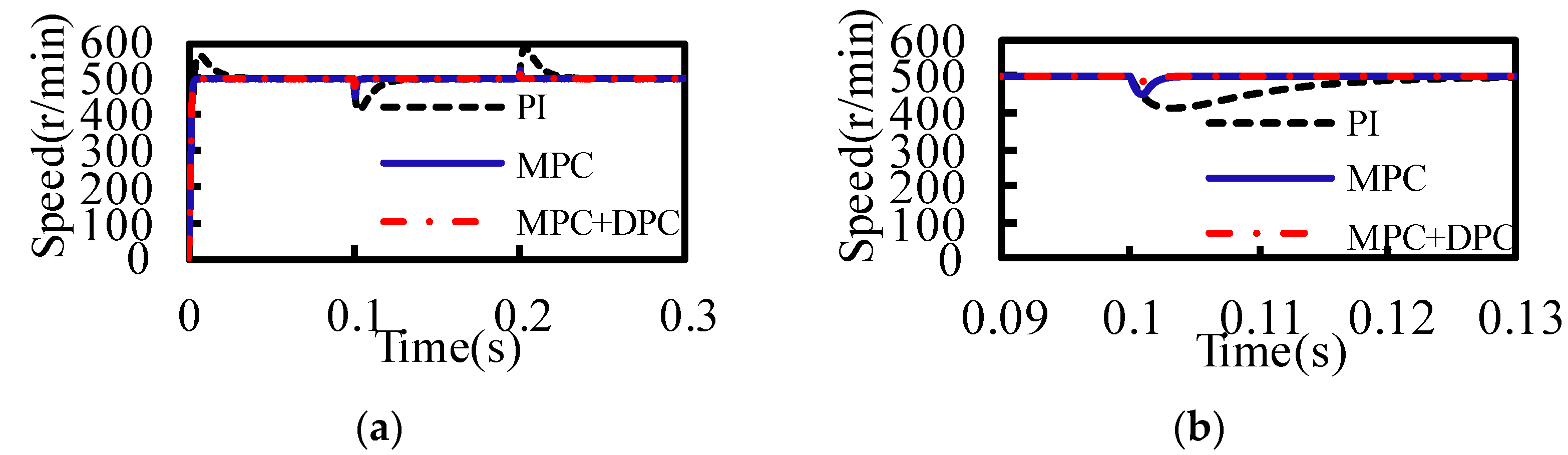
This paper is organized as follows. In Section 2, based on the mathematical model of PMSM, a speed loop model predictive control (MPC) and a current loop DPC are designed to form a double closed-loop predictive control system. The performance of the three control strategies MPC+DPC, MPC, and PI is compared and verified by a simulation model. Then, the sensitivity of the parameter change of traditional current predictive control is analyzed in Section 3. In order to improve the anti-parameter disturbance performance of the system, parameter disturbance sliding mode observer (DSMO) and parameter disturbance internal model observer (DIMO) are proposed. Section 4 is devoted to the experimental verification of proposed predictive control system. Finally, conclusions are drawn in Section 5.

2. Design of the Predictive Controller

2.1. MPC Controller

The electromagnetic torque equation and mechanical motion equation of PMSM in dq-coordinate can be expressed as

$$\{\begin{array}{c}{T}_e=\frac{3}{2}{P}_n{\psi }_f{i}_q\hfill \\ \frac{d{\omega }_m}{dt}=\frac{T_e-B{\omega }_m-T_L}{J}\hfill \end{array}$$

(1)

where T_e and T_L are the electromagnetic torque and the load torque, respectively, Ψ_f is the flux linkage due to the permanent magnets, p_n is the number of pole pairs, i_q is the current component of the q-axis, B is the friction coefficient, ω_m is the mechanical angular velocity, and J is the moment of inertia.

By simplifying the above equations as a predictive model and discretizing, one can get

$$\omega (k+1)=(1-\frac{BT}{J})\omega (k)+\frac{3P_n{\psi }_{f}T}{2J}{i}_q(k)-\frac{T_L}{J}$$

(2)

where T represents the sampling time. It is approximately considered that T_L remains unchanged when T is short, and the discrete equation at the previous moment is

$$\omega (k)=(1-\frac{BT}{J})\omega (k-1)+\frac{3P_n{\psi }_{f}T}{2J}{i}_q(k-1)-\frac{T_L}{J}$$

(3)

Subtracting (3) from (2), one can get

$$\omega (k+1)=(2-\frac{BT}{J})\omega (k)-(1-\frac{BT}{J})\omega (k-1)+\frac{3P_n{\psi }_{f}T}{2J}\Delta i_q(k)$$

(4)

where $\Delta i_q(k)=i_q(k)-i_q(k-1)$, $a=1-\frac{BT}{J}$, $b=\frac{3P_n{\psi }_{f}T}{2J}$.

The prediction model of the first step can be expressed as

$${\omega }_m(k+1)=(a+1)\omega (k)-a\omega (k-1)+b\Delta i_q(k)$$

(5)

The prediction model of the step N can be expressed as

$${\omega }_m(k+N)={\displaystyle \sum _{i=0}^N{a}^i}\omega (k)-{\displaystyle \sum _{j=1}^N{a}^j}\omega (k-1)+{\displaystyle \sum _{n=k}^{N-1}(N-n)a^{n}b}\Delta i_q(n)$$

(6)

Considering the influence of external disturbances and parameter changes, such as changes in motor resistance, inductance, and flux linkage, there will be a certain error between the predicted speed and the actual speed. The predicted error value e(k) can be defined as

$$e(k)=\omega (k)-{\omega }_m(k)$$

(7)

Assuming that the prediction error value of N steps in the future will not change, one can get

$$e(k+N)=\cdots =e(k+1)=e(k)$$

(8)

The revised output prediction of the Nth step can be expressed as

$${\omega }_s(k+N)={\omega }_m(k+N)+e(k)$$

(9)

In order to make the predicted output close to the reference trajectory, and so that the control increment will not change drastically, the quadratic performance index function is selected as follows.

$$J={\displaystyle \sum _{i=1}^N{q}_i^2}{[{\omega }_r(k+i)-{\omega }_s(k+i)]}^2+r{[\Delta i_q(k)]}^2$$

(10)

where q_i is the weighting coefficient of the error between the prediction and the actual value, and r is the weighting coefficient of the control variable current change. The smaller the weighting coefficient is, the weaker the restraining ability of the control variable changes.

In order to minimize the performance index value, generally let $dJ/d\Delta i_q(k)=0$, and the final optimal control quantity can be expressed as

$$\Delta i_q(k)={(r+W_b{}^{T}Q{W}_b)}^{-1}{W}_b{}^{T}Q(W_r-W_0-E)$$

(11)

where $W_r={[{\omega }_r(k+1),{\omega }_r(k+2),\cdots {\omega }_r(k+N)]}^T$, $W_b=\left[\begin{array}{c}b\\ (a+2)b\\ ⋮\\ {\displaystyle \sum _k^{N-1}(N-k)a^{k}b}\end{array}\right]$, $Q=\left[\begin{array}{cccc}{q}_1^2& 0& 0& 0\\ 0& q_2^2& 0& 0\\ 0& 0& ⋮& 0\\ 0& 0& 0& q_N^2\end{array}\right]$,$E=\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]e(k)$, $W_0=\left[\begin{array}{c}a+1\\ a^2+a+1\\ ⋮\\ {\displaystyle \sum _{i=0}^N{a}^i}\omega (k)\end{array}\right]\omega (k)-\left[\begin{array}{c}a\\ a^2+a\\ ⋮\\ {\displaystyle \sum _{j=1}^N{a}^j}\omega (k)\end{array}\right]\omega (k-1)$.

Therefore, the actual current control quantity at time k is

$$i_q(k)=\Delta i_q(k)+i_q(k-1)$$

(12)

2.2. DPC Controller

According to the voltage equation of the motor, the flux linkage equation and the mechanical motion equation, one can get

$$\{\begin{array}{c}L\frac{d{i}_d}{dt}=-R{i}_d+{\omega }_{e}L{i}_q+u_d\hfill \\ L\frac{d{i}_q}{dt}=-R{i}_q-{\omega }_e({\psi }_f+L{i}_d)+u_q\hfill \\ J\frac{d{\omega }_m}{dt}=T_e-T_L-B{\omega }_m\hfill \end{array}$$

(13)

where u_d and u_q are dq-axes applied voltages, i_d and i_q are dq-axes currents, respectively, R is the stator resistance, p_n is the number of pole pairs, ω_e is the electrical angular velocity, which satisfies ${\omega }_e=p_n{\omega }_m$, L is the inductance.

Changing (13) into a matrix form, one can obtain

$$\left[\begin{array}{c}\frac{d{i}_d}{dt}\\ \frac{d{i}_q}{dt}\end{array}\right]=\left[\begin{array}{cc}-\frac{R}{L}& {\omega }_e\\ -{\omega }_e& -\frac{R}{L}\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& 0\\ 0& \frac{1}{L}\end{array}\right]\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]+\left[\begin{array}{c}0\\ -\frac{{\omega }_e{\psi }_f}{L}\end{array}\right]$$

(14)

When the sampling time T is small enough, the first-order Taylor formula can be used to discretize the differential term of Equation (14), and the differential term can be approximated as

$$\{\begin{array}{c}\frac{d{i}_d}{dt}=\frac{i_d(k+1)-i_d(k)}{T}\\ \frac{d{i}_q}{dt}=\frac{i_q(k+1)-i_q(k)}{T}\end{array}$$

(15)

Assuming that the voltage and back electromotive force remain unchanged during a control period T, the discretized current prediction model at time T(k + 1) can be written as

$$\{i(k+1)=A(k)\cdot i(k)+B\cdot u(k)+C(k)$$

(16)

where $i(k)={[i_d(k),i_q(k)]}^T$, $u(k)={[u_d(k),u_q(k)]}^T$, $A(k)=\left[\begin{array}{cc}1-\frac{RT}{L}& T{\omega }_{\mathrm{e}}(k)\\ -T{\omega }_e(k)& 1-\frac{RT}{L}\end{array}\right]$, $B=\left[\begin{array}{cc}\frac{T}{L}& 0\\ 0& \frac{T}{L}\end{array}\right]$, $C(k)=\left[\begin{array}{c}0\\ -\frac{{\psi }_{f}T{\omega }_e(k)}{L}\end{array}\right]$.

When the delay effect is not considered, the reference current $i_d^{*}(k)$, $i_q^{*}\left(k\right)$ can be used as the input quantity i_d(k + 1), i_q(k + 1) at the next time T(k + 1), which is

$$\{\begin{array}{c}{i}_d(k+1)=i_d^{*}(k)\\ i_q(k+1)=i_q^{*}(k)\end{array}$$

(17)

Finally, the fast-tracking closed-loop control of the current loop is realized. In principle, a given current signal can be followed after a T period.

$$u(k)=B^{-1}[i^{*}(k)-A(k)\cdot i(k)-C(k)]$$

(18)

2.3. Simulation Analysis

The first two sections design a speed loop MPC controller and a current loop DPC controller. The former acts on the outer speed loop, and the latter acts on the inner current loop to form a double closed-loop predictive control system, which uses i_d = 0 control strategy. Pulse width modulation control adopts space vector, and the designed control system is shown in Figure 1.

A simulation model is established to compare the control performance of dual prediction loop (MPC+DPC), single speed prediction loop (MPC) and dual PI loop. The main parameters of motor under simulation are shown in

Table 1. Main Parameters of PMSM.

Symbol	Quantity	Value
Rs	phase resistance	4 Ω
L	dq-axis inductance	11.6 mH
Ψf	rotor flux	0.1827 Wb
J	rotational inertia	4.07 × 10−5 kg·m2
pn	pole pairs	4
Tn	rated torque	1.27 N·m
Kt	torque constant	0.48 (N·m)/A
Nn	rated speed	3000 r/min
Pn	rated power	0.4 kW
T	sampling time interval	10−4 s

.

When the given speed is 500 r/min under no-load conditions, the speed curves of three control strategies are shown in Figure 2. It can be seen that traditional PI controller has a large overshoot and a longer adjustment time, while MPC and MPC+DPC controller has no overshoot. The comparison speed curves at start show that when MPC and MPC+DPC controller are adopted, the adjustment time and rise time are significantly reduced. It is obvious from the comparison speed curves at steady-state that under the traditional PI and single MPC controller, the speed error is larger than that of the MPC+DPC controller, and the steady-state accuracy is lower. Therefore, the MPC+DPC controller has better dynamic and steady-state performance.

In order to further demonstrate the control performance, it is necessary to consider the influence of load changes. Therefore, a load simulation experiment is carried out. When the given speed is 500 r/min, the motor starts at no load, and a load of 1 Nm is suddenly added at 0.1 s, which is removed at 0.2 s. Figure 3 shows the speed curves of different controllers. Specific speed comparison performance of the three control methods is shown in

Table 2. Comparison of three control methods.

Parameter	PI	MPC	MPC+DPC
Startup time(s)	0.015	0.004	0.004
Steady-state speed fluctuation (r/min)	−0.5~1.2	−0.4~0.3	−0.2~0.2
Load change (1 Nm) speed fluctuation (r/min)	80	25	10

. It can be seen that under the same load disturbance, the traditional PI controller has large fluctuations in speed, long adjustment time, and poor disturbance rejection performance. The speed fluctuation under the MPC controller is small, which can recover to the given speed faster. Under the MPC+DPC controller, the speed fluctuation is smaller, the recovery time is shorter, and the ability of disturbance rejection is stronger. Figure 4 shows the corresponding electromagnetic torque curves, and it can be seen that the electromagnetic torque under MPC controller and MPC+DPC controller can quickly track the load torque. The steady-state fluctuation of MPC+DPC controller is smaller and the accuracy is higher, indicating the higher robustness of the MPC+DPC controller.

3. Design of the Disturbance Observer

3.1. Parameter Mismatch Analysis

From the current DPC model, the actual current values i_d(k + 1) and i_q(k + 1) at the next moment under the actual motor parameters can be calculated as follows:

$$\{\begin{array}{c}{u}_d(k)=\frac{L_0}{T}{i}_d(k+1)+(R_0-\frac{L_0}{T})i_d(k)-L_0{\omega }_e(k)i_q(k)\hfill \\ u_q(k)=\frac{L_0}{T}{i}_q(k+1)+(R_0-\frac{L_0}{T})i_q(k)+L_0{\omega }_e(k)i_d(k)+{\psi }_{f0}{\omega }_e(k)\hfill \end{array}$$

(19)

where L₀ is the actual inductance, R₀ is the actual resistance, and Ψ_f0 is the actual rotor flux linkage.

Actually, there is a gap between nameplate parameters and actual parameters. The equations under the nameplate parameters can be expressed as

$$\{\begin{array}{c}{u}_d(k)=\frac{L_{\mathrm{mod}}}{T}{i}_{{}_d}^{*}(k+1)+(R_{\mathrm{mod}}-\frac{L_{\mathrm{mod}}}{T})i_d(k)-L_{\mathrm{mod}}{\omega }_e(k)i_q(k)\hfill \\ u_q(k)=\frac{L_{\mathrm{mod}}}{T}{i}_{{}_q}^{*}(k+1)+(R_{\mathrm{mod}}-\frac{L_{\mathrm{mod}}}{T})i_q(k)+L_{\mathrm{mod}}{\omega }_e(k)i_d(k)+{\psi }_{f\mathrm{mod}}{\omega }_e(k)\hfill \end{array}$$

(20)

where L_mod is the nameplate inductance, R_mod is the nameplate resistance, and Ψ_fmod is the nameplate rotor flux linkage.

If the calculated voltage values of Equations (19) and (20) are equal, the error relationship equations between the actual current and the predicted current can be expressed as

$$\{\begin{array}{l}{i}_d(k+1)=\frac{L_{\mathrm{mod}}}{L_0}{i}_d^{*}(k+1)+\frac{\Delta RT-\Delta L}{L_0}{i}_d(k)-\frac{\Delta L}{L_0}T{\omega }_e(k)i_q(k)\\ i_q(k+1)=\frac{L_{\mathrm{mod}}}{L_0}{i}_q^{*}(k+1)+\frac{\Delta RT-\Delta L}{L_0}{i}_q(k)+\frac{\Delta L}{L_0}T{\omega }_e(k)i_d(k)+\frac{\Delta {\psi }_f}{L_0}T{\omega }_e(k)\end{array}$$

(21)

where $\Delta R=R_{\mathrm{mod}}-R_0$, $\Delta L=L_{\mathrm{mod}}-L_0$, $\Delta {\psi }_f={\psi }_{f\mathrm{mod}}-{\psi }_{f0}$.

Since T is very small, items related to T can be ignored in Equation (21). Performing Z transformation, one can get

$$\{\begin{array}{l}z{i}_d(z)=\frac{L_{\mathrm{mod}}}{L_0}z{i}_d^{*}(z)+\frac{-\Delta L}{L_0}{i}_d(z)\\ z{i}_q(z)=\frac{L_{\mathrm{mod}}}{L_0}z{i}_q^{*}(z)+\frac{-\Delta L}{L_0}{i}_q(z)\end{array}$$

(22)

Then, the transfer function between the predicted current value and the actual value can be expressed as

$$G_{dq}(z)=\frac{i_{dq}(z)}{i_{dq}^{*}(z)}=\frac{(L_{\mathrm{mod}}/L_0)z}{z+(L_{\mathrm{mod}}/L_0-1)}$$

(23)

It is obvious that there is a closed-loop pole z = 1 − L_mod/L₀ in the closed-loop transfer function. The closed-loop system can remain stable only if the pole is in the unit circle, so 0 < L_mod < 2L₀.

When the system is running in a steady-state, assuming i_d(k + 1) = i_d(k) and i_q(k + 1) = i_q(k), one can get

$$\{\begin{array}{l}{i}_d(k+1)=\frac{L_{\mathrm{mod}}}{L_{\mathrm{mod}}-T\Delta R}{i}_d^{*}(k+1)-\frac{\Delta L}{L_{\mathrm{mod}}-T\Delta R}T{\omega }_e(k)i_q(k)\\ i_q(k+1)=\frac{L_{\mathrm{mod}}}{L_{\mathrm{mod}}-T\Delta R}{i}_q^{*}(k+1)+\frac{\Delta L}{L_{\mathrm{mod}}-T\Delta R}T{\omega }_e(k)i_d(k)+\frac{\Delta {\psi }_f}{L_{\mathrm{mod}}-T\Delta R}T{\omega }_e(k)\end{array}$$

(24)

When only considering the influence of resistance parameters, combined with the system using i_d = 0, one can get

$$\{\begin{array}{l}{i}_d(k+1)-i_d^{*}(k+1)=\frac{T\Delta R}{L_0-T\Delta R}{i}_d^{*}(k+1)=0\\ i_q(k+1)-i_q^{*}(k+1)=\frac{T\Delta R}{L_0-T\Delta R}{i}_q^{*}(k+1)\end{array}$$

(25)

Then, the error of dq-axes currents is less affected by the resistance.

When only considering the influence of inductance parameters, one can get

$$\{\begin{array}{l}{i}_d(k+1)-i_d^{*}(k+1)=\frac{-\Delta L}{L_0+\Delta L}T{\omega }_e(k)i_q(k)\\ i_q(k+1)-i_q^{*}(k+1)={(\frac{\Delta L}{L_0+\Delta L}T{\omega }_e)}^2(k)i_q(k)\end{array}$$

(26)

Although the changes of T and inductance are small, ω_e may be very large, so the error of i_d current is greatly affected by the inductance.

When only considering the influence of rotor flux parameters, one can get

$$\{\begin{array}{l}{i}_d(k+1)-i_d^{*}(k+1)=0\\ i_q(k+1)-i_q^{*}(k+1)=\frac{\Delta {\psi }_f}{L_0}T{\omega }_e(k)\end{array}$$

(27)

Then, the error of the i_q current is proportional to the deviation of the rotor flux linkage and the speed, which is greatly affected by the rotor flux linkage.

In this paper, the influence of the resistor, inductance, and flux parameter mismatch on the static current error is deduced based on the current discrete equation, and the closed-loop transfer function between the predicted and actual current values in the discrete domain is used to obtain that the inductance should meet 0 < L_mod < 2L₀ to ensure the stability of the system.

From the above, the parameters mismatch will have a significant impact on the error of dq-axes currents. The disturbance observers are designed to compensate in the paper.

3.2. Design of Disturbing Sliding Mode Observer

The dq-axes stator voltage equations under actual parameters can be expressed as

$$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=L_0\left[\begin{array}{c}{\dot{i}}_d\\ {\dot{i}}_q\end{array}\right]+R_0\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_0{i}_q\\ {\omega }_e{L}_0{i}_d+{\omega }_e{\psi }_{f0}\end{array}\right]$$

(28)

When the motor parameters are disturbed, one can get

$$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=L_{\mathrm{mod}}\left[\begin{array}{c}{\dot{i}}_d\\ {\dot{i}}_q\end{array}\right]+R_{\mathrm{mod}}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_{\mathrm{mod}}{i}_q+m_d\\ {\omega }_e{L}_{\mathrm{mod}}{i}_d+{\omega }_e{\psi }_{f\mathrm{mod}}+m_q\end{array}\right]$$

(29)

$$\left[\begin{array}{c}{\dot{m}}_d\\ {\dot{m}}_q\end{array}\right]=\left[\begin{array}{c}{M}_d\\ M_q\end{array}\right]$$

(30)

where m_d and m_q are the compensation amounts of the dq-axes voltage vector when the motor parameters are disturbed, M_d and M_q are the differentials of m_d and m_q, which are close to zero.

Then, the compensation of voltage and the observation of current can be obtained as

$$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=L_{\mathrm{mod}}\left[\begin{array}{c}{\dot{\widehat{i}}}_d\\ {\dot{\widehat{i}}}_q\end{array}\right]+R_{\mathrm{mod}}\left[\begin{array}{c}{\widehat{i}}_d\\ {\widehat{i}}_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_{\mathrm{mod}}{i}_q+{\widehat{m}}_d+M_{ds}\\ {\omega }_e{L}_{\mathrm{mod}}{i}_d+{\omega }_e{\psi }_{f\mathrm{mod}}+{\widehat{m}}_q+M_{qs}\end{array}\right]$$

(31)

$$\left[\begin{array}{c}{\dot{\widehat{m}}}_d\\ {\dot{\widehat{m}}}_q\end{array}\right]=\left[\begin{array}{c}{k}_d{M}_{ds}\\ k_q{M}_{qs}\end{array}\right]$$

(32)

where ${\widehat{i}}_d$ and are the observed values of the dq-axes current, ${\widehat{m}}_d$ and ${\widehat{m}}_q$ are the observed values of the dq-axes voltage compensation, M_ds and M_qs are the sliding mode control functions of the dq-axes, k_d and k_q are the sliding mode coefficients, respectively.

By subtracting Equation (31) from Equation (29) and subtracting Equation (32) from Equation (30), one can get

$$\left[\begin{array}{c}\Delta {\dot{i}}_d\\ \Delta {\dot{i}}_q\end{array}\right]=-\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}\left[\begin{array}{c}\Delta i_d\\ \Delta i_q\end{array}\right]-\frac{1}{L_{\mathrm{mod}}}\left[\begin{array}{c}\Delta m_d-M_{ds}\\ \Delta m_q-M_{qs}\end{array}\right]$$

(33)

$$\left[\begin{array}{c}\Delta {\dot{m}}_d\\ \Delta {\dot{m}}_q\end{array}\right]=\left[\begin{array}{c}{M}_d-k_d{M}_{ds}\\ M_q-k_q{M}_{qs}\end{array}\right]$$

(34)

where $\{\begin{array}{c}\Delta i_d=i_d-{\widehat{i}}_d\\ \Delta i_q=i_d-{\widehat{i}}_q\end{array}$ are the difference between the actual values of the dq-axes current and the observed one, $\{\begin{array}{c}\Delta m_d=m_d-{\widehat{m}}_d\\ \Delta m_q=m_q-{\widehat{m}}_q\end{array}$ are the error between the actual values of the dq-axes compensation voltages and the observed values, respectively.

The sliding mode surface is selected as $\{\begin{array}{c}{s}_d=\Delta i_d\\ s_q=\Delta i_q\end{array}$. In order to obtain better observation results, the exponential reaching law is chosen to design the sliding mode control function, which can be expressed as

$$\frac{ds}{dt}=-\epsilon \mathrm{sgn}(s)-\lambda s \epsilon >0, \lambda >0$$

(35)

where $\epsilon$ and $\lambda$ are both reaching law parameters.

Substituting Equation (35) into Equations (33) and (34), one can get

$$\left[\begin{array}{c}{M}_{ds}\\ M_{qs}\end{array}\right]=\left[\begin{array}{c}(R_{\mathrm{mod}}-L_{\mathrm{mod}}{\lambda }_d)\Delta i_d--{\epsilon }_d{L}_{\mathrm{mod}}\mathrm{sgn}(\Delta i_d)+\Delta m_d\\ (R_{\mathrm{mod}}-L_{\mathrm{mod}}{\lambda }_q)\Delta i_q--{\epsilon }_q{L}_{\mathrm{mod}}\mathrm{sgn}(\Delta i_q)+\Delta m_q\end{array}\right]$$

(36)

Since Δm_d and Δm_q are included in the sliding mode control function, which can be ignored. Then, Equation (36) can be expressed as

$$\left[\begin{array}{c}{M}_{ds}\\ M_{qs}\end{array}\right]=\left[\begin{array}{c}(R_{\mathrm{mod}}-L_{\mathrm{mod}}{\lambda }_d)\Delta i_d--{\epsilon }_d{L}_{\mathrm{mod}}\mathrm{sgn}(\Delta i_d)\\ (R_{\mathrm{mod}}-L_{\mathrm{mod}}{\lambda }_q)\Delta i_q--{\epsilon }_q{L}_{\mathrm{mod}}\mathrm{sgn}(\Delta i_q)\end{array}\right]$$

(37)

In order to converge the disturbance compensation voltage error and current error and ensure the stability of the control system, it is necessary to analyze the stability of the designed sliding mode observer. According to the Lyapunov function, Equation (38) needs to be satisfied to achieve the reachability of the sliding mode surface.

$$\{\begin{array}{l}{s}_d\cdot {\dot{s}}_d=\Delta i_d\cdot \Delta {\dot{i}}_d\le 0\\ s_q\cdot {\dot{s}}_q=\Delta i_q\cdot \Delta {\dot{i}}_q\le 0\end{array}$$

(38)

Then, one can get

$$\{\begin{array}{c}\Delta i_d({\epsilon }_d\mathrm{sgn}(\Delta i_d)+\Delta m_d/L_{\mathrm{mod}})\ge 0\\ \Delta i_q({\epsilon }_q\mathrm{sgn}(\Delta i_q)+\Delta m_q/L_{\mathrm{mod}})\ge 0\end{array}$$

(39)

The range of ${\epsilon }_d$ and ${\epsilon }_q$ can be expressed as

$$\{\begin{array}{c}{\epsilon }_d>\frac{\left|\Delta m_d\right|}{L_{\mathrm{mod}}}\\ {\epsilon }_q>\frac{\left|\Delta m_q\right|}{L_{\mathrm{mod}}}\end{array}$$

(40)

When Equation (40) is satisfied, the system can reach the sliding mode surface. Then, the errors between the observed and actual values of the dq-axes currents and the errors between their derivatives can all converge to zero, one can get

$$\{\begin{array}{c}\underset{s\to 0}{\lim }\Delta i_{dq}=0\\ \underset{s\to 0}{\lim }\Delta {\dot{i}}_{dq}=0\end{array}$$

(41)

Then, Equations (33) and (34) can be simplified as

$$\left[\begin{array}{c}{M}_d\\ M_q\end{array}\right]=\left[\begin{array}{c}\Delta {\dot{m}}_d+k_d\Delta m_d\\ \Delta {\dot{m}}_q+k_q\Delta m_q\end{array}\right]$$

(42)

Solving Equation (42), one can get

$$\left[\begin{array}{c}\Delta m_d\\ \Delta m_q\end{array}\right]=\left[\begin{array}{c}{e}^{-k_{d}t}(A-\int M_d{e}^{k_{d}t}dt)\\ e^{-k_{q}t}(A-\int M_q{e}^{k_{q}t}dt)\end{array}\right]$$

(43)

When both k_d and k_q are greater than zero, Δm_d and Δm_d can approach zero at a steady state. The reasonable selection of the above parameters can ensure the stability of the designed observer.

The sliding mode observer for dq-axes voltage compensation and current when considering parameter disturbance can be expressed as

$$\{\begin{array}{c}\begin{array}{ll}{\widehat{i}}_d(k+1)=\hfill & (1-\frac{R_{\mathrm{mod}}T}{L_{\mathrm{mod}}}){\widehat{i}}_d(k)+T{\omega }_e(k)i_q(k)\hfill \\ & -\frac{T}{L_{\mathrm{mod}}}[{\widehat{m}}_d(k)+M_{ds}(k)-u_d(k)]\hfill \end{array}\hfill \\ {\widehat{m}}_d(k+1)=k_{d}T{M}_{ds}(k)+{\widehat{m}}_d(k)\hfill \end{array}$$

(44)

$$\{\begin{array}{c}\begin{array}{ll}{\widehat{i}}_q(k+1)=\hfill & (1-\frac{R_{\mathrm{mod}}T}{L_{\mathrm{mod}}}){\widehat{i}}_q(k)-T{\omega }_e(k)i_d(k)\hfill \\ & -\frac{T}{L_{\mathrm{mod}}}[{\psi }_{f\mathrm{mod}}{\omega }_e(k)+{\widehat{m}}_q(k)+M_{qs}(k)-u_q(k)]\hfill \end{array}\hfill \\ {\widehat{m}}_q(k+1)=k_{q}T{M}_{qs}(k)+{\widehat{m}}_q(k)\hfill \end{array}$$

(45)

Then, the dq-axes voltage vector can be expressed as

$$\{\begin{array}{l}{u}_d^{\prime }(k)=u_d(k)+{\widehat{m}}_d(k+1)\\ u_q^{\prime }(k)=u_q(k)+{\widehat{m}}_q(k+1)\end{array}$$

(46)

3.3. Design of Disturbing Internal Mode Observer

When the motor parameters are disturbed, the error term can be expressed as

$$\left[\begin{array}{c}{m}_d\\ m_q\end{array}\right]=\left[\begin{array}{c}\Delta L{\dot{i}}_d+\Delta R{i}_d-\Delta L{\omega }_e{i}_q\\ \Delta L{\dot{i}}_q+\Delta R{i}_q+\Delta L{\omega }_e{i}_d+\Delta {\psi }_f{\omega }_e\end{array}\right]$$

(47)

According to Equation (34), the state observation equation can be constructed as

$$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=L_{\mathrm{mod}}\left[\begin{array}{c}{\dot{\widehat{i}}}_d\\ {\dot{\widehat{i}}}_q\end{array}\right]+R_{\mathrm{mod}}\left[\begin{array}{c}{\widehat{i}}_d\\ {\widehat{i}}_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_{\mathrm{mod}}{i}_q+{\widehat{m}}_d\\ {\omega }_e{L}_{\mathrm{mod}}{i}_d+{\omega }_e{\psi }_{f\mathrm{mod}}+{\widehat{m}}_q\end{array}\right]$$

(48)

The error variables that define the actual value and the observed value are as follows:

$$\{\begin{array}{l}\Delta i_d=i_d-{\widehat{i}}_d\\ \Delta i_q=i_q-{\widehat{i}}_q\end{array},\{\begin{array}{l}\Delta m_d=m_d-{\widehat{m}}_d\\ \Delta m_q=m_q-{\widehat{m}}_q\end{array}$$

(49)

Subtracting Equation (48) from Equation (29), the error state equation can be expressed as

$$\left[\begin{array}{c}\Delta {\dot{i}}_d\\ \Delta {\dot{i}}_q\end{array}\right]=-\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}\left[\begin{array}{c}\Delta i_d\\ \Delta i_q\end{array}\right]-\frac{1}{L_{\mathrm{mod}}}\left[\begin{array}{c}\Delta m_d\\ \Delta m_q\end{array}\right]$$

(50)

According to the derivation of the first line in Equation (50), a new state equation can be constructed as

$$\left[\begin{array}{c}\Delta {\dot{i}}_d\\ \Delta {\ddot{i}}_d\end{array}\right]=\overrightarrow{A}\left[\begin{array}{c}\Delta i_d\\ \Delta {\dot{i}}_d\end{array}\right]+\overrightarrow{B}\Delta {\dot{m}}_d$$

(51)

where $\overrightarrow{A}=\left[\begin{array}{cc}0& 1\\ 0& -\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}\end{array}\right]$, $\overrightarrow{B}=\left[\begin{array}{c}0\\ -\frac{1}{L_{\mathrm{mod}}}\end{array}\right]$.

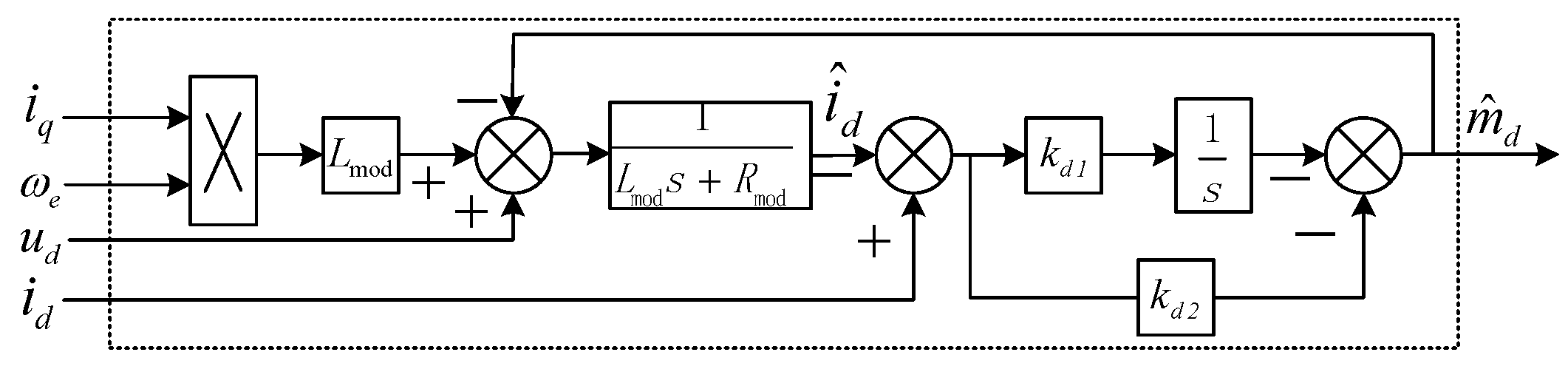
Because of $rank\left[\begin{array}{cc}\overrightarrow{B}& \overrightarrow{A}\overrightarrow{B}\end{array}\right]=2$, the system is completely controllable. According to the principle of state feedback, state feedback control can be realized. Let $\Delta {\dot{m}}_d=\overrightarrow{K}\left[\begin{array}{c}\Delta i_d\\ \Delta {\dot{i}}_d\end{array}\right]$, where $\overrightarrow{K}=\left[\begin{array}{cc}{k}_{d1}& k_{d2}\end{array}\right]$, k_d1 and k_d2 are the parameters to be optimized in the observer. Then, there is $\Delta {\dot{m}}_d=k_{d1}\Delta i_d+k_{d2}\Delta {\dot{i}}_d$.

Since the sampling period is very small, it can be assumed that the d-axis disturbance compensation voltage value remains unchanged within a sampling period, which means ${\dot{m}}_d=0$.

The derivative of the estimated d-axis disturbance compensation voltage value can be expressed as

$${\dot{\widehat{m}}}_d=-k_{d1}\Delta i_d-k_{d2}\Delta {\dot{i}}_d$$

(52)

Let its characteristic equation $\det [s\overrightarrow{I}-(\overrightarrow{A}+\overrightarrow{B}\overrightarrow{K})]$ = 0 and one can get

$$s^2+\frac{R_{\mathrm{mod}}+k_{d2}}{L_{\mathrm{mod}}}s+\frac{k_{d1}}{L_{\mathrm{mod}}}=0$$

(53)

Let the expected poles of the observer be x_d1 and x_d2, then the values of k_d1 and k_d2 can be obtained as

$$\{\begin{array}{l}{k}_{d1}=x_{d1}{x}_{d2}{L}_{\mathrm{mod}}\\ k_{d2}=-R_{\mathrm{mod}}-(x_{d1}+x_{d2})L_{\mathrm{mod}}\end{array}$$

(54)

According to Equations (48) and (52), the d-axis disturbance compensation voltage observer equation can be expressed as

$$\{\begin{array}{c}{\dot{\widehat{i}}}_d=-\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}{\widehat{i}}_d+\frac{u_d}{L_{\mathrm{mod}}}+{\omega }_e{i}_q-\frac{{\widehat{m}}_d}{L_{\mathrm{mod}}}\hfill \\ {\dot{\widehat{m}}}_d=-k_{d1}(i_d-{\widehat{i}}_d)-k_{d2}({\dot{i}}_d-{\dot{\widehat{i}}}_d)\hfill \end{array}$$

(55)

Then, by Laplace transform performing, Equation (55) can be transformed into

$$\{\begin{array}{c}s{\widehat{i}}_d(s)=-\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}{\widehat{i}}_d(s)+\frac{u_d(s)}{L_{\mathrm{mod}}}+{\omega }_e(s)i_q(s)-\frac{{\widehat{m}}_d(s)}{L_{\mathrm{mod}}}\hfill \\ s{\widehat{m}}_d(s)=-k_{d1}[i_d(s)-{\widehat{i}}_d(s)]-k_{d2}[s{i}_d(s)-s{\widehat{i}}_d(s)]\hfill \end{array}$$

(56)

The observer structure can be designed as shown in Figure 5. It can be seen that the control quantity of the observer is obtained in the form of integration and proportion, and the compensation control effect is excellent.

Assuming that the sampling period T is small, the differential term can be approximated by difference, so Equation (55) can be discretized, one can obtain

$$\{\begin{array}{c}{\widehat{i}}_d(k+1)=(1-\frac{R_{\mathrm{mod}}T}{L_{\mathrm{mod}}}){\widehat{i}}_d(k)+\frac{T}{L_{\mathrm{mod}}}{u}_d(k)\hfill \\ +T{\omega }_e(k)i_q(k)-\frac{T}{L_{\mathrm{mod}}}{\widehat{m}}_d(k)\\ {\widehat{m}}_d(k+1)={\widehat{m}}_d(k)+(k_{d2}-k_{d1}T)[i_d(k)-{\widehat{i}}_d(k)]\hfill \\ -k_{d2}[i_d(k+1)-{\widehat{i}}_d(k+1)]\end{array}$$

(57)

Then, the d-axis voltage vector can be expressed as

$$u_d^{\prime }(k)=u_d(k)+{\widehat{m}}_d(k+1)$$

(58)

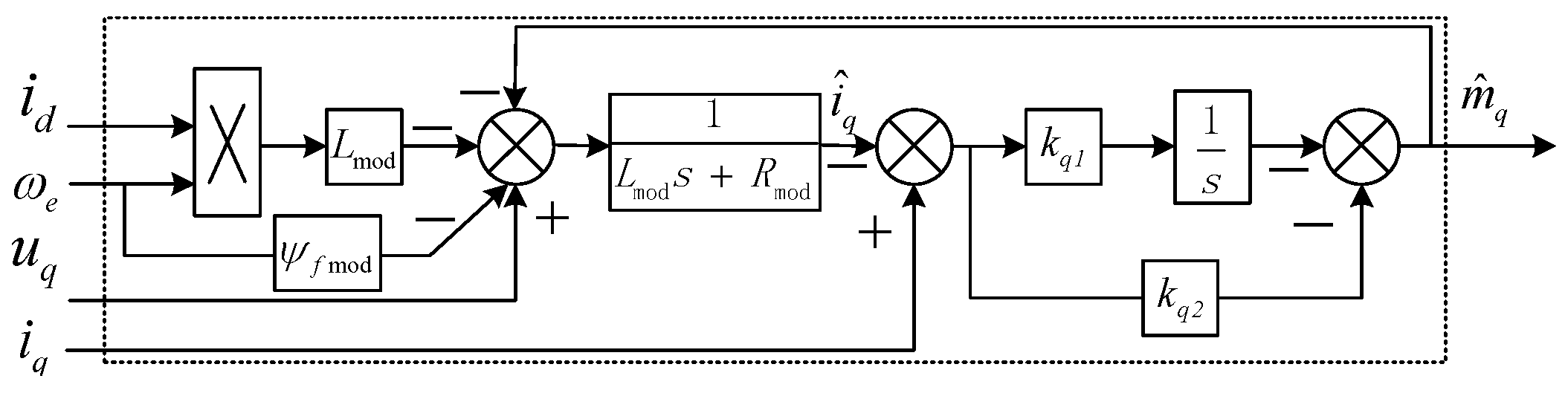
Similar to the construction method of the d-axis disturbance observer, the q-axis parameter disturbance compensation voltage observer equation can be obtained as

$$\{\begin{array}{c}{\dot{\widehat{i}}}_q=-\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}{\widehat{i}}_q+\frac{u_q}{L_{\mathrm{mod}}}-\frac{{\widehat{m}}_q+L_{\mathrm{mod}}{\omega }_e{i}_d+{\omega }_e{\psi }_{f\mathrm{mod}}}{L_{\mathrm{mod}}}\hfill \\ {\dot{\widehat{m}}}_q=-k_{q1}(i_q-{\widehat{i}}_q)-k_{q2}({\dot{i}}_q-{\dot{\widehat{i}}}_q)\hfill \end{array}$$

(59)

Then, by Laplace transform performing, (59) can be transformed into

$$\{\begin{array}{c}s{\widehat{i}}_q(s)= -\frac{R_{\mathrm{mod}}}{L_{\mathrm{mod}}}{\widehat{i}}_q(s)+ \frac{u_q(s)}{L_{\mathrm{mod}}}-\frac{{\widehat{m}}_q(s)+L_{\mathrm{mod}}{\omega }_e(s)i_d(s)+{\psi }_{f\mathrm{mod}}{\omega }_e(s)}{L_{\mathrm{mod}}}\hfill \\ s{\widehat{m}}_q(s)=-k_{q1}[i_q(s)-{\widehat{i}}_q(s)]-k_{q2}[s{i}_q(s)-s{\widehat{i}}_q(s)]\hfill \end{array}$$

(60)

The observer can be designed as shown in Figure 6.

Assuming that the sampling period T is small, the differential term can be approximated by difference, so Equation (59) can be discretized, one can get

$$\{\begin{array}{cc}{\widehat{i}}_q(k+1)=\hfill & (1-\frac{R_{\mathrm{mod}}T}{L_{\mathrm{mod}}}){\widehat{i}}_q(k)+\frac{T}{L_{\mathrm{mod}}}{u}_q(k)\hfill \\ & -T{\omega }_e(k)i_d(k)-\frac{T[{\psi }_{f\mathrm{mod}}{\omega }_e(k)+{\widehat{m}}_q(k)]}{L_{\mathrm{mod}}}\hfill \\ {\widehat{m}}_q(k+1)=\hfill & {\widehat{m}}_q(k)+(k_{q2}-k_{q1}T)[i_q(k)-{\widehat{i}}_q(k)]\hfill \\ & -k_{q2}[i_q(k+1)-{\widehat{i}}_q(k+1)]\hfill \end{array}$$

(61)

Then, the q-axis voltage vector can be expressed as

$$u_q^{\prime }(k)=u_q(k)+{\widehat{m}}_q(k+1)$$

(62)

3.4. Simulation Analysis

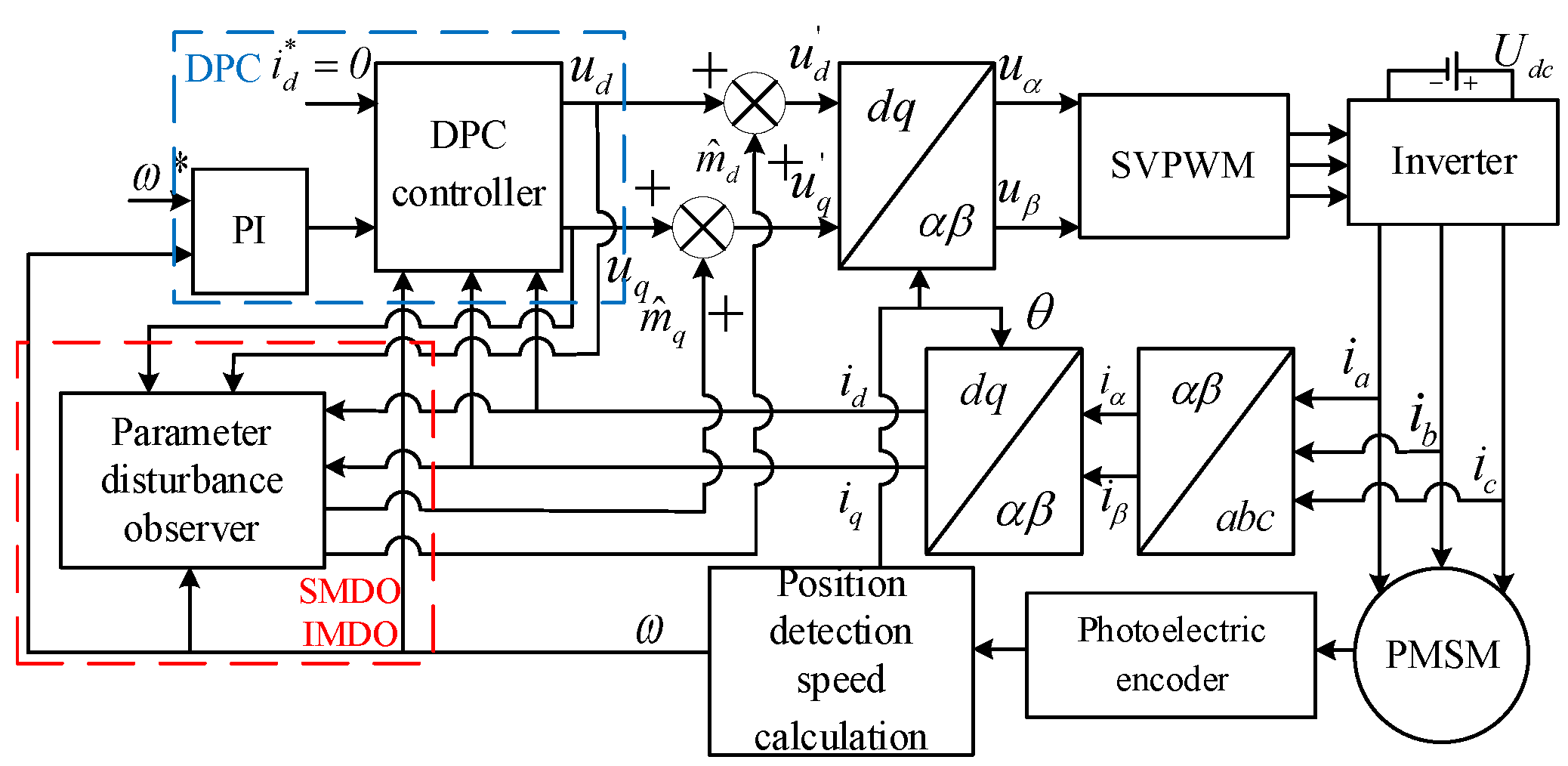
The deadbeat current predictive control system based on parameter disturbance observer is shown in Figure 7. Simulation models of parameter disturbance sliding mode observer and internal model observer are built to verify whether the proposed parameter disturbance observer can improve the control performance of PMSM under the condition of motor parameter mismatch. From the aspects of resistance mismatch, inductance mismatch, rotor flux mismatch, and various motor parameter mismatch, the performance of predictive control with disturbance observer and traditional predictive control on the static error of dq-axes currents is compared.

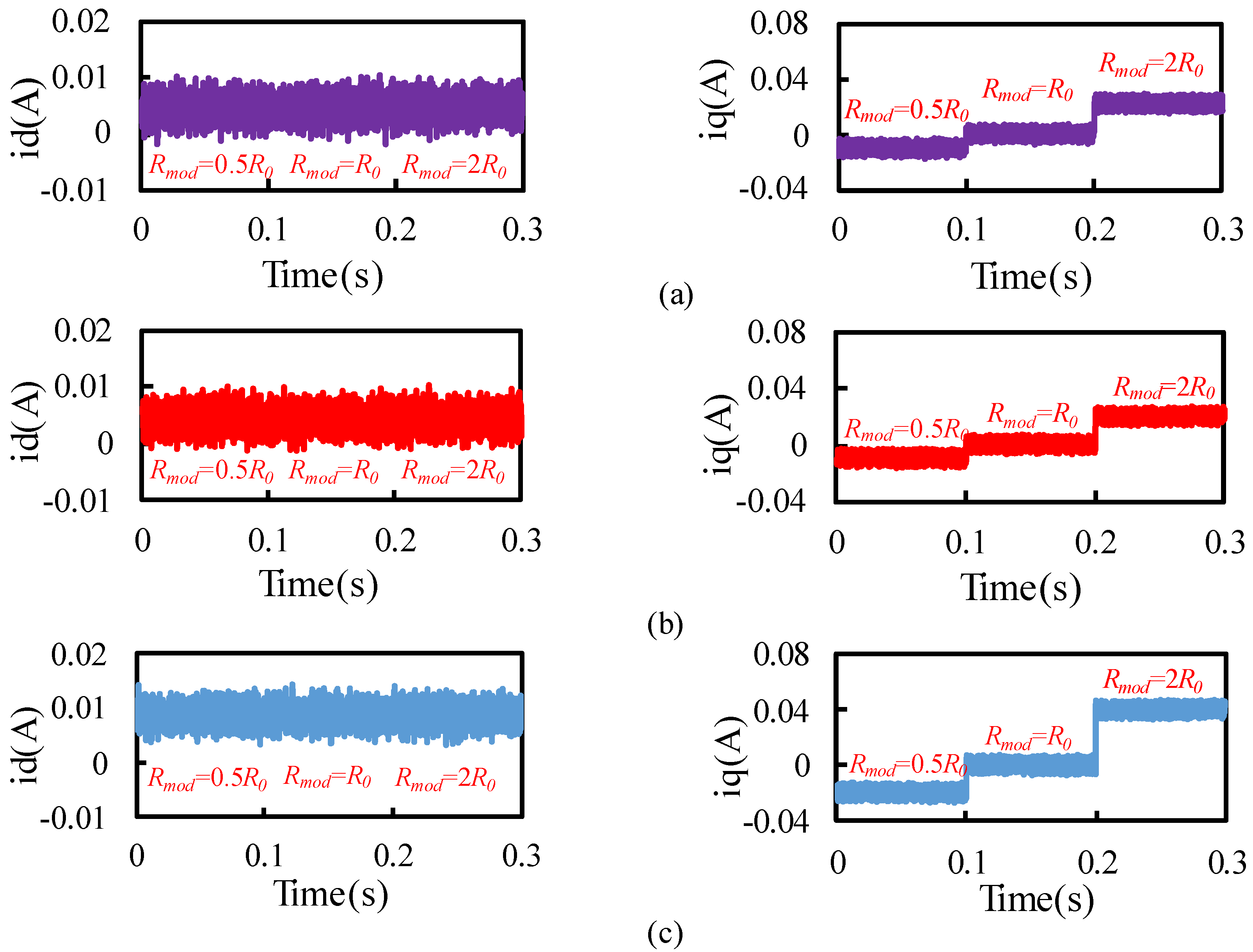
Assuming that the nominal and actual values of the inductance and rotor flux linkage are equal, the error of the dq-axes currents is affected by the mismatch of motor resistance parameter. The nominal value of the resistance is set to be 0.5, 1, and 2 times of the actual value. The results are shown in Figure 8. It can be seen that the i_d current error is almost not affected by the resistance change. When the nominal resistance and the actual resistance are greater, the i_q current static error is also larger, which is consistent with the theoretical analysis result. After the disturbance observer is added, the static error between i_d and i_q currents is significantly reduced.

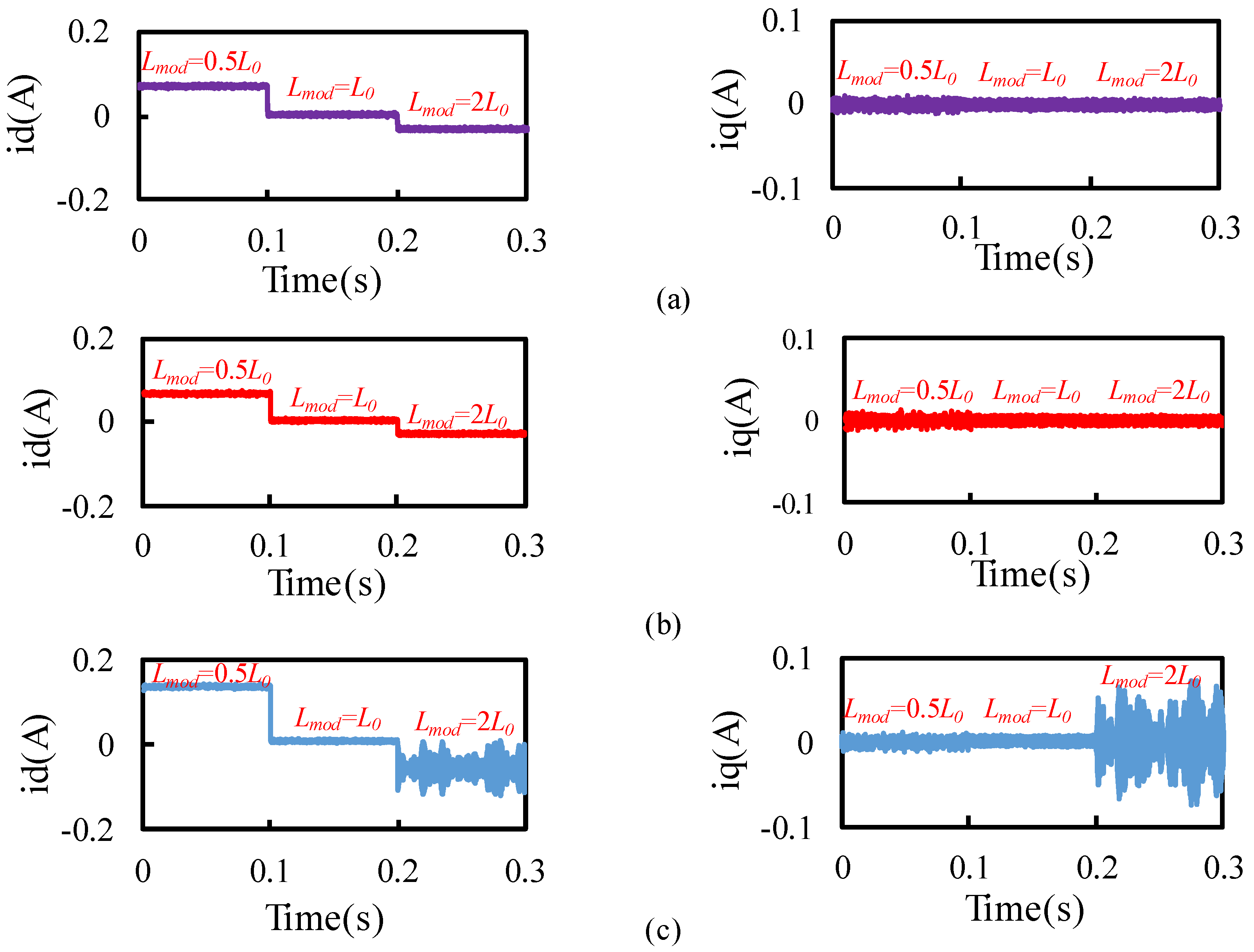
When only considering the error of the dq-axes currents due to the mismatch of the inductance parameter, the results are shown in Figure 9. It can be seen that in the stable range, the i_d current error is greatly affected by the inductance change, and the i_q current error is almost unaffected, and when the nominal inductance is twice of the actual value, the system begins to be unstable. After adding the disturbance observer, the i_d and i_q current errors are significantly reduced, the system is not unstable, and the current error under the internal model disturbance observer is smaller.

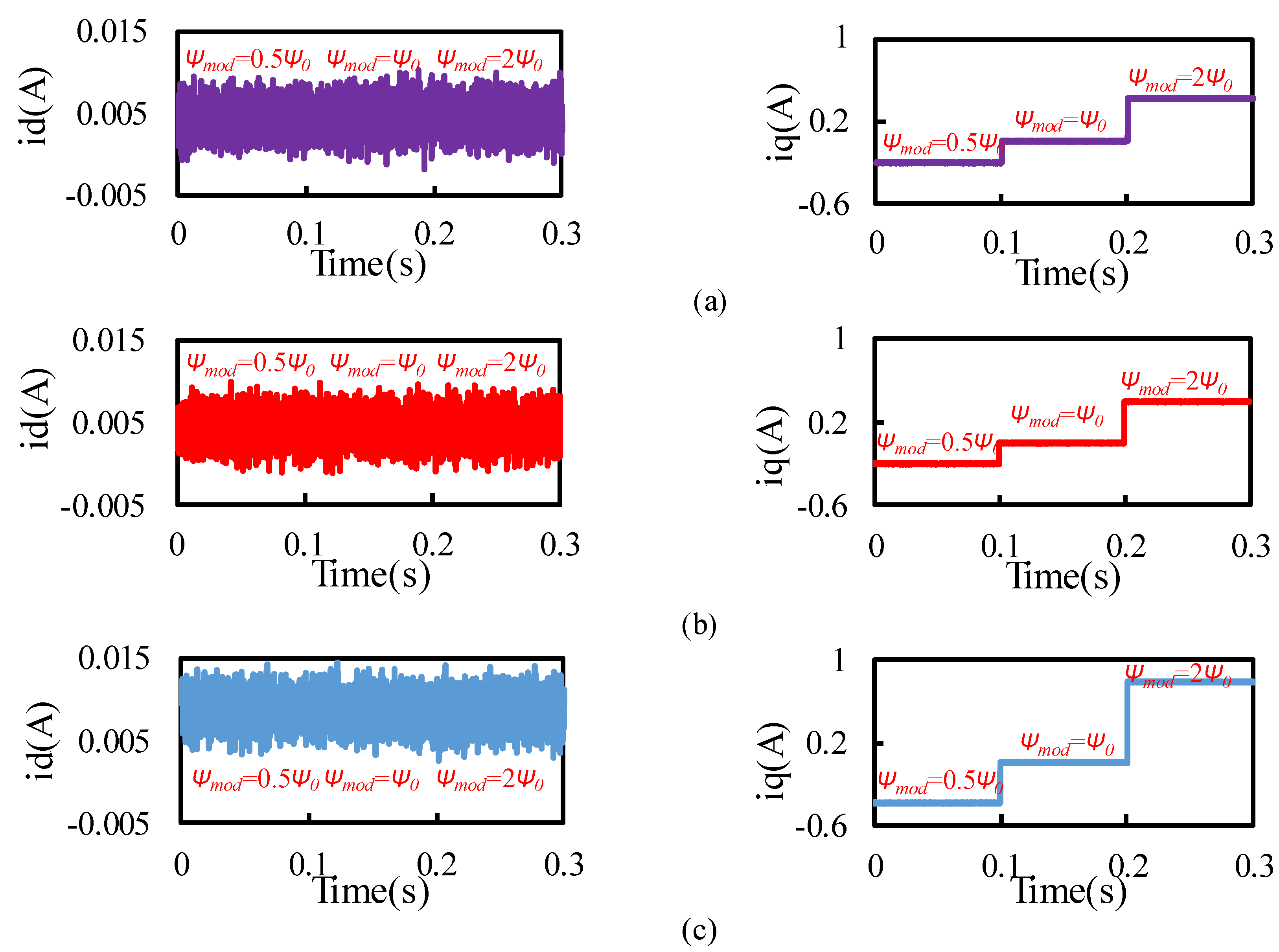
When only considering the error of the dq-axes currents due to the mismatch of the flux linkage parameter, the results are shown in Figure 10. It can be seen that the i_d current error is almost unaffected by the flux linkage change, and the i_q current static error is greatly affected by the flux linkage change. When the error between the nominal flux linkage value and the actual value is larger, the i_q current error value is also greater. After adding the disturbance observer, the i_d and i_q current errors are obviously improved, and the current error under the internal model disturbance observer is smaller. Figure 8, Figure 9 and Figure 10 are summarized in

Table 3. Comparison of current tracking performance.

Value	Parameter	DPC		DPC+SMDO		DPC+IMDO
		id(A)	iq(A)	id(A)	iq(A)	id(A)	iq(A)
Rmod	0.5R0	0.008 ± 0.0054	−0.02 ± 0.006	0.0042 ± 0.0052	−0.01 ± 0.006	0.004 ± 0.0051	−0.011 ± 0.006
	R0		±0.006		±0.006		±0.006
	2R0		0.04 ± 0.006		0.025 ± 0.006		0.02
Lmod	0.5L0	0.15 ± 0.004	±0.075	0.06 ± 0.004	±0.073	0.058 ± 0.004	±0.074
	L0	±0.004		±0.004		±0.004
	2L0	0.05 ± 0.004	±0.1 ± 0.005	0.03 ± 0.004		−0.28 ± 0.004
ψmod	0.5Ψ0	0.008 ± 0.005	−0.39	0.0045 ± 0.004	−0.21 ± 0.005	0.004 ± 0.0042	−0.2 ± 0.005
	Ψ0		±0.005		±0.005		±0.005
	2Ψ0		0.79 ± 0.005		0.415 ± 0.005		0.392 ± 0.005

, and the current fluctuation range under parameter mismatch is given. It can be seen from the figure and table that the static errors of dq axes are consistent with the theoretical analysis of Section 3.1, and the influence of parameters on current static errors can be reduced by adding the observer. In addition, the performance of IMDO is better than that of SMDO.

4. Experimental Verification

In order to verify the effectiveness and feasibility of the proposed predictive control system, an experimental platform and the hardware circuit platform are built as shown in Figure 11, which consist of a microcontroller unit TMS320F28335, some circuits, and some power supplies, etc. The speed servo system experimental control platform is set up, and the DPC controller is compared with the traditional PI controller, the controller parameters of which are manually fine-tuned from the simulated parameters.

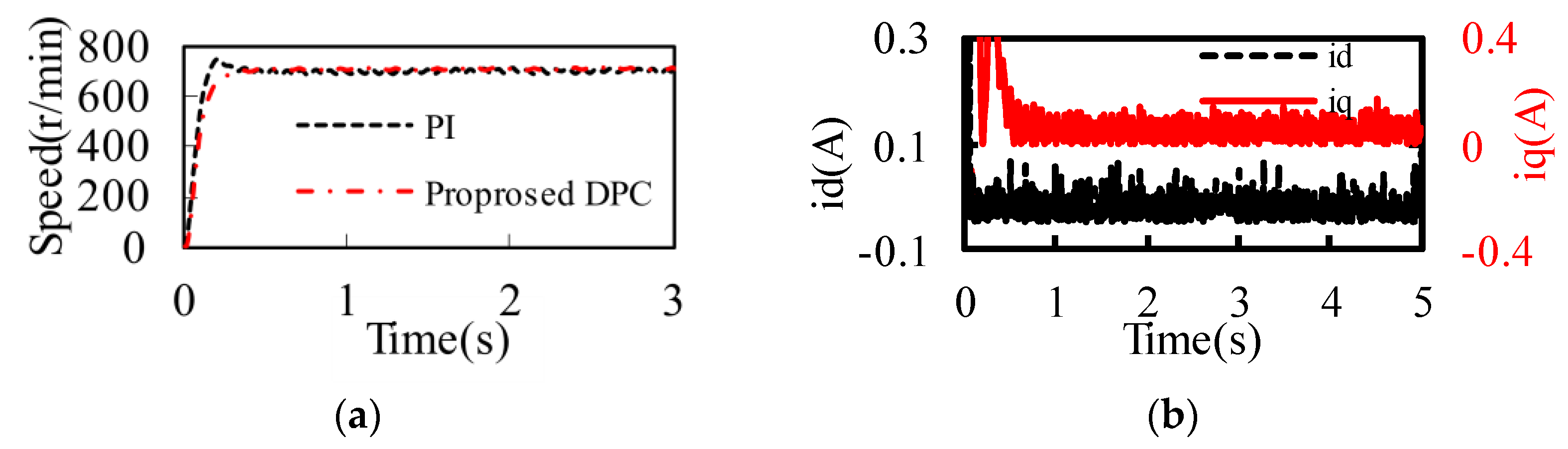
When the given reference speed is 700 r/min, Figure 12a shows the comparison of the speeds under the two control strategies. It can be seen that, compared with the traditional PI controller, the DPC controller has a faster speed response, the system does not overshoot, and the steady-state speed error is smaller, indicating that the DPC controller has better dynamic and steady-state control performance. Figure 12b shows the dq-axes current, and it can be seen that the i_q current will increase temporarily during the motor startup stage, but when the motor is stable, the i_q current almost remains unchanged, indicating that the system has a fast response speed and good dynamic performance.

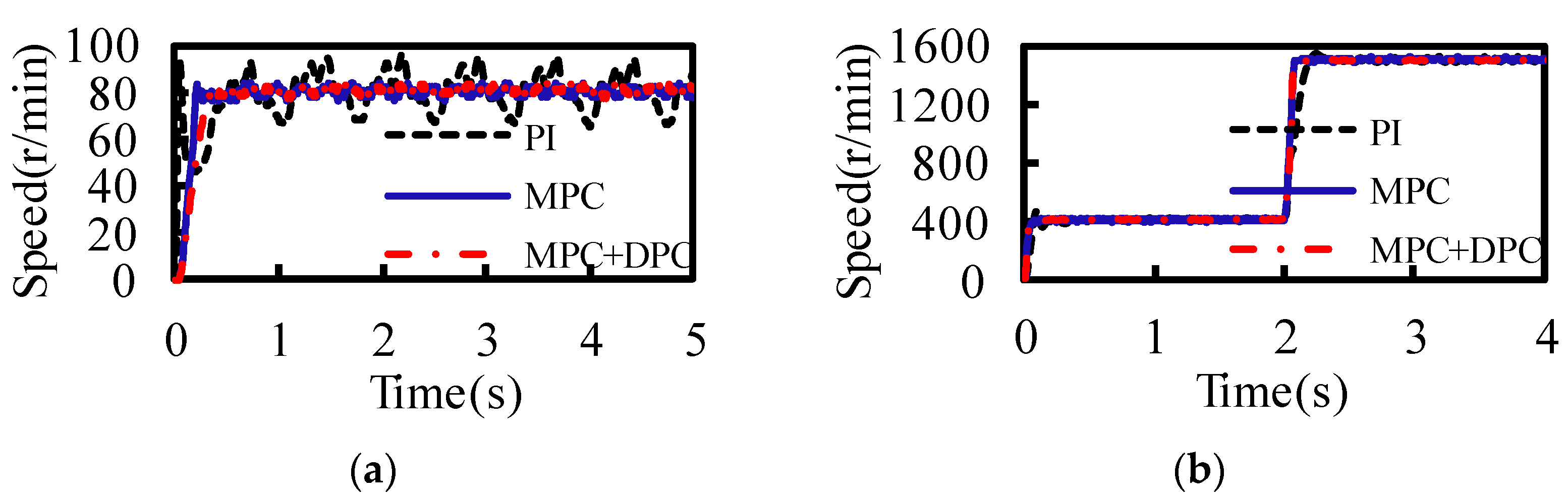
When the given reference speed is 80 r/min, the difference in control performance of the two control algorithms at low speed is considered. Figure 13a shows the speed comparison under the three control strategies, and the speed fluctuates significantly compared with the previous high-speed conditions, mainly due to the influence of factors such as cogging torque. The PI control has a severe overshoot, initial velocity has reached 90 r/min. However, compared with the PI controller, the overshoot of conventional DPC becomes smaller, and the steady-state error is reduced from ±9 r/min to ±4 r/min. The proposed DPC has almost no overshoot and the steady-state speed error is ±3 r/min, which can effectively reduce the steady-state error, indicating that the proposed DPC controller has better control performance, high control accuracy, and excellent wide speed adjustment capability.

In order to test the speed regulation performance of the control system, the reference speed is set to be initially 400 r/min, suddenly increases to 1500 r/min at 2 s. The comparison response of the speed under the three control algorithms is shown in Figure 13b. It can be seen that speed can track the given speed under the three control strategies, but compared with the traditional PI controller, the conventional DPC controller has no overshoot of the speed fluctuation and start-up response time is 0.34 s, and the steady-state error is reduced from ±12 r/min to ±9 r/min. Moreover, the proposed MPC in this paper can reduce the speed fluctuation more effectively, the steady-state error is reduced to ±7 r/min, and the speed regulation performance and the robustness are strong.

5. Conclusions

This paper has successfully proposed a double closed-loop predictive control scheme for permanent-magnet synchronous motor system, which consists of a speed loop MPC and a current loop DPC. In particular, when the load is suddenly applied at 500 r/min, the motor speed fluctuation is reduced to 10 r/min by using double loop predictive control. Aiming at the influence of motor parameter mismatch on control performance, based on the principles of internal model control and sliding mode control, two parameter disturbance observers are designed, which achieve accurate speed tracking of the servo motor. The simulation results show that the improved control strategy can improve the dq axis current static error when the resistance inductance and flux mismatch, and the current static error of the internal model disturbance observer is smaller. Experimental results show that the proposed control strategy has better dynamic and steady-state performance.