Analysis of Crowded Propagation on the Metro Network
Abstract
:1. Introduction
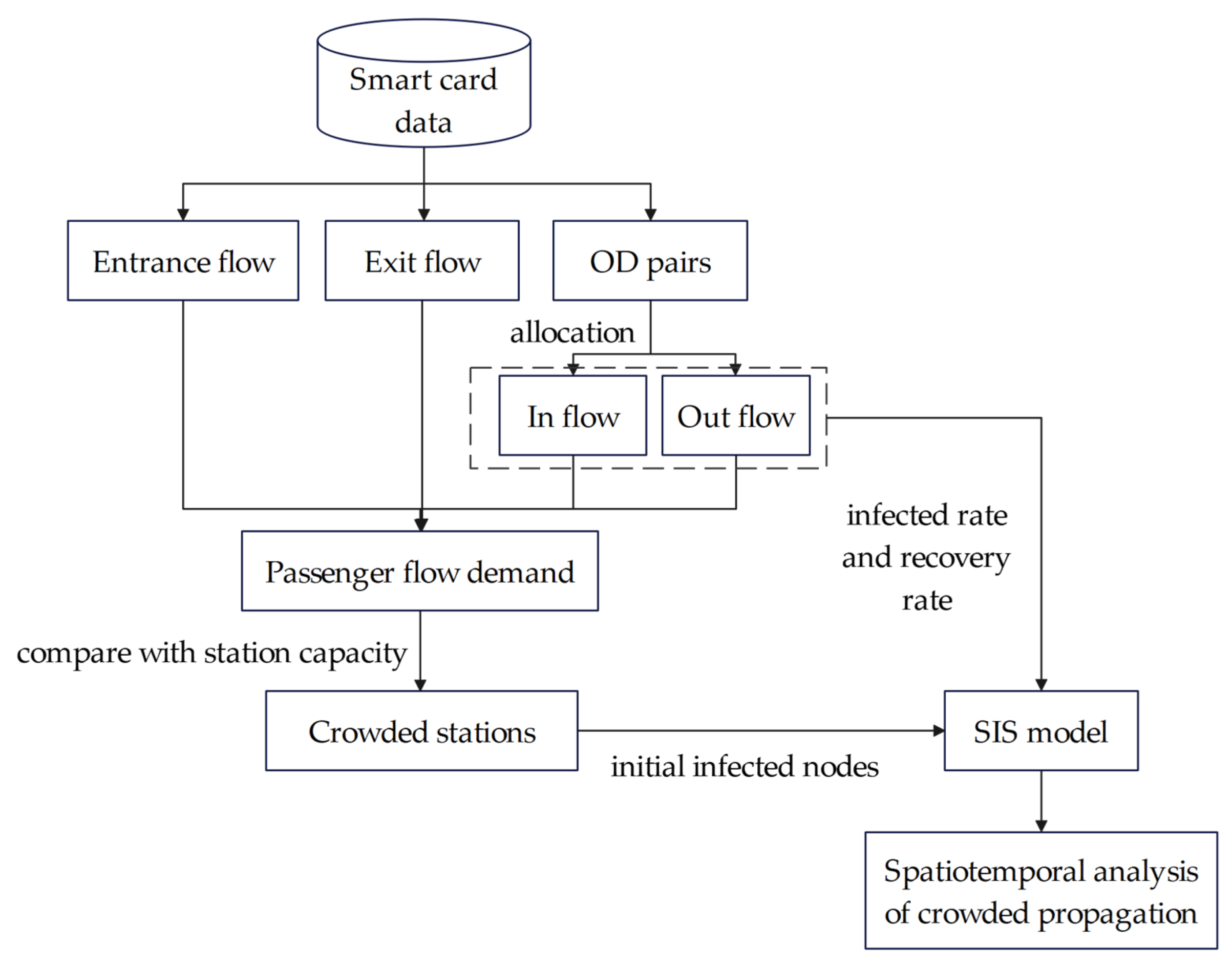
2. Materials and Methods
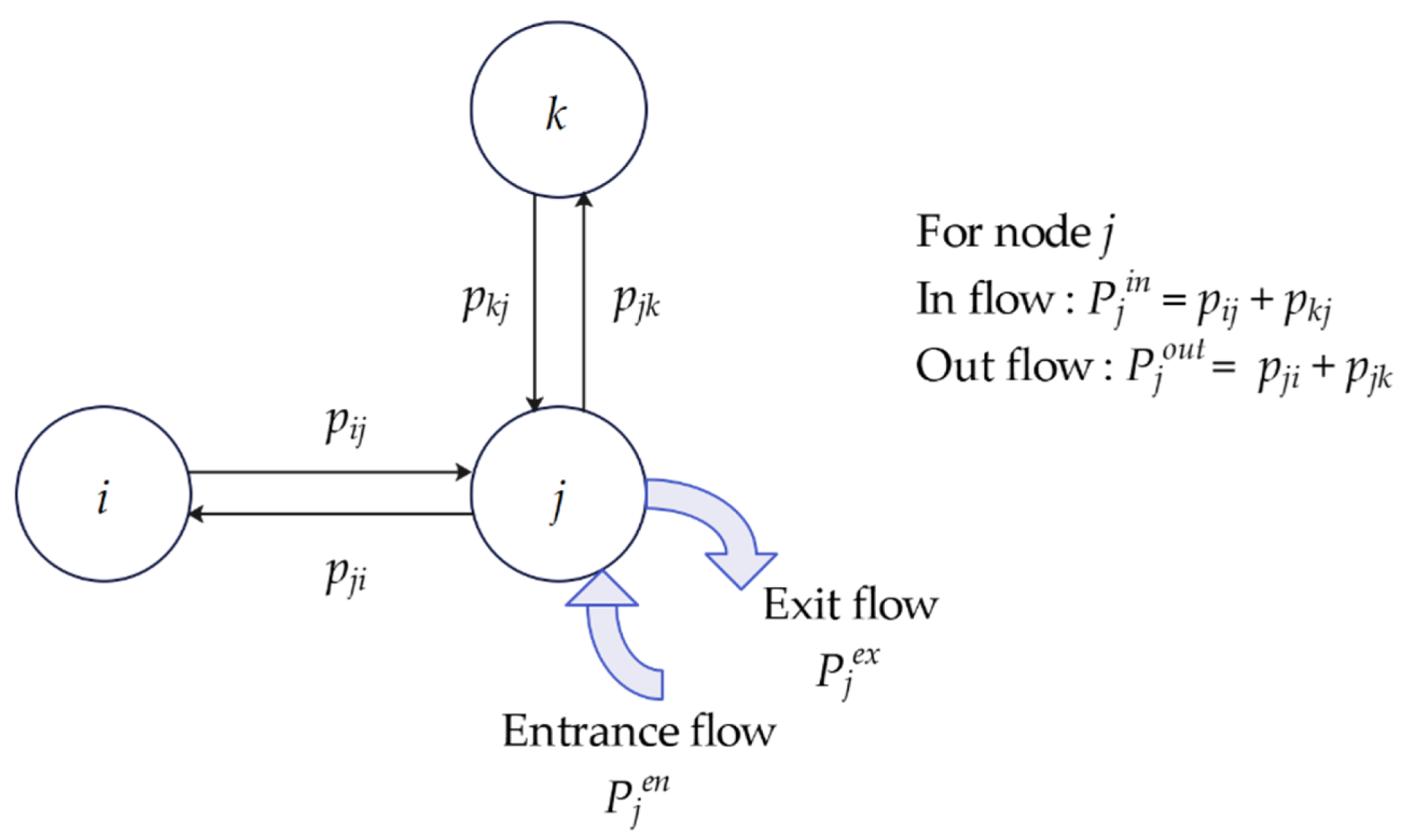
2.1. Notations and Definitions
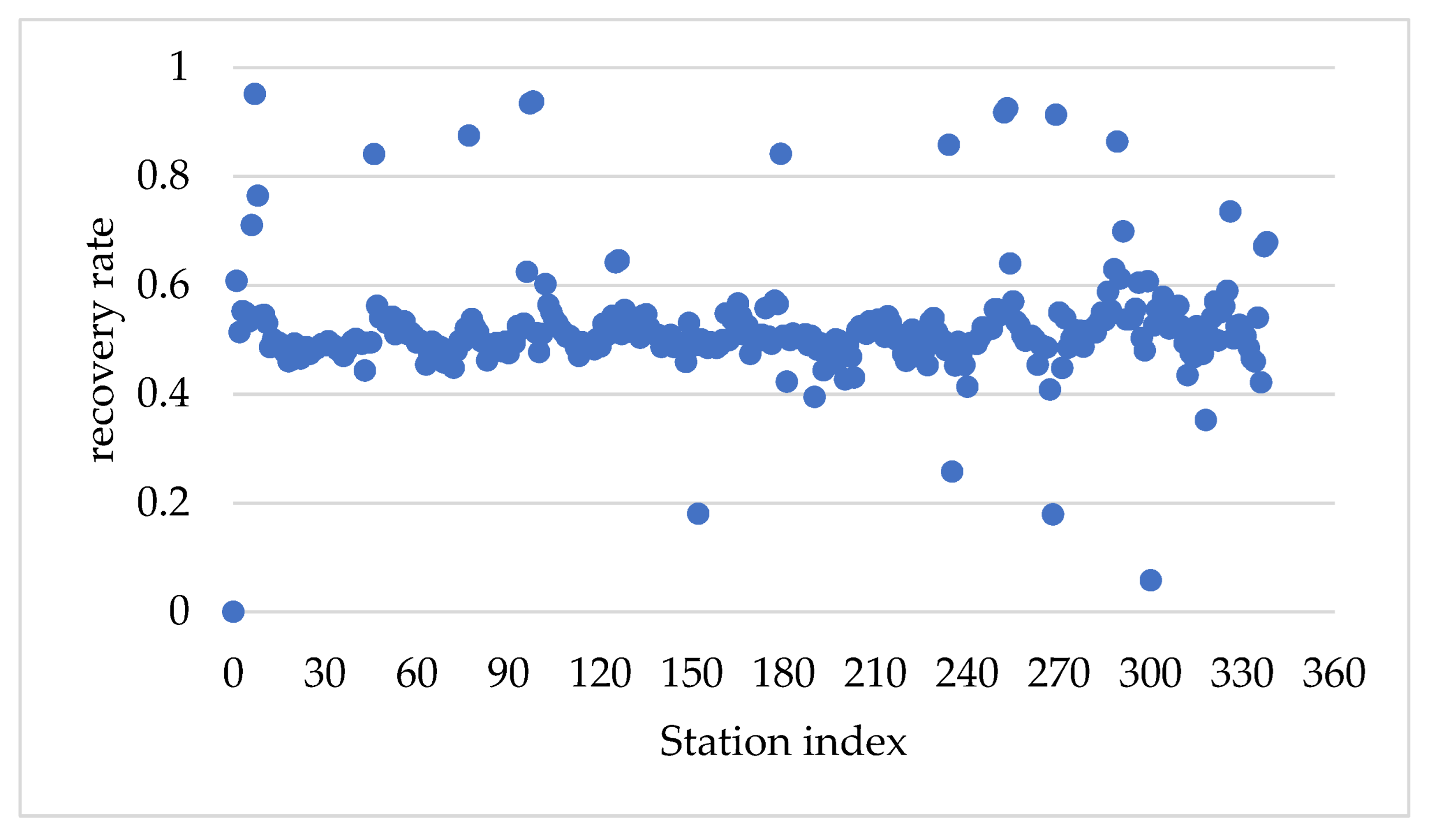
2.2. Passenger Flow Allocation
2.3. Passenger Flow Propagation Based on SIS Model
3. Experiment and Results
3.1. The Initial Setting
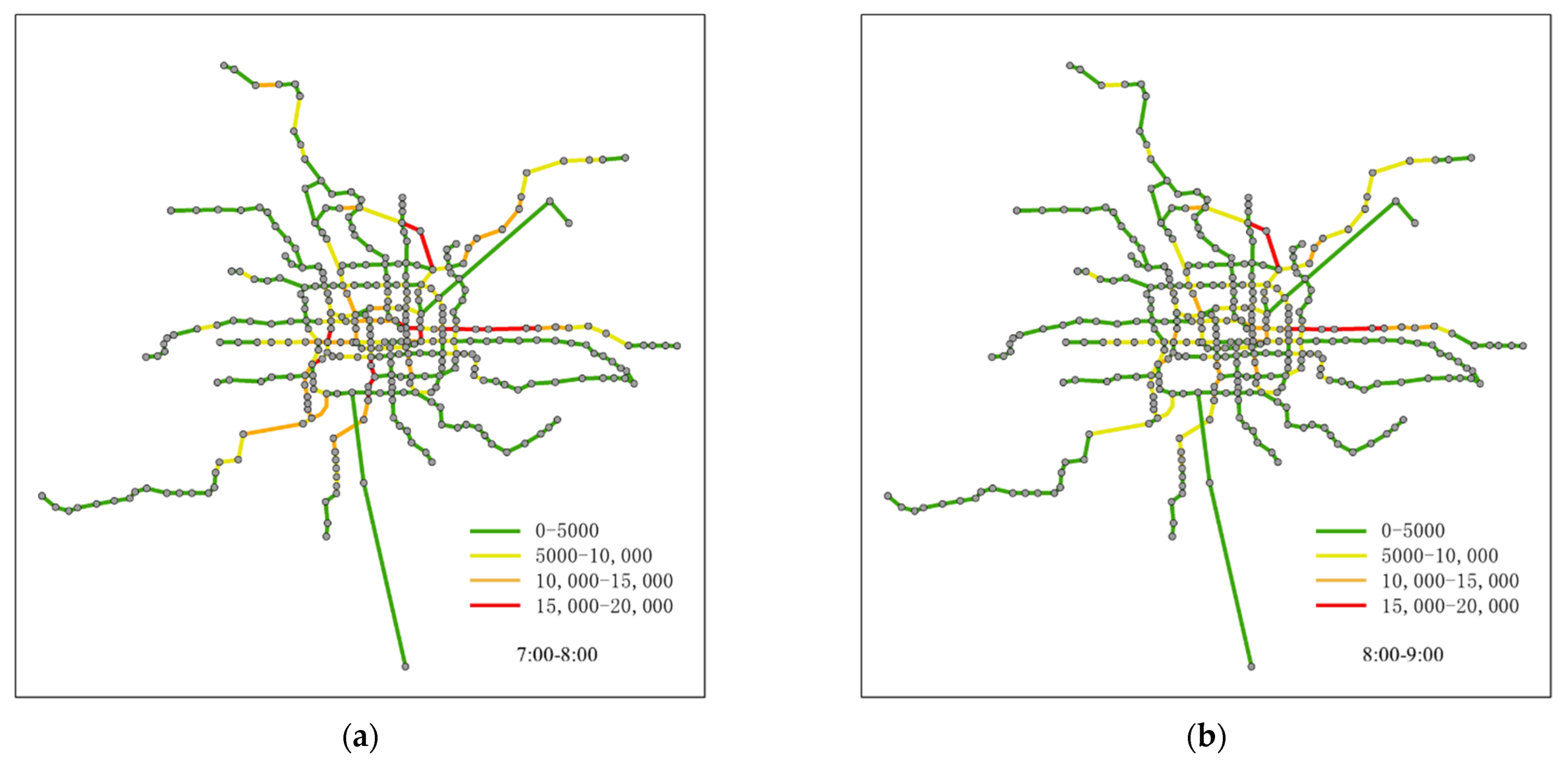
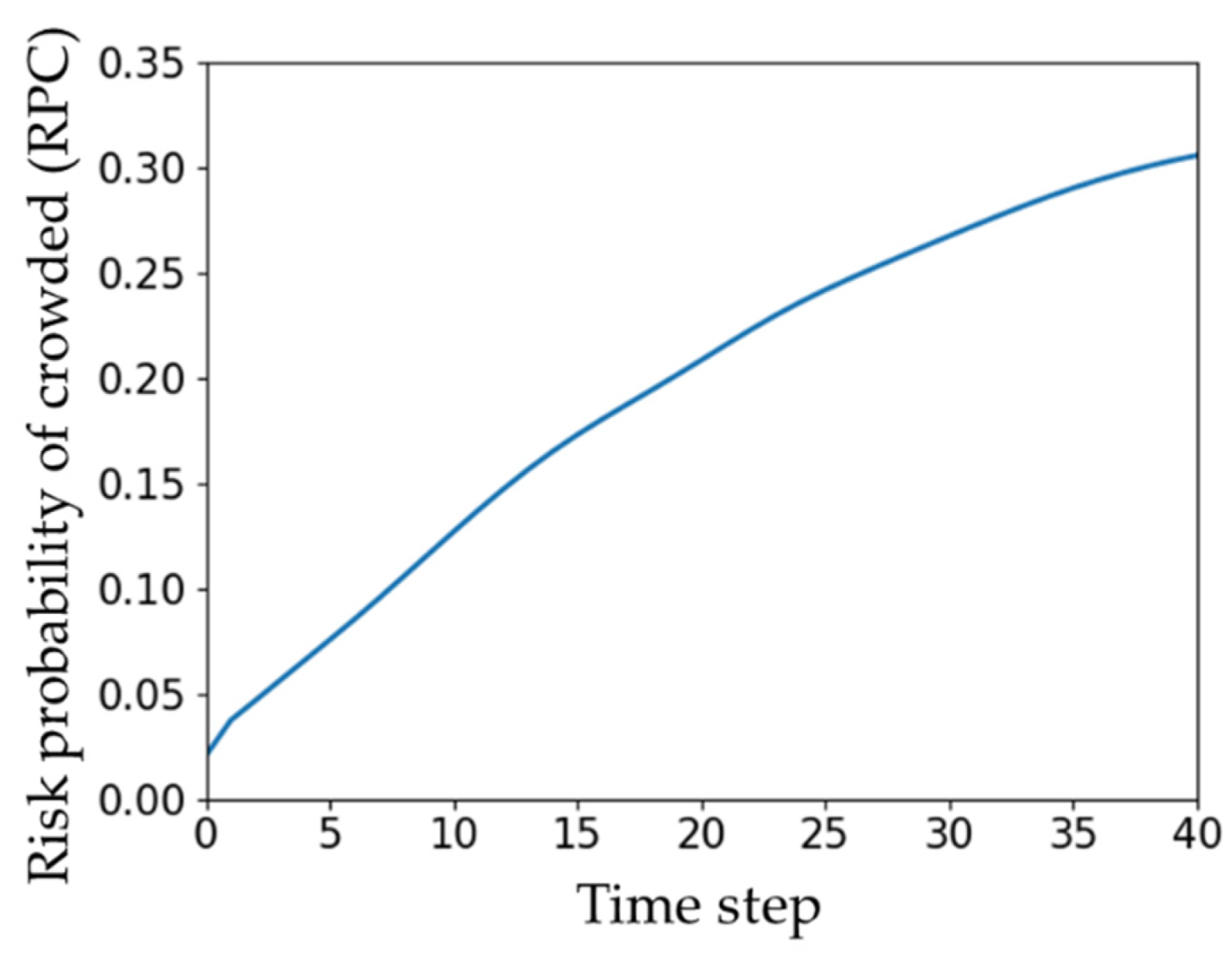
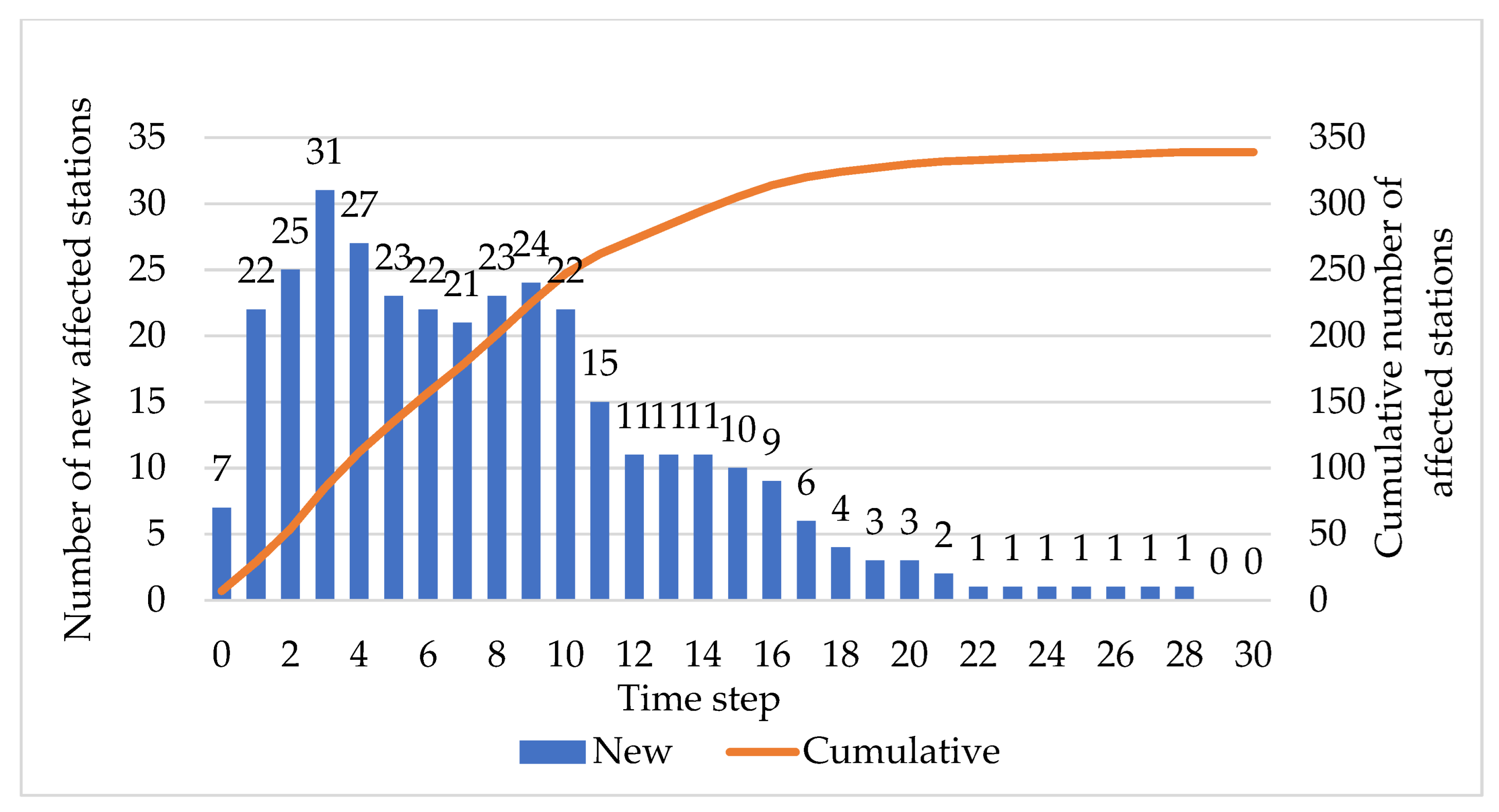
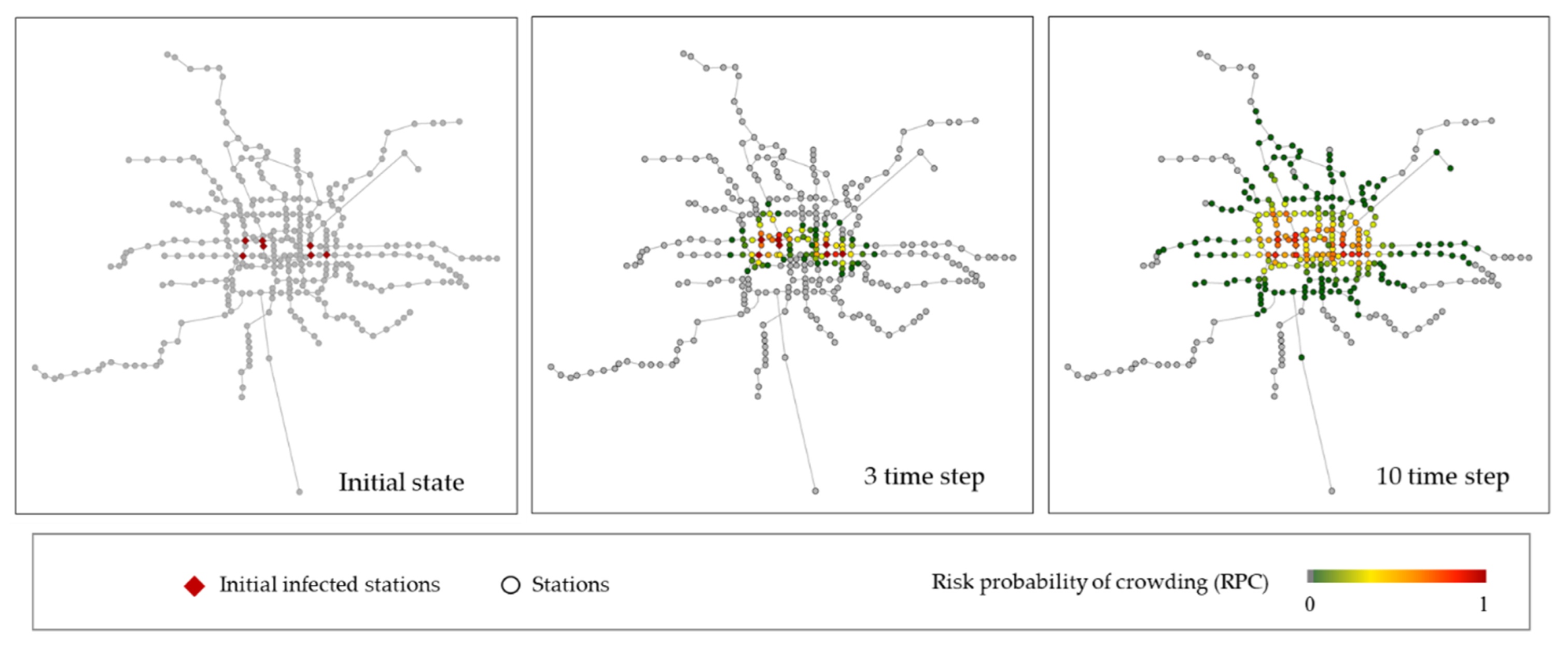
3.2. Spatiotemporal Analysis of Crowding Propagation
- (1)
- After the crowd occurs at some stations, it will spread to the majority of the network within half an hour. Then the propagation speed decreases and spreads throughout the network for about one and a half hours.
- (2)
- The propagation distance outward is limited, and the propagation strength decreases as the distance increases. The transfer nodes are more affected during propagation.
4. Discussion
5. Conclusions
- (1)
- Within half an hour, the majority of the network will become affected once it starts to happen at some stations. Following then, the propagation speed slows down.
- (2)
- The propagation strength diminishes with increasing distance. During propagation, the transfer nodes are significantly impacted.
- (3)
- Imposing control at the nodes with the highest demand or relatively peripheral nodes is more effective than other nodes.
Author Contributions
Funding
Conflicts of Interest
References
- Bačić, T. China: Metro Openings Hit Record High. Metro Report. 2021. Available online: https://www.railwaygazette.com/long-reads/china-metro-openings-hit-record-high/58572.article (accessed on 26 February 2021).
- Luo, Q.; Hou, Y.; Li, W.; Zhang, X. In Study on the Propagation Mechanism of Large Passenger Flow in Urban Rail Transit. In Proceedings of the 2018 3rd IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 3–5 September 2018; pp. 100–104. [Google Scholar]
- Norgate, S.H.; Cooper-Ryan, A.M.; Lavin, S.; Stonier, C.; Cooper, C.L. The impact of public transport on the health of work commuters: A systematic review. Health Psychol. Rev. 2020, 14, 325–344. [Google Scholar] [CrossRef] [PubMed]
- Higgins, C.D.; Sweet, M.N.; Kanaroglou, P.S. All minutes are not equal: Travel time and the effects of congestion on commute satisfaction in Canadian cities. Transportation 2018, 45, 1249–1268. [Google Scholar] [CrossRef]
- Nagy, A.M.; Simon, V. A novel congestion propagation modeling algorithm for smart cities. Pervasive Mob. Comput. 2021, 73, 101387. [Google Scholar] [CrossRef]
- Shang, P.; Li, R.; Guo, J.; Xian, K.; Zhou, X. Integrating Lagrangian and Eulerian observations for passenger flow state estimation in an urban rail transit network: A space-time-state hyper network-based assignment approach. Transp. Res. Part B Methodol. 2019, 121, 135–167. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Y.; Liu, Z.; Hu, H. The modeling of urban rail transit emergency delay propagation scope under network operation mode. Concurr. Comput. Pract. Exp. 2020, 32, e5530. [Google Scholar] [CrossRef]
- Li, M.; Zhou, X.; Wang, Y.; Jia, L.; An, M. Modelling cascade dynamics of passenger flow congestion in urban rail transit network induced by train delay. Alex. Eng. J. 2022, 61, 8797–8807. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Yu, Z.; Wang, S. Traffic Flow Prediction with Big Data: A Learning Approach Based on SIS-Complex Networks. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; pp. 550–554. [Google Scholar]
- Saberi, M.; Hamedmoghadam, H.; Ashfaq, M.; Hosseini, S.A.; Gu, Z.; Shafiei, S.; Nair, D.J.; Dixit, V.; Gardner, L.; Waller, S.T.; et al. A simple contagion process describes spreading of traffic jams in urban networks. Nat. Commun. 2020, 11, 1616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, M.; Liu, J.; Cenedese, C.; Sun, Z.; Cao, M. A Network SIS Meta-Population Model with Transportation Flow. IFAC-Pap. 2020, 53, 2562–2567. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, H.; Feng, T.; Witlox, F. A Network Modelling Approach to Flight Delay Propagation: Some Empirical Evidence from China. Sustainability 2019, 11, 4408. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Zhang, N.; Zhu, L. Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model. Information 2019, 10, 258. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Ye, X.; Chen, J.; Yan, X.; Wang, T. Evaluation Indexes and Correlation Analysis of Origination–Destination Travel Time of Nanjing Metro Based on Complex Network Method. Sustainability 2020, 12, 1113. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Xu, R.; Fan, W.; Zhou, F.; Liu, W. Service-Oriented Load Balancing Approach to Alleviating Peak-Hour Congestion in a Metro Network Based on Multi-Path Accessibility. Sustainability 2019, 11, 1293. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Zhu, Y. Intercity Train Operation Schemes Based on Passenger Flow Dynamic Assignment. J. Transp. Syst. Eng. Inf. Technol. 2013, 13, 111–117. [Google Scholar] [CrossRef]
- Sun, L.; Lu, Y.; Jin, J.G.; Lee, D.; Axhausen, K.W. An integrated Bayesian approach for passenger flow assignment in metro networks. Transp. Res. Part C Emerg. Technol. 2015, 52, 116–131. [Google Scholar] [CrossRef]
- Poulhès, A. Dynamic assignment model of trains and users on a congested urban-rail line. J. Rail Transp. Plan. Manag. 2020, 14, 100178. [Google Scholar] [CrossRef]
- Deng, L.; Zeng, J.; Mei, H. Passenger Flow Pushing Assignment Method for an Urban Rail Network Based on Hierarchical Path and Line Decomposition. Sustainability 2019, 11, 6441. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Li, T. Analyzing Congestion Propagation on Urban Rail Transit Oversaturated Conditions: A Framework Based on SIR Epidemic Model. Urban Rail Transit 2018, 4, 130–140. [Google Scholar] [CrossRef]
- Wu, J.; Gao, Z.; Sun, H. Simulation of Traffic Congestion with SIR Model. Mod. Phys. Lett. B 2004, 30, 1537–1542. [Google Scholar] [CrossRef]
- Baspinar, B.; Koyuncu, E.; Reyhanoglu, M. A Data-Driven Air Transportation Delay Propagation Model Using Epidemic Process Models. Int. J. Aerosp. Eng. 2016, 2016, 4836260. [Google Scholar] [CrossRef]


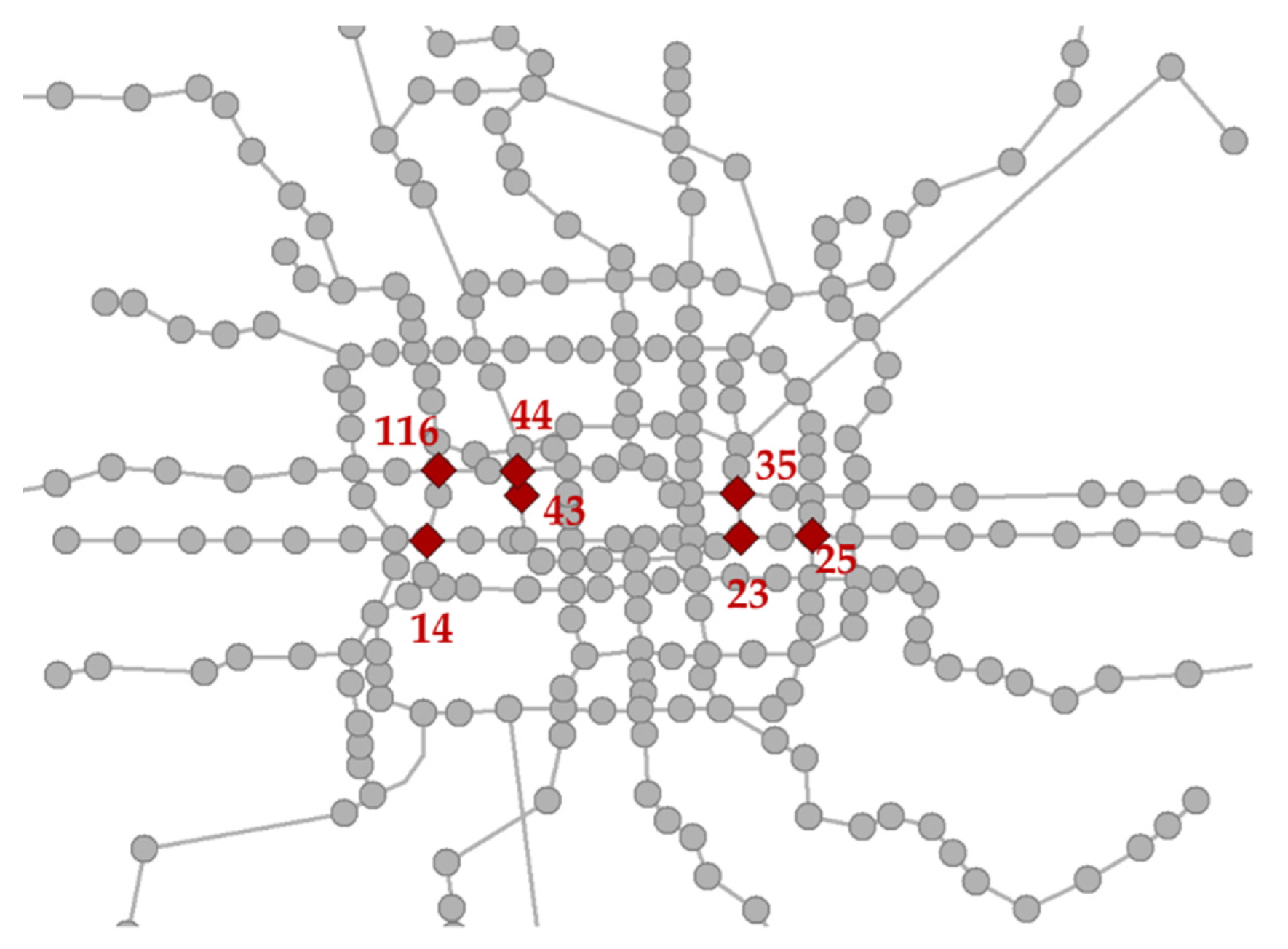

| Intervention Station Number | 14 | 23 | 25 | 35 | 43 | 44 | 116 |
| Average RPC of the whole network among two hours | 0.185 | 0.190 | 0.184 | 0.190 | 0.191 | 0.189 | 0.190 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Zheng, S.; Qian, H.; Cao, B.; Zhang, K. Analysis of Crowded Propagation on the Metro Network. Sustainability 2022, 14, 9829. https://doi.org/10.3390/su14169829
Jia C, Zheng S, Qian H, Cao B, Zhang K. Analysis of Crowded Propagation on the Metro Network. Sustainability. 2022; 14(16):9829. https://doi.org/10.3390/su14169829
Chicago/Turabian StyleJia, Cai, Shuyan Zheng, Hanqiang Qian, Bingxin Cao, and Kaiting Zhang. 2022. "Analysis of Crowded Propagation on the Metro Network" Sustainability 14, no. 16: 9829. https://doi.org/10.3390/su14169829
APA StyleJia, C., Zheng, S., Qian, H., Cao, B., & Zhang, K. (2022). Analysis of Crowded Propagation on the Metro Network. Sustainability, 14(16), 9829. https://doi.org/10.3390/su14169829





