Optimal Selection of Short- and Long-Term Mitigation Strategies for Buildings within Communities under Flooding Hazard
Abstract
1. Introduction
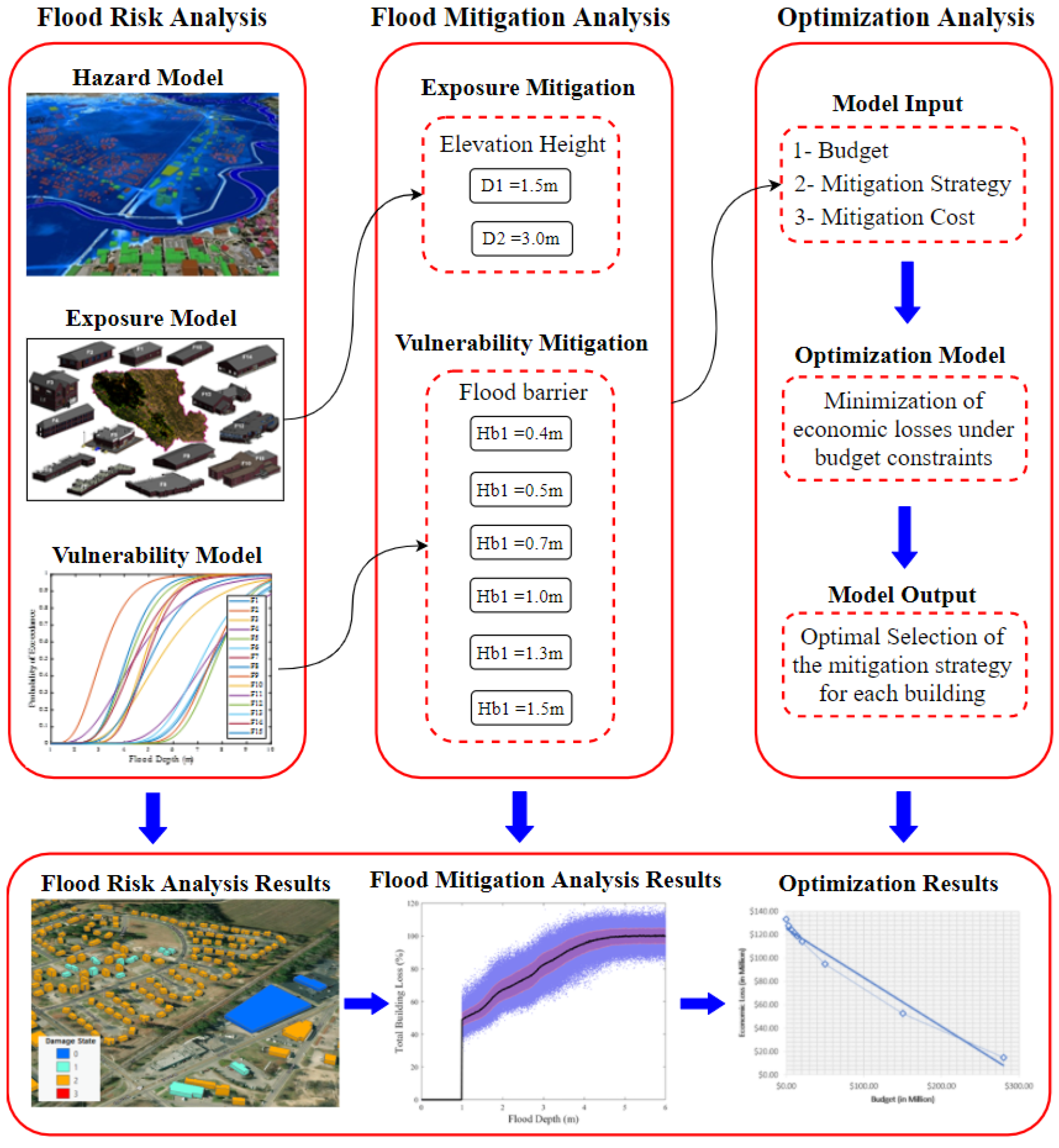
2. Research Methodology
2.1. Flood Risk and Mitigation Model
2.2. Optimization Model
2.2.1. Objective of the Optimization Model
2.2.2. Constraints of the Optimization Model
3. Illustrative Example of Lumberton, NC
3.1. Flood Hazard and Damage Analysis Results
3.2. Comparative Analysis of Short- and Long-Term Mitigation Strategies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walters, P. The Problem of Community Resilience in Two Flooded Cities: Dhaka 1998 and Brisbane 2011. Habitat Int. 2015, 50, 51–56. [Google Scholar] [CrossRef]
- Hemmati, M.; Ellingwood, B.R.; Mahmoud, H.N. The Role of Urban Growth in Resilience of Communities Under Flood Risk. Earth’s Future 2020, 8, e2019EF001382. [Google Scholar] [CrossRef] [PubMed]
- Mullins, A.; Soetanto, R. Enhancing Community Resilience to Flooding through Social Responsibility. Int. J. Saf. Secur. Eng. 2011, 1, 115–125. [Google Scholar] [CrossRef][Green Version]
- Magis, K. Community Resilience: An Indicator of Social Sustainability. Soc. Nat. Resour. 2010, 23, 401–416. [Google Scholar] [CrossRef]
- Lindell, M.K.; Prater, C.S. Assessing Community Impacts of Natural Disasters. Nat. Hazards Rev. 2003, 4, 176–185. [Google Scholar] [CrossRef]
- Elms, D.; McCahon, I.; Dewhirst, R. Improving Infrastructure Resilience. Civ. Eng. Environ. Syst. 2019, 36, 83–99. [Google Scholar] [CrossRef]
- González, A.D.; Dueñas-Osorio, L.; Medaglia, A.L.; Sánchez-Silva, M. Resource allocation for infrastructure networks within the context of disaster management. In Proceedings of the International Conference on Structural Safety and Reliability (ICOSSAR), New York, NY, USA, 16 June 2013; pp. 1–8. [Google Scholar]
- Koliou, M.; van de Lindt, J.W.; McAllister, T.P.; Ellingwood, B.R.; Dillard, M.; Cutler, H. State of the Research in Community Resilience: Progress and Challenges. Sustain. Resilient Infrastruct. 2020, 5, 131–151. [Google Scholar] [CrossRef]
- Melendez, A.; Caballero-Russi, D.; Gutierrez Soto, M.; Giraldo, L.F. Computational Models of Community Resilience. Nat. Hazards 2022, 111, 1121–1152. [Google Scholar] [CrossRef]
- Liao, T.Y.; Hu, T.Y.; Ko, Y.N. A Resilience Optimization Model for Transportation Networks under Disasters. Nat. Hazards 2018, 93, 469–489. [Google Scholar] [CrossRef]
- Nozhati, S.; Sarkale, Y.; Ellingwood, B.; Chong, E.K.P.; Mahmoud, H. Near-Optimal Planning Using Approximate Dynamic Programming to Enhance Post-Hazard Community Resilience Management. Reliab. Eng. Syst. Saf. 2019, 181, 116–126. [Google Scholar] [CrossRef]
- Sen, M.K.; Dutta, S.; Kabir, G. Flood Resilience of Housing Infrastructure Modeling and Quantification Using a Bayesian Belief Network. Sustainability 2021, 13, 1026. [Google Scholar] [CrossRef]
- Sen, M.K.; Dutta, S.; Kabir, G. Modelling and Quantification of Time-Varying Flood Resilience for Housing Infrastructure Using Dynamic Bayesian Network. J. Clean. Prod. 2022, 361, 132266. [Google Scholar] [CrossRef]
- Abdel-Mooty, M.N.; El-Dakhakhni, W.; Coulibaly, P. Data-Driven Community Flood Resilience Prediction. Water 2022, 14, 2120. [Google Scholar] [CrossRef]
- Gudipati, V.K.; Cha, E.J. A resilience-based framework for design optimization of interdependent buildings. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering, ICASP, Seoul, Korea, 26–30 May 2019; pp. 1–8. [Google Scholar]
- Nofal, O.M.; van de Lindt, J.W. Minimal Building Flood Fragility and Loss Function Portfolio for Resilience Analysis at the Community Level. Water 2020, 12, 2277. [Google Scholar] [CrossRef]
- Pistrika, A.; Tsakiris, G.; Nalbantis, I.; Tsakiris, G.; Nalbantis, I. Flood Depth-Damage Functions for Built Environment. Environ. Processes 2014, 1, 553–572. [Google Scholar] [CrossRef]
- Romali, N.S.; Sulaiman, M.; Khushren, S.A.; Yusop, Z.; Ismail, Z. Flood damage assessment: A review of flood stage–Damage function curve. In Proceedings of the International Symposium on Flood Research and Management, ISFRAM 2014; Springer: Singapore, 2015; pp. 147–159. [Google Scholar] [CrossRef]
- Scawthorn, C.; Asce, F.; Flores, P.; Blais, N.; Seligson, H.; Tate, E.; Chang, S.; Mifflin, E.; Thomas, W.; Murphy, J.; et al. HAZUS-MH Flood Loss Estimation Methodology. II. Damage and Loss Assessment. Nat. Hazards Rev. 2006, 7, 72–81. [Google Scholar] [CrossRef]
- De Risi, R.; Jalayer, F.; de Paola, F.; Iervolino, I.; Giugni, M.; Topa, M.E.; Mbuya, E.; Kyessi, A.; Manfredi, G.; Gasparini, P. Flood Risk Assessment for Informal Settlements. Nat. Hazards 2013, 69, 1003–1032. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W. High-Resolution Approach to Quantify the Impact of Building-Level Flood Risk Mitigation and Adaptation Measures on Flood Losses at the Community-Level. Int. J. Disaster Risk Reduct. 2020, 51, 101903. [Google Scholar] [CrossRef]
- Shane Crawford, P.; Mitrani-Reiser, J.; Sutley, E.J.; Do, T.Q.; Tomiczek, T.; Nofal, O.M.; Weigand, J.M.; Watson, M.; van de Lindt, J.W.; Graettinger, A.J. Measurement Approach to Develop Flood-Based Damage Fragilities for Residential Buildings Following Repeat Inundation Events. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2022, 8. [Google Scholar] [CrossRef]
- Marvi, M.T. A Review of Flood Damage Analysis for a Building Structure and Contents. Nat. Hazards 2020, 102, 967–995. [Google Scholar] [CrossRef]
- Figueiredo, R.; Romão, X.; Paupério, E. Component-Based Flood Vulnerability Modelling for Cultural Heritage Buildings. Int. J. Disaster Risk Reduct. 2021, 61, 102323. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W. High-Resolution Flood Risk Approach to Quantify the Impact of Policy Change on Flood Losses at Community-Level. Int. J. Disaster Risk Reduct. 2021, 62, 102429. [Google Scholar] [CrossRef]
- Nofal, O.M. High-Resolution Multi-Hazard Approach to Quantify Hurricane-Induced Risk for Coastal and Inland Communities. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2021. [Google Scholar]
- Zhang, W.; Nicholson, C. A Multi-Objective Optimization Model for Retrofit Strategies to Mitigate Direct Economic Loss and Population Dislocation. Sustain. Resilient Infrastruct. 2016, 1, 123–136. [Google Scholar] [CrossRef]
- Najarian, M.; Lim, G.J. Optimizing Infrastructure Resilience under Budgetary Constraint. Reliab. Eng. Syst. Saf. 2020, 198, 106801. [Google Scholar] [CrossRef]
- Almoghathawi, Y.; González, A.D.; Barker, K. Exploring Recovery Strategies for Optimal Interdependent Infrastructure Network Resilience. Netw. Spat. Econ. 2021, 21, 229–260. [Google Scholar] [CrossRef]
- Wen, Y. Development of Multi-Objective Optimization Model of Community Resilience on Mitigation Planning. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2021. [Google Scholar]
- Adluri, T. Multi-Objective Optimization of Building Mitigation Strategies to Address Multiple Hazards. Master’s Thesis, University of Oklahoma, Norman, OK, USA, 2021. [Google Scholar]
- Zhang, W.; Lin, P.; Wang, N.; Nicholson, C.; Xue, X. Probabilistic Prediction of Postdisaster Functionality Loss of Community Building Portfolios Considering Utility Disruptions. J. Struct. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Wiebe, D.M.; Cox, D.T. Application of Fragility Curves to Estimate Building Damage and Economic Loss at a Community Scale: A Case Study of Seaside, Oregon. Nat. Hazards 2014, 71, 2043–2061. [Google Scholar] [CrossRef]
- Onan, K.; Ülengin, F.; Sennaroğlu, B. An Evolutionary Multi-Objective Optimization Approach to Disaster Waste Management: A Case Study of Istanbul, Turkey. Expert Syst. Appl. 2015, 42, 8850–8857. [Google Scholar] [CrossRef]
- Gupta, H.S. Optimal Selection of Short-and Long-Term Mitigation Strategies for Flooding Hazard. Master’s Thesis, University of Oklahoma, Norman, OK, USA, 2022. [Google Scholar]
- Nofal, O.M.; van de Lindt, J.W.; Cutler, H.; Shields, M.; Crofton, K. Modeling the Impact of Building-Level Flood Mitigation Measures Made Possible by Early Flood Warnings on Community-Level Flood Loss Reduction. Buildings 2021, 11, 475. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W.; Do, T.Q. Multi-Variate and Single-Variable Flood Fragility and Loss Approaches for Buildings. Reliab. Eng. Syst. Saf. 2020, 202, 106971. [Google Scholar] [CrossRef]
- Snyman, J.A.; Wilke, D.N. Practical Mathematical Optimization; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 9783319775852. [Google Scholar]
- Calle, P.M.; Norman, C. A Comparative Analysis of Population Dislocation Models for Multi-Objective Community Resilience Optimization. Master’s Thesis, Universiy of Oklahoma, Norman, OK, USA, 2019. [Google Scholar]
- Mejjaouli, S.; Alzahrani, M. Decision-Making Model for Optimum Energy Retrofitting Strategies in Residential Buildings. Sustain. Prod. Consum. 2020, 24, 211–218. [Google Scholar] [CrossRef]
- Deniz, D.; Sutley, E.; van de Lindt, J.W.; Peacock, W.G.; Rosenheim, N.; Gu, D.; Mitrani-Reiser, J.; Dillard, M.; Koliou, M.; Hamideh, S. Flood Performance and Dislocation Assessment for Lumberton Homes after Hurricane Matthew. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP13), Seoul, Korea, 26–30 May 2019. [Google Scholar]
- ID. 41—Modeling Business Recovery after Natural Disasters: The Case Study of Lumberton, NC Following Hurricane Matthew—ICONHIC. 2019. Available online: https://iconhic.com/2019/2019/11/id-41-modeling-business-recovery-after-natural-disasters-the-case-study-of-lumberton-nc-following-hurricane-matthew/ (accessed on 16 November 2021).
- Khajehei, S. Recovery Challenges of Public Housing Residents after Disasters: Lumberton, North Carolina after Hurricane Matthew. Master’s Thesis, Iowa State University, Ames, IA, USA, 2019. [Google Scholar]
- Cuny, F.C. Living with Floods Alternatives for Riverine Flood Mitigation. Land Use Policy 1991, 8, 331–342. [Google Scholar] [CrossRef]
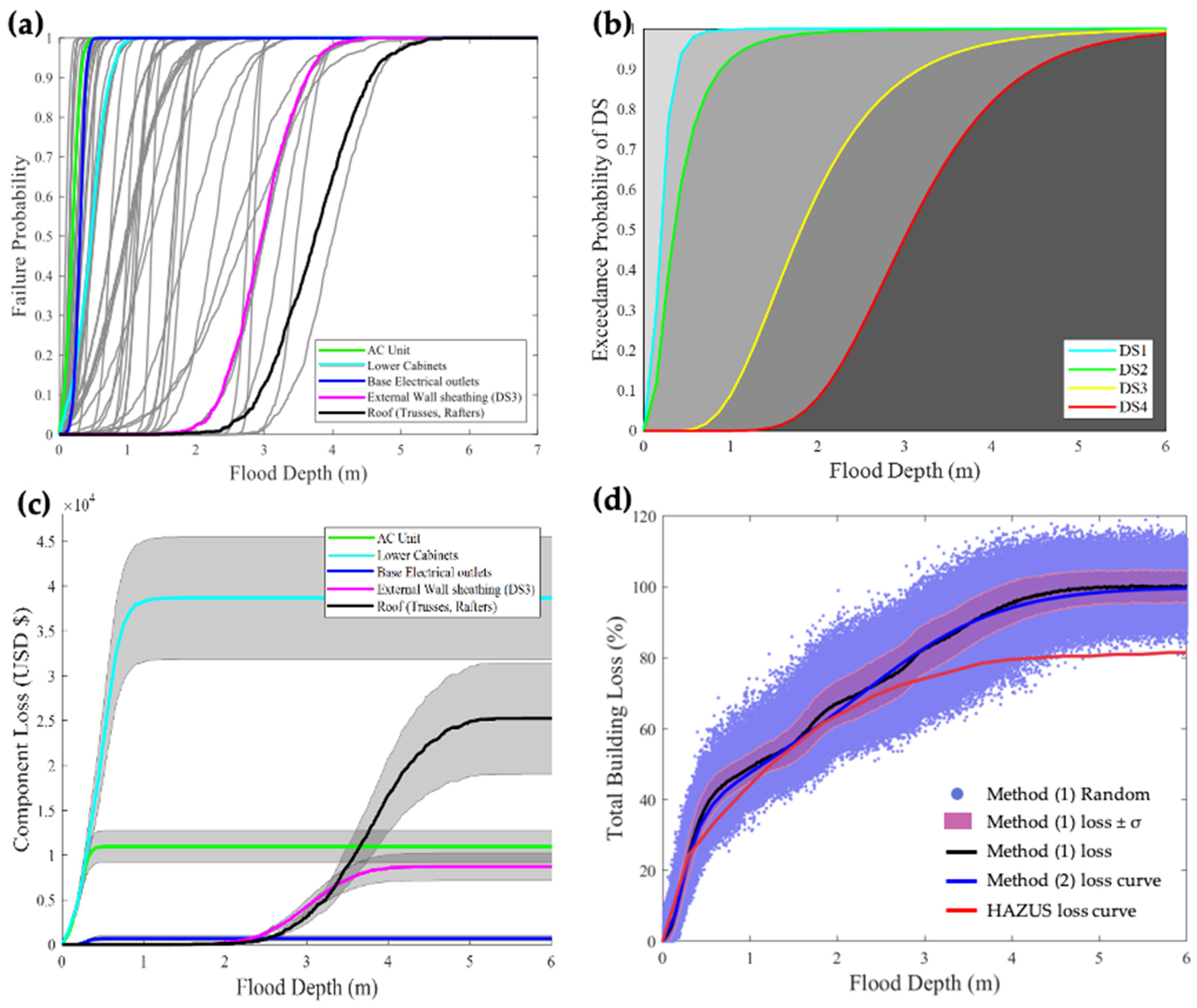

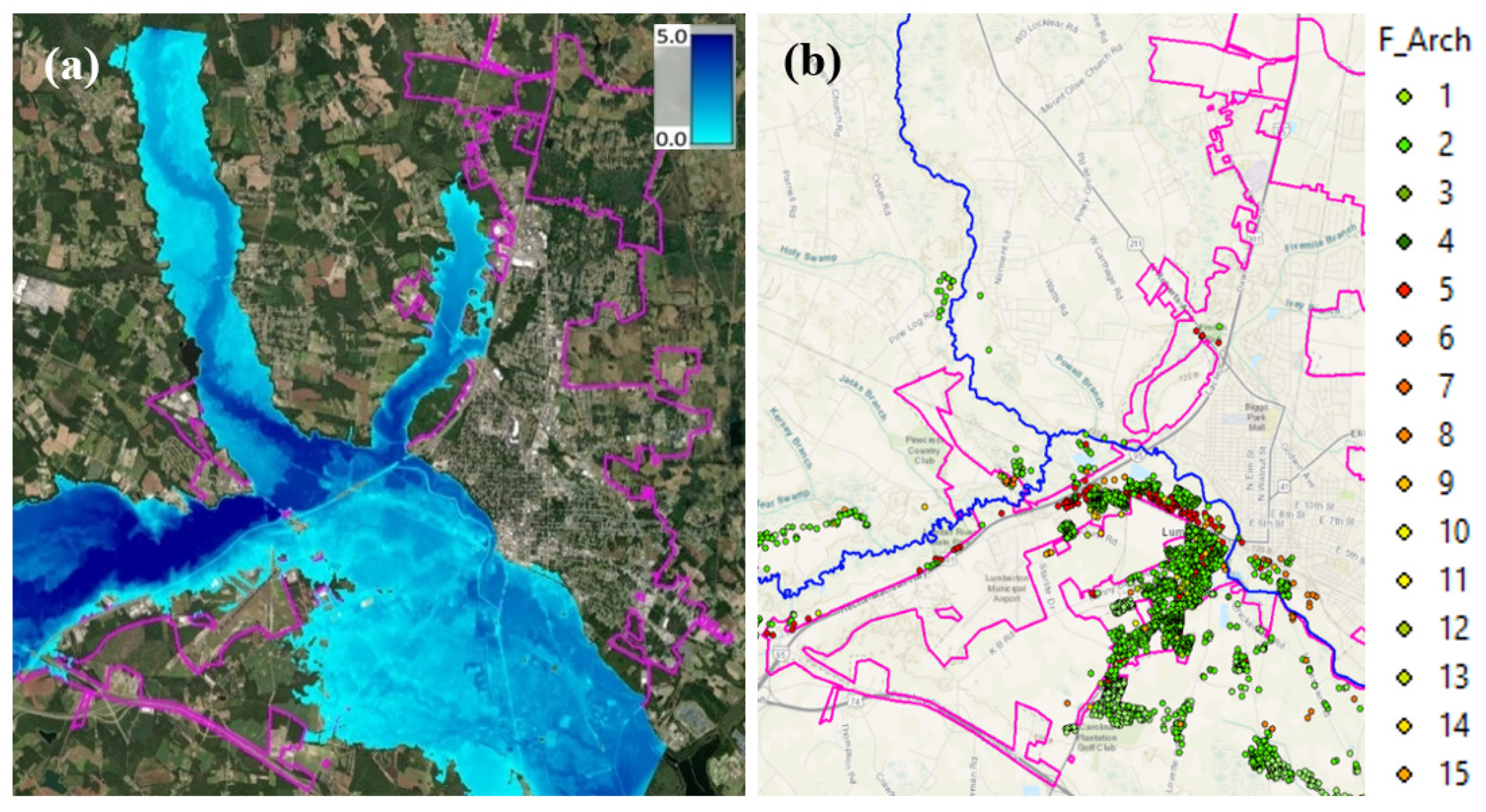
| Damage State Level | Functionality | Damage Scale | Loss Ratio |
|---|---|---|---|
| DS-0 | Operational | Insignificant | 0.00–0.03 |
| DS-1 | Limited Occupancy | Slight | 0.03–0.15 |
| DS-2 | Restricted Occupancy | Moderate | 0.15–0.50 |
| DS-3 | Restricted Use | Extensive | 0.50–0.70 |
| DS-4 | Restricted Entry | Complete | 0.70–1.00 |
| Archetype | Number of Buildings | Total Current Replacement Value | Total Base Flood Losses |
|---|---|---|---|
| F1: One-Story Single-Family Residential Building | 665 | $37,527,864 | $10,097,519 |
| F2: One-Story Multi-Family Residential Building | 1741 | $194,990,289 | $80,651,358 |
| F3: Two-Story Single-Family Residential Building The | 7 | $1,059,617 | $316,074 |
| F4: Two-Story Multi-Family Residential Building | 96 | $21,174,848 | $5,548,556 |
| F5: Small Grocery Store/Gas Station with a Convenience Store | 157 | $62,855,685 | $7,921,982 |
| F6: Multi-Unit Retail Building (Strip Mall) | 1 | $7,195,517 | $0 |
| F7: Small Multi-Unit Commercial Building | 1 | $256,600 | $157,864 |
| F8: Super Retail Center The | 2 | $408,318 | $176,194 |
| F9: Industrial Building | 62 | $124,562,628 | $12,002,943 |
| F10: One-Story School | 8 | $7,429,091 | $2,495,461 |
| F11: Two-Story School | 3 | $23,456,627 | $3,621,603 |
| F12: Hospital/Clinic The | 0 | $0 | $0 |
| F13: Community Center (Place of Worship) | 44 | $23,381,452 | $6,720,040 |
| F14: Office Building | 17 | $8,782,066 | $2,565,452 |
| F15: Warehouse (Small/Large Box) | 53 | $40,975,016 | $860,940 |
| Exceedance Probability of a DS (Fragility) | Number of Buildings (Total = 2858) | ||||
|---|---|---|---|---|---|
| DS0 | DS1 | DS2 | DS3 | DS4 | |
| 0% < P_DS < 20% | 2201 | 396 | 567 | 2071 | 2822 |
| 20% < P_DS < 40% | 5 | 72 | 115 | 355 | 25 |
| 40% < P_DS < 60% | 7 | 72 | 144 | 293 | 7 |
| 60% < P_DS < 80% | 30 | 108 | 290 | 121 | 3 |
| 80% < P_DS < 100% | 614 | 2209 | 1741 | 17 | 0 |
| Number of Buildings Mitigated | |||||
|---|---|---|---|---|---|
| Budget (Million) | No Intervention | Elevate 5 ft (1.5 m) | Elevate 10 ft (3 m) | Total # of Mitigated Buildings | Economic Loss |
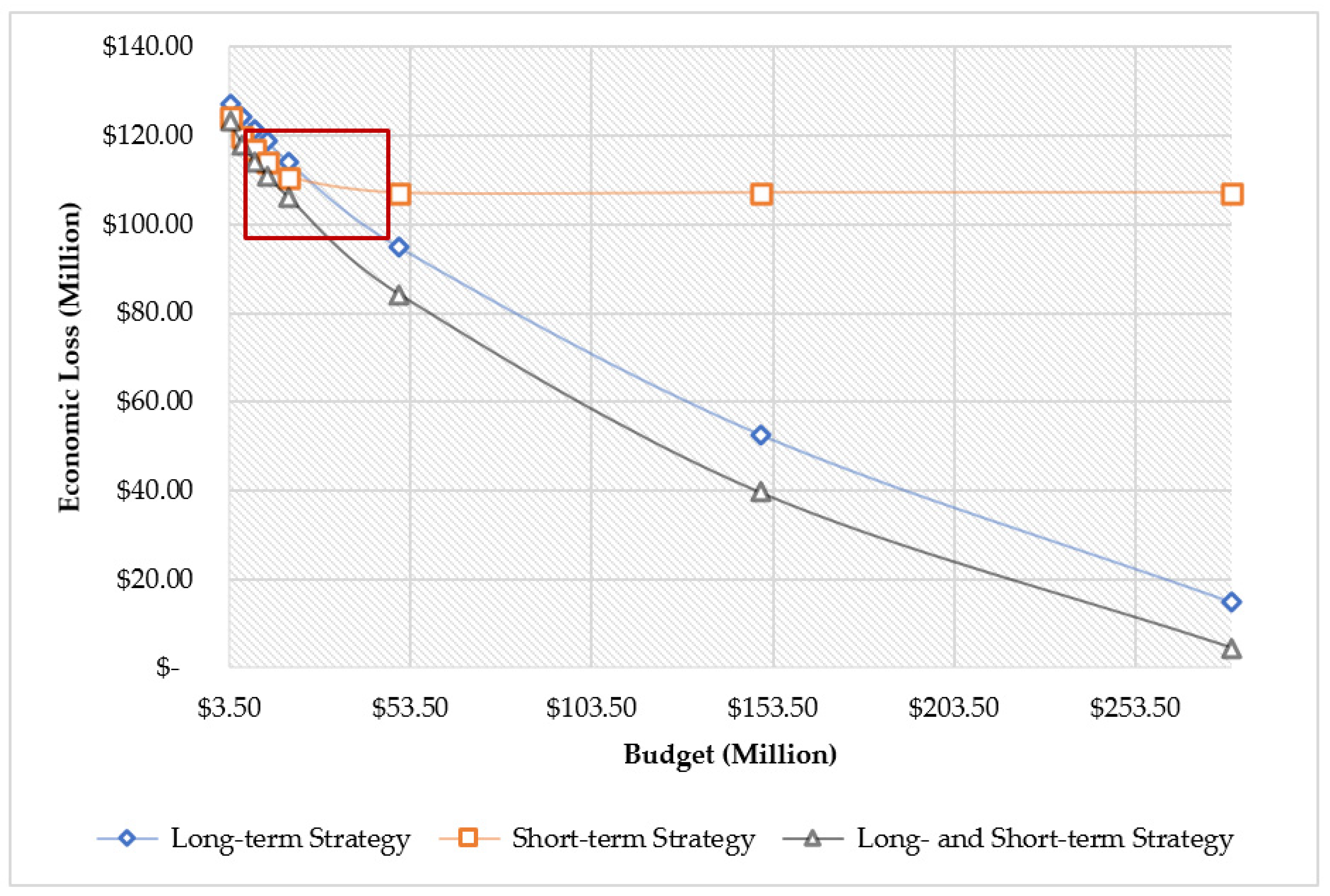
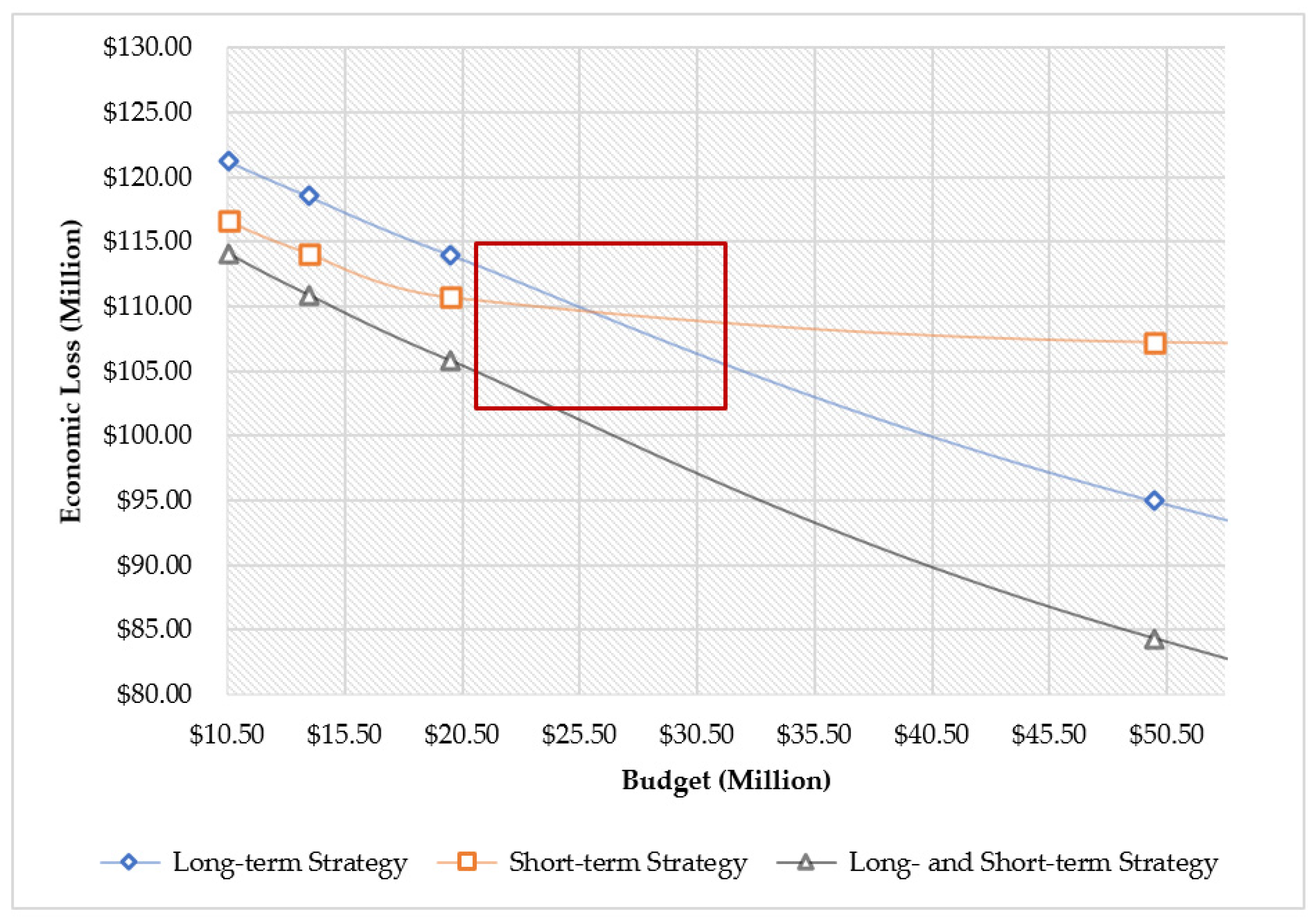
| $0 | 2858 | 0 | 0 | 0 | $133,135,992 |
| $3.5 | 2837 | 17 | 4 | 21 | $127,398,555 |
| $7 | 2818 | 33 | 7 | 40 | $124,164,674 |
| $10.5 | 2787 | 57 | 14 | 71 | $121,268,774 |
| $14 | 2762 | 81 | 16 | 97 | $118,517,884 |
| $ 20 | 2718 | 123 | 18 | 141 | $114,017,769 |
| $50 | 2524 | 288 | 46 | 334 | $94,973,886 |
| $150 | 1797 | 726 | 335 | 1061 | $52,520,789 |
| $280 | 1120 | 1329 | 409 | 1738 | $14,704,547 |
| Number of Buildings Mitigated | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Buildings Surrounded by a Barrier of Height (Hb) | |||||||||
| Budget (Million) | No Intervention | Hb = 0.4 m | Hb = 0.5 m | Hb = 0.7 m | Hb = 1.0 m | Hb = 1.3 m | Hb = 1.5 m | Total # of Mitigated Buildings | Economic Loss |
| $0 | 2858 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | $133,135,992 |
| $3.5 | 2827 | 0 | 0 | 5 | 4 | 7 | 15 | 31 | $124,118,022 |
| $7 | 2767 | 1 | 0 | 9 | 16 | 26 | 39 | 91 | $119,675,195 |
| $10.5 | 2707 | 1 | 0 | 12 | 29 | 47 | 62 | 151 | $116,597,842 |
| $14 | 2638 | 1 | 0 | 14 | 37 | 74 | 94 | 220 | $114,059,986 |
| $20 | 2514 | 2 | 1 | 16 | 47 | 116 | 162 | 344 | $110,680,315 |
| $50 | 2027 | 33 | 8 | 70 | 146 | 264 | 311 | 832 | $107,224,597 |
| $150 | 2027 | 33 | 8 | 70 | 146 | 264 | 311 | 832 | $107,224,597 |
| $280 | 2027 | 33 | 8 | 70 | 146 | 264 | 311 | 832 | $107,224,597 |
| Number of Buildings Mitigated | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Buildings Surrounded by a Barrier of Height (Hb) | |||||||||||
| Budget (Million) | No Intervention | Hb = 0.4 m | Hb = 0.5 m | Hb = 0.7 m | Hb = 1.0 m | Hb = 1.3 m | Hb = 1.5 m | Elevate 5 ft | Elevate 10 ft | Total # of Mitigated Buildings | Economic Loss |
| $0 | 2858 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | $133,135,992 |
| $3.5 | 2834 | 0 | 0 | 4 | 3 | 4 | 9 | 3 | 1 | 24 | $ 123,380,846 |
| $7 | 2788 | 1 | 0 | 7 | 8 | 15 | 28 | 8 | 3 | 70 | $ 118,059,178 |
| $10.5 | 2746 | 1 | 0 | 9 | 16 | 28 | 39 | 15 | 4 | 112 | $ 114,175,819 |
| $14 | 2716 | 1 | 0 | 10 | 22 | 34 | 44 | 24 | 7 | 142 | $ 110,893,178 |
| $20 | 2650 | 1 | 0 | 10 | 27 | 45 | 60 | 51 | 14 | 208 | $ 105,849,491 |
| $50 | 2378 | 2 | 1 | 14 | 39 | 80 | 106 | 212 | 26 | 480 | $ 84,368,342 |
| $150 | 1539 | 2 | 1 | 18 | 53 | 131 | 184 | 601 | 329 | 1319 | $ 39,452,522 |
| $280 | 788 | 5 | 3 | 23 | 75 | 185 | 239 | 1091 | 446 | 2067 | $ 4,539,084 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, H.S.; Nofal, O.M.; González, A.D.; Nicholson, C.D.; van de Lindt, J.W. Optimal Selection of Short- and Long-Term Mitigation Strategies for Buildings within Communities under Flooding Hazard. Sustainability 2022, 14, 9812. https://doi.org/10.3390/su14169812
Gupta HS, Nofal OM, González AD, Nicholson CD, van de Lindt JW. Optimal Selection of Short- and Long-Term Mitigation Strategies for Buildings within Communities under Flooding Hazard. Sustainability. 2022; 14(16):9812. https://doi.org/10.3390/su14169812
Chicago/Turabian StyleGupta, Himadri Sen, Omar M. Nofal, Andrés D. González, Charles D. Nicholson, and John W. van de Lindt. 2022. "Optimal Selection of Short- and Long-Term Mitigation Strategies for Buildings within Communities under Flooding Hazard" Sustainability 14, no. 16: 9812. https://doi.org/10.3390/su14169812
APA StyleGupta, H. S., Nofal, O. M., González, A. D., Nicholson, C. D., & van de Lindt, J. W. (2022). Optimal Selection of Short- and Long-Term Mitigation Strategies for Buildings within Communities under Flooding Hazard. Sustainability, 14(16), 9812. https://doi.org/10.3390/su14169812








