Numerical Simulation of the Hydraulic Characteristics and Fish Habitat of a Natural Continuous Meandering River
Abstract
Highlights
- To study the hydraulic characteristics of natural continuous curved river flows;
- To study the influence of the hydraulic characteristics of natural continuous curved river flows on fish habitats;
- To evaluate the impact of channel regulation on the construction of ecological waterways.
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.1.1. Hydrodynamic Control Equations
2.1.2. Boundary Conditions and Model Parameter Settings
2.1.3. Grid Division
2.2. The Shannon Diversity Index
2.3. Experimental Parameter Selection
2.4. Experimental Conditions
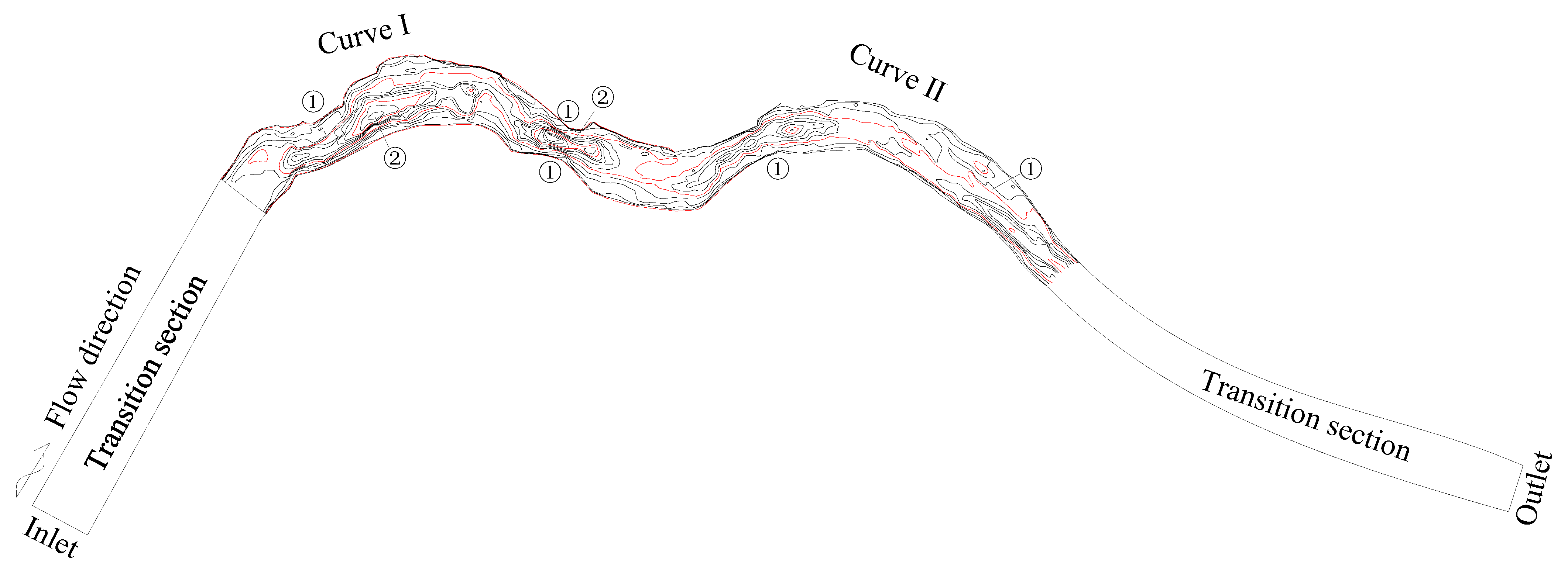
3. Results
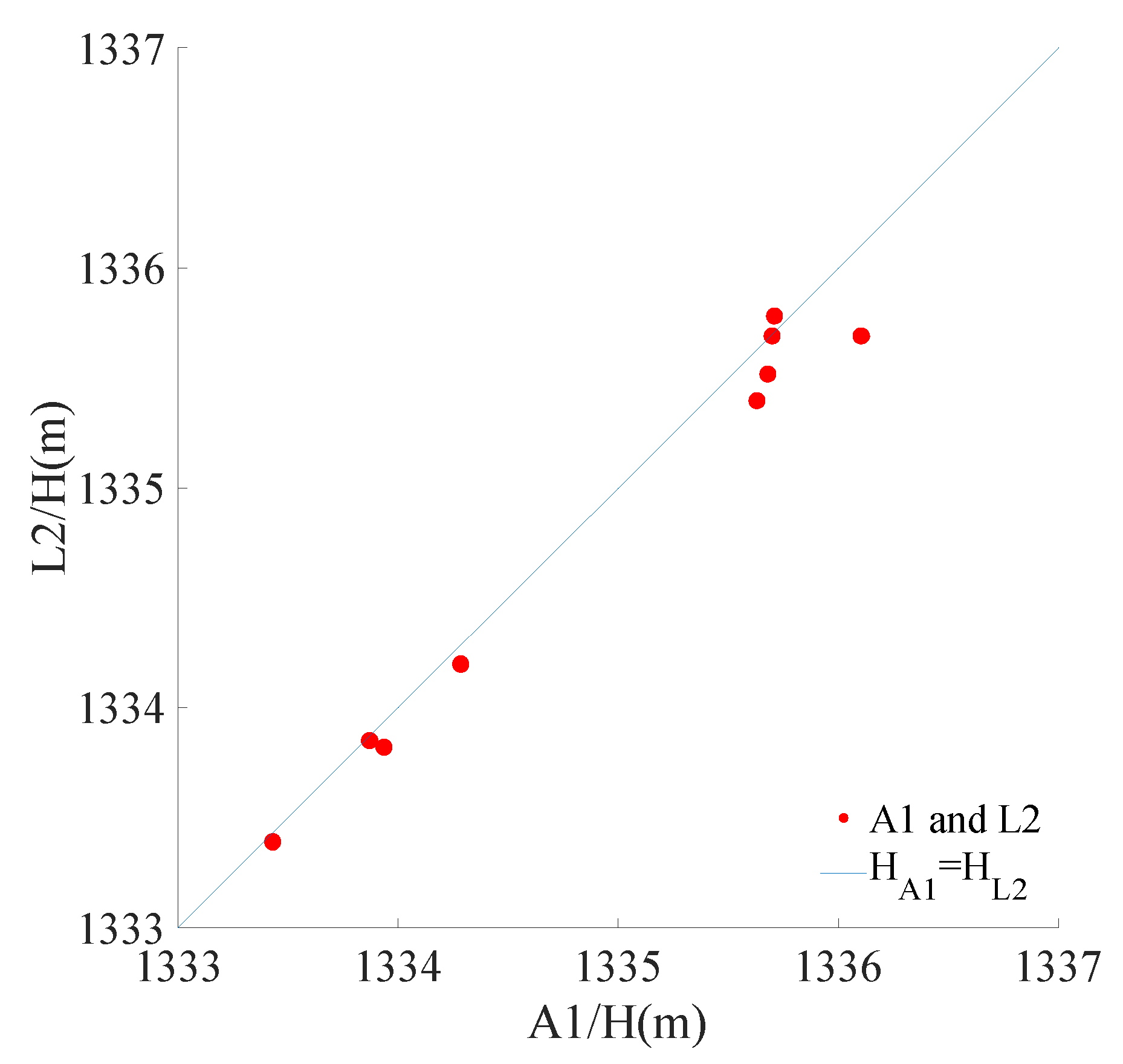
3.1. Feasibility Analysis of the Mathematical Model
3.2. Numerical Simulation of Natural Rivers
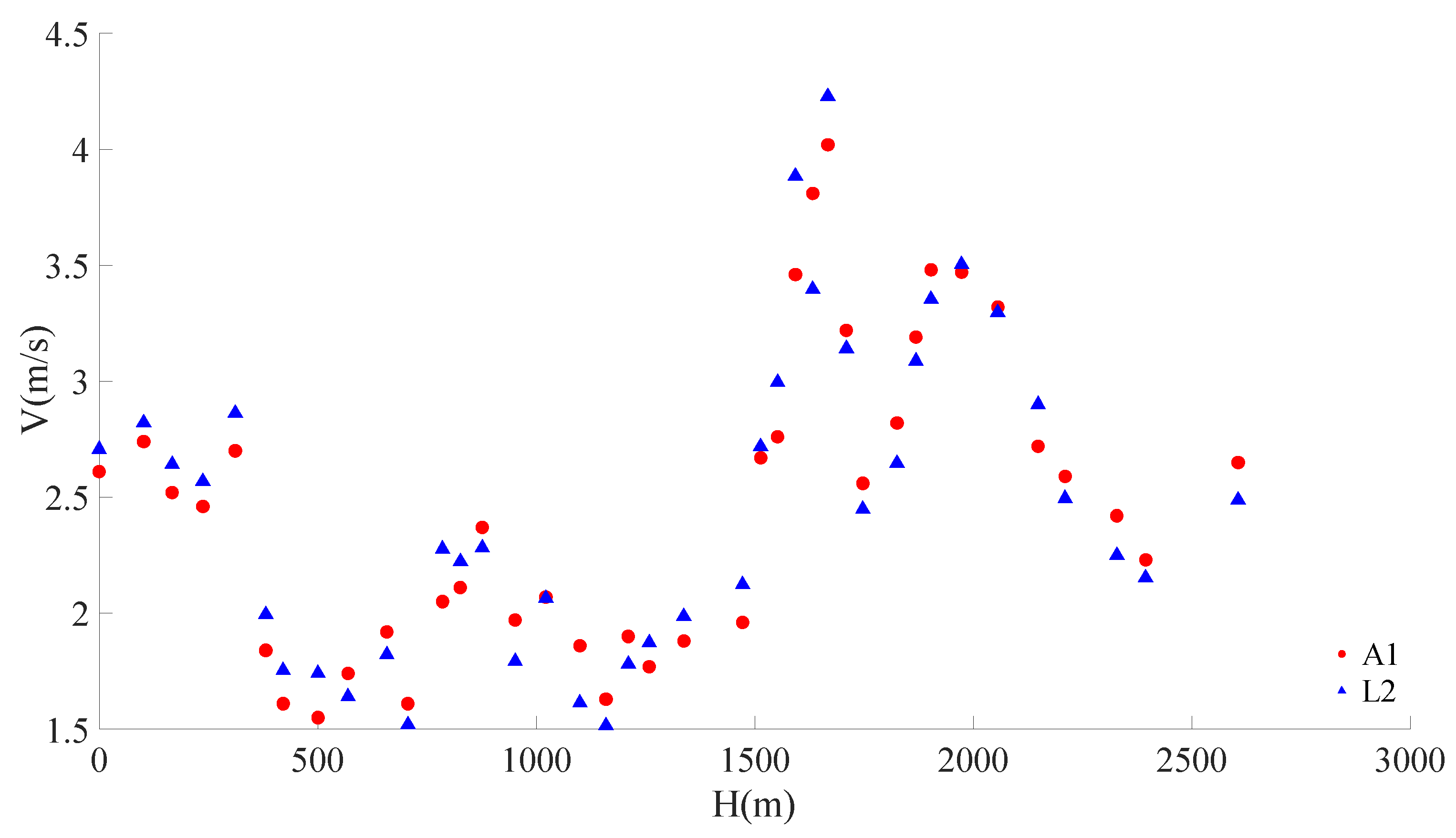
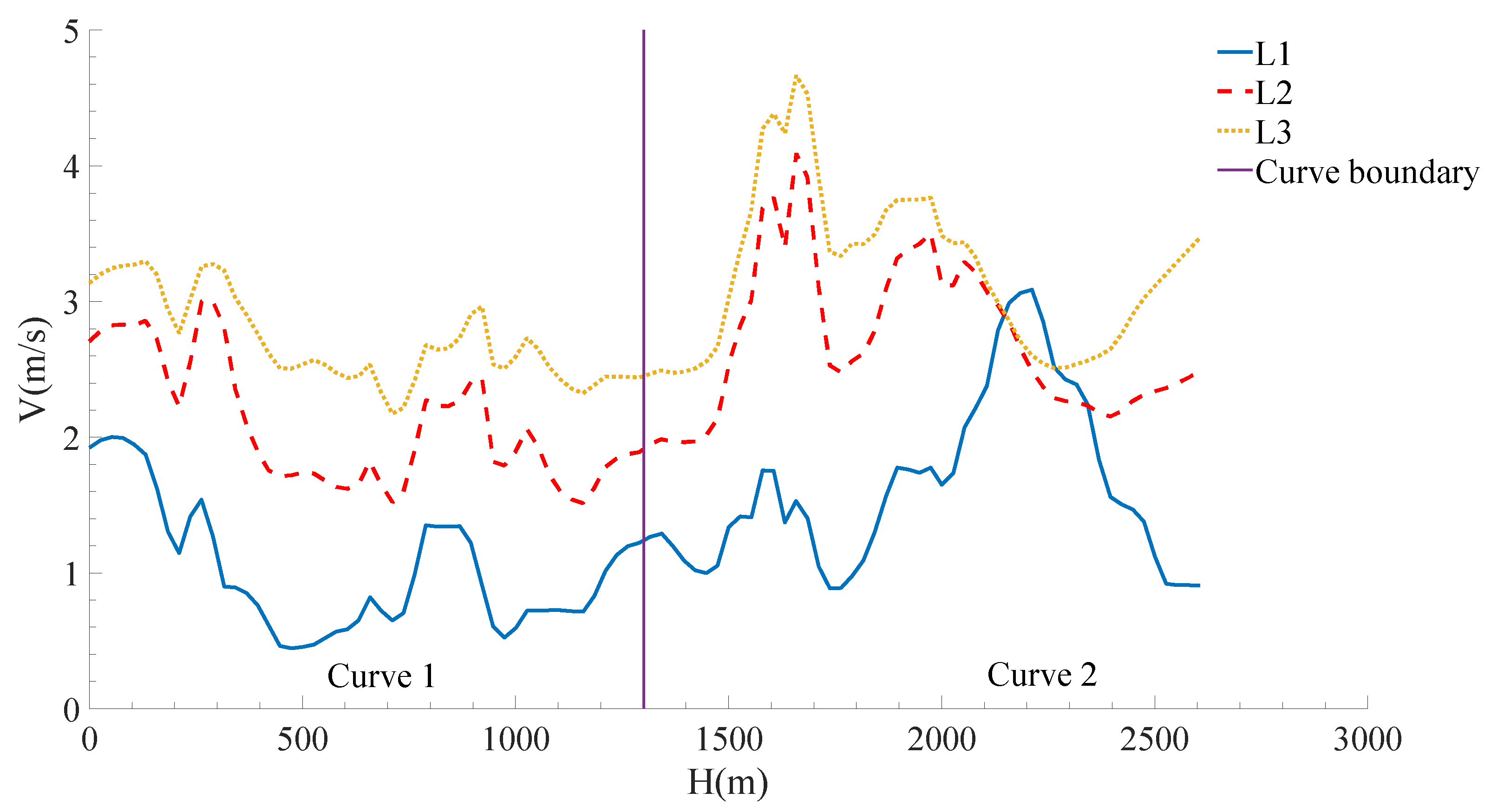
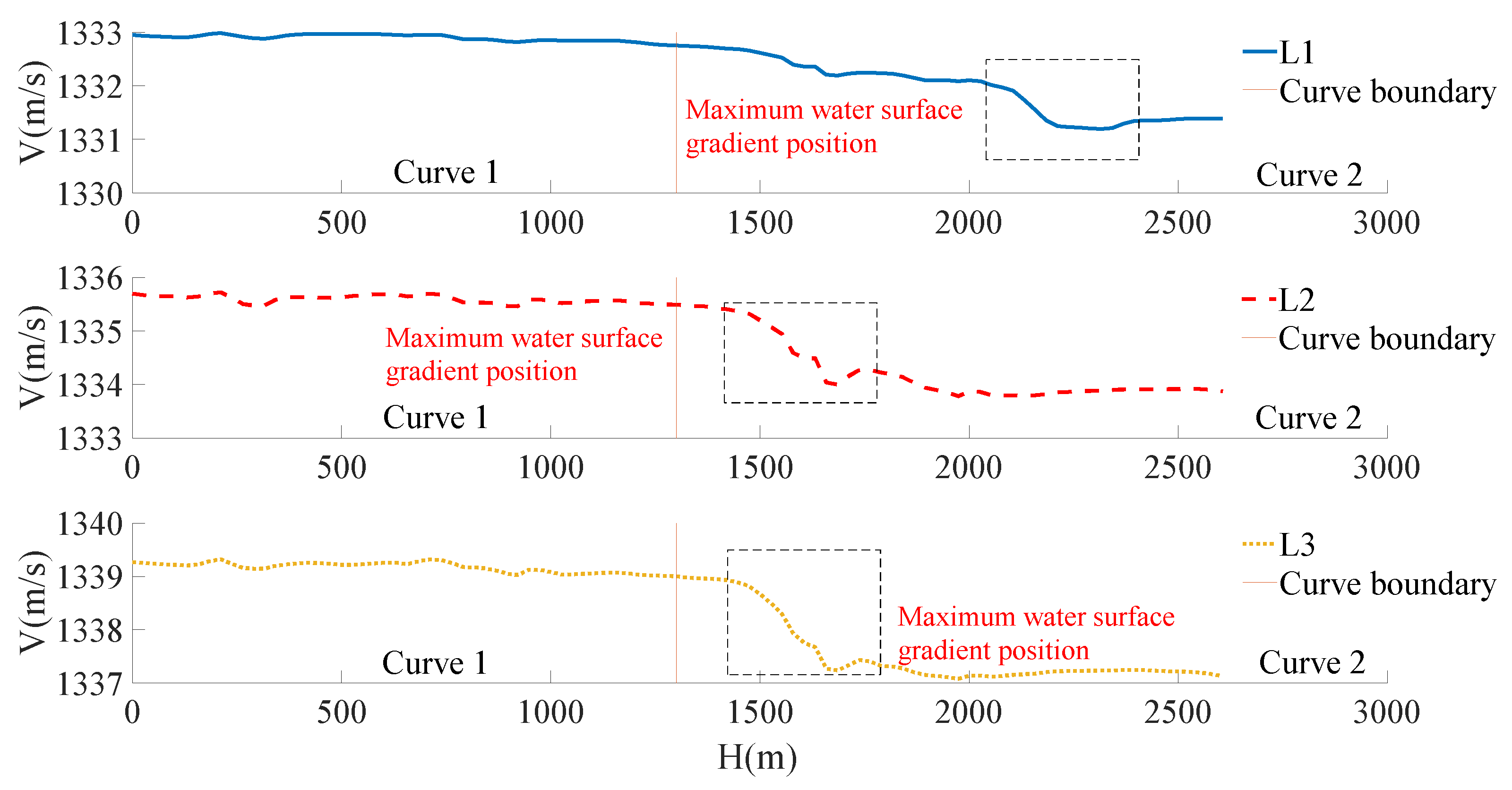
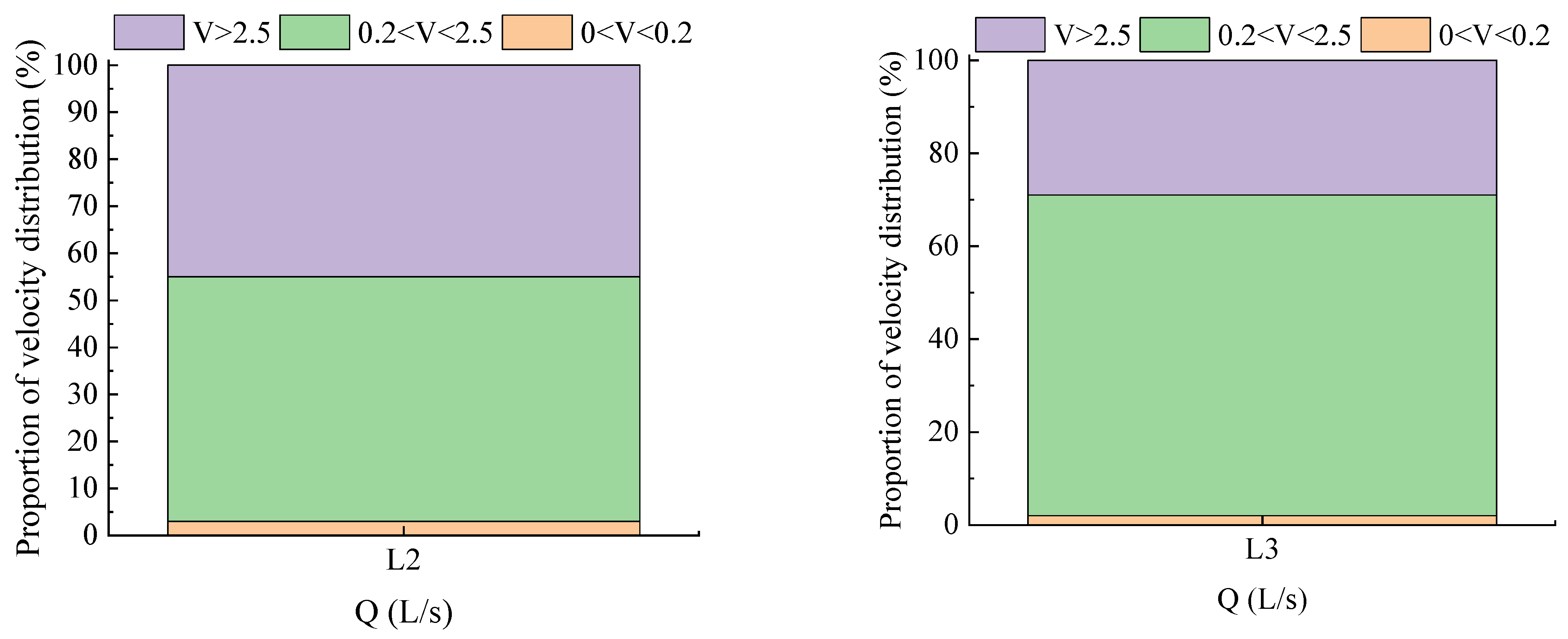
3.2.1. Flow Velocity
3.2.2. Water Level and Depth
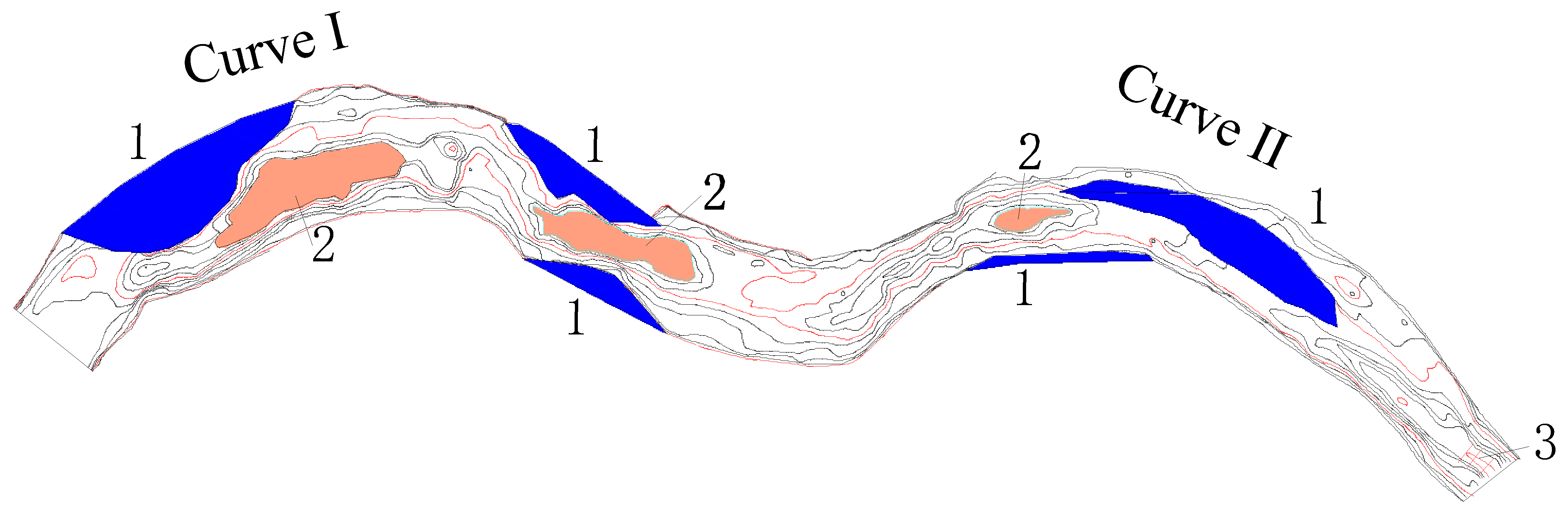
3.2.3. Flow Pattern
3.2.4. Fish Living Environment
3.3. Numerical Simulation Analysis after River Regulation
3.3.1. Flow Velocity
3.3.2. Water Level and Depth
3.3.3. Flow Pattern
3.3.4. Fish Living Environment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, M. Flow Characteristics and Influence of Geometric Factors in a Bend. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2017. [Google Scholar]
- Liu, X.X.; Bai, Y.C. Turbulent structure and bursting process in multi-bend meander channel. J. Hydrodyn. Ser. B 2014, 26, 207–215. [Google Scholar] [CrossRef]
- Cao, Y.F. Hydrodynamic Instability and Short-Term Evolution Properties of Bed Surface in Curved Channel. Ph.D. Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Van Balen, W.; Blanckaert, K.; Uijttewaal, W.S.J. Analysis of the role of turbulence in curved open-channel flow at different water depths by means of experiments, LES and RANS. J. Turbul. 2010, 11, N12. [Google Scholar] [CrossRef]
- Stoesser, T.; Ruether, N.; Olsen, N.R.B. Calculation of primary and secondary flow and boundary shear stresses in a meandering channel. Adv. Water Resour. 2010, 33, 158–170. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, Y.-T.; Ji, X. Hydrodynamic characteristics of flow over emergent vegetation in a strongly curved channel. J. Hydraul. Res. 2022, 60, 240–257. [Google Scholar] [CrossRef]
- He, Y.; Cheng, H.; Chen, J. Morphological evolution of mouth bars on the Yangtze estuarine waterways in the last 100 years. J. Geogr. Sci. 2013, 23, 219–230. [Google Scholar] [CrossRef]
- Breen, M.; Dyson, J.; O’Neill, F.G.; Jones, E.; Haigh, M. Swimming endurance of haddock (Melanogrammus aeglefinus L.) at prolonged and sustained swimming speeds, and its role in their capture by towed fishing gears. ICES J. Mar. Sci. 2004, 61, 1071–1079. [Google Scholar] [CrossRef]
- Bretón, F.; Baki, A.; Link, O.; Zhu, D.; Rajaratnam, N. Flow in nature-like fishway and its relation to fish behaviour. Can. J. Civ. Eng. 2013, 40, 567–573. [Google Scholar] [CrossRef]
- Winger, P.D.; He, P.; Walsh, S.J. Factors affecting the swimming endurance and catchability of Atlantic cod (Gadus morhua). Can. J. Fish. Aquat. Sci. 2000, 57, 1200–1207. [Google Scholar] [CrossRef]
- Smith, D.L. The Shear Flow Environment of Juvenile Salmonids. Ph.D. Thesis, University of Idaho, Moscow, ID, USA, 2003. [Google Scholar]
- Haro, A.; Odeh, M.; Noreika, J.; Castro-Santos, T. Effect of water acceleration on downstream migratory behavior and passage of Atlantic salmon smolts and juvenile American shad at surface bypasses. Trans. Am. Fish. Soc. 1998, 127, 118–127. [Google Scholar] [CrossRef]
- He, D.R. Fish Behavior; Xiamen University Press: Xiamen, China, 1998. [Google Scholar]
- Hammer, C. Fatigue and exercise tests with fish. Comp. Biochem. Physiol. Part A Physiol. 1995, 112, 1–20. [Google Scholar] [CrossRef]
- Plaut, I. Critical swimming speed: Its ecological relevance. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2001, 131, 41–50. [Google Scholar] [CrossRef]
- Yang, N.-L.; Dou, X.-P.; Zhang, X.-Z.; Luo, X.-F. Hydrodynamic effect of the regulation project of Yangtze River deepwater channel downstream of Nanjing. China Ocean Eng. 2013, 27, 767–779. [Google Scholar] [CrossRef]
- Jian, L.; Wang, P.; Wang, M.; Han, L. Experimental study on hydraulic characteristics of new ecological slope protection structure. Mar. Georesources Geotechnol. 2021. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Alonso, C.V.; Shields, F.D. Local scour associated with angled spur dikes. Hydraulic Eng. 2002, 128, 1087–1093. [Google Scholar] [CrossRef]
- Kang, J.; Yeo, H.; Jung, S. Flow characteristic variations on groney types for aquatic habitat. Sci. Res. 2012, 4, 811–812. [Google Scholar] [CrossRef][Green Version]
- Liu, C.H.; Liu, S.; Li, D.; Yan, J.; Lu, C. An Analysis of the Impact of Zhonghuan Sewage Outlet on Water Quality of the Yangtze River Based On MIKE21 Model. China Rural. Water Conserv. Hydropower 2020, 1, 72–76. [Google Scholar]
- Li, T.Y.; Li, Z.H.; Huang, B.B. Simulation on water quantity and quality of Shahe Reservoir by Mike21 model. Acta Sci. Circumstantiae 2021, 41, 293–300. [Google Scholar] [CrossRef]
- Tan, W.; Hu, S. Implementation of first-order finite-volume Osher scheme in shallow water flow computation. Adv. Water Sci. 1994, 5, 262–270. (In Chinese) [Google Scholar]
- Zhou, J.G.; Causon, D.M.; Ingram, D.M.; Mingham, C.G. Numerical solutions of the shallow water equations with discontinuous bed topography. Int. J. Numer. Methods Fluids 2002, 38, 769–788. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V.; Zanni, A.A. Case study: Malpasset dam-break simulation using a two-dimensional finite volume method. J. Hydraul. Eng. ASCE 2002, 128, 460–472. [Google Scholar] [CrossRef]
- Hu, J.L. Hydraulic Characteristics of a New Permeable Spur Dike and Its Effect on Fish Behavior. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 3–55. [Google Scholar] [CrossRef]



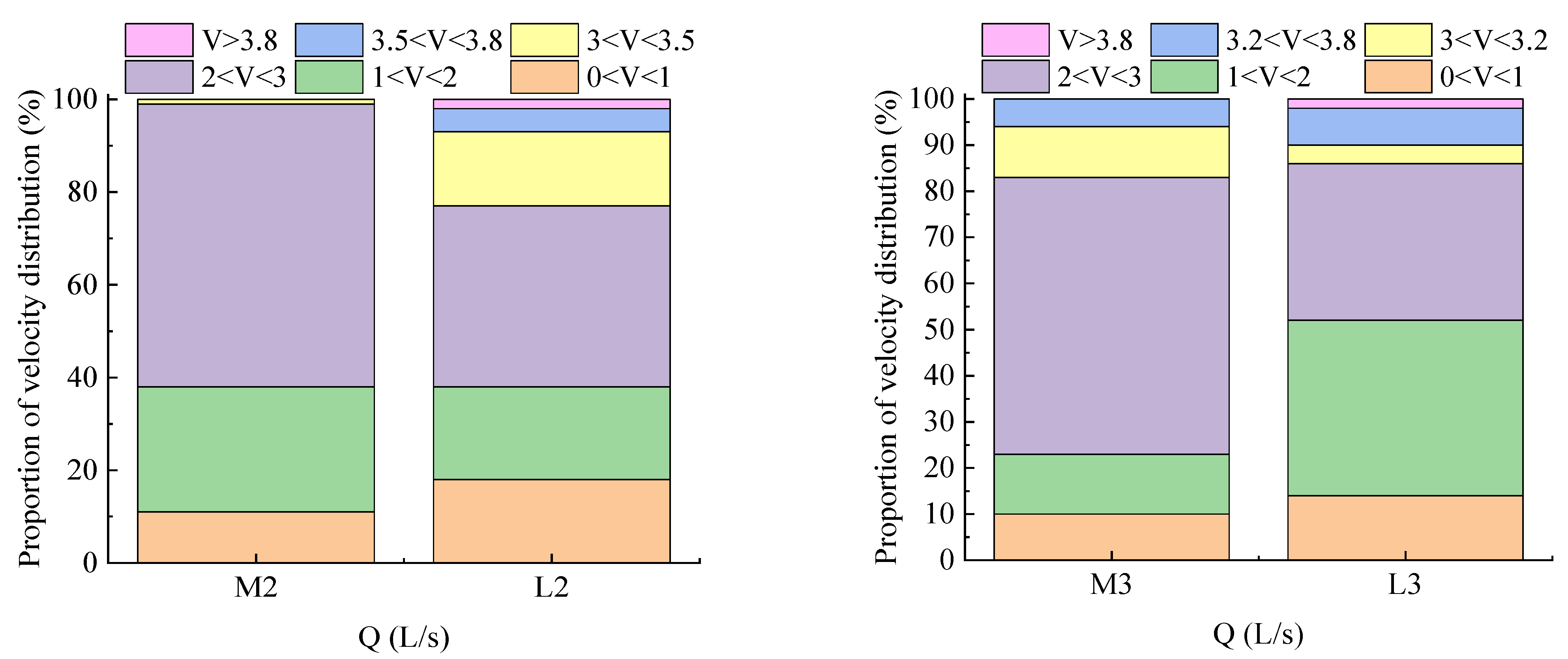
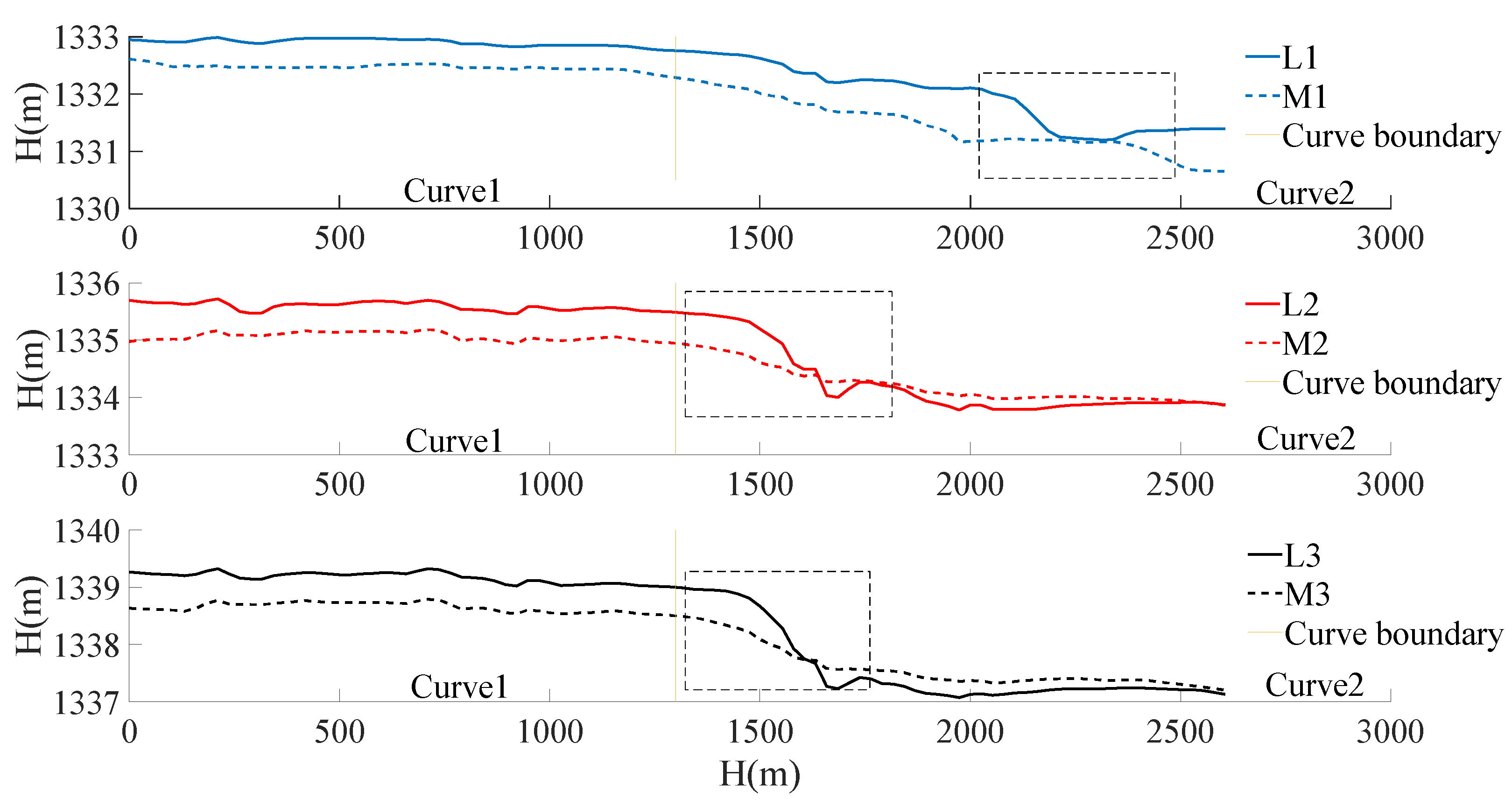
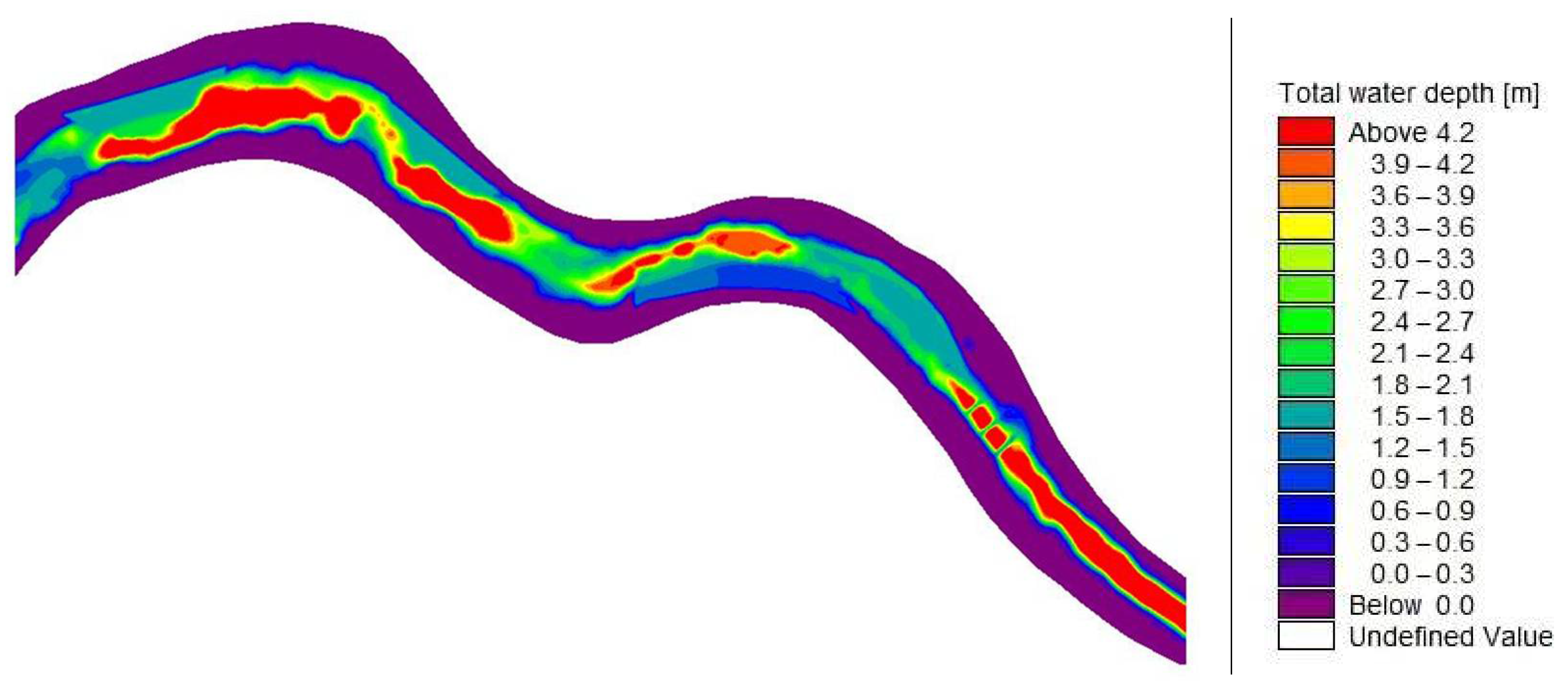

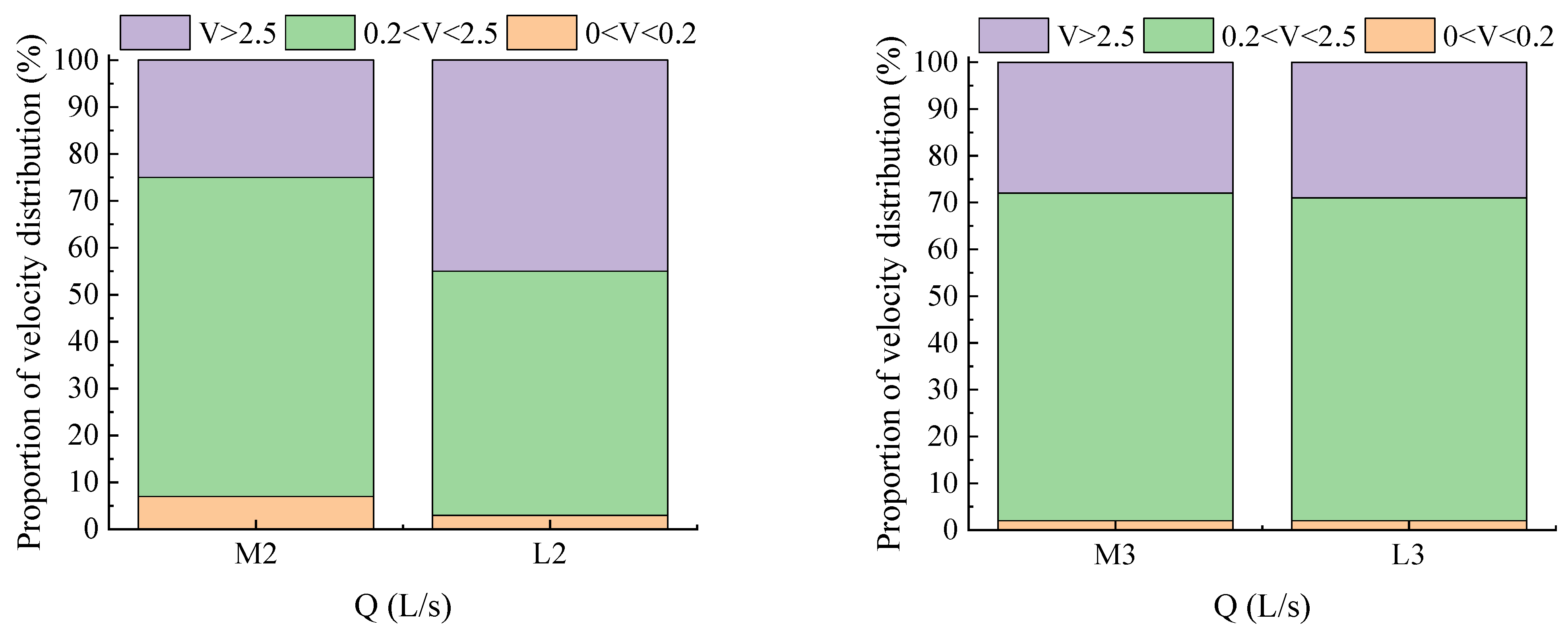
| Prototype Condition | Mathematical Model Test Conditions | ||||
|---|---|---|---|---|---|
| Natural Conditions | Natural Conditions | After Remediation | |||
| Working Condition | Flow (m3/s) | Working Condition | Flow (m3/s) | Working Condition | Flow (m3/s) |
| - | - | L1 | 374 | M1 | 374 |
| A1 | 1520 | L2 | 1520 | M2 | 1520 |
| - | - | L3 | 3410 | M3 | 3410 |
| Gradient (‰) | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
| Velocity (m/s) | 4 | 3.8 | 3.5 | 3.2 | 2.9 | 2.5 | 2.1 |
| Location | Error Value | Location | Error Value |
|---|---|---|---|
| C1 | −0.5% | C6 | 1.2% |
| C2 | 0.1% | C7 | 1.8% |
| C3 | 0.2% | C8 | 0.6% |
| C4 | 0.3% | C9 | 0.9% |
| C5 | 3.1% |
| H (m) | Error Value | H (m) | Error Value | H (m) | Error Value |
|---|---|---|---|---|---|
| 0 | −3.73% | 876.6821 | 3.69% | 1667.3218 | −5.16% |
| 101.8836 | −2.96% | 952.0129 | 9.00% | 1709.6348 | 2.45% |
| 166.9831 | −4.83% | 1022.0596 | 0.28% | 1747.4577 | 4.35% |
| 237.3158 | −4.38% | 1100.1048 | 13.22% | 1825.6284 | 6.17% |
| 311.4188 | −6.02% | 1159.6542 | 7.08% | 1868.7288 | 3.21% |
| 381.3038 | −8.39% | 1210.8155 | 6.25% | 1903.3225 | 3.61% |
| 420.921 | −8.94% | 1258.7356 | −5.78% | 1973.2406 | −0.97% |
| 500.7897 | −12.32% | 1337.7123 | −5.63% | 2056.0031 | 0.72% |
| 569.4314 | 5.71% | 1472.2932 | −8.39% | 2148.2125 | −6.63% |
| 658.2227 | 5.11% | 1513.4778 | −1.80% | 2210.2138 | 3.66% |
| 706.4791 | 5.62% | 1552.1245 | −8.57% | 2328.5594 | 7.02% |
| 785.4862 | −11.08% | 1593.023 | −12.25% | 2394.4765 | 3.48% |
| 826.5563 | −5.36% | 1632.6447 | 10.85% | 2606.0386 | 6.09% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Li, J.; Wang, M.; Hu, J.; Zhang, F. Numerical Simulation of the Hydraulic Characteristics and Fish Habitat of a Natural Continuous Meandering River. Sustainability 2022, 14, 9798. https://doi.org/10.3390/su14169798
Wang P, Li J, Wang M, Hu J, Zhang F. Numerical Simulation of the Hydraulic Characteristics and Fish Habitat of a Natural Continuous Meandering River. Sustainability. 2022; 14(16):9798. https://doi.org/10.3390/su14169798
Chicago/Turabian StyleWang, Pingyi, Jian Li, Meili Wang, Jielong Hu, and Fan Zhang. 2022. "Numerical Simulation of the Hydraulic Characteristics and Fish Habitat of a Natural Continuous Meandering River" Sustainability 14, no. 16: 9798. https://doi.org/10.3390/su14169798
APA StyleWang, P., Li, J., Wang, M., Hu, J., & Zhang, F. (2022). Numerical Simulation of the Hydraulic Characteristics and Fish Habitat of a Natural Continuous Meandering River. Sustainability, 14(16), 9798. https://doi.org/10.3390/su14169798






