Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model
Abstract
:1. Introduction
2. Background of the Case
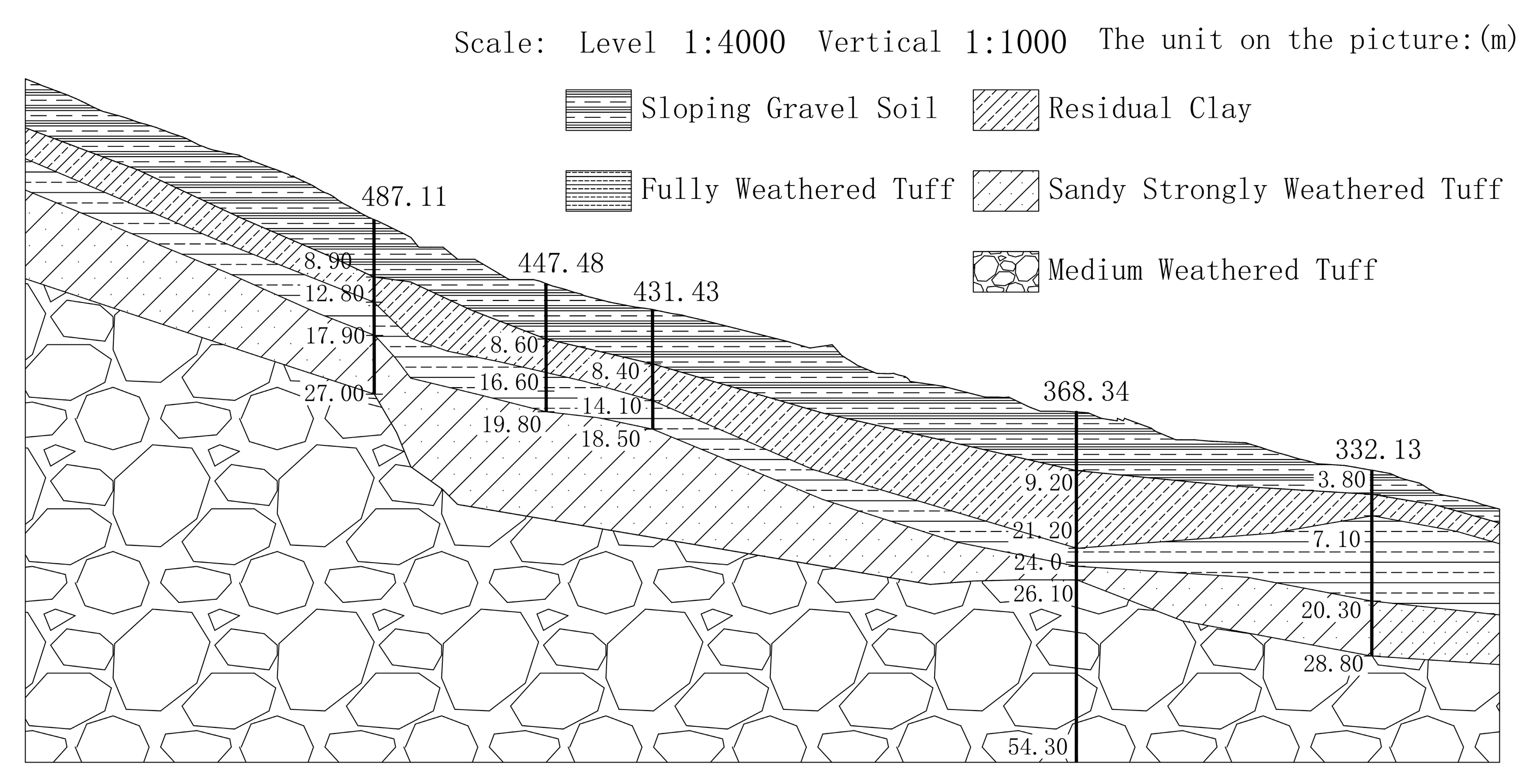
2.1. Research Area
2.2. Monitoring Methods
3. Displacement Prediction Model
3.1. SSA
3.2. LSTM
- (1)
- Forgetting gate: used to determine whether to retain the value of the memory unit through the sigmoid function to determine the input information and the previous moment of information forgotten or retained. Its formula is shown in (4):
- (2)
- Input gates: used to control the addition of new information on the training process to obtain the cell state at that moment. The sigmoid layer in the input gate determines the content of the information update, and the tanh layer generates a new vector of candidate values to be added to the current state. The formulas are shown in (5) and (6):
- (3)
- output gate: the output value determined by the sigmoid function is multiplied with the tanh functions to obtain the final output value. The formula is shown in (8):
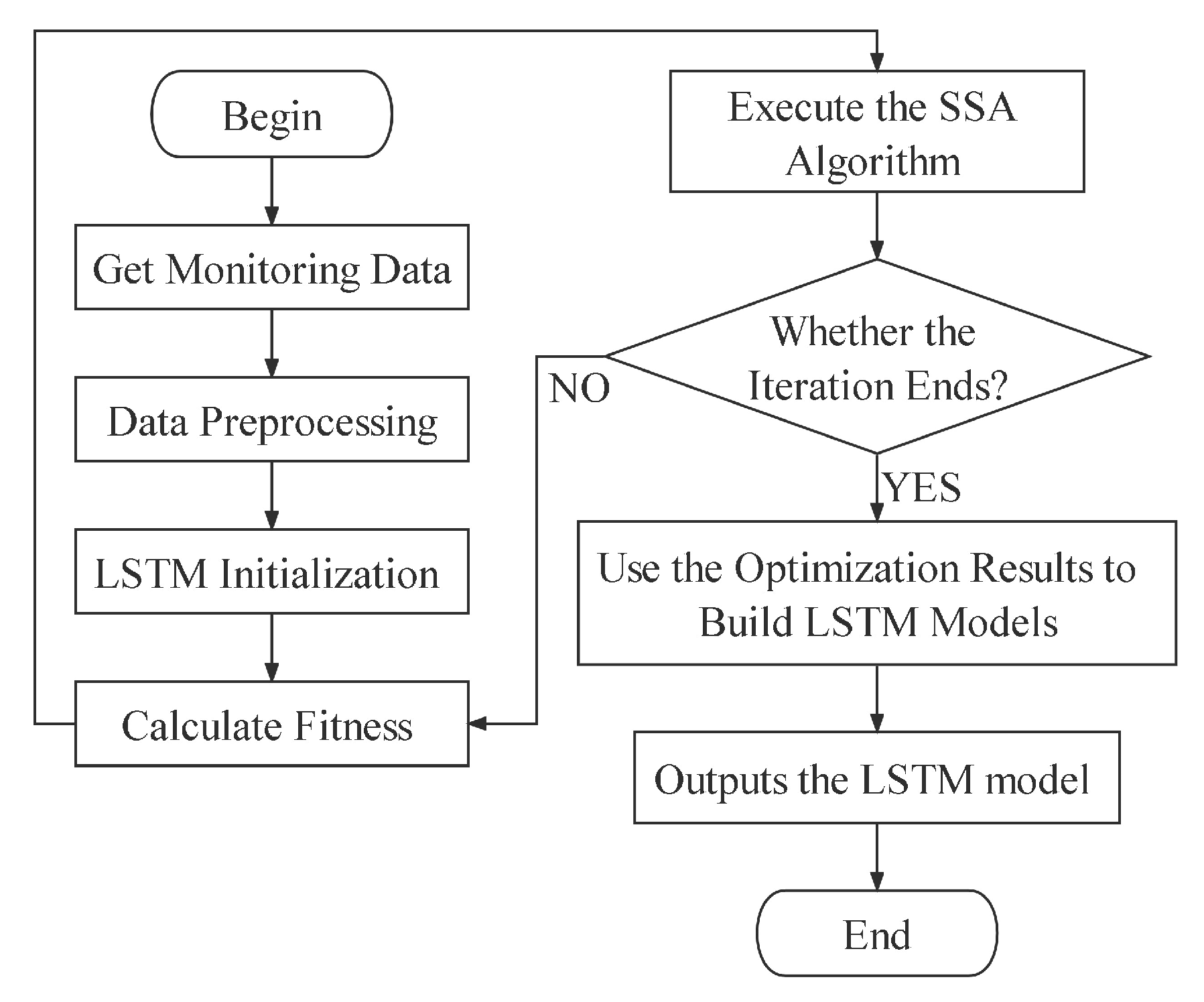
3.3. SSA-LSTM
- Reading of monitoring data;
- Data pre-processing, including filtering and normalization of monitoring data;
- Population initialization, including population size, maximum number of iterations, percentage of discoverers and scouts, and optimization parameters of LSTM;
- Execution of SSA algorithm;
- If the algorithm reaches the preset maximum number of iterations or the best fitness is continuously maintained at 10% of the total number of iterations, the algorithm search ends and returns the sparrow location information of the best fitness, which is the best optimization parameter of the LSTM; otherwise, skip to 4;
- The optimization results are used to build the LSTM model and saved.
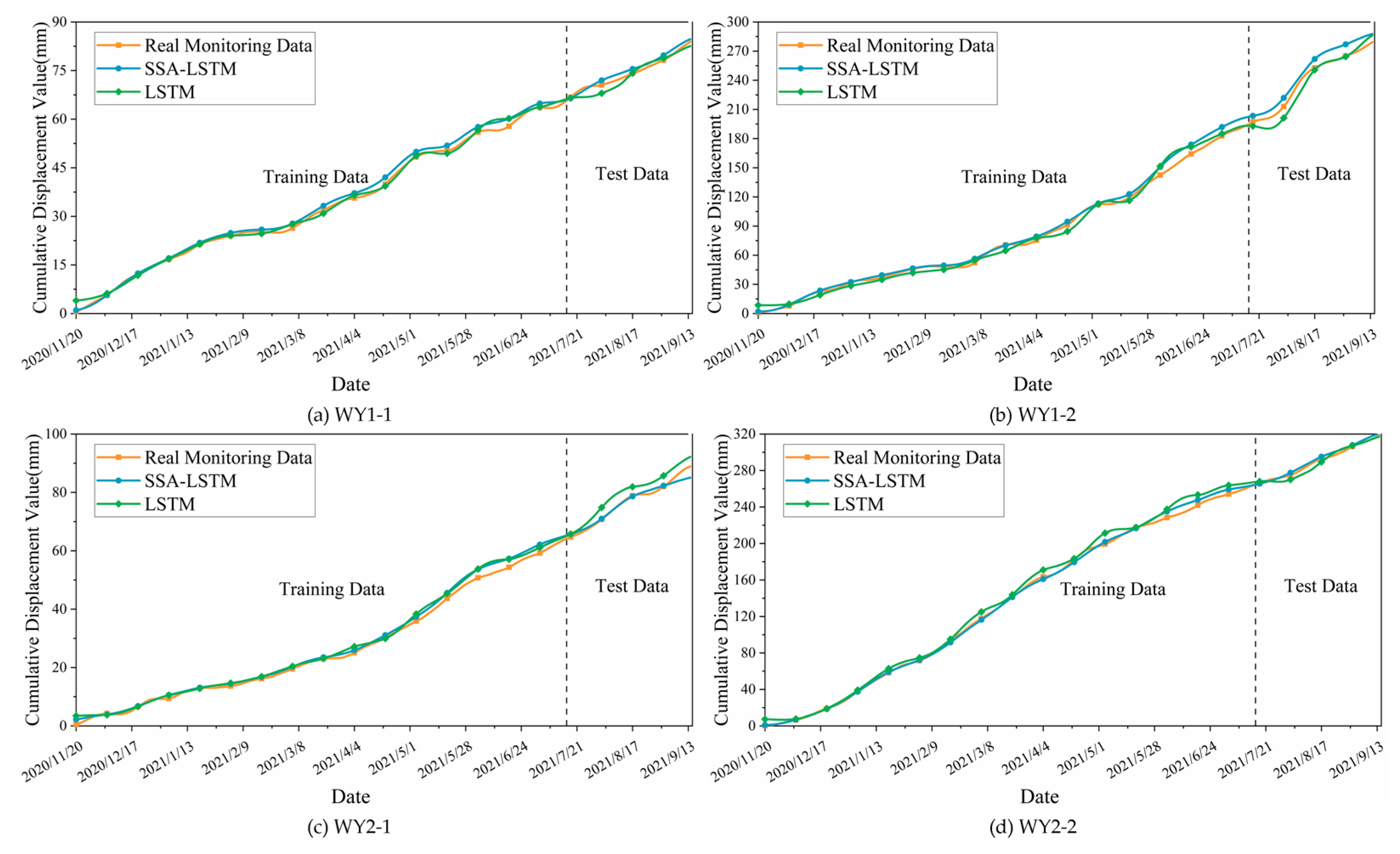
3.4. Comparison of Predicted Results
4. Building Early Warning Models
4.1. Model Updates
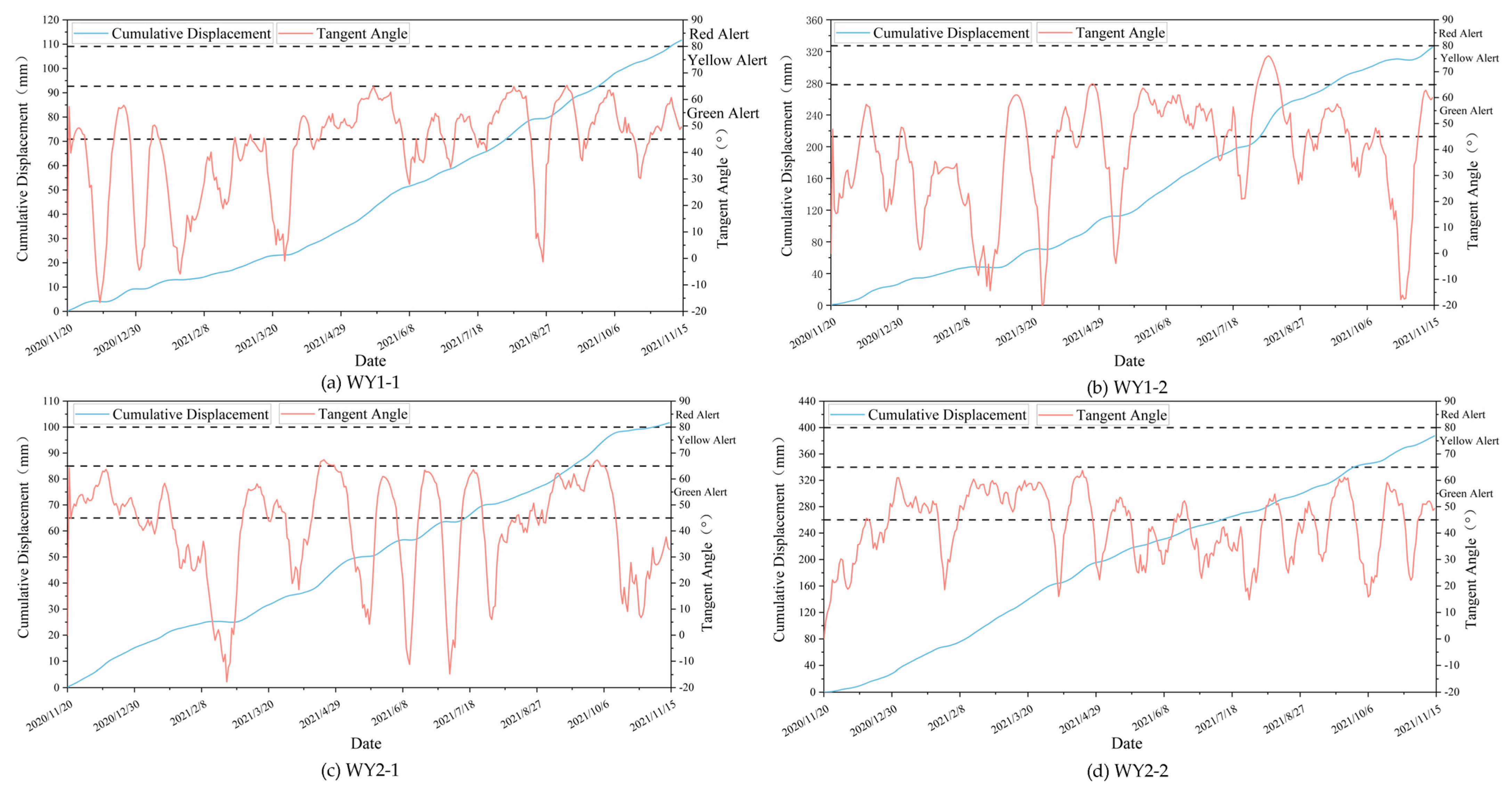
4.2. Early Warning Level Classification
4.3. Early Warning Model Workflow
- Data pre-processing, including noise reduction, normalization, and extraction of the first 300 data;
- Optimize the online migration learning of the initial model using the SSA algorithm to update the weights within the initial model to adapt it to the latest monitoring data using the 300 most recent data monitored;
- Predict the displacement value for the coming day and obtain the warning level of displacement for that day using the improved tangent angle model;
- Transmission of alert levels to the server side for alerting.
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazard Earth Syst. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Huning, L.S.; Chiang, F.; Sadegh, M.; Vahedifard, F.; Mazdiyasni, O.; Moftakhari, H.; Mallakpour, I. How do natural hazards cascade to cause disasters? Nature 2018, 561, 458–460. [Google Scholar] [CrossRef] [PubMed]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Kanungo, D.P.; Sharma, S. Rainfall thresholds for prediction of shallow landslides around Chamoli-Joshimath region, Garhwal Himalayas, India. Landslides 2014, 11, 629–638. [Google Scholar] [CrossRef]
- Harilal, G.T.; Madhu, D.; Ramesh, M.V.; Pullarkatt, D. Towards establishing rainfall thresholds for a real-time landslide early warning system in Sikkim, India. Landslides 2019, 16, 2395–2408. [Google Scholar] [CrossRef]
- Herrera, G.; Fernández-Merodo, J.A.; Mulas, J.; Pastor, M.; Luzi, G.; Monserrat, O. A landslide forecasting model using ground based SAR data: The Portalet case study. Eng. Geol. 2009, 105, 220–230. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. 2010, 115, F03013. [Google Scholar] [CrossRef]
- Siqing, Q. Nonlinear Evolution Mechanism and Physical Prediction of Slope Instability Process. Chin. J. Geotech. Eng. 2005, 27, 6–13. (In Chinese) [Google Scholar]
- Qiang, X.; Yuping, Z.; Jiangpeng, Q.; Chengjun, W.; Chengjiang, H. An Improved Tangent Angle and Corresponding Landslide Warning Criterion. Geol. Bull. 2009, 28, 501–505. (In Chinese) [Google Scholar]
- Zhang, X.; Zhu, C.; He, M.; Dong, M.; Zhang, G.; Zhang, F. Failure Mechanism and Long Short-Term Memory Neural Network Model for Landslide Risk Prediction. Remote Sens. 2022, 14, 166. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y.; Zhou, C.; Hong, H.; Glade, T.; Yin, K. Landslide Displacement Prediction Combining LSTM and SVR Algorithms: A Case Study of Shengjibao Landslide from the Three Gorges Reservoir Area. Appl. Sci. 2020, 10, 7830. [Google Scholar] [CrossRef]
- Niu, X.; Ma, J.; Wang, Y.; Zhang, J.; Chen, H.; Tang, H. A Novel Decomposition-Ensemble Learning Model Based on Ensemble Empirical Mode Decomposition and Recurrent Neural Network for Landslide Displacement Prediction. Appl. Sci. 2021, 11, 4684. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Hongtao, N. Smart safety early warning model of landslide geological hazard based on BP neural network. Saf. Sci. 2020, 123, 104572. [Google Scholar] [CrossRef]
- Yan, Y.; Ashraf, M.A. The application of the intelligent algorithm in the prevention and early warning of mountain mass landslide disaster. Arab. J. Geosci. 2020, 13, 79. [Google Scholar] [CrossRef]
- Huang, L.; Xiang, L. Method for Meteorological Early Warning of Precipitation-Induced Landslides Based on Deep Neural Network. Neural Process. Lett. 2018, 48, 1243–1260. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Zhu, C.H.; Hu, G.D. Time Series Prediction of Landslide Displacement Using SVM Model: Application to Baishuihe Landslide in Three Gorges Reservoir Area, China. Appl. Mech. Mater. 2012, 239–240, 1413–1420. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, K.; Alexander, D.E.; Zhou, C. Using an extreme learning machine to predict the displacement of step-like landslides in relation to controlling factors. Landslides 2016, 13, 725–736. [Google Scholar] [CrossRef]
- Li, H.; Xu, Q.; He, Y.; Deng, J. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models. Landslides 2018, 15, 2047–2059. [Google Scholar] [CrossRef]
- Lian, C.; Zeng, Z.; Yao, W.; Tang, H. Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level. Stoch. Environ. Res. Risk Assess. 2014, 28, 1957–1972. [Google Scholar] [CrossRef]
- Dai, B.; Wang, J.; Gu, X.; Xu, C.; Yu, X.; Zhang, H.; Yuan, C.; Nie, W. Development of Modified LSTM Model for Reservoir Capacity Prediction in Huanggang Reservoir, Fujian, China. Geofluids 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, Y.; Wang, Z.; Cao, G.; Wang, R.; Lu, S.; Li, W.; Nie, W.; Zhang, Z. A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism. Water 2022, 2022, 1229. [Google Scholar] [CrossRef]
- Mao, Y.; Qin, G.; Ni, P.; Liu, Q. Analysis of road traffic speed in Kunming plateau mountains: A fusion PSO-LSTM algorithm. Int. J. Urban Sci. 2022, 26, 87–107. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Zhen, H.; Niu, D.; Wang, K.; Shi, Y.; Ji, Z.; Xu, X. Photovoltaic power forecasting based on GA improved Bi-LSTM in microgrid without meteorological information. Energy 2021, 231, 120908. [Google Scholar] [CrossRef]
- Taorui, Z.; Hongwei, J.; Qingli, L.; Kunlong, Y. Landslide displacement prediction based on Variational mode decomposition and MIC-GWO-LSTM model. Stoch. Environ. Res. Risk Assess. 2022, 36, 1353–1372. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Liu, Q.; Jian, W.; Nie, W. Rainstorm hazard early warning system in mountainous cities based on groundwater level change fast prediction. Sustain. Cities Soc. 2021, 69, 102817. [Google Scholar] [CrossRef]
- Hou, B.; Zhou, Z. Learning with Interpretable Structure from Gated RNN. IEEE Trans. Neural Netw. Learn. Syst. 2020, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Turkoglu, M.O.; D’Aronco, S.; Wegner, J.; Schindler, K. Gating Revisited: Deep Multi-layer RNNs That Can Be Trained. IEEE Trans. Pattern. Anal. 2021, 44, 4081–4092. [Google Scholar] [CrossRef] [PubMed]
- Tong, W.; Li, L.; Zhou, X.; Hamilton, A.; Zhang, K. Deep learning PM2.5 concentrations with bidirectional LSTM RNN. Air Qual. Atmos. Health 2019, 12, 411–423. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.S.J. Long Short-Term Memory. Neural Comput. 1997, 8, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Wang, Z.; Wang, P.; Liu, Z.; Li, N.; Zhang, C. An Initial Value Estimation Method for the Kalman and Extended Kalman Filters in Underground Metal Detection. Appl. Sci. 2019, 9, 4113. [Google Scholar] [CrossRef]
- Chen, B.; Dang, L.; Gu, Y.; Zheng, N.; Principe, J.C. Minimum Error Entropy Kalman Filter. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5819–5829. [Google Scholar] [CrossRef]
- Matthias Katzfuss, J.R.S.C. Understanding the Ensemble Kalman Filter. Am. Stat. 2016, 70, 350–357. [Google Scholar] [CrossRef]
- Yang, F.; Cui, Y.; Wu, F.; Zhang, R. Fault Monitoring of Chemical Process Based on Sliding Window Wavelet Denoising GLPP. Processes 2021, 9, 86. [Google Scholar] [CrossRef]
- Gradolewski, D.; Magenes, G.; Johansson, S.; Kulesza, W. A Wavelet Transform-Based Neural Network Denoising Algorithm for Mobile Phonocardiography. Sensors 2019, 19, 957. [Google Scholar] [CrossRef]
- Priyadarshani, N.; Marsland, S.; Castro, I.; Punchihewa, A. Birdsong Denoising Using Wavelets. PLoS ONE 2016, 11, e146790. [Google Scholar] [CrossRef] [PubMed]
- John, A.; Sadasivan, J.; Seelamantula, C.S. Adaptive Savitzky-Golay Filtering in Non-Gaussian Noise. IEEE Trans. Signal Process. 2021, 69, 5021–5036. [Google Scholar] [CrossRef]
- Niedźwiecki, M.J.; Ciołek, M.; Gańcza, A.; Kaczmarek, P. Application of regularized Savitzky–Golay filters to identification of time-varying systems. Automatica 2021, 133, 109865. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rashid, M.A.; Ahmad, M. Selecting the optimal conditions of Savitzky–Golay filter for fNIRS signal. Biocybern. Biomed. Eng. 2019, 39, 624–637. [Google Scholar] [CrossRef]
- Qiang, X.; Dalei, P.; Chaoyang, H.; Xing, Q.; Kuanyao, Z.; Dehao, X. Research on the theory and method of monitoring and early warning of sudden loess landslides—Taking Heifangtai, Gansu Province as an example. Chin. J. Eng. Geol. 2020, 28, 111–121. (In Chinese) [Google Scholar]
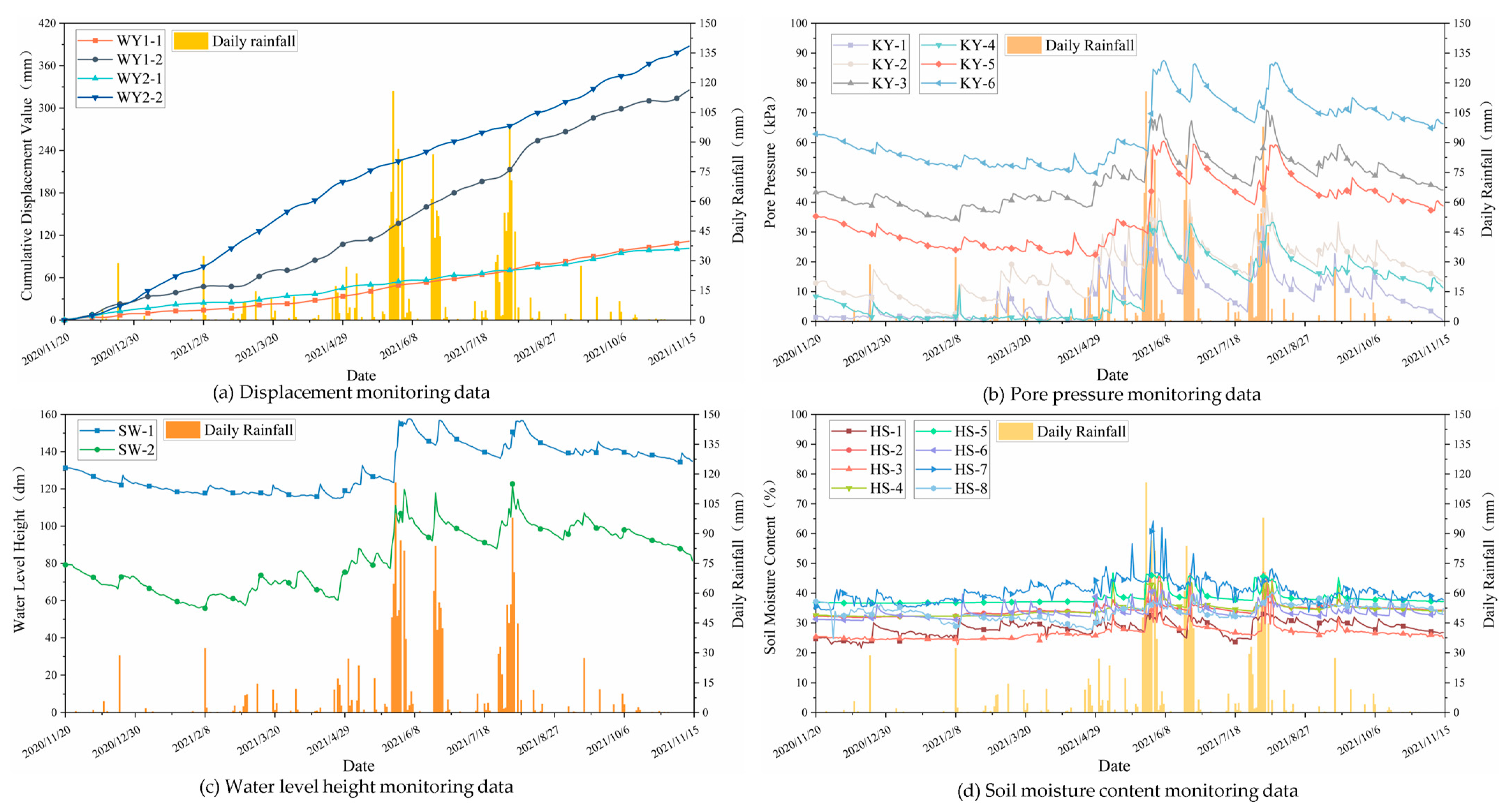


| Monitoring Content | Monitoring Equipment | Monitoring Site | Number of Sensors |
|---|---|---|---|
| Displacement | Guide wheel type fixed measurement | Landslide body | 4 |
| Pore water pressure | Pore water pressure gauge | Landslide body | 6 |
| Water-level monitoring | Water level gauge | Landslide body | 2 |
| Soil water content | Moisture meter | Landslide body | 8 |
| Rainfall monitoring | Rain gauge | Side slope area | 1 |
| Type of Error | SSA-LSTM | LSTM |
|---|---|---|
| MAE | 0.875 | 3.276 |
| RMSE | 1.307 | 3.393 |
| R2 | 0.965 | 0.766 |
| Type of Error | SSA-LSTM | LSTM |
|---|---|---|
| MAE | 9.063 | 5.997 |
| RMSE | 9.439 | 7.563 |
| R2 | 0.880 | 0.923 |
| Type of Error | SSA-LSTM | LSTM |
|---|---|---|
| MAE | 1.200 | 1.421 |
| RMSE | 1.269 | 1.700 |
| R2 | 0.922 | 0.860 |
| Type of Error | SSA-LSTM | LSTM |
|---|---|---|
| MAE | 2.168 | 2.927 |
| RMSE | 2.375 | 3.612 |
| R2 | 0.978 | 0.949 |
| Type of Error | Online Learning | Off-Line Learning | Upgraded |
|---|---|---|---|
| Average error | 0.935 | 5.057 | 4.122 |
| Maximum Error | 5.859 | 12.701 | 6.842 |
| Type of Error | Online Learning | Off-Line Learning | Upgraded |
|---|---|---|---|
| Average error | 2.275 | 10.304 | 8.030 |
| Maximum Error | 4.489 | 14.235 | 9.746 |
| Type of Error | Online Learning | Off-Line Learning | Upgraded |
|---|---|---|---|
| Average error | 1.530 | 9.550 | 8.021 |
| Maximum Error | 5.838 | 14.522 | 8.683 |
| Type of Error | Online Learning | Off-Line Learning | Upgraded |
|---|---|---|---|
| Average error | 0.765 | 8.063 | 7.298 |
| Maximum Error | 1.727 | 9.562 | 7.835 |
| Early Warning Thresholds | ||||
|---|---|---|---|---|
| Early warning level | None | Green alert | Yellow alert | Red alert |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Jin, A.; Nie, W.; Liu, C.; Li, Y. Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model. Sustainability 2022, 14, 10246. https://doi.org/10.3390/su141610246
Yang S, Jin A, Nie W, Liu C, Li Y. Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model. Sustainability. 2022; 14(16):10246. https://doi.org/10.3390/su141610246
Chicago/Turabian StyleYang, Shasha, Anjie Jin, Wen Nie, Cong Liu, and Yu Li. 2022. "Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model" Sustainability 14, no. 16: 10246. https://doi.org/10.3390/su141610246
APA StyleYang, S., Jin, A., Nie, W., Liu, C., & Li, Y. (2022). Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model. Sustainability, 14(16), 10246. https://doi.org/10.3390/su141610246






