The Multi-Depot Traveling Purchaser Problem with Shared Resources
Abstract
:1. Introduction
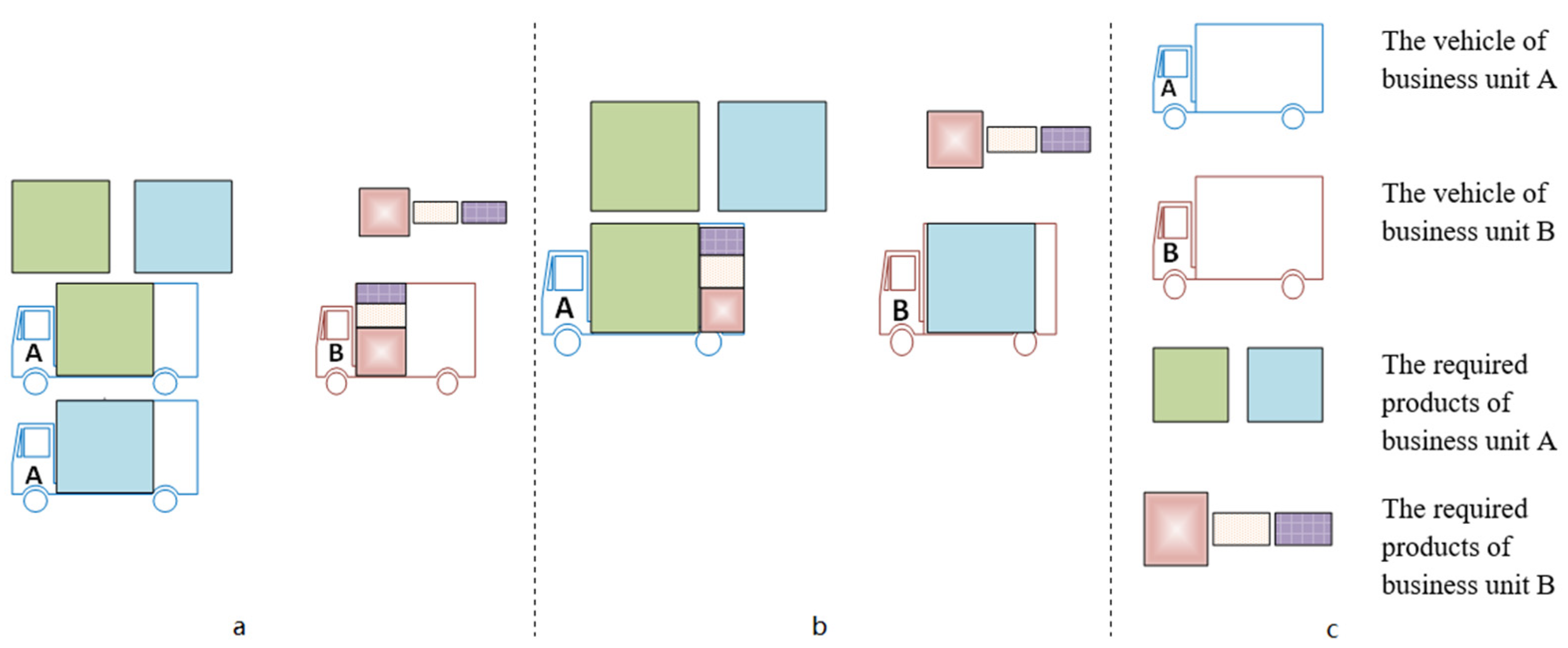
- First approach—Each dispatched vehicle should return to its depot (its starting node) at the end of its route. Indeed, the route of each vehicle is a “closed route” or “circuit”. One drawback associated with this approach is that the corresponding depot of the vehicle is the last one that receives its purchased products (Figure 3a);
- Second approach—Each vehicle can stay at the depot of the last purchaser whose products are delivered by this vehicle. Contrary to the first approach, the vehicle does not have to return to its starting depot (Figure 3b).
- -
- Since each vehicle might continue its route after returning to its starting depot to deliver the products of others, each vehicle might make more than one trip (as is also the case with the Multi-trip Vehicle Routing Problem);
- -
- Suppose the vehicle returns to its initial depot and provides products to it, and then delivers the products to others. In that case, the routes are a combination of closed and open routes (similar to Figure 3b). We call the second proposed approach a “Multi-Trip, Open Vehicle Routing Problem”.
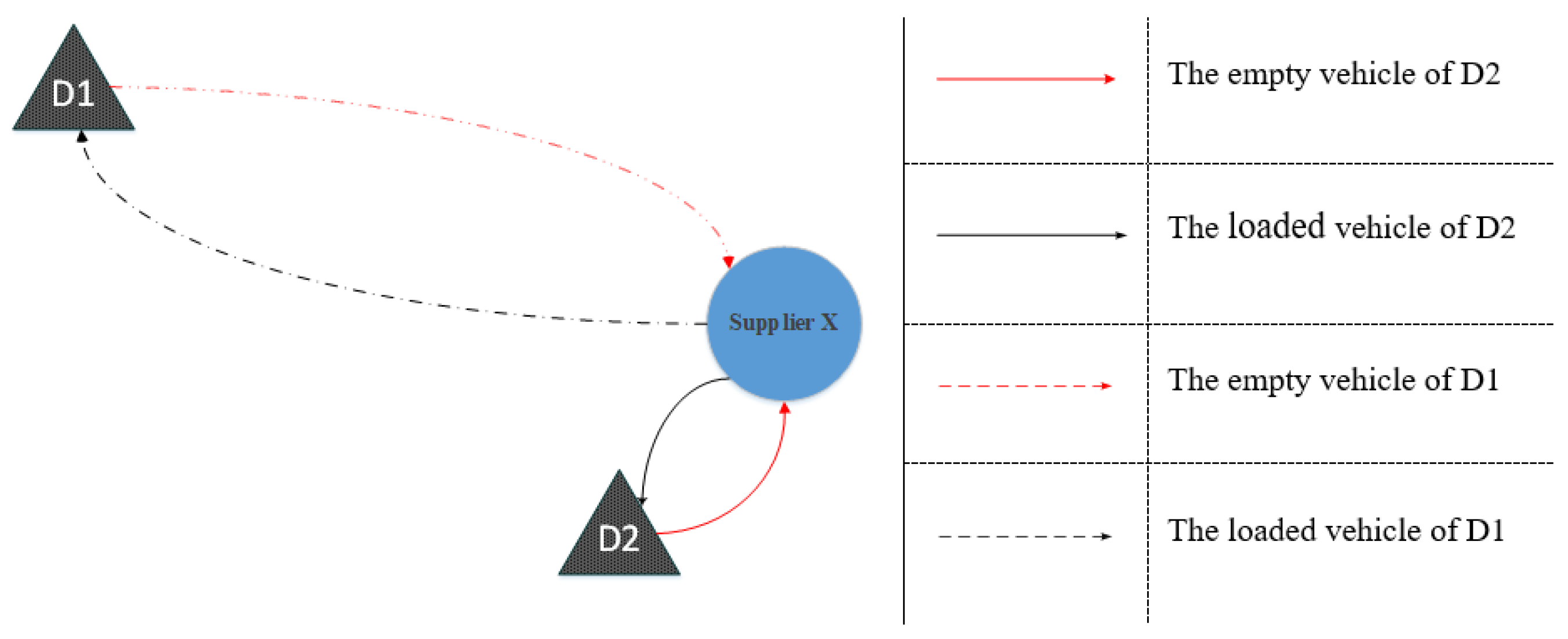
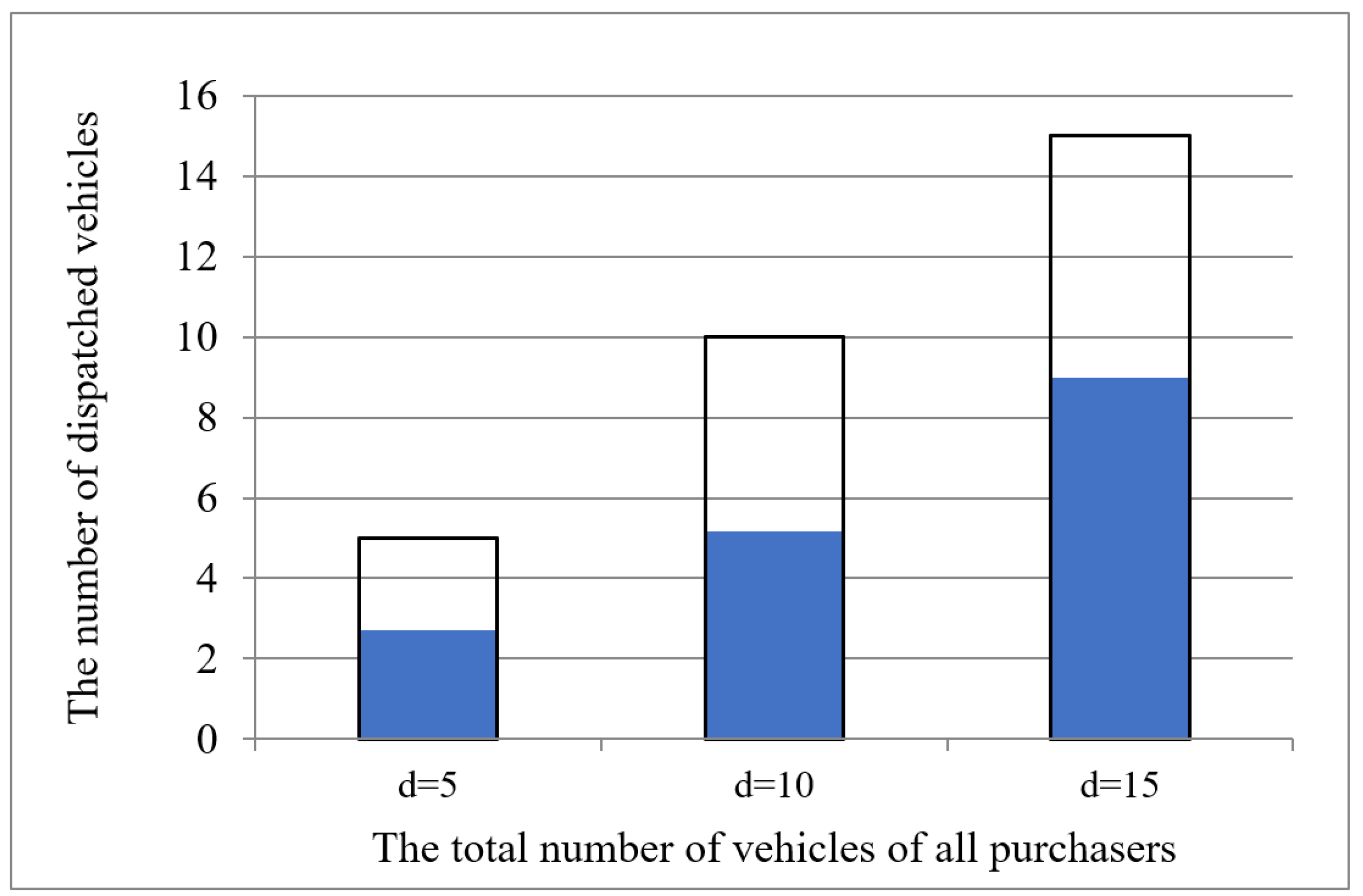
- Modeling—In this paper, we design a collaborative structure between multiple purchasers for the sustainable development of procurement and the inbound logistics network. In this regard, we propose a mathematical model for MDTPPSR. In our model, we also define a collaborative rate () between depots, which ranges from 0 (a multi independent TPP) to 1 (full collaboration). In complete cooperation, the vehicle of a depot can load the products of other depots, even without loading one product from its depot. We perform some logical analysis to estimate the minimum number of required vehicles in partial collaboration ();
- Introducing a new variant of the vehicle routing problem—As mentioned earlier, the collaboration structure between members is not just about using the shared vehicle capacities. Rather, it is also about the shared parking spaces of other depots. Regarding the second dimension of the collaboration framework (using the shared parking spaces), we introduce a new type of vehicle routing problem, “Multi-Trip, Open Vehicle Routing Problem”, which, to the best of the authors’ knowledge, has not been adequately addressed so far in the relevant literature. In this new type of routing problem, the vehicle of a particular depot is allowed to end at another depot’s parking space after delivering its products and those of other depots;
- Algorithm—Since our problem is an outgrowth of the classical TPP, it is NP-hard [1]. However, this problem is more complex because of its collaborative nature. We propose a decomposition-based algorithm that breaks down the problem, based on its specific structure, into two manageable pieces to tackle this complexity. Generally, tactical decisions are made at the first stage of the algorithm, regarding supplier selection and the type of collaboration. In the subsequent step, operational decisions about the route vehicle are made, and departing vehicles are assigned to available depot parking spaces. Moreover, to rectify the decisions made in phase 1, two types of heuristic algorithms based on the removal and insertion of an operator are developed to amend the selection of suppliers and redesign the collaboration structure in phase 1.
2. Literature Review
3. Problem Definition
- -
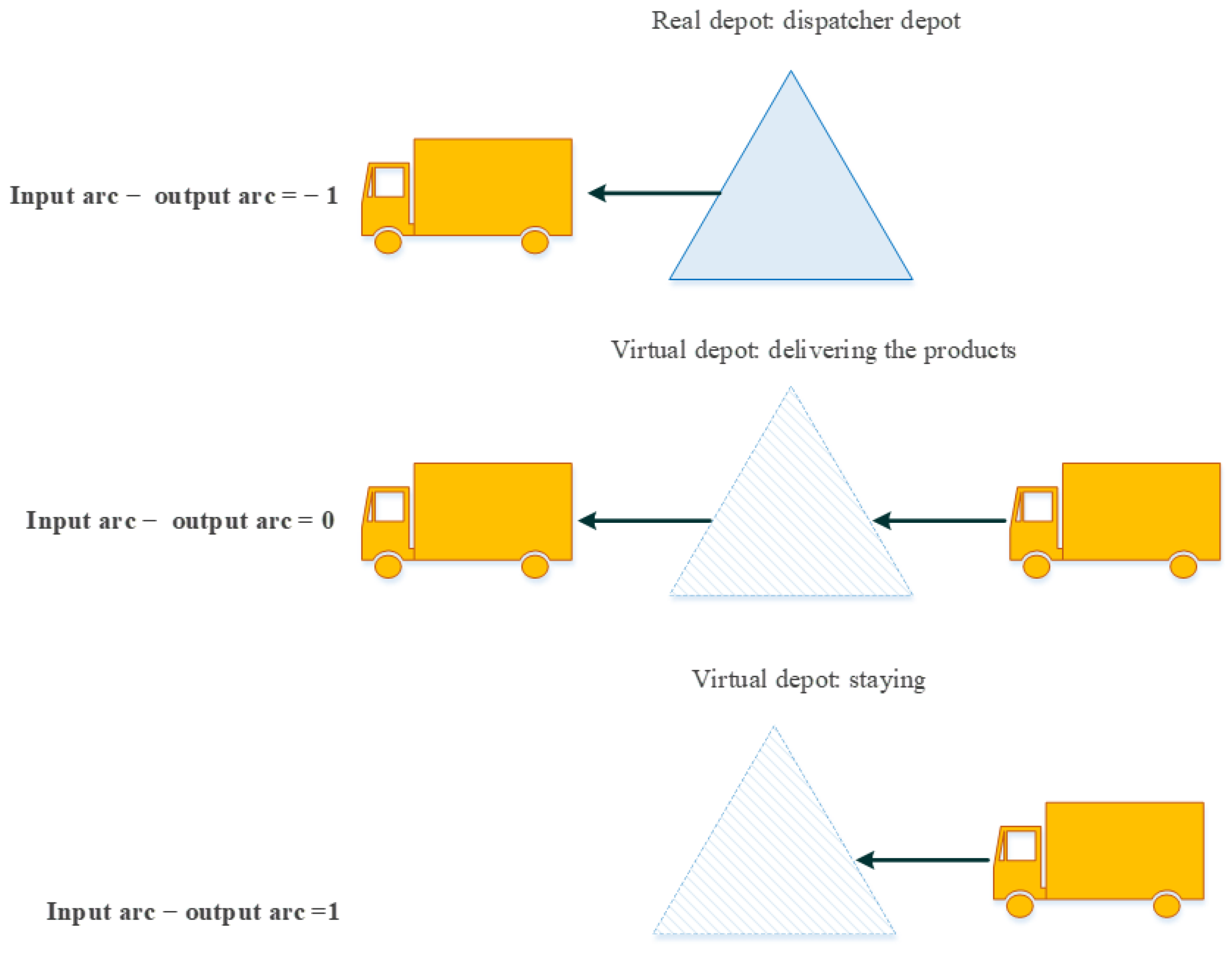
- The distance of each virtual depot to its corresponding depot is zero, and the distance to the other nodes of the network (suppliers and other depots) is equal to the distance of its real depot to those nodes;
- -
- The virtual depot acts as a delivery depot or a staying depot, where a vehicle delivers the purchased products to the depot, or stays at the end of its route. It should be noted that the latter is only possible if the vehicle has already delivered the products of other depots;
- -
- No vehicles can be dispatched from virtual depots—they can only be dispatched from real depots (if necessary). In fact, real depots just act as dispatchers, and no vehicle is allowed to enter them.
4. Mathematical Modeling
- -
- The demands of all products are unitary;
- -
- Each depot has only one vehicle with a limited capacity, and without a loss of generality, the index of each vehicle is equal to the index of its corresponding depot;
- -
- Each depot has a limited parking space;
- -
- Each product is supplied by at least one supplier.
5. The Proposed Heuristic Algorithm for the MDTPPSR
5.1. Decomposition Algorithm
5.2. Improvement Heuristics
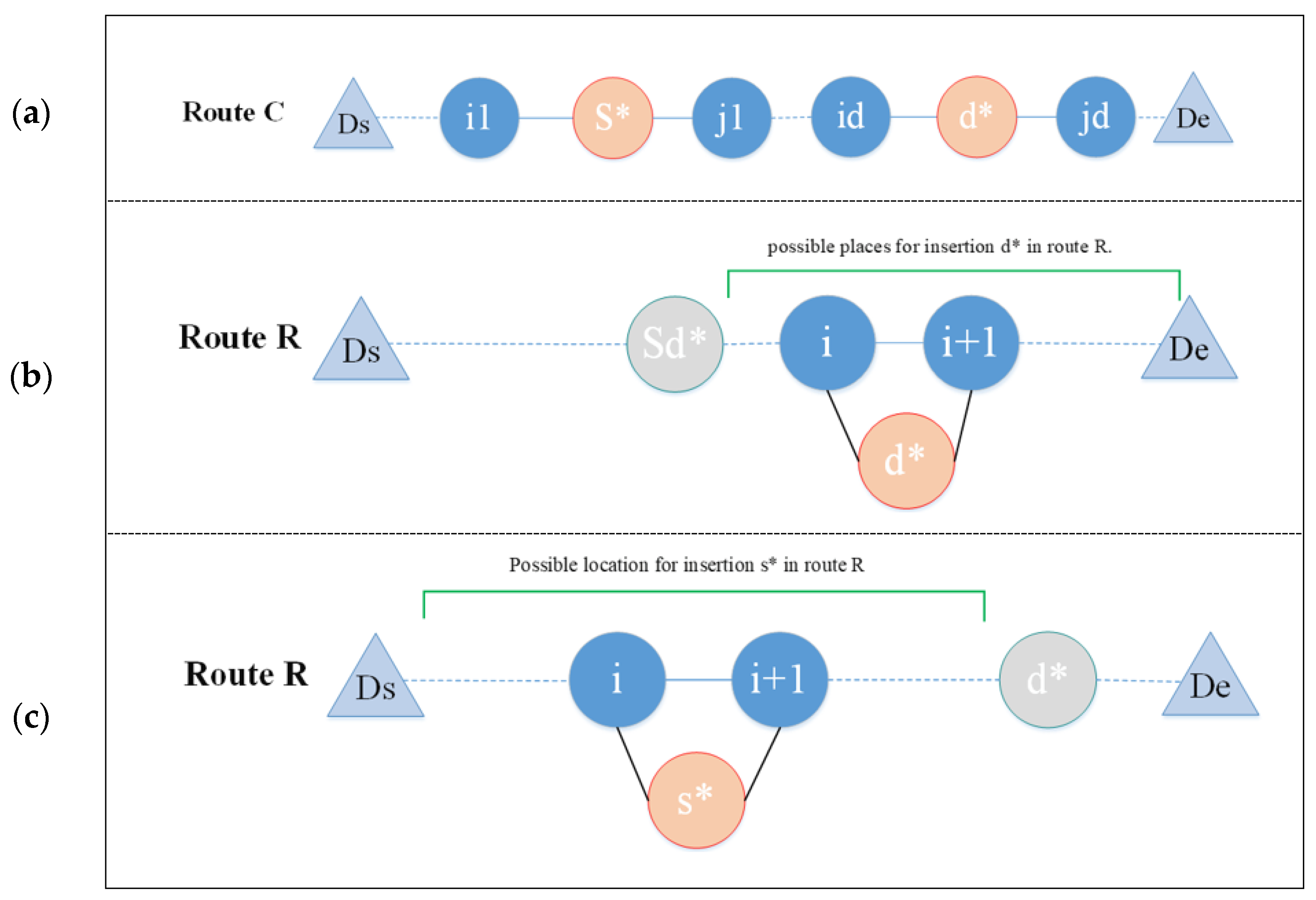
- Heuristic approach for selected suppliers—in this algorithm, we replace the supplier of each product with another supplier of that product, resulting in maximum saving. Consider route r in Figure 5.
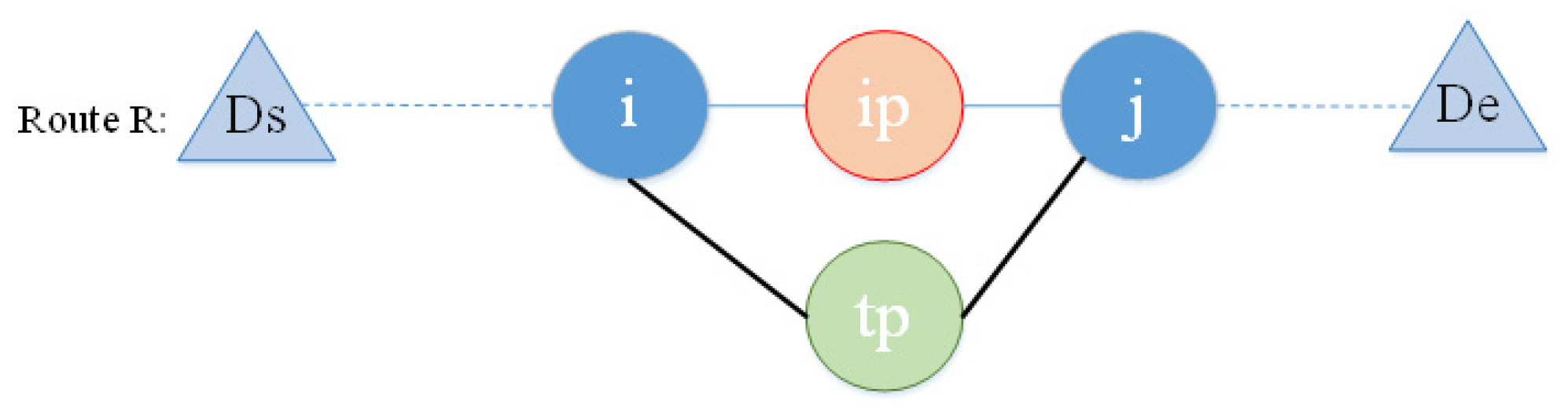
- Heuristic approach for assigning products to the vehicles of the other depots—as mentioned earlier, in the case of assigning a product to a depot’s vehicle, a better assignment (supplier assignment to a depot’s vehicle) might be set. So, this heuristic algorithm tests the reassigning of the suppliers of products to a route with less transportation costs. It is clear that the purchasing cost is not changed by changing the position of a particular supplier on another route.
- Scenario 1: supplier and its corresponding depot ae present on the optional route .
- Scenario 2: supplier exists on the optional route , but its corresponding depot does not exist.
- Scenario 3: supplier is not included on the optional route R, while its depot is. In this scenario, the supplier can be located before depot (Figure 6c).
- Scenario 4: neither supplier nor depot exists on route R.
6. Computational Experiments
6.1. Structure of Instances
6.2. Computational Results
7. Sensitivity Analysis
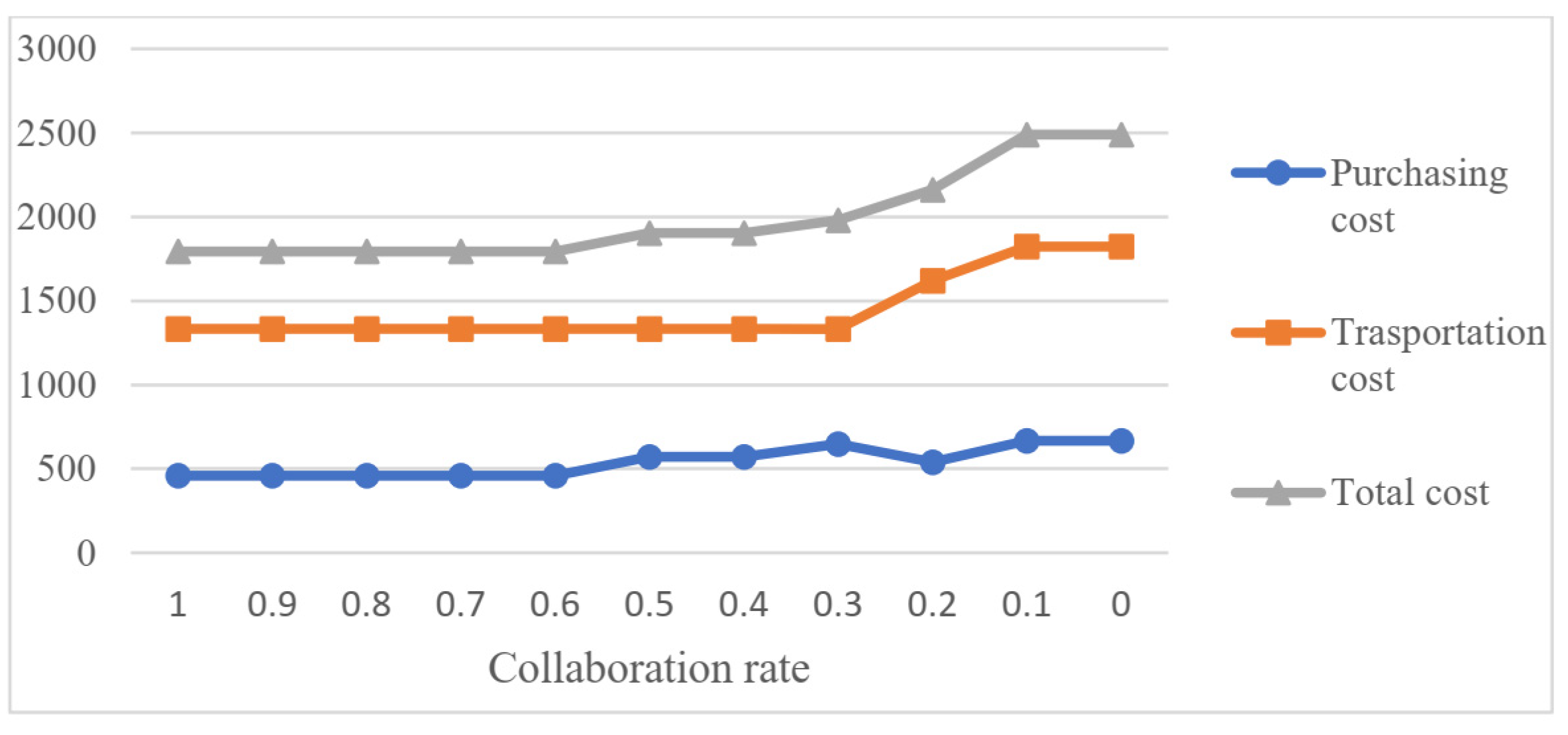
7.1. Sensitivity Analysis of the Collaboration Rate
7.2. The Optimal Range of the Partial Collaboration Rate
8. Conclusions and Suggestions for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Proof of Minimum Required Vehicles in Partial Collaboration
References
- Manerba, D.; Mansini, R.; Riera-Ledesma, J. The traveling purchaser problem and its variants. Eur. J. Oper. Res. 2017, 259, 1–18. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Shared resources in collaborative vehicle routing. TOP 2020, 28, 1–20. [Google Scholar] [CrossRef]
- Schmelzer, H.; Bütikofer, S.; Hollenstein, L. Kooperieren? Ja! Aber wie?: Chancen und Herausforderungen bei der Entwicklung einer Kooperationsplattform für urbane Güterlogistik in der Stadt Zürich. Logist. Innov. 2016, 2016, 16–19. [Google Scholar]
- NextTrust. What is NextTrust? 2AD. 2018. Available online: https://nextrust-project.eu/ (accessed on 8 August 2022).
- Li, J.; Wang, R.; Li, T.; Lu, Z.; Pardalos, P.M. Benefit analysis of shared depot resources for multi-depot vehicle routing problem with fuel consumption. Transp. Res. Part D Transp. Environ. 2018, 59, 417–432. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Collaborative vehicle routing: A survey. Eur. J. Oper. Res. 2018, 268, 1–12. [Google Scholar] [CrossRef]
- HasanpourJesri, Z.; Eshghi, K. The Multi-Vehicle Traveling Purchaser Problem with Priority in Purchasing and Uncertainty in Demand. Int. J. Logist. Syst. Manag. 2021, 39, 359–389. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; Franco, J.L.; Isaza, S.N.; Jiménez, H.F.; Herazo-Padilla, N. A literature review on the vehicle routing problem with multiple depots. Comput. Ind. Eng. 2015, 79, 115–129. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Pardalos, P.M. Multi-depot vehicle routing problem with time windows under shared depot resources. J. Comb. Optim. 2016, 31, 515–532. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Z.; Geng, N. A hybrid genetic algorithm for the multi-depot open vehicle routing problem. OR Spectr. 2014, 36, 401–421. [Google Scholar] [CrossRef]
- Sombuntham, P.; Kachitvichyanukul, V. Multi-depot vehicle routing problem with pickup and delivery requests. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2010; Volume 1285, pp. 71–85. [Google Scholar]
- European Commission. Guidelines on the Applicability of Article 101 of the Treaty on the Functioning of the European Union to Horizontal Co-Operation Agreements. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:C:2011:011:0001:0072:EN:PDF (accessed on 8 August 2022).
- Buijs, P.; Alvarez, J.A.L.; Veenstra, M.; Roodbergen, K.J. Improved collaborative transport planning at dutch logistics service provider fritom. Interfaces 2016, 46, 119–132. [Google Scholar] [CrossRef]
- Cruijssen, F.; Bräysy, O.; Dullaert, W.; Fleuren, H.; Salomon, M. Joint route planning under varying market conditions. Int. J. Phys. Distrib. Logist. Manag. 2007, 37, 287–304. [Google Scholar] [CrossRef]
- Almeida, C.P.; Gonçalves, R.A.; Delgado, M.R.; Goldbarg, E.F.; Goldbarg, M.C. A transgenetic algorithm for the bi-objective traveling purchaser problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Lin, C.K.Y. A cooperative strategy for a vehicle routing problem with pickup and delivery time windows. Comput. Ind. Eng. 2008, 55, 766–782. [Google Scholar] [CrossRef]
- Gouveia, L.; Paias, A.; Voß, S. Models for a traveling purchaser problem with additional side-constraints. Comput. Oper. Res. 2011, 38, 550–558. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Z.; Fung, R.Y.K.; Chen, F.; Liu, X. Two-phase heuristic algorithms for full truckloads multi-depot capacitated vehicle routing problem in carrier collaboration. Comput. Oper. Res. 2010, 37, 950–959. [Google Scholar] [CrossRef]
- Cambazard, H.; Penz, B. A constraint programming approach for the traveling purchaser problem. In Principles and Practice of Constraint Programming; Springer: Berlin/Heidelberg, Gemany, 2012; pp. 735–749. [Google Scholar]
- Hernández, S.; Peeta, S.; Kalafatas, G. A less-than-truckload carrier collaboration planning problem under dynamic capacities. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 933–946. [Google Scholar] [CrossRef]
- Kang, S.; Ouyang, Y. The traveling purchaser problem with stochastic prices: Exact and approximate algorithms. Eur. J. Oper. Res. 2011, 209, 265–272. [Google Scholar] [CrossRef]
- Sprenger, R.; Mönch, L. A methodology to solve large-scale cooperative transportation planning problems. Eur. J. Oper. Res. 2012, 223, 626–636. [Google Scholar] [CrossRef]
- Riera-Ledesma, J.; Salazar-González, J.-J. Solving school bus routing using the multiple vehicle traveling purchaser problem: A branch-and-cut approach. Comput. Oper. Res. 2012, 39, 391–404. [Google Scholar] [CrossRef]
- Nadarajah, S.; Bookbinder, J.H. Less-than-truckload carrier collaboration problem: Modeling framework and solution approach. J. Heuristics 2013, 19, 917–942. [Google Scholar] [CrossRef]
- Batista-Galván, M.; Riera-Ledesma, J.; Salazar-González, J.J. The traveling purchaser problem, with multiple stacks and deliveries: A branch-and-cut approach. Comput. Oper. Res. 2013, 40, 2103–2115. [Google Scholar] [CrossRef]
- Bianchessi, N.; Mansini, R.; Speranza, M.G. The distance constrained multiple vehicle traveling purchaser problem. Eur. J. Oper. Res. 2014, 235, 73–87. [Google Scholar] [CrossRef]
- Defryn, C.; Sörensen, K.; Cornelissens, T. The selective vehicle routing problem in a collaborative environment. Eur. J. Oper. Res. 2016, 250, 400–411. [Google Scholar] [CrossRef]
- Gendreau, M.; Manerba, D.; Mansini, R. The multi-vehicle traveling purchaser problem with pairwise incompatibility constraints and unitary demands: A branch-and-price approach. Eur. J. Oper. Res. 2016, 248, 59–71. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Vindigni, M. The stochastic and dynamic traveling purchaser problem. Transp. Sci. 2016, 50, 642–658. [Google Scholar] [CrossRef]
- Lai, M.; Cai, X.; Hu, Q. An iterative auction for carrier collaboration in truckload pickup and delivery. Transp. Res. Part E Logist. Transp. Rev. 2017, 107, 60–80. [Google Scholar] [CrossRef]
- Beraldi, P.; Bruni, M.E.; Manerba, D.; Mansini, R. A stochastic programming approach for the traveling purchaser problem. IMA J. Manag. Math. 2017, 28, 41–63. [Google Scholar] [CrossRef]
- Fernández, E.; Roca-Riu, M.; Speranza, M.G. The shared customer collaboration vehicle routing problem. Eur. J. Oper. Res. 2018, 265, 1078–1093. [Google Scholar] [CrossRef]
- Angelelli, E.; Gendreau, M.; Mansini, R.; Vindigni, M. The traveling purchaser problem with time-dependent quantities. Comput. Oper. Res. 2017, 82, 15–26. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F.; Salzmann, P.E.H. Exact solutions for the collaborative pickup and delivery problem. Cent. Eur. J. Oper. Res. 2018, 26, 357–371. [Google Scholar] [CrossRef]
- Hamdan, S.; Larbi, R.; Cheaitou, A.; Alsyouf, I. Green traveling purchaser problem model: A bi-objective optimization approach. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, 4–6 April 2017; pp. 1–6. [Google Scholar]
- Wang, Y.; Yuan, Y.; Assogba, K.; Gong, K.; Wang, H.; Xu, M.; Wang, Y. Design and profit allocation in two-echelon heterogeneous cooperative logistics network optimization. J. Adv. Transp. 2018, 2018, 4607493. [Google Scholar] [CrossRef]
- Bernardino, R.; Paias, A. Metaheuristics based on decision hierarchies for the traveling purchaser problem. Int. Trans. Oper. Res. 2018, 25, 1269–1295. [Google Scholar] [CrossRef]
- Vaziri, S.; Etebari, F.; Vahdani, B. Development and optimization of a horizontal carrier collaboration vehicle routing model with multi-commodity request allocation. J. Clean. Prod. 2019, 224, 492–505. [Google Scholar] [CrossRef]
- Palomo-Martínez, P.J.; Salazar-Aguilar, M.A. The bi-objective traveling purchaser problem with deliveries. Eur. J. Oper. Res. 2019, 273, 608–622. [Google Scholar] [CrossRef]
- Quintero-Araujo, C.L.; Gruler, A.; Juan, A.A.; Faulin, J. Using horizontal cooperation concepts in integrated routing and facility-location decisions. Int. Trans. Oper. Res. 2019, 26, 551–576. [Google Scholar] [CrossRef]
- Yang, T.; Wang, W. Logistics Network Distribution Optimization Based on Vehicle Sharing. Sustainability 2022, 14, 2159. [Google Scholar] [CrossRef]
- Kang, H.-Y.; Lee, A.H.I.; Yeh, Y.-F. An optimization approach for traveling purchaser problem with environmental impact of transportation cost. Kybernetes 2020, 50, 2289–2317. [Google Scholar] [CrossRef]
- Wang, Y.; Zhe, J.; Wang, X.; Sun, Y.; Wang, H. Collaborative Multidepot Vehicle Routing Problem with Dynamic Customer Demands and Time Windows. Sustainability 2022, 14, 6709. [Google Scholar] [CrossRef]
- Pradhan, K.; Basu, S.; Thakur, K.; Maity, S.; Maiti, M. Imprecise Modified Solid Green Traveling Purchaser Problem for Substitute Items using Quantum-inspired Genetic Algorithm. Comput. Ind. Eng. 2020, 147, 106578. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.; Xu, M.; Liu, Y.; Wang, H. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Cheaitou, A.; Hamdan, S.; Larbi, R.; Alsyouf, I. Sustainable traveling purchaser problem with speed optimization. Int. J. Sustain. Transp. 2021, 15, 621–640. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Guan, X.; Xu, M.; Liu, Y.; Wang, H. Two-echelon collaborative multi-depot multi-period vehicle routing problem. Expert Syst. Appl. 2021, 167, 114201. [Google Scholar] [CrossRef]
- Hamdan, S.; Cheaitou, A.; Larbi, R.; Alsyouf, I. Moving toward sustainability in managing assets: A sustainable travelling purchaser problem. In Proceedings of the 2018 4th International Conference on Logistics Operations Management (GOL), Le Havre, France, 10–12 April 2018; pp. 1–5. [Google Scholar]
- Wang, Y.; Ma, X.; Li, Z.; Liu, Y.; Xu, M.; Wang, Y. Profit distribution in collaborative multiple centers vehicle routing problem. J. Clean. Prod. 2017, 144, 203–219. [Google Scholar] [CrossRef]
- Roy, A.; Gao, R.; Jia, L.; Maity, S.; Kar, S. A noble genetic algorithm to solve a solid green traveling purchaser problem with uncertain cost parameters. Am. J. Math. Manag. Sci. 2020, 40, 17–31. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Z. The close–open mixed vehicle routing problem. Eur. J. Oper. Res. 2012, 220, 349–360. [Google Scholar] [CrossRef]
- Azadeh, A.; Farrokhi-Asl, H. The Close–Open Mixed Multi Depot Vehicle Routing Problem Considering Internal and External Fleet of Vehicles. Transp. Lett. 2019, 11, 78–92. [Google Scholar] [CrossRef]
- Archetti, C.; Bertazzi, L.; Speranza, M.G. Reoptimizing the traveling salesman problem. Networks 2003, 42, 154–159. [Google Scholar] [CrossRef]
- Reinhelt, G. {TSPLIB}: A Library of Sample Instances for the TSP (and Related Problems) from Various Sources and of Various Types. 2014. Available online: http//comopt.ifi.uniheidelberg.de/software/TSPLIB95 (accessed on 8 August 2022).
- I.A.P.S.A. AP14-0427. IBM ILOG CPLEX Optimization Studio V12.6.1 Delivers Better Performance and a New Licensing Option. Available online: https://www.ibm.com/common/ssi/ShowDoc.wss?docURL=/common/ssi/rep_ca/7/872/ENUSAP14-0427/index.html (accessed on 8 August 2022).
- Anand, R.; Aggarwal, D.; Kumar, V. A comparative analysis of optimization solvers. J. Stat. Manag. Syst. 2017, 20, 623–635. [Google Scholar] [CrossRef]


| Collaborative VRP | TPP | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | LTL | FTL | Objective | Cost Allocation Allocation | Case Study | Methodology | Reference | Collaboration | Depot | Deterministic | Uncertain | Objective | Unitary Demand | Non-Unitary Demand | Single Vehicle | Multi Vehicle |
| [14] | ✓ | cost | ✓ | Empirical analysis | [15] | single | ✓ | Bi-objective (travel distance and purchasing cost) | ✓ | ✓ | ||||||
| [16] | ✓ | cost | ✓ | Heuristic algorithm | [17] | single | ✓ | Total cost | ✓ | ✓ | ||||||
| [18] | ✓ | minimizing empty vehicle movements | Heuristic algorithms | [19] | single | ✓ | Total cost | ✓ | ✓ | |||||||
| [20] | ✓ | cost | Exact algorithm | [21] | single | ✓ | Expected total cost | ✓ | ✓ | |||||||
| [22] | ✓ | cost | ✓ | Heuristic algorithms | [23] | single | ✓ | Total cost | ✓ | ✓ | ||||||
| [24] | ✓ | cost | Heuristic algorithms | [25] | single | ✓ | Total cost | ✓ | ✓ | |||||||
| [13] | ✓ | cost | ✓ | ✓ | Heuristic algorithms | [26] | single | ✓ | Total cost | ✓ | ✓ | |||||
| [27] | ✓ | cost | ✓ | Heuristic algorithms | [28] | single | ✓ | Total cost | ✓ | ✓ | ||||||
| [9] | ✓ | cost | Hybrid metaheuristic algorithm | [29] | single | ✓ | Total cost | ✓ | ✓ | |||||||
| [30] | ✓ | cost | ✓ | Heuristic algorithms | [31] | single | ✓ | Total cost | ✓ | ✓ | ||||||
| [32] | ✓ | cost | Exact algorithm | [33] | single | ✓ | Total cost | ✓ | ✓ | |||||||
| [34] | ✓ | cost | Exact algorithm | [35] | single | ✓ | Bi-objective (total cost and CO2 emissions) | ✓ | ✓ | |||||||
| [36] | ✓ | cost | ✓ | ✓ | Hybrid metaheuristic algorithm | [37] | single | ✓ | Total cost | ✓ | ✓ | |||||
| [38] | ✓ | cost | ✓ | ✓ | Hybrid metaheuristic algorithm | [39] | single | ✓ | Bi-objective (total cost and waiting time of customers) | ✓ | ✓ | |||||
| [40] | ✓ | cost | A hybrid metaheuristic algorithm | [7] | single | ✓ | Total cost | ✓ | ✓ | |||||||
| [41] | ✓ | cost | Metaheuristic algorithm | [42] | single | ✓ | Cost (assigning cost, traveling cost and purchasing cost, emission cost, earliness and tardiness) | ✓ | ✓ | |||||||
| [43] | ✓ | cost | ✓ | Hybrid metaheuristic algorithm | [44] | single | ✓ | Total cost with hard constraint on maximum emission level | ✓ | ✓ | ||||||
| [45] | ✓ | minimizing total carbon emission and operating cost | ✓ | Hybrid heuristic algorithm | [46] | single | ✓ | Minimizing total cost, Co2 emission and maximizing total sustainability value | ✓ | ✓ | ||||||
| [47] | ✓ | Minimizing operational cost and service time | ✓ | ✓ | Hybrid heuristic algorithm | [48] | single | ✓ | Minimizing total cost and maximizing total sustainability score | ✓ | ✓ | |||||
| [49] | ✓ | minimizing the total network costs | ✓ | ✓ | Multi-phase hybrid approach | [50] | single | ✓ | Minimizing cost by considering the environmental impact | ✓ | ✓ | |||||
| This paper | ✓ | cost | Heuristic algorithms | This paper | ✓ | multiple | ✓ | Total collaborative cost | ✓ | ✓ | ||||||
| Basis Features | Collaborative Inbound Logistics (CIL) | Collaborative Outbound Logistics (COL) |
|---|---|---|
| Collaboration | Product’s Demand Aggregation | Order Exchange |
| Final Delivery | Purchaser | Customer |
| Dimension | Multi-Products | Single Product |
| Interaction | Different Potential Suppliers and Purchasers | Known Set of Customers and Distributors |
| Potential Opportunities | Resource Sharing and Group Purchasing | Resource Sharing |
| Set | |
|---|---|
| The set of arcs | |
| The set and index of depots (Each depot corresponds to a certain purchaser) (: number of depots) | |
| The set of suppliers (: number of suppliers) | |
| The set and index of purchasers’ vehicles | |
| The set and index of all purchasers’ products | |
| The set of real network nodes () | |
| The set of all nodes in the network (including suppliers, depots, and virtual depots, =2) | |
| Para-meters | |
| The allowed collaboration rate between depots () | |
| The traveling cost between two nodes and () | |
| The demand for product of depot | |
| The number of parking spaces of depot | |
| The capacity of vehicle | |
| The purchasing cost of product () from supplier () | |
| Decisionvariables: | |
| The number of loadings (unloadings) of vehicle at the time of visiting node (). | |
| The upper limit of the vehicle’s load when entering node (). | |
| 1, if vehicle parks at virtual depot corresponding to real depot , 0 otherwise. | |
| An arbitrary variable for subtour elimination in the Miller–Tucker–Zemlin method (). | |
| 1, if vehicle goes from node to node , 0 otherwise (). | |
| 1, if supplier is visited by vehicle , 0 otherwise (). | |
| 1, if product of depot is purchased from supplier by the purchaser’s vehicle , 0 otherwise. |
| Set and Parameters | |
|---|---|
| The set of delivery depots in phase 1 | |
| The virtual starting depot | |
| The set of selected suppliers in phase 1 | |
| Take value 1 if a product of depot is purchased from supplier . | |
| The vehicle capacity | |
| The demand for node () (the demand for the virtual depot is zero) | |
| The set of network nodes () | |
| Decision variables | |
| The sequence of visiting node on the route | |
| 1 if the vehicle goes directly from node to node , 0 otherwise |
| Row | Instance | Heuristic Result | CPU Time of Heuristic (s) | Exact Result of CPLEX | CPU Time of CPLEX (s) | Optimality Gap (%) |
|---|---|---|---|---|---|---|
| 1 | V10-d3-s7-p15-park2 | 4061.43 | 7.42 | 4046.94 | 13.49 | 0.03 |
| 2 | V10-d3-s7-p25-park2 | 5025.65 | 17.65 | 4980.83 | 25.68 | 0.91 |
| 3 | V10-d4-s6-p15-park2 | 3871.5 | 21.14 | 3871.99 | 39.77 | 0 |
| 4 | V10-d5-s5-p15-park2 | 4971.12 | 47.65 | 4971.23 | 421.16 | 0 |
| 5 | V10-d5-s5-p25-park2 | 6189.03 | 63.08 | 6105.38 | 6540.26 | 1.37 |
| 6 | V11-d5-s6-p15-park2 | 4263.71 | 50.64 | 4193.26 | 6103.78 | 1.68 |
| 7 | V11-d6-s5-p15-park2 | 5313.46 | 57.13 | 5276.53 | 6973.13 | 0.7 |
| 8 | V12-d5-s7-p15-park2 | 4463.98 | 70.34 | 4376.45 | 4920.37 | 2 |
| 9 | V13-d5-s8-p15-park2 | 4671.33 | 53.67 | 4246.67 | 5451.74 | 1.01 |
| 10 | V15-d5-s10-p15-park2 | 4346.14 | 61.73 | Out of memory | 866 | - |
| Row | Instance | Phases 1 and 2 (without Heuristic) | Number of Dispatched Vehicles | Saving A (without Heuristic) | Phases 1 and 2 (with Heuristic 1 and 2) | Saving B (with Heuristic 1 and 2) | Independent Case (Collaboration = 0) |
|---|---|---|---|---|---|---|---|
| 1 | V10-d3-s7-p15-park2 | 4594.4 | 2 out of 3 | 9.03% | H1 + = 4061.11 H2 ++ = 4416.40 | SH1 * = 19.60% SH2 ** = 12.56% | 5050.5 |
| 2 | V10-d5-s5-p15-park2 | 5170.11 | 2 out of 5 | 13.20% | H1 = 5075.80 H2 = 4971.11 | SH1 = 14.78% SH2 = 16.53% | 5956.08 |
| 3 | V10-d5-s5-p20-park2 | 5719.6 | 2 out of 5 | 22.81% | H1 = 5713.60 H2 = 5332.69 | SH1 = 22.88% SH2 = 28.02% | 7409.36 |
| 4 | V15-d5-s10-p15-park2 | 4909.1 | 2 out of 5 | −5.41% * | H1 = 4836.30 H2 = 4346.14 | SH1 = −3.85% * SH2 = 6.68% | 4657.09 |
| 5 | V15-d5-s10-p25-park2 | 9329.53 | 5 out of 5 | 0.10% | H1 = 9280.54 H2 = 7837.82 | SH1 = 0.61% SH2 = 16.07% | 9339.13 |
| 6 | V20-d5-s15-p15-park2 | 4264.49 | 2 out of 5 | 25.32% | H1 = 4201.50 H2 = 4126.16 | SH1 = 26.42% SH2 = 27.73% | 5710.15 |
| 7 | V20-d10-s10-p25-park2 | 9302.47 | 5 out of 10 | 9.30% | H1 = 9266.47 H2 = 8112.27 | SH1 = 9.65% SH2 = 20.90% | 10,256.65 |
| 8 | V25-d10-s15-p25-park2 | 7512.26 | 5 out of 10 | 9.44% | H1 = 7512.26 H2 = 6397.76 | SH1 = 9.44% SH2 = 22.87% | 8295.14 |
| 9 | V25-d10-s15-p35-park2 | 8920.15 | 5 out of 10 | 1.17% | H1 = 8920.10 H2 = 7821.83 | SH1 = 1.17% SH2 = 13.34% | 9026.05 |
| 10 | V25-d5-s20-p20-park2 | 4523.68 | 3 out of 5 | −1.98% * | H1 = 4235.23 H2 = 4068.62 | SH1 = 4.51% SH2 = 8.27% | 4435.67 |
| 11 | V30-d10-s20-p25-park2 | 8873.24 | 5 out of 10 | −9.99% * | H1 = 6094.34 H2 = 8691.45 | SH1 = 24.45% SH2 = −7.73% * | 8067.68 |
| 12 | V30-d10-s20-p40-park2 | 14,090.22 | 7 out of 10 | −18.48% * | H1 = 14,041.01 H2 = 11,619.46 | SH1 = −18.06% * SH2 = 2.30% | 11,892.48 |
| 13 | V35-d10-s25-p20-park2 | 5436.02 | 4 out of 10 | 21.53% | H1 = 5353.12 H2 = 4911.17 | SH1 = 22.73% SH2 = 29.11% | 6927.85 |
| 14 | V35-d5-s30-p20-park2 | 4018.29 | 3 out of 5 | 14.14% | H1 = 3990.69 H2 = 3910.78 | SH1 = 14.73% SH2 = 16.44% | 4680.12 |
| 15 | V30-d15-s15-p20-park2 | 9546.97 | 10 out of 15 | 5.55% | H1 = 9380.82 H2 = 7440.36 | SH1 = 7.19% SH2 = 26.38% | 10,107.45 |
| 16 | V35-d15-s20-p30-park2 | 12,556.9 | 8 out of 15 | −22.05% * | H1 = 12,443.30 H2 = 9691.02 | SH1 = −20.94% SH2 = 5.81% | 10,288.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasanpour Jesri, Z.S.; Eshghi, K.; Rafiee, M.; Van Woensel, T. The Multi-Depot Traveling Purchaser Problem with Shared Resources. Sustainability 2022, 14, 10190. https://doi.org/10.3390/su141610190
Hasanpour Jesri ZS, Eshghi K, Rafiee M, Van Woensel T. The Multi-Depot Traveling Purchaser Problem with Shared Resources. Sustainability. 2022; 14(16):10190. https://doi.org/10.3390/su141610190
Chicago/Turabian StyleHasanpour Jesri, Zahra Sadat, Kourosh Eshghi, Majid Rafiee, and Tom Van Woensel. 2022. "The Multi-Depot Traveling Purchaser Problem with Shared Resources" Sustainability 14, no. 16: 10190. https://doi.org/10.3390/su141610190
APA StyleHasanpour Jesri, Z. S., Eshghi, K., Rafiee, M., & Van Woensel, T. (2022). The Multi-Depot Traveling Purchaser Problem with Shared Resources. Sustainability, 14(16), 10190. https://doi.org/10.3390/su141610190






