Impact of Producer Service Agglomeration on Carbon Emission Efficiency and Its Mechanism: A Case Study of Urban Agglomeration in the Yangtze River Delta

Abstract

As an important part of the economic system of urban agglomeration, the agglomeration of producer services (APS) has become a key contributor to regional low-carbon development. This study analyzes the spatial effect of APS on carbon emission efficiency (CEE) as well as its mechanism and heterogeneity using the panel data of 41 cities in the Yangtze River Delta (YRD) region from 2005 to 2019. First, a U-shaped relationship exists between APS and CEE in both local and neighboring areas. Second, the non-linear relationship between APS and CEE is generated by allocation effects, structural effects and technology effects. Third, the effect of APS on CEE is constrained by the heterogeneity of urban characteristics, in which human capital, fiscal expenditure, and information infrastructure all support and positively moderate the energy-saving and carbon-reduction effect of APS. Fourth, the impact of externalities of APS on CEE varies, both the Marshall–Arrow–Romer (MAR) and Porter externalities having a U-shaped relationship with the CEE of neighboring areas but Jacobs externalities having no significant influence on the CEE of the surrounding areas. The findings of this study indicate that increasing the scale of APS in urban agglomeration, promoting the diversification and division of labor and the cooperation of industries across areas, and promoting the process of city–industry integration are important for achieving the goal of carbon peaking and carbon neutrality in the YRD region.

1. Introduction

The Yangtze River Delta (YRD) urban agglomeration is one of China’s major strategic development regions, including Anhui Province, Jiangsu Province, Zhejiang Province and Shanghai (Figure 1a), with a total of 41 prefecture-level and above cities (Figure 1b), and occupies an important position in China’s economic and social development [1]. There are many big cities in the YRD region (Figure 1b), the sufficient labor supply and perfect infrastructure provide good conditions for the economic development of the urban agglomeration [2]. With a Gross Domestic Product (GDP) of 27.61 trillion yuan (about 4.28 trillion dollars) in 2021, the YRD region generates 24.14% of China’s GDP on less than 4% of its land area, making it one of the growth poles driving China’s economic development [3]. However, the huge economic and city scale also bring serious challenges to the ecological environment of the YRD region. The energy structure is not clean enough and the industrial structure of most cities is still dominated by high-energy-consuming industries, resulting in high carbon emissions in the YRD region, with the overall emission level already accounting for more than 20% of China’s total carbon emissions. Especially during the 13th Five-Year Plan period, the average annual growth rate of carbon emissions in the YRD region is as high as 2.4% [4]. It can be seen that the contradiction between economic growth and carbon emissions in the YRD region is becoming increasingly prominent.

Many scholars have pointed out that the essence of low-carbon development lies in adjusting the regional industrial structure [5]. The producer service has strong knowledge-intensive attributes, and its agglomeration and development is an important way to achieve the transformation and upgrading of industrial structure [6]. Therefore, paying attention to the interaction between the agglomeration of producer services (APS) and carbon emission efficiency (CEE) not only can observe the regular changes in the evolution of APS, but also can provide empirical evidence for APS to support low-carbon economic growth, and thus explore a new path for the green development of the YRD region.

2. Literature Review

It is generally believed that producer services are rooted in the intermediate demand of the manufacturing industry and are an industrial form gradually developed around the manufacturing industry [7]. With the continuous improvement of transportation conditions and information technology, the intrinsic requirements such as geographical proximity and “face-to-face” contact between production services and the manufacturing industry have been weakened, and the scope of transactions has expanded, showing a significant trend of spatial agglomeration [8].

First, many scholars have focused on the impact of the APS on green development and explored the mechanisms between them [9]. A study by Gao and Yuan on 285 cities in China from 2006 to 2017 found a significant inverted U-shaped relationship between APS and resource misallocation [10]. This means that the APS can contribute to the quality development of regional economy by improving resource mismatch. This view is also corroborated by the study of Li et al. [11]. Guo et al. found that the APS can significantly optimize the local industrial structure [12]. Zhou et al., Cheng et al., and Li et al. further indicated that industrial upgrading would have a positive impact on the achievement of carbon emission reduction, which suggested that the positive effect of the APS on green development was likely to be realized through the adjustment of industrial structure [13,14,15]. In addition, Chen et al. found that productive service enterprises can improve regional eco-efficiency through technical cooperation with manufacturing enterprises [16]. This finding is also reflected in the study of Lu and Wang, which knowledge and technology spillovers from the APS can contribute to reduce the pollution emissions [17].

Second, the impact of the APS on regional green development is also reflected in the spatial spillover [18]. On the one hand, Xie et al. and Shen et al. found that the APS can positively influence the green production efficiency of surrounding areas through the effect of economies of scale [19,20]. On the other hand, Ren et al. and Huang and Guo argued that the economic competition between regions can also make the APS have a negative effect on the economic efficiency of the surrounding areas [21,22]. Therefore, the direction of the influence of the APS on neighboring places’ green development is uncertain and needs to be sorted out through theoretical analysis.

Third, under the constraint of city characteristics variables, the APS can have a heterogeneous impact on green development. Chen et al. constructed an analytical framework for APS and found that urban knowledge intensity, fiscal expenditure scale and information infrastructure construction would have significant influences on the formation of the APS [23]. This suggests that under the constraints of human capital, government intervention and information technology, the APS can have a non-linear impact on green development [24,25,26].

In conclusion, although the economic and environmental effects of the APS have been discussed in the literature, most of them relate to the total pollution emissions and ecological efficiency but fail to specifically reflect the input–output relationship between carbon emissions and economic growth in detail. The essence of low-carbon economic development is to accelerate economic growth as much as possible while reducing total carbon emissions. This study investigates the spatial effect of APS on CEE and the corresponding mechanism and heterogeneity. The main contributions of this paper are as follows. First, a super-efficiency slack-based measure (SBM) model with undesirable outputs is constructed to measure the CEEs of 41 cities in the YRD region. Second, spatial effects of APS and its externalities on CEE are analyzed quantitatively using the spatial econometric model to overcome the estimation bias of traditional econometric methods that ignore the impact of spatial interactions between cities. Third, the mediating effect model and panel threshold model are used to analyze the influence mechanism and heterogeneity constraints between APS and CEE, and to answer the question of how to better improve CEE of the YRD region through APS at a deeper level.

3. Theoretical Framework

According to the agglomeration economy theory and new economic geography theory, APS can influence CEE through the labor market pooling, input-output linkages, and technology spillovers [27]. Moreover, under the effect of polarization and trickle-down effect, APS can also have spatial spillover on CEE of surrounding cities. Finally, under the constraints of urban characteristics, APS can have a nonlinear impact on CEE. Figure 2 illustrates the theoretical framework of this study.

3.1. APS, Intermediary Mechanisms and CEE

First, labor market pooling (allocative effect). On the one hand, APS promotes the convergence of labor in the agglomeration area, which helps to reduce the extra cost incurred by enterprises in matching labor, reduce the level of labor mismatch within cities and realize the optimal allocation of resources [28]. In turn, it improves the production efficiency of enterprises and enhances the level of CEE. On the other hand, APS is conducive to the specialized division of labor and collaboration between regions, which not only improves the degree of labor mismatch between regions, but also helps each city to improve the quality of producer services [29]. More carbon-reducing production technologies and producer services are put into the manufacturing production process, which promotes the construction of low-carbon production systems in cities.

Second, input-output linkages (structure effect). As a “lubricant” for the secondary and tertiary industries, the producer services can transform the “invisible knowledge” created by researchers in universities and research institutes into “explicit services” that can be absorbed by the manufacturing industry [30]. It can make the manufacturing industry gradually change to knowledge-intensive, talent-intensive and technology-intensive, which is conducive to upgrading the regional industrial structure and achieving the ultimate goal of energy saving and carbon reduction [31].

Third, technology spillovers (technology effect). On the one hand, the deep integration of producer services and manufacturing industry can outsource non-core business in the manufacturing process, enabling the manufacturing industry to focus on core competitiveness enhancement such as R&D and innovation [32]. On the other hand, APS expands the competitive behavior of similar enterprises, forcing them to design cleaner production technologies through green innovations [33]. The diffusion of knowledge and technology between industries contributes to the CEE of cities by reducing regional energy demand and increasing production efficiency [34].

According to the cluster life cycle theory, different stages of APS will have different impacts on CEE. Therefore, the relationship between them is not always linear, and there is a distinction between short-term and long-term impacts [35]. At the early stage of APS, the scale of agglomeration is relatively small and the resource allocation is not yet optimal [36]. At this time, the interaction between producer services and manufacturing industry is inadequate, and it is difficult to make full use of the allocative effect, structural effect and technology effect of APS on CEE. Therefore, instead of achieving the expected carbon emission reduction effect, APS at this stage is likely to lead to an increase in carbon emissions, thus inhibiting or even reducing CEE. The results of this analysis are consistent with the theoretical elaboration and empirical analysis of Han and Xie, who showed a positive relationship between APS and carbon emissions in 283 cities in China [37]. However, considering the regional heterogeneity, the YRD region has a relatively high level of economic development, a superior market business environment and more developed producer services [38]. Therefore, along with the deepening APS, the allocative effect, structure effect and technology effect of APS begin to appear. The producer services gradually form a positive interaction with the manufacturing industry, the manufacturing process is continuously optimized and the industrial chain is extended to the high-end [39]. Therefore, the impact of APS on CEE has changed from negative to positive. In conclusion, the following hypothesis is proposed:

Hypothesis 1.

There is a U-shaped relationship between APS and CEE in the YRD region, and the non-linear effects between them mainly arise through the allocative effect, structure effect and technology effect.

3.2. APS, Spatial Spillover and CEE

As shown in Figure 2, according to polarization and trickle-down effects, at different stages of APS, the spatial spillover effects on the surrounding areas are different [40,41]. In the early stage of regional development, producer services usually gather in some central areas such as mega-cities and big cities [42]. With the rapid development of economy and the improvement of infrastructure, a large amount of capital, labor and other high-quality factors of production are constantly pouring into the central region. The formation of economies of scale significantly reduces the production costs in the central region, causing the “polarization effect” on CEE in the peripheral regions due to the loss of production factors [43]. When the producer services in the central area has reached a certain scale, due to the limited carrying capacity of the city, the central area is often accompanied by a strong “involuntary” desire to expand outward [44]. The producer services such as logistics and warehousing, commercial leasing, wholesale and retail, financial lending, information transmission, and scientific research to the peripheral regions provides a favorable opportunity for manufacturing enterprises in the surrounding cities to acquire outsourcing services, which enables them to focus on technological innovation in energy conservation and emission reduction. Therefore, the industrial linkage between regions makes APS have a “trickle-down effect” on CEE of neighboring regions. In conclusion, the following hypothesis is proposed:

Hypothesis 2.

According to the polarization and trickle-down effects, there is a U-shaped non-linear relationship between APS and CEE of surrounding areas, which is first inhibited and then promoted.

3.3. APS, Heterogeneity Constraints and CEE

APS cannot be developed without the support of human (human capital), financial (fiscal expenditure) and material (information infrastructure) resources of the city (Figure 2). First, as a knowledge and technology-intensive industry, producer services require high quality of labor. If the human capital stock of a city is low, it is difficult for producer services to form a positive interaction with manufacturing industries, thus limiting the positive externalities of agglomeration [45]. Therefore, due to the high labor threshold, APS always tend to be located in areas with high human capital stock. Second, financial support is also particularly crucial for APS. The fiscal sector can rationally allocate the accumulated funds to all areas of society and use public expenditure instruments to influence the effective demand for producer services [46]. Especially for high-tech industries with high uncertainty and strong positive externalities, increased fiscal support can also stimulate their further development through tax breaks, subsidies and transfer payments. Finally, according to the “information hinterland theory”, the construction of information infrastructure can provide the necessary technical support for the cross-border transmission of producer services, which means that the information economy with the Internet as the carrier has become an important engine and emerging force to promote the further deepening of producer services [47]. In conclusion, the following hypothesis is proposed:

Hypothesis 3.

The impact of APS on CEE is constrained by the heterogeneity of human (human capital), financial (fiscal expenditure) and physical (information infrastructure) support of cities.

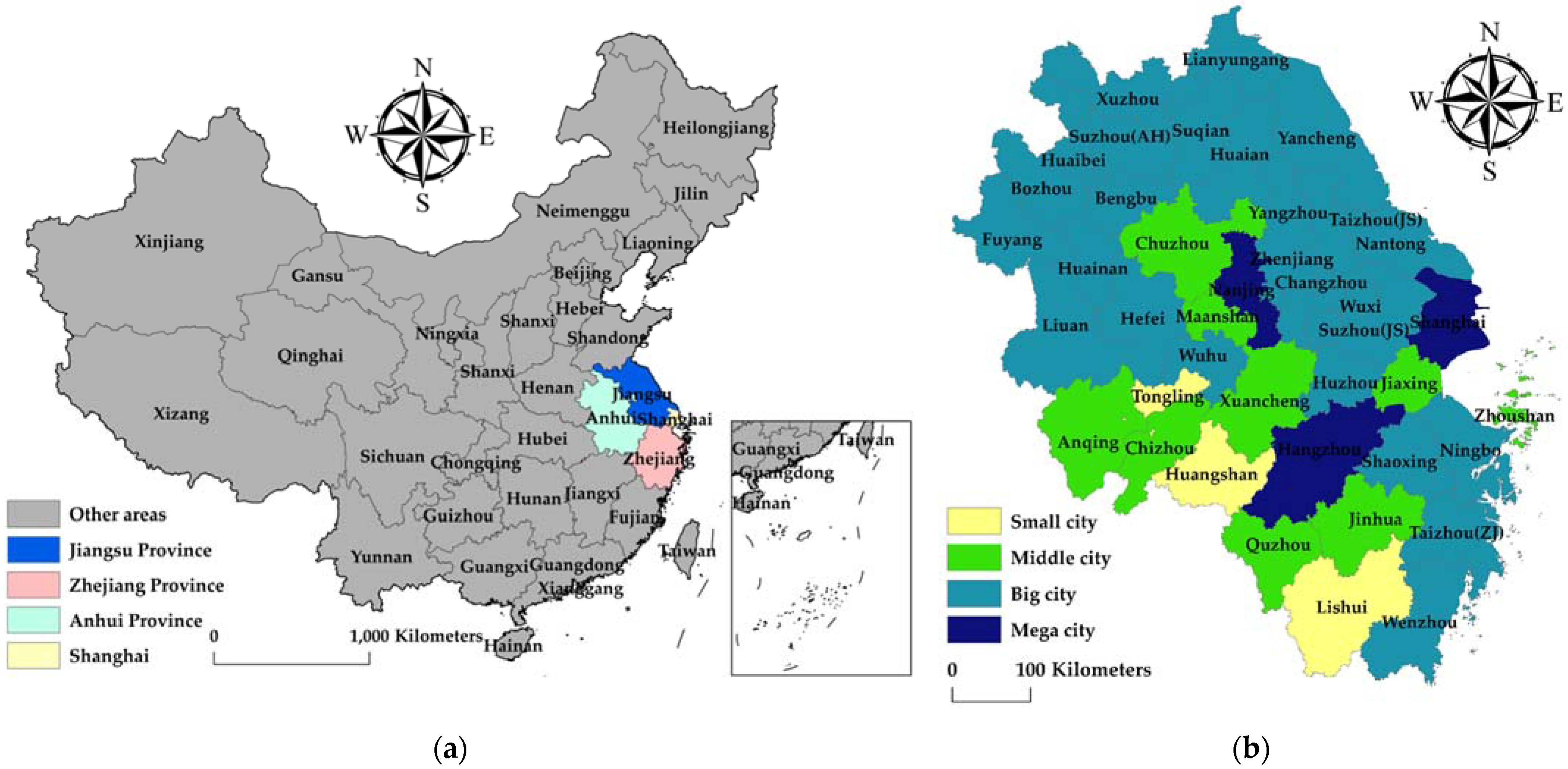
4. Methodology and Data

4.1. Model Setting

4.1.1. Spatial Durbin Model

Based on the STIRPAT model, which is widely used in the field of environmental economics [48], this study constructs the following baseline model:

$$I=a{P}^{{\lambda }_1}{A}^{{\lambda }_2}{T}^{{\lambda }_3}e$$

(1)

where $I$ represents a city’s $CEE$; $a$ is a constant term; $P$ is the population factor; $A$ is the affluence factor; $T$ is the technology factor. ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ represent the elasticity coefficients of the population, affluence and technology factors, respectively. Additionally, $e$ is the random error term. Referring to Han et al., the technology factor is regarded as an increasing function of $APS$ [49]:

$$T=T_0{\left(AP{S}_i\right)}^{\alpha }, \alpha >0$$

(2)

where $T_0$ is a constant, and $\alpha$ is the elasticity coefficient. Combining Equations (1) and (2), we can obtain the following equation:

$$CEE=a{P}^{{\lambda }_1}{A}^{{\lambda }_2}{T}_0^{{\theta }_1}{\left(AP{S}_i\right)}^{{\theta }_2}e$$

(3)

where ${\theta }_1={\lambda }_3$, ${\theta }_2=\alpha {\lambda }_3$ denotes the elasticity coefficient of $APS$ to the city’s $CEE$. Taking the logarithm of Equation (3) yields the following form:

$$\ln CE{E}_{it}=S_0+{\lambda }_1\ln P_{it}+{\lambda }_2\ln A_{it}+{\theta }_2\ln AP{S}_{it}+{\epsilon }_{it}$$

(4)

where $S_0=a{\theta }_1\ln T_0$ and ${\epsilon }_{it}$ is the random error term. In addition, according to the relevant literature, the variables that affect $CEE$ may include environmental regulation ($ER$), industrial structure ($IN$) and transportation condition ($TR$) [50]. Therefore, the above control variables are further introduced into the model:

$$\begin{array}{c}\ln CE{E}_{it}=S_0+{\lambda }_1\ln P_{it}+{\lambda }_2\ln A_{it}+{\theta }_2\ln AP{S}_{it}+{\phi }_1\ln E{R}_{it}\\ +{\phi }_2\ln I{N}_{it}+{\phi }_3\ln T{R}_{it}+{\epsilon }_{it}\end{array}$$

(5)

where ${\phi }_1\sim {\phi }_3$ represent the estimated coefficients of $ER$, $IN$ and $TR$, respectively.

According to the life cycle theory of the industrial cluster, a quadratic term of $APS$ is introduced into the model to examine the nonlinear relationship between $APS$ and $CEE$:

$$\begin{array}{c}\ln CE{E}_{it}=S_0+{\lambda }_1\ln P_{it}+{\lambda }_2\ln A_{it}+{\theta }_2\ln AP{S}_{it}+{\theta }_3{\left(\ln AP{S}_{it}\right)}^2+{\phi }_1\ln E{R}_{it}\\ +{\phi }_2\ln I{N}_{it}+{\phi }_3\ln T{R}_{it}+{\epsilon }_{it}\end{array}$$

(6)

As an externality of economic development, carbon emissions are not only spread between regions with natural climatic conditions, but also in the spatial dimension with intercity transportation and trade transactions. In addition, according to the theoretical analysis, APS can also be spatially linked to the surrounding areas through industrial linkages, economies of scale and technology spillover effects. Therefore, this study constructs a spatial Durbin model to analyze the correlation effect between $APS$ and $CEE$:

$$\begin{array}{c}\ln CE{E}_{it}={\beta }_0+\rho W_{it}\ln CE{E}_{it}+{\beta }_1\ln AP{S}_{it}+{\beta }_2{\left(\ln AP{S}_{it}\right)}^2+{\beta }_c\ln X_{it}\\ +{\varphi }_1{W}_{it}\ln AP{S}_{it}+{\varphi }_2{W}_{it}{\left(\ln AP{S}_{it}\right)}^2+{\varphi }_c{W}_{it}\ln X_{it}+{\mu }_i+v_t+{\epsilon }_{it}\end{array}$$

(7)

where ${\beta }_0$ is the intercept term; $\ln CE{E}_{it}$ and $\ln AP{S}_{it}$ represent the carbon emission efficiency and agglomeration of producer services in city $i$ during the period $t$, respectively; $\ln X_{it}$ represents a set of control variables including population factor, affluence factor, environmental regulation, industrial structure, and transportation condition; ${\beta }_1$, ${\beta }_2$ and ${\beta }_c$ represent the estimated coefficient of $\ln AP{S}_{it}$, its quadratic term and the control variables, respectively; ${\varphi }_1$, ${\varphi }_2$ and ${\varphi }_c$ represent the estimated coefficient of the spatial lag term of $\ln AP{S}_{it}$, its quadratic term and the control variables, respectively; $W_{it}$ is the spatial weight matrix of size $41\times 41$; $\rho$ is the coefficient of the spatial lag term of $\ln CE{E}_{it}$; ${\mu }_i$, $v_t$ and ${\epsilon }_{it}$ represent the individual fixed effect, time fixed effect, and random disturbance term, respectively.

4.1.2. Mediating Effect Model

The form for the analysis and test of the mechanism is set based on the mediating effect test model [51]. The $\ln CE{E}_{it}$ is considered the explained variable, the $\ln AP{S}_{it}$ is the explanatory variable, and the other variables are considered the control variables of the mediating effect model. The mediating effect test process is set up as follows:

$$\ln CE{E}_{it}={\omega }_0+{\omega }_1\ln AP{S}_{it}+{\omega }_2{\left(\ln AP{S}_{it}\right)}^2+{\omega }_c\ln X_{it}+{\mu }_i+v_t+{\epsilon }_{it}$$

(8)

$$M_{it}={\tau }_0+{\tau }_1\ln AP{S}_{it}+{\tau }_2{\left(\ln AP{S}_{it}\right)}^2+{\tau }_c\ln X_{it}+{\mu }_i+v_t+{\epsilon }_{it}$$

(9)

$$\ln CE{E}_{it}={\psi }_0+{\psi }_1\ln AP{S}_{it}+{\psi }_2{\left(\ln AP{S}_{it}\right)}^2+{\psi }_3{M}_{it}+{\psi }_c\ln X_{it}+{\mu }_i+v_t+{\epsilon }_{it}$$

(10)

where $M_{it}$ is the mediating variable; ${\omega }_0$, ${\tau }_0$ and ${\psi }_0$ represent the intercept terms of models (8) to (10), respectively; ${\omega }_1$, ${\tau }_1$ and ${\psi }_1$ represent the estimated coefficients of the primary term of $\ln AP{S}_{it}$ in models (8) to (10), respectively; ${\omega }_2$, ${\tau }_2$ and ${\psi }_2$ represent the estimated coefficients of the squared term of $\ln AP{S}_{it}$ in models (8) to (10), respectively; ${\omega }_c$, ${\tau }_c$ and ${\psi }_c$ represent the estimated coefficients of the control variables (8) to (10), respectively; ${\psi }_3$ represents the estimated coefficients of mediating variables on $\ln CE{E}_{it}$ in model (10); the rest of the variables are explained as in model (7).

4.1.3. Threshold Effect Model

This study empirically analyzes the threshold characteristics and heterogeneous impact of $APS$ on $CEE$ using a panel threshold model of the following form [52]:

$$\begin{array}{c}\ln CE{E}_{it}={\sigma }_0+{\sigma }_{th1}\ln AP{S}_{it}\cdot I\left(q_{it}\le {\lambda }_1\right)+{\sigma }_{th2}\ln AP{S}_{it}\cdot I\left({\lambda }_1<q_{it}\le {\lambda }_2\right)+\cdots \\ +{\sigma }_{thn}\ln AP{S}_{it}\cdot I\left(q_{it}>{\lambda }_n\right)+{\sigma }_c\ln X_{it}+{\mu }_i+{\epsilon }_{it}\end{array}$$

(11)

where $q_{it}$ is the threshold variable; ${\lambda }_1\cdots {\lambda }_n$ are the thresholds to be estimated; ${\sigma }_{th1}\cdots {\sigma }_{thn}$ are the parameter estimates under different thresholds; $I(\cdot )$ is the indicator function; and other parameters are the same as in Equation (7).

4.2. Variable Selection

4.2.1. Explained Variable

Carbon emission efficiency ($CEE$). This study measures $CEE$ using the super-efficiency SBM model with undesirable outputs, where the input indicators are labor, capital, and energy and the output indicators are the GDP and carbon emissions of a city [53,54].

Table 1. CEE indicator evaluation system.

Indicator Type	Primary Indicators	Secondary Indicators
Input indicators	Capital input	Fixed capital stock
	Labor input	Number of employed people at the end of the year
	Energy input	Electricity consumption of the whole society Natural gas Liquefied petroleum gas
Output types	Desirable output	GDP
	Undesirable output	Carbon emissions

reports the selection of input and output indicators, respectively.

4.2.2. Core Explanatory Variable

Agglomeration of producer services ($APS$). First, according to the Statistical Classification of Producer Services (2019) issued by China’s National Bureau of Statistics, the transportation warehousing and postal services, wholesale and retail, leasing and commercial services, finance, information transmission and computer software and science and technology services are selected as representative of producer services. Second, APS level is measured using the location entropy model [55], which is specifically calculated as follows:

$$AP{S}_i=\frac{q_{ij}/q_i}{q_j/q}$$

(12)

where $AP{S}_i$ is the location entropy index of the producer service industry at city $i$, $q_{ij}$ is the number of employed people in (producer service) industry $j$ in city $i$; $q_i$ is the total number of employed people in city $i$, $q_j$ is the number of employed people in (producer service) industry $j$ in the country, and $q$ is the total number of employed people in the country.

In addition, the producer services can also influence CEE through agglomeration externalities. According to Yu, agglomeration externalities of producer services can be divided into Marshall–Arrow–Romer (MAR), Jacobs and Porter externalities in the following forms [56]:

$$MA{R}_i=Ma{x}_j\left(E_{ij}/E_i\right)$$

(13)

$$Jacob{s}_i=1/{\displaystyle \sum _j\left|E_{ij}-E_i\right|}$$

(14)

$$Porte{r}_i=AP{S}_i\times co{m}_i$$

(15)

where $E_{ij}$ is the share of employment in productive service sector $j$ in the total employment in the city $i$; $E_i$ is the share of productive service sector $j$ in the total employment in the country; $co{m}_i$ is the degree of market competition, which is characterized by the average wage of city employees.

4.2.3. Mediating Variables

(1)

Allocation effect (RM), which is characterized by the labor misallocation index [57].

(2)

Structure effect (IH), which is measured as the ratio of the output value of the tertiary industry to the output value of the secondary industry [58].

(3)

Technology effect (GI), which is measured by the number of “green” patent applications per 10,000 people [59].

4.2.4. Threshold Variables

(1)

Human factor (HC), we use the number of students in colleges and universities to measure the level of human capital [60].

(2)

Financial factor (FS), we use the ratio of fiscal expenditure to regional GDP to measure the scale of fiscal expenditure [61].

(3)

Material factor (IT), we use the number of Internet broadband access users to measure the amount of regional information infrastructure [62].

4.2.5. Control Variables

Referring to Feng et al. and Yuan et al.’s study [63,64], we select the following control variables:

(1)

Population factor (P), we use the land area, total population at the end of the year and the location entropy method to measure the population agglomeration.

(2)

Affluence factor (A), which is measured by the ratio of regional GDP to the total population at the end of the year.

(3)

Environmental regulation (ER), which is measured as the comprehensive utilization rate of industrial solid waste.

(4)

Industrial structure (IN), which is the ratio of industrial value added to regional GDP.

(5)

Traffic condition (TR), which are measured by the number of buses per capita.

4.2.6. Spatial Weight Matrix

In this study, we refer to the Lesage and Pace, the spatial adjacency weight matrix is used for the baseline regression analysis, and the geographical distance and economic distance spatial weight matrices are used for the robustness test [65].

(1)

The spatial adjacency weight matrix (W₀₋₁) is defined as follows:

$$W_{0-1}=\{\begin{array}{l}1, when region i adjacent to j.\\ 0, when region i is not adjacent to j.\end{array}$$

(16)

(2)

The geographical distance weight matrix (W_d) is defined as follows:

$$W_d=\{\begin{array}{l}\frac{1}{d_{ij}^2}, i\ne j\\ 0, i=j\end{array}$$

(17)

where $d_{ij}$ is the distance between two cities calculated from the geographical longitude and latitude.

(3)

The economic distance weight matrix (W_e) is defined as follows:

$$W_e=\{\begin{array}{l}\frac{1}{{\left|Y_i-Y_j\right|}^2}, i\ne j\\ 0, i=j\end{array}$$

(18)

where $Y_i$ and $Y_j$ are the average per capita GDP of city $i$ and $j$ from 2005 to 2019.

4.3. Data Sources

The data in this study are mainly obtained from the 2006–2020 China City Statistical Yearbook, China Regional Economic Statistical Yearbook (2019), China Electric Power Yearbook, China Environment Yearbook, the statistical yearbooks of various provinces (municipalities directly under the central government), and statistical bulletins of national economic and social development. In particular, the total number of green patent applications in each city is obtained by obtaining the green patent code from the green patent list issued by the World Intellectual Property Organization (WIPO) and then finding the data on the patent search and service platform of the State Intellectual Property Office. In this study, the time value variable is converted to 2003 as the base period, according to the GDP deflator of each city.

Table 2. Descriptive statistics of main variables.

Type	Variables	Observation	Mean	Std.Dev	Min	Max
Explained variable	$CEE$	615	0.7177	0.2350	0.2390	1.4147
Core explanatory variable	$APS$	615	0.8228	0.2926	0.2905	2.1089
	$MAR$	615	1.3941	0.6051	0.4213	3.9781
	$Jacobs$	615	14.0883	6.3941	4.2105	76.1037
	$Porter$	615	31,189.9900	24,331.8900	5714.1310	205,457.0000
Mediating variable	$RM$	615	0.3678	0.3128	0.0003	1.5569
	$IH$	615	0.8918	0.3001	0.3127	2.6946
	$GI$	615	2.1222	3.2829	0.0000	22.4099
Threshold variable	$HC$	615	10.1496	15.0685	0.1700	87.7894
	$FS$	615	0.1489	0.0814	0.0553	1.4852
	$IT$	615	2166.8400	2358.7660	70.2454	36,634.7600
Control variable	$P$	615	2.5762	1.3513	0.5449	10.2922
	$A$	615	43,956.7400	37,280.4900	2831.1020	204,350.1000
	$ER$	615	92.2484	8.6617	40.0700	100.0000
	$IN$	615	0.4210	0.0886	0.1687	0.6966
	$TR$	615	7.9038	4.4964	0.4330	25.0724
Spatial weight matrix	$\mathrm{Geographical} \mathrm{adjacency} \mathrm{spatial} \mathrm{weight} \mathrm{matrix} \left(W_{0-1}\right)$		Matrix element in which two places are adjacent is 1, otherwise is 0.
	$\mathrm{Inverse} \mathrm{distance} \mathrm{weight} \mathrm{matrix} (W_d$)		The elements of the matrix are the square of the inverse of the distance between the centers of mass of the two places.
	$\mathrm{Economic} \mathrm{distance} \mathrm{weight} \mathrm{matrix} (W_e$)		The matrix element is the square of the inverse of the difference between the annual average GDP per capita of the two places.

reports the results of descriptive statistics of each variable.

5. Empirical Analysis

5.1. Spatial Correlation Analysis

First, Moran’s I and Geary’s C are used to test the spatial correlation between variables in order to initially investigate the applicability of the spatial econometric model [66]. Second, the geographic analysis software ArcGIS10.7 is used to analyze the distribution of CEE in the YRD region. The Moran’s I and Geary’s C indices are calculated as follows:

$$Moran’s I=\frac{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}}}\left(x_i-\overline{x}\right)\left(x_j-\overline{x}\right)}{S^2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}}}}$$

(19)

$$Geary’s C=\frac{\left(n-1\right){\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}}}{\left(x_i-x_j\right)}^2}{2\left({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}}}\right)\left[{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}\right]}$$

(20)

where $S^2$ is the sample variance and $W_{ij}$ the element in row $i$ and column $j$ of the geographical adjacency spatial weight matrix ($W_{0-1}$).

Moran’s I and Geary’s C statistics in

Table 3. Moran’s I and Geary’s C of CEE in 2005–2019 ($W_{0-1}$ ).

Year	Moran’s I		Geary’s C
	Statistic Value	p-Value	Statistic Value	p-Value
2005	0.171 **	0.027	0.779 **	0.015
2006	0.064	0.193	0.901	0.165
2007	0.054	0.219	0.907	0.179
2008	0.059	0.206	0.910	0.188
2009	0.072	0.169	0.885	0.128
2010	0.103	0.104	0.868 *	0.097
2011	0.183 **	0.020	0.775 **	0.014
2012	0.267 ***	0.002	0.679 ***	0.001
2013	0.381 ***	0.000	0.573 ***	0.000
2014	0.322 ***	0.000	0.623 ***	0.000
2015	0.393 ***	0.000	0.556 ***	0.000
2016	0.370 ***	0.000	0.585 ***	0.000
2017	0.399 ***	0.000	0.559 ***	0.000
2018	0.400 ***	0.000	0.556 ***	0.000
2019	0.412 ***	0.000	0.550 ***	0.000

Note: * p < 0.1, ** p < 0.05, *** p < 0.01.

indicate that CEE showes a spatial dispersion trend before 2010 and changed to a spatial clustering trend after 2010, which means that the spatial distribution of the YRD region during the sample study period is not completely random, but has obvious spatial dependence characteristics and dynamic evolution characteristics. Thus, it is initially judged that it is appropriate and accurate to use the spatial econometric model for empirical testing of both.

Figure 3 further shows the specific spatial distribution of CEE in the YRD region during the sample period 2005–2019 using the natural breakpoint method in ArcGIS10.7. We named them as low level, lower level, general level, higher level, and high level according to CEE values from the lowest to the highest. It can be seen that the high value areas of CEE in Anhui Province are decreasing, while the distribution of high value areas of CEE in Jiangsu Province, Zhejiang Province and Shanghai is more stable, with Shanghai, Taizhou(ZJ) and Nanjing as the center and spreading around. It gradually makes CEE of the YRD region show a binary spatial distribution pattern of “Anhui Province-Jiangsu Province, Zhejiang Province and Shanghai”.

5.2. Model Testing and Selection

In this study, the Moran’s I, Lagrange multiplier, likelihood ratio, Wald, and Hausman tests are performed sequentially to determine the optimal form of the spatial econometric model [67].

First,

Table 4. Identification test of spatial panel econometrics model ($W_{0-1}$ ).

Contents	Methods	Statistic Value	p-Value
Panel spatial correlation test	Moran’s I	3.395 ***	0.001
SLM model and SEM model test	LM-lag test	213.182 ***	0.000
	R-LM-lag test	25.488 ***	0.000
	LM-err test	215.023 ***	0.000
	R-LM-err test	27.329 ***	0.000
Simplified test of SDM model	Wald-lag test	77.95 ***	0.000
	LR-lag test	73.98 ***	0.000
	Wald-err test	80.22 ***	0.000
	LR-err test	74.71 ***	0.000
Hausman test of SDM model	Hausman test	293.85 ***	0.000

Note: *** p < 0.01.

shows that the panel Moran’s I value based on the Geographical adjacency spatial weight matrix is 3.395 with a concomitant probability of 0.001, which again validates the test result of cross-sectional spatial correlation in Section 5.1 that a large number of cities with high CEE are also bound to cluster around cities with high CEE.

Second, the LM test and LM robustness test results jointly indicate that the spatial lag model (SLM) and spatial error model (SEM) are accepted for the setting, and the spatial Durbin model (SDM) needs to be further considered.

Third, the Wald statistic and LR statistic are significantly positive, indicating that the SDM is not degradable to the SEM and SLM, and the SDM should be selected for estimation.

Fourth, the Hausman test result is 293.85 with a concomitant probability of 0.000, rejecting the original hypothesis of using random effects, and a fixed-effects model should be used for analysis.

Comprehensive above, the spatiotemporally fixed SDM is selected as the object of analysis in this study and is fitted using maximum likelihood.

5.3. Spatial Effect Analysis

SLM and SDM contain global effects, the parameter estimate of the explanatory variable does not represent its marginal effect. Therefore, this study uses partial differential decomposition to further estimate the direct and indirect effects of APS and other control variables on CEE in the SLM and SDM (

Table 5. Overall regression results ($W_{0-1}$ ).

Type	Variable	OLS	SEM	SLM	SDM
	$\ln APS$	0.0724 (1.20)	−0.0082 (−0.15)	0.0309 (0.56)	0.1086 ** (2.01)
	$\ln AP{S}^2$	0.1768 *** (2.93)	0.0839 (1.56)	0.1233 ** (2.35)	0.1971 *** (3.89)
	$\ln P$	0.2902 ** (2.43)	0.2127 ** (2.00)	0.2301 ** (2.19)	0.1867 * (1.83)
	$\ln A$	0.3391 *** (4.78)	0.3421 *** (6.07)	0.3281 *** (5.87)	0.3372 *** (6.18)
	$\ln ER$	−0.0013 (−0.02)	−0.0253 (−0.51)	−0.0100 (−0.20)	−0.0210 (−0.44)
	$\ln IN$	−0.4383 *** (−7.36)	−0.4450 *** (−9.27)	−0.3947 *** (−8.89)	−0.4099 *** (−7.68)
	$\ln TR$	−0.0520 ** (−2.48)	−0.0567 *** (−3.62)	−0.0609 *** (−3.79)	−0.0486 *** (−3.00)
	$W\times \ln APS$				0.8730 *** (7.08)
	$W\times \ln AP{S}^2$				0.9191 *** (7.80)
	$W\times \ln P$				0.2483 (1.27)
	$W\times \ln A$				0.0913 (0.78)
	$W\times \ln ER$				0.2107 ** (2.00)
	$W\times \ln IN$				0.1999 ** (2.51)
	$W\times \ln TR$				0.0362 (1.03)
	City FE	YES	YES	YES	YES
	Year FE	YES	YES	YES	YES
	Observation	615	615	615	615
Direct effect	$\ln APS$	0.0724 (1.20)	−0.0082 (−0.15)	0.0332 (0.58)	0.1359 ** (2.49)
	$\ln AP{S}^2$	0.1768 *** (2.93)	0.0839 (1.56)	0.1251 ** (2.37)	0.2244 *** (4.57)
	$\ln P$	0.2902 ** (2.43)	0.2127 ** (2.00)	0.2420 ** (2.39)	0.2032 ** (2.09)
	$\ln A$	0.3391 *** (4.78)	0.3421 *** (6.07)	0.3304 *** (6.24)	0.3396 *** (6.62)
	$\ln ER$	−0.0013 (−0.02)	−0.0253 (−0.51)	−0.0093 (−0.19)	−0.0140 (−0.30)
	$\ln IN$	−0.4383 *** (−7.36)	−0.4450 *** (−9.27)	−0.3969 *** (−9.01)	−0.4030 *** (−7.77)
	$\ln TR$	−0.0520 ** (−2.48)	−0.0567 *** (−3.62)	−0.0619 *** (−3.61)	−0.0479 *** (−2.76)
Indirect effect	$\ln APS$			0.0080 (0.52)	0.9864 *** (7.46)
	$\ln AP{S}^2$			0.0318 ** (2.10)	1.0571 *** (8.77)
	$\ln P$			0.0624 ** (2.09)	0.3121 (1.47)
	$\ln A$			0.0860 *** (3.39)	0.1415 (1.08)
	$\ln ER$			−0.0030 (−0.22)	0.2372 * (1.95)
	$\ln IN$			−0.1032 *** (−3.77)	0.1614 ** (2.13)
	$\ln TR$			−0.0163 ** (−2.45)	0.0360 (0.87)

Note: * p < 0.1, ** p < 0.05, *** p < 0.01; ( ) values for z or t statistics. In order to make it more visual, the meanings of the variables in the table are as follows: $\ln APS$ stands for agglomeration of producer services; $\ln P$ stands for population Agglomeration; $\ln A$ stands for GDP per capita; $\ln ER$ stands for environmental regulation; $\ln IN$ stands for the ratio of industrial value added to regional GDP; $\ln TR$ stands for traffic condition.

) [68]. In particular, the direct effect reflects the influence of local explanatory variables on the explained variable, while the indirect effect represents the influence of neighboring explanatory variables on the local explained variable or the influence of local explanatory variables on the neighboring explained variable.

In terms of direct effect, there is a nonlinear (first decreasing and then increasing) relationship between local APS and CEE. In the early stage of APS, neither the economy-of-scale effect nor the benign interaction between producer services and the manufacturing industry arises, which causes unfavorable factors such as rising costs and increasing energy consumption, inhibiting the green and low-carbon transformation of regional economy. With the further deepening of APS, the synergistic effect between the producer services and the manufacturing industry gradually appears, the technology spillover related to energy saving and emission reduction continuously provides innovative support for the low-carbon development of manufacturing enterprises, and the role of APS in promoting CEE begins to appear. The calculation of the inflection point of APS shows that the promoting effect of APS on CEE becomes apparent only when the threshold of −0.3028 is exceeded. Comparison with the data at the end of 2019 reveals that 20 cities in the YRD region have crossed to the right side of the inflection point, showing the promoting effect of APS on CEE, but nearly half of the cities are still located on the left side of the inflection point, inhibiting the improvement of CEE. This implies that local governments need to formulate corresponding industrial transformation policies to accelerate the guidance of the spatial aggregation of producer services in the YRD region and fully stimulate the positive impact of APS on regional low-carbon economic development.

Among indirect effects, there is also a significant U-shaped relationship between APS in an area and CEE of the surrounding areas. The influence of APS on the surrounding areas shows a two-stage change from attraction to diffusion. In the early stage of agglomeration, the concentration of resource elements in the central area leads to a siphon effect, which in turn forms a negative spatial spillover on CEE of neighboring cities. After the agglomeration reaches a certain level, the infrastructure becomes increasingly improved, the trade circulation is more and more close, and the exchange of people becomes increasingly frequent. As a result, industrial linkages between producer services and manufacturing industry in the YRD cities are gradually forged, and positive externalities such as knowledge spillover, labor sharing, and technological innovation generated by APS bring the ability to improve CEE of the surrounding areas. Therefore, there is also a nonlinear trend (first decreasing and then increasing) between APS and CEE of the neighboring areas. Therefore, partial Hypothesis 1 and Hypothesis 2 are confirmed.

5.4. Robustness and Endogeneity Tests

Table 6. Robust test.

Type	Variable	Replace the Spatial Weight Matrix		Substitution of Explained Variable		Substitution of Core Explanatory Variable		Excluding Regression Samples		Instrumental Variable Regression
		${\mathit{W}}_{\mathit{d}}$	${\mathit{W}}_{\mathit{e}}$	$\mathbf{ln}\mathit{C}\mathit{E}{\mathit{E}}_2$	$\mathbf{ln}\mathit{C}\mathit{E}{\mathit{E}}_3$	$\mathbf{ln}\mathit{A}\mathit{P}{\mathit{S}}_2$	$\mathbf{ln}\mathit{A}\mathit{P}{\mathit{S}}_3$	$\mathbf{ln}\mathit{C}\mathit{E}\mathit{E}$	$\mathbf{ln}\mathit{C}\mathit{E}\mathit{E}$	$\mathit{S}\mathit{L}\mathit{X}$	$2\mathit{S}\mathit{L}\mathit{S}$
		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Direct effect	$\ln APS$	0.0743 (1.29)	0.0489 (0.90)	−0.1317 ** (−2.47)	0.0600 (1.48)	0.0985 ** (2.17)	−0.2924 *** (−5.69)	0.0306 (0.52)	0.0738 (1.33)	0.1344 (1.10)	0.1659 ** (2.26)
	$\ln AP{S}^2$	0.1642 *** (3.16)	0.1760 *** (3.58)	−0.0907 * (−1.87)	0.0736 ** (2.02)	0.1956 *** (4.42)	0.0659*** (7.93)	0.1248 ** (2.33)	0.1937 *** (3.80)	0.2264 * (1.85)	0.3174 *** (4.03)
Indirect effect	$\ln APS$	0.2669 (1.60)	0.0595 (0.87)	−0.3590 ** (−2.35)	0.2440 *** (2.64)	0.7628 *** (6.32)	−0.0687 (−0.70)	0.6979 *** (5.22)	0.9173 *** (7.14)	0.9195 *** (3.50)	0.9599 *** (7.45)
	$\ln AP{S}^2$	0.3994 *** (2.91)	0.2605 *** (4.37)	−0.4786 *** (−3.28)	0.3327 *** (3.88)	0.8256 *** (7.37)	0.0330 ** (2.17)	0.8160 *** (6.55)	1.0255 *** (8.56)	0.9950 *** (4.26)	1.0085 *** (8.42)
Kleibergen-Paap rk LM statistic											39.929 [0.0000]
Kleibergen-Paap rk Wald F statistic											46.966 {7.03}
Control		YES	YES	YES	YES	YES	YES	YES	YES	YES	YES
City FE		YES	YES	YES	YES	YES	YES	YES	YES	YES	YES
Year FE		YES	YES	YES	YES	YES	YES	YES	YES	YES	YES
Observation		615	615	615	615	615	615	600	615	615	615

Note: * p < 0.1, ** p < 0.05, *** p < 0.01; ( ) values for z or t statistics; [ ] values are p-values; { } values are critical values at the 10% level of the Stock-Yogo weak identification test.

reports the results of robustness and endogeneity tests of this paper:

First, the spatial weight matrix is replaced. The geographical distance and economic distance spatial weight matrices are used to conduct regression analysis again to obtain Model (1) and Model (2), respectively, which show that there is still a significant U-shaped relationship between APS and local–neighboring CEE.

Second, the explained variable is replaced. The explained variable is directly measured by total carbon emissions ($\ln CE{E}_2$) and carbon productivity ($\ln CE{E}_3$, which is the ratio of non-agricultural output to carbon emissions) to result in Model (3) and Model (4), respectively. Model (3) shows that there is a significant inverted U-shaped relationship between APS and local neighboring carbon emissions, and Model (4) indicates that there is a significant U-shaped relationship between APS and local–neighboring carbon productivity.

Third, the explanatory variable is replaced. After excluding wholesale/retail trade ($\ln AP{S}_2$), Model (5) shows that the U-shaped relationship still holds. In Model (6), the measure of APS is replaced with employment density ($\ln AP{S}_3$, ratio of the number of employed people in producer services to land area), and the results show that the nonlinear (first negative and then positive) relationship between the APS and the local–neighboring CEE still holds.

Fourth, a regression sample is excluded. The municipalities directly under the central government have a higher administrative level and are superior to other cities in terms of resource accumulation. For this reason, Shanghai is excluded and the regression is performed again. Model (7) shows that the local–neighboring effect of APS still exhibits a U-shaped relationship. This study also eliminates the sample outliers via 1% winsorization. Model (8) shows that the quadratic term of APS and its spatial lag is still significantly positive.

Fifth, the endogeneity test is conducted. The spatial lag of X (SLX) model has a flexible form and can be combined with panel data econometric methods. The spatial lag term of its explanatory variable reflects the spatial spillover effect and hence is an ideal variable for testing the endogeneity of the SDM. Model (9) reports the initial estimation results of the SLX model. On this basis, by drawing on the approach of Zeng et al., we carry out a two-stage least squares estimation using APS and its squared term lagged by one period as instrumental variables to control for any endogeneity problem [69]. Model (10) shows that the positive U-shaped relationship between APS and local–neighboring CEE still holds. In the test of the null hypothesis “insufficient identification of instrumental variables”, the p-value of the Kleibergen-Paap rk Lagrange multiplier statistic is 0.0000, which significantly rejects the null hypothesis. In the weak identification test of instrumental variables, the Kleibergen-Paap rk Wald F-statistic is greater than the Stock-Yogo weak identification test critical value at the 10% significance level.

In summary, the above multiple robustness tests indicate that the findings of this study are robust and reliable.

6. Discussions

6.1. Mechanistic Analysis

This study uses stepwise regression to verify the mediating mechanism by which APS affects CEE (

Table 7. Estimated of mediating effect analysis.

Variable	Allocative Effect		Structure Effect		Technology Effect
	$\mathit{R}\mathit{M}$ (1)	$\mathbf{ln}\mathit{C}\mathit{E}\mathit{E}$ (2)	$\mathit{I}\mathit{H}$ (3)	$\mathbf{ln}\mathit{C}\mathit{E}\mathit{E}$ (4)	$\mathit{G}\mathit{I}$ (5)	$\mathbf{ln}\mathit{C}\mathit{E}\mathit{E}$ (6)
$\ln APS$	0.4300 *** (4.38)	0.0968 (1.50)	0.1901 *** (5.07)	0.0317 (0.51)	3.3756 *** (3.46)	0.0113 (0.19)
$\ln AP{S}^2$	−0.2056 * (−1.74)	0.1652 *** (2.77)	0.1747 *** (4.74)	0.1394 ** (2.32)	1.8315 ** (2.11)	0.1437 ** (2.43)
$RM$		−0.0568 * (−1.92)
$IH$				0.2141 ** (1.99)
$GI$						0.0181 *** (6.47)
Control	YES	YES	YES	YES	YES	YES
City FE	YES	YES	YES	YES	YES	YES
Year FE	YES	YES	YES	YES	YES	YES
Observation	615	615	615	615	615	615

Note: * p < 0.1, ** p < 0.05, *** p < 0.01; ( ) values for t statistics.

). First, the allocation effect: Model (1) shows that the linear and quadratic terms of APS are significantly positive and significantly negative, respectively, indicating that APS has a significant inverted U-shaped impact on resource misallocation. That is, only after APS reaches a certain level can its effect of mitigating resource misallocation be exerted. Model (2) incorporates resource misallocation into the baseline model, and regression is performed again. In this case, the influence of resource misallocation on CEE is significantly negative, indicating that resource misallocation has an indirect negative effect in the mechanism by which APS affects CEE.

Second, the structure effect: In Model (3), both the linear and quadratic terms of APS are significantly positive. In Model (4), the squared term of APS remains positive at the 5% significance level, and industrial upgrading also has a positive impact on CEE. These results indicate that industrial structure transformation is an effective mediating mechanism by which APS promotes the improvement of urban CEE, so the structural effect is verified by the test.

Third, the technology effect: As in the analysis of the structural effect, the quadratic terms of the influence of APS on green technological innovation in Model (5) are positive at the 5% significance level. After including the mediating variable in the regression model, Model (6) shows that the green technological innovation also has a significant positive impact on the improvement of CEE. The U-shaped relationship between APS and CEE still holds, indicating that APS has a positive impact on the low-carbon transformation of regional economic structure through the diffusion and spillover of green research and development (R&D) technology between industries. Therefore, Hypothesis 1 is confirmed.

6.2. Heterogeneity Analysis

We use the panel threshold model to test the heterogeneity of the impact of APS on CEE under the constraints of urban human capital, fiscal expenditure, and information infrastructure (

Table 8. Estimated of heterogeneity analysis.

Panel A: Threshold Effect Test
$\mathrm{The} \mathrm{threshold} \mathrm{variable} \mathrm{is} HC$	F-value	p-value	BS	1%	5%	10%	Threshold value
Single threshold	41.81	0.0667	300	57.6858	44.3625	35.2492	24.3788
Double threshold	11.73	0.7800	300	50.7724	37.9895	32.4624	1.6022
Triple threshold	23.15	0.4633	300	59.6886	49.0570	42.6643	0.9722
$\mathrm{The} \mathrm{threshold} \mathrm{variable} \mathrm{is} FS$	F-value	p-value	BS	1%	5%	10%	Threshold value
Single threshold	64.76	0.0067	300	61.5269	41.3541	36.0535	0.2086
Double threshold	37.54	0.0533	300	45.1751	37.5892	32.5775	0.1505
Triple threshold	8.59	0.8400	300	42.0390	33.1135	28.2986	0.1239
$\mathrm{The} \mathrm{threshold} \mathrm{variable} \mathrm{is} IT$	F-value	p-value	BS	1%	5%	10%	Threshold value
Single threshold	31.67	0.0533	300	52.5238	32.1567	28.1236	394.3066
Double threshold	15.95	0.3033	300	39.2158	28.8934	22.8907	1402.0537
Triple threshold	9.13	0.5933	300	42.3442	28.8167	23.9055	6961.6519
Panel B: Estimation Results of Threshold Effect
Variable		(1)		(2)		(3)
$HC\le 24.3788$		−0.2055 *** (−5.39)
$HC>24.3788$		0.9562 *** (5.28)
$FS\le 0.1505$				−0.2425 *** (−6.58)
$0.1505<FS\le 0.2086$				0.0037 (0.08)
$FS>0.2086$				0.3754 *** (5.72)
$IT\le 394.3066$						−0.5236 *** (−6.81)
$IT>394.3066$						−0.1447 *** (−3.84)
Control		YES		YES		YES
Observation		615		615		615
Panel C: Threshold Interval Division
Threshold interval	City (in 2005)			City (in 2019)
$HC\le 24.3788$	Hefei, Anqing, Bengbu, Chizhou, Chuzhou, Fuyang, Huaibei, Huainan, Huangshan, Liuan, Maanshan, Suzhou(AH), Tongling, Wuhu, Xuancheng, Bozhou, Changzhou, Huaian, Lianyungang, Nantong, Suzhou(JS), Suqian, Taizhou(JS), Wuxi, Xuzhou, Yancheng, Yangzhou, Zhenjiang, Huzhou, Jiaxing, Jinhua, Lishui, Ningbo, Shaoxing, Taizhou(ZJ), Wenzhou, Zhoushan, Quzhou (Total 38 cities)			Anqing, Bengbu, Chizhou, Chuzhou, Fuyang, Huaibei, Huainan, Huangshan, Liuan, Maanshan, Suzhou(AH), Tongling, Wuhu, Xuancheng, Bozhou, Changzhou, Huaian, Lianyungang, Nantong, Suzhou(JS), Suqian, Taizhou(JS), Wuxi, Xuzhou, Yancheng, Yangzhou, Zhenjiang, Huzhou, Jiaxing, Jinhua, Lishui, Ningbo, Shaoxing, Taizhou(ZJ), Wenzhou, Zhoushan, Quzhou (Total 37 cities)
$HC>24.3788$	Nanjing, Shanghai, Hangzhou (Total 3 cities)			Hefei, Nanjing, Shanghai, Hangzhou (Total 4 cities)
$FS\le 0.1505$	Hefei, Anqing, Bengbu, Chizhou, Chuzhou, Fuyang, Huaibei, Huainan, Huangshan, Liuan, Maanshan, Suzhou(AH), Tongling, Wuhu, Xuancheng, Bozhou, Nanjing, Changzhou, Huaian, Lianyungang, Nantong, Suzhou(JS), Suqian, Taizhou(JS), Wuxi, Xuzhou, Yancheng, Yangzhou, Zhenjiang, Hangzhou, Huzhou, Jiaxing, Jinhua, Lishui, Ningbo, Shaoxing, Taizhou(ZJ), Wenzhou, Zhoushan, Quzhou (Total 40 cities)			Hefei, Maanshan, Wuhu, Changzhou, Huaian, Lianyungang, Nanjing, Nantong, Suzhou(JS), Taizhou(JS), Wuxi, Xuzhou, Yangzhou, Zhenjiang, Hangzhou, Huzhou, Jiaxing, Jinhua, Ningbo, Shaoxing, Taizhou(ZJ) (Total 21 cities)
$0.1505<FS\le 0.2086$	Shanghai (Total 1 cities)			Anqing, Bengbu, Chizhou, Chuzhou, Huaibei, Huainan, Tongling, Suqian, Yancheng, Wenzhou (Total 10 cities)
$FS>0.2086$	None			Fuyang, Huangshan, Liuan, Suzhou(AH), Xuancheng, Bozhou, Shanghai, Lishui, Zhoushan, Quzhou (Total 10 cities)
$IT\le 394.3066$	Anqing, Chizhou, Chuzhou, Fuyang, Huaibei, Huainan, Huangshan, Liuan, Suzhou(AH), Tongling, Xuancheng, Bozhou, Huaian, Lianyungang, Nantong, Suqian, Xuzhou, Yancheng (Total 18 cities)			None
$IT>394.3066$	Hefei, Bengbu, Maanshan, Wuhu, Nanjing, Changzhou, Suzhou(JS), Taizhou(JS), Wuxi, Yangzhou, Zhenjiang, Shanghai, Hangzhou, Huzhou, Jiaxing, Jinhua, Lishui, Ningbo, Shaoxing, Taizhou(ZJ), Wenzhou, Zhoushan, Quzhou (Total 23 cities)			Hefei, Anqing, Bengbu, Chizhou, Chuzhou, Fuyang, Huaibei, Huainan, Huangshan, Liuan, Maanshan, Suzhou(AH), Tongling, Wuhu, Xuancheng, Bozhou, Nanjing, Changzhou, Huaian, Lianyungang, Nantong, Suzhou(JS), Suqian, Taizhou(JS), Wuxi, Xuzhou, Yancheng, Yangzhou, Zhenjiang, Shanghai, Hangzhou, Huzhou, Jiaxing, Jinhua, Lishui, Ningbo, Shaoxing, Taizhou(ZJ), Wenzhou, Zhoushan, Quzhou (Total 41 cities)

Note: *** p < 0.01; ( ) values for t statistics.

).

Panel A shows that there is at least a single threshold effect for the three heterogeneity variables, that is, the impact of APS on CEE is indeed influenced by human capital, fiscal expenditure, and information infrastructure. Specifically, human capital and information infrastructure each exhibit a single threshold effect, while fiscal expenditure exhibits a double threshold effect. The threshold for human capital is 24.3788, the threshold for information infrastructure is 394.3066, and the thresholds for fiscal expenditure are 0.1505 and 0.2086.

Panel B reports the estimation results of the threshold regression coefficients for different intervals:

First, when human capital is less than the threshold, APS has a significant negative impact on CEE; when human capital exceeds the threshold, the impact of APS on CEE turns from negative to positive, indicating that under a human capital constraint, the impact of APS on CEE shows gradient enhancement from inhibition to promotion. Second, when fiscal expenditure is below the first threshold, the impact of APS on CEE is significantly negative and passes the significance test at the 1% level; when fiscal expenditure is between the first and second thresholds, the impact of APS on CEE becomes positive but is not significant; and when fiscal expenditure exceeds the second threshold, the impact of APS on CEE is significantly positive, indicating that the negative impact of APS on CEE is mitigated to some extent and the positive impact of APS on CEE is enhanced continuously under the local government’s financial intervention. Finally, when information infrastructure does not exceed the first threshold, the impact of APS on CEE is significantly negative; when information infrastructure exceeds the second threshold, the impact of APS on CEE remains negative, but the absolute value of the coefficient is reduced. Therefore, Hypothesis 3 is confirmed.

Panel C reports the specific distribution of cities in the YRD region under each threshold interval in 2005 and 2019:

In terms of the threshold constraint of human capital, most cities in the YRD region did not cross the threshold of human capital in 2005, and the only three cities that crossed the threshold were Shanghai, Nanjing and Hangzhou. Only Hefei was added to the region that crossed the threshold in 2019, which indicates that there is still more room to improve the development of human capital in the YRD region. In terms of the threshold constraint of fiscal expenditure, no city crossed the second threshold in 2005, and only Shanghai crossed the first threshold. As of 2019, 10 regions such as Shanghai and Zhoushan have crossed the second threshold, and 10 regions such as Anqing and Wenzhou have crossed the first threshold, but nearly half of the cities are still under the first threshold. It can be seen that the fiscal expenditure of the YRD region has improved to a certain extent during the sample period, but still needs to continue to be enhanced. In terms of the constraints of information infrastructure, 18 cities, including Anqing and Nantong, did not cross the threshold in 2005, while in 2019 all cities in the YRD region crossed the threshold, and there is a substantial improvement in the level of information and communication technology.

6.3. Further Discussion Based on Agglomeration Externalities

Producer services can be divided into specialized and diversified agglomeration models, which generate different externalities. Specialized agglomeration refers to the agglomeration of the same industry in the same area. On the one hand, it enables the industry to quickly achieve economy of scale, reduce the production cost of the manufacturing industry through specialized services, and expand the scope of knowledge and technology spillover while promoting the improvement of CEE (Marshall–Arrow–Romer (MAR) externalities). On the other hand, the market competition and interaction triggered by specialized agglomeration accelerates the innovation and R&D process, and the cluster competitive advantage of local producer services is gradually enhanced, thereby promoting the steady growth of the overall quality of the industrial chain and the CEE of the area (Porter externalities). In comparison, diversified agglomeration focuses more on multi-industry interaction and cross-industry technology penetration, thereby attracting the agglomeration of related industries and professionals and further enhancing the regional market capacity, innovation momentum, and growth potential (Jacobs externalities).

As shown in

Table 9. Impact of externalities of APS on CEE($W_{0-1}$).

Variable	MAR			Jacobs			Porter
	Direct Effect	Indirect Effect	Total Effect	Direct Effect	Indirect Effect	Total Effect	Direct Effect	Indirect Effect	Total Effect
$\ln N$	−0.0824 *** (−3.51)	−0.1559 *** (−2.85)	−0.2383 *** (−4.00)	−0.6598 *** (−5.63)	−0.3242 (−1.15)	−0.9840 *** (−3.17)	−2.4057 *** (−9.54)	−1.4358 ** (−2.57)	−3.8415 *** (−6.13)
$\ln N^2$	0.1571 *** (6.27)	0.2454 *** (4.02)	0.4025 *** (5.82)	0.1038 *** (4.92)	0.0248 (0.47)	0.1287 ** (2.22)	0.1140 *** (9.43)	0.0767 *** (2.85)	0.1906 *** (6.40)
Control	YES			YES			YES
City FE	YES			YES			YES
Year FE	YES			YES			YES
Observation	615			615			615

Note: ** p < 0.05, *** p < 0.01; ( ) values for z statistics. In addition, N stands for MAR, Jacobs, Porter externalities, respectively.

, the MAR and Porter externalities of APS each show a U-shaped nonlinear relationship with the CEE of both local and neighboring areas, as expected, while the Jacobs externalities of APS have a significant U-shaped relationship with the CEE of the area but do not have the expected reduction-promoting effect on the surrounding areas. One possible reason is that the diversified agglomeration model of large and complete or small and complete producer services in most cities makes it difficult to reap complementary advantages with the manufacturing industry in the surrounding areas, which greatly weakens the spatial correlation effect as well as the pollution- and carbon-emission-reducing effect of producer services on the manufacturing industry, thus failing to have a significant impact on the improvement of the CEE of the surrounding cities.

7. Conclusions and Policy Recommendations

7.1. Conclusions

This study constructs a theoretical framework for the impact of APS on CEE based on the theories of the agglomeration economy and new economic geography. A panel data of 41 cities in the YRD region from 2005 to 2019 is selected as the sample, a super-efficiency SBM model with undesirable outputs is employed to construct a CEE evaluation system, a spatial Durbin model is adopted to analyze in depth the direct local impact and indirect intercity impact of APS and its externalities on CEE, and mechanisms by which APS affects CEE is elucidated using a mediating effect model. In addition, in order to find the constraints on heterogeneity characteristics among cities more scientifically and reasonably, this study examines the nonlinear impact of APS on CEE through a panel threshold model. The findings of this study are as follows:

APS not only promotes local CEE through the allocation effect, structure effect, and technology effect but also has a significant spatial spillover effect on CEE of surrounding areas. The heterogeneity analysis based on human capital, fiscal expenditure, and information infrastructure shows that a high level of human capital stock, fiscal expenditure scale and information infrastructure is conducive to the exertion of the energy-saving and carbon-reducing effects of APS. Further discussion of the externalities of APS finds that the local–neighborhood U-shaped relationship between the MAR and Porter externalities of specialized agglomeration of APS and CEE still holds, while the Jacobs externalities of diversified agglomeration do not have a significant spatial spillover effect on the surrounding cities.

7.2. Policy Recommendations

First, the scale and quality of APS should be improved, and the synergy and cooperation among cities should be strengthened. Research results show that the impact of APS on CEE in the YRD region is influenced by the degree and mode of agglomeration. Therefore, in the process of using APS to promote CEE in the YRD region, it is especially important to formulate differentiated regional policies. On the one hand, for cities that have not yet crossed the inflection point, they should further increase the proportion of producer services in the process of structural adjustment, so as to realize the positive externalities of APS on CEE as early as possible. Meanwhile, cities that have already crossed the inflection point should strengthen the optimization of the internal structure of producer services, improve the quality of APS, and contribute to the improvement of CEE in the surrounding areas through the spatial flow of human capital and the spatial spillover of low-carbon technology. On the other hand, the YRD region should actively guide the free flow of production factors, and gradually eliminate the long-standing regional market segmentation and administrative system barriers. Through the industrial linkage of producer services and manufacturing industries between regions, a diversified industrial layout with complementary advantages and clear division of labor is formed to fully stimulate the impact of Jacobs’ externalities to achieve the joint improvement of CEE in each region of the YRD region.

Second, the allocative, structural and technological effects of APS on CEE need to be fully exploited. The results of the mediating effect analysis in Table 7 show that there is a two-stage change from agglomeration diseconomies to agglomeration economies with significant nonlinear characteristics between APS and intermediary variables in the YRD region. This indicates that actively promoting APS and crossing the inflection point in the process of non-linear change is the primary goal to open the intermediate channel. In terms of allocation effect, government departments in each region of the YRD region should create a favorable market environment to guide healthy competition in the producer services by improving the efficiency of resource allocation and thus promoting CEE of the YRD cities. In terms of structural effect, the YRD region should give full play to the supporting role of APS in promoting the transformation and upgrading of manufacturing industries, and provide help to improve the regional industrial structure. In terms of technology effect, government departments should increase support for low-carbon technology research in producer services, improve laws and regulations on intellectual property protection and other invention incentive systems, and enhance the core motivation for green and low-carbon development.

Third, we should accurately identify the threshold constraints of each city and then solve these problems in turn. In terms of human capital, the four cities of Shanghai, Hangzhou, Nanjing and Hefei need to give full play to their high human capital advantages, focus on strengthening the training of specialized talents, and provide sufficient talent reserves for the R&D of carbon reduction technologies for producer services enterprises. In addition, the four cities need to further exert the radiation effect to drive the development of low-carbon economy in other areas of the YRD region through the spatial flow of human capital. Each city in the YRD region can refer to the threshold range in Table 8 to adjust local fiscal policies. On the one hand, cities with smaller fiscal expenditures should moderately expand the scale of fiscal expenditures to promote the agglomeration effect of local producer services. On the other hand, cities with larger fiscal expenditures should maintain their current spending status while preventing potential problems such as rent-seeking, bureaucracy, resource mismatch and inefficiency caused by excessive government intervention. Through differentiated fiscal policies, the role of fiscal expenditures in assisting the CEE driven by APS in the YRD region can be fully exploited. In terms of information infrastructure, Table 8 shows that all cities in the YRD region have crossed the threshold value in 2019, which indicates that the YRD region should now avoid the crude growth of information technology and focus more on the connotative development. Specifically, the YRD region should strengthen the research and development of 5G network base stations, big data centers, artificial intelligence and other high-tech information technology, and promote the diffusion of green production technology with the help of “Internet +”, create a high-level low-carbon economy industry chain, and establish a long-term mechanism of CEE in the YRD region driven by APS.

7.3. Limitations and Future Directions

Even though this paper adds to the research on APS and CEE, and provides a theoretical and empirical reference for the low carbon development of producer services industry in the YRD region, there are still some shortcomings for further improvement:

In terms of direct effect, there are many sub-sectors in the producer services, and different sectors have different levels of knowledge and technology intensity. Therefore, the impact of different producer services on CEE varies. The main service targets of low-end producer services are labor- and capital-intensive manufacturing industries, while high-end productive services are mainly for knowledge- and technology-intensive manufacturing industries [70]. Since labor- and capital-intensive manufacturing industries are in the low end of the value chain, the energy consumption and carbon emissions per unit of product are relatively high, and thus the allocation effect, structural effect and technology effect of APS on CEE will be limited if the low-end industries account for a large proportion of the internal structure of producer services. On the contrary, APS with a large share of high-end industries in the internal structure contributes to the expected positive externality of agglomeration, which has a positive impact on the improvement of CEE. Therefore, subsequent studies can demonstrate the direct impact and mechanism of heterogeneous producer services’ low-carbon development from a more detailed perspective of industry heterogeneity, and provide a more microscopic empirical basis for the implementation of industrial policies in the YRD region.

In terms of spatial spillover effect, although this study analyzes the spatial relationship between APS and CEE, the empirical part of the discussion is still insufficient due to the limitation of space. The spillover boundaries of CEE under different geographical thresholds need to be explored in more detail in subsequent studies, which is of profound significance for regional integration and coordinated development.