An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation
Abstract
1. Introduction
2. Methodology
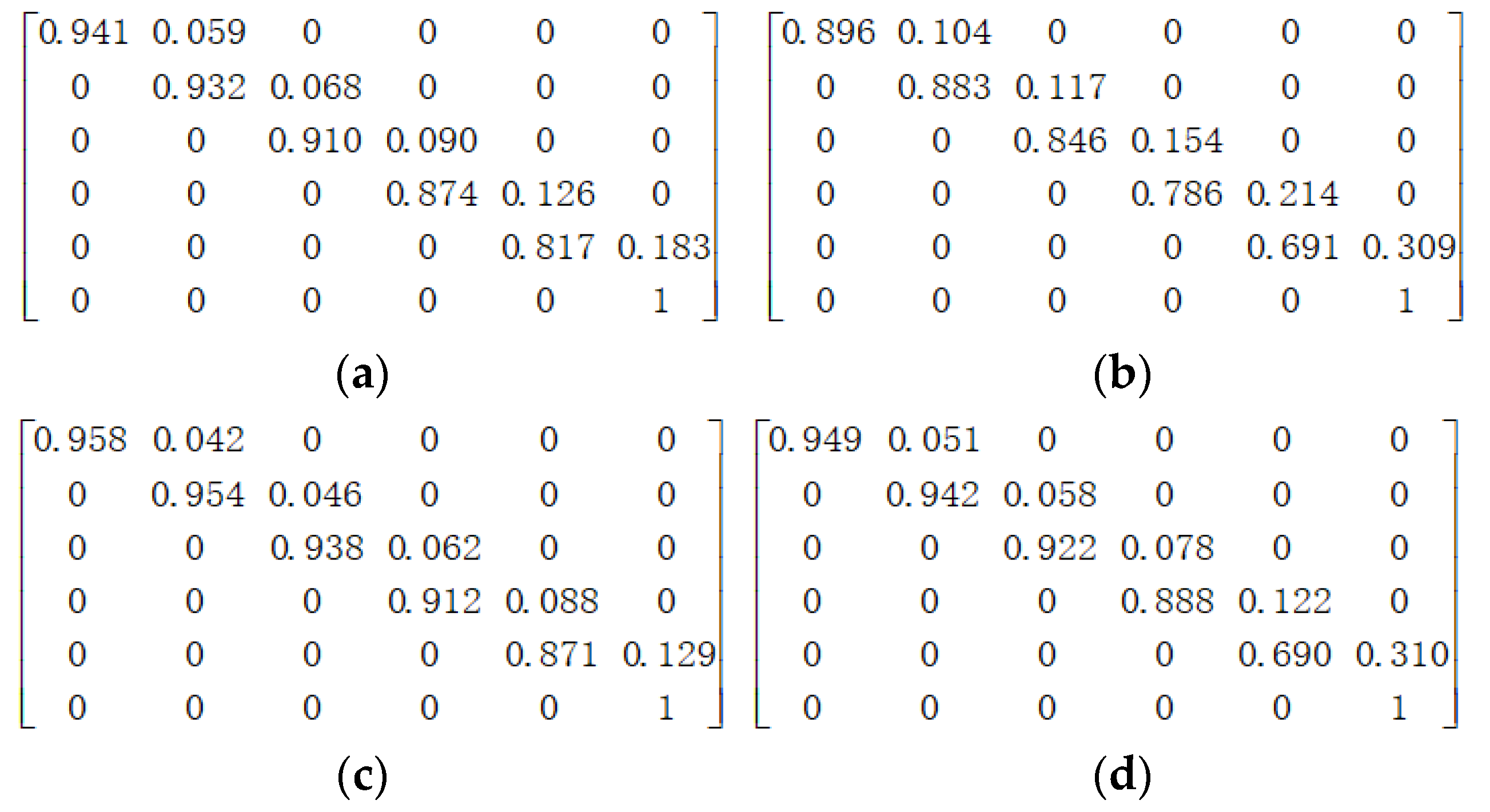
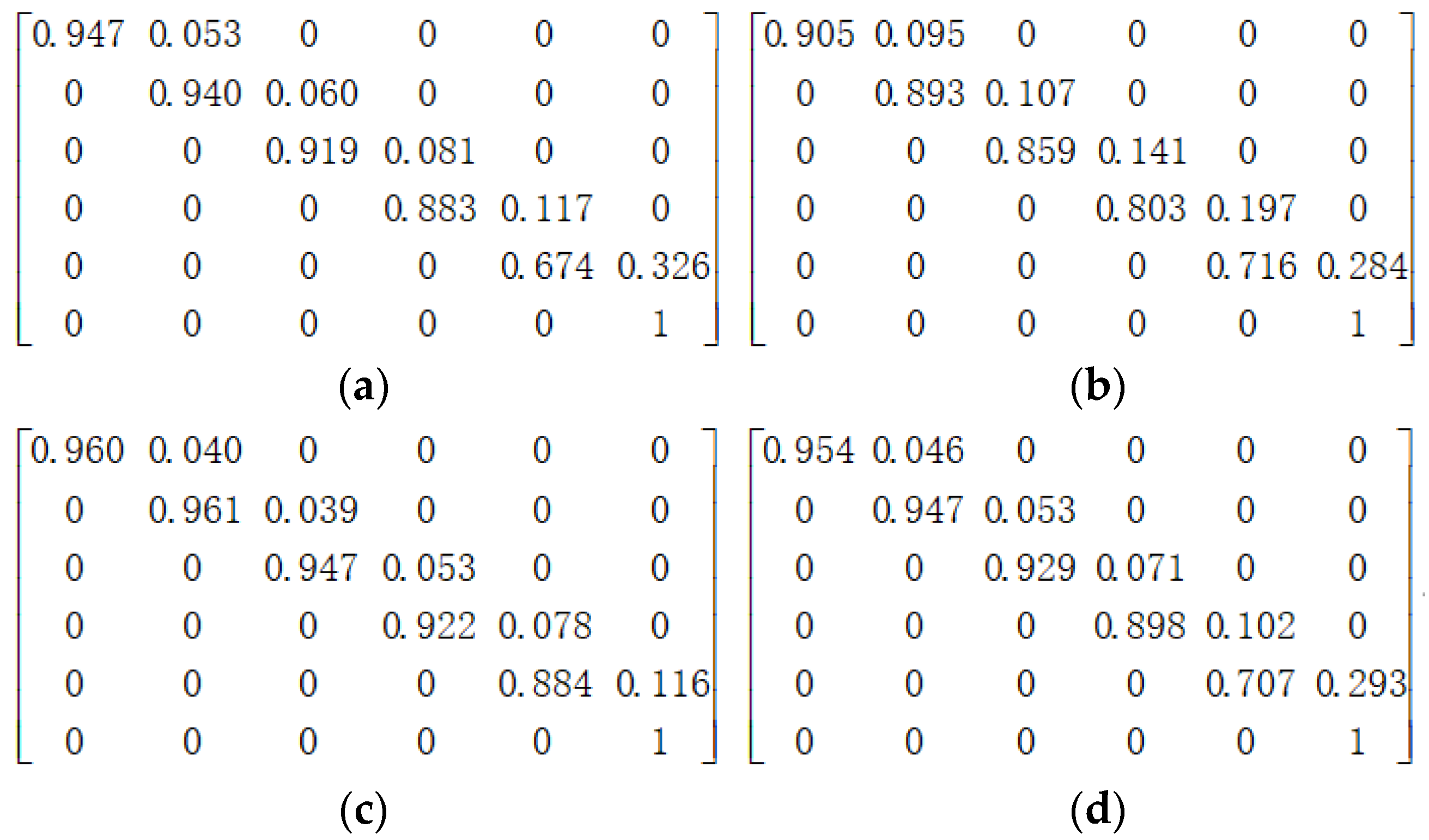
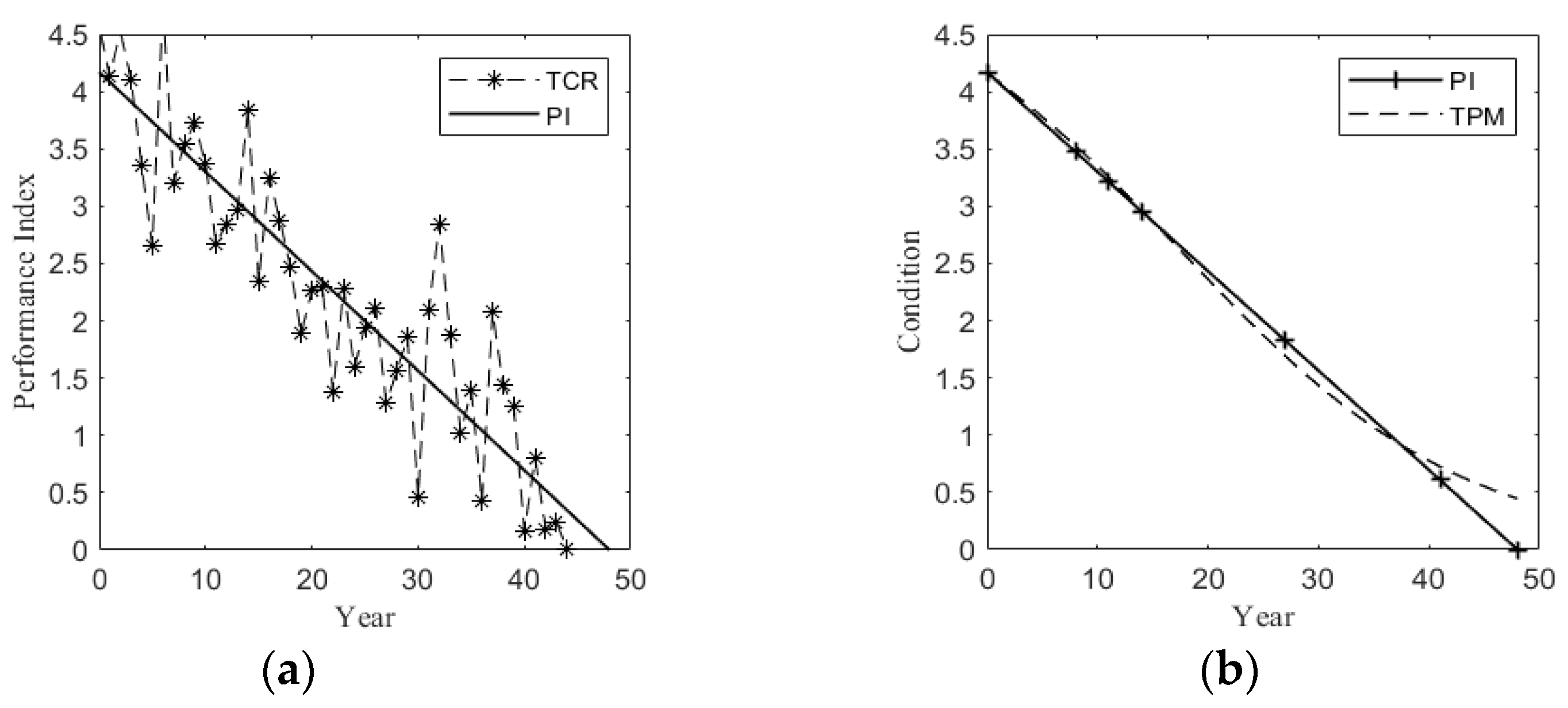
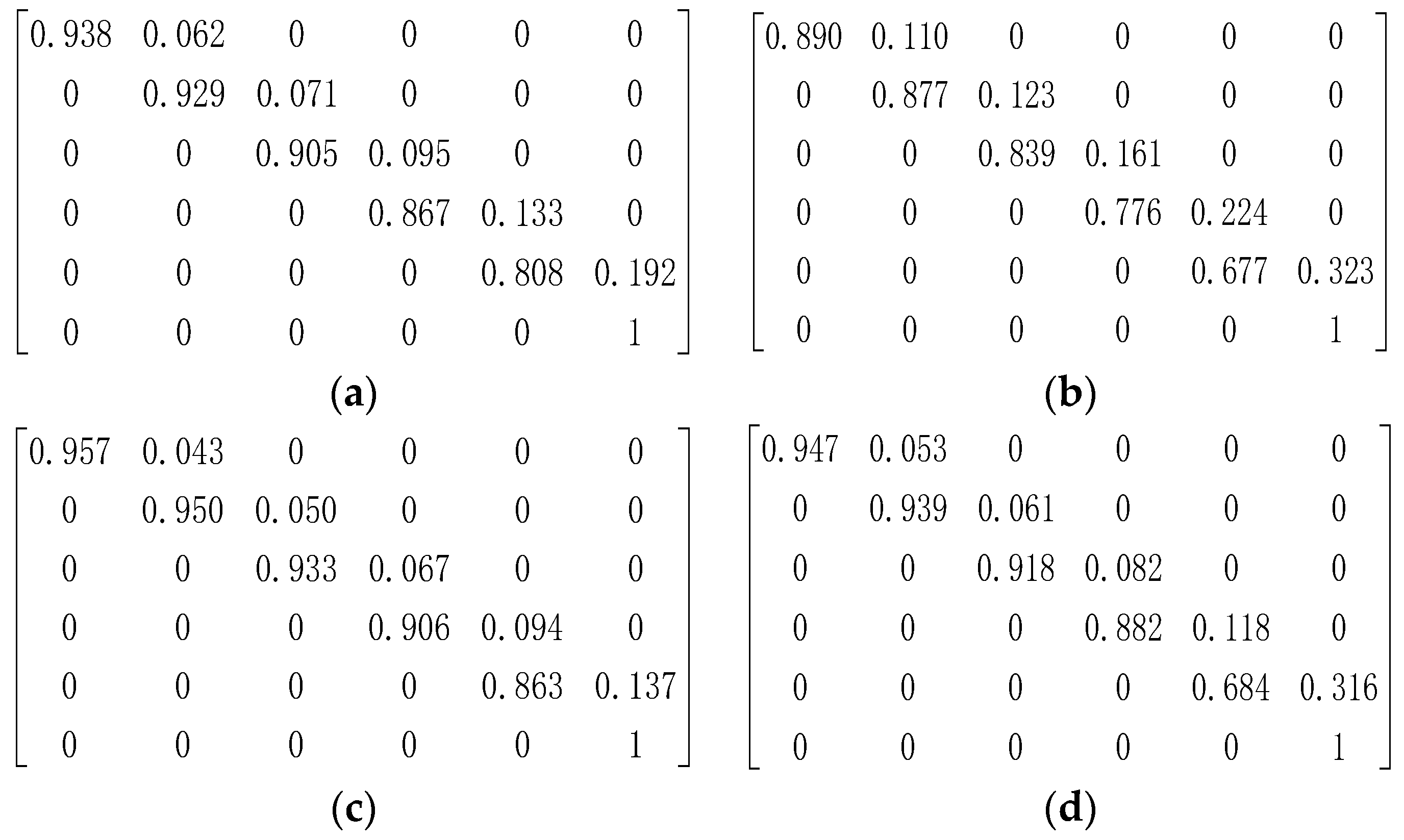
2.1. Deterioration Model
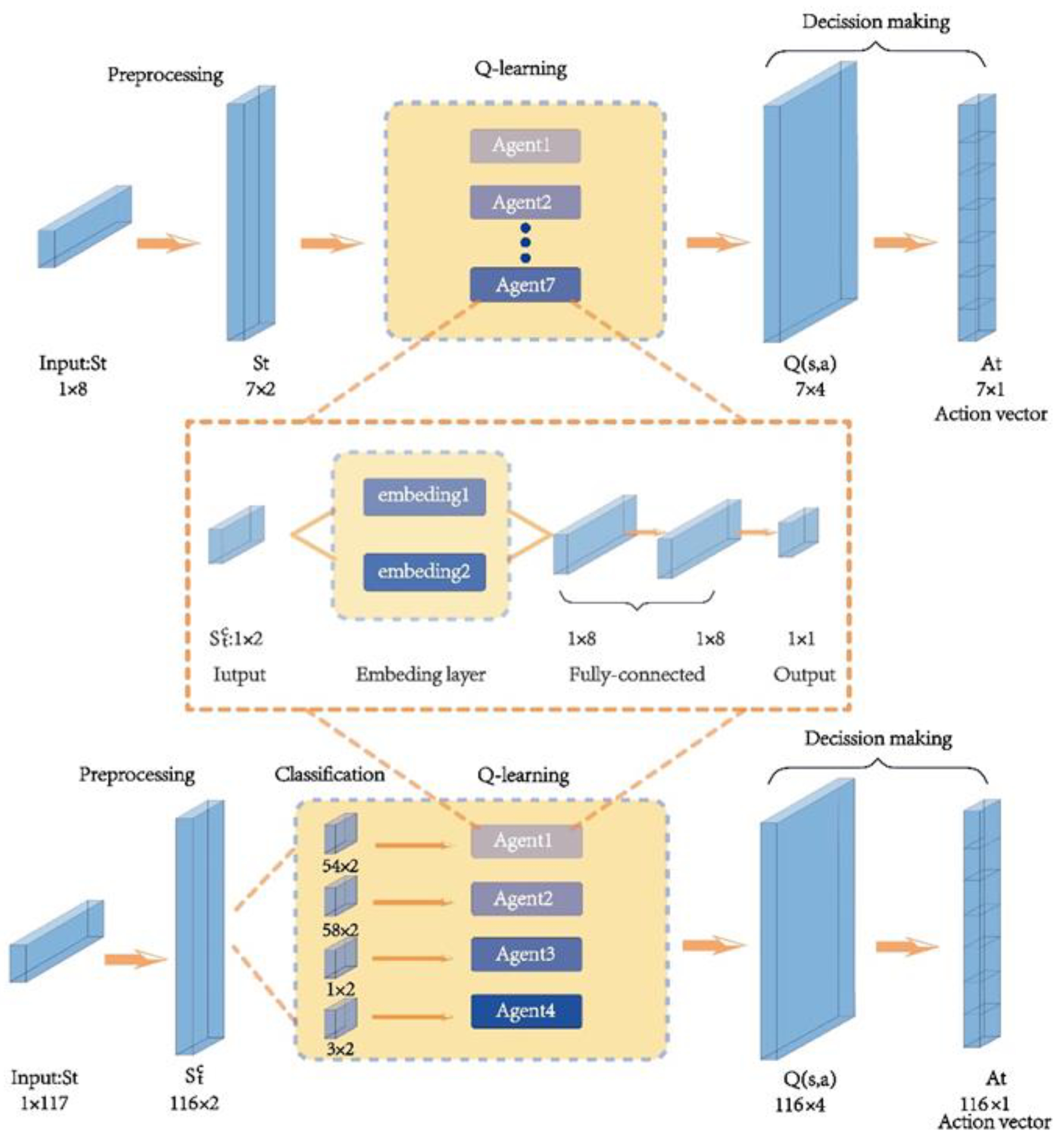
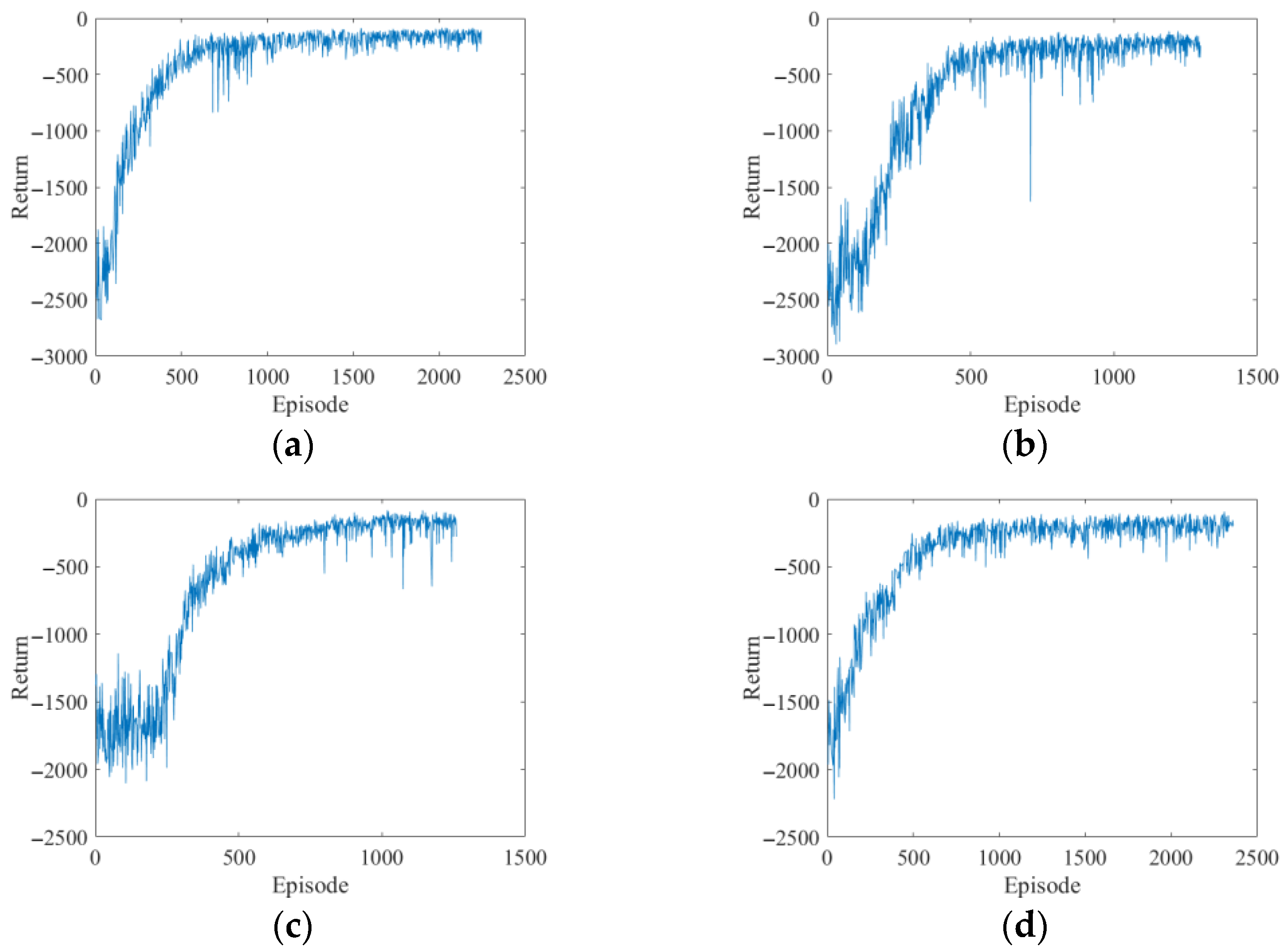
2.2. Reinforcement Learning
2.3. Q-Learning and Deep Q-Learning
2.4. Multiple-Agent in Parallel
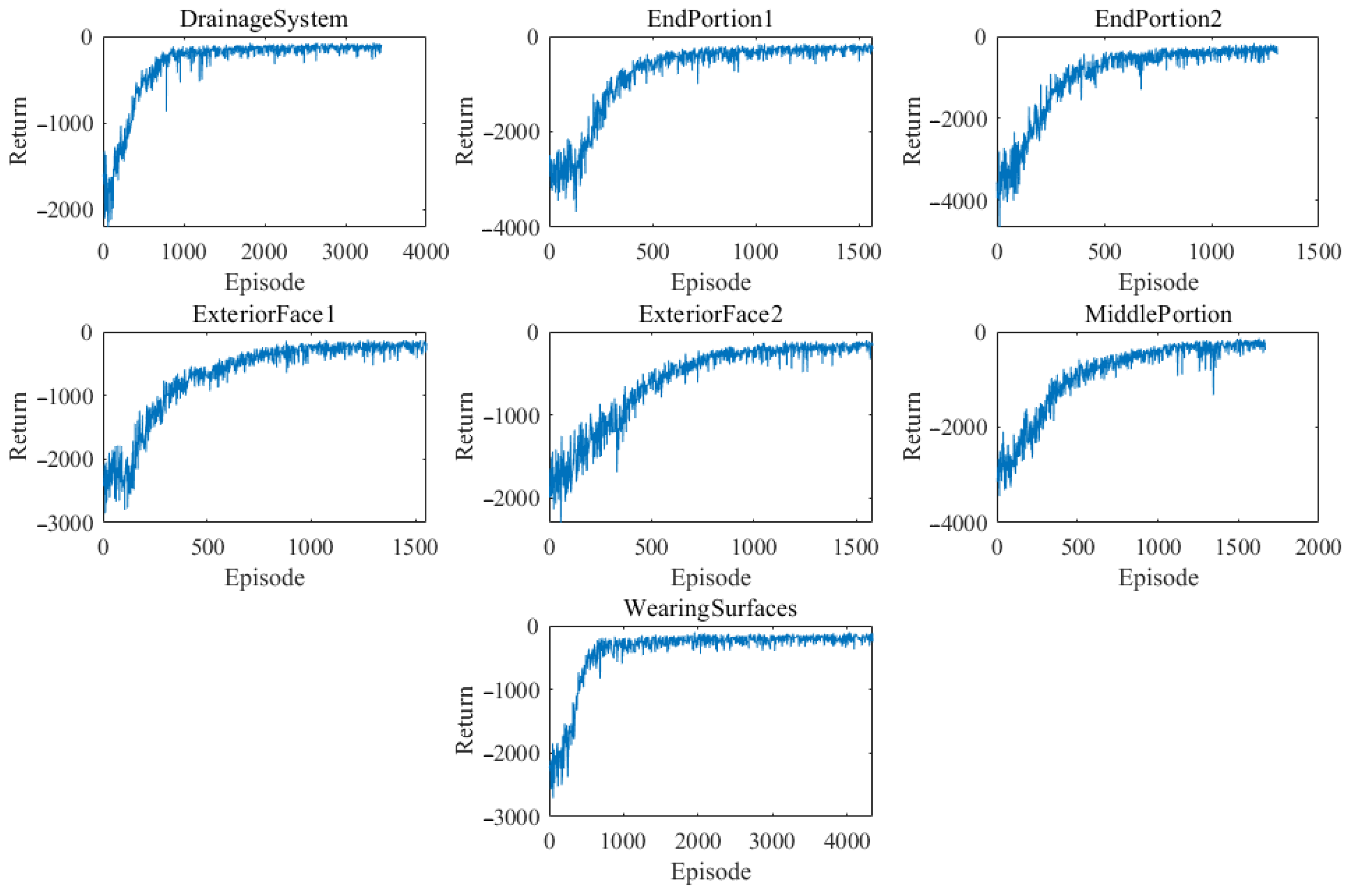
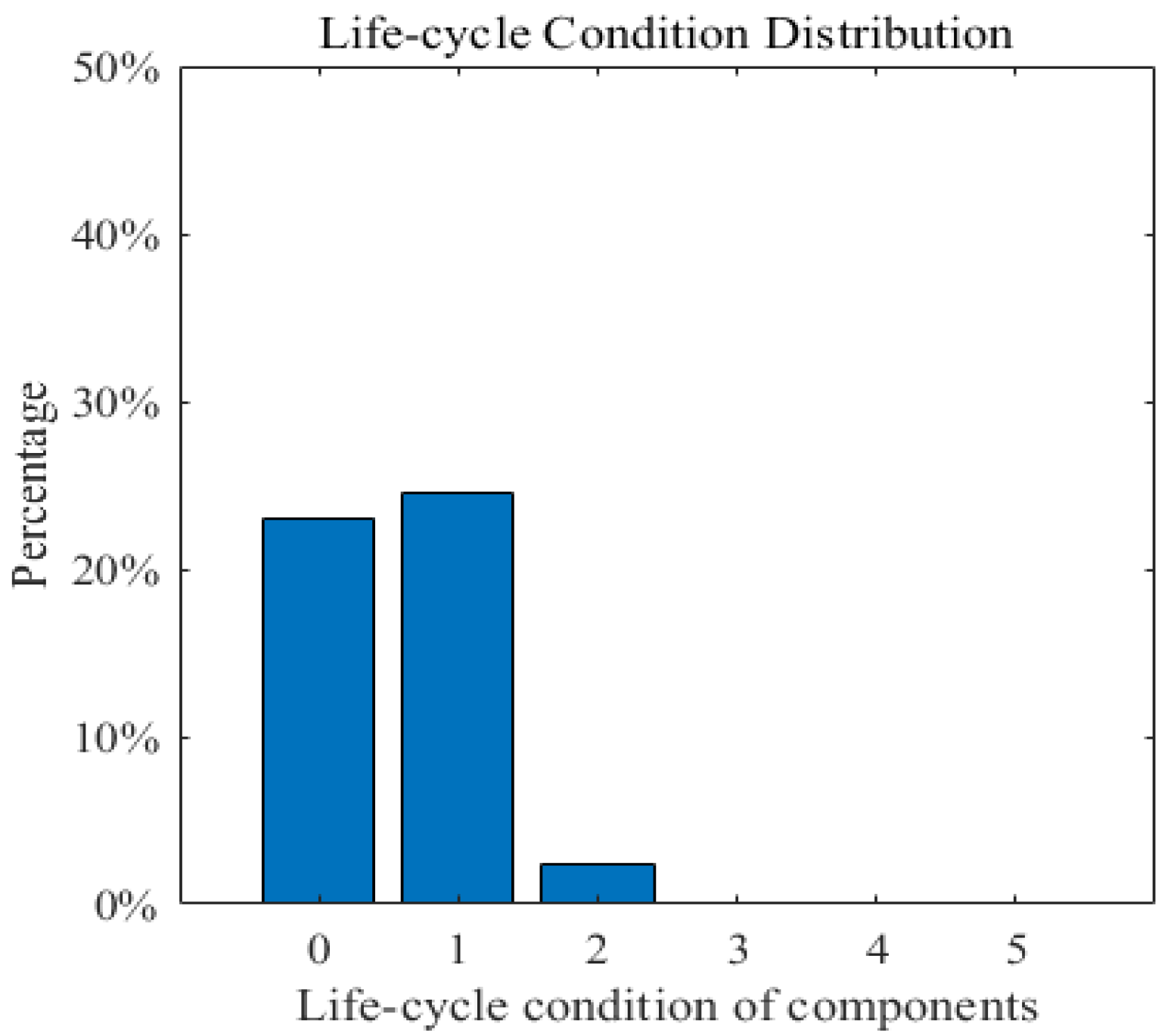
3. Case Study
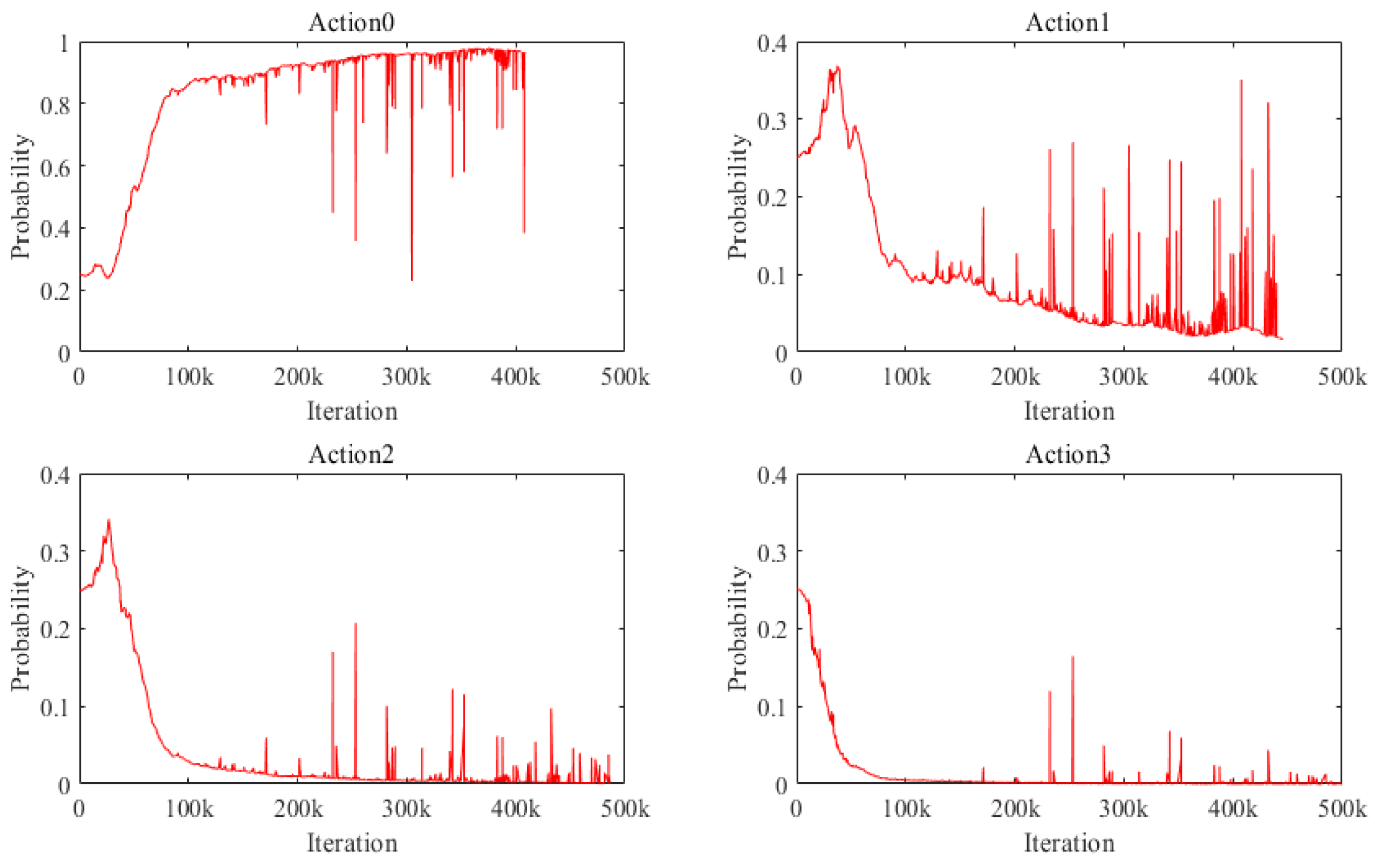
3.1. Case I: A Simple Bridge Deck System
| Algorithm 1 Pseudocode |
| Repeat (for each sample episode): |
| Initialize t = start year (random), (depend on t) |
| Preprocessing: |
| Single agent parallelism |
| Initialize arbitrarily |
| Repeat (for t < T) |
| Choose using policy derived from Q (epsilon greedy) |
| Take action , observe , sample next state =*) |
| and collect state <,,,>; |
| t = t + 1; |
| Util t = T; |
| Calculate for each step t in the episode, save the tuple |
| <, , , , > to memory |
| Update using Equation (16) |
| Calculate |
| Output optimal maintenance policy |
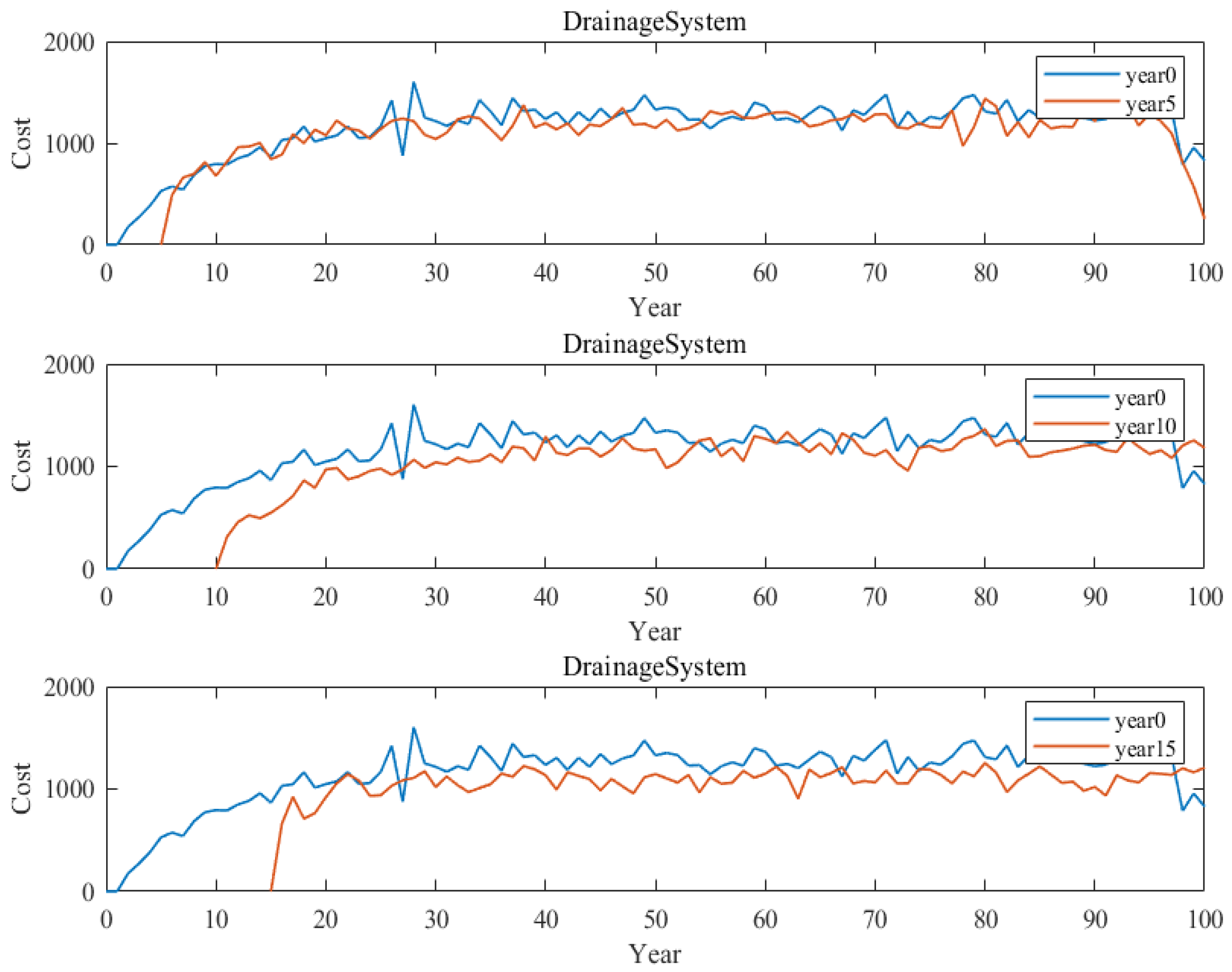
3.2. Case II: Taiping Lake Bridge
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimisation and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Wong, K.Y.; Lau, C.K.; Flint, A.R. Planning and implementation of the structural health monitoring system for cable-supported bridges in Hong Kong. In Proceedings of the SPIE-The International Society for Optical Engineering, San Diego, CA, USA, 31 July–2 August 2000; Volume 3995, pp. 266–275. [Google Scholar]
- Bao, Y.; Chen, Z.; Wei, S.; Xu, Y.; Tang, Z.; Li, H. The state of the art of data science and engineering in structural health monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Tsuda, Y.; Kaito, K.; Aoki, K.; Kobayashi, K. Estimating markovian transition probabilities for bridge deterioration forecasting. Kagaku Kogaku Ronbun 2006, 23, 241–256. [Google Scholar] [CrossRef]
- Mirzaei, Z. Overview of Existing Bridge Management Systems-Report by the IABMAS Bridge Management Committee. 2014. Available online: https://www.research-collection.ethz.ch (accessed on 7 February 2022).
- Robert, W.E.; Marshall, A.R.; Shepard, R.W.; Aldayuz, J. The Pontis Bridge Management System: State-of-the-Practice in Implementation and the Pontis Bridge Management System: State-of-the-Practice in Implementation and Development. 2002. Available online: https://trid.trb.org/view/644472 (accessed on 7 February 2022).
- Andersen, N.H. Danbro—A Bridge Management System for Many Levels; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Kim, S.K. Intelligent Bridge Maintenance System Development for Seo-Hae Grand Bridge//Cable-Supported Bridges: Challenging Technical Limits. In Proceedings of the Cable-Supported Bridges—Challenging Technical Limits, Seoul, Korea, 12–14 June 2001. [Google Scholar]
- Frangopol, D.M. Life-cycle performance, management, and optimisation of structural systems under uncertainty: Accomplishments and challenges. Struct. Infrastruct. Eng. 2011, 7, 389–413. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Kallen, M.J.; Noortwijk, J.M.V. Probabilistic models for life-cycle performance of deteriorating structures: Review and future directions. Prog. Struct. Eng. Mat. 2004, 6, 197–212. [Google Scholar] [CrossRef]
- Kuhn, K.D. Network-level infrastructure management using approximate dynamic programming. J. Infrastruct. Syst. 2010, 6, 103–111. [Google Scholar] [CrossRef]
- Medury, A.; Madanat, S. Simultaneous network optimization approach for pavement management systems. J. Infrastruct. Syst. 2014, 20, 04014010.1–04014010.7. [Google Scholar] [CrossRef]
- Robelin, C.A.; Madanat, S.M. Dynamic programming based maintenance and replacement optimization for bridge decks using history-dependent deterioration models. Am. Soc. Civil Eng. 2006, 13–18. [Google Scholar] [CrossRef][Green Version]
- Mozer, M.C.; Touretzky, D.S.; Hasselmo, M. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 2005, 16, 285–286. [Google Scholar]
- Canese, L.; Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-agent reinforcement learning: A review of challenges and applications. Appl. Sci. 2021, 11, 4948. [Google Scholar] [CrossRef]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning algorithms: A comprehensive classification and applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Bao, Y.; Li, H. Optimal policy for structure maintenance: A deep reinforcement learning framework. Struct. Saf. 2020, 83, 101906. [Google Scholar] [CrossRef]
- Madanat, S.; Mishalani, R.; Ibrahim, W.H.W. Estimation of infrastructure transition probabilities from condition rating data. J. Infrastruct. Syst. 1995, 1, 120–125. [Google Scholar] [CrossRef]
- Chung, S.-H.; Hong, T.-H.; Han, S.-W.; Son, J.-H.; Lee, S.-Y. Life cycle cost analysis based optimal maintenance and rehabilitation for underground infrastructure management. KSCE J. Civ. Eng. 2006, 10, 243–253. [Google Scholar] [CrossRef]
- Wellalage, N.K.W.; Zhang, T.; Dwight, R. Calibrating Markov Chain-based deterioration models for predicting future conditions of railway bridge elements. J. Bridge Eng. 2015, 20, 04014060. [Google Scholar] [CrossRef]
- Veshosky, D.; Beidleman, C.R.; Buetow, G.W.; Demir, M. Comparative analysis of bridge superstructure deterioration. J. Struct. Eng. 1994, 120, 2123–2136. [Google Scholar] [CrossRef]
- Park, T.; Saad, W. Kolkata paise restaurant game for resource allocation in the internet of things. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 16 April 2018; pp. 1774–1778. [Google Scholar]
- Kastampolidou, K.; Papalitsas, C.; Andronikos, T. The distributed Kolkata paise restaurant game. Games 2022, 13, 33. [Google Scholar] [CrossRef]
- Qiu, J.; Yu, C.; Liu, W.; Yang, T.; Yu, J.; Wang, Y.; Yang, H. Low-cost multi-agent navigation via reinforcement learning with multi-fidelity simulator. IEEE Access 2021, 9, 84773–84782. [Google Scholar] [CrossRef]
- Tham, C.K.; Prager, R.W. A modular Q-Learning architecture for manipulator task decomposition. In Proceedings of the Eleventh International Conference, Rutgers University, New Brunswick, NJ, USA, 10–13 July 1994; pp. 309–317. [Google Scholar]
- Machado, L.; Schirru, R. The Ant-Q algorithm applied to the nuclear reload problem. Ann. Nucl. Energy 2002, 29, 1455–1470. [Google Scholar] [CrossRef]
- Yang, L.; Sun, Q.; Ma, D.; Wei, Q. Nash Q-learning based equilibrium transfer for integrated energy management game with We-Energy. Neurocomputing 2020, 396, 216–223. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Gopinath, D. Modeling infrastructure performance and user costs. J. Infrastruct. Syst. 1995, 1, 33–43. [Google Scholar] [CrossRef]
- Kobayashi, K.; Do, M.; Han, D. Estimation of Markovian transition probabilities for pavement deterioration forecasting. KSCE J. Civ. Eng. 2010, 14, 343–351. [Google Scholar] [CrossRef]
- Jiang, Y.; Saito, M.; Sinha, K.C. Bridge Performance Prediction Model Using the Markov Chain. 1988. Available online: https://trid.trb.org/view/300339 (accessed on 7 February 2022).
- Walgama Wellalage, N.K.; Zhang, T.; Dwight, R.; El-Akruti, K. Bridge deterioration modeling by Markov Chain Monte Carlo (MCMC) simulation method. In Proceedings of the 8th World Congress on Engineering Asset Management & 3rd International Conference on Utility Management & Safety, Hong Kong, China, 30 October–1 November 2013; pp. 545–556. [Google Scholar]
- Morcous, G. Performance prediction of bridge deck systems using Markov Chains. J. Perform. Constr. Fac. 2006, 20, 146–155. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
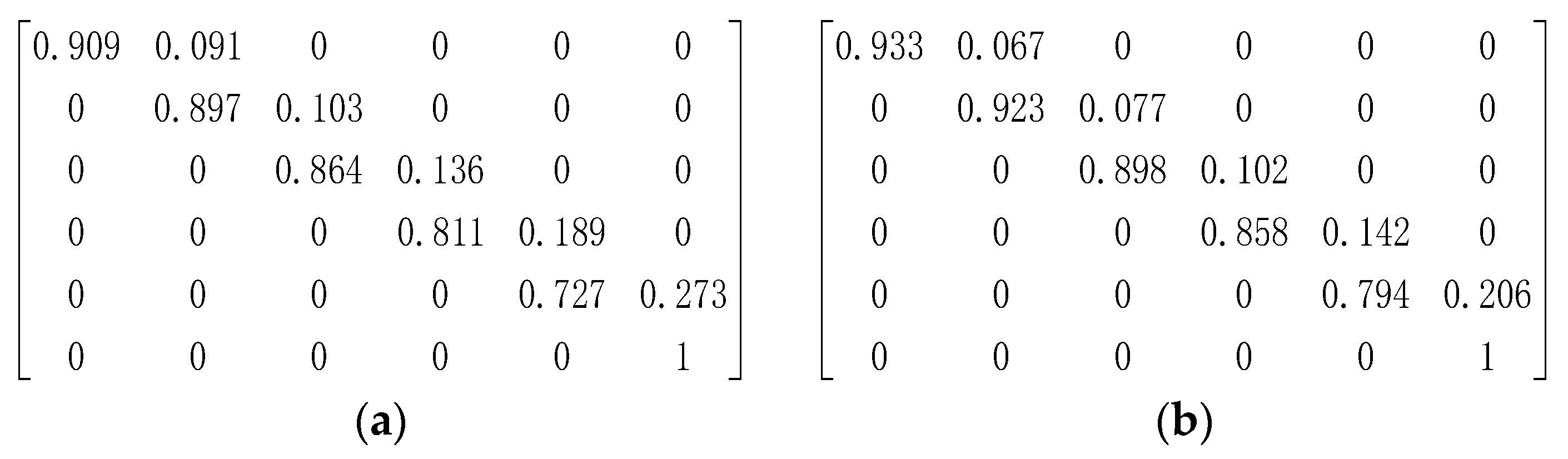
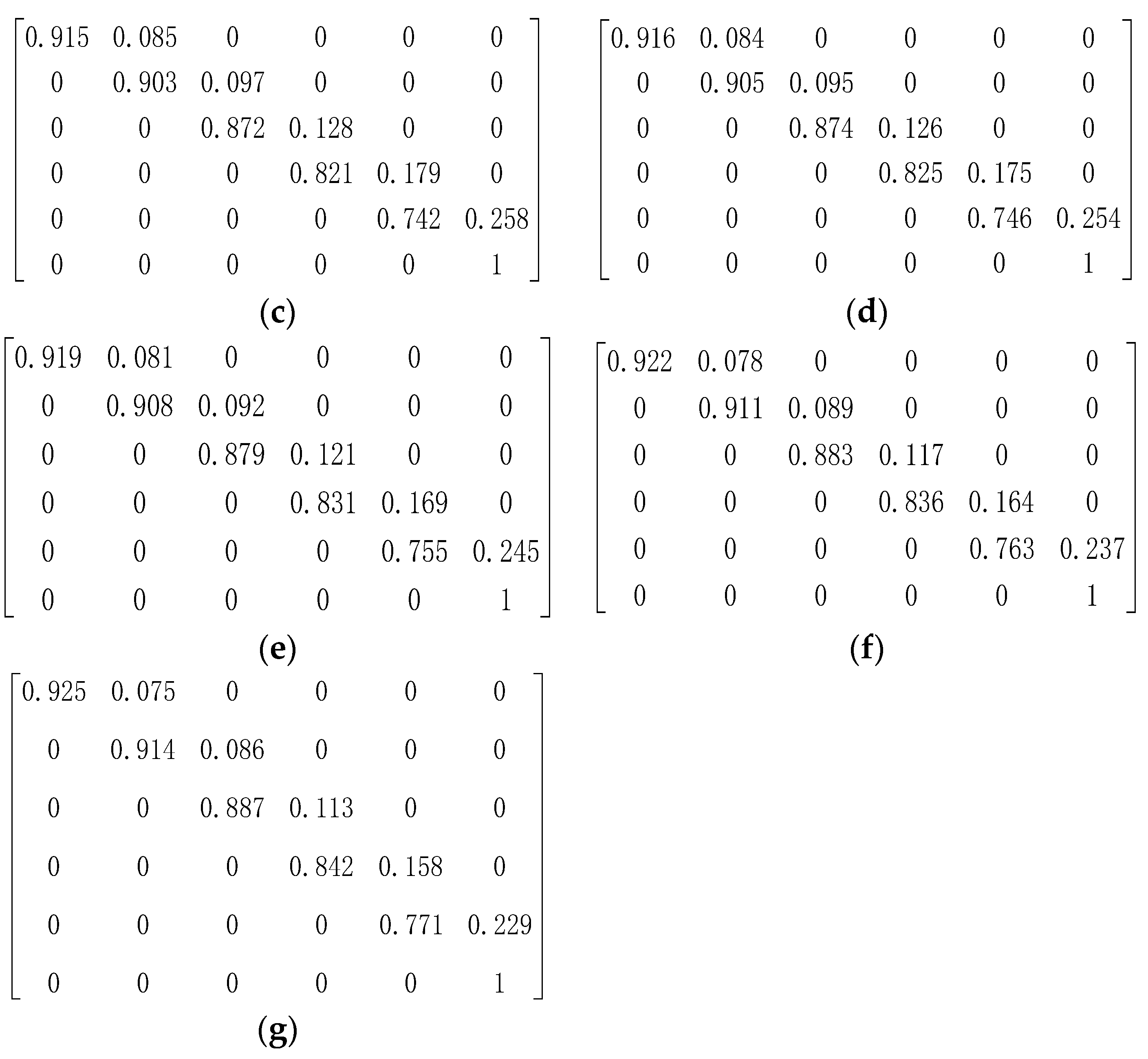




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.-N.; Yuan, Y.; Yang, D.; Zhang, J. An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation. Sustainability 2022, 14, 10050. https://doi.org/10.3390/su141610050
Zhou Q-N, Yuan Y, Yang D, Zhang J. An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation. Sustainability. 2022; 14(16):10050. https://doi.org/10.3390/su141610050
Chicago/Turabian StyleZhou, Qi-Neng, Ye Yuan, Dong Yang, and Jing Zhang. 2022. "An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation" Sustainability 14, no. 16: 10050. https://doi.org/10.3390/su141610050
APA StyleZhou, Q.-N., Yuan, Y., Yang, D., & Zhang, J. (2022). An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation. Sustainability, 14(16), 10050. https://doi.org/10.3390/su141610050





