Impact of Transformer Topology on Short-Circuit Analysis in Distribution Systems with Inverter-Based Distributed Generations
Abstract
:1. Introduction
- A detailed approach that can conduct fault analyses with IBDGs is presented while considering the interconnection transformer topology that can impact the symmetric components of fault currents. This thorough approach helps engineers or researchers to study any types of distribution systems with SBDGs or IBDGs.
- Different fault behaviors caused by various transformer topologies are studied, including D-Yg, Yg-D, Yg-D-Yg, D-D-Yg, and Y-D-Yg.
- The transformer grounding impact on the zero-sequence fault current contributions of DERs and the total fault current are analyzed.
- Ultimately, this study can give insights on how to practically design a transformer topology and its grounding in distribution systems.
2. Materials and Methods
3. Impact of Interconnection Transformer Topology on Fault Current Contribution
4. Investigation of Fault Behaviors of the IBDG
4.1. Short-Circuit Analysis of the SBDG-Based System
4.2. Short-Circuit Analysis of the IBDG-Based System
4.2.1. Decomposition and Short-Circuit Analysis: Voltage Source
4.2.2. Decomposition and Short-Circuit Analysis: Current Source
4.2.3. Superposition
4.3. Comparison of the SBDG and IBDG Cases
4.4. Accuracy Test
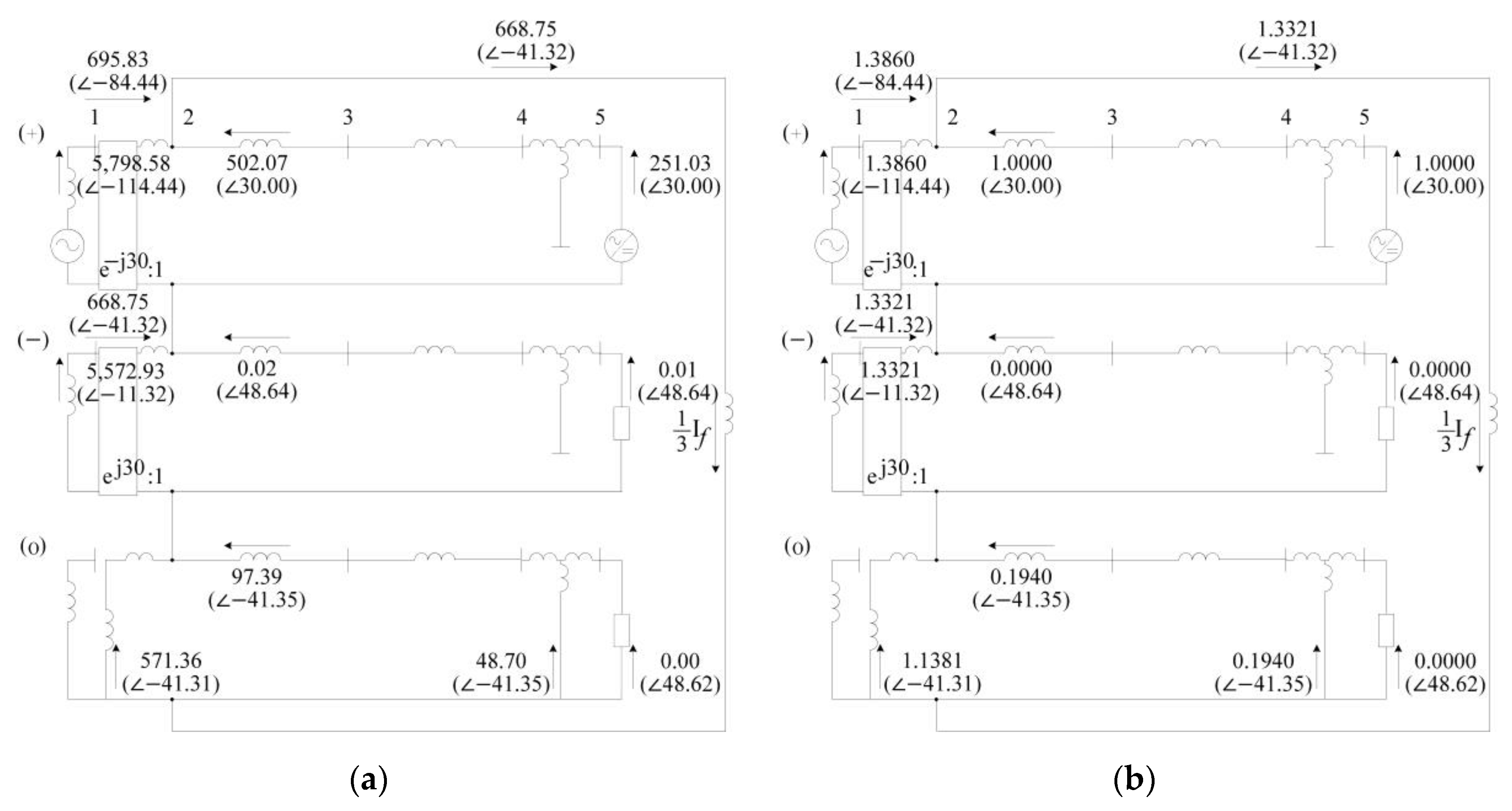
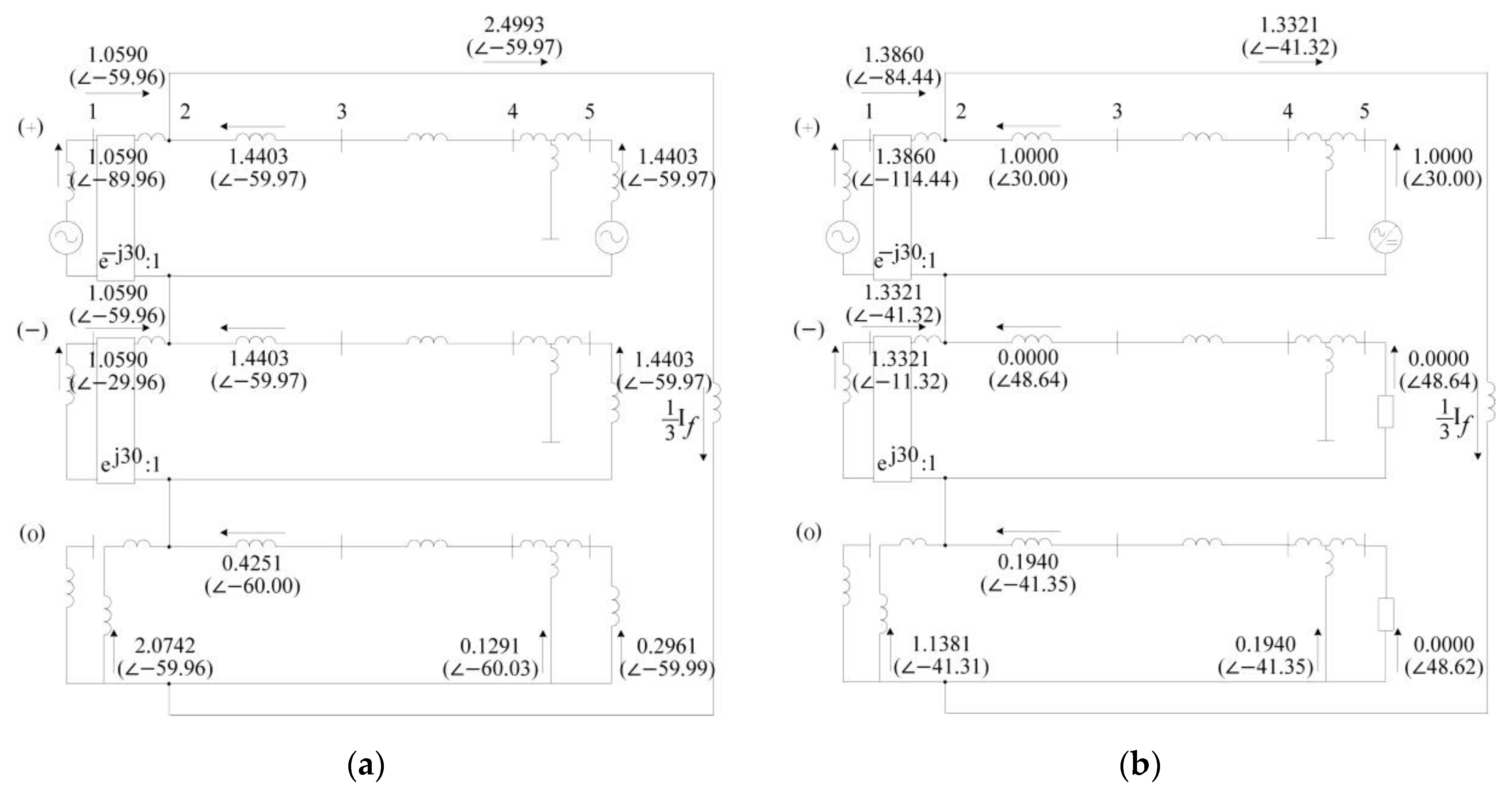
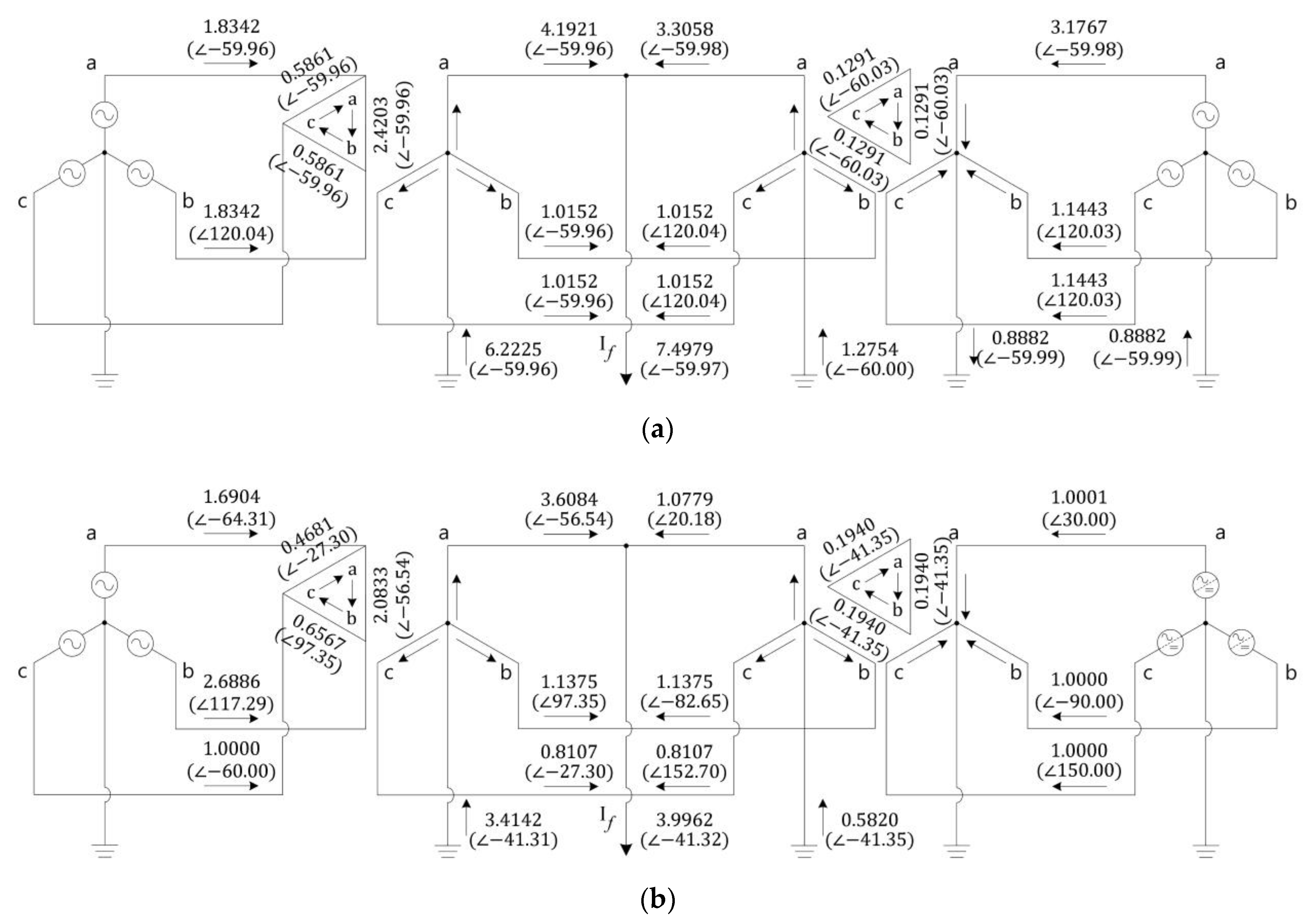
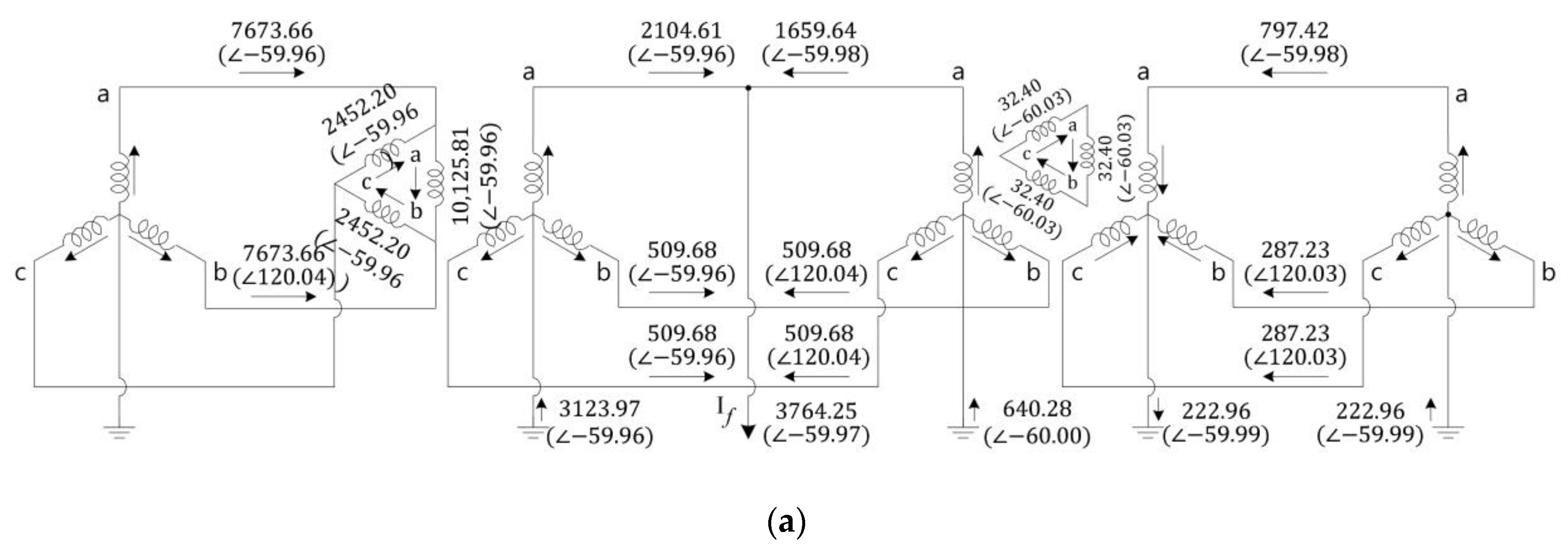
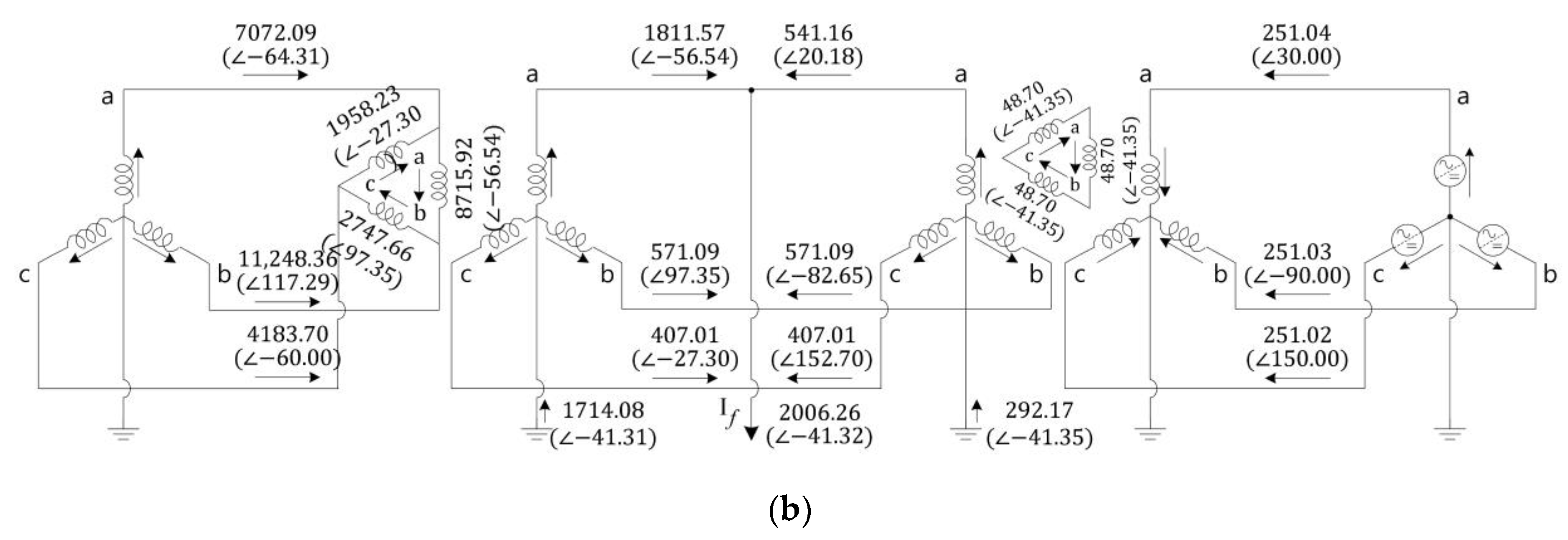
5. Short-Circuit Analysis with Consideration of the Interconnection Transformer
5.1. Case Study with Different Topologies of the Interconnection Transformer
5.2. Case Study Analyses
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DER | Distributed energy resource |
| SBDG | Synchronous-based distributed generation |
| IBDG | Inverter-based distributed generation |
| DG | Distributed generation |
| SLG | Single-line-to-ground |
References
- D’Adamo, I.; Rosa, P. Current state of renewable energies performances in the European Union: A new reference framework. Energy Convers. Manag. 2016, 121, 84–92. [Google Scholar] [CrossRef]
- Pinson, P.; Mitridati, L.; Ordoudis, C.; Østergaard, J. Towards fully renewable energy systems: Experience and trends in Denmark. CSEE J. Power Energy Syst. 2017, 3, 26–35. [Google Scholar] [CrossRef]
- Marafao, F.P.; Alonso, A.M.D.S.; Goncalves, F.A.S.; Brandao, D.I.; Martins, A.C.G.; Paredes, H.K.M. Trends and constraints on Brazilian photovoltaic industry: Energy policies, interconnection codes, and equipment certification. IEEE Trans. Ind. Applicat. 2018, 54, 4017–4027. [Google Scholar] [CrossRef]
- Holdmann, G.P.; Wies, R.W.; Vandermeer, J.B. Renewable energy integration in Alaska’s remote islanded microgrids: Economic drivers, technical strategies, technological Niche development, and policy implications. Proc. IEEE 2019, 107, 1820–1837. [Google Scholar] [CrossRef]
- Ozarisoy, B.; Altan, H. Developing an evidence-based energy-policy framework to assess robust energy-performance evaluation and certification schemes in the South-eastern Mediterranean countries. Energy Sustain. Develop. 2021, 64, 65–102. [Google Scholar] [CrossRef]
- Burke, M.J.; Stephens, J.C. Energy democracy: Goals and policy instruments for sociotechnical transitions. Energy Res. Soc. Sci. 2017, 33, 35–48. [Google Scholar] [CrossRef]
- Abrishambaf, O.; Lezama, F.; Faria, P.; Vale, Z. Towards transactive energy systems: An analysis on current trends. Energy Strategy Rev. 2019, 26, 100418. [Google Scholar] [CrossRef]
- Bayer, B.; Matschoss, P.; Thomas, H.; Marian, A. The German experience with integrating photovoltaic systems into the low-voltage grids. Renew. Energy 2018, 119, 129–141. [Google Scholar] [CrossRef]
- Kennedy, J.; Ciufo, P.; Agalgaonkar, A. A review of protection systems for distribution networks embedded with renewable generation. Renew. Sustain. Energy Rev. 2016, 58, 1308–1317. [Google Scholar] [CrossRef] [Green Version]
- Manditereza, P.T.; Bansal, R. Renewable distributed generation: The hidden challenges—A review from the protection perspective. Renew. Sustain. Energy Rev. 2016, 58, 1457–1465. [Google Scholar] [CrossRef]
- Sidhu, T.S.; Bejmert, D. Short-circuit current contribution from large scale PV power plant in the context of distribution power system protection performance. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011; pp. 1–6. [Google Scholar] [CrossRef]
- IEEE 1547.2-2008; IEEE Application Guide for IEEE std 1547(TM), IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems. IEEE: New York, NY, USA, 2009. [CrossRef]
- Popadic, B.; Dumnic, B.; Strezoski, L. Modeling of initial fault response of inverter-based distributed energy resources for future power system planning. Int. J. Electr. Power Energy Syst. 2020, 117, 105722. [Google Scholar] [CrossRef]
- Haj-Ahmed, M.A.; Illindala, M.S. The influence of inverter-based DGs and their controllers on distribution network protection. IEEE Trans. Ind. Applicat. 2014, 50, 2928–2937. [Google Scholar] [CrossRef]
- Haddadi, A.; Zhao, M.; Kocar, I.; Karaagac, U.; Chan, K.W.; Farantatos, E. Impact of inverter-based resources on negative sequence quantities-based protection elements. IEEE Trans. Power Deliv. 2020, 36, 289–298. [Google Scholar] [CrossRef]
- Behnke, M.R.; Custer, G.; Farantatos, E.; Fischer, N.; Guttromson, R.; Isaacs, A.; Majumder, R.; Pant, S.; Patel, M.; Venkat, R.-K.; et al. Impact of Inverter-Based Resource Negative-Sequence Current Injection on Transmission System Protection; United States Department of Energy: Oak Ridge, TN, USA, 2020. [Google Scholar]
- Saleh, K.A.; Zeineldin, H.H.; Al-Hinai, A. A three-phase fault currents calculation method used for protection coordination analysis. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Kou, G.; Jordan, J.; Cockerham, B.; Patterson, R.W.; VanSant, P. Negative-sequence current injection of transmission solar farms. IEEE Trans. Power Deliv. 2020, 35, 2740–2743. [Google Scholar] [CrossRef]
- Erlich, I.; Neumann, T.; Shewarega, F.; Schegner, P.; Meyer, J. Wind turbine negative sequence current control and its effect on power system protection. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, X. Fault current negative contribution method for inverter-based distributed generators under grid unbalanced fault. IEEE Access 2020, 8, 220807–220815. [Google Scholar] [CrossRef]
- Rajaei, N.; Ahmed, M.H.; Salama, M.M.A.; Varma, R.K. Analysis of fault current contribution from inverter based distributed generation. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Kim, I. A calculation method for the short-circuit current contribution of current-control inverter-based distributed generation sources at balanced conditions. Electr. Power Syst. Res. 2021, 190, 106839. [Google Scholar] [CrossRef]
- Mathur, A.; Das, B.; Pant, V. Fault analysis of unbalanced radial and meshed distribution system with inverter based distributed generation (IBDG). Int. J. Electr. Power Energy Syst. 2017, 85, 164–177. [Google Scholar] [CrossRef]
- Kim, I. Short-circuit analysis models for unbalanced inverter-based distributed generation sources and loads. IEEE Trans. Power Syst. 2019, 34, 3515–3526. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D. A fast fault current calculation method for distribution networks connected with inverter interfaced distributed generators. MethodsX 2021, 8, 101176. [Google Scholar] [CrossRef]
- Blackburn, J.L.; Domin, T.J. Protective Relaying—Principles and Applications, 4th ed.; CRC Press LLC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Cho, N.; Yun, S.; Jung, J. Shunt fault analysis methodology for power distribution networks with inverter-based distributed energy resources of the Korea Electric Power Corporation. Renew. Sustain. Energy Rev. 2020, 133, 110–140. [Google Scholar] [CrossRef]
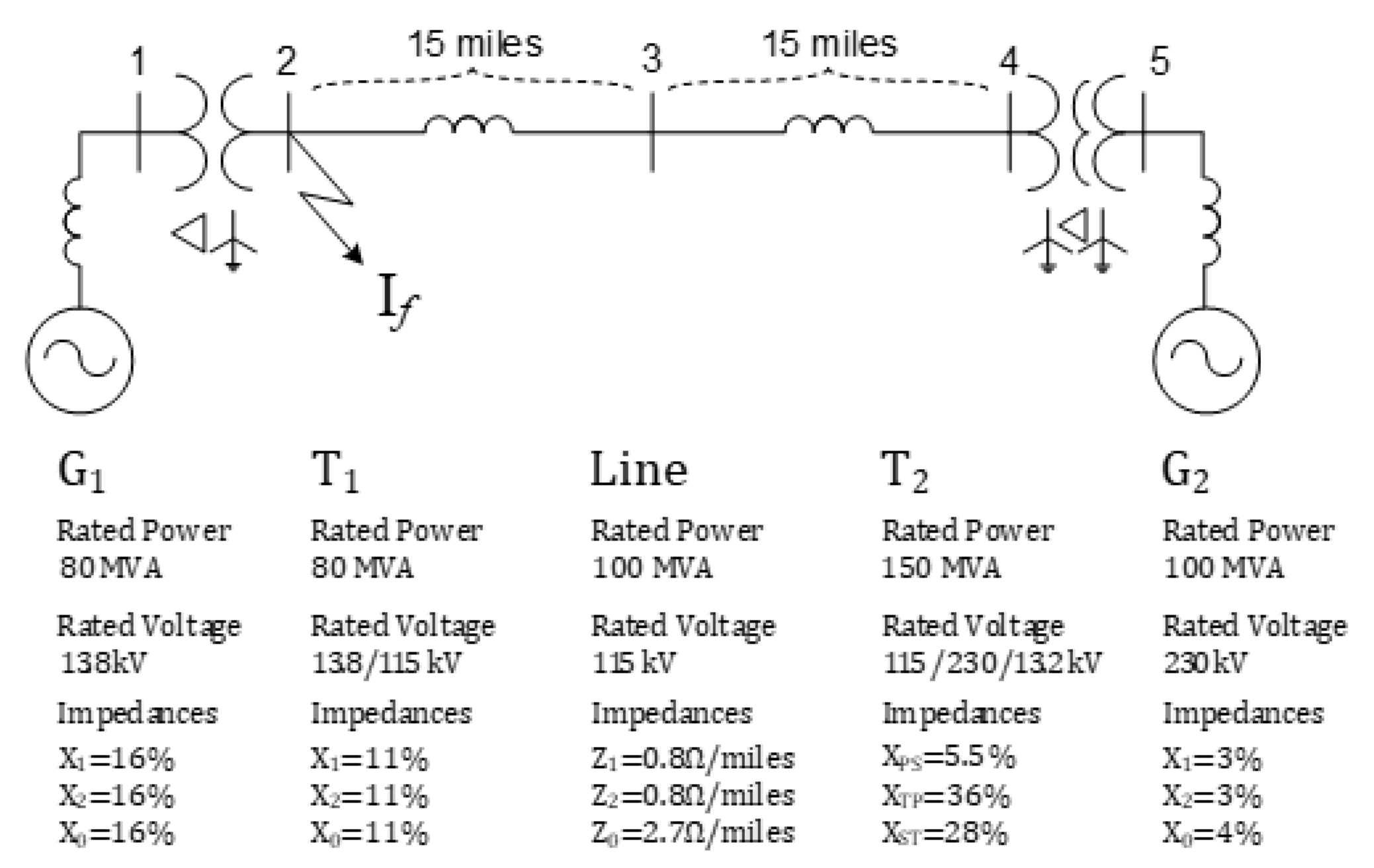
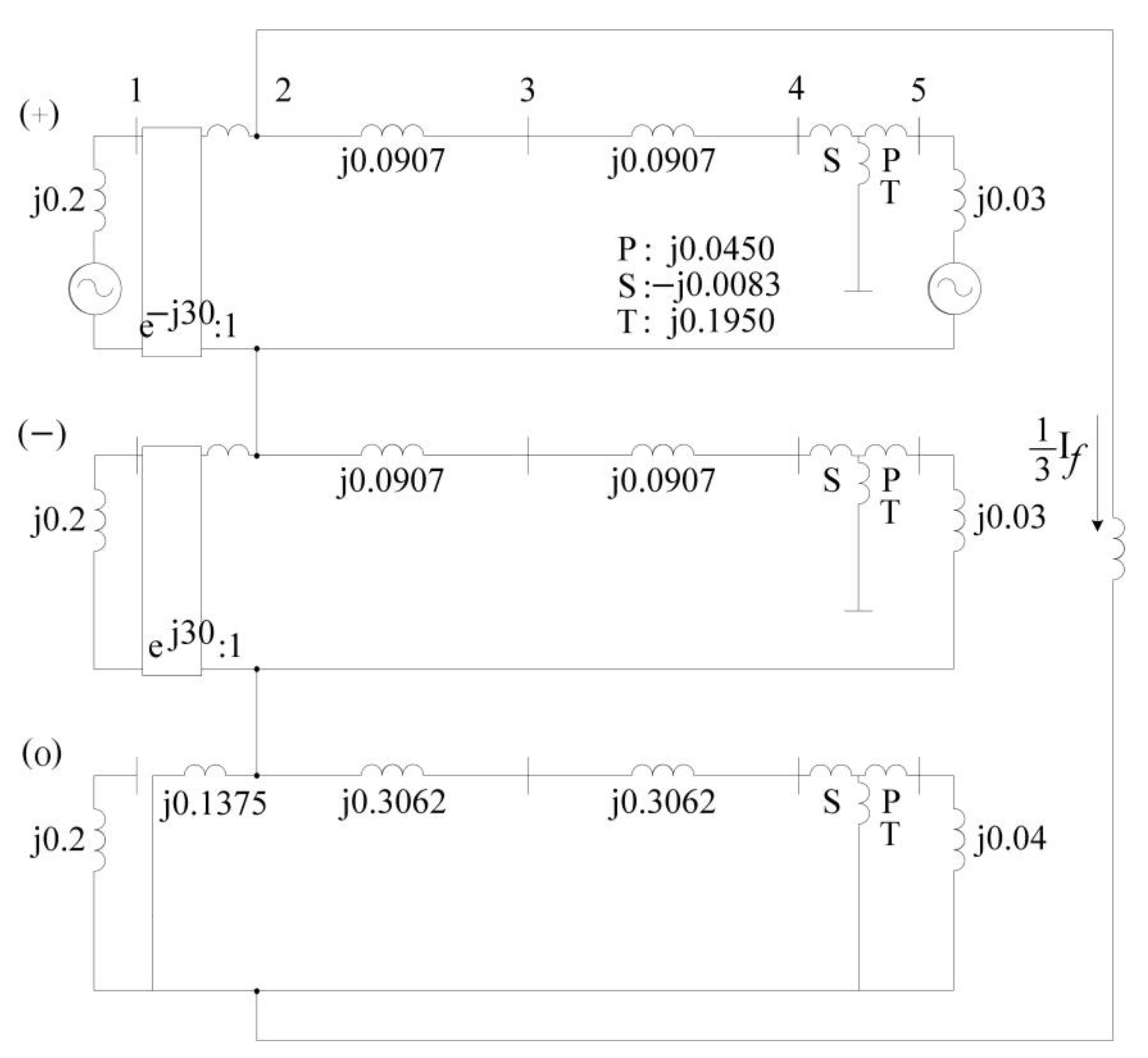
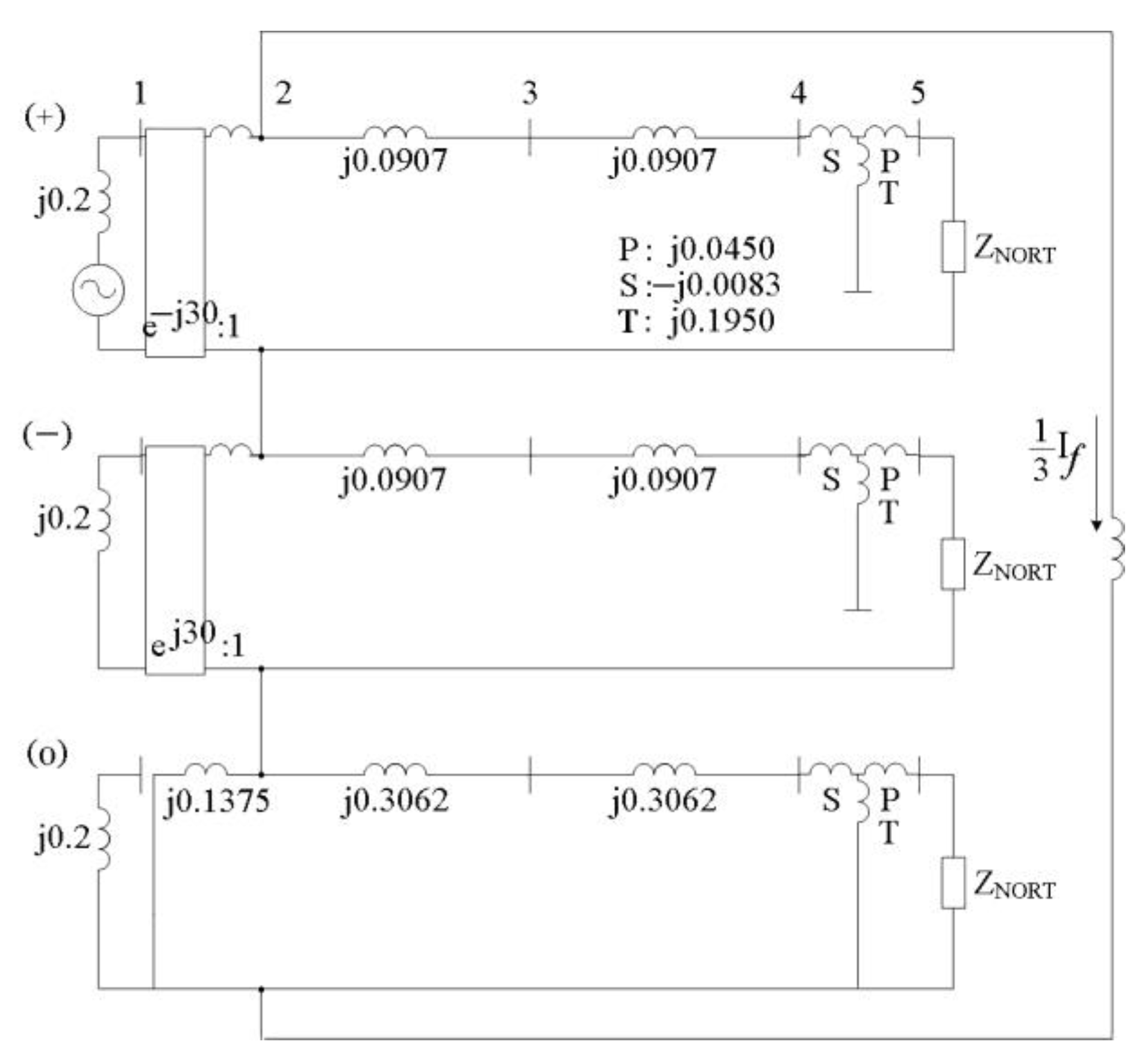
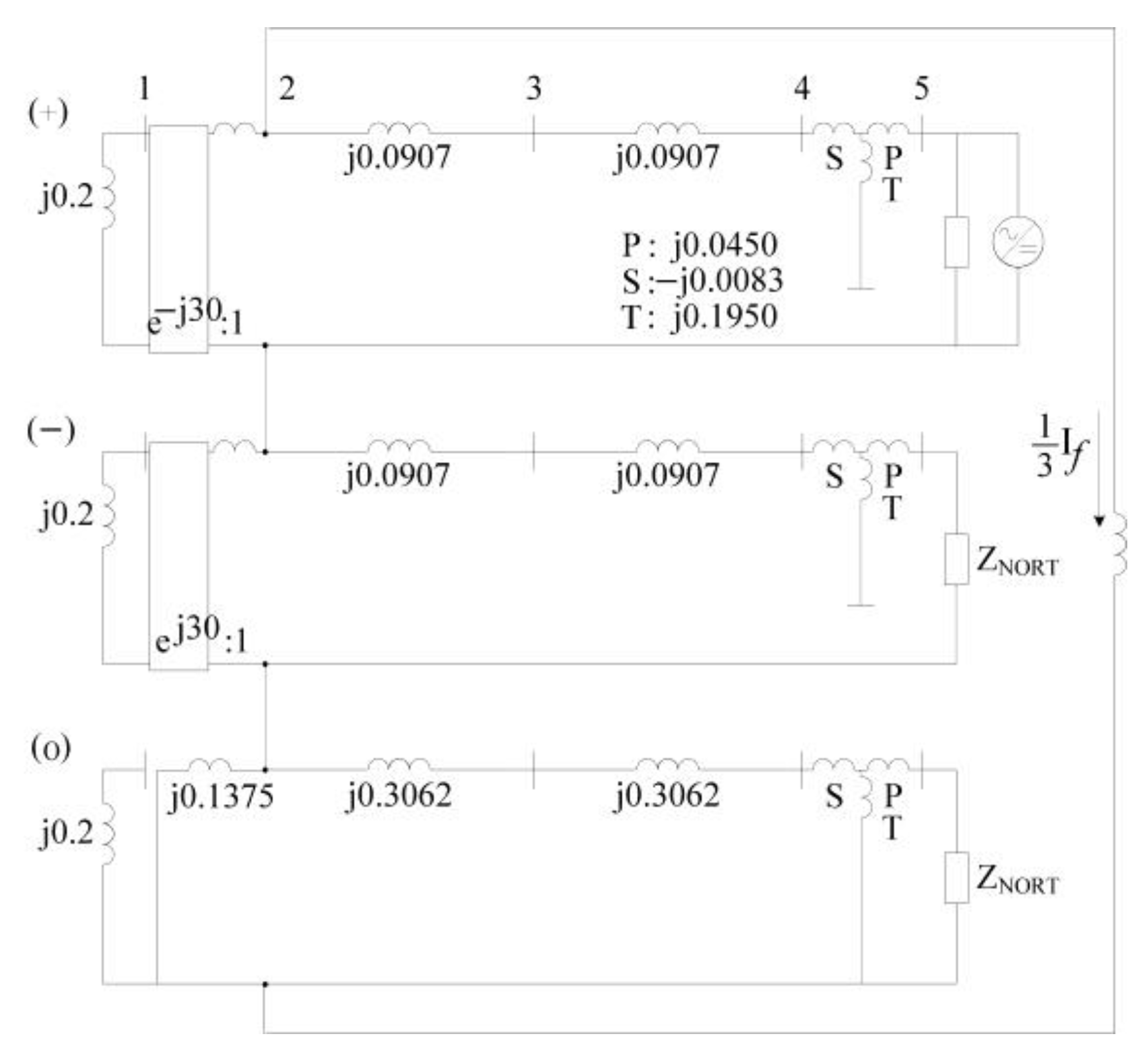
| Previous Studies | Summary |
|---|---|
| [19] | Observed that the wind turbine controller may reduce the negative-sequence component of fault currents; injected negative-sequence currents |
| [20] | Presented the method that changed the fault current phase angle to minimize the system fault current |
| [21] | Quantified the fault current contributions due to IBDGs using steady-state and transient analyses |
| [22] | Conducted fault analysis due to IBDGs under balanced conditions |
| [23] | Considered IBDG’s voltage-dependent control modes for short-circuit analysis of radial and meshed networks |
| [24] | Considered fault contributions from unbalanced IBDGs |
| [25] | Improved computational speed for fault analysis with IBDGs |
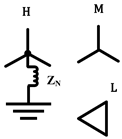
| Transformer Bank Connection | Positive/Negative Sequence | Zero Sequence |
|---|---|---|
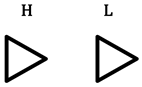
 |  |  |
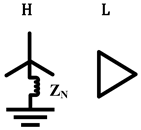 | Same as above | 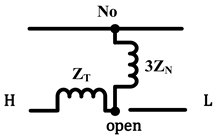 |
 | Same as above | 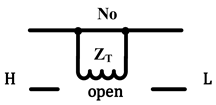 |
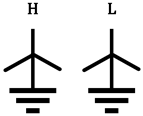 | Same as above |  |
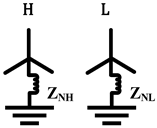 | Same as above | 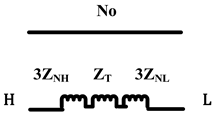 |
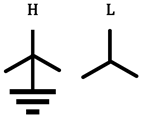 | Same as above | 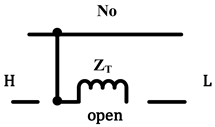 |
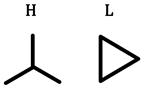 | Same as above | 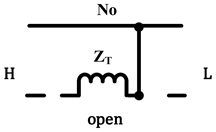 |
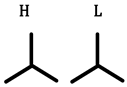 | Same as above | 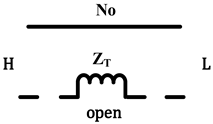 |
| Transformer Bank Connection | Positive/Negative Sequence | Zero Sequence |
|---|---|---|
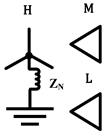 |  | 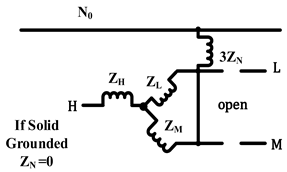 |
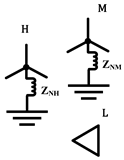 | Same as above | 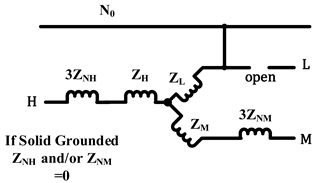 |
 | Same as above | 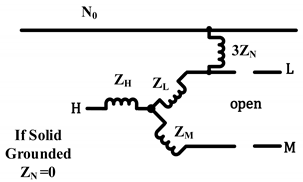 |
| Transformer Type | Topology | Fault Current Behavior in the Zero-Sequence Network |
|---|---|---|
| Two-winding transformer | D-Yg | 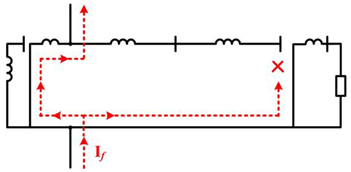 |
| Yg-D | 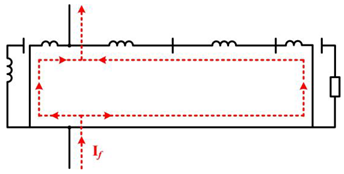 | |
| Three-winding transformer | Y-D-Yg | 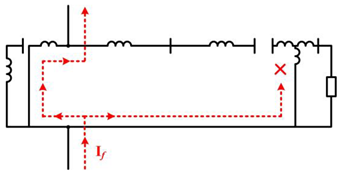 |
| D-D-Yg | 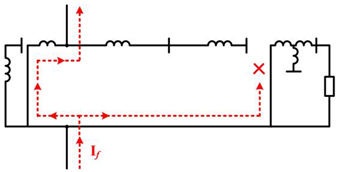 | |
| Yg-D-Yg | 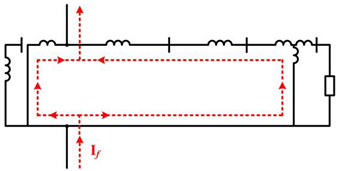 |
| Sequence | Impedance of G1 | Impedance of T1 | Impedance of Line | Secondary Impedance of T2 | Primary Impedance of T2 | Tertiary Impedance of T2 | Impedance of G2 |
|---|---|---|---|---|---|---|---|
| Positive (symbol) | |||||||
| Negative (symbol) | |||||||
| Zero (symbol) |
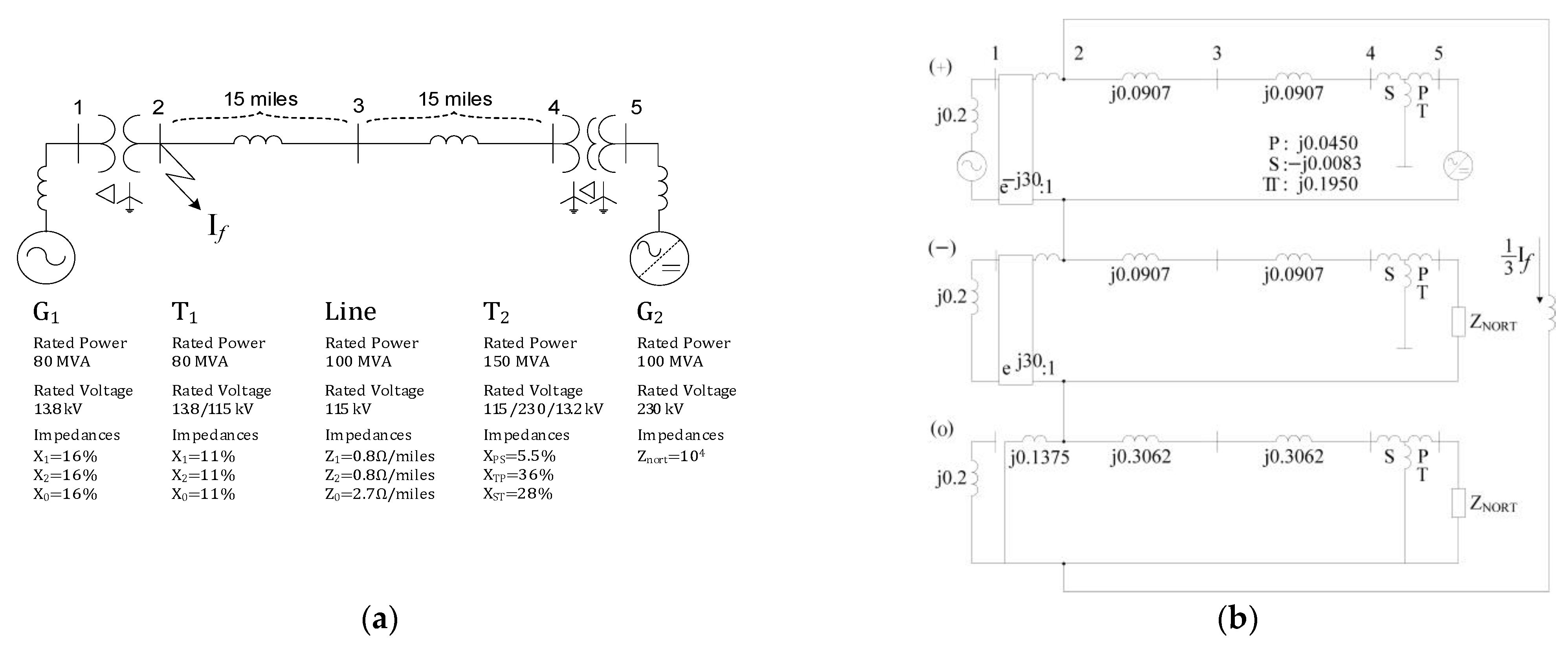
| Sequence | Impedance of G1 | Impedance of T1 | Impedance of Line | Secondary Impedance of T2 | Primary Impedance of T2 | Tertiary Impedance of T2 | Norton Impedance of G2 |
|---|---|---|---|---|---|---|---|
| Positive (symbol) | |||||||
| Negative (symbol) | |||||||
| Zero (symbol) |
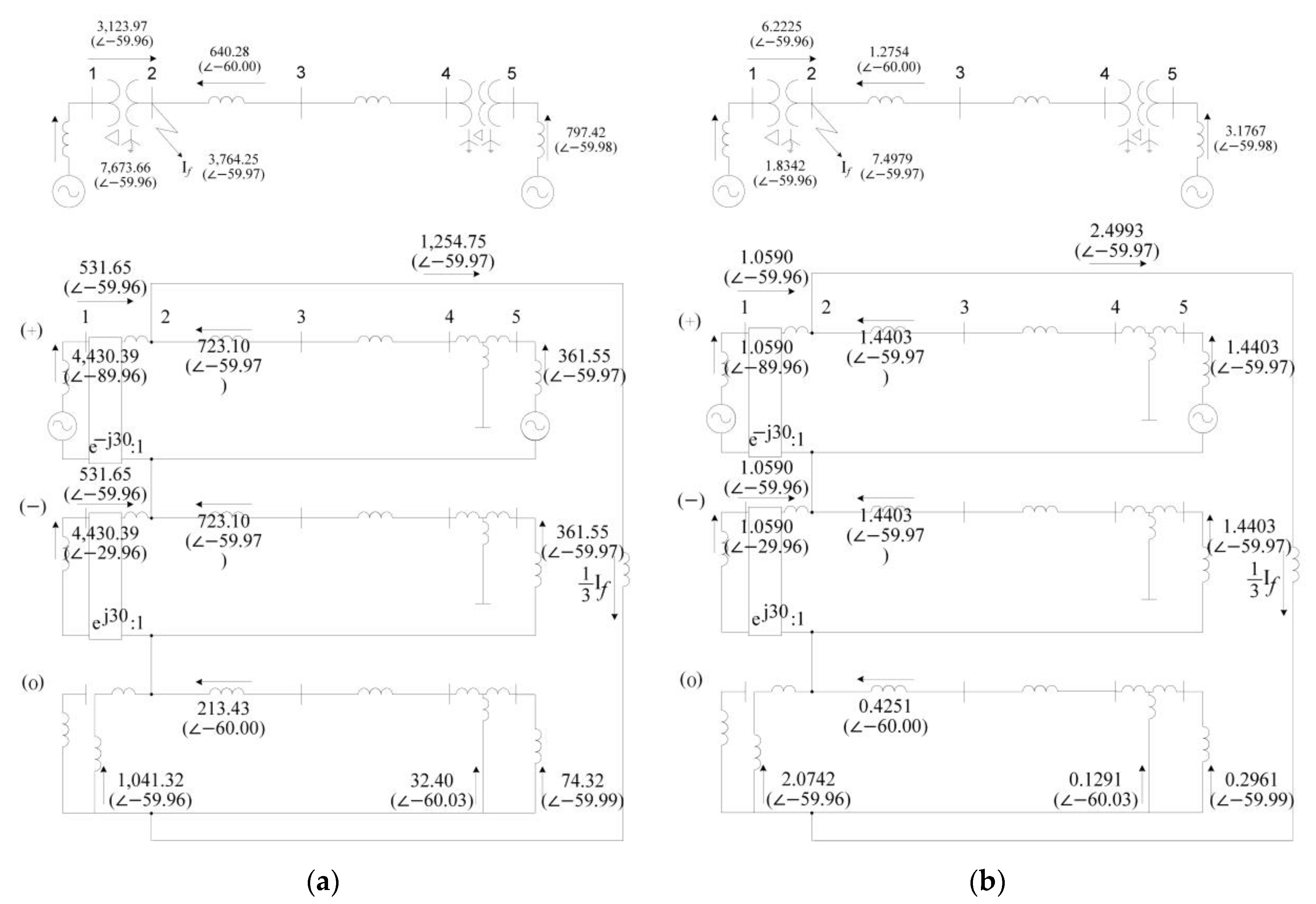
| Bus No. | Va | Vb | Vc | 3V0 | V0 | V1 | V2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Magnitude (Mag) (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | |
| 1 | 0.7105 | −11.89 | 0.6201 | −92.03 | 1.0199 | 131.31 | 0.0000 | 0 | 0.0000 | 0 | 0.7565 | 8.73 | 0.2664 | −101.35 |
| 2 | 0.0000 | 0 | 0.9438 | −55.75 | 0.9439 | 153.05 | 0.4695 | −131.35 | 0.1565 | −131.35 | 0.6061 | 48.65 | 0.4496 | −131.35 |
| 3 | 0.1239 | 92.61 | 0.9890 | −48.01 | 0.9343 | 155.03 | 0.2890 | −131.36 | 0.0963 | −131.36 | 0.6409 | 56.36 | 0.4496 | −131.35 |
| 4 | 0.2477 | 92.61 | 1.0504 | −41.06 | 0.9259 | 157.05 | 0.1086 | −131.38 | 0.0362 | −131.38 | 0.6860 | 63.16 | 0.4496 | −131.36 |
| 5 | 0.2797 | 96.30 | 1.0783 | −39.86 | 0.9317 | 159.39 | 0.1135 | −131.38 | 0.0378 | −131.38 | 0.7067 | 65.65 | 0.4496 | −131.36 |
| From | To | Ia | Ib | Ic | 3I0 | I0 | I1 | I2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus No. | Bus No. | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) |
| 1 | 2 | 3.6084 | −56.54 | 1.1375 | 97.35 | 0.8107 | −27.30 | 3.4142 | −41.31 | 1.1381 | −41.31 | 1.3860 | −84.44 | 1.3321 | −41.32 |
| 2 | F | 3.9962 | −41.32 | 0.0000 | 0.00 | 0.0000 | 0.00 | 3.9962 | −41.32 | 1.3321 | −41.32 | 1.3321 | −41.32 | 1.3321 | −41.32 |
| 3 | 2 | 1.0779 | 20.18 | 1.1375 | −82.65 | 0.8107 | 152.70 | 0.5820 | −41.35 | 0.1940 | −41.35 | 1.0000 | 30.00 | 0.0000 | 48.64 |
| 4 | 3 | 1.0779 | 20.18 | 1.1375 | −82.65 | 0.8107 | 152.70 | 0.5820 | −41.35 | 0.1940 | −41.35 | 1.0000 | 30.00 | 0.0000 | 48.64 |
| 5 | 4 | 1.0001 | 30.00 | 1.0000 | −90.00 | 1.0000 | 150.00 | 0.0000 | 48.62 | 0.0000 | 48.62 | 1.0000 | 30.00 | 0.0000 | 48.64 |
| MATLAB Code (Frequency Domain) | PSCAD/EMTDC (Time Domain) | ||||||||||||
| V0 | V1 | V2 | V0 | V1 | V2 | ||||||||
| Voltage | Bus | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) |
| 2 | 0.1565 | −131.35 | 0.6061 | 48.65 | 0.4496 | −131.35 | 0.1576 | −132.40 | 0.6067 | 48.41 | 0.4491 | −133.27 | |
| 3 | 0.0963 | −131.36 | 0.6409 | 56.36 | 0.4496 | −131.35 | 0.0971 | −130.96 | 0.6443 | 56.00 | 0.4493 | −131.29 | |
| 4 | 0.0362 | −131.38 | 0.6860 | 63.16 | 0.4496 | −131.35 | 0.0365 | −124.72 | 0.6912 | 62.67 | 0.4489 | −131.28 | |
| MATLAB code (Frequency Domain) | PSCAD/EMTDC (Time Domain) | ||||||||||||
| I0 | I1 | I2 | I0 | I1 | I2 | ||||||||
| Current | Bus | Mag (pu) | Phase angle (°) | Mag (pu) | Phase angle (°) | Mag (pu) | Phase angle (°) | Mag (pu) | Phase angle (°) | Mag (pu) | Phase angle (°) | Mag (pu) | Phase angle (°) |
| 1→2(F) | 3.4142 | −41.31 | 1.3860 | −84.44 | 1.3321 | −41.32 | 3.4322 | −42.37 | 1.3841 | −84.36 | 1.3404 | −41.27 | |
| 3→2(F) | 0.5820 | −41.35 | 1.0000 | 30.00 | 0.0000 | 48.64 | 0.5847 | −34.71 | 0.9980 | 30.11 | 0.0015 | −41.36 | |
| 4→3 | 0.5820 | −41.35 | 1.0000 | 30.00 | 0.0000 | 48.64 | 0.5862 | −34.72 | 0.9942 | 30.50 | 0.0067 | −41.27 | |
| Bus Location | Fault Current Magnitude in MATLAB Code | Bus Location | Fault Current Magnitude in MATLAB Code |
|---|---|---|---|
| 2 | 3.4142 | 3.4322 | 0.52 |
| 3 | 0.5820 | 0.5847 | 0.46 |
| 4 | 0.5820 | 0.5862 | 0.76 |
| Transformer Bank Connection | Sequence Network |
|---|---|
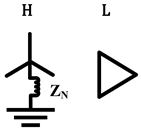 D-Yg | 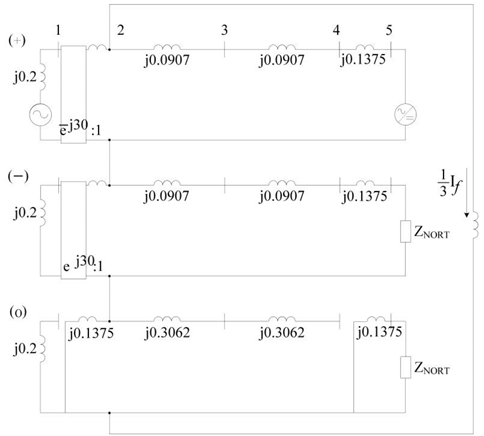 |
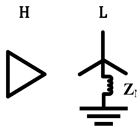 Yg-D | 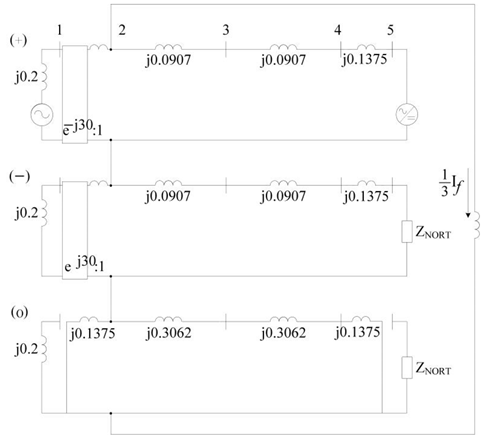 |
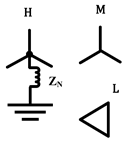 Y-D-Yg | 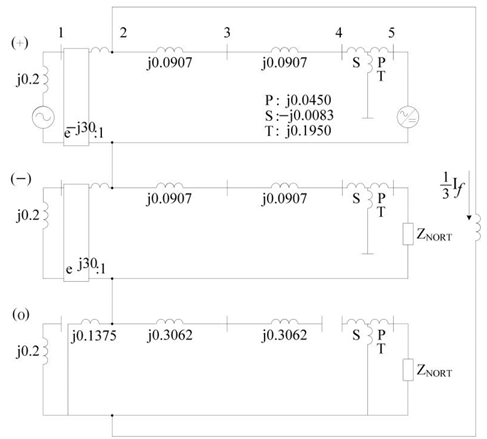 |
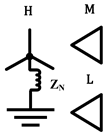 D-D-Yg |  |
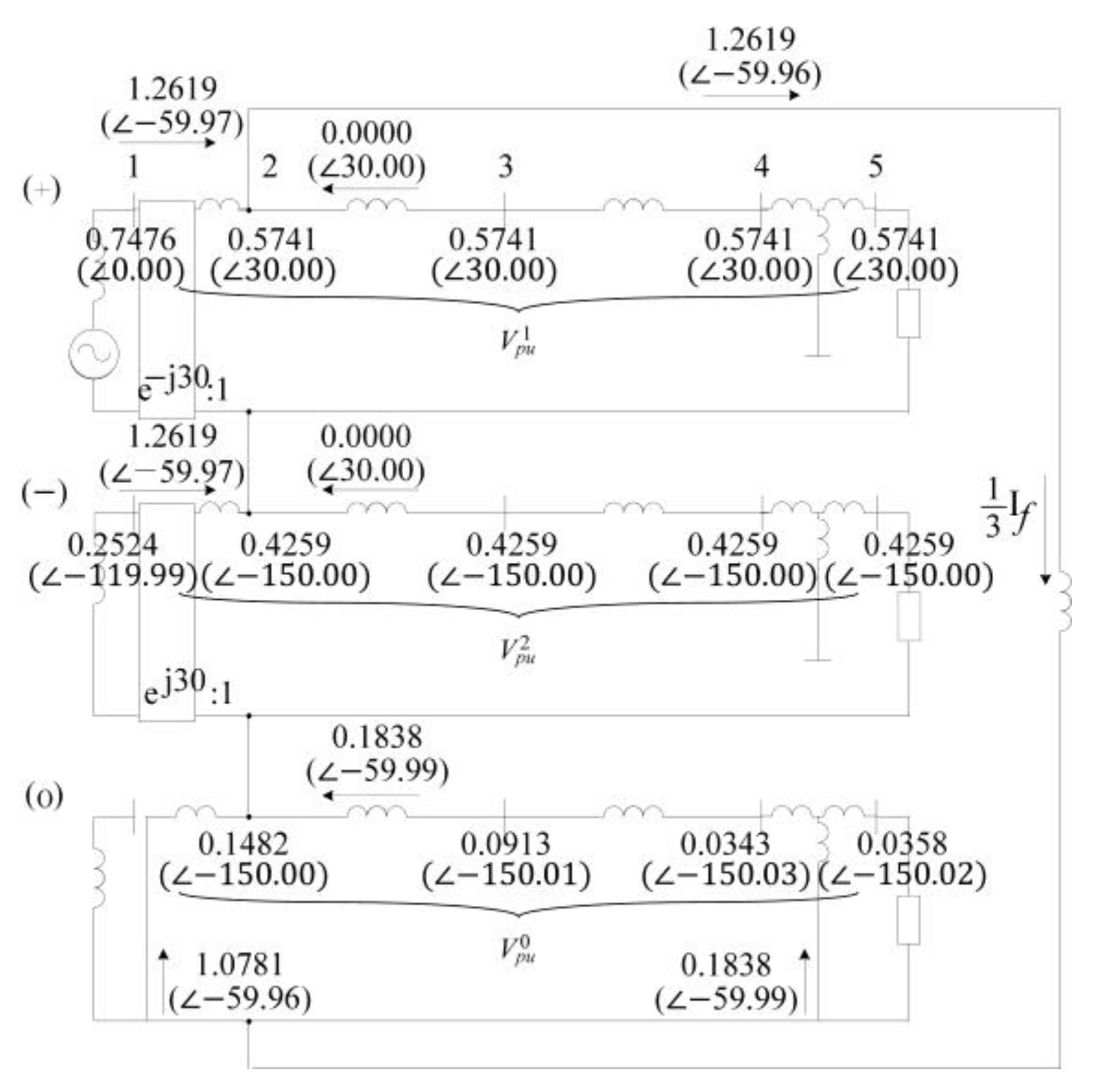
| Bus No. | Va | Vb | Vc | 3V0 | V0 | V1 | V2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | |
| 1 | 0.7161 | −11.09 | 1.0198 | 131.31 | 1.0198 | 131.31 | 0.0000 | 0 | 0.0000 | 0.00 | 0.7629 | 8.82 | 0.2598 | −101.35 |
| 2 | 0.0000 | 0 | 0.9525 | 154.99 | 0.9525 | 154.99 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6170 | 48.65 | 0.4384 | −131.35 |
| 3 | 0.0907 | 120.00 | 0.9646 | 160.36 | 0.9646 | 160.36 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6517 | 56.23 | 0.4384 | −131.35 |
| 4 | 0.1815 | 120.00 | 0.9850 | 165.56 | 0.9850 | 165.56 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6966 | 62.94 | 0.4384 | −131.35 |
| 5 | 0.8455 | 132.41 | 0.5058 | −170.16 | 0.505 | −170.16 | 0.0000 | 0.00 | 0.0000 | 0.00 | 0.7800 | 101.45 | 0.4384 | −161.35 |
| From | To | Ia | Ib | Ic | 3I0 | I0 | I1 | I2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus No. | Bus No. | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) |
| 1 | 2 | 1.6383 | −65.13 | 2.6358 | 116.81 | 1.0000 | −60.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.3625 | −115.41 | 1.2990 | −11.35 |
| 2 | F | 3.8970 | −41.35 | 0.0000 | 0.00 | 0.0000 | 0.00 | 3.8970 | −41.35 | 1.2990 | −41.35 | 1.2990 | −41.35 | 1.2990 | −41.35 |
| 3 | 2 | 1.0001 | −150.00 | 1.0000 | 89.99 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 4 | 3 | 1.0001 | −150.00 | 1.0000 | 89.99 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 5 | 4 | 1.0001 | −150.00 | 1.0000 | 89.99 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
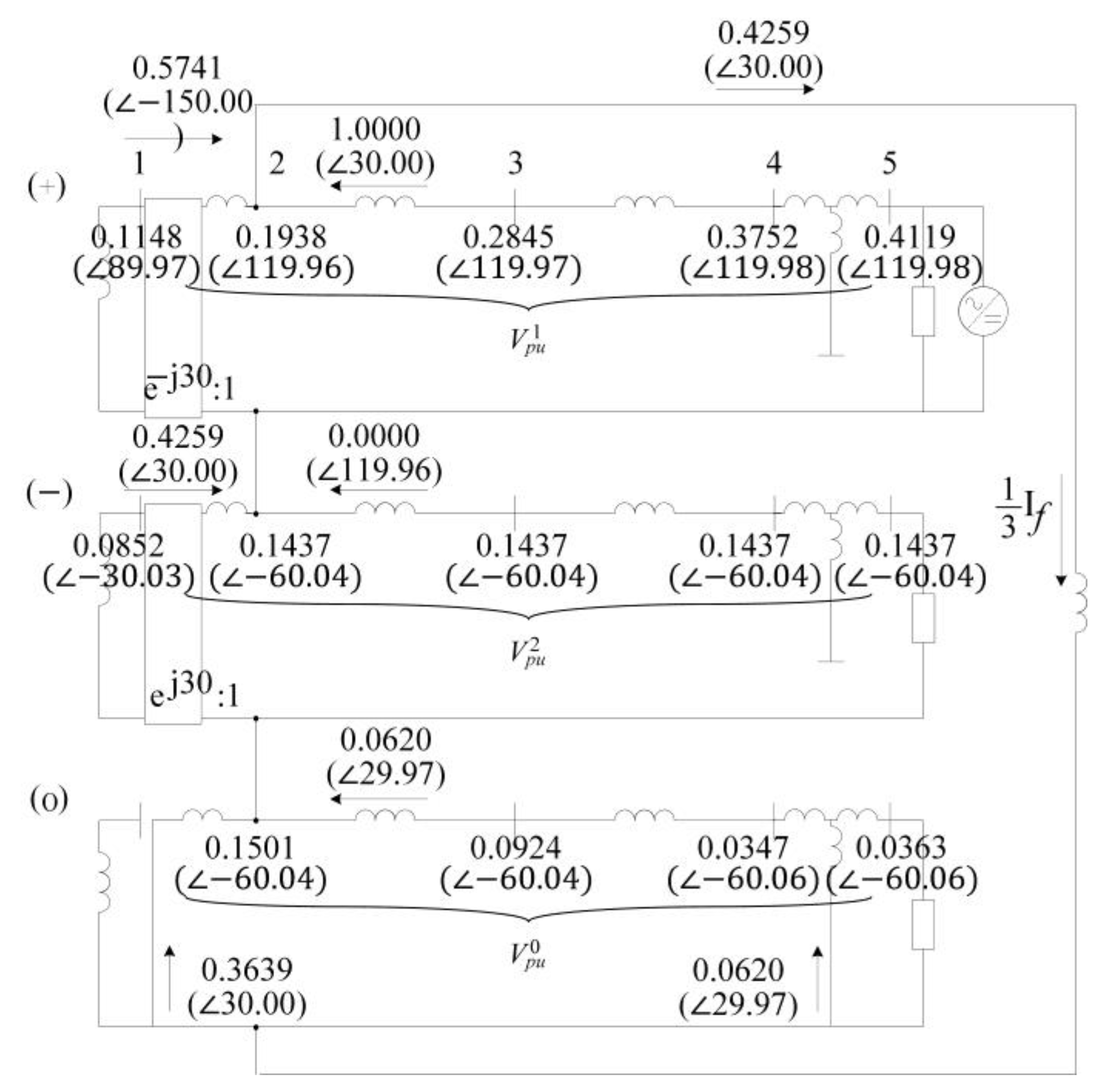
| Bus No. | Va | Vb | Vc | 3V0 | V0 | V1 | V2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | |
| 1 | 0.7090 | −12.10 | 0.6177 | −91.85 | 1.0198 | 131.31 | 0.0000 | 0.00 | 0.0000 | 0.00 | 0.7547 | 8.71 | 0.2681 | −101.35 |
| 2 | 0.0000 | 0.00 | 0.9415 | −55.23 | 0.9415 | 152.53 | 0.4516 | −131.35 | 0.1505 | −131.35 | 0.6030 | 48.65 | 0.6030 | 48.65 |
| 3 | 0.1352 | 88.16 | 0.9863 | −46.62 | 0.9276 | 153.61 | 0.2258 | −131.36 | 0.0753 | −131.36 | 0.6378 | 56.40 | 0.4525 | −131.35 |
| 4 | 0.2703 | 88.16 | 1.0512 | −38.92 | 0.9141 | 154.73 | 0.0001 | 138.66 | 0.0000 | 138.66 | 0.6830 | 63.23 | 0.4525 | −131.35 |
| 5 | 0.8432 | 134.05 | 1.1963 | −26.72 | 0.4871 | −171.95 | 0.0000 | 0.00 | 0.0000 | 0.00 | 0.7671 | 101.85 | 0.4525 | −161.35 |
| From | To | Ia | Ib | Ic | 3I0 | I0 | I1 | I2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus No. | Bus No. | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) |
| 1 | 2 | 1.7045 | −64.15 | 2.7028 | 117.38 | 1.0000 | −60.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.3927 | −114.22 | 1.3406 | −11.35 |
| 2 | F | 4.0218 | −41.35 | 0.0000 | 0.00 | 0.0000 | 0.00 | 4.0218 | −41.35 | 1.3406 | −41.35 | 1.3406 | −41.35 | 1.3406 | −41.35 |
| 3 | 2 | 1.1036 | −162.18 | 1.1769 | 99.02 | 0.7605 | −26.36 | 0.7374 | 138.66 | 0.2458 | 138.66 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 4 | 3 | 1.1036 | −162.18 | 1.1769 | 99.02 | 0.7605 | −26.36 | 0.7374 | 138.66 | 0.2458 | 138.66 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 5 | 4 | 1.0001 | −150.00 | 1.0000 | 89.99 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| Bus No. | Va | Vb | Vc | 3V0 | V0 | V1 | V2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | |
| 1 | 0.7161 | −11.09 | 0.6289 | −92.69 | 1.0198 | 131.31 | 0.0000 | 0.00 | 0.0000 | 0.00 | 0.7629 | 8.82 | 0.2598 | −101.35 |
| 2 | 0.0000 | 0.00 | 0.9525 | −57.69 | 0.9525 | 154.99 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6170 | 48.65 | 0.4384 | −131.35 |
| 3 | 0.0907 | 120.00 | 1.0039 | −53.31 | 0.9646 | 160.36 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6517 | 56.23 | 0.4384 | −131.35 |
| 4 | 0.1815 | 120.00 | 1.0607 | −49.37 | 0.9850 | 165.56 | 0.5358 | −131.35 | 0.1786 | −131.35 | 0.6966 | 62.94 | 0.4384 | −131.35 |
| 5 | 0.3231 | 88.42 | 1.0792 | −38.44 | 0.9224 | 157.84 | 0.0000 | 0.00 | 0.0000 | 0.00 | 0.7172 | 65.40 | 0.4384 | −131.35 |
| From | To | Ia | Ib | Ic | 3I0 | I0 | I1 | I2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus No. | Bus No. | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) | Mag (pu) | Phase Angle (°) |
| 1 | 2 | 1.6383 | −65.13 | 2.6358 | 116.81 | 1.0000 | −60.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.3625 | −115.41 | 1.2990 | −11.35 |
| 2 | F | 3.8970 | −41.35 | 0.0000 | 0.00 | 0.0000 | 0.00 | 3.8970 | −41.35 | 1.2990 | −41.35 | 1.2990 | −41.35 | 1.2990 | −41.35 |
| 3 | 2 | 1.0001 | −150.00 | 1.0000 | 90.00 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 4 | 3 | 1.0001 | −150.00 | 1.0000 | 90.00 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
| 5 | 4 | 1.0001 | −150.00 | 1.0000 | 90.00 | 1.0000 | −30.00 | 0.0000 | 0.00 | 0.0000 | 0.00 | 1.0000 | −150.00 | 0.0000 | −131.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, N.; Yoon, M.; Choi, S. Impact of Transformer Topology on Short-Circuit Analysis in Distribution Systems with Inverter-Based Distributed Generations. Sustainability 2022, 14, 9781. https://doi.org/10.3390/su14159781
Cho N, Yoon M, Choi S. Impact of Transformer Topology on Short-Circuit Analysis in Distribution Systems with Inverter-Based Distributed Generations. Sustainability. 2022; 14(15):9781. https://doi.org/10.3390/su14159781
Chicago/Turabian StyleCho, Namhun, Myungseok Yoon, and Sungyun Choi. 2022. "Impact of Transformer Topology on Short-Circuit Analysis in Distribution Systems with Inverter-Based Distributed Generations" Sustainability 14, no. 15: 9781. https://doi.org/10.3390/su14159781
APA StyleCho, N., Yoon, M., & Choi, S. (2022). Impact of Transformer Topology on Short-Circuit Analysis in Distribution Systems with Inverter-Based Distributed Generations. Sustainability, 14(15), 9781. https://doi.org/10.3390/su14159781






