Research on China’s Carbon Emission Efficiency and Its Regional Differences
Abstract
:1. Introduction
2. Methodology
2.1. Introduction to the Research Methods
2.1.1. The First Stage of DEA
2.1.2. The Second Stage of DEA
2.1.3. The Third Stage of DEA
2.2. Data Description
2.2.1. Introduction of Related Variables
2.2.2. Data Source
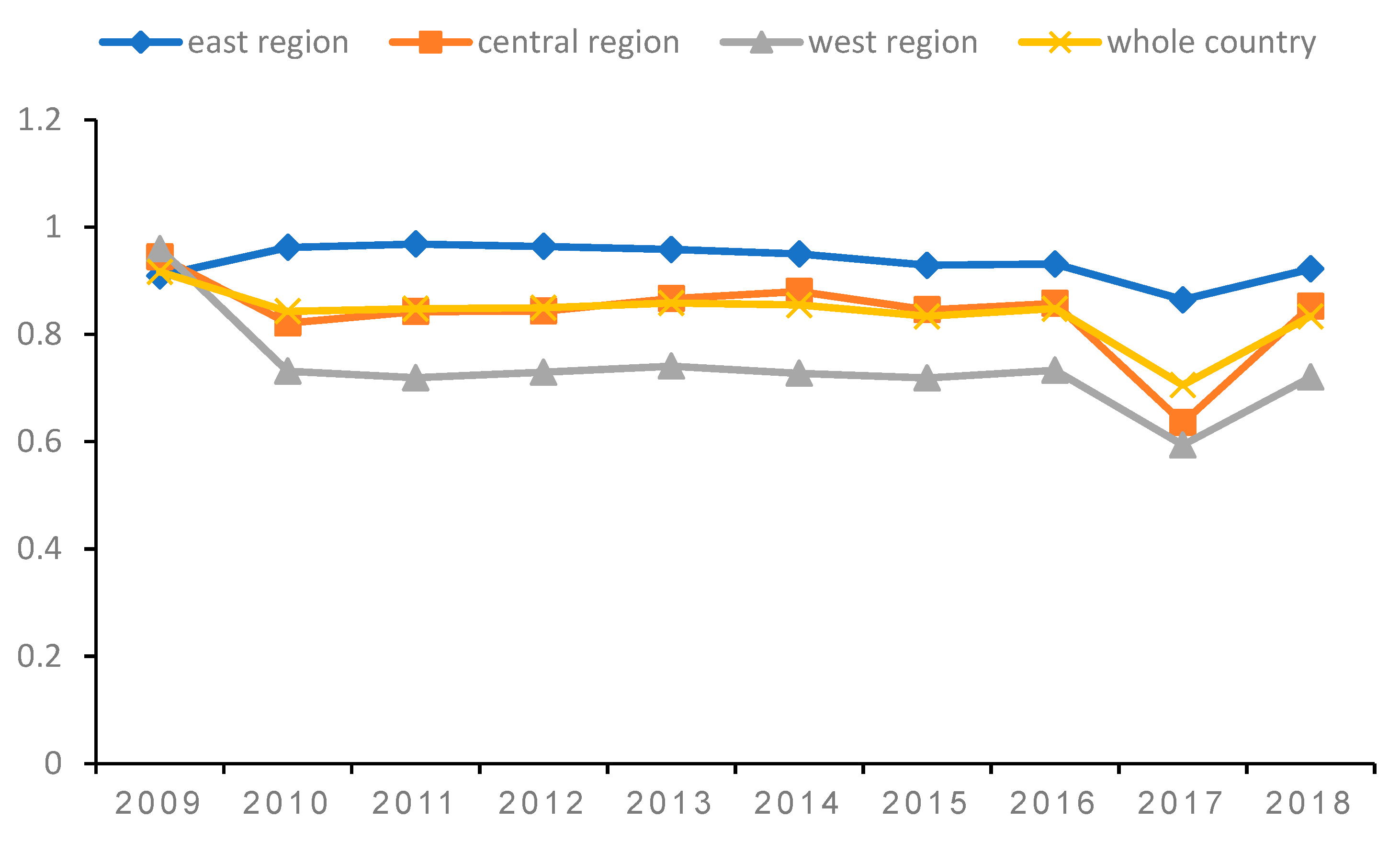
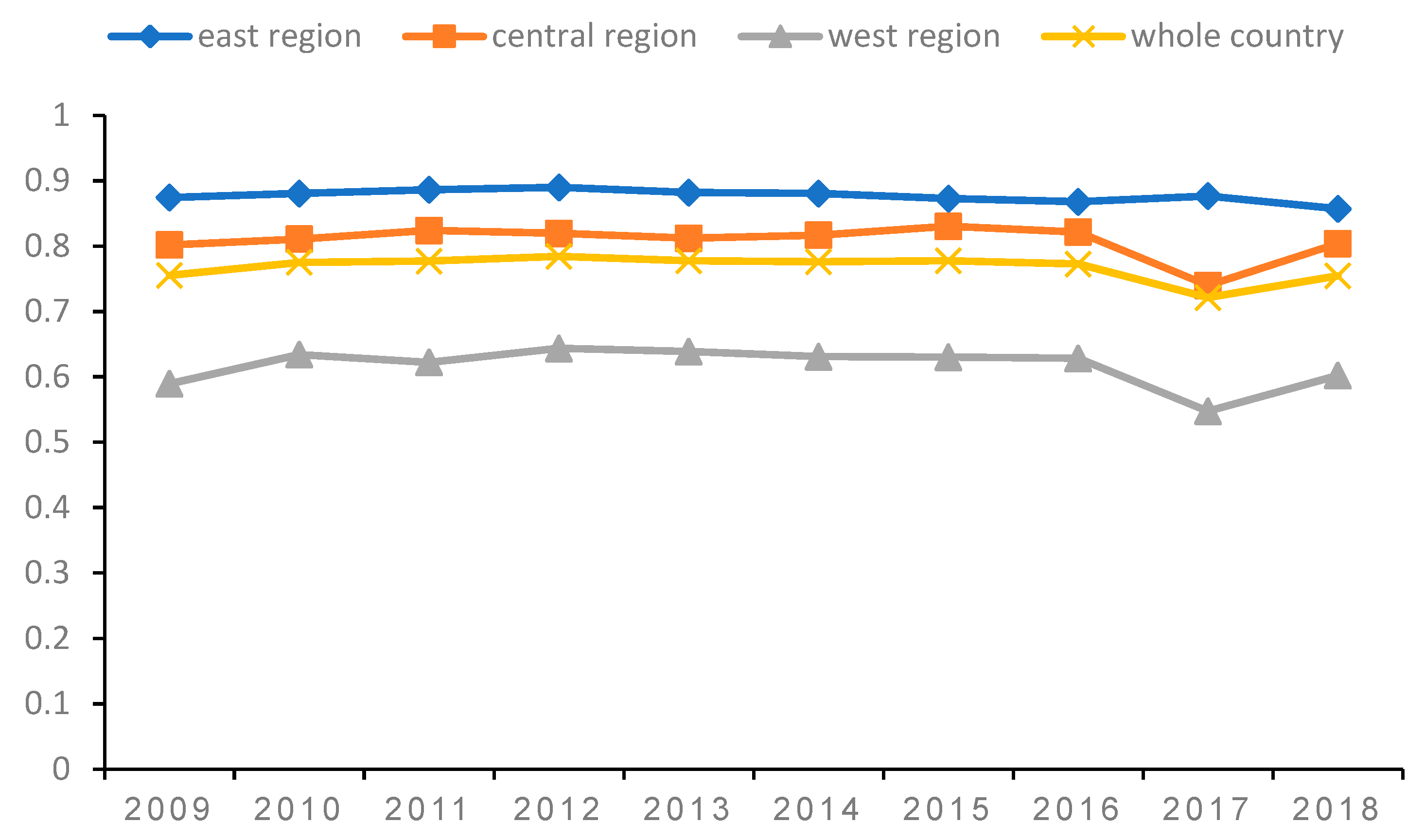
3. Results
3.1. The First Stage of the Traditional DEA Analysis
3.2. The Second Stage of the SFA Analysis
3.3. Empirical Results of DEA after Adjustment in the Third Stage
4. Conclusions and Suggestions
4.1. Conclusions
4.2. Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 22 April 2016).
- Zheng, X.; Lu, Y.; Yuan, J.; Baninla, Y.; Zhang, S.; Stenseth, N.C. Drivers of change in China’s energy-related CO2 emissions. Proc. Natl. Acad. Sci. USA 2020, 117, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Chien, F.; Anwar, A.; Hsu, C.C.; Sharif, A.; Razzaq, A.; Sinha, A. The role of information and communication technology in encountering environmental degradation: Proposing an SDG framework for the BRICS countries. Technol. Soc. 2021, 65, 101587. [Google Scholar] [CrossRef]
- Kirikkaleli, D.; Adebayo, T.S. Do public-private partnerships in energy and renewable energy consumption matter for consumption-based carbon dioxide emissions in India? Environ. Sci. Pollut. Res. 2021, 28, 30139–30152. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhu, X.; Wang, Y. China’s agricultural green total factor productivity based on carbon emission: An analysis of evolution trend and influencing factors. J. Clean. Prod. 2021, 278, 123692. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Sayed, E.T.; Elsaid, K.; Abdelkareem, M.A. Progress in carbon capture technologies. Sci. Total Environ. 2021, 761, 143203. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, P.; Wu, C. Driving Factors behind Energy-Related Carbon Emissions in the US Road Transport Sector: A Decomposition Analysis. Int. J. Environ. Res. Public Health 2022, 19, 2321. [Google Scholar] [CrossRef]
- Wang, L.; Yang, D.; Meng, Q.; Zhao, Y.; He, L. Effects of supercritical carbon dioxide under different conditions on mechanical properties and energy evolution of coal. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 93. [Google Scholar] [CrossRef]
- Yang, H.; Lin, Q.; Zhang, C.; Yu, X.; Cheng, Z.; Li, G.; Hu, Q.; Ren, X.; Zhang, Q.; Liu, J.; et al. Carbon dioxide electroreduction on single-atom nickel decorated carbon membranes with industry compatible current densities. Nat. Commun. 2020, 11, 593. [Google Scholar] [CrossRef] [Green Version]
- Jiao, X.; Zheng, K.; Liang, L.; Li, X.; Sun, Y.; Xie, Y. Fundamentals and challenges of ultrathin 2D photocatalysts in boosting CO2 photoreduction. Chem. Soc. Rev. 2020, 49, 6592–6604. [Google Scholar] [CrossRef]
- Modise, R.K.; Mpofu, K.; Adenuga, O.T. Energy and Carbon Emission Efficiency Prediction: Applications in Future Transport Manufacturing. Energies 2021, 14, 8466. [Google Scholar] [CrossRef]
- Qiang, W.; Fza, B. Does increasing investment in research and development promote economic growth decoupling from carbon emission growth? An empirical analysis of BRICS countries. J. Clean. Prod. 2019, 252, 119853. [Google Scholar]
- Sun, Y.; Kamran, H.W.; Razzaq, A.; Qadri, F.S.; Suksatan, W. Dynamic and causality linkages from transportation services and tourism development to economic growth and carbon emissions: New insights from Quantile ARDL approach. Integr. Environ. Assess. Manag. 2021, 00, 1–15. [Google Scholar] [CrossRef]
- Kirikkaleli, D.; Güngr, H.; Adebayo, T.S. Consumption-based carbon emissions, renewable energy consumption, financial development and economic growth in Chile. Bus. Strategy Environ. 2021, 31, 1123–1137. [Google Scholar] [CrossRef]
- Mielnik, O.; Goldemberg, J. Communication The evolution of the “carbonization index” in developing countries. Energy Policy 1999, 27, 307–308. [Google Scholar] [CrossRef]
- Yamaji, K.; Matsuhashi, R.; Nagata, Y.; Kaya, Y. A study on economic measures for CO2 reduction in Japan. Energy Policy 1993, 21, 123–132. [Google Scholar] [CrossRef]
- Chen, J.; Xie, Q.; Shahbaz, M.; Song, M.; Li, L. Impact of bilateral trade on fossil energy consumption in BRICS: An extended decomposition analysis. Econ. Model. 2022, 106, 105698. [Google Scholar] [CrossRef]
- Lin, Y.; Huang, J.; Li, M.; Lin, R. Does lower regional density result in less CO2 emission per capita? Environ. Sci. Pollut. Res. 2022, 29, 29887–29903. [Google Scholar] [CrossRef]
- Ji, Q.; Zhang, D. How much does financial development contribute to renewable energy growth and upgrading of energy structure in China? Energy Policy 2019, 128, 114–124. [Google Scholar] [CrossRef]
- Wurlod, J.-D.; Noailly, J. The impact of green innovation on energy intensity: An empirical analysis for 14 industrial sectors in OECD countries. Energy Econ. 2018, 71, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Ning, Z.A.; Peng, Z.B.; Cck, A. Total-factor carbon emission performance of the Chinese transportation industry: A bootstrapped non-radial Malmquist index analysis—ScienceDirect. Renew. Sustain. Energy Rev. 2015, 41, 584–593. [Google Scholar]
- Chen, S.; Golley, J. ‘Green’ productivity growth in China’s industrial economy. Energy Econ. 2014, 44, 89–98. [Google Scholar] [CrossRef]
- Nassar, R.; Napier-Linton, L.; Gurney, K.R.; Andres, R.J.; Oda, T.; Vogel, F.R.; Deng, F. Improving the temporal and spatial distribution of CO2 emissions from global fossil fuel emission data sets. J. Geophys. Res. Atmos. 2013, 118, 917–933. [Google Scholar] [CrossRef]
- Uddin, M.S.; Smirnov, O. Spatial Distribution of the Annual Atmospheric Carbon Dioxide in the Contiguous USA and Their Controlling Factors. Environ. Modeling Assess. 2022, 27, 57–76. [Google Scholar] [CrossRef]
- Yu, Z. Measurement of carbon emission efficiency of China’s energy consumption and its spatial distribution pattern. IOP Conf. Ser. Earth Environ. Sci. 2020, 546, 022050. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, Q.; Huang, F.; Qiu, R.; Lin, Y.; Zhang, L.; Hu, X. Understanding spatial variation in the driving pattern of carbon dioxide emissions from taxi sector in great Eastern China: Evidence from an analysis of geographically weighted regression. Clean Technol. Environ. Policy 2020, 22, 979–991. [Google Scholar] [CrossRef]
- Liu, F.; Tang, L.; Liao, K.; Ruan, L.; Liu, P. Spatial Distribution and Regional Difference of Carbon Emissions Efficiency of Industrial Energy in China. Sci. Rep. 2021, 11, 19419. [Google Scholar] [CrossRef]
- Wang, B.; Yu, M.; Zhu, Y.; Bao, P. Unveiling the driving factors of carbon emissions from industrial resource allocation in China: A spatial econometric perspective. Energy Policy 2021, 158, 112557. [Google Scholar] [CrossRef]
- Li, Y.; Hou, W.; Zhu, W.; Li, F.; Liang, L. Provincial carbon emission performance analysis in China based on a Malmquist data envelopment analysis approach with fixed-sum undesirable outputs. Ann. Oper. Res. 2021, 304, 233–261. [Google Scholar] [CrossRef]
- Iram, R.; Zhang, J.; Erdogan, S.; Abbas, Q.; Mohsin, M. Economics of energy and environmental efficiency: Evidence from OECD countries. Environ. Sci. Pollut. Res. 2020, 27, 3858–3870. [Google Scholar] [CrossRef]
- Wang, K.; Wu, M.; Sun, Y.; Shi, X.; Sun, A.; Zhang, P. Resource abundance, industrial structure, and regional carbon emissions efficiency in China. Resour. Policy 2019, 60, 203–214. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.-M. China’s regional industrial energy efficiency and carbon emissions abatement costs. Appl. Energy 2014, 130, 617–631. [Google Scholar] [CrossRef]
- Zhang, C. Total-factor carbon emission performance of fossil fuel power plants in China: A metafrontier non-radial Malmquist index analysis. Energy Econ. 2013, 40, 549–559. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, C.; Wang, Z.; Feng, K.; Hubacek, K. The characteristics and drivers of fine particulate matter (PM2.5) distribution in China. J. Clean. Prod. 2017, 142, 1800–1809. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data development analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Liu, C.; Tang, R.; Guo, Y.; Sun, Y.; Liu, X. Research on the Structure of Carbon Emission Efficiency and Influencing Factors in the Yangtze River Delta Urban Agglomeration. Sustainability 2022, 14, 6114. [Google Scholar] [CrossRef]
- Minviel, J.J.; Sipiläinen, T. A dynamic stochastic frontier approach with persistent and transient inefficiency and unobserved heterogeneity. Agric. Econ. 2021, 52, 575–589. [Google Scholar] [CrossRef]
- Jin, S.; Wang, X.; Wang, Z.; Xu, Y. Bayesian piecewise stochastic frontier model to estimate initial public offering pricing efficiency under issuance policy reforms. Appl. Stoch. Models Bus. Ind. 2021, 37, 545–559. [Google Scholar] [CrossRef]
- Hao, C.; Evelyn, A.; Ahakwa, I.; Musah, M.; Salakpi, A.; Alfred, M.; Atingabili, S. Does energy consumption, economic growth, urbanization, and population growth influence carbon emissions in the BRICS? Evidence from panel models robust to cross-sectional dependence and slope heterogeneity. Environ. Sci. Pollut. Res. 2022, 29, 37598–37616. [Google Scholar]
- He, Y.; Fu, F.; Liao, N. Exploring the path of carbon emissions reduction in China’s industrial sector through energy efficiency enhancement induced by R&D investment. Energy 2021, 225, 120208. [Google Scholar]
- Xu, Q.; Dong, Y.X.; Yang, R. Urbanization impact on carbon emissions in the Pearl River Delta region: Kuznets curve relationships. J. Clean. Prod. 2018, 180, 514–523. [Google Scholar] [CrossRef]
- Zhu, J. Analysis of carbon emission efficiency based on DEA model. J. Discret. Math. Sci. Cryptogr. 2018, 21, 405–409. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Wang, D.; Jz, B. Digital economy and carbon emission performance: Evidence at China’s city level. Energy Policy 2022, 165, 112927. [Google Scholar] [CrossRef]
- Ooi, J.Y.; Wolfenden, L.; Sutherland, R.A. Systematic Review of the Recent Consumption Levels of Sugar-Sweetened Beverages in Children and Adolescents from the World Health Organization Regions with High Dietary–Related Burden of Disease. Asia Pac. J. Public Health 2022, 34, 11–24. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.J.; Sun, Y.F.; Huang, J. Energy efficiency, carbon emission performance, and technologygaps: Evidence from CDM project investment. Energy Policy 2018, 115, 119–130. [Google Scholar] [CrossRef]
- China Energy Statistical Yearbook. Available online: https://navi.cnki.net/knavi/yearbooks/YCXME/detail (accessed on 6 June 2022).
- China Environmental Statistical Yearbook. Available online: https://navi.cnki.net/knavi/yearbooks/YHJSD/detail (accessed on 6 June 2022).
- China Science and Technology Statistical Yearbook. Available online: https://navi.cnki.net/knavi/yearbooks/YBVCX/detail (accessed on 6 June 2022).
- Pan, C.; Wang, H.; Guo, H.; Pan, H. How Do the Population Structure Changes of China Affect Carbon Emissions? An Empirical Study Based on Ridge Regression Analysis. Sustainability 2021, 13, 3319. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, C.C.; Lin, I.F.; Lin, J.Y. Dynamic assessment of agro-industrial sector efficiency and productivity changes among G20 nations. Energy Environ. 2021. [Google Scholar] [CrossRef]
- Fu, Y.; He, C.; Luo, L. Does the low-carbon city policy make a difference? Empirical evidence of the pilot scheme in China with DEA and PSM-DID. Ecol. Indic. 2021, 122, 107238. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, R.; Wang, S. How technological progress affects the carbon emission efficiency? Evidence from national panel quantile regression. J. Clean. Prod. 2021, 307, 127133. [Google Scholar] [CrossRef]
- Luo, Y. Will infrastructure construction cause environmental pollution in China? IOP Conf. Ser. Earth Environ. Sci. 2020, 450, 012109. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Liu, W.; Lv, X.; Cheng, X.; Shen, M. Investigating interior driving factors and cross-industrial linkages of carbon emission efficiency in China’s construction industry: Based on Super-SBM DEA and GVAR model. J. Clean. Prod. 2019, 241, 118322. [Google Scholar] [CrossRef]
- Akbar, U.; Li, Q.L.; Akmal, M.A.; Shakib, M.; Iqbal, W. Nexus between agro-ecological efficiency and carbon emission transfer: Evidence from China. Environ. Sci. Pollut. Res. 2021, 28, 18995–19007. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.J.; Li, X.Y.; Tang, B.J. Assessing the operational performance and maturity of the carbon trading pilot program: The case study of Beijing’s carbon market. J. Clean. Prod. 2017, 161, 1263–1274. [Google Scholar] [CrossRef]
- Kusadokoro, M.; Chitose, A. The Impact of Road Infrastructure Development on Economic Growth and Urban-Rural Income Inequality in Inner Mongolia, China. Jpn. J. Agric. Econ. 2022, 24, 29–34. [Google Scholar]
- Abid, A.; Mehmood, U.; Tariq, S.; Haq, Z.U. The effect of technological innovation, FDI, and financial development on CO2 emission: Evidence from the G8 countries. Environ. Sci. Pollut. Res. 2022, 29, 11654–11662. [Google Scholar] [CrossRef]
- Fu, Y.; Huang, G.; Liu, L.; Zhai, M.A. factorial CGE model for analyzing the impacts of stepped carbon tax on Chinese economy and carbon emission. Sci. Total Environ. 2020, 759, 143512. [Google Scholar] [CrossRef]
| Level 1 Indicators | Secondary Indicators | Level 3 Indicators |
|---|---|---|
| Input indexes | Size of population | Total population at the end of the year (/10,000) |
| Stock of capital | Industrial energy investment (/RMB 100 million) | |
| Energy use | Total regional energy consumption (/Million tons) | |
| Output indexes | Carbon emission | Carbon emissions from each region (/Ton) |
| GDP | Total GDP (/100 million yuan) | |
| External environment variables | Economic development | Per capita GDP (/Ten thousand yuan) |
| National consumption | Total social consumer goods (/100 million yuan) | |
| Scientific and technological | Patent valid (/Piece) |
| Area | Carbon Emission Efficiency | Pure Technical Efficiency | Scale Efficiency | Area | Carbon Emission Efficiency | Pure Technical Efficiency | Scale Efficiency |
|---|---|---|---|---|---|---|---|
| Beijing | 1.000 | 1.000 | 1.000 | Henan | 0.775 | 0.813 | 0.923 |
| Tianjin | 0.992 | 0.998 | 0.990 | Hubei | 0.761 | 0.765 | 0.953 |
| Hebei | 0.839 | 0.858 | 0.975 | Hunan | 0.693 | 0.708 | 0.934 |
| Shanxi | 0.985 | 0.998 | 0.987 | Guangdong | 0.857 | 1.000 | 0.846 |
| Nei Monggol | 1.000 | 1.000 | 1.000 | Guangxi | 0.715 | 0.720 | 0.946 |
| Liaoning | 0.992 | 1.000 | 1.000 | Hainan | 0.975 | 1.000 | 0.983 |
| Jilin | 0.877 | 0.878 | 0.980 | Chongqing | 0.696 | 0.675 | 0.974 |
| Heilongjiang | 0.821 | 0.834 | 0.964 | Sichuan | 0.616 | 0.619 | 0.928 |
| Shanghai | 0.992 | 1.000 | 1.000 | Guizhou | 0.738 | 0.756 | 0.947 |
| Jiangsu | 0.986 | 1.000 | 0.988 | Yunnan | 0.608 | 0.609 | 0.944 |
| Zhejiang | 0.891 | 0.916 | 0.969 | Shaanxi | 0.961 | 0.967 | 0.986 |
| Anhui | 0.834 | 0.905 | 0.912 | Gansu | 0.714 | 0.712 | 0.971 |
| Fujian | 0.865 | 0.869 | 0.972 | Qinghai | 0.524 | 1.000 | 0.477 |
| Jiangxi | 0.819 | 0.838 | 0.955 | Ningxia | 0.999 | 1.000 | 0.997 |
| Shandong | 0.965 | 1.000 | 0.973 | Xinjiang | 0.807 | 0.821 | 0.991 |
| Average | Carbon emission efficiency: 0.843 | Pure technical efficiency: 0.875 | Scale efficiency: 0.949 | ||||
| Population | Coefficient | Standard Error | T-Ratio | p-Value |
|---|---|---|---|---|
| Cow distance item | −944 | 158 | −6 | 0 |
| per capita GDP | 4 | 20 | 0 | 1 |
| Total retail sales of consumer goods | 0 | 0 | 5 | 0 |
| Number of valid patents | 0 | 0 | −3 | 0 |
| sigmasq | 34,900,000 | 1 | 3,490,000 | 0 |
| gamma | 1 | 0 | 524 | 0 |
| Log- likelihood function | −2190 | |||
| LR test of the one-sided error | 716 | |||
| One-sided likelihood ratio test for p-values | 0 | |||
| Energy Consumption | Coefficient | Standard Error | T-Ratio | p-Value |
| Cow distance item | −17,000 | 417 | −4 | 0 |
| per capita GDP | 92 | 56 | 2 | 0 |
| Total retail sales of consumer goods | 0 | 0 | 4 | 0 |
| Number of valid patents | 0 | 0 | −2 | 0 |
| Sigmasq | 79,600,000 | 1 | 7,960,000 | 0 |
| Gamma | 1 | 0 | 58 | 0 |
| Log -likelihood function | −26,000 | |||
| LR test of the one-sided error | 229 | |||
| One-sided likelihood ratio test for p-values | 0.000 | |||
| Energy Industry Investment | Coefficient | Standard Error | T-Ratio | p-Value |
| Cow distance item | −177 | 50 | −4 | 0 |
| per capita GDP | 11 | 7 | 2 | 0 |
| Total retail sales of consumer goods | 0 | 0 | 3 | 0 |
| Number of valid patents | 0 | 0 | −2 | 0 |
| Sigmasq | 868,000 | 1 | 841,000 | 0 |
| Gamma | 1 | 0 | 31 | 0 |
| Log- likelihood function | −1974 | |||
| LR test of the one-sided error | 143 | |||
| One-sided likelihood ratio test for p-values | 0 |
| Area | Population | Energy Consumption | Investment Amount in Industrial Energy Sources | Area | Population | Energy Consumption | Investment Amount in Industrial Energy Sources |
|---|---|---|---|---|---|---|---|
| Beijing | 3480 | 11,600 | 1184 | Henan | 10,100 | 25,000 | 2320 |
| Tianjin | 2870 | 12,000 | 1220 | Hubei | 6600 | 19,200 | 1520 |
| Hebei | 8300 | 33,900 | 2550 | Hunan | 7660 | 18,300 | 1444 |
| Shanxi | 4890 | 24,600 | 1950 | Guangdong | 12,200 | 37,600 | 2320 |
| NeiMonggol | 3680 | 27,300 | 2770 | Guangxi | 5990 | 14,300 | 1400 |
| Liaoning | 5310 | 26,500 | 1510 | Hainan | 2330 | 6710 | 886 |
| Jilin | 3820 | 11,100 | 1280 | Chongqing | 4260 | 12,000 | 1090 |
| Heilongjiang | 4810 | 14,800 | 1360 | Sichuan | 9030 | 22,100 | 19,601 |
| Shanghai | 3570 | 15,600 | 907 | Guizhou | 4890 | 13,700 | 1230 |
| Jiangsu | 8850 | 35,600 | 2310 | Yunnan | 5960 | 14,800 | 1320 |
| Zhejiang | 6680 | 24,700 | 1700 | Shaanxi | 4980 | 17,100 | 2190 |
| Anhui | 7340 | 17,200 | 1670 | Gansu | 3950 | 11,700 | 1080 |
| Fujian | 4910 | 16,400 | 1520 | Qinghai | 2040 | 890 | 1190 |
| Jiangxi | 5792 | 13,100 | 1290 | Ningxia | 2120 | 11,700 | 1330 |
| Shandong | 10,700 | 44,400 | 4100 | Xinjiang | 3820 | 21,200 | 1970 |
| The First Stage | The Third Stage | ||||||
|---|---|---|---|---|---|---|---|
| Area | Carbon Emission Efficiency | Pure Technical Efficiency | Scale Efficiency | Area | Carbon Emission Efficiency | Pure Technical Efficiency | Scale Efficiency |
| Beijing | 1.000 | 1.000 | 1.000 | Beijing | 0.959 | 1.000 | 0.959 |
| Tianjin | 0.992 | 0.998 | 0.990 | Tianjin | 0.747 | 1.000 | 0.747 |
| Hebei | 0.839 | 0.859 | 0.976 | Hebei | 0.883 | 0.909 | 0.972 |
| Shanxi | 0.985 | 0.998 | 0.987 | Shanxi | 0.993 | 0.998 | 0.995 |
| Nei Monggol | 1.000 | 1.000 | 1.000 | Nei Monggol | 1.000 | 1.000 | 1.000 |
| Liaoning | 0.992 | 1.000 | 1.000 | Liaoning | 1.000 | 1.000 | 1.000 |
| Jilin | 0.877 | 0.878 | 0.980 | Jilin | 0.713 | 0.957 | 0.745 |
| Heilongjiang | 0.821 | 0.834 | 0.964 | Heilongjiang | 0.761 | 0.929 | 0.818 |
| Shanghai | 0.992 | 1.000 | 1.000 | Shanghai | 0.928 | 1.000 | 0.928 |
| Jiangsu | 0.986 | 1.000 | 0.988 | Jiangsu | 1.000 | 1.000 | 1.000 |
| Zhejiang | 0.891 | 0.913 | 0.969 | Zhejiang | 0.913 | 0.952 | 0.959 |
| Anhui | 0.834 | 0.905 | 0.912 | Anhui | 0.800 | 0.957 | 0.837 |
| Fujian | 0.865 | 0.869 | 0.972 | Fujian | 0.817 | 0.946 | 0.864 |
| Jiangxi | 0.819 | 0.838 | 0.955 | Jiangxi | 0.669 | 0.939 | 0.711 |
| Shandong | 0.965 | 1.000 | 0.973 | Shandong | 1.000 | 1.000 | 1.000 |
| Henan | 0.775 | 0.814 | 0.923 | Henan | 0.852 | 0.918 | 0.929 |
| Hubei | 0.761 | 0.765 | 0.953 | Hubei | 0.958 | 0.899 | 0.844 |
| Hunan | 0.693 | 0.708 | 0.934 | Hunan | 0.728 | 0.857 | 0.848 |
| Guangdong | 0.857 | 1.000 | 0.846 | Guangdong | 1.000 | 1.000 | 1.000 |
| Guangxi | 0.715 | 0.720 | 0.946 | Guangxi | 0.634 | 0.876 | 0.723 |
| Hainan | 0.975 | 1.000 | 0.983 | Hainan | 0.361 | 1.000 | 0.361 |
| Chongqing | 0.696 | 0.675 | 0.974 | Chongqing | 0.592 | 0.875 | 0.677 |
| Sichuan | 0.616 | 0.619 | 0.928 | Sichuan | 0.669 | 0.755 | 0.887 |
| Guizhou | 0.739 | 0.756 | 0.947 | Guizhou | 0.625 | 0.892 | 0.700 |
| Yunnan | 0.608 | 0.609 | 0.944 | Yunnan | 0.578 | 0.801 | 0.720 |
| Shaanxi | 0.961 | 0.967 | 0.986 | Shaanxi | 0.903 | 0.979 | 0.922 |
| Gansu | 0.714 | 0.712 | 0.971 | Gansu | 0.569 | 0.883 | 0.645 |
| Qinghai | 0.524 | 1.000 | 0.477 | Qinghai | 0.247 | 1.000 | 0.247 |
| Ningxia | 0.999 | 1.000 | 0.997 | Ningxia | 0.588 | 1.000 | 0.588 |
| Xinjiang | 0.807 | 0.821 | 0.991 | Xinjiang | 0.764 | 0.895 | 0.855 |
| Average value | 0.843 | 0.875 | 0.949 | Average value | 0.775 | 0.941 | 0.816 |
| High Efficiency Area | Beijing | Shanxi | Nei Monggol | Liaoning |
| Shaanxi | Hubei | Zhejiang | Shandong | |
| Shanghai | Guangdong | Jiangsu | ||
| Medium Efficiency Area | Tianjin | Hebei | Jilin | Henan |
| Jiangxi | Guangxi | Sichuan | Guizhou | |
| Heilongjiang | Xinjiang | Anhui | Hunan | |
| Low Efficiency Area | Hainan | Chongqing | Yunnan | Gansu |
| Qinghai | Ningxia |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Xu, H.; Sun, Q. Research on China’s Carbon Emission Efficiency and Its Regional Differences. Sustainability 2022, 14, 9731. https://doi.org/10.3390/su14159731
Zhao X, Xu H, Sun Q. Research on China’s Carbon Emission Efficiency and Its Regional Differences. Sustainability. 2022; 14(15):9731. https://doi.org/10.3390/su14159731
Chicago/Turabian StyleZhao, Xiaochun, Huixin Xu, and Qun Sun. 2022. "Research on China’s Carbon Emission Efficiency and Its Regional Differences" Sustainability 14, no. 15: 9731. https://doi.org/10.3390/su14159731
APA StyleZhao, X., Xu, H., & Sun, Q. (2022). Research on China’s Carbon Emission Efficiency and Its Regional Differences. Sustainability, 14(15), 9731. https://doi.org/10.3390/su14159731





