Network Structure Features and Influencing Factors of Tourism Flow in Rural Areas: Evidence from China

Abstract

Exploring the spatial network structure of tourism flow and its influencing factors is of great significance to the transmission of characteristic culture and the sustainable development of tourism in tourist destinations, especially in backward rural areas. Taking Qiandongnan Miao and Dong Autonomous Prefecture (hereinafter referred to as Qiandongnan Prefecture) as an example, this paper adopts social network analysis and Quadratic Assignment Procedure regression analysis to study the network structural characteristics and influencing factors of tourism flow using online travel blog data. The results show that: (1) There are seasonal changes in tourism flow, but the attractions that tourists pay attention to do not change with the seasons. (2) The tightness of the tourism flow network structure is poor. The core nodes are unevenly distributed, and there are obvious structural holes. (3) The density of the tourism flow network is low. There is a clear core–periphery structure in the network, and the core area has a weak driving effect on the periphery area. There are more cohesive subgroups in the network, but the degree of connectedness between the subgroups varies greatly. (4) Geographical adjacency, transportation accessibility, and tourism resource endowment influence tourism flow network structure. The study found that the influencing factors of tourism flow in rural areas are different from those in urban areas. These results provide useful information for the marketing and development of tourism management departments in rural areas.

1. Introduction

With the rapid development of the global economy and the increase in urbanization, rural areas are facing problems such as hollowing out of villages, labor force loss, and deterioration of the rural environment [1]. Rural tourism, which is an emerging industry that straddles the primary, secondary, and tertiary industries and takes into account production, life, and ecology, has been proven in many countries and regions to be an important outlet for economic development and economic diversification in rural areas. For example, in 2019, China’s rural leisure tourism industry received 3.3 billion visitors with a business income of more than 850 billion yuan [2]. The development of rural tourism is an important decision for the development of mainland China and minority regions and an important driving force for the implementation of the rural revitalization strategy [3]. Tourism flow, as the foundation of the tourism industry [4], is directly related to the development of rural tourism and affects the process of implementing the rural revitalization strategy.

Tourism flows are collective displacements of tourists that occur in space, accompanied by certain changes in time, direction, and scale [5]. During the trip, material and immaterial flows such as energy flows, financial flows, information flows, and cultural flows occur between tourists and their travel behavior. Thus, tourism behavior is not an isolated process but a complex network [6]. A “network” is a system for studying multiple objects and the associations between them, consisting of objects (i.e., nodes) and connections between objects (i.e., links between nodes). In tourism flow networks, nodes are usually used to represent tourism attractions, and the connection between nodes is used to represent the tourism flow linkage between tourism attractions [7]. The tourism flow network structure refers to the complex network system formed by the flow of tourists through spatial movements between several tourist attractions (i.e., nodes) following tourism routes (i.e., connecting lines) [8]. The network structure of tourism flows is concerned with three main aspects: tourism nodes, routes, and the relationship between each tourism node [9]. The tourism nodes are not simply connected by tourism routes but are intrinsically linked. The same tourism nodes are connected by the different intensity of tourism flows according to different tourism routes (i.e., different flows and directions of tourism flows) and form a network structure with different functions. Since the 21st century, the social network analysis method based on the idea of network structure has been widely used to explore the network structure characteristics of tourism flows and reveal the spatial distribution pattern of tourism flows, spatial characteristics, and the relationship between tourism nodes [10,11], because the social network theory can better analyze the complex spatial movement of tourism flows. However, most studies concentrated on major tourist cities or famous tourist attractions [12,13].

Most of the early studies on tourism flow used quantitative data such as statistical yearbooks [14,15] or questionnaire surveys [16,17]. However, these data are difficult to capture the spatial distribution and flow characteristics of tourists accurately. In recent years, with the rapid development of information technology, more and more tourists share their travel blogs (including text information, pictures, travel methods, geographic location, etc.) on travel websites, providing a new data source for the study of tourism flow. Therefore, many scholars used online travel blogs to study the characteristics and spatial distribution of tourism flows [18,19,20].

Although the study of tourism flows has attracted the attention of scholars, few studies have been conducted on rural areas. Moreover, the rural ethnic areas in southwest China have a special geographical location, rich natural resources, but backward economic development. The region urgently needs new theories to guide the development of tourism in order to consolidate China’s poverty alleviation achievements and promote rural revitalization.

In view of this, this paper obtained data information from online travel blogs and uses social network analysis to study the structural characteristics of tourism flow networks and their influencing factors in Qiandongnan Miao and Dong Autonomous Prefecture (hereinafter referred to as Qiandongnan Prefecture), located in the southwest region of China, focusing on answering the following questions: (1) In the era of big data, how to fully explore and utilize the geospatial information contained in online travel blogs? (2) What are the characteristics of the network structure of tourism flow in rural tourism as a special form of tourism? Is there any difference in the network structure of tourism flow in different seasons? (3) What are the influencing factors of tourism flow network structure? Addressing these issues provides an effective reference for developing tourism products, designing tourism itineraries, and sustainable development in rural tourism destinations. The findings contribute to the experience of China and can also be extended to other developing countries and regions.

The structure of this paper is as follows: Section 2 reviews the existing studies on tourism flow. Section 3 presents the case study area, data, and methodology. Section 4 demonstrates the analysis results. Section 5 discusses the significance of the main results and presents suggestions. The final Section 6 concludes the research efforts and limitations.

2. Literature Review

Research on tourism flows started in the 1960s. For example, Campbell [21] proposed a spatial model of tourism flow in recreational and holiday destinations. Williams [22] attempted to reveal several major tourism flow patterns in selected groups of countries that dominate the international tourism market. Pearce [23] first proposed the concept of tourism flow, and then it was widely used in tourism research, which greatly expanded the research perspective. Early research data on tourism flows were mainly from traditional sources such as questionnaire surveys, statistical yearbooks, and second-hand panel data. For example, Shih [24] used questionnaires to collect data on self-driving travel in Nantou, Taiwan, studied the network characteristics of self-driving tourism flow, and made recommendations for tourism facilities and services of each destination. Alderighi and Gaggero [25] collected data from official airline guides and statistical yearbooks to analyze the impact of flight supply on international tourism flows. Connell and Page [17] investigated the spatial characteristics of tourism flows through questionnaire data collected from tourists traveling by car in Loch Lomond and the Trossachs Mountains National Park, Scotland.

However, these data collection approaches fail to accurately reflect the network characteristics of the tourism flow. With the emergence of interactive tourism websites and social software, scholars began to mine tourists’ digital footprints so as to accurately reflect the tourists’ spatio-temporal behaviors. This new data collection approach is based on big data and has attracted increasing attention from the academic community. It addresses the limitations of insufficient sample data and low accuracy and has been applied in various fields of tourism flow research. For example, Zheng [26] focused on Chinese tourists in Nordic countries and used travel blog data collected from Qunar.com (https://www.qunar.com/ (accessed on 31 December 2019)) to investigate tourists’ spatio-temporal behavior characteristics and complex network effects of the tourism flow. Thus far, research based on digital tourism footprint, a new data source, has become a hot spot and has obtained abundant achievements. Orama et al. [27] collected data from the social platform Twitter and used artificial intelligence to reveal tourist mobility patterns and visit preferences. Using this tool, destination management organizations can provide visitors with personalized services and information to enhance the visitor experience.

From the perspective of research content, the studies on tourism flow mainly fall into the following three aspects: (1) Simulation and prediction of tourism flows: Zhang [28] combined econometrics and judgment methods to predict Hong Kong’s tourism flow and possible ways of recovery. In the context of the tourism industry severely affected by unforeseen events such as COVID-19, Turtureanu et al. [29] applied the ARMA model approach to analyze the evolution of tourism flows in Romania between January 2020 and September 2021 in order to find the best way to forecast tourism demand. (2) Spatial flow and pattern of tourism flow: Lee [30] used geographic information system (GIS) and network analysis to measure the centrality of 43 villages in Jangheung-gun and Jeollanam-do in Korea. Mou [31] mined online travel diaries from Qunar.com and analyzed the spatial patterns of tourism flows in Qingdao by using the gravity center model, association rules mining, and social network analysis. Jeon and Yang [32] examined the structural changes in local tourism networks before and after COVID-19, using Gangwon Province, Korea, as an example. It was found that tourists traveling after the COVID-19 outbreak simplified their travel routes and concentrated their demand for tourism on the beaches. (3) Influencing factors of tourism flows: Wang [33] used the Baidu Index to obtain daily visitor data of 73 scenic spots in Beijing and constructed a new theoretical framework for investigating the effects of haze weather on tourism. Ivanov et al. [34] analyzed the impact of COVID-19 on tourism flows and spatial structure in Finland and Estonia in 2020. Khalid et al. [35] explored the impact of languages of different origins on international tourism flows. It was found that the use of a common language derived from a common mother tongue, a common official language, and linguistic proximity promotes international tourism flows.

The methodology adopted for tourism flow studies varies depending on the research perspective and type of data. In the study of the causes of tourism flows, the analysis was carried out with the help of “push-pull” and “O-D” theories. For example, Roy and Sharma [36] presented people’s motivation to travel during COVID-19 based on the push–pull theory. The study provided insight into the emotional state of travelers in the context of day trips. Wu et al. [6] studied the spatial and temporal differences in tourism flows on May Day holidays using the “O-D” theory and differential indices with China as the study area. The system dynamics approach is mostly used in the study of the dynamic operating mechanism of tourism flows to promote the sustainability of tourism flows by adjusting the input elements so that the system output results in meeting development expectations [17,37]. GIS and social network analysis are mostly applied to the study of the spatial structure of tourism flows. For example, Wang et al. [5] used a combination of social network and spatial analysis to analyze the spatial structure, evolutionary patterns, and influencing factors of tourism flow networks. Zhong et al. [38] visualized tourism flows in Tibet through social network analysis to identify the inflow and outflow of tourists in the destination.

In terms of time scales, most scholars focus on studying tourism flows concerning long-time scales. There are more studies on the long-term change characteristics, seasonal change characteristics, and holiday change characteristics of tourism flow. For example, Mou et al. [31] proposed a new framework for studying tourism flows and verified the validity of the model with tourism flows in Qingdao city from 2012 to 2018. Yang et al. [39] investigated the impact of air and rail intermodal connections on urban tourism flows during the National Day holidays in China in 2014.

From the perspective of view of case study areas, most studies used international tourism flows, or tourism flows in major tourist cities. For example, Seok [40] used social network analysis to explore the changes in the structure of international tourism flows. Mou [41] collected Flickr photos of China’s inbound tourism flows from 2004 to 2018 and used the R-HDBSCAN clustering algorithm and complex network to study the spatio-temporal evolution process of the inbound tourism flow network in Shanghai. It was found that the spatial structure of tourism flows in urban tourism destinations has typical common features, such as strong connections within the network. The development of tourism in rural ethnic areas is more influenced by the spatial distribution of tourist attractions and basic transportation construction, and its network structure will show different characteristics from urban tourism flows. How to scientifically design tourism routes and create tourism products for rural ethnic areas based on tourists’ preferences is very important.

The existing studies on tourism flow have laid a solid theoretical foundation for this paper, but they have suffered from some shortcomings. First, the case study areas are mostly tourist cities. Studies on rural tourism have focused more on sustainable rural tourism development [42], stakeholder research [43], and spatial patterns of rural tourism destinations [44], while few studies have been conducted on tourism flows in rural areas. Second, most studies identified only a single influencing factor of tourism flow, and there are few comprehensive studies on the identification of multiple factors. This paper aims to address the above shortcomings by utilizing online travel blogs data to analyze the network structure characteristics and influencing factors of the tourism flow with a case study of Qiandongnan Prefecture so as to promote regional coordination and sustainable development of rural tourism.

3. Methodology

3.1. Study Area

Qiandongnan Miao and Dong Autonomous Prefecture are located in the southeast of Guizhou Province, China, and at the intersection of Guizhou, Hunan, and Guangxi provinces (Figure 1). It has jurisdiction over 16 counties and cities, with a total area of 30,282.34 km². It has a population of about 4,811,900, of which ethnic minorities account for 80.3%. Qiandongnan Prefecture is rich in tourism resources and cultural heritage. There are many tourist attractions, traditional villages, and famous historical towns in the territory. The local ethnic customs are strong, and 128 festivals with a scale of over 10,000 people are held every year. In 2019, the prefecture received 129,929,800 tourists, and the total revenue of tourism reached 121.21 billion yuan (equaling USD 17.57 billion), with year-on-year growth of 19.3% and 29.3%, respectively. Tourism has become the main economic industry in the prefecture, and most of the well-known tourist attractions in the region are rural ones. Therefore, Qiandongnan Prefecture is a highly representative case study site for studying tourism flows in southwest ethnic regions.

3.2. Data Sources and Database Construction

We chose the online travel blogs from three travel websites as the data sources: mafengwo.com (http://www.mafengwo.cn/ (accessed on 1 January 2020)), Ctrip.com (https://www.ctrip.com/ (accessed on 1 January 2020)), and Qunar.com (https://www.qunar.com/ (accessed on 1 January 2020)). These three websites are the leading tourism search engines in China and have accumulated a large amount of user-generated content (UGC) in tourism. In order to avoid the impact of COVID-19 on this study, this paper adopted a data mining method to collect tourist travel blogs from January 2019 to December 2019, totaling 738 articles. Since there may be information errors in the online travel blogs, we used the following rules to clean up the data: (1) remove travel blogs that do not fully record the itinerary, (2) remove travel blogs that have duplicate content and are not related to Qiandongnan Prefecture, and (3) remove travel blogs that have plagiarism and advertisements. After cleaning up in terms of these rules, we finally obtained 289 travel blogs.

Tourist routes in 289 travel blogs were extracted. The tourist attractions were abstracted as nodes (i.e., the attractions and nodes are the same object), and the number of tourism flows between two attractions was abstracted as edges with weights. According to the order of visits, it was split into directed node pairs. If there was a direct flow between nodes, it was recorded as 1; otherwise, it was recorded as 0, and the result is recorded in the Excel cell in the form of a matrix. Considering that tourism nodes with fewer visits are of less significance in the analysis, the node with one visit was discarded. Finally, 42 tourism nodes are involved in this study; that is, a 42 × 42 multi-valued directed relation matrix was obtained in this study.

3.3. Research Methods

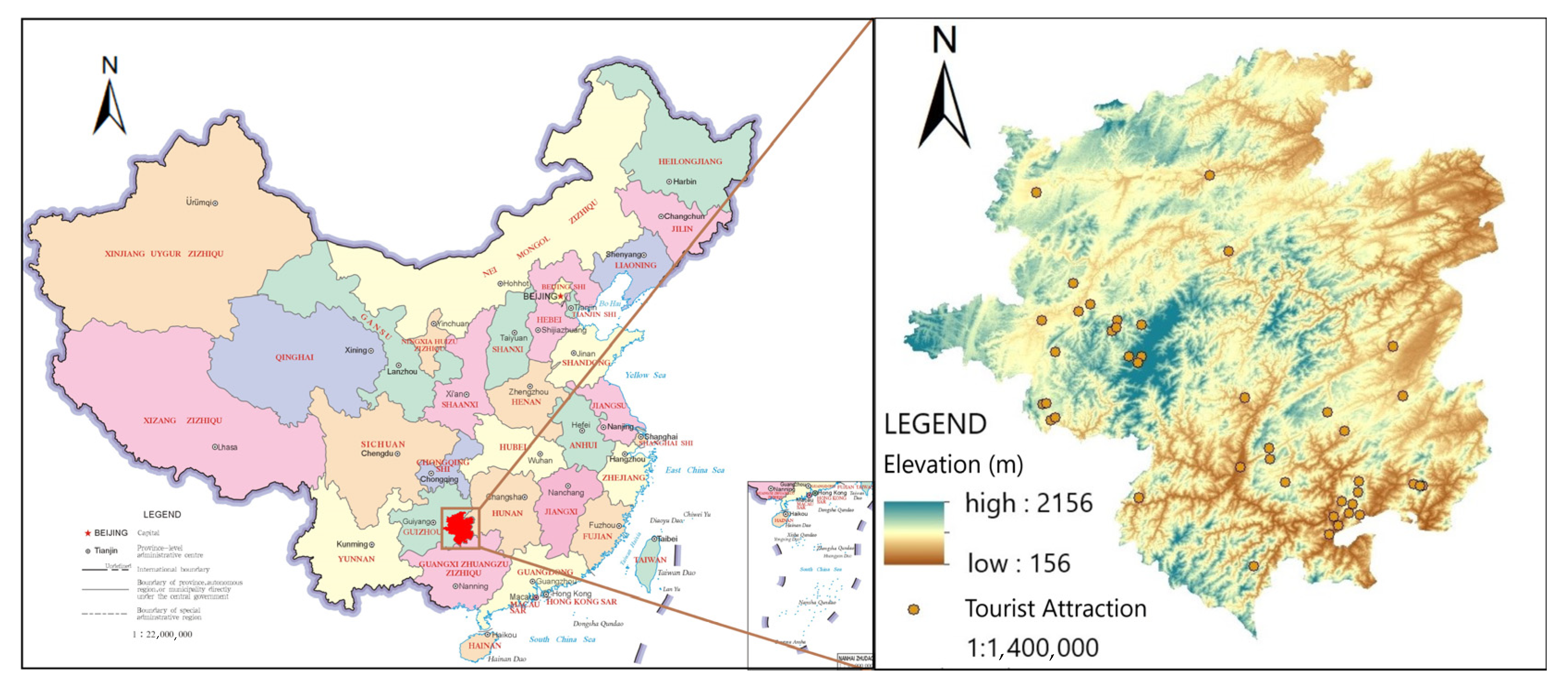
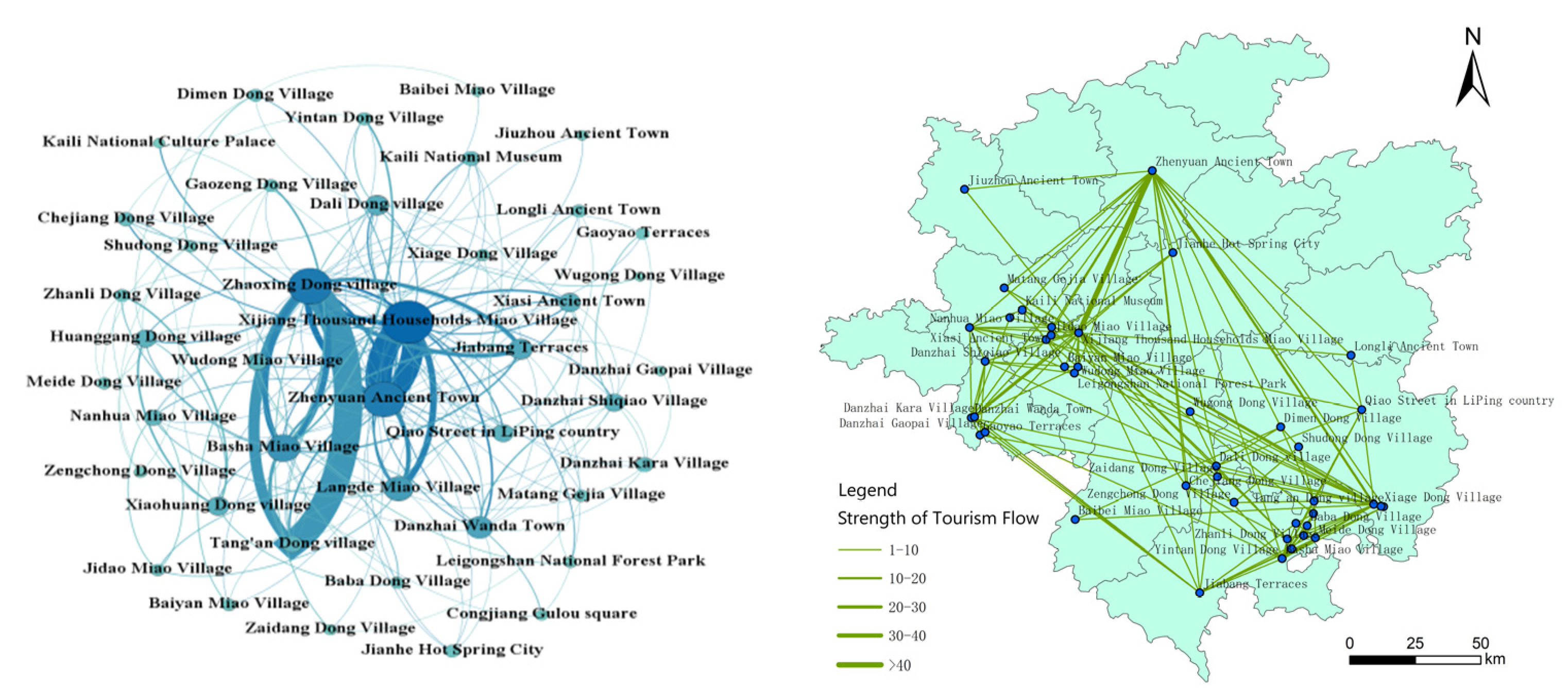
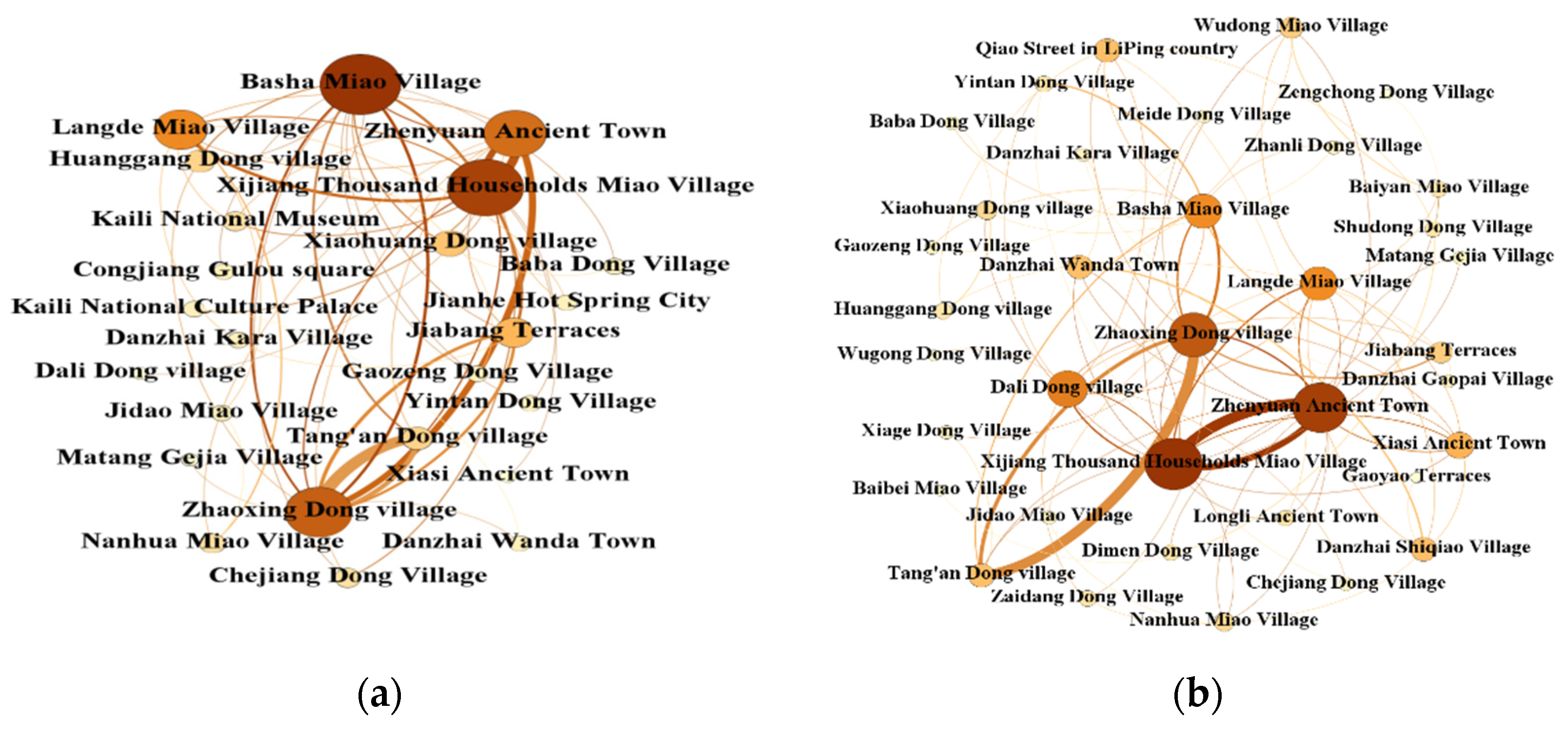
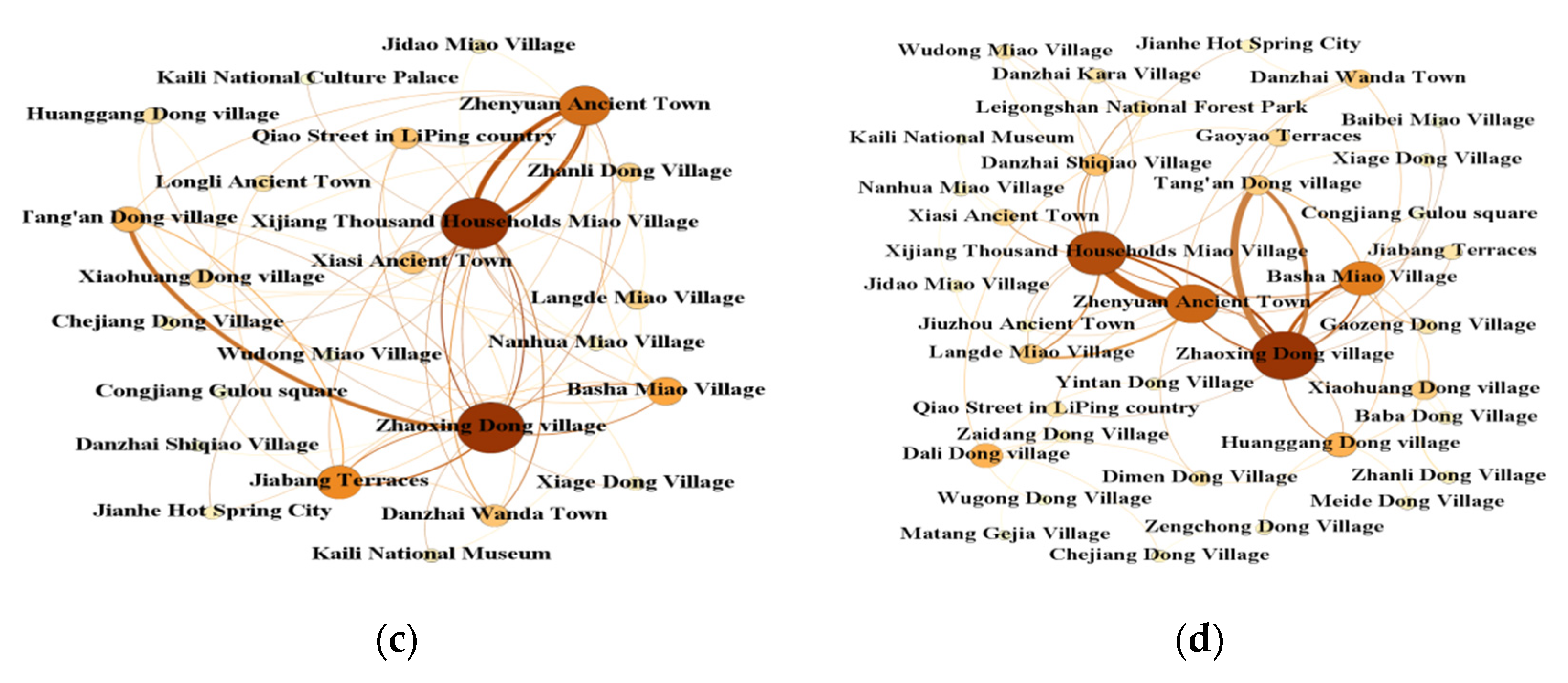
3.3.1. Social Network Analysis

A social network is a collection of social actors and their relationships. It is mainly used to describe and analyze the relationship characteristics and types of social things and analyze the influence of relationships on the network [45]. Currently, social network analysis has been widely used in the fields of sociology, management, and economics. The flow of tourists makes tourism destinations spatially constitute a network structure including tourism nodes and the connecting lines between tourism nodes. The social network analysis method can precisely combine graph theory and mathematical models to study such network relationships. It can not only describe the overall spatial distribution pattern of tourism flows but also discover the characteristics of the intrinsic connections between tourism nodes. Social network analysis can realize the accurate and quantitative analysis of various relationships in tourist flows, thus providing quantitative tools for theoretical construction and practical tests [5]. Therefore, the social network analysis method is gradually becoming a popular paradigm for studying the network structure of tourism flows. Specifically, we used the social network analysis method to study the node structure characteristics and overall structure characteristics of the tourism flow in Qiandongnan Prefecture from the perspective of geography. Centrality analysis and structural hole index were used to analyze the node structure characteristics of tourism flow in Qiandongnan Prefecture. Network density, core–periphery structure model, and cohesive subgroups were used to analyze the overall structure characteristics of tourism flow in Qiandongnan Prefecture.

• Individual network characteristics index.

Degree centrality is the number of nodes directly connected to other nodes. If a node has the highest degree, it is regarded as the center and has a great influence on other nodes. In a directed graph, the degree of each node can be divided into point-in degree and point-out degree. Equation (1) shows how to calculate the degree of centrality $C_D\left(i\right)$ of node i,

$$C_D\left(i\right)={{\displaystyle \sum }}_{j=1}^n{r}_{ij}$$

(1)

where ${\displaystyle \sum }_{j=1}^n{r}_{ij}$ represents the number of direct connections between nodes and $j$ ($i\ne j$).

Closeness centrality is a measure that is not controlled by other nodes. If the distance between a node and all other nodes in the network is very short, the node has a high closeness centrality. The closeness centrality is the sum of the shortest path distances between the node and other nodes in the network. Equation (2) shows how to calculate closeness centrality $C_C\left(i\right)$ of node i,

$$C_C\left(i\right)=\frac{1}{{{\displaystyle \sum }}_{j=1}^n{z}_{ij}}$$

(2)

where z_ij represents the distance between nodes i and j $(i\ne j$).

Betweenness centrality is an index to measure the control degree of nodes on the whole network. If a node is on the shortest path of many other node pairs, we say that the node has a high betweenness centrality. Equation (3) shows how to calculate betweenness centrality $C_B\left(i\right)$ of node i,

$$C_B\left(i\right)={{\displaystyle \sum }}_j^n{{\displaystyle \sum }}_k^n\frac{g_{jk}\left(i\right)}{g_{jk}},j\ne k\ne i,j<k$$

(3)

where $g_{jk}$ represents the number of shortest paths that exist between nodes j and k, $g_{jk}\left(i\right)$ represents the number of paths that exist between nodes j and k through node i.

Structural holes represent non-redundant connections and can be used to identify nodes that are at an advantage or disadvantage in the network. Nodes with structural holes are generally more competitive than nodes in other locations in the network and are irreplaceable [46]. Measuring structural holes helps identify potential bottlenecks in the network. The index of the structural hole should generally consider the following three aspects: effective size, efficiency, and constraint, among which the third index is the most important.

2.

Overall network characteristic indexes

Network density can be used to measure the overall tightness of the network structure. It is calculated as the ratio of the number of connections in the network to the total number of possible connections [47]. The lower the density value, the worse the coordination between the nodes. Equation (4) shows how to calculate the network density,

Density = L/N(N − 1)

(4)

where L represents the number of arrows in the network, and N represents the number of nodes in the network.

The core–periphery structure model divides nodes into core area and periphery area according to the closeness among nodes in the network [48]. The core area is the dominant cluster, while the periphery area has relatively few node connections. Core–periphery structure analysis can quantitatively analyze the location of nodes in the network and distinguish which nodes are in the core position in the social network and which nodes are in the periphery position.

Cohesive subgroups are important analytical measures in social networks, which can reveal actual or potential relationships between social actors [49]. Cohesive subgroups are an important link between individuals and organizations. When the relationship between certain actors in the network is so close that they are combined into a sub-group, social network analysis calls such groups cohesive subgroups. If there are cohesive subgroups in the network, and the density is high, it means that the nodes in this cohesive subgroup are closely connected.

3.3.2. Quadratic Assignment Procedure

• The Quadratic Assignment Procedure Analysis Method.

The quadratic assignment procedure (QAP) is a method that compares the values of the corresponding elements in two or more square matrices based on the replacement of matrix data. It compares the corresponding grid values of each square matrix, gives the correlation coefficient between the two matrices, and performs non-parametric tests on the coefficients at the same time. Since there is no need to assume that the independent variables are independent of one another, the QAP can effectively avoid the inherent autocorrelation errors in the data and obtain a more reliable result than the parametric method. Since the tourism flow network structure and its influencing factors are a kind of relational data, in this case, the use of ordinary least squares (OLS) for analysis leads to deviations in the estimates. On the contrary, QAP explicitly considers the autocorrelation error in the network data; therefore, it can circumvent this problem to a large extent [50]. The QAP is usually divided into two steps: QAP correlation analysis and QAP regression analysis. QAP correlation analysis studies whether two matrices are correlated or not. It permutes the matrix, calculates the correlation coefficient by comparing the similarity of matrix lattice values, and carries out a non-parametric test [51]. QAP regression analysis is to study the regression relationships between multiple matrices and one matrix. In a calculation, a standard multiple regression analysis is first carried out for the corresponding elements of the independent variable matrix and the dependent variable matrix. Then, the rows and columns of the dependent variable matrix are randomly and simultaneously replaced. Subsequently, the regression is recalculated, and all coefficient values and decision coefficient r² values are saved. This step is repeated hundreds of times to estimate the standard errors of the statistics [52].

2.

Theoretical model.

Although the formation of tourism flow is a subjective choice of tourists, it is actually influenced by multiple factors. After referring to the existing literature [5,53,54] and combining it with the actual situation of Qiandongnan Prefecture, this paper selected geographical adjacency, traffic accessibility, tourism reception capacity, tourism resource endowment, the popularity of tourist attractions, and ticket price of attractions as independent variables, and takes the spatial correlation matrix of tourism flow in Qiandongnan Prefecture as dependent variables and constructs the QAP model:

$$\mathrm{Y}=\mathrm{f}\left(\mathrm{GA},\mathrm{TA},\mathrm{TRC},\mathrm{TRE},\mathrm{TAP},\mathrm{TP}\right)$$

(5)

In the above model, the data of all indicators are a series of matrices. Y denotes the spatial correlation matrix of the tourism flow network. GA, TA, TRC, TRE, TAP, and TP denote the dichotomous matrices of geographical adjacency, traffic accessibility, tourism reception capacity, tourism resource endowment, the popularity of tourist attractions, and ticket price of attractions, respectively.

In this paper, whether the nodes are in the same county or not is used to represent the geographic adjacency.

In this paper, the distance from the node to the train station (DTS) and the average travel time of the node (ATT) are used to represent traffic accessibility. The railway station in the case study area is Kaili South Station. The distance from the node to the train station is based on the shortest time shown on amap (https://ditu.amap.com/ (accessed on 1 January 2020)). The average travel time of the node is calculated by Equation (6) [55].

$$A_i=\frac{{{\displaystyle \sum }}_{j=1}^n{T}_{ij}}{n}$$

(6)

where $A_i$ is the average travel time of node i; i and j represent tourist nodes; $T_{ij}$ represents the shortest travel time from node i to node j calculated using amap to select the driving mode; and n represents the number of tourist nodes.

In this paper, tourism reception capacity is replaced by the number of hotels within five kilometers of the node.

China assesses the quality level of tourist attractions according to the “Standard of rating for the quality of tourist attractions” (GB/T17775-2003), which classifies them into national 5A, 4A, 3A, 2A, and 1A level tourist attractions. Whether a tourist attraction is A-level is an important measure of resource endowment. Therefore, this paper uses whether the node is an A-level tourist attraction to represent tourism resource endowment.

This paper uses the average Baidu index of tourist attractions in 2019 to represent the popularity of tourist attractions.

Sometimes, ticket prices can also affect tourism flow. This paper used the average off-season and peak season ticket prices of tourist attractions in 2019 to represent it. The above indicator data came from the website of the Ministry of Culture and Tourism of the People’s Republic of China (https://mct.gov.cn/ (accessed on 1 January 2020).), Baidu.com (http://www.baidu.com/ (accessed on 1 January 2020).), Ctrip.com, Mafengwo.com, and amap.com.

The dichotomous matrix is constructed as follows. If the nodes are in the same region, the matrix value is 1; otherwise, it is 0. If the nodes are all A-level attractions, the value is 1; otherwise, it is 0. We took the mean value of the variable data as the dividing point. If the node is above the mean value, it is coded as 1; otherwise, it is 0.

3.

Variable assumptions.

Since there are many factors affecting tourism flow, this paper proposes the following hypotheses with reference to the existing literature:

Hypothesis 1. (H1)

Geographic adjacency is an important factor affecting tourism. If two tourist attractions are geographically close to each other, it has a positive impact on tourism flows development. The scenic spots in Qiandongnan Prefecture are scattered, and tourists need to spend a lot of time on transportation. The geographical proximity can promote tourist flow between tourist attractions.

Hypothesis 2. (H2)

The improvement of traffic accessibility has a positive impact on the improvement of tourist flows. Traffic facilities, as the infrastructure of tourist attractions, play an important role in improving the accessibility of tourist attractions and expanding the tourism market. Generally speaking, tourists tend to prefer to travel to attractions with high transportation accessibility. Traffic accessibility will directly affect the formation of tourist flows in the two tourist attractions.

Hypothesis 3. (H3)

The improvement of tourism reception capacity has a positive impact on the increase in tourist flows. Tourism reception capacity refers to the equipment and facilities of the tourism sector, which usually reflects the number of tourists received and the service level of the tourist attractions. Tourist reception capacity is one of the important indexes to attract tourists. It plays an important role in publicizing the culture of tourist destinations and promoting the comprehensive competitiveness of scenic spots.

Hypothesis 4. (H4)

The improvement of tourism resource endowment has a positive influence on the improvement of tourism flow. Tourism resource endowment is an important condition to attract tourists. Tourism resources with special characteristics can help tourists effectively overcome the resistance of spatial distance and form a tourist flow.

Hypothesis 5. (H5)

The improvement in popularity of tourist attractions has a positive impact on the improvement of tourist flows. The popularity of tourist attractions has an important impact on expanding the influence of the attractions and increasing revenue. Generally speaking, most tourists prefer to go to tourist attractions that are well known and popular.

Hypothesis 6. (H6)

The reduction in ticket prices of attractions has a positive impact on the improvement of tourist flows. Ticket prices in attractions are directly related to tourists’ vital interests. In recent years, the number of tourists in some high-ticket scenic spots has begun to decline, which indicates that high ticket prices restrict the growth of tourism consumption, and it has become an urgent problem to be solved. Generally speaking, the lower the ticket price, the more tourists.

4. Results

4.1. Construction of Tourism Flow Network

The multi-valued directed relationship matrix constructed in Excel was processed by Ucinet software and imported into Netdraw to draw a network structure diagram of the tourism flow in Qiandongnan Prefecture (Figure 2). As shown in Figure 2, the larger the circle representing the node, the greater the number of visits and preference of tourists for that node. The thicker the line between the nodes, the more frequent the flow of tourists between the nodes. According to Figure 1, the nodes that tourists frequently visit include Xijiang Thousand Households Miao Village, Zhenyuan Ancient Town, Zhaoxing Dong Village, Tang’an Dong Village, Basha Miao Village, Langde Miao Village, Jiabang Terrace, Xiasi Ancient Town, Danzhai Wanda Town, Dali Dong Village, Xiaohuang Dong Village, Huanggang Dong Village, and Danzhai Shiqiao Village. These 13 key nodes that tourists visit constitute the tourism flow network of Qiandongnan Prefecture. When comparing these 13 nodes with the 18 tourist attractions introduced in the “Tourist Attractions” section on the homepage of the Qiandongnan Prefecture Culture, Sports, Radio, Film, and Tourism Bureau official website, it was found that 13 of the 18 tourist attractions promoted by the government are not the tourist attractions that tourists focus on. Among the 13 nodes with high visit volume and preference, eight nodes are not promoted by the government; that is, there exists a big difference between the actual tourist hot spots and the promoted spots by the government (

Table 1. Comparison of tourist focus nodes and government promotion nodes in Qiandongnan.

Number	Node	Tourists Focus Node	Government Promotion Node	Number	Node	Tourists Focus Node	Government Promotion Node
1	Xijiang Thousand Households Miao Village	√	√	14	Huangping Feiyunya Scenic Area		√
2	Zhenyuan Ancient Town	√	√	15	Baishuidong Waterfall		√
3	Zhaoxing Dong village	√		16	Jianhe Hot Spring City Scenic Area		√
4	Tang’an Dong village	√		17	Baili Primitive Broadleaf Forest Gallery		√
5	Basha Miao Village	√		18	Hongyang Grassland		√
6	Langde Miao Village	√	√	19	Sister Lake Scenic Area		√
7	Jiabang Terraces	√		20	Taijiang Multi-voice Love Song		√
8	Xiasi Ancient Town	√		21	Podong Modern Ecological Agriculture Park		√
9	Danzhai Wanda Town	√	√	22	Jiepai Rural Tourism Demonstration Zone		√
10	Dali Dong village	√		23	Shanshan River Scenic Area		√
11	Xiaohuang Dong village	√		24	Qiandongnan Grand Canyon Scenic Area		√
12	Huanggang Dong village	√		25	Longquan Chiyou Cultural Park		√
13	Danzhai Shiqiao Village	√	√	26	Jiuzhou Ancient Town		√

). We further found that the nodes promoted by the government but not the foci of tourists are mainly distributed in areas far away from the core nodes, and the transportation is relatively inconvenient. Most of them are natural landscapes, which are not attractive to outbound tourists. These results reflect the deviation between the official tourism marketing department’s understanding of tourist behavior and the perception of tourists themselves. Therefore, the official tourism department should proceed from the perspective of tourists and conduct reasonable tourism marketing to enhance the attractiveness and competitiveness of tourist attractions.

4.2. Seasonal Network

By extracting and analyzing the travel time information in the blogs, it is known that there are seasonal changes in the tourism flow in Qiandongnan Prefecture. The tourism flow is mainly concentrated in February, April, and July to August (Figure 3). The Spring Festival holiday in February is the main reason for the large tourism flow. In April, Qiandongnan Prefecture has a suitable climate and pleasant scenery, and ethnic minorities will hold large-scale programs. From July to August, most areas have a hot climate, while Qiandongnan Prefecture attracts a large number of tourists to escape the summer heat due to its high altitude and suitable temperature. In winter, the tourism flow of Qiandongnan Prefecture is relatively small, which puts pressure on tourism development in Qiandongnan Prefecture.

From the perspective of the tourism flow network structure in the four seasons, it was found that the main attractions that tourists visit have not changed due to seasonal changes. Xijiang Thousand Households Miao Village, Zhenyuan Ancient Town, Zhaoxing Dong Village, Basha Miao Village, and other nodes are still the main tourist attractions. It can be seen from Figure 4a,c that there are too many isolated nodes in the network structure diagrams in spring and autumn (nodes that have no connection with other nodes are isolated nodes, such as Qiao Street in LiPing country and Wudong Miao Village in Figure 4a, a total of 18 nodes). Although there are fewer isolated nodes in winter, the connections between the main nodes are thinner. It shows that the links between the nodes in the tourism flow network in spring, autumn, and winter are not close enough, and the links between tourist attractions should be actively strengthened.

4.3. Network Structure

In order to more intuitively and clearly reflect the structural characteristics of the tourism flow network in Qiandongnan Prefecture, the 42 × 42 multi-value directed relationship matrix was converted into a binary matrix. After several tests, it was finally determined that 1 was selected as the breakpoint value. If the connection frequency between nodes is greater than 1, 1 is assigned to it; otherwise, 0 is assigned to it. Then UCINET software was used to analyze and calculate the network structure.

4.3.1. Characteristics of the Network Node Structure

UCINET was used to obtain the node metrics of network structure evaluation in Qiandongnan Prefecture (

Table 2. Indicators of tourism nodes in Qiandongnan Prefecture.

Node	Degree Centrality		Closeness Centrality		Betweenness Centrality	Structural Holes
	Out	In	Out	In		Effective Size	Efficiency	Constraint
Xijiang Thousand Households Miao Village	16	20	37.273	63.077	561.505	20.944	0.838	0.162
Zhaoxing Dong Village	15	14	37.273	56.164	406.896	17.138	0.816	0.178
Zhenyuan Ancient Town	13	15	36.283	54.667	282.918	14.964	0.788	0.213
Langde Miao Village	10	7	33.884	45.055	103.918	8.471	0.706	0.306
Basha Miao Village	10	10	35.043	49.398	235.010	11.450	0.763	0.243
Jiabang Terraces	8	5	34.167	42.268	105.709	7.577	0.689	0.339
Dali Dong Village	7	5	33.607	44.086	143.782	8.333	0.758	0.313
Tang’an Dong Village	6	3	33.607	39.806	16.350	3.000	0.500	0.561
Danzhai Wanda Town	6	9	32.283	50.000	94.148	8.067	0.672	0.324
Xiasi Ancient Town	6	5	30.370	45.556	12.019	4.636	0.515	0.440
Xiaohuang Dong Village	6	5	32.031	45.556	100.582	4.818	0.803	0.406
Huanggang Dong Village	6	4	30.370	41.414	108.668	6.350	0.794	0.367
Danzhai Shiqiao Village	4	6	26.623	44.086	30.817	6.350	0.706	0.419
Qiao Street in LiPing country	4	6	30.827	44.086	27.900	4.400	0.629	0.510
Wudong Miao Village	4	5	32.031	41.837	51.286	4.389	0.549	0.480
Nanhua Miao Village	4	4	29.710	42.708	24.998	2.500	0.500	0.603
Kaili National Museum	4	3	32.031	40.594	2.223	1.571	0.314	0.684
Chejiang Dong Village	4	2	30.370	41.000	48.910	3.833	0.639	0.483
Longli Ancient Town	3	2	29.286	37.615	1.452	1.600	0.533	0.933
Baiyan Miao Village	3	1	28.276	39.048	0	1.250	0.417	1.022
Danzhai Kara Village	3	4	28.873	39.048	44.410	3.786	0.631	0.523
Dimen Dong Village	2	3	27.703	35.965	83.917	4.200	0.840	0.400
Yintan Dong Village	2	3	28.671	41.837	4.435	2.500	0.500	0.663
Jidao Miao Village	2	2	25.786	31.783	0.333	1.500	0.750	0.889
Zhanli Dong Village	2	3	27.333	36.607	26.461	3.000	0.750	0.633
Jianhe Hot Spring City	2	3	29.078	38.679	0	1.400	0.350	0.848
Zengchong Dong Village	2	1	24.118	29.927	6.742	2.333	0.778	0.611
Gaoyao Terraces	2	2	28.671	38.679	3.340	2.000	0.500	0.805
Xiage Dong Village	2	2	27.703	36.607	0	1.000	0.500	1.125
Leigongshan National Forest Park	2	1	25.625	39.423	0	1.333	0.444	0.997
Matang Gejia Village	2	2	28.082	40.196	3.033	2.125	0.531	0.791
Meide Dong Village	2	2	22.527	38.318	5.054	3.125	0.781	0.594
Baba Dong Village	2	2	24.699	35.965	1.200	1.250	0.417	0.956
Kaili National Culture Palace	1	1	24.848	39.423	0	1.000	0.500	1.389
Zaidang Dong Village	1	2	25.625	37.273	3.111	1.667	0.556	0.840
Baibei Miao Village	1	1	27.891	26.974	8.333	2.000	1.000	0.500
Jiuzhou Ancient Town	1	1	27.703	35.965	0	1.000	0.500	1.389
Wugong Dong Village	1	0	33.884	2.381	0	1.000	1.000	1.000
Danzhai Gaopai Village	1	1	23.034	30.597	0	1.000	0.500	1.125
Shudong Dong Village	1	2	22.283	30.597	2.700	1.667	0.556	0.840
Congjiang Gulou Square	1	2	26.282	34.746	0	1.000	0.500	1.235
Gaozeng Dong Village	1	4	26.452	39.806	17.839	3.300	0.660	0.614
Mean	4.167	4.167	29.339	39.734	61.190	-	-	-
Std Dev	3.760	4.047	3.879	9.006	114.468	-	-	-
Variance	14.139	16.377	15.044	81.106	13,103.015	-	-	-
Maximum	16.000	20.000	37.273	63.077	561.505	-	-	-
Minimum	1.000	0.000	22.283	2.381	0	-	-	-
Network Centralization	29.566%	39.560%	-	-	31.25%	-	-	-

). We analyzed the centrality of the nodes through degree centrality, closeness centrality, and betweenness centrality. We analyzed the structural hole level of each node through effective size, efficiency, and constraint.

(1)

Node centrality

It can be seen from Table 2 that the mean value of degree centrality is 4.167, which means that each node has an inflow and outflow relationship with 4.167 other nodes on average. The large variance of degree centrality indicates that Qiandongnan Prefecture has a strong imbalance in the structure of the tourism flow network. The higher the out-degree centrality, the more tourism flow from this node to other nodes. It indicates that the node has a stronger radiation ability. The higher the in-degree centrality, the more tourism flow from other nodes to this node. The results of out-degree centrality and in-degree centrality of tourism flow network nodes are basically consistent. It indicates that the node has a stronger agglomeration ability. The Xijiang Thousand Households Miao Village has the highest out-degree centrality and in-degree centrality, indicating that it is the distribution center of the tourism flow in Qiandongnan Prefecture, and it has a strong agglomeration and radiation effect on the tourism flow. This also shows that Xijiang Thousand Households Miao Village is the most popular attraction because of its unique architecture and Miao culture.

From the calculation result of closeness centrality, we can see that the patency of tourism flows between nodes in the tourism network is quite different (Table 2). Seventeen nodes had higher than average out-closeness centrality and in-closeness centrality, indicating that these nodes had high out-closeness centrality (29.339~37.273) and in-closeness centrality (39.734~63.077). This shows that these nodes are closely connected with other nodes and have good flow patency with other nodes. They are at the center of the tourism network, and the combination of different tourists’ travel routes usually includes these nodes.

From the calculation result of the betweenness centrality, each node acts as an intermediary 27.21 times in the network on average (Table 2). The standard deviation of betweenness centrality is 114.468, which shows that the control ability of tourism nodes is quite different. There were 11 nodes with above-average mesoscopic centrality of travel nodes, indicating that they had high mesoscopic centrality (61.19~561.505). It shows that these nodes are in a key position in the tourism network of Qiandongnan Prefecture, and other nodes rely on them. The attraction with the highest betweenness centrality, Xijiang Thousand Households Miao Village, plays the role of a core intermediary in the tourism flow network. In contrast, the betweenness centrality of nine tourist nodes, such as Kaili National Culture Palace and Leigongshan National Forest Park, is 0. They have a strong dependence on other tourist nodes, weaker control capabilities, and a lack of attractiveness to tourists.

Generally speaking, the network structure of tourism flow in Qiandongnan Prefecture has poor tightness and strong imbalance. Moreover, there are big differences among these nodes. The core nodes in the tourism flow are Xijiang Thousand Households Miao Village, Zhaoxing Dong Village, Zhenyuan Ancient Town, Langde Miao Village, Basha Miao Village, Dali Dong Village, and Jiabang Terraces (i.e., they have high node centrality values). They are in an obviously advantageous position in the network, acting as agglomeration and radiating centers. Most other tourism nodes need to flow through these nodes.

(2)

Structural Holes

According to the calculation results of the structural hole (Table 2), it can be seen that Xijiang Thousand Households Miao Village has a large effect size and efficiency values but low constraint values. This shows that it has the highest structural hole level in the tourism flow network of Qiandongnan Prefecture and has strong competitiveness. There are also more structural holes in the tourist nodes, such as Zhenyuan Ancient Town, Zhaoxing Dong village, Baasha Miao Village, and Langde Miao Village, which occupy a favorable position in the whole network and can better connect with other tourist nodes. Baiyan Miao Village, Jiuzhou Ancient Town, Xiage Dong Village, Kaili National Culture Palace, Danzhai Gaopai Village, Congjiang Gulou Square, and Jianhe Hot Spring City have fewer structural holes and are in a disadvantaged position. Hence, the tourism department should actively promote these attractions and improve the level of tourism facilities and services. At the same time, cooperation should be strengthened with tourism nodes that are close and have more structural holes to enhance the competitiveness of attractions.

4.3.2. Characteristics of the Overall Network Structure

(1)

Network density

For a network with a size of 42 × 42, there are 1722 possible paths at most, but only 175 are actually observed. The density of the tourism flow network in Qiandongnan Prefecture is 0.1016, indicating that the closeness of the network structure is relatively low, the connections between tourism nodes are relatively sparse, and the tourism routes are relatively small. Combined with the tourism flow network structure of Qiandongnan Prefecture (Figure 2), it can be known that tourism flow has a tendency to gather in the Xijiang Thousand Households Miao Village, Zhenyuan Ancient Town, Zhaoxing Dong Village, Basha Miao Village, and Langde Miao Village, while the connections between other nodes are relatively sparse. This is probably due to the fact that each of these attractions has its own characteristics, and with the strong support and promotion of the government, many tourists come to visit them.

(2)

Core–Periphery Structure Model

By using the core–periphery model in UCINET to analyze the tourism flow network structure of Qiandongnan Prefecture, the results show that there is an obvious core–periphery structure in the network (

Table 3. Core–periphery areas of tourism flow.

Category	Node
Core Class Memberships (12)	Xijiang Thousand Households Miao Village, Zhenyuan Ancient Town, Zhaoxing Dong village, Tang’an Dong village, Basha Miao Village, Langde Miao Village, Jiabang Terraces, Xiasi Ancient Town, Danzhai Wanda Town, Dali Dong village, Qiao Street in LiPing country, and Wudong Miao Village
Periphery Class Memberships (30)	Xiaohuang Dong village, Huanggang Dong village, Danzhai Shiqiao Village, Nanhua Miao Village, Yintan Dong Village, Chejiang Dong Village, Zhanli Dong Village, Baiyan Miao Village, Gaozeng Dong Village, Dimen Dong Village, Longli Ancient Town, Jidao Miao Village, and Danzhai Kara Village, Kaili National Museum, Jiuzhou Ancient Town, Gaoyao Terraces, Xiage Dong Village, Zaidang Dong Village, Matang Gejia Village, Kaili National Culture Palace, Baba Dong Village, Baibei Miao Village, Leigongshan National Forest Park, Wugong Dong Village, Zengchong Dong Village, Meide Dong Village, Danzhai Gaopai Village, Shudong Dong Village, Congjiang Gulou square, and Jianhe Hot Spring City

). The nodes of the core area are Xijiang Thousand Households Miao Village, Zhenyuan Ancient Town, Zhaoxing Dong Village, Tang’an Dong Village, Basha Miao Village, Langde Miao Village, Jiabang Terrace, Xiasi Ancient Town, Danzhai Wanda Town, Dali Dong Village, Qiao Street in LiPing country, Wudong Miao Village, and other nodes are in the periphery area (Table 3). The density between nodes in the core area is 0.455, indicating that the links among tourist attractions are relatively close, and there are many interactions. The density between nodes in the periphery area is 0.030, indicating that there are fewer connections among tourist attractions and the connections are not close. The density between the nodes in the core area and the periphery area is 0.125, indicating that the core area has a weak driving effect on the periphery area, and there is less interaction between the core area and the periphery area (

Table 4. Core–periphery density matrix.

Category	Core	Periphery
Core	0.455	0.125
Periphery	0.122	0.030

). In summary, it can be inferred that tourists visiting the core area attractions are more inclined to move to other attractions in the core area. Tourists visiting the periphery area attractions are more likely to move to the periphery area attractions. The probability of visiting other nodes in the periphery area is lower. The tourism flow network has a clear structural stratification.

(3)

Cohesive Subgroups

By using the concor algorithm in the UCINET, it was learned that Qiandongnan Prefecture has eight cohesive subgroups at three levels, but the closeness of the connections among the cohesive subgroups is quite different and loose. As shown in

Table 5. Cohesive Subgroups Density Matrix.

Subgroups	1	2	3	4	5	6	7	8
1	0.250	0.280	0.267	0.240	0.000	0.029	0.000	0.000
2	0.080	0.100	0.133	0.080	0.000	0.086	0.000	0.000
3	0.200	0.000	0.000	0.433	0.000	0.048	0.067	0.000
4	0.360	0.060	0.300	0.122	0.075	0.057	0.120	0.067
5	0.100	0.000	0.333	0.075	0.250	0.107	0.050	0.000
6	0.057	0.000	0.000	0.029	0.143	0.357	0.057	0.190
7	0.000	0.000	0.067	0.140	0.050	0.000	0.000	0.000
8	0.000	0.000	0.111	0.000	0.000	0.095	0.067	0.167

Note: R-squared = 0.130. 1: Xijiang Thousand Households Miao Village, Danzhai Shiqiao Village, Jidao Miao Village, Baiyan Miao Village, Kaili National Museum; 2: Yintan Dong Village, Chejiang Dong Village, Leigongshan National Forest Park, Wudong Miao Village, Kaili National Culture Palace; 3: Zhenyuan Ancient Town, Gaoyao Terraces, Danzhai Kara Village; 4: Danzhai Wanda Town, Langde Miao Village, Nanhua Miao Village, Jiuzhou Ancient Town, Xiasi Ancient Town, Zhaoxing Dong village, Dali Dong village, Jianhe Hot Spring City, Matang Gejia Village, Longli Ancient Town; 5: Danzhai Gaopai Village, Tang’an Dong village, Jiabang Terraces, Congjiang Gulou square; 6: Huanggang Dong village, Xiaohuang Dong village, Gaozeng Dong Village, Zhanli Dong Village, Basha Miao Village, Baba Dong Village, Zengchong Dong Village; 7: Zaidang Dong Village, Baibei Miao Village, Qiao Street in LiPing country, Xiage Dong Village, Wugong Dong Village; 8: Meide Dong Village, Shudong Dong Village, Dimen Dong Village.

, there are three subgroups (subgroups 1, 5, and 6) in the tourism flow network of Qiandongnan Prefecture that have a higher connection density than the entire network, and their internal connections are closer. It is mainly because the subgroup contains core nodes and the internal nodes are close in geographical space. By observing the density among cohesive subgroups, it can be found that there are three pairs of subgroups that are closely related, namely, subgroup 1 and subgroup 4, subgroup 3 and subgroup 4, and subgroup 3 and subgroup 5, indicating that tourists tend to combine tourism nodes in these three pairs of subgroups.

4.4. Analysis of Influencing Factors

4.4.1. QAP Correlation Analysis

UCINET software was used to analyze the factors affecting the network structure of tourism flow in Qiandongnan Prefecture. Five thousand random permutations were selected for QAP correlation analysis, and the results are shown in

Table 6. QAP correlation analysis results of the spatial correlation matrix Y and its influencing factors.

Variable	Obs Value	Significa	Average	Std Dev	Minimum	Maximum	Prop ≥ 0	Prop ≤ 0
GA	0.212	0.000 ***	0.000	0.030	−0.094	0.125	0.000	1.000
DTS	0.195	0.000 ***	0.000	0.026	−0.085	0.107	0.000	1.000
ATT	0.002	0.498	0.000	0.025	−0.091	0.102	0.498	0.562
TRC	−0.036	0.206	0.000	0.042	−0.122	0.146	0.820	0.206
TRE	0.238	0.000 ***	−0.000	0.058	−0.137	0.271	0.000	1.000
TAP	−0.188	0.001 **	−0.000	0.057	−0.218	0.140	0.999	0.001
TP	−0.160	0.001 **	0.000	0.052	−0.176	0.143	0.999	0.001

Note: “Obs Value” represents the correlation coefficient. “Significa” represents the level of significance. “Average” represents the average value of the correlation coefficient. “Std Dev” stands for standard deviation. “Minimum” represents the minimum value of the correlation coefficient. “Maximum” represents the maximum value of the correlation coefficient. “Prop ≥ 0” represents the probability that the randomly calculated correlation coefficient is greater than or equal to the actual correlation coefficient. “Prop ≤ 0” represents the probability that the randomly calculated correlation coefficient is less than or equal to the actual correlation coefficient. **, and *** represent significance at the levels of 5% and 1%, respectively.

. As can be seen from Table 6, the correlation coefficients of geographical adjacency, the distance from the node to the train station, and tourism resource endowment all pass the 1% significance level test. The popularity of tourist attractions and ticket prices all pass the 5% significant level test. This indicates that all five factors significantly affect the formation of the tourism flow network structure. The correlation coefficients of GA, DTS, and TRE are positive, indicating a positive correlation between them and the structure of the tourism flow network. The correlation coefficients of TAP and TP are negative, indicating a negative correlation between them and the structure of the tourism flow network. The correlation coefficients of the average travel time of nodes and tourist reception capacity are not significant, indicating their insignificant effects on network formation.

4.4.2. QAP Regression Analysis

QAP regression analysis was performed using UCINET software, setting the number of random permutations to 10,000 times. The regression results are shown in

Table 7. Quadratic assignment procedure regression analysis results.

Independent	Unstandardized Coefficient	Standardized Coefficient	Significance	Proportion as Large	Proportion as Small
Intercept	0.092	0.000	-	-	-
GA	0.162	0.179	0.000 ***	0.000	1.000
DTS	0.084	0.139	0.000 ***	0.000	1.000
ATT	−0.009	−0.015	0.268	0.732	0.268
TRC	0.007	0.011	0.367	0.367	0.633
TRE	0.157	0.216	0.000 ***	0.000	1.000
TAP	−0.089	−0.133	0.007 **	0.993	0.007
TP	−0.034	−0.054	0.127	0.873	0.127

Note: Adj-R² = 0.150. **, and *** represent significance at the levels of 5% and 1%, respectively.

. The adjusted R² is 0.150, indicating that the regression equation explains 15% of the structure of the tourism flow network in Qiandongnan Prefecture. In previous studies, the R² values were mostly between 12.5% and 40.3% [5,49]. The R² value of this study is moderate, which indicates its explanatory power.

The results of the QAP regression analysis were generally consistent with the correlation analysis, but some variables failed the significance test, which was similar to the findings of previous studies [5,49,50]. Geographic adjacency, distance from the node to the train station, and tourism resource endowment all passed the 1% significance test. The popularity of tourist attractions passed the significance test with 5%. This indicates that these indicators are important factors in attracting tourists.

Specifically, the regression coefficient of geographic proximity passed the 1% significance level test and was positive, indicating that geographic proximity plays a significant role in promoting the formation of a tourism flow network. The reason for this is that tourists prefer to move between attractions in the same region. Tourists moving to the same region can visit more attractions in less time and reduce travel costs.

The regression coefficient of the distance from the node to the train station is significantly positive at the 1% level. This is because Qiandongnan Prefecture is located in the mountainous region of southwest China. The distance from the node to the train station has a great influence on the accessibility of the attractions. The farther the distance from the node to the train station, the less favorable the communication between the nodes.

Tourism resource endowment is significant at the 1% level with a positive regression coefficient, indicating that the differentiation of this indicator is also a key factor in the formation of a tourism flow network. The higher the rating of a tourist attraction, the better its resource endowment and infrastructure, and the more attractive it is to tourists.

The popularity of tourist attractions is at the 5% level with a negative regression coefficient. It implies that the widening of the difference in the popularity of tourist attractions has a positive impact on the formation of the network. The reason is that most of the attractions in Qiandongnan Prefecture are less well-known attractions, such as villages. Tourists know less about these and need to use the Internet to obtain information about the attractions. To a certain extent, it can reflect the attention of tourists to attractions.

The three indicators of the node’s average travel time, tourist reception capacity, and ticket price have not passed the significance test on the tourism flow network structure of Qiandongnan Prefecture and have no effect on the tourism flow. The main reason is that the various scenic spots in Qiandongnan Prefecture are far away. Tourist resources are the key factor based on which tourists make decisions, rather than the convenient transportation between scenic spots. On the one hand, Qiandongnan Prefecture is located in a mountainous ethnic area with fewer hotels. Tourists pay more attention to the scenic spots themselves and do not have excessive requirements on the number of hotels near the scenic spots. On the other hand, most tourists travel by self-driving or group tours. The reception level of most hotels is not high, and many tourists do not choose to stay near scenic spots. There are many tourist attractions in Qiandongnan Prefecture involved in this study, and tickets are not charged. Tourists seldom give up visiting the famous attractions that must be “checked in” because of expensive ticket prices, so the influence of ticket prices is relatively weak.

5. Discussion

Tourism flow is a current research hotspot. The analysis of tourism flow networks in typical regions can enrich the research of tourism geography and also provide practical guidance for the rapid development of tourism. This study aimed to explore the network structure characteristics of tourism flows in Qiandongnan Prefecture from the perspective of social networks and identify the factors affecting the structure characteristics by using the data information from online travel blogs.

First, unlike the previous literature that uses panel data or distributes questionnaires to obtain sampling data [14,16], this study used travel blogs shared by tourists on social media as a data source. Travel blog data are easy to collect and have a large sample size. By using these data, researchers can obtain tourists’ trajectories and accurately grasp the spatial structure of the tourism flow network.

Secondly, the results show that there are obvious deficiencies in tourism marketing. The significant difference between the tourist attractions promoted by the government and the tourist attractions that tourists prefer to visit indicates a bias in the government’s marketing strategy. Several studies also identified deficiencies in government marketing of tourism [56,57]. In particular, rural tourism is different from urban tourism. Tourists are mostly unaware of rural tourist attractions, which increases the need for tourism marketing to play a role.

Third, there are seasonal fluctuations in tourist flows in terms of travel time. There are more tourists in summer, which is consistent with the findings of Liu et al. [58] and Ahas et al. [59]. In fact, the influence of seasonal factors has become a major obstacle that seriously restricts the sustainable development of rural tourism [60]. On the one hand, the natural resource landscape of rural tourism varies greatly due to seasonal changes; on the other hand, there is a temporal concentration of rural tourism resources with folklore festivals as the main brand. Therefore, extending the peak tourism season as much as possible and reducing the adverse effects caused by seasonal fluctuations have become important ways to crack the rural tourism dilemma.

Fourth, the analysis of the tourism flow network structure reveals that the tourism flow network structure of Qiandongnan Prefecture is low in closeness and has a strong imbalance. The connections between tourist attractions are relatively sparse. In a previous study, Mou et al. [31] found that the regional development of tourism in Qingdao is unbalanced, and tourists are mostly concentrated in the east coast area. The findings are similar to the results of this study. Therefore, establishing how to deal with the unbalanced development of different tourist attractions correctly is particularly important for the future development of tourism.

Finally, through analysis of influencing factors, it was found that the influencing factors of tourism flow in rural areas are different from those in cities. For example, the study of Zhao and Liu [61] found that the structure of Beijing’s tourism flow network is not affected by the attention of the scenic spot network, while we found that the result of Qiandongnan Prefecture is the opposite. The reason may be that tourists are relatively familiar with the scenic spots in the famous tourist city of Beijing, while most of the scenic spots in Qiandongnan Prefecture are less well-known. Tourists need to use the Internet to obtain information about scenic spots. This proves that the tourism flow in ethnic rural areas has its own characteristics and is different from tourist cities. Therefore, we believe that tourist attractions in rural areas can be optimized according to their own characteristics.

In summary, these findings provide a theoretical basis for building tourism facilities in rural areas and provide practical insights for local governments to formulate sound policies. First, local governments can set up visitor feedback channels on official websites and publicity platforms to collect visitor suggestions. According to the statistical data such as passenger flow, the more attractive attractions can be introduced and recommended in a comprehensive manner. Second, diversified tourism products with distinctive characteristics are developed to meet the needs of different seasons and to improve the rationalization of tourism resources. For example, tourism management can strengthen public service management during the peak tourism season. In the off-season, they can reduce the entrance fees and carry out cultural performances and activities with local characteristics to attract tourists. Finally, tourism promotion centers for attractions in peripheral areas can be established in core areas. Infrastructure construction can also be carried out in peripheral tourist attractions to improve accessibility and tourism services in order to solve the problem of uneven tourism development. In addition, a comparative analysis with the previous literature revealed that the methodology and results used in this study to examine tourism flow networks are applicable not only to the Qiandongnan Prefecture of China but also to multiple destinations. However, this needs to be verified by other scholars in future empirical studies.

6. Conclusions

This paper constructed a framework for studying rural tourism flow networks. By mining online travel blog data, social network analysis methods were applied to reveal the structural characteristics of tourism flow networks. QAP correlation and regression analysis methods were used to analyze the influencing factors of tourism flow networks. This paper verified the rationality of this research framework by taking Qiandongnan Prefecture as an example. The following conclusions are drawn:

(1) The key nodes of tourist arrivals differ greatly from those advertised by the government, reflecting a bias in official tourism marketing;

(2) There are seasonal fluctuations in tourist flow. There are more tourists in summer, but the attractions visited by tourists do not change with the seasons. Rural tourism attractions should pay great attention to the promotion of off-season tourism products while fully creating tourism resources in peak seasons to promote the sustainable development of rural tourism;

(3) In the tourism flow network, the core nodes are unevenly distributed, and there are obvious structural voids. The tightness of the network structure is relatively low, and there are relatively few tourist routes. There is an obvious core–periphery structure in the network. Additionally, the core area has a weak driving effect on the peripheral areas, and there is less interaction between the core and peripheral areas. There are more cohesive groups in the network, but the closeness of ties among the cohesive groups varies greatly and is loose. This is common in rural tourism destinations. Efforts to narrow these differences and solve the problem of unbalanced and unsustainable development of tourist attractions are important ways to develop rural tourism and achieve rural revitalization in the future;

(4) In terms of influencing factors, geographic adjacency, traffic accessibility, and tourism resource endowment influence tourism flow network structure. Tourist attractions in rural areas can refer to the above influencing factors for construction. For example, tourist attractions develop tourism products in depth according to their own resources, create unique tourism resources according to their own characteristics, and improve traffic accessibility and tourism service level.

In conclusion, the research framework of this paper is feasible and can comprehensively capture the characteristics and development of tourism flow in rural areas from individual nodes to the whole network. The framework can be applied to other rural areas. It can also provide reasonable guidance and suggestions for tourism planning, infrastructure planning, and scientific development of tourism in rural areas. Ultimately, it promotes the sustainable development of rural areas and realizes rural revitalization.

However, this work also has several limitations. First, there is less information extracted from online travel blogs. It is impossible to analyze the characteristics of tourists’ ages, occupations, and so on. Moreover, some unpopular attractions are not included, which may be due to insufficient publicity or high travel costs. This also shows that there are certain deficiencies in the data. In future research, data will be further mined and combined with those from statistical yearbooks and official tourism data sources to improve their accuracy and comprehensiveness. Secondly, this article does not consider that the structure of the tourism flow network is a dynamically changing system and only analyzes its structural characteristics from a static perspective based on online travel blogs. Therefore, in further research, we will consider dynamic tourism flow that changes over time. In addition, tourism flow is affected by both subjective wills and objective conditions. This paper only constructs an indicator system from objective conditions without considering the tourists’ subjective wills. Future research will use online travel blogs’ text information and questionnaire surveys to investigate the influence of tourists’ subjective wills.