3.1. Analysis of Multiphysics Simulations
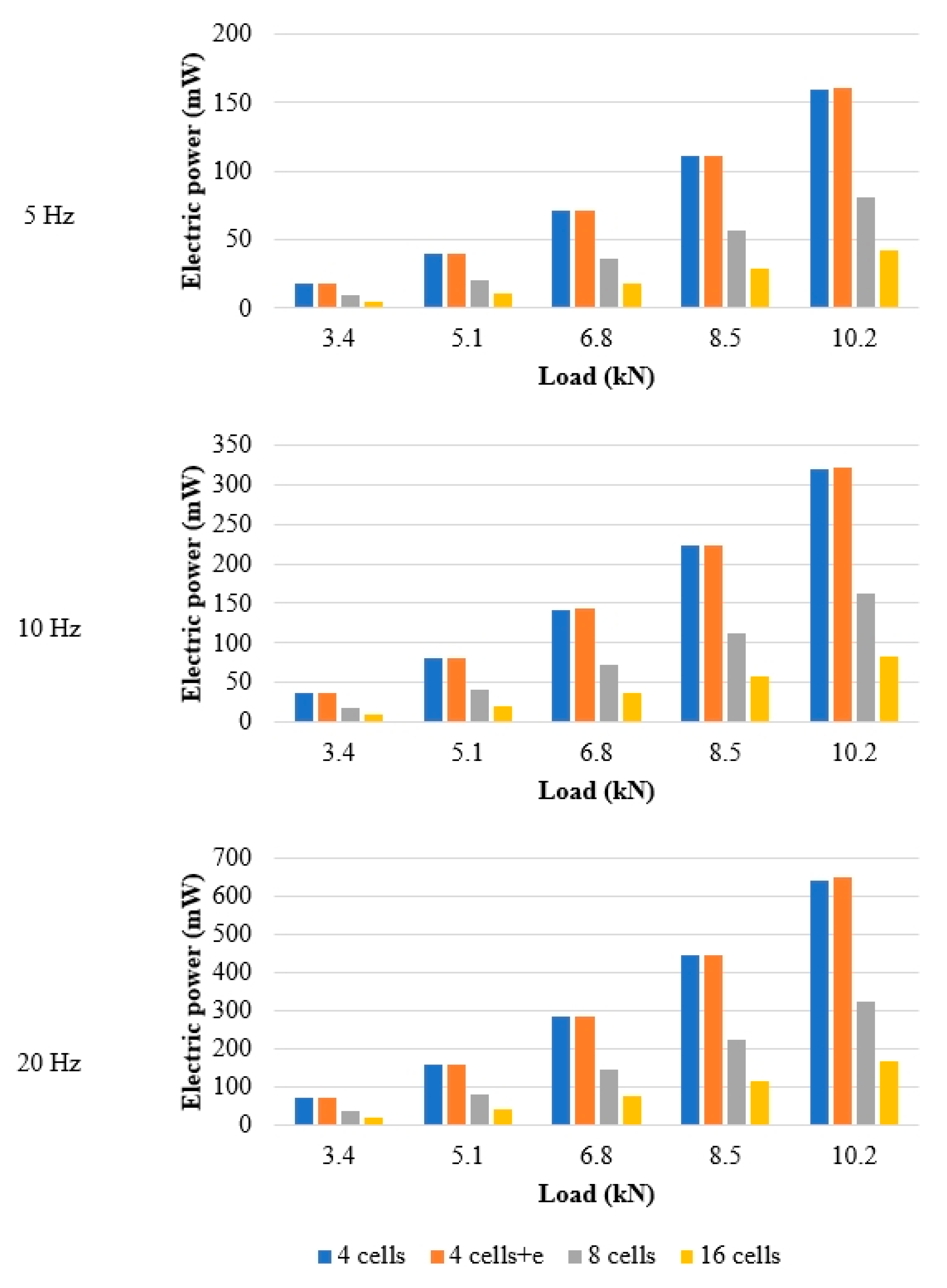
The first stage was performed by applying forces of 3.4 kN, 5.1 kN, 6.8 kN, 8.5 kN, and 10.2 kN according to the number of cells and the frequency values of 5 Hz, 10 Hz, and 20 Hz. The results obtained were plotted in
Figure 4. The power values were obtained for the internal resistance corresponding to each frequency and cell combination, as in
Table 3, and previously presented in
Section 2.1.2. The resistances adopted were calculated in such a way that it would be possible to return to the maximum power values for each frequency combination and number of cells. The group of the four most widely spaced cells was represented by “+e”.
In view of the values presented in
Figure 4, it was observed that the power generated decreases with the increase in the number of cells applied. This occurs as the applied force distributes itself equally over a wider area of piezoelectric cells. However, this decrease in electric power does not occur proportionally. When compared to the four-cell arrangement, the combinations of eight and sixteen cells produced a reduction of the electric potential by an average of 49% and 74%, respectively.
Another important observation is related to the spacing of the piezoelectric cells. Two positioning configurations were tested for the group of four piezoelectrics and the cell arrangement with wider spaces between cells generated slightly higher power outputs. This is an average increase of 0.39% over the configuration with cells closer together. This increase in power happens because the piezoelectric effect of a cell interferes less with the behavior of the others around it.
The interference between the piezoelectric effect of the cells occurs due to the magnetic field between them. When they move closer together, the effect of one interferes with the effect of the other. However, it was observed that the stiffness of the asphalt mixture contributes to decreasing the difference in electrical output when the spacing is varied.
About the power values obtained with the optimized results of the resistance, the highest value obtained was 10.2 kN and 20 Hz with four more widely spaced cells, resulting in 648.8 mW. Following the same trend, the lowest value obtained was 3.4 kN and 5 Hz with sixteen cells producing 4.7 mW. Thus, it was found that the power increases directly with the increase of load and frequency. However, it falls with the increase in the number of cells.
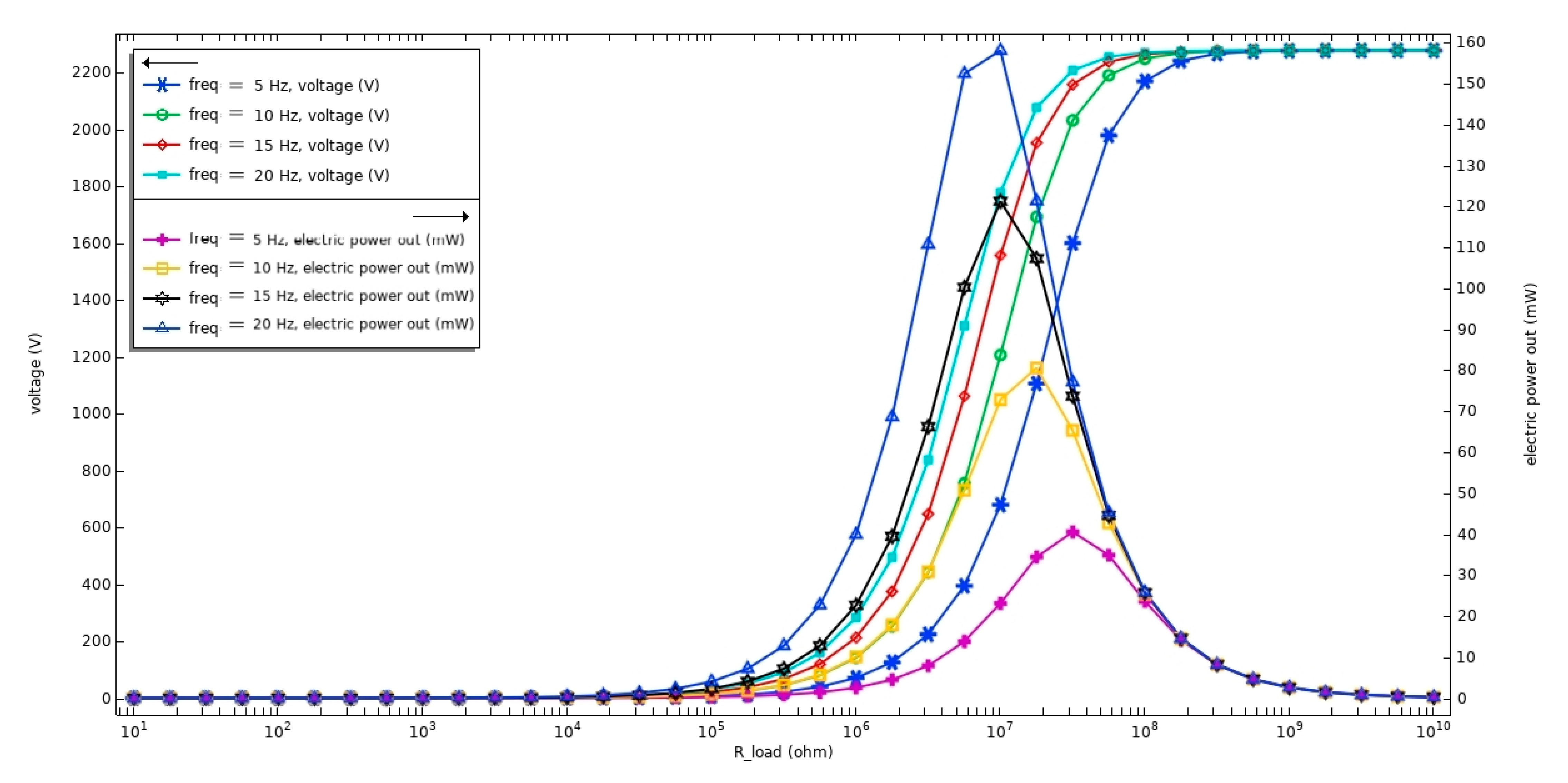
Furthermore, the power and the maximum electric voltage obtained from the variation of resistance in the x-axis were simulated, fixing the frequency and the load.
Figure 5 shows this variation for the force of 10.2 kN with four more widely spaced cells. The same behavior pattern is observed for the rest of the force and cell combinations.
The electric power demonstrated is dependent on variables such as the frequency (or speed of the vehicle) of application, applied load, electric resistance, and the number of cells that relate to each other. The relationship of dependence on more than one variable precludes a simpler analysis. However, it is possible to assert, based on the Multiphysics analysis provided by the software, that the higher the load and frequency variables, the better the results for the electric power obtained.
On the other hand, when the number of cells is increased, the electric generation of the prototype is reduced, since the stress applied on the top of the specimen is equally distributed over a larger area, meaning each piezoelectric cell receives a smaller load. The results are consistent with what has been observed by some studies in the area [
4,
13,
17,
18,
28,
29,
30]. The difference was noted concerning cell spacing responses. In the reported studies, different stiffnesses of the asphalt mixtures were not studied. In this analysis, the replacement of the initially used asphalt mix with another paving material with a 300 MPa resilient modulus was simulated. Thus, it was realized that a greater spacing between the piezoelectric cells would not cause a percentage difference in the electrical response for stiffer materials.
Another factor that contributes to the decrease of electric power is the electric resistance of the prototype. When the number of cells is increased, the electric resistance of the prototype is decreased, caused by the inverse relationship with the capacitance, demonstrated by Equation (3).
Based on the power value behavior with the variations aforementioned, 12 equations were derived to obtain the electric power from the application of different loads, fixing the other variables.
Table 9 shows the equations created (14 to 25), in which L is the load applied (in kN) and y is the electric power generated. The results of R² were equal to 1.0 due to this being the optimal situation for obtaining the electrical output, represented by the values of external resistance equal to the internal resistance. These resistances were calculated as presented previously in
Table 3.
The equations presented in
Table 8 have a limitation. They are valid only for the specified quantities of cells and internal resistances. However, the authors recognize the need to formulate equations that cover all the variables involved (loads, frequencies, resistances, number of cells, and spacing). This may be possible by deriving constitutive models and introducing artificial intelligence methods to verify the influence of each variable on the output.
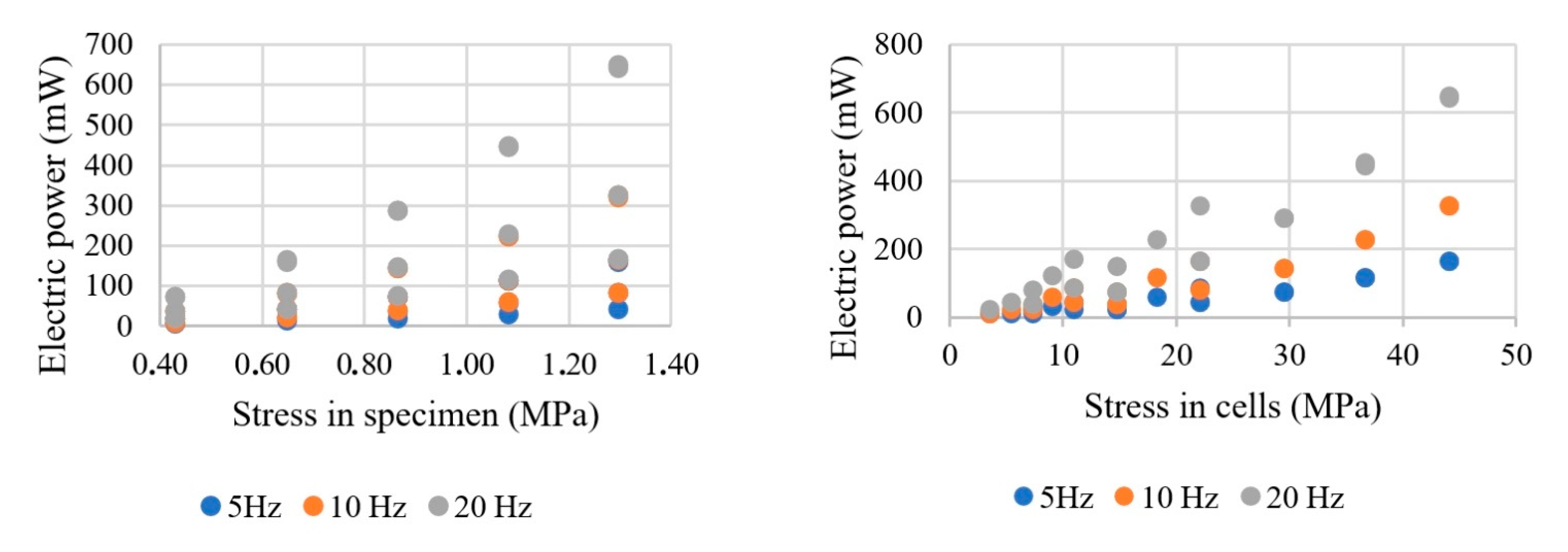
It is possible to analyze the power results based on the stresses applied. Once again, the forces were limited to 10.2 kN. However, when applied to the area of the AC specimen, stresses that vary from 0.43 MPa to 1.30 MPa were obtained. The tire pressure varies between 0.15 MPa to 0.70 MPa on the pavement [
38,
39]. When these same forces are distributed across the area of the piezoelectric cells, stresses varied from 3.96 MPa to 44.31 MPa-
Table 2.
Figure 6 displays the electric responses according to the stresses exerted over the entire area of the cells and of the specimen, respectively.
The results allow us to record the electric power produced by the system from the application of all stresses on the pavement. These values ranged from 4.7 mW for 5 Hz and 0.43 MPa to 648.8 mW for 20 Hz and 1.30 MPa, with sixteen and four+e cells, respectively. Thus, the mechanical stresses to which the prototype was subjected comprise a percentage of the reference range and superior values, mainly when the whole area of the cells is considered. That analysis allows us to measure the effect of overloaded vehicles traveling on the road and to verify the mechanical resistance of the piezoelectric element. Higher stress values, such as 1.30 MPa in the specimen, would still be supported by the elements, which did not fracture.
3.2. Laboratory Tests
The laboratory tests were performed according to the material and methods section and with the limitations discussed. The results were presented according to the changes in variables, such as load, frequency, number of cells, and spacing.
Figure 7 shows the power numbers according to the load applied for each cell situation with frequencies of 5 Hz, 10 Hz, and 20 Hz, respectively.
According to
Figure 7, it is possible to observe the variation in power, given the different combinations of piezoelectric elements. Considering the limitations coming from not controlling the electric resistance and the irregularities of the copper board, the prototype with eight cells yielded the highest electric power generation. The combination of four widely spaced cells (four cells+e) was the second-ranking combination in terms of electric response, except for the last three force levels at 20 Hz, at which point this combination was slightly outperformed by the standard four-cell and sixteen-cell combination.
As in the simulation stage, the equations were created to obtain the electric power according to the load variation. The electrical resistance and frequency values were fixed for the prototype configuration situations.
Table 10 shows the equations obtained from the laboratory tests, in which L is the load applied (in kN) and y is the electric power generated. The resistance was obtained through the values of electric current and voltage captured by the multimeter. The constant of Equation (28) is high due to the high numbers of power obtained for this situation, which is the closest to the results observed in the Multiphysics simulations stage.
As for the setup with four cells, the highest value for electric power is obtained for the situation of applying 10.2 kN and 20 Hz, returning to 47.53 mW, in which each piezoelectric cell is responsible for generating up to 11.88 mW. The electric resistances vary from 0.39 kΩ to 0.77 kΩ, resulting in an average of 0.49 kΩ.
Along with 4 more widely spaced cells the highest electric power obtained was 33.47 mW for the situation of 20 Hz and 10.2 kN, in which each piezoelectric cell generates 8.37 mW. The results for these electric resistances are almost double those found in the four-cell layout. The values vary from 0.65 kΩ to 1.07 kΩ, resulting in an average of 0.91 kΩ, an increase of 46% when compared to the four cells.
For each situation of eight cells, it is interesting to highlight the fact that the electric power was six times higher on average than the four-cell arrangement and four times more than the widely spaced cells (for 20 Hz and 10.20 kN: four cells returned 47.53 mW, four+e cells, 33.47 mW, and eight cells, 226.95 mW). This behavior was not expected, considering that there is an overlap of the piezoelectric effect and the dissipation of mechanical power to a larger area due to the sum of the eight elements. However, what justifies these higher values is the irregularity of the copper board. For the four piezoelectric cell layout, there is a lower probability that all the cells will be directly in contact with the copper board. When eight cells are used, the stability may be greater, meaning more elements are affected piezoelectrically. Nonetheless, the existence of more cells decreases the optimal electric resistance of the prototype. The external resistance equaled 0.75 kΩ, due to the impossibility of controlling it.
Another element that contributes to the obtaining of higher values in the laboratory stage for the combination of eight cells is the low rate of fracturing of the piezoelectric elements. During the 30 tests performed (15 for voltage and 15 for current), only 2 elements broke. For the arrangement with four wider spaced elements, the number of broken cells increased to eight, requiring substitution between the change of load levels and frequency applied. Thus, the best electric power was obtained with this layout, which generated 226.95 mW, each element producing 28.37 mW. When this is compared to the power values of the eight- and four-cell layouts, there was an increase of 377.5% when applying 20 Hz and 10.2 kN.
As expected, with sixteen cells, the electric response was lower than the combination of eight cells, representing a reduction of 69.5% in the power, applying 20 Hz, and 10.2 kN. This result is directly connected to the external resistance of the prototype; because it is not directly equal to the internal one, the layout generates different voltages, current, and power about the expected proportion since more elements are included. Moreover, since eight more piezoelectric cells were inserted, a reduction of approximately 50% was expected. Thus, the electric resistance varied between 0.81 kΩ and 1.79 kΩ, resulting in an average of 1.32 kΩ, the highest of all the combinations of tested cells.
To test the piezoelectric cell resistance, a load cell of 5.0 kN was applied with 0.1 mm of displacement steps, until reaching the stop limit of the software (approximately 4.9 kN) or until the element breakage. Thus, the equipment controller reached the stop limit, and the piezoelectric cell did not fail, reaching a stress of 46.23 MPa, superior to all of those simulated in the laboratory in the stage of electric response. This result is important to demonstrate that the piezoelectric cell is resistant and that the problem that occurred in the laboratory in the UTM-25 was due to the irregularities of the boards, distributing uneven stresses to the elements and causing them to break.
With the second step (laboratory tests), it was possible to relate the irregularity of the copper plates to the longitudinal irregularity of the pavement. At sites where there will be no direct contact of the vehicle wheel with the structure, a higher strain is exerted, causing the cells to fracture. It can also cause some cells to not operate in the system, decreasing the amount of energy generated. Thus, it is suggested that the prototype be applied to roads with low longitudinal irregularity (IRI).
From the laboratory tests, it was found that the uneven distribution of mechanical stress can result in early fracture of the piezoelectric elements, even though they have high compressive strength (greater than 46 MPa for the tested cell). This distribution also caused higher power values than those simulated in the software in the situation of eight cells and 20 Hz, even with low resistance and without control. This occurs due to the non-direct contact of the cells with the plate, reducing the number of them transforming the mechanical voltage into electrical voltage. This analysis was demonstrated by the Multiphysics simulations that fewer piezoelectric cells increase the electrical power values.
Despite the limitations caused by unavailable equipment, such as the oscilloscope and a resistance box and flat copper boards, the laboratory results followed the same behavior pattern when compared to the load and frequency applied. The greatest difference is related to the electric power obtained from the number of cells. It was expected that the increase in the number of piezoelectric elements would reduce the electric power and voltage.
However, in the laboratory stage, the best results were observed in the application of eight piezoelectric cells, resulting in a power of 226.95 mW for 20 Hz and with 10.2 kN of load applied. When it was possible to observe the maximum electric power obtained for the same combination in the stage of the computer simulation, we expected to obtain 324.40 mW. The reduction, in this case, was 30%, which is considered low when the difference between the resistances is analyzed, which is 0.81 kΩ in the test phase in UTM-25, and 3.5615 MΩ, calculated by using Equation (3) with optimal resistance. This resistance reduction is equivalent to 99.98%.
Another important observation is related to the increase of power with the variation of the space between the piezoelectric cells. For the computer simulation stage, a larger space between the piezoelectric elements represented an average increase of 0.39% in electric power. However, in the laboratory stage, this average increase was 30%, even after considering that the last three applications of force for the frequency of 20 Hz resulted in greater power for the layout with four cells.
In the Multiphysics simulations, the combination of more widely spaced cells resulted in the highest levels of harvested energy, reaching a response of 648.80 mW for 20 Hz and 10.2 kN. When the same application is compared to the laboratory test, the value obtained was 33.47 mW, which is a reduction of 94.84%. Again, it is worth noting that this difference is directly related to the electric resistance, which, for the computer simulation, had an optimum of 7.1230 MΩ, and in the laboratory, only 0.99 kΩ was obtained, which is a reduction of 99.99%.
While varying the frequency of 5 Hz to 10 Hz in the computer simulation stage, there was an average increase of 72%, 167%, and 249% in the electric power for the three ranges of resistance simulated in each frequency and combination of cells from largest to smallest, respectively. When the same interval was analyzed in the laboratory stage, the increase was 44% on average. This percentage rose above 72% only with the application of four cells and eight cells, representing 89.20% and 75.80%, respectively.
By performing the same analysis of the variation from 5 Hz to 20 Hz in the simulation stage, an average increase of 110%, 359%, and 832% occurred for the same ranges of resistance. In the laboratory, this increase was an average of 3450.00%, mainly due to the differentiation of the curve of 20 Hz about the other.
As far as the frequency variation is concerned, ranging from 10 Hz to 20 Hz resulted in an increase of 22%, 72%, and 167% in the harvested energy for the same resistances in descending order. The results obtained in the UTM-25 demonstrated an average increase of 2256.00% in the power value for the duplication of the frequency adopted.
It is therefore possible to observe that for the four-cell and four widely spaced cell arrangements, the reduction was around 97%. It was noticeable that the decrease was less for the frequency of 20 Hz. In the layout with sixteen cells, the percentage difference also decreases with the increase in force applied. At the other frequencies, this behavior can also be observed. However, it does not occur proportionally, as there is some inference. It was also possible to observe that the curves presented a similar behavior, mainly in the 20 Hz curve, which had an exponential trend. As for the combination of eight cells, the results showed an inverse behavior. The percentage difference increased with the growth of the force applied. However, results were lower when compared to the other three situations.
As for the 20 Hz frequency, the lowest difference was obtained with the application of 8.5 kN, resulting in a reduction of 15.86%. Thus, positive results were obtained for loads of 3.4 kN, 5.1 kN, and 6.8 kN, which shows that power values were being obtained above the optimal ones found by the software. This can occur because even if the same load is applied to the specimen, this force might be unevenly distributed to the piezoelectric cells, resulting in higher stresses and, thus, increasing the voltage and the electric power as a consequence.
It is worth noting that, despite the high percentage differences, the power and electric voltage values follow the same behavior as those obtained from the computer simulation, which allows us to compare them, even though they present different electric resistances. This problem would be solved with the use of a resistance box to equalize the internal and external resistances, the assistance of an oscilloscope to measure the voltage, and flat copper boards for even contact with the piezoelectric cell.
The results demonstrate that the electric piezoelectric prototype will respond effectively and efficiently to situations where the road speed is as high as possible, while considering issues related to road safety and for higher load applications such as trucks. Additionally, by controlling the electrical resistance, it becomes possible to obtain the optimum power values for any load application situation. In the
supplementary material all the data obtained in the laboratory tests and the comparisons with the computer simulations were made available, from
Tables S1–S6 and Figure S1.
3.3. Simulation of Energy Production
It was possible to determine the ideal combination to apply in the prototype in the field through a comparative analysis. At this stage, the real-life application scenario was decided according to the Multiphysics simulation. The pavement of the BR-222 highway had small or insignificant longitudinal irregularity and the electric resistance was controlled by resistance boxes inserted close to the edge of the road. The resistance adopted was the one that yielded the highest energy values in the 10 Hz simulation, given the enforced speed limit of 60 km/h.
The prototypes were inserted 5 cm beneath the top coating layer, i.e., between it and the binder course. The copper boards did not have any irregularities, providing even contact with the piezoelectric cells.
Considering the dimensions (10 × 10 cm) of the prototype, it was installed in the average contact location of the tire/pavement, spaced evenly, 10 cm apart. In order to perform a maximum simulation, it was established that at least one wheel of all the vehicles would pass over each of the prototypes installed on the road. Thus, for a 1 km length of the road, 10,000 prototypes would be installed, 5000 on each side of the road.
As per
Section 2.3, the traffic considered was 296 vehicles per hour of passenger cars with wheel load equal to 1.98 kN, and 47 vehicles per hour of two-axle bus and truck types with wheel loads equal to 24.50 kN. The total traffic was allocated 50% for each direction with all vehicles traveling at the enforced speed of 60 km/h.
Therefore, for this case, the four more widely spaced cell layout was used with the frequency of 10 Hz and resistance of 14.2460 MΩ. Thus, the electric power would be obtained by Equation (12) (y = 3.1061 × L
1.9977), in which L is the load applied. The entire load of the car wheels was transmitted to the piezoelectric elements. For trucks and buses, which have a tire contact area of approximately 355 cm
2, we performed a ratio of absorption of the energy generated by the prototype equal to 28.17% of the load applied, given the copper boards had an area of 100 cm
2.
Table 11 presents the power obtained for the simulated situation at this stage.
If 10,000 prototypes were applied on the road, in one year it would be possible to generate up to 918.76 MWh, which is 76.56 MWh per month. In 2021, the average monthly electric energy consumption in the Brazilian northeast region was 125.20 kWh per household [
44], which means that the energy harvested from 1 km of the road would be able to supply up to 611 residences. The number of residences (NR) was calculated from the average consumption of electricity in the state of Ceará, Brazil. It was obtained from the application of the accumulated monthly energy values, derived from the vehicle traffic in
Table 8 and the results of
Table 11 in relation to the mentioned monthly electric consumption Equation (32).