Cantilever Soldier Pile Design: The Multiobjective Optimization of Cost and CO₂ Emission via Pareto Front Analysis

Abstract

In the context of this study, it is focused on the design of cantilever soldier piles under the concept of Pareto optimality with multiobjective analyses of cost and CO₂ emission considering the change in the excavation depth, the shear strength parameters of the foundation soil strata, and the unit costs and unit emission amounts of structural materials. Considering this aim, the harmony search algorithm was used as a tool to achieve the integrated effects of the solution variants. The lateral response of the soil mass was determined based on the active Rankine earth pressure theory and the design process was shaped according to the beams on the elastic foundation soil assumption. Moreover, the specification envisaged by the American Concrete Institute (ACI 318-11) was used to control the structural requirements of the design. Pareto front graphs and also design charts were created to achieve the eco- and cost optimization, simultaneously, for the design with arbitrarily selected cases to compare the results of the multiobjective analysis to minimize both the cost and the CO₂ emission.

1. Introduction

Cantilever soldier piles (CSP) are frequently used structures to support the generated lateral thrust of soil mass through excavation works. CSPs can be penetrated into a wide range of soil strata, including layered stratification, in addition to easing the construction works by using special equipment that ensures reducing labor. The simple design process of laterally loaded supporting piles can be generally defined as the same as other classical-retaining-structures’ design process, which is starting with the calculation of activated lateral pressures through the wall surfaces to check the stability conditions based on the foreseen dimensions. This kind of process, referred to as proportioning, ensures the application of an iterative design process takes place where the sections are adjusted at the end of the calculations if needed [1]. Then, the calculations are followed by the implementation of structural necessities to assess structural design limits. Several studies have been performed to design CSP retaining systems depending on the determination of the lateral earth pressures along the pile length, which depend upon the soil’s geotechnical properties and the environmental conditions, analyzed using different kinds of techniques such as theoretical or experimental and so on. The single-soldier-pile walls are sometimes analyzed like sheet pile walls, although the structural components of both systems are different. In that condition, the selected type of the retaining system has to satisfy the force and moment equilibrium simultaneously [2]. Moreover, the free embedded cantilever walls are basically used to support relatively low heights of cohesionless soils. Traditionally, these kinds of walls are designed based on limit equilibrium analysis depending on the stress distribution along the wall. Sisson et al. [3] shaped a research study about the design of CSP retaining walls embedded in stiff clays and clay stones by taking into consideration the long-term loading conditions, the strength of the soil, and the method of analysis for design.

Wen-Ai and De-Ling [4] applied a different design process for CSP based on the principle of minimum potential energy. An analytic determination of the pile head’s maximum displacement was produced. The relationship between the design and the excavation depth was also investigated. Gajan [2] studied both sheet pile and soldier pile walls penetrated into cohesionless soils and used Rankine earth pressure theory to determine the lateral pressures activated for active and passive states. Relationships were developed to calculate the depth of embedment in terms of nondimensional parameters that can be used for various soil conditions, pile dimensions, and depths of excavation. Lee et al. [5] analyzed cantilever double-soldier-pile walls with a proposed model, including an equivalent single-soldier-pile system, and centrifuge model tests were conducted in the sand to measure the performance of the suggested study.

The reinforced concrete material is assumed to be the economical and safe choice for retaining the system design in most of the projects. This situation necessitates determining the reinforcing bars’ number and diameters to calculate the volume of the concrete that is needed to complete the whole design process. This necessity shows that the said sequential geotechnical and structural design process also creates the need to provide economic control. However, it can be seen from the actual literature sources that the conceptions of the design of the CSP and the economy of the structural system do not take into consideration an integrated view. Moreover, beginning from the 20th century, the huge increase in the amount of reinforced concrete throughout the world has begun, due to the unforeseen growth of sheltering and industrialization needs. Therefore, it has become significant to design structural systems in an eco-friendly manner to protect human life from the harmful effects of global warming. In this respect, construction materials made of both steel and concrete have caused carbon dioxide emissions, which increase global warming and have destructive effects on the environment.

The mentioned mixed relationship leads designers to use many discrete design variables for the solution of related cases. For this reason, generally, the practicability of optimization-based techniques means they are preferred to be used by designers to model structural design problems to ensure enough safety, cost efficiency, and eco-friendly solutions.

In structural design, optimization-based techniques usually use the power of computer science technologies to obtain ideal design values by generating random designs. Thuswise, the structure’s type is validated and automatically calculated, and afterward, the redefinition process of the design by conducting the process of the envisaged algorithm, which controls the process of iteration numbers through the investigation of the optimum, can be carried out [6]. Specifically, the advantage of metaheuristic algorithms, such as a genetic algorithm [7,8], harmony search algorithm [9,10], particle swarm optimization [11,12], and firefly algorithm [13,14], are preferred to be used to maintain the design analysis of retaining structures. Some of the conducted studies are focused on the optimal design of reinforced-concrete retaining structures depending on the minimization of only the cost. Sasidhar et al. [7] performed an optimization analysis for the design of cantilever retaining walls with different heights using a GA to compare the effectiveness of the method with traditional design predictions. The single-objective algorithms optimize scalar variables; in that case, the fitness function returns scalar values, and the algorithm finds the optimum solution to minimize a scalar variable.

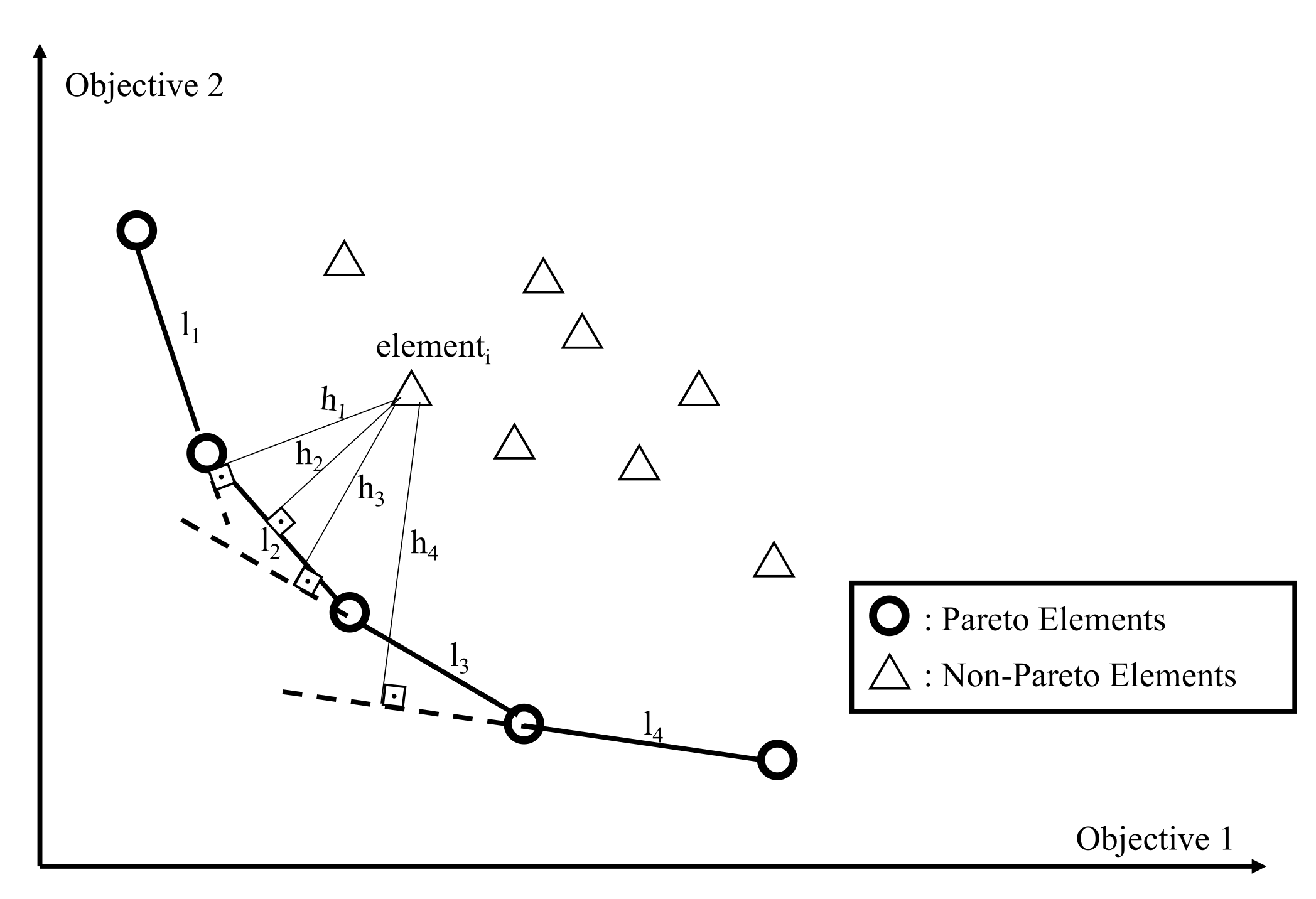
In multiobjective optimizations, Pareto optimality exhibits an opportunity to synchronize the optimality considering multiple objectives. In this sense, there are various studies on the civil engineering field by using multiobjective meta-heuristic algorithms. Especially in the energy modeling of a building, multiobjective algorithms have important practical outcomes. Wang et al. [15] applied the GA multiobjective optimization model to support green building designing. Another study about green building objects to minimizes energy consumption on the other hand thermal comfort is maximized [16]. In some studies such as [17], multiobjective GA is used along with building heat simulation software. In the study, optimum solutions were searched to satisfy minimum energy consumption with minimum cooling equipment.

According to the documented methods, cantilever soldier piles are not optimized for multiple objectives. In this study, the total cost and ultimate CO₂ emission values are simultaneously minimized by using multiobjective HS and GA algorithms. Moreover, investigations are conducted to measure the differentiation abilities of the design variants to achieve the sustainable design objective, such as the shear friction angle of the foundation soil strata, the unit costs of the construction materials, and the unit CO₂ emission values of the construction materials on the CSP wall design. Pareto-optimal solutions are obtained with the investigation of the trade-off relations among the design objectives. Moreover, comparative analyses are conducted to search for the effectiveness of the used algorithm on the Pareto-optimal analyses of CSP wall designs. As a result of the study, in light of the mentioned aims, design charts and tables are arranged to easily obtain an environmentally friendly and lower-cost design at the same time.

2. Design and Methodology

2.1. The Design of Cantilever Soldier Pile Walls

The geotechnical design of CSPs is subjected to the stability of the generated lateral earth pressures on both faces of the wall system [18,19]. A classical geometrical section of a single CSP is shown in Figure 1a. h is the depth of excavation, L_pnt is the depth of the penetration of the pile, ΣL illustrates the length of the pile that is determined by the sum of the excavation and penetration depths of the pile, and D is the diameter of the pile. Figure 1b illustrates the stress distribution along with both active and passive sides of the pile depending on beams on the elastic soil. In Figure 1b, q_a defines the surcharge loading that is converted to F_qa as a lateral surcharge force. In addition, F_sa and F_p define the lateral soil reaction forces generated in the active and passive states, respectively. Φ and γ represent the shear strength angle (friction angle) and the unit weight of the envisaged frictional soil strata, respectively.

Rankine earth pressure theory was used for the problem of determining the lateral earth pressures. The lateral active and passive earth coefficients are abbreviated by K_a and K_p, respectively (Equations (1) and (2)).

$$K_a=ta{n}^2\left(45-\frac{\varphi }{2}\right)$$

(1)

$$K_p=ta{n}^2\left(45+\frac{\varphi }{2}\right)$$

(2)

The stability of such a CSP wall results from to the activation of the lateral soil pressures along with both active and passive faces of the wall system [20]. Subjected to the beams on the elastic soil approach, the CSPs are assumed to locate tangents to constitute a continuous wall and the soil is described by a continuum of elastic media [1]. The depth of penetration and the location of the pivot point are only connected with the equilibrium of forces which exist throughout the penetrated length of the CSP. The flexural rigidity of the single pile is defined by EI and the characteristic length of the CSP is described by L₀. E represents the elasticity modulus and I is the inertia of the pile material. In Figure 1c, a single lateral force, F_0, and in Figure 1d, a moment M_0, is applied at the edge of the beam depending on the beams on the elastic soil approach. The change in the system deflection, rotation, bending moment, and shear force can be calculated with the use of Equations (3)–(6), respectively. The terms a_wp, a_wm, a_tp, a_tm, a_mp, a_mm, a_vp, and a_vm characterize the coefficients which refer to deflection, rotation, bending moment, and shear force, respectively, that were proposed by Celeb and Kumbasar [21].

$$w\left(x\right)=\frac{F_0{L}_0^3}{EI}{a}_{wp}\left(x\right) w\left(x\right)=\frac{M_0{L}_0^2}{EI}{a}_{wm}\left(x\right)$$

(3)

$$Q\left(x\right)=\frac{F_0{L}_0^2}{EI}{a}_{tp}\left(x\right) Q\left(x\right)=\frac{M_0{L}_0}{EI}{a}_{tm}\left(x\right)$$

(4)

$$M\left(x\right)=\frac{F_0{L}_0}{EI}{a}_{mp}\left(x\right) M\left(x\right)=\frac{M_0{L}_0}{EI}{a}_{mm}\left(x\right)$$

(5)

$$V\left(x\right)=F{a}_{vp}\left(x\right) V\left(x\right)=\frac{M_0}{L_0}{a}_{vm}\left(x\right)$$

(6)

Moreover, Equation (7) is given to determine the L₀ if the soil reaction coefficient k·(k = k₀·z) remains constant along the depth z. In addition, Equation (8) is preferred to be used in a case if the coefficient of soil reaction k·(k = k₀′z/D) is increasing linearly along with the depth. The length of the penetration of CSP is obtained mathematically by the multiplication of the characteristic length of the CSP with “π” to behave like a beam that is supported by an elastic soil stratum.

$$L_0^4=4EI/k$$

(7)

$$L_0^5=4EI/\left(k_0^{\prime }\right)$$

(8)

2.2. Multiobjective Optimal Design of Cantilever Soldier Piles

In this study, a multiobjective approach was used to design a CSP to obtain both optimized CO₂ emission and total cost values to reach a sustainable design. HS was used to control the minimization process of cost and CO₂ emission through the attainment of geotechnical stability conditions and the supplementation of structural design requirements. A multivariant analysis was also performed to compare the effects of design parameters on the design loop and the effectiveness of the algorithms. As a result, the applicability of the HS algorithm for Pareto-front analysis was controlled depending on the variants of the analysis.

2.2.1. Harmony Search Algorithm (HS)

In the context of this study, alongside the classical application of HS, a modified version for multiobjective optimizations is used. Figure 2 shows a detailed flowchart for the multiobjective HS algorithm procedures used in this study. The number of unknown parameters equals 3. The multiobjective HS starts with generating random harmony elements to constitute the initial harmony memory. The harmony memory size equals 100. Additionally, for each of these 100 elements, two fitness values are calculated according to Equation (9).

$${\left[f_{cost}\left(x\right), f_{C{O}_2}\left(x\right)\right]}^T={\left[C_{C,Cost}\times V_c+C_{S,Cost}\times W_s, C_{C,C{O}_2}\times V_c+C_{S,C{O}_2}\times W_S\right]}^T$$

(9)

In Equation (9), there are two single outputs as fitness values. These two values of total steel weight ($W_s$) and total concrete volume ($V_c$) are used for construction. Due to the difference in calculating these output values, the required coefficients are different. In the formulation for calculating $f_{cost}\left(x\right)$, $C_{c,cost}$ is the unit cost of concrete, $C_{s,cost}$ shows the cost value of unit steel production and calculating $f_{C{O}_2}\left(x\right)$; and $C_{C,C{O}_2}$ and $C_{S,C{O}_2}$ are the coefficients for unit concrete and steel production resulting in emitting CO₂ gas to the atmosphere. In the next step of HS, a distinctive harmony element is produced. HMCR and PAR parameters are used for generating a new harmony element similar to a single-objective HS. The HMCR value equals 0.7, and the PAR value equals 0.2. The main difference, in this case, is a distinct element is generated that is different from any harmony elements in the memory to eliminate dealing with duplicated elements. After the element is generated as a new harmony, fitness values are calculated for this new element. Generating the Pareto front is an additional procedure in multiobjective algorithms. As shown in Figure 3, Pareto front elements are dominant elements in the population taking into account whole objectives, i.e., in this study, an element in the Pareto front is cheaper and emits less CO₂ compared to every non-Pareto element. To determine the worst element in the harmony memory, distances from non-Pareto elements to the Pareto front are calculated. Figure 3 shows the Pareto front with line parts between Pareto elements. In addition, the curve of the Pareto front is divided into four parts of the lines. To calculate the distance from a non-Pareto element to the Pareto front, firstly, all perpendicular distances (i.e., h₁, h₂, h₃, and h₄ values in Figure 4) between these line parts $l_i$ (i.e., the line segments between Pareto elements in Figure 3) and the non-Pareto element are calculated. Then, the minimum value of these perpendicular distances is asserted as the distance from this non-Pareto element to the Pareto front. The element with a maximum distance to the Pareto front is labeled as the worst element in HM. The fitness function returns fitness values as a vector containing two elements, as shown in Equation (1). After the Pareto front is generated, the stop criterion is checked. In this study, the upper limit of the iteration number equals 10,000. If the total cycle count does not reach the upper limit, the HS continues. It may model the bases of the selection of iteration numbers by focusing on the study by Geem et al. [9], which shows that after 1095 iterations, the optimization finds the same solution.

In the next step, the new harmony is compared with the worst element in the HM to determine whether the new harmony element dominates the worst one, i.e., both fitness values of the new harmony’s fitness values are lower than the worst ones’ fitness values. The new harmony is replaced with this worst element. In the case of all elements located in the Pareto front, the new harmony is compared with these elements. If the new harmony dominates one of the harmony elements, the new one is replaced with this harmony element.

2.2.2. The Variables and the Constraints of the Cantilever Soldier Pile Design Problem

To solve the CSP wall design problem, three different parameters have to be identified. The diameter of the CSP (X1) is about the geometrical section dimension of the wall and the diameter of the reinforcing bars and the number of the reinforcing bars (X2, X3) form the variables of the reinforced concrete. These three variables of the CSP design are given in

Table 1. The parameters of CSP design.

Symbol	Parameter Description
X1	Diameter of the CSP (D)
X2	Diameter of the reinforcing bars of the CSP (ϕp)
X3	Number of the reinforcing bars of the CSP

with the abbreviations.

The necessities of the reinforced-concrete design are described considering the American Concrete Institute design code (ACI 318-05) [22]. The mentioned code proposes analyzing the case with the equivalent rectangular compressive distribution of stress. The use of the mentioned distribution allows the calculation of the moment capacity. The flexural moment of the soldier pile is abbreviated as Mu, the shear force is defined by Vu, the area of the reinforcing bars is identified by As, and the diameter of the reinforcing bars is abbreviated as ϕp. The constraints of the CSP wall design which are used in the solution of the algorithms are shown in

Table 2. Design constraints of the problem.

Description of the Constraints	Constraints
Flexural-strength capacities of critical sections (Md)	g1(X): Md ≥ Mu
Shear strength capacities of critical sections (Vd)	g2(X): Vd ≥ Vu
Minimum reinforcement areas of critical sections (Asmin)	g3(X): As ≥ Asmin
Maximum reinforcement areas of critical sections (Asmax)	g4(X): As ≤ Asmax

.

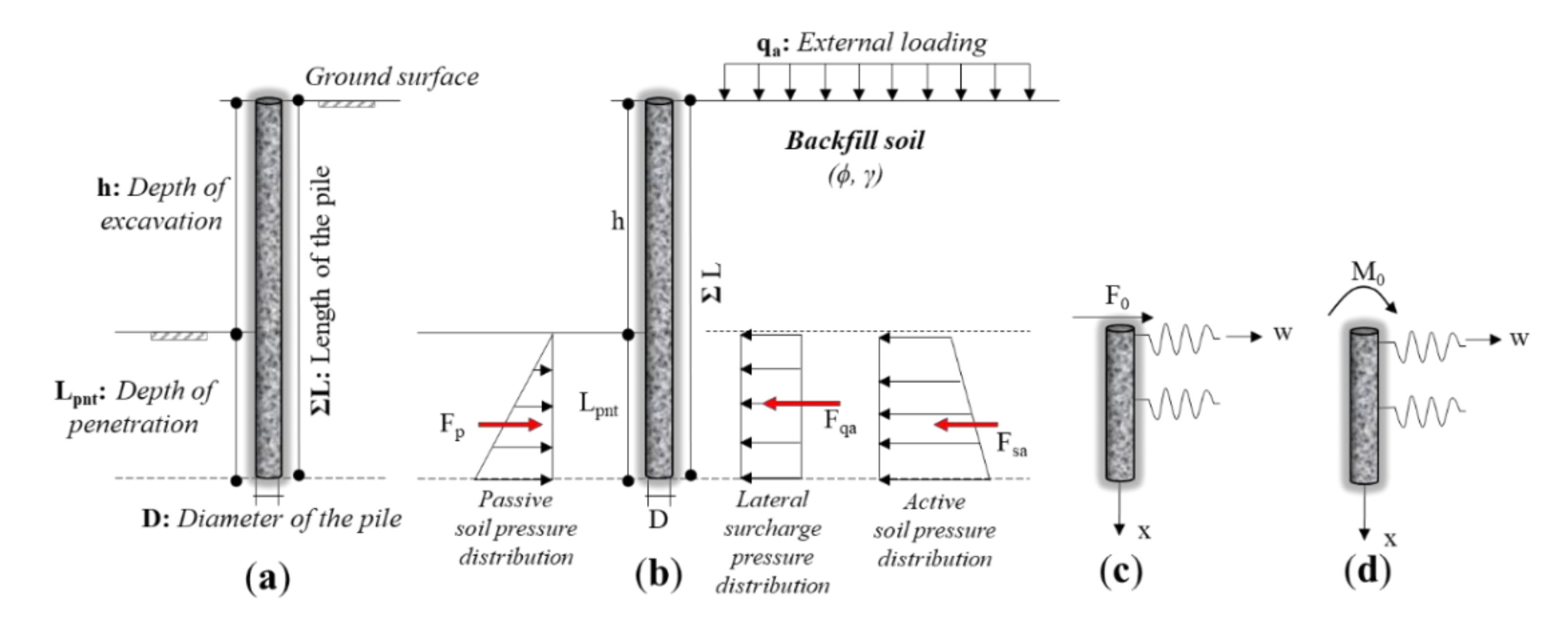
3. Parametrical Analysis

Multivariate parametrical analyses are conducted in this comparative study for exemplifying the optimal design process of CSP systems. It is assumed that the foundation soil is purely homogeneous frictional. Therefore, the design variants that concern the soil remain only the shear strength angle (ϕ) and the unit weight of the soil (γ). ϕ is assumed to be 20°, 25°, 30°, 35°, and 40°, respectively, but γ is taken as a constant 18 kN/m³. The analyses are also focused on the holistic solution of cost and CO₂ emission for different depths of excavation. The depth of excavations is selected beginning from 4 and reaching 12 m based on the construction limits defined in the national and international references [23,24]. The characteristic length of the CSP can be determined by the use of the Ks, which is assumed to be 200 MN/m³ in this study. The amount of the surcharge loading is assumed constant, at 10 kPa. The integrated alteration of relationships was investigated by the use of different unit costs and unit CO₂ emission values of the structural materials. The unit cost of the concrete per m³ was assumed as USD 50, 75, 100, 125, and 150, respectively, and the unit cost of the steel of the reinforcing bars per ton was defined as USD 700, 800, 900, 1000, and 1100, respectively. The constants and variables of the CSP wall design are also given in

Table 3. The variables and the constraints of the design.

Symbol	Definition	Value	Unit
h	Depth of excavation	4 to 12	m
fy	Yield strength of steel	420	MPa
f’c	Compressive strength of concrete	30	MPa
cc	Concrete cover	30	mm
Esteel	The elasticity modulus of steel	200	GPa
Econcrete	Elasticity modulus of concrete	23,5	GPa
γsteel	Unit weight of steel	7.85	t/m3
γconcrete	Unit weight of concrete	25	kN/m3
Cc	Cost of concrete per m3	50, 75, 100, 125, 150	USD
Cs	Cost of steel per ton	700, 800, 900, 1000, 1100	USD
q	Surcharge load	10	kPa
ϕ	Shear strength angle of soil	20, 25, 30, 35, 40	°
γ	Unit weight of soil	18	kN/m3
D	Diameter of pile	0.3–2	m
ϕp	Diameter of reinforcing bars of soldier pile	14–40	-
n	Number of reinforcing bars of soldier pile	6–20	-

. In addition, some cases are modeled with the assumption that the CO₂ emission values are selected to be different based on two different literature sources. Yeo and Potra [25] used 376 kg as the CO₂ emission amount of concrete and 352 kg as the CO₂ emission amount of steel for the recycled type of steel. Paya et al. [26] suggested using a CO₂ emission amount of steel of 3010 kg and a CO₂ emission amount of 143.48 kg for the concrete.

The chosen values of the CO₂ emissions approximately exhibit the upper and lower limits of the available values envisaged within the literature sources. These unit amounts of CO₂ emission values for both steel and concrete were used to arrange four different emission couples. The couples of CO₂ emission values are shown in

Table 4. Unit values of CO₂ emissions of concrete and steel.

The CO2 Emission Couples	Concrete (C30)	Steel (S420)
Couple 1 (C1)	376	352
Couple 2 (C2)	143.48	3010
Couple 3 (C3)	143.48	352
Couple 4 (C4)	376	3010

. Couple 3 represents the lower limits and couple 4 represents the upper limits of material emission values.

In total, in the context of the study, 4500 case analyses were fictionalized and 250,000 different solutions were searched depending on the huge variety in the design parameters. However, to reduce the informational convergence that can occur during the interpretation process of the outcomes of the analyses, some special cases were selected to explain the main theme of the study.

Figure 4 shows a pseudocode for generating the different cases to generate optimum design(s) regarding the related case. There are four different encapsulated loops that generate variations in conditions. The first loop generates different excavation depths. The second loop generates concrete and steel cost couples. C_c and C_s are concrete and steel cost prices, and a cost couple is picked in order from the 9th and 10th rows in Table 3. Different shear strength angles “ϕ” are selected by using the third loop. Additionally, in the last loop, each of the emission couples is selected in order from Table 4. By these loops, conditions are generated. For each condition, a Pareto front of optimum designs is obtained by using each genetic algorithm and harmony search algorithm. The term “Generate optimum results based on the condition” includes the whole optimization process (by using both GA and HS methods) that finds optimum pile designs under the related condition.

Figure 5 shows a Pareto front for the optimum designs for 7 m excavation depths. The other values are given at the right side of the graph. Each data point represents cost and CO₂ emission values of each design. These Pareto fronts for other conditions are obtained by applying loops in Figure 4. These values constitute a Pareto front given in figure which represents a trade-off between the cost and emission values.

4. Results and Discussions

For each iteration, a Pareto front of optimum solutions is obtained. For instance, Figure 6a,b include six different Pareto fronts regarding different excavation depths. The related condition is given on the upper-left side of the graphs. There is no possible optimum design for excavation depths larger than 9 m.

The output file is inserted into a spreadsheet file. By using a pivot table, whole data are filtered and can be directly viewed. After the graphs are generated, a curve-fitting tool is used for obtaining the optimum relationship between the output variables. Some special cases are envisaged to show the applicability of Pareto HS analyses have been used to discuss the assessment of the sustainable design of CSP via multiobjective Pareto front optimal analysis. The first type of analysis is conducted to compare the effects of selected amounts of the design variants. The relationships between the total cost and the ultimate CO₂ emission (Figure 6), the total length of the pile and the total cost (Figure 7), the diameter of the pile and the ultimate CO₂ emission (Figure 8), the total length of the pile and the diameter of the pile (Figure 9), the total cost and the diameter of the pile (Figure 10), and the total cost and the total length of the pile (Figure 11) are evaluated depending on the lower and upper limits of all the foreseen parameters of the whole design process. The Pareto fronts of these mentioned parameters were evaluated by performing regression analyses and proper design expressions are suggested depending upon the Pareto graphs.

Regression analyses are conducted with the use of Microsoft front analysis for the CSP design problem. The abbreviations a and b are used to define the arranged lower- and upper-limit conditions of the fictionalized cases. The lower- and upper-limit definitions can be described by the selected parameter specifications. The lower limit of the parameters is the smallest value of the design parameters. In such a case that if the application of the lower limits is admissible, the shear strength angle of the foundation soil is 20°, the unit costs of the concrete and steel are USD 50 and USD 700, respectively, and couple 3 is chosen as the unit emission values of the materials. However, on the contrary, if the application of the upper limits is admissible, the shear strength angle of the foundation soil is 35°, the unit costs of the concrete and steel are USD 150 and USD 1100, respectively, and couple 4 is chosen as the unit emission values of the materials. In Figure 6a,b, the relationship between ΣC and ΣE_CO2 is given against the change in excavation depth. All the axes of the graphs are fixed at special values to ease the comparison of the use of similar limits. The increase in the design parameters leads the analyses to scan more members in the Pareto sets and also enlarge the scanned range of the Pareto sets. The linear-curve-fitting option gives more accurate solutions for the lower limits of the design variables and, also, the polynomial-curve-fitting option gives more applicable results for the upper limits of the design variables to predict the relationship between ΣC and the ΣE_CO2. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.85 for both situations. This result strengthens the applicability of the given mathematical expressions for the design problem of CSP.

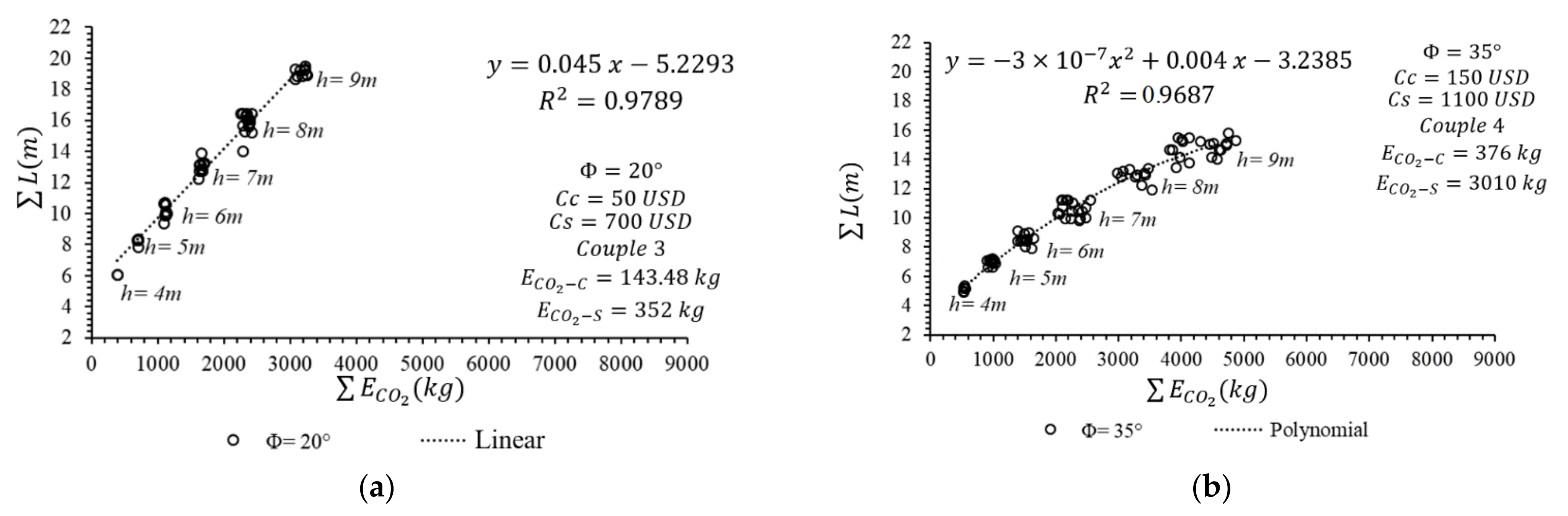
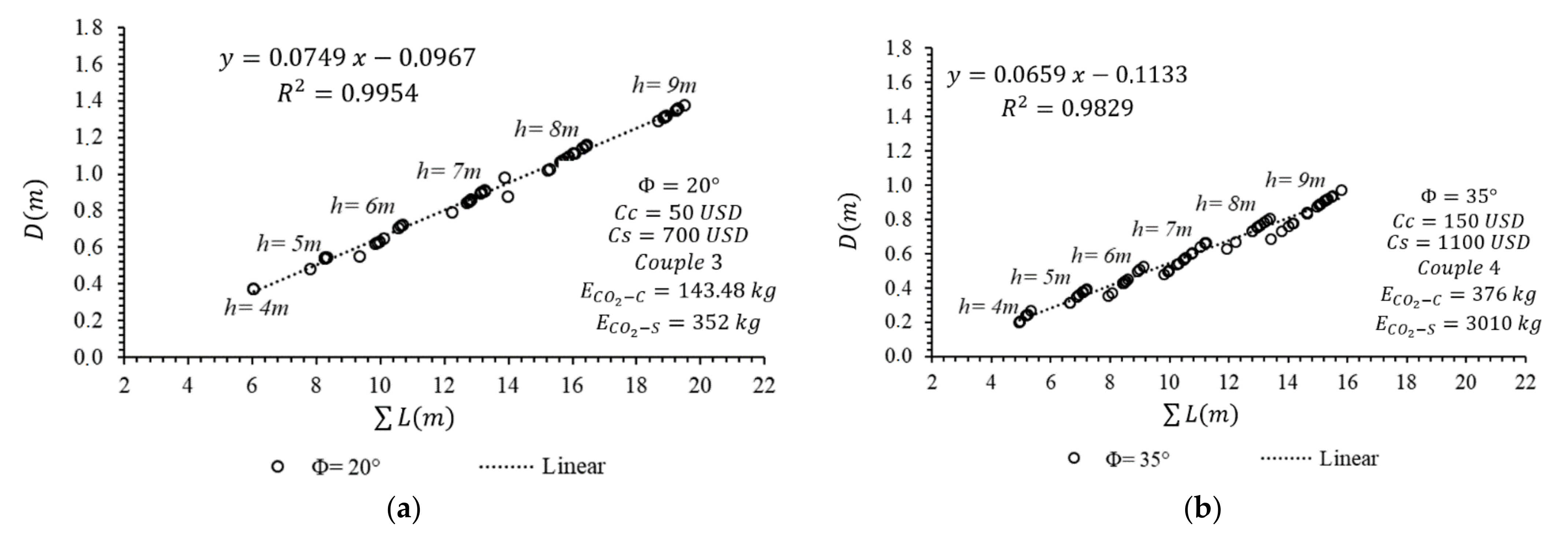
In Figure 7, the relationship between ΣL and ΣE_CO2 is investigated against the change in the excavation depth for both the lower and upper limits of the design variants. The exact solution for the expression of the relation between ΣL and ΣE_CO2 is derived with the use of the linear-curve-fitting and polynomial-curve-fitting options, respectively, for the lower and upper boundaries of the design variants. Similar to Figure 6b, the use of design parameters at the upper-limit values causes the Pareto data set to become dispersed and the number of data obtained to increase in Figure 7b. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.96 for both of the situations. This situation enables us to predict the ultimate CO₂ emission value directly from the total length of the pile with an admissible accuracy. Therefore, these mentioned simple Pareto expressions can make it possible to design eco-friendly structures when utilized. Herein, if the trend in the acquired relationships for both lower and upper limits is compared, it can be seen that these expressions are only valid for the envisaged conditions. The bigger the design parameters, the more difficult it is to reach the optimal design solutions. Therefore, in the context of this study, numerous relationships are derived in consideration of all the foreseen design variables. In addition, the applicability of the obtained mathematical expressions is controlled against the conducted regression analysis by the coefficient-of-determination values which are determined as approximately equal to or bigger than 0.85 at each time.

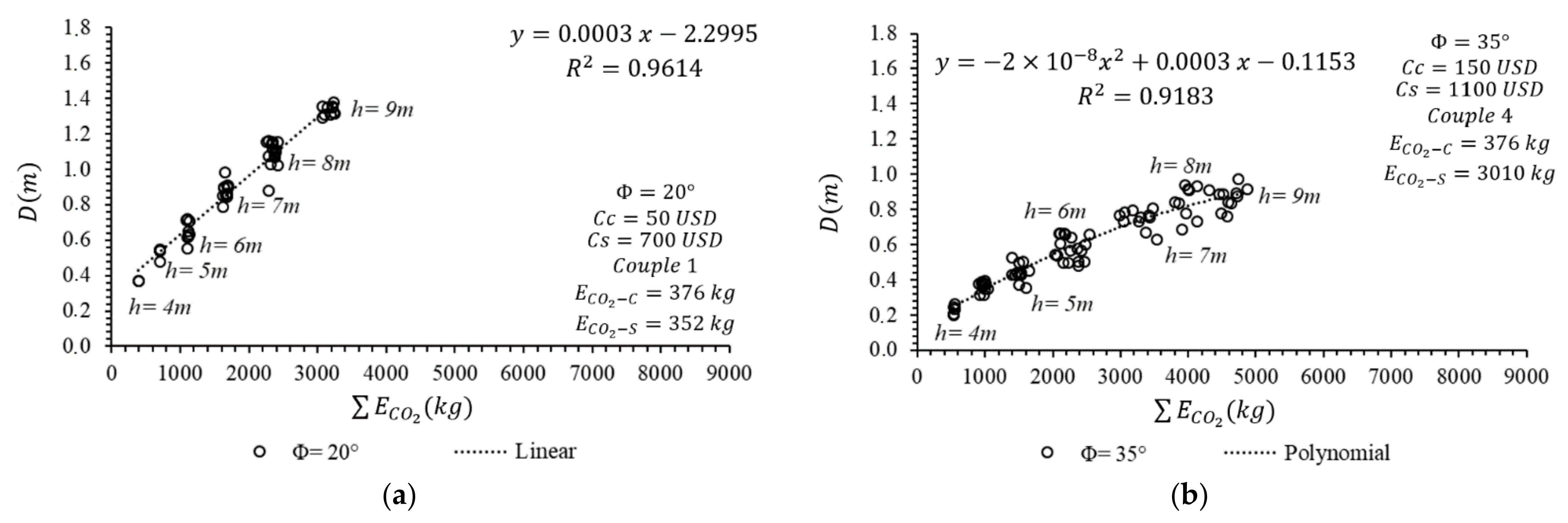
In Figure 8, the relationship between D and ΣE_CO2 is investigated against the change in the excavation depth for both the lower and upper limits of design variants. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.91 for both of the situations. These relations show that although the diameter of the pile seems to be a smaller dimension compared with the length of the pile, it has a direct effect on the emission of CO₂.

In Figure 8, the relationship between ΣL and D is investigated against the change in the excavation depth for both the lower and upper limits of design variants. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.98 for both of the situations. In Figure 9a,b, the Pareto-optimal dimensional design can be directly obtained by the use of linear relationships. These graphs can ease the sustainable design of CSP systems by using an integrated usage process with other derived expressions. In such a case, if there is a known shear strength angle of the foundation soil strata, the length of the pile can be expressed with a preadmitted diameter value. Moreover, this identification can be also related to Figure 8 to predict the ultimate CO₂ emission value and can be related to Figure 6 to predict the total cost value of the system. This process may be useful in the predesign stage to achieve both eco-friendly and cost-effective solutions. Moreover, Figure 9 is direct proof of the decrement in both the length and diameter of the pile depending on the increase in any design variant.

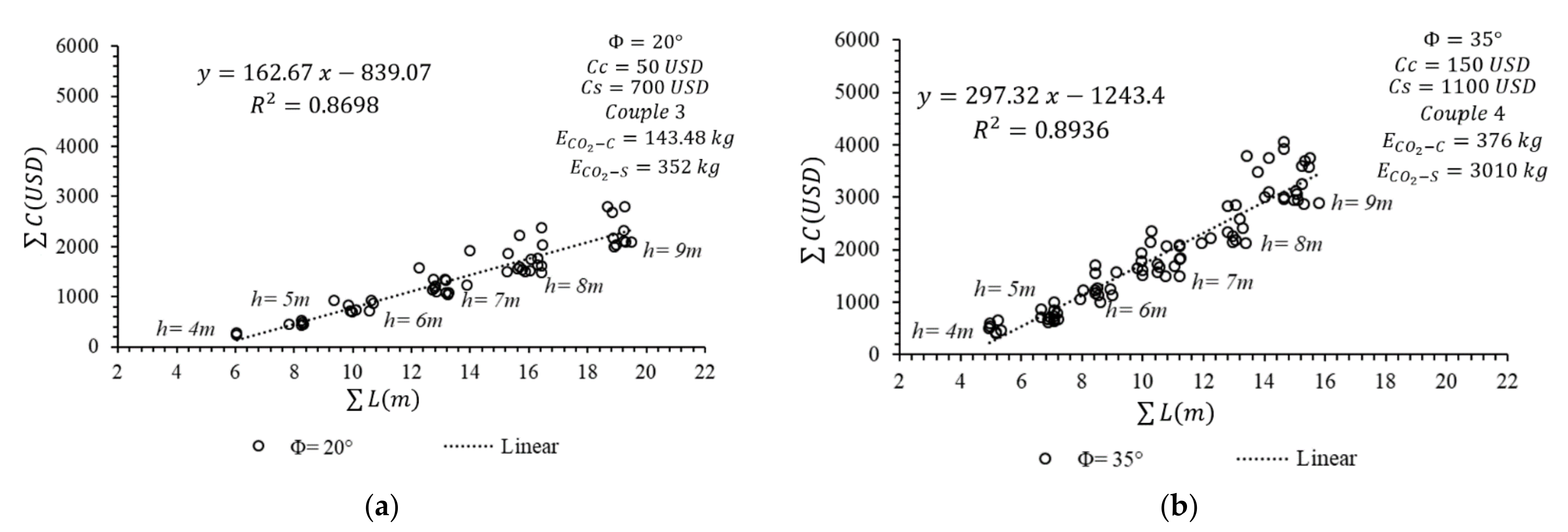
In Figure 10, the relationship between ΣC and D is investigated against the change in the excavation depth for both the lower and upper limits of design variants. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.84 for both of the situations. The Pareto of the ΣC and D relation can be described with a linear-curve-fitting option. However, a striking situation in these analyses is that if the design variables are accepted at the upper-limit values, the Pareto data set obtained for each depth is gradually spreading over a wider range.

In Figure 11, the relationship between ΣC and ΣL is investigated against the change in the excavation depth for both the lower and upper limits of the design variants. The coefficient of determination, denoted R², has been calculated as approximately bigger than 0.86 for both of the situations. In Figure 11, a relation like Figure 10 is obtained. The change in excavation depth leads to the spread of the Pareto data.

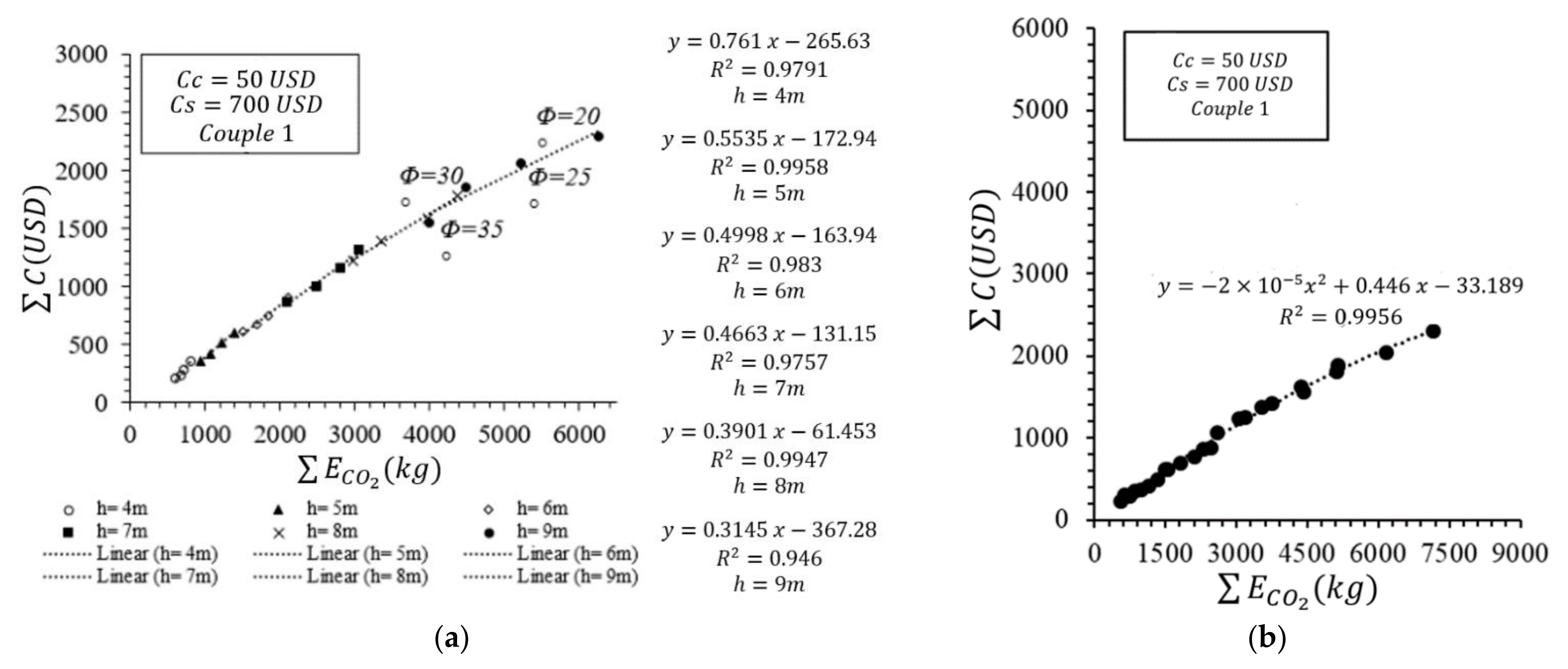
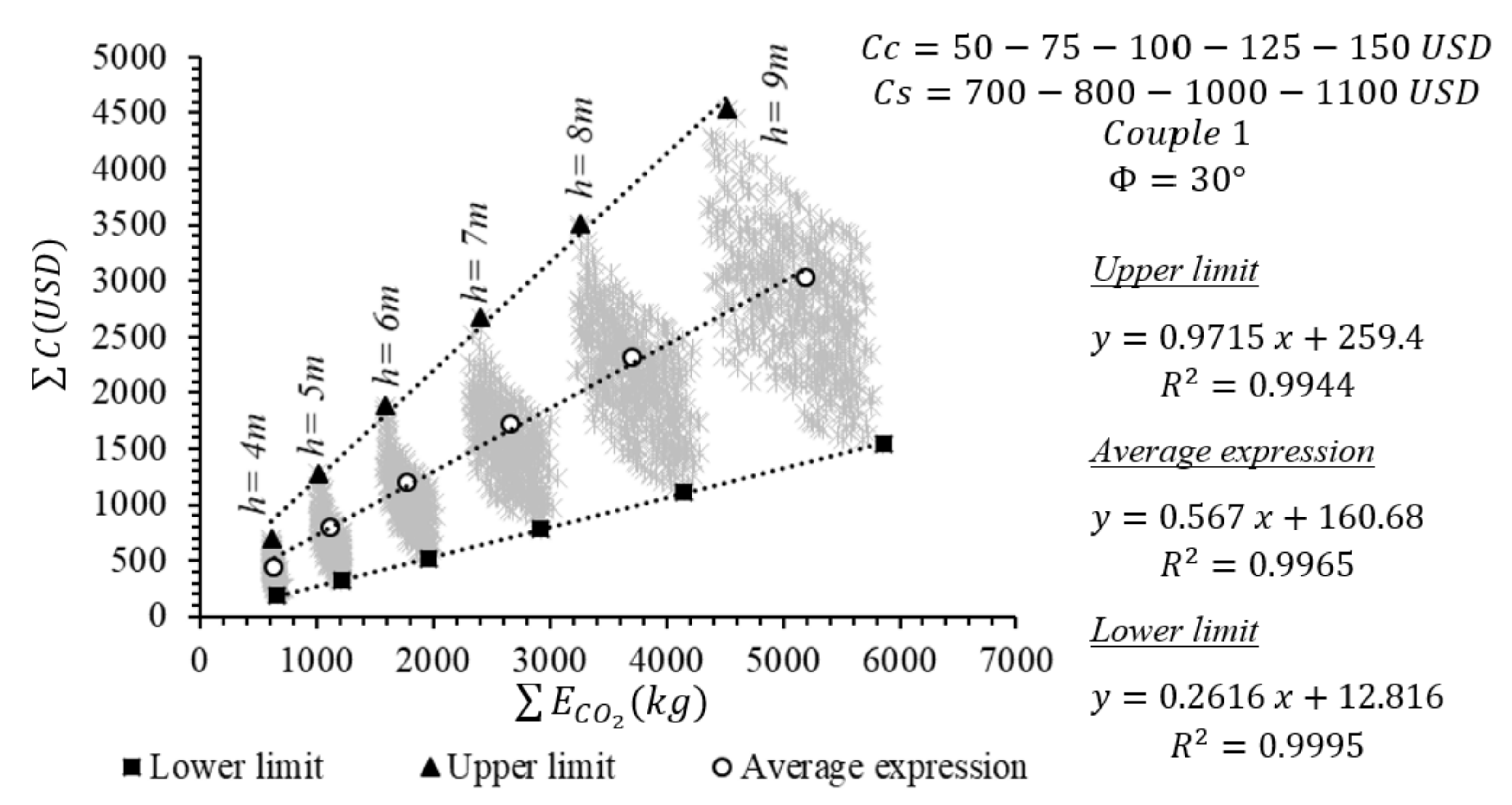
In addition to these evaluations, the effect of the change in the shear strength angle of the foundation soil was also investigated individually. The upper and lower boundaries of the design variants were also used, respectively, for the interpretation of the change in different CO₂ emission couples. In Figure 12, the emission couple 1 is taken into consideration and the lower limit of the unit costs is assumed to be used to search for the effect of the change in Φ. The Pareto graphs were drawn for the evaluation of ΣC and ΣE_CO2 against the change in excavation depths. In addition, representative mathematical expressions were obtained for each excavation depth (stated by “a” subdivision of the related figures) and a total expression was derived to represent all the excavation depths and shear-strength-angle changes (stated by “b” subdivision of the related figures). These Pareto graphs were obtained with the use of average values that were determined using the arithmetic means of the Pareto data to reduce the data densities. The change in the shear strength angles is exemplified in the graphs for only one representative excavation depth so as not to complicate the illustrations. As an example, the change in the Φ is shown in Figure 12a for only a 9 m excavation depth. As seen from Figure 12a, that linear relationship can be derived for every single excavation depth with a coefficient-of-determination value minimum of 0.95. Moreover, with the use of a polynomial function, a single integrated expression can state the ΣC and ΣE_CO2 relation for different depth and shear strength angles. In addition, the increase in the shear strength angle relatively decreases the total cost and ultimate emission values significantly.

Figure 13a,b represent the analyses conducted for the lower limits of the costs and the emission couple 2. The same logic is also used to specify the average Pareto points in Figure 13 as above mentioned. The coefficient-of-determination values (minimum 0.9999) show that the prediction rates for the foreseen conditions have been determined almost exactly.

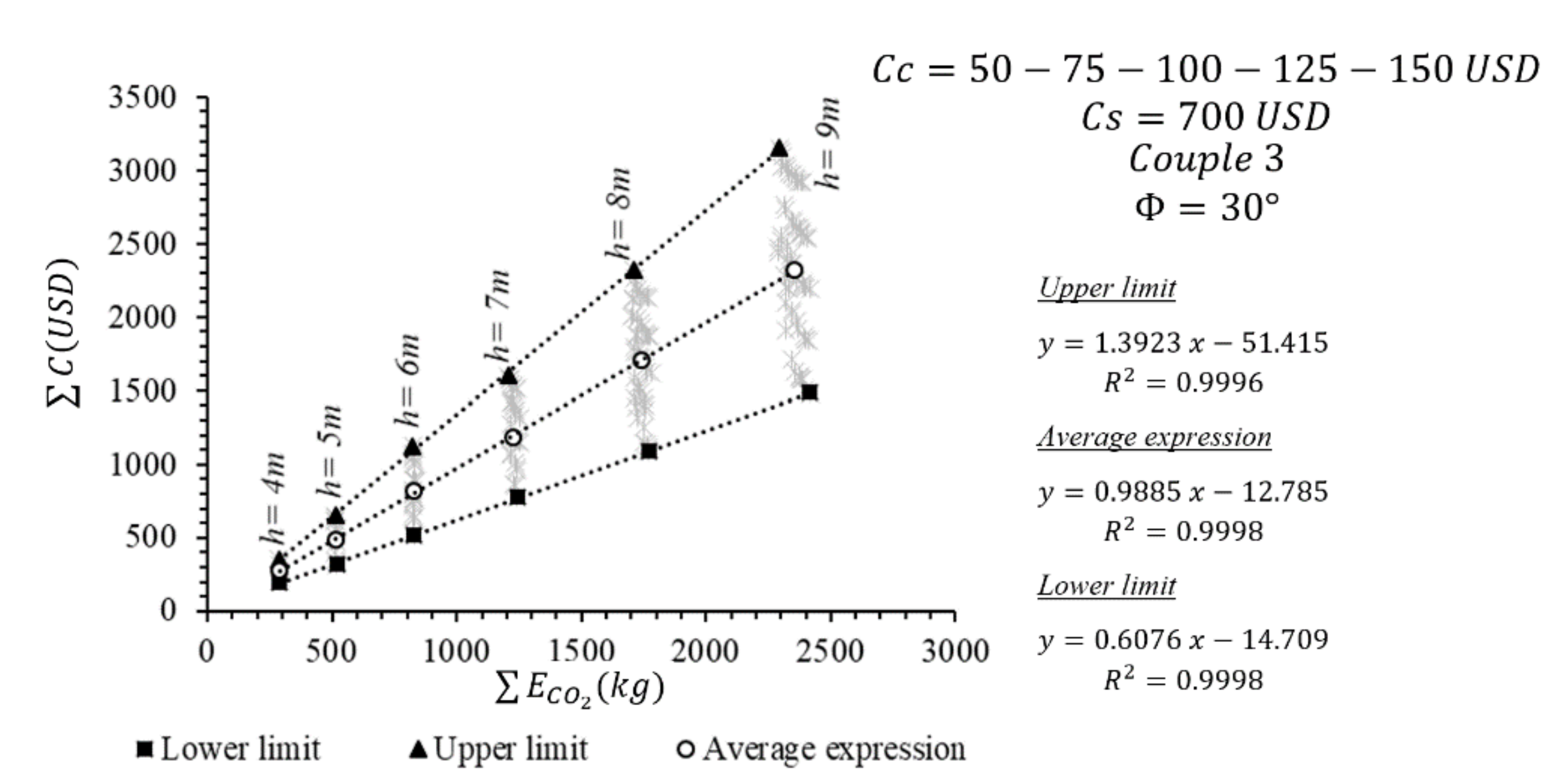
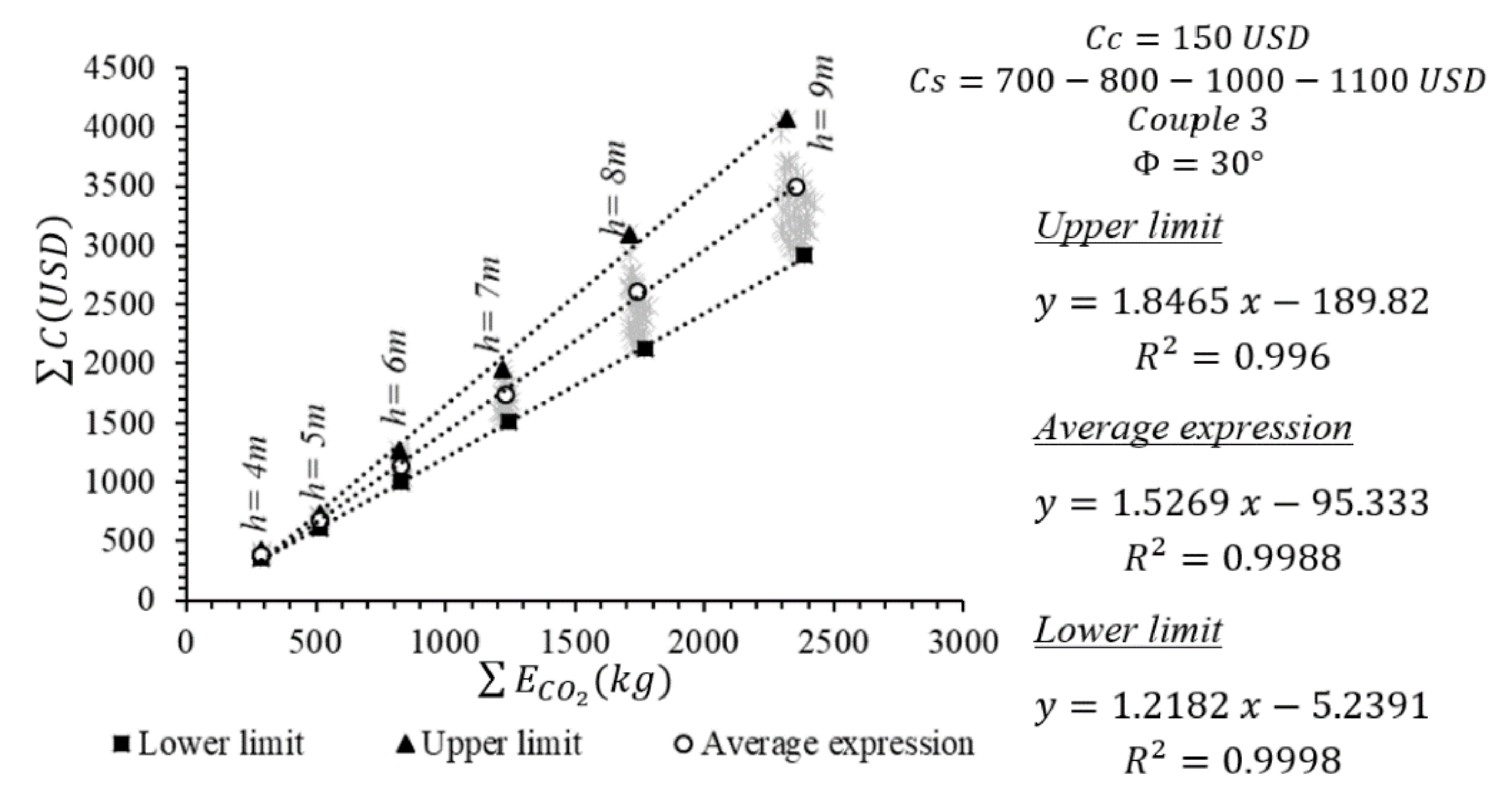
Figure 14a,b represent the analyses conducted for the lower limits of the costs and the emission couple 3. The coefficient-of-determination values (minimum 0.92) show that the prediction rates for the foreseen conditions have been determined almost exactly, too. It has to be noted that emission couple 3 consists of the minimum CO₂ emission values of the construction materials. Therefore, it is appropriate to compare the obtained numerical values of ΣC and ΣE_CO2 with other emission couples. The minimization of the emission values leads to a decrease in the ultimate CO₂ emission amount by approximately 250%, but in conjunction with the emission amount, the total cost values are increased in a predictable range.

Figure 15a,b represent the analyses conducted for the lower limits of the costs and the emission couple 4. It has to be noted that the emission couple 4 consists of the maximum CO₂ emission values of the construction materials. The usage of the upper limits of material emission values for the determination of the Pareto optimization analyses causes an increase in the ultimate emission value in comparison with the usage of the minimum limits of the emissions. However, there are approximately no differences that occurred in the conditions that are analyzed by the use of couple 1, couple 2, and couple 4 in terms of the determined ultimate emissions and total costs. This situation may be the result of a change in the structural design depending on the aim of the minimization process. Therefore, the evaluations have to be conducted in an integrated relationship with the dimensional options.

The same Pareto-optimal analyses were repeated for the upper limits of the material costs. The unit cost of the concrete and steel was assumed to be USD 150 and USD 1100 for the continuing Pareto-optimal analyses. In Figure 16, Figure 17, Figure 18 and Figure 19, the results of the analyses are shown for the emission couples 1, 2, 3, and 4, respectively. The huge increase in the total cost of the construction is the remarkable point of the analyses.

The coefficient-of-determination values are bigger than 0.99 for all the conducted analyses and this condition can convince the designers to use the envisaged mathematical expressions to use at the design stage of the CSP systems.

It is a significant point that the inclination of the achieved curve-fitting line and the accuracy rate of the representative linear mathematical expressions are increased depending on the rise in the material costs except for the condition of the usage of the maximum emission values (Figure 19). Moreover, the usage of emission couple 3 remarkably decreases the amount of ultimate CO₂ emission as expected (Figure 18b).

These above-mentioned expressions only belong to the used values of the design parameters and all different parameter usage processes lead to creating new correlations. In this context, the excavation depth and shear strength angle are also effective parameters from the first step of the analysis, but the derivation of an integrated relationship is possible with the use of different values of the specified parameters as seen from the given graph. The solution of the objective function is directly proportional to the amounts of costs and emissions; therefore, there arises a new requirement to generate design graphs or charts to estimate the outcomes of CSP design directly. In this connection, design charts are also given in

Table 5. Design chart 1.

Cc = USD 50 and Cs = USD 700		Couple 1				Couple 2
		D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)	D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)
h = 4 m	Φ = 20°	0.34	838.90	357.63	5.86	0.41	875.00	241.57	6.28
	Φ = 25°	0.32	739.36	293.20	5.73	0.35	799.44	218.08	5.93
	Φ = 30°	0.30	627.56	300.21	5.60	0.32	730.01	197.34	5.69
	Φ = 35°	0.26	556.15	231.85	5.28	0.30	732.51	196.46	5.55
h = 5 m	Φ = 20°	0.47	1487.35	616.64	7.74	0.55	1597.32	440.45	8.31
	Φ = 25°	0.44	1330.01	493.05	7.53	0.50	1359.65	374.88	7.96
	Φ = 30°	0.40	1140.39	417.10	7.27	0.45	1157.62	319.06	7.59
	Φ = 35°	0.37	978.32	359.50	7.01	0.39	991.33	272.94	7.20
h = 6 m	Φ = 20°	0.68	2450.54	872.75	10.34	0.76	2537.52	699.84	10.96
	Φ = 25°	0.60	2100.66	768.23	9.74	0.64	2186.33	603.07	10.06
	Φ = 30°	0.54	1810.32	686.31	9.28	0.59	1883.63	519.18	9.65
	Φ = 35°	0.46	1535.87	621.53	8.64	0.53	1576.60	435.38	9.22
h = 7 m	Φ = 20°	0.84	3534.35	1371.71	12.71	0.93	3789.14	1045.34	13.44
	Φ = 25°	0.77	3040.87	1228.84	12.11	0.85	3244.72	896.63	12.78
	Φ = 30°	0.67	2591.12	1064.26	11.29	0.75	2789.64	770.37	11.90
	Φ = 35°	0.59	2285.70	867.60	10.64	0.64	2382.45	656.59	11.06
h = 8 m	Φ = 20°	1.07	5120.19	1817.27	15.72	1.14	5351.55	1478.54	16.27
	Φ = 25°	1.00	4368.82	1617.13	15.02	1.03	4596.35	1269.34	15.31
	Φ = 30°	0.85	3741.03	1424.62	13.75	0.92	3988.92	1099.31	14.34
	Φ = 35°	0.72	3195.20	1243.84	12.70	0.81	3382.50	932.23	13.42
h = 9 m	Φ = 20°	1.32	7166.50	2312.24	18.94	1.38	7309.53	2013.84	19.51
	Φ = 25°	1.18	6164.62	2048.37	17.71	1.23	6289.53	1737.25	18.16
	Φ = 30°	1.12	5138.84	1884.60	16.45	1.10	5393.80	1487.76	16.91
	Φ = 35°	0.88	4420.71	1565.74	15.04	0.96	4581.94	1264.22	15.71
Cc = USD 50 and Cs = USD 700		Couple 3				Couple 4
		D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)	D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)
h = 4 m	Φ = 20°	0.37	391.95	257.43	6.04	0.34	839.20	374.05	5.85
	Φ = 25°	0.34	334.87	217.56	5.83	0.33	738.13	291.70	5.76
	Φ = 30°	0.32	288.57	196.59	5.67	0.28	636.24	256.28	5.42
	Φ = 35°	0.28	256.13	195.20	5.42	0.27	560.41	219.26	5.36
h = 5 m	Φ = 20°	0.53	702.71	466.35	8.18	0.45	1472.74	632.92	7.63
	Φ = 25°	0.50	605.85	410.05	7.93	0.44	1278.39	553.62	7.54
	Φ = 30°	0.43	516.34	334.85	7.48	0.40	1127.05	432.68	7.27
	Φ = 35°	0.40	438.39	281.71	7.21	0.36	975.94	363.53	6.95
h = 6 m	Φ = 20°	0.65	1115.48	803.96	10.13	0.65	2339.40	996.31	10.15
	Φ = 25°	0.63	968.07	655.72	9.96	0.62	2097.61	779.16	9.86
	Φ = 30°	0.57	826.30	562.00	9.46	0.52	1785.22	697.08	9.10
	Φ = 35°	0.50	704.18	434.77	8.99	0.47	1538.44	616.95	8.77
h = 7 m	Φ = 20°	0.88	1660.88	1224.45	13.00	0.83	3534.57	1372.64	12.63
	Φ = 25°	0.80	1439.31	989.41	12.34	0.74	3084.81	1163.27	11.87
	Φ = 30°	0.73	1230.84	895.15	11.73	0.71	2744.30	966.92	11.56
	Φ = 35°	0.61	1055.10	711.19	10.80	0.60	2252.50	940.67	10.71
h = 8 m	Φ = 20°	1.09	2349.02	1744.68	15.85	1.06	5184.75	1788.43	15.58
	Φ = 25°	0.97	2021.56	1511.07	14.75	0.93	4430.03	1606.75	14.48
	Φ = 30°	0.87	1746.74	1220.93	13.92	0.80	3702.39	1446.62	13.31
	Φ = 35°	0.79	1487.05	1045.76	13.24	0.74	3193.07	1258.60	12.83
h = 9 m	Φ = 20°	1.33	3166.57	2345.37	19.10	1.29	7189.82	2269.49	18.66
	Φ = 25°	1.14	2742.12	1961.46	17.34	1.16	5945.58	2145.63	17.44
	Φ = 30°	1.00	2357.97	1764.10	16.02	1.01	5161.12	1900.92	16.10
	Φ = 35°	0.92	2022.00	1389.70	15.34	0.90	4389.98	1602.59	15.16

and

Table 6. Design chart 2.

Cc = USD 150 and Cs = USD 1100		Couple 1				Couple 2
		D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)	D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)
h = 4 m	Φ = 20°	0.36	854.87	676.40	5.96	0.41	875.19	543.91	6.30
	Φ = 25°	0.31	734.29	584.98	5.60	0.35	799.44	480.88	5.90
	Φ = 30°	0.27	631.03	533.80	5.37	0.32	729.83	429.75	5.73
	Φ = 35°	0.24	544.24	489.00	5.21	0.31	734.38	417.35	5.61
h = 5 m	Φ = 20°	0.49	1466.65	1212.08	7.87	0.55	1573.83	977.23	8.36
	Φ = 25°	0.43	1313.93	1020.53	7.49	0.50	1359.60	840.91	7.99
	Φ = 30°	0.38	1112.08	909.71	7.14	0.47	1157.40	714.24	7.73
	Φ = 35°	0.35	964.44	782.78	6.91	0.39	991.59	612.89	7.20
h = 6 m	Φ = 20°	0.62	2299.67	1922.43	9.88	0.75	2538.04	1572.80	10.92
	Φ = 25°	0.57	2013.28	1677.16	9.47	0.65	2190.76	1357.81	10.11
	Φ = 30°	0.52	1755.54	1449.43	9.10	0.58	1878.18	1155.61	9.56
	Φ = 35°	0.46	1533.39	1211.13	8.68	0.52	1576.41	978.29	9.09
h = 7 m	Φ = 20°	0.79	3453.94	2810.57	12.27	0.93	3786.58	2351.82	13.42
	Φ = 25°	0.71	3004.59	2415.12	11.60	0.82	3261.06	2019.45	12.48
	Φ = 30°	0.67	2653.39	2046.73	11.27	0.74	2795.82	1738.26	11.82
	Φ = 35°	0.55	2222.12	1861.22	10.32	0.66	2382.84	1474.39	11.22
h = 8 m	Φ = 20°	1.03	5097.77	3721.04	15.27	1.13	5357.60	3321.14	16.17
	Φ = 25°	0.86	4227.64	3390.74	13.86	1.03	4608.59	2867.28	15.28
	Φ = 30°	0.83	3730.58	2851.10	13.57	0.91	3985.00	2466.12	14.22
	Φ = 35°	0.71	3188.26	2482.86	12.59	0.79	3382.17	2088.35	13.21
h = 9 m	Φ = 20°	1.27	7094.63	4847.67	18.53	1.35	7281.64	4513.61	19.23
	Φ = 25°	1.13	6055.69	4256.64	17.22	1.23	6283.85	3888.48	18.17
	Φ = 30°	0.98	5088.89	3794.27	15.91	1.10	5392.48	3334.49	16.97
	Φ = 35°	0.85	4271.36	3363.08	14.79	0.96	4586.72	2840.12	15.68
Cc = USD 150 and Cs = USD 1100		Couple 3				Couple 4
		D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)	D (m)	ΣECO2 (kg)	ΣC (USD)	ΣL (m)
h = 4 m	Φ = 20°	0.38	391.74	557.62	6.13	0.35	849.91	674.02	5.91
	Φ = 25°	0.33	336.90	489.67	5.76	0.32	746.37	553.08	5.69
	Φ = 30°	0.34	288.03	423.05	5.80	0.27	634.81	520.41	5.40
	Φ = 35°	0.26	252.11	399.82	5.30	0.23	542.59	515.98	5.11
h = 5 m	Φ = 20°	0.52	698.26	1049.06	8.13	0.48	1471.05	1217.76	7.84
	Φ = 25°	0.49	602.96	876.55	7.89	0.45	1298.00	1027.97	7.59
	Φ = 30°	0.43	513.69	714.31	7.47	0.40	1118.10	911.04	7.22
	Φ = 35°	0.39	438.09	610.33	7.15	0.36	974.13	742.98	6.98
h = 6 m	Φ = 20°	0.71	1114.66	1701.85	10.57	0.63	2334.79	1928.00	9.96
	Φ = 25°	0.60	959.96	1505.01	9.70	0.98	1917.18	1907.71	16.26
	Φ = 30°	0.56	825.16	1217.10	9.41	0.57	1813.46	1367.67	9.45
	Φ = 35°	0.51	705.67	1020.54	9.01	0.44	1507.62	1273.01	8.53
h = 7 m	Φ = 20°	0.86	1668.71	2542.89	12.83	0.84	3555.94	2741.11	12.67
	Φ = 25°	0.74	1427.16	2231.99	11.85	0.69	2967.25	2460.43	11.45
	Φ = 30°	0.70	1234.84	1819.20	11.52	0.67	2622.00	2080.24	11.24
	Φ = 35°	0.64	1054.47	1515.04	11.03	0.58	2262.52	1808.06	10.57
h = 8 m	Φ = 20°	1.06	2345.24	3591.19	15.58	1.00	5069.91	3714.12	15.07
	Φ = 25°	0.99	2020.73	3108.28	14.92	0.91	4278.56	3350.59	14.27
	Φ = 30°	0.85	1742.08	2660.49	13.75	0.82	3766.09	2823.68	13.54
	Φ = 35°	0.79	1497.31	2180.83	13.26	0.74	3279.98	2369.96	12.87
h = 9 m	Φ = 20°	1.29	3181.93	4747.67	18.68	1.27	7176.81	4803.42	18.51
	Φ = 25°	1.18	2744.23	4214.54	17.63	1.12	5956.37	4318.99	17.09
	Φ = 30°	1.02	2365.03	3571.15	16.25	0.98	4925.80	3952.83	15.89
	Φ = 35°	0.90	2019.77	3020.58	15.20	0.86	4320.60	3340.01	14.81

to ease the sustainable design process of the CSP walls. Table 5 represents the design chart for the lower limit of the material costs, and Table 6 includes the same analyses for the upper limit of the material costs considering different excavation depths and shear strength angles.

The linear proportional interpolation can be applicable for unavailable intermediate values. Table 5 represents the design chart for the upper limit of the material costs and the emission couple 1 and 2, and Table 6 includes the same analyses for couple 3 and couple 4 for different excavation depths and shear strength angles. The linear proportional interpolation is also applicable for unavailable intermediate values.

The Pareto-optimal analyses were evaluated with a different perspective by also the consideration of some special cases. In Figure 20, the Pareto data are investigated with the change in ΣC and ΣE_CO2 against the excavation depth. An investigation of the effects of the change in the unit cost of the concrete material is also attempted. According to this purpose, the unit cost of the steel is taken as a constant value of USD 700. In addition, the shear strength angle of the foundation soil strata is assumed to be 30°, and emission the Couple 3 is selected to conduct the analyses. The unit cost of the concrete is envisaged to be USD 50, USD 75, USD 100, USD 125, and USD 150, respectively. To eliminate the illustration of the random distribution of the Pareto data and prevent the disorder of the data spread, upper and lower values of the determined results are used to illustrate the following graphs. Representative mathematical expressions are also derived by the performed regression analysis for both upper and lower limits of the results depending on the change in the excavation depth. As a result, an average mathematical expression is generated based on the upper and lower limits of the analysis results by examining the sufficient applicability according to the coefficient-of-determination value. It is an apparent and expectable situation that the increase in the cost of the concrete raises the total costs of the design in a manner directly proportional to the increment of the excavation depth. The coefficient-of-determination values, denoted as R², is calculated as bigger than 0.99 for all the conditions.

In Figure 21, the rise in the unit cost of concrete is also investigated with the assumption of a constant unit cost of steel value. In these analyses, the unit cost of the steel material is assumed to be at its upper limit of USD 1100. The comparison of Figure 20 and Figure 21 shows that the increase in the steel costs only affects the total cost of the CSP but does not lead to a change in the design of the CSP system. Moreover, the prediction rate of the mathematical expressions obtained from regression analyses for the upper, average, and lower limits of the Pareto data results is high.

The effects of the change in the steel costs are also investigated with the assumption of a constant concrete cost. The concrete cost is selected as USD 50 and USD 150, respectively, and the results of the Pareto-optimal solution are given in Figure 22 and Figure 23.

The comparison of Figure 22 with Figure 19 shows that the change in the unit cost of the steel is not an important factor to change the whole design of the CSP if the unit cost of the concrete remains at its envisaged lower limit. However, the increase in the unit cost of the concrete causes a narrowing in the range of Pareto sets. In Figure 23, the average values of the ultimate CO₂ emission values are not changed but the total cost values are directly affected by the rise in the unit cost of the steel if the unit cost of the concrete remains at the upper level of the envisaged values. In addition to all these, the possibility of generating an integrated graph was also investigated with the change in both the unit costs of the concrete and the unit cost of the steel material. Figure 24 represents this mentioned relationship within the evaluation process of emission couple 1. The clusters of the Pareto data are also shown as grey crosses in Figure 24. The distribution of the Pareto sets is proportional to the excavation depth and the density of the Pareto data is not changed with depth. The distribution range of the data enlarges with the increased excavation depth. This condition increases the relative difference between the obtained upper and lower limits of the results. In that situation, the coefficient-of-determination value that is calculated for the average conditions makes it possible to obtain an applicable mathematical expression for the design of CSP walls.

Figure 25 represents this mentioned relationship within the evaluation process of emission couple 2. The distribution of the Pareto sets is differentiated from the data set that is obtained in Figure 24. The distribution of the data is highly regular and linear. This condition increases the prediction rate of the relationship between ΣC and ΣE_CO2 according to conducted regression analyses.

Figure 26 represents this mentioned relationship within the evaluation process of emission couple 3 and Figure 27 represents this mentioned relationship within the evaluation process of emission couple 4. It should be remembered that couple 3 represents the minimum limit of the emission values and couple 4 represents the maximum of the emission values. The distribution of the Pareto data is similar for Figure 25 and Figure 26 which have the same amount of emission values for the concrete material. However, the amounts of the total cost and ultimate CO₂ emission are differentiated from the solution results. Moreover, the distribution of Pareto data is also similar for Figure 24 and Figure 27 wherein the amount of the unit emission value of the concrete is the same. Therefore, it may be stated that the unit emission value of the concrete material forms the general shape of the distribution of the Pareto data for the design problem of CSP. This may be related to the volume content of the construction materials. The concrete material plays a dominant role in terms of volume rendering during the construction of CSP wall systems. This situation has to be also controlled with the change in design dimensions.

To evaluate the dimensional variance in the CSP designs, integrated graphs were drawn considering different unit costs, emission values, and excavation depths together. Figure 28a,b represent the mentioned kind of relationship of ΣL and D within the limits of emission couple 1 and emission couple 2, respectively. In addition, Figure 29a,b represent the mentioned kind of relationship of ΣL and D within the limits of emission couple 3 and emission couple 4, respectively.

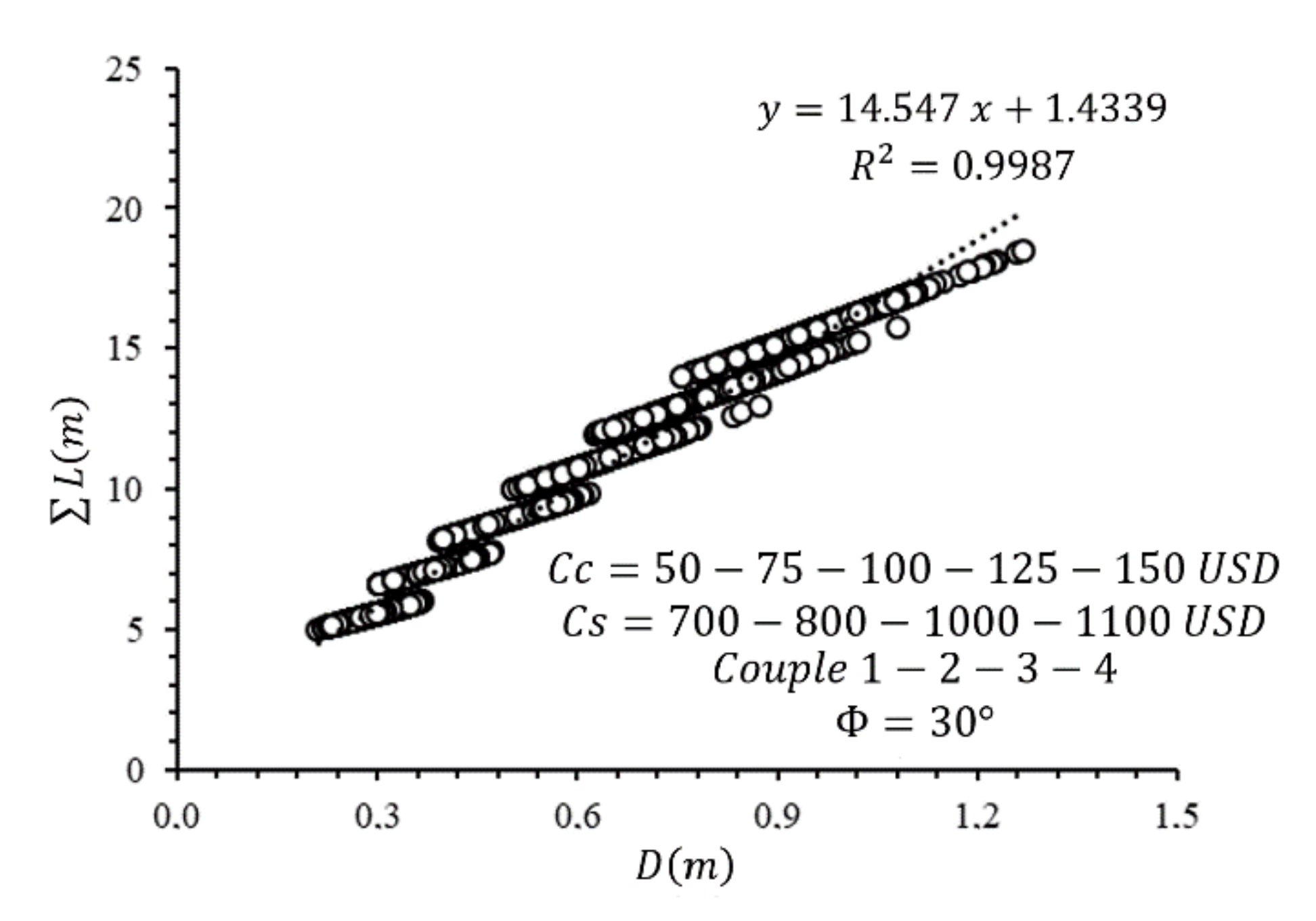
Figure 28 and Figure 29 show the relationships between the diameter and the length of CSP structures that are obtained from Pareto front designs. Additionally, there is a similar linear relationship which appears between the length and the diameter. The calculated coefficient-of-determination values are bigger than 0.98 for all the fictionalized cases. Therefore, this situation may lead to the thought that these graphs can be used for the predesign of CSP systems and can be adapted for different shear-strength-angle values. The envisaged mathematical expressions can be associated based on the similarity of the coefficients and constraints values in the equation. Hence, Figure 30 is produced to query the expressibility situation of the integrated relationship with the use of a simple ordinary expression. Figure 30 shows the general dimensional change in the CSP walls depending on the change in unit cost, emission, and depth values. The integrated relation can ease the design process by producing charts or graphs for only different shear strength values.

5. Conclusions

In this paper, HS was used as a tool to derive a Pareto-optimal solution to the problem of cantilever soldier pile wall design considering several conditions described in Figure 4. As a basic outcome of multiobjective optimization techniques, it was aimed towards reaching the optimal design by simultaneously considering both the total cost and ultimate CO₂ emission amount minimization. Additionally, the optimum results were obtained and the whole data were stored in the spreadsheet file. All combinations and their outcomes were recorded. The graphs were plotted that represent various relationships between the total cost and the ultimate CO₂ emission; the total length of the pile and the total cost; the diameter of the pile and the ultimate CO₂ emission; the total length of the pile and the diameter of the pile; the total cost and the diameter of the pile; and the total cost and the total length of the pile, which were evaluated depending on all the foreseen parameters of the whole design process by the usage of HS. The Pareto fronts of trade-offs between total costs and CO₂ emissions were categorized based on the generated combinations and evaluated by performing regression analyses, and proper design expressions were suggested depending upon the Pareto graphs and charts. All the conducting regression analyses led to attaining a coefficient-of-determination number bigger than 0.85 which seems to be a satisfactory amount for an expression to be applicable for the design problem of cantilever soldier piles. Consequently, the analyses performed within this study ensure the development of more exhaustive mathematical expressions; hence, it allows the process of seeking the design of a cantilever soldier pile wall to be automated. Two practical comparative-design objectives were considered with relevant applicable results to involve the most proper design application of the pile, and this system could be extended to the design of other soil-supporting structures and other metaheuristic algorithms with the use of more objective functions.

6. Recommendations for Further Studies

This study is a preliminary study that aimed to design CSPs by simultaneously considering the multiobjective optimization of cost and CO₂ emission minimization. Therefore, it aimed to be a guide to designers and researchers to focus on the design problem of CSPs with the multiobjective approach. In this context, within this study, it was utilized from the logic of Pareto optimality, and the HS algorithm was used as the tool of solution. Although the factors such as the excavation depth, the shear strength parameters of foundation soil strata, and the unit costs and unit emission amounts of structural materials were considered during the analysis, it is a clear fact that factors such as the existence of groundwater, the change in the loading type, environmental effects, etc., affect the design, performance, and cost of the structural system. On the other hand, the applicability of other more powerful methods can be controlled and the statistical optimum estimation techniques can also be used to justify the number of numerical tests required to provide a solution. In addition, the control parameters’ sensitivity analysis can be conducted to clarify the quality of the final solution. Further studies in which these above-mentioned factors are also considered are ongoing.