Abstract
The quality of the photovoltaic (PV) cell model impacts many simulation studies for PV systems, such as maximum power point tracking and other assessments. Moreover, due to limited information found in the datasheets of the PV cells, several parameters of the model are unavailable. Thus, this paper introduces a novel approach using a hybrid Particle Swarm and Grey Wolf Optimization algorithm to figure out these parameters under different environmental conditions. The proposed algorithm is used with two types of PV cells–Kyocera KC200GT and Canadian solar cell CS6K-280M–and can be used with any commercial type of PV module needing only parameters in the datasheet. The absolute error of the model’s simulation results is compared to the actual results collected from sites in Egypt, in an attempt to investigate the effectiveness of the suggested approach.
1. Introduction
Renewables are spreading worldwide due to several reasons such as minimal operating costs and privileged access to electricity grids. They were the only source of electricity to record demand growth worldwide over the last year by around 256 giga watts (GW), consisting of 54.4% solar PV, around 36.3% wind power, 7.6% hydropower, around 1.8% biopower, and less than 1% geothermal power and concentrated solar power (CSP); in total, the use of renewables has increased nearly 29%. This was recorded as the highest share of renewables among global electricity sources in history [1,2]. According to recent operational measurements, a monthly decrease of more than 20% of the worldwide electricity demand was observed due to the effects of COVID-19. Moreover, around 4% of universal electricity demand decreased in 2020, and the demand for coal and oil decreased by nearly 8% and 5%, respectively [3]. Investments in renewable energy resources increased in 2019 by 2%, reaching around 300 billion USD, with 32 countries having a minimum of 10 GW of renewable power capacity, in contrast with only 19 countries ten years before [4]. The expansion of the PV market over the past few years is a result of several factors, such as (a) the increasing number of PV manufacturers leading to a decrease in the cost of PV modules, (b) a rising demand for electricity, (c) the ongoing wars and events all over the world, and (d) the desire to decrease the effects of carbon dioxide and other greenhouse gases [5]. Several applications use PV modules such as Earth-orbiting Solar Power Satellites (SPSs), photovoltaic pumps for irrigation systems, and remote off-grid systems. Large PV farms have been installed worldwide, such as the New and Renewable Energy Agency (NREA)’s 37.5 km2 Benban Solar Park in Egypt, which reaches around 1.8 GW [6]. To study these systems thoroughly, an accurate model for the PV cell model is needed under different environmental conditions to obtain data on several aspects, such as Maximum Power Point Tracking (MPPT) and various grid operations [7]. All losses inside the cell and I–V characteristics should be considered in order to accurately model PV cells during the study. The ideal PV cell is represented by a photo-generated current supply (Iph) affected by the solar irradiance (G) landing on the cell [8,9]. Furthermore, different losses such as optical losses in the PN (positive–negative) junction of the cell (represented in the single diode model) [10], recombination losses due to the space charge region (SCR), which is defined in the double-diode (DD) model [11,12], and losses in the defect region and grain boundaries (described in the triple-diode (TD) model) [13,14] must be taken into consideration.
The main five parameters in the single diode (SD) model are photo-generated current (Iph), ideality factor (a), the diode cut-off region current (Io), which represents the diode parameters, along with series resistance (Rs) which indicates the summation of the resistance of the terminals on the external surfaces, and the resistances of the bulk and diffuse layers for the PN junction on the outer sides. Additionally, parallel resistance (Rp) arises from the PV surface and bulk irregularities, along with current losses across the edge of the cell [10]. Another couple of variables representing the second diode are added for the DD model. In comparison, another two variables for the third diode (TD) are added to the model, making it nine parameters in total for this model.
The single diode (SD) model was widely used because of its directness in parameter calculations, simple nature, and adequate accuracy level. However, this model had less accuracy in open-circuit voltage at low irradiances due to recombination losses [15]. This effect was considered when considering the double diode (DD) model by introducing a further diode standing for the recombination losses. This extra diode increases the precision of the DD model, but it also leads to more complexity, with two additional parameters added to the previous five; the second diode cut-off region current and its ideality factor [16]. Furthermore, the triple diode (TD) model was introduced with greater precision by adding a third diode representing the leakage current and the effect of grain boundaries [17]. While this model addresses most of the losses, it has more complicated calculations to calculate its parameters with an additional two parameters (reverse saturation current and ideality factor) added to represent the third diode [18].
Multiple methods have been used to deduce the previously mentioned parameters. Generally, elements from the datasheet (Isc, Voc, Im, Vm) are used to extract the parameters at standard conditions (G = 1000 W/m2 and T = 25 °C) using analytical, iterative, and meta-heuristic optimization strategies.
Meta-heuristic techniques are used to acquire the parameters of the SD model [19], DD model [20] and TD model [21] by using the root-mean-square deviation, which requires the difference between the actual and calculated current values. These algorithms, such as the genetic algorithm (GA) [22], particle swarm optimization (PSO) technique [23], bacterial foraging (BF) technique [24], hybrid artificial bee colony (ABC) and trust-region-reflective (TRR) technique [25], whale optimization algorithm (WOA) [26], shuffled frog leaping algorithm (SFLA) [27], hybrid firefly technique and pattern search technique [28], harmony search algorithm (HSA) [29], artificial fish swarm algorithm (AFSA) [30], trust-region-reflective (TRR) algorithm [25], and cuckoo search (CS) algorithm [31] aim to minimize the error. However, each of the techniques above has its limitations and merits. Using the conventional GA has the benefit of simplifying the limitation, but the finite length of the bit string provides an obstacle to obtaining the real values of the variables [32]. The use of a penalty function was presented as a solution to the major drawback of using standard DE: the premature convergence of parameters to local minima [33]. HSA is impacted deeply by the initial population [29], PSO is prone to premature convergence as it lacks the right mechanism for balancing exploration between the local and global particles search [34], and ABC has a poor response under operating conditions [35]. CS has a slow convergence rate as it does not use local search to enhance the convergence speed when the confined search is close to global or local minima but relies solely on Lévy flight to find new parameter solutions [36]. For AFSA, it was deduced that the accumulation of few fishes in local optima leads to slow convergence speed [35]. It was deduced that the use of the analytical methods is complicated in the TD model due to the number of parameters. Therefore, the use of the meta-heuristic algorithms was met with appreciation, especially the new algorithms.
In this paper, the advantages and disadvantages of the single, double, and triple diode model (reported in previous studies) prompted the authors to apply the hybrid optimization technique to deduce the parameters for the TD model. For a realistic study of the TD model, two well-known commercial PV modules were picked to be studied (Kyocera KCG200T and Canadian solar CS6K-280M). Experimental readings for temperature, irradiance, and output current and voltage were taken for these modules in 2019. To ensure the study’s credibility, the parameters obtained using the proposed optimization technique and datasheet parameters are compared to those obtained from the measured readings. The hybrid particle swarm grey wolf optimization (PSOGWO) technique is applied in this study as the hybridization of optimization techniques is a trending direction these days and is used in multiple studies, as hybridization merges the merits of several optimization techniques and diminishes the weak points in each technique [37,38]. These hybrid techniques are especially beneficial for renewable energy studies due to the intermittence of these energy sources and their non-linear nature.
The remainder of this paper is organized in the following sequence, with Section 2 explaining the mathematical representation of the triple diode model for the PV module and formulating the problem. Section 3 discusses and demonstrates the PSO and GWO optimization techniques leading to the hybrid PSOGWO optimization technique. In Section 4, the results are displayed and discussed, then verified by comparing them to results obtained from other techniques (e.g., WOA and SFO); they are also compared to results from experimental readings for further verification.
2. Modeling of PV Module
Single, Double, and Triple Diode Models are the most used models when representing the I–V characteristics of the PV module. As mentioned before, the triple diode model is used in this paper due to its greater accuracy, where it considers most of the factors responsible for the cell losses. In the next section, a brief explanation of each model is presented.
2.1. PV Models
2.1.1. Single Diode Model
Although this PV model is accurate, it is considered a straightforward model [39]. It consists of one diode, a current source, a series, and shunt resistances, as depicted in Figure 1a. The diffusion and recombination losses in the emitter and bulk in the P–N junction are represented as the diode current (Id). The terminal and the emitter and bulk regions are represented by series resistance, Rs, while the shunt resistance, Rp, represents the leakage current in the P–N junction. The output current of this model is calculated as follows [39]:
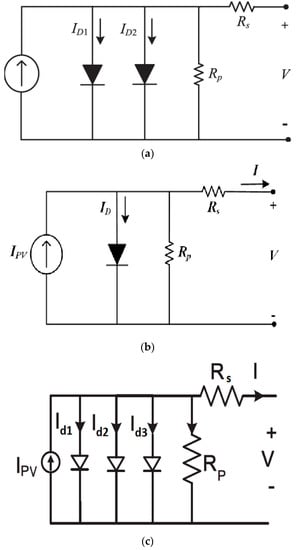
Figure 1.
(a) SD PV Model. (b) DD PV Model. (c) TD PV Model.
In the above equation, Ipv represents the cell photocurrent, Io represents the reverse saturation current, a is the ideality factor and Vth = NskT/q represents the thermal voltage. Ns is the number of the series-connected cells in the module, k is the Boltzmann constant, and q is the electron charge. The five needed parameters for this model are Ipv, Io, Rp, Rs, and a.
2.1.2. Double Diode Model
A double diode PV model is introduced for higher accuracy [40]. It also represents the effect of charge recombination by adding an extra diode. The DD model is shown in Figure 1b. The output current is calculated using the following equation [40]:
In this case, diffusion and recombination currents are represented by Io1 and Io2. Io2 stands for the extra recombination losses in this model. The ideality factors for the two diodes are a1 and a2, respectively. Despite its higher accuracy, this model needs the extraction of the SD parameters and two additional parameters, which are Io2, and a2.
2.1.3. Triple Diode Model
As previously mentioned, the TD model considers the impact of the grain boundaries and the defect region [41]. Figure 1c demonstrates the model. The model’s output current is obtained utilizing Equation (3) [41]. This model meets the majority of the solar cell’s specifications. However, it necessitates the computation of nine parameters, including Ipv, Io1, Io2, Io3, Rp, Rs, a1, a2, a3.
2.2. Parameters Variation
The below equations illustrate the effect of temperature and irradiance on some parameters [42,43]:
where Ipvn, Egn, Gn, Rshn, and Tn stand for the photo-generated current, energy gap, irradiance, parallel resistance, and cell temperature at standard conditions. Ki is the short-circuit current coefficient, Egn equals 1.21 eV [44] for silicon, and ΔT denotes the deviation between T and Tn. These equations are implemented to interpret the I–V characteristics of the SD, DD, and TD PV module models at various temperatures and solar irradiation levels. Calculating the parameters of the models above from the I–V curves, an interpretation for the fitness function is necessary to utilize the optimization techniques.
Eg = Egn (1 − 0.0002677 ΔT)
In this paper, the root-mean-square deviation method [45] interprets the objective function, which stands for the disparity between the actual and calculated currents.
The objective function is illustrated in Equation (7) [45]:
where the number of samples of actual data is symbolized by N, while the parameters to be calculated are included in the decision vector that is represented by Ø. is expressed by Equation (8) in the case of the triple-diode model [45]:
where
This paper aims to optimize Equation (8). To retrieve the parameters of the TD-based PV model, the hybrid PSOGWO is employed to solve these objective functions.
3. Hybrid Particle Swarm–Grey Wolf Optimization
3.1. Grey Wolf Optimization Algorithm
GWO was inspired by the ranking conduct of grey wolves, who live in packs of up to 12 wolves, as detailed in [46]. This algorithm introduces four levels to imitate the GWO’s leadership hierarchy: alpha, beta, delta, and omega. Alpha refers to the leaders of a group, with the alphas having primary responsibility for decisions such as hunting and sleeping. Betas are presented to aid alphas in making judgments, with feedback ideas being their primary job. Scouts, caregivers, elders, and hunters are all roles deltas play, by conforming to the needs of alpha and beta wolves. Betas govern omegas. Every other wolf must obey the omega-ranked. In the GWO, the hunting process is guided by the highest three ranks, and the lower-ranked wolves follow them. The following formula can be used to calculate GWO’s encircling conduct [46]:
where and represent coefficient vectors, the prey’s position vector is referred to as , The location of wolves in d-dimensional space is represented by Z, where d is the number of variables, (t) is the number of iterations, and the following equation defines Y [46]:
where and are represented as follows:
where the vectors r1, r2 are generated at random in the range [0, 1]. Over a number of iterations, the value of declines uniformly between 2 and 0. The best candidates for the solution in the grey wolf hunting process are alpha, beta, and delta, who are depicted to be aware of the prey’s likely location. As a result, the three best solutions found for a given iteration are preserved, forcing other wolves to adjust their locations in the hunting space to match the optimal spot. The following is the approach for updating positions [46]:
where , , and are calculated using the below equations [46]:
where , , and represent the finest solutions in the pack at certain iteration t. Where , , and are depicted using Equation (3). , , and are depicted using the following equations [44]:
where , , and are calculated according to Equation (4).
The vector is one of the most essential components of GWO for regulating exploration and hunting. It is recommended in the primary publication of this approach to reduce . The following is the equation to update it [46]:
where t denotes the number of iterations and ter is the total number of optimization iterations.
3.2. Particle Swarm Optimization
PSO was first established in [47]. It resembles the perception of bird swarms and fish schools in nature as a swarm intelligence technique. Each position and velocity vector in PSO symbolizes a particle. Every particle has its conduct and traverses a search space centered on the best answer it has found. Particles also know the best place the entire particle swarm has discovered thus far. The following equations are used to update the location and velocity vectors [47]:
3.3. The Applied Hybrid PSOGWO Algorithm
The authors of [37] proposed the hybrid PSOGWO algorithm. The primary idea behind PSOGWO is to improve the technique’s ability to use PSO while also exploring GWO to attain the optimization strength of both. The exploitation and exploration of the GW were governed by the inertia constant in PSOGWO; rather than utilizing traditional mathematical calculations, the primary agents’ location in the hunting area was updated. This was numerically expressed as follows [37]:
The velocity and locations have been adjusted to integrate PSO and GWO variations as follows [37]:
A flowchart for the proposed algorithm is shown in Figure 2.
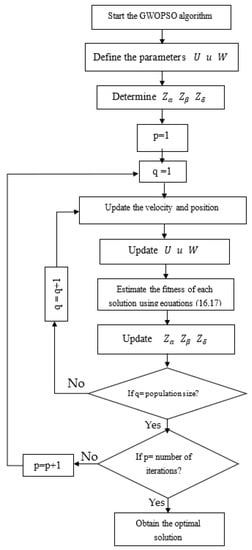
Figure 2.
Flow diagram of the PSGWO- algorithm.
4. Results
The hybrid PSGWO- algorithm determines the parameters of a TD model of two commonly-used PV modules. These PV modules (Kyocera KC200GT and Canadian Solar CS6K-280M) have different power capacities, cell types, and manufacturers. The electrical characteristics for these cells under the STCs (G = 1000 W/m2 and T = 25 °C) are presented in Table 1.

Table 1.
Datasheet of the studied PV modules at STC.
These PV modules were chosen because the suppliers are well-known PV module manufacturers, such as the Canadian solar cell [48], which was ranked among the top five PV providers in 2020. The two modules’ datasheet parameters (Isc, Voc, Im, Vm, Pm) are acquired at standard conditions, as clarified in Table 1.
When the population size is 30, and the iterations are 500, the hybrid PSOGWO is utilized to minimize the fitness function. These hybrid PSOGWO ideal settings are derived using the designer’s experience to fine-tune the configuration. Figure 3 shows the objective function convergence curves for the TD model of the Kyocera and Canadian Solar PV modules. The curves displayed are quite smooth and end with a zero-fitness value.
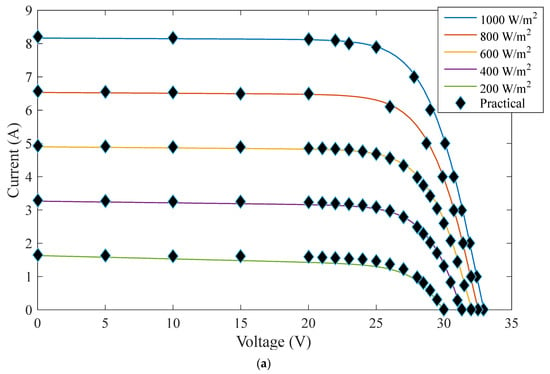
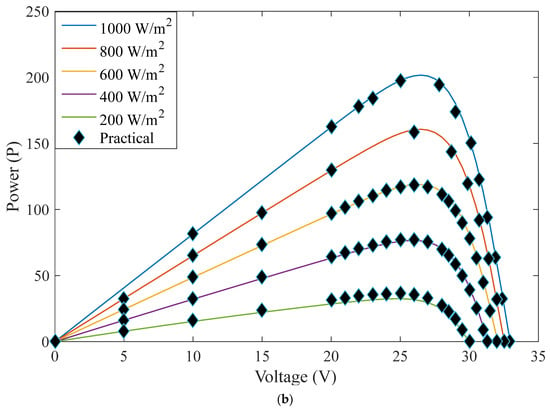
Figure 3.
Simulation and practical outcomes of the Kyocera KCG200T module under various irradiances at 25 °C. (a) I–V Curves. (b) P–V Curves.
MATLAB 2015b on a PC with the following specs was used to optimize and simulate results: 8 GB RAM, Intel(R) Core (TM) i5 @ 1.60 GHz processor, and 64-bit operating system. Table 2 shows the boundary conditions of the proposed hybrid PSGWO approach for the two PV modules. Table 3 shows the optimized parameters using the proposed hybrid PSGWO approach.

Table 2.
Boundary conditions of the proposed hybrid PSOGWO approach.

Table 3.
Optimized parameters using the proposed hybrid PSOGWO approach.
5. Discussion
5.1. Kyocera KC200GT
The suggested method’s optimal parameters are compared to those determined using GA, SA, WOA [18], and the sunflower optimization algorithm (SFO) [49] for KC200GT modules, as depicted in Table 4. The optimal configuration for the TD model for CS6K-280M is compared to the configuration deduced by WOA and SFO [49] in Table 5. The proposed approach is further authenticated by comparing its absolute current error to other approaches recording values of less than 0.4% and reaching 0.08%, with a fitness value of 3.14 × 10−10. The absolute error for the current is compared to the WOA [18] and the SFO [49] for the KC200GT module. Furthermore, the suggested approach’s I–V and P–V curves are compared with experimental curves under varied T and G to prove its effectiveness [50,51]. The I–V and P–V curves are produced and verified using actual data at a fixed temperature of 25 °C and variable irradiances ranging from 200 to 1000 W/m2 in Figure 3. The given approach is evaluated in the KC200GT module at fixed irradiance of 1000 W/m2 and various temperatures of (25, 50, and 75 degrees Celsius), after which the illustrated I–V and P–V curves are verified with observed outcomes, as depicted in Figure 4. We may conclude that the results for the proposed TD model’s optimized parameters showed better outcomes, more realistic curves regarding the experimental readings, and good accuracy when compared to those obtained using existing meta-heuristic optimization procedures.

Table 4.
Comparison of optimum parameters of triple diode PV model for KC200GT.

Table 5.
Comparison of optimum parameters of triple diode PV model for CS6K-280M.
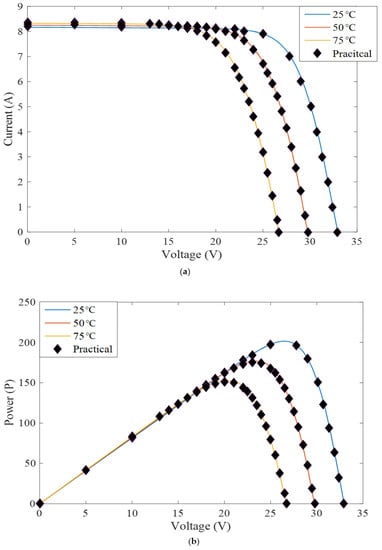
Figure 4.
Simulation and practical outcomes of the Kyocera KCG200T under various temperatures, at 1000 W/m2. (a) I–V Curves. (b) P–V Curves.
5.2. Canadian Solar Cell CS6K-280M
The TD model’s optimum parameters for CS6K-280M are compared to WOA and SFO-derived values. This comparison shows fewer errors for the offered approach than for the other approaches. Meanwhile, the CS6K-280 derived I–V and P–V curves for T = 25 °C and varied irradiances ranging from 400 to 1000 W/m2) are illustrated in Figure 5 and then justified using observed data. Also presented are the I–V and P–V curves with a fixed irradiance of 1000 W/m2 and varied temperatures (25, 45, and 65 degrees Celsius), which are then validated with observed data in Figure 6. The offered method is verified by comparing its absolute current error to the WOA and SFO [49] methods in Figure 7. This comparison confirms the effectiveness of the results for the proposed approach, with the error within the results being less than 0.4%, reaching 0.07% with a fitness value of 1.59 × 10−10. Results were of excellent accuracy compared to the other mentioned techniques and the experimental results.
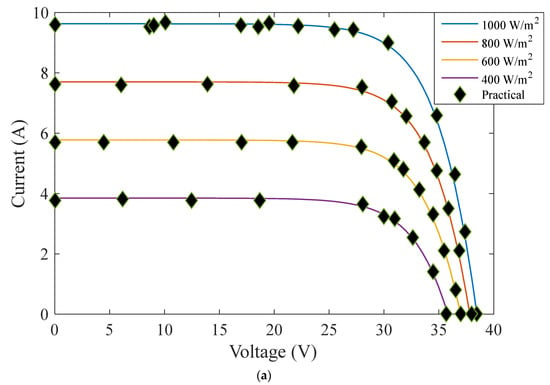
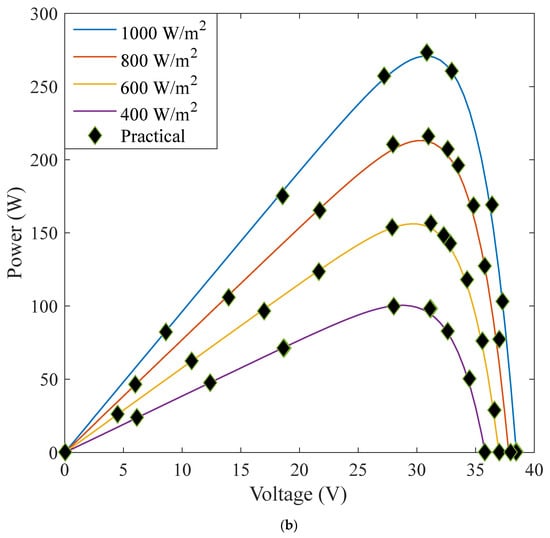
Figure 5.
Simulation and practical outcomes of the Canadian CS6K-280M cell under various irradiances at 25 °C. (a) I–V Curves. (b) P–V Curves.
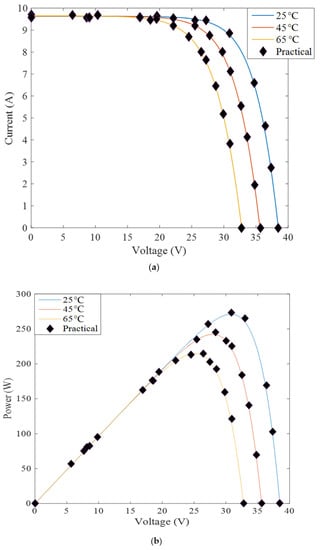
Figure 6.
Simulation and practical outcomes of the Canadian CS6K-280M cell under various temperatures, at 1000 W/m2. (a) I–V Curves. (b) P–V Curves.
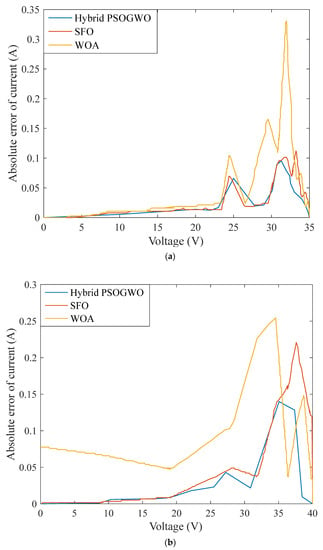
Figure 7.
Absolute current deviation levels of PV module. (a) KCG200T. (b) CS6K-280M.
The proposed approach has led us to find a more accurate model for the two PV modules with lower error and fitness functions than other techniques. As a result, a precise model was obtained, which is beneficial for the PV simulation, which can be used in power electronic studies and grid-connected PV systems [40,51].
6. Conclusions
The main target is to obtain the optimal configuration of the TD model of the PV module. These parameters are beneficial for obtaining an accurate PV model, which is extremely important for PV-powered systems’ modeling studies. Due to the lack of data presented by the PV suppliers, the hybrid PSOGWO algorithm is utilized to reach the optimal configuration of the TD model. The model is built using equations for the TD model and parameters from the datasheet (Isc, VOC, etc.). The objective of using the optimization technique is to minimize the current deviation. Aiming for a realistic study, the proposed technique is applied to two well-known PV modules, Kyocera and Canadian. The obtained parameters are validated and compared with those obtained from other recent algorithms such as SFO, GA, and WOA. The simulation outcomes ensure the competitiveness and robustness of the proposed model over the other techniques under comparison.
Moreover, the analytical results are evaluated concerning experimental results, and the error was proved to be satisfactory and within acceptable ranges, recording values below 0.5% and reaching in certain cases 0.07% and 0.08% with fitness values of 3.14 × 10−10 in the case of Kyocera and 1.59 × 10−10 in case of the Canadian solar cell. Accordingly, with the help of the hybrid PSOGWO algorithm, an accurate PV model was obtained. This model may also be useful for power electronics studies that need an accurate, efficient, and dependable PV model, and in studies for grid-connected PV systems.
Finally, reducing greenhouse gas emissions requires reliance on renewable energy resources such as solar energy, which is regarded as a clean and sustainable energy source. However, the efficient use of solar PV necessitates accurate modeling of the PV cells to correctly estimate the parameters of equivalent circuit models, particularly in the TD model, which is one of the most precise PV models. The mathematical and experimental results obtained in this work clearly verified that the hybrid PSOGWO algorithm performed well at different irradiance and temperature levels for the investigated commercial PV modules. This allows for the proper and efficient use of solar PV modeling in different studies..
Author Contributions
Conceptualization, H.H.E., M.A.A. and H.M.H.; methodology, H.H.E. and H.M.H.; software, H.H.E.; validation, H.M.H., A.M.T., A.E.-S. and M.A.A.; formal analysis, H.H.E. and A.E.-S.; investigation, H.H.E.; resources, H.M.H. and H.H.E.; data curation, H.H.E.; writing—original draft preparation, H.H.E. and S.H.E.A.A.; writing—review and editing, H.H.E., H.M.H., A.E.-S. and M.A.A.; visualization, H.H.E.; supervision, H.M.H., A.E.-S. and A.M.T.; project administration, H.M.H., A.E.-S. and S.H.E.A.A.; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Ideality factor of diode |
| Eg | Band gap energy (eV) |
| G | Solar Irradiance(W/m2) |
| Id | Diode Current (A) |
| Im | Maximum output current of PV Array (A) |
| Io | Reverse saturation current of diode (A) |
| Iph | Photo-generated current (A) |
| Isc | Short circuit current of PV module (A) |
| k | Boltzmann constant (1.38065 × 10−23 J/K) |
| Ki | Short-circuit current coefficient |
| Ns | Number of the series-connected cells in the module |
| P | Output power of PV module (W) |
| Pm | Maximum Output power of PV Module (W) |
| q | Electron charge (1.6022 × 10−19 C) |
| Rs | Series resistance (Ω) |
| Rp | Shunt resistance (Ω) |
| T | Cell Temperature (K) |
| Vm | Maximum output voltage of PV Array (V) |
| Voc | Open circuit voltage of PV module (V) |
| Vth | Thermal voltage (V) |
| Abbreviations | |
| PV | Photovoltaic |
| CSP | Concentrated Solar Power |
| SPS | Solar Power Satellite |
| NREA | New and Renewable Energy Agency |
| MPPT | Maximum Power Point Tracking |
| SCR | Space charge region |
| WOA | Whale optimization algorithm |
| SFO | Sunflower optimization algorithm |
| SD | Single Diode |
References
- Data & Statistics. Available online: http://resourceirena.irena.org/gateway/dashboard/?topic=4&subTopic=54 (accessed on 10 July 2022).
- Jones, D. Global Electricity Review 2021. Available online: https://ember-climate.org/project/global-electricity-review-2021 (accessed on 10 December 2021).
- IEA. Global Energy Review 2021—Analysis. Available online: https://www.iea.org/reports/global-energy-review-2021. (accessed on 10 December 2021).
- IEA. Renewables—Global Energy Review 2020—Analysis. Available online: https://www.iea.org/reports/global-energy-review-2020/renewables (accessed on 10 July 2022).
- Wang, S. Current status of PV in China and its future forecast. CSEE J. Power Energy Syst. 2020, 6, 72–82. [Google Scholar]
- Mustafaa, A.; Rashad, A.; Kamel, S.; Nasrat, L.; Jurado, F. Performance Analysis of Small Signal of Benban Solar Park Integrated with Battery ESS Optimized by EMS during Uncertainty Condition. In Proceedings of the 2021 12th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 26–28 October 2021. [Google Scholar]
- Khursheed, M.-U.-N.; Alghamdi, M.A.; Khan, M.F.N.; Khan, A.K.; Khan, I.; Ahmed, A.; Kiani, A.T.; Khan, M.A. PV Model Parameter Estimation Using Modified FPA With Dynamic Switch Probability and Step Size Function. IEEE Access 2021, 9, 42027–42044. [Google Scholar] [CrossRef]
- Enaganti, P.K.; Nambi, S.; Behera, H.K.; Dwivedi, P.K.; Kundu, S.; Imamuddin, M.; Srivastava, A.K.; Goel, S. Performance Analysis of Submerged Polycrystalline Photovoltaic Cell in Varying Water Conditions. IEEE J. Photovolt. 2020, 10, 531–538. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S.M. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef] [Green Version]
- Hara, S. Parameter Extraction of Single-Diode Model from Module Datasheet Information Using Temperature Coefficients. IEEE J. Photovolt. 2021, 11, 213–218. [Google Scholar] [CrossRef]
- Barbosa, E.J.; Cavalcanti, M.C.; Azevedo, G.M.; Barbosa, E.A.; Bradaschia, F.; Limongi, L.R. Global Hybrid Maximum Power Point Tracking for PV Modules Based on a Double-Diode Model. IEEE Access 2021, 9, 158440–158455. [Google Scholar] [CrossRef]
- Abbassi, A.; Ben Mehrez, R.; Touaiti, B.; Abualigah, L.; Touti, E. Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik 2022, 253, 168600. [Google Scholar] [CrossRef]
- Kumar, C.; Mary, D.M. A novel chaotic-driven Tuna Swarm Optimizer with Newton-Raphson method for parameter identification of three-diode equivalent circuit model of solar photovoltaic cells/modules. Optik 2022, 264, 169379. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Alkuhayli, A. Marine Predators Algorithm for Parameters Identification of Triple-Diode Photovoltaic Models. IEEE Access 2020, 8, 155832–155842. [Google Scholar] [CrossRef]
- Mathew, L.E.; Panchal, A.K. A Complete Numerical Investigation on Implicit and Explicit PV Single-Diode-Models Using I- and V-Approaches. IEEE J. Photovolt. 2021, 11, 827–837. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, R.; Li, C.; Zhang, L.; Cui, Z. Hybrid Symbiotic Differential Evolution Moth-Flame Optimization Algorithm for Estimating Parameters of Photovoltaic Models. IEEE Access 2020, 8, 156328–156346. [Google Scholar] [CrossRef]
- Ismaeel, A.A.K.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-Based Optimizer for Parameter Extraction in Photovoltaic Models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single- and multiple-diode photovoltaic model using whale optimization algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, J.; Duck, B.C.; Fell, C.J. An Adaptive Wind-Driven Optimization Algorithm for Extracting the Parameters of a Single-Diode PV Cell Model. IEEE Trans. Sustain. Energy 2019, 11, 1054–1066. [Google Scholar] [CrossRef]
- Li, L.; Xiong, G.; Yuan, X.; Zhang, J.; Chen, J. Parameter Extraction of Photovoltaic Models Using a Dynamic Self-Adaptive and Mutual- Comparison Teaching-Learning-Based Optimization. IEEE Access 2021, 9, 52425–52441. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Hussein, M.M.; Hassan, M.H. A New Application of Chaos Game Optimization Algorithm for Parameters Extraction of Three Diode Photovoltaic Model. IEEE Access 2021, 9, 51582–51594. [Google Scholar] [CrossRef]
- Kumar, M.; Shiva Krishna Rao, K.D.V. Modelling and Parameter Estimation of Solar Cell Using Genetic Algorithm. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019. [Google Scholar]
- Qin, H.; Kimball, J.W. Parameter Determination of Photovoltaic Cells from Field Testing Data Using Particle Swarm Optimization. In Proceedings of the 2011 IEEE Power and Energy Conference at Illinois, Urbana, IL, USA, 25–26 February 2011. [Google Scholar]
- Subudhi, B.; Pradhan, R. Bacterial Foraging Optimization Approach to Parameter Extraction of a Photovoltaic Module. IEEE Trans. Sustain. Energy 2018, 9, 381–389. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Z.; Long, C.; Cheng, S.; Lin, P.; Chen, Y.; Chen, H. Parameter extraction of photovoltaic models from measured I-V characteristics curves using a hybrid trust-region reflective algorithm. Appl. Energy 2018, 232, 36–53. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Hasanien, H.M. Shuffled Frog Leaping Algorithm for Photovoltaic Model Identification. IEEE Trans. Sustain. Energy 2015, 6, 509–515. [Google Scholar] [CrossRef]
- Beigi, A.M.; Maroosi, A. Parameter identification for solar cells and module using a Hybrid Firefly and Pattern Search Algorithms. Sol. Energy 2018, 171, 435–446. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Han, W.; Wang, H.-H.; Chen, L. Parameters Identification for Photovoltaic Module Based on an Improved Artificial Fish Swarm Algorithm. Sci. World J. 2014, 2014, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, T.; Yao, J.; Yang, S.; Duong, T.; Zhu, X. Novel Cuckoo Search Algorithm with Quasi-Oppositional Population Initialization Strategy for Solar Cell Parameters Identification. In Proceedings of the 13th World Congress on Intelligent Control and Automation (WCICA), Changsha, China, 4–8 July 2018. [Google Scholar]
- Ulaganathan, M.; Devaraj, D. Real Coded Genetic Algorithm for Optimal Parameter Estimation of Solar Photovoltaic Model. In Proceedings of the International Conference on Emerging Trends in Engineering, Technology and Science (ICETETS), Pudukkottai, India, 24–26 February 2016. [Google Scholar]
- Ishaque, K.; Salam, Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Sol. Energy 2011, 85, 2349–2359. [Google Scholar] [CrossRef]
- Wei, H.; Cong, J.; Lingyun, X.; Deyun, S. Extracting Solar Cell Model Parameters Based on Chaos Particle Swarm Algorithm. In Proceedings of the International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011. [Google Scholar]
- Saha, C.; Agbu, N.; Jinks, R. Review article of the solar PV parameters estimation using evolutionary algorithms. MOJ Sol. Photoenergy Syst. 2018, 2, 66–78. [Google Scholar]
- Jovanovic, R.; Kais, S.; Alharbi, F. Cuckoo Search Inspired Hybridization of the Nelder- Mead Simplex Algorithm Applied to Optimization of Photovoltaic Cells. Appl. Math. Inf. Sci. 2016, 10, 961–973. [Google Scholar] [CrossRef] [Green Version]
- Singh, N.; Singh, S.B. Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer for Improving Convergence Performance. J. Appl. Math. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Kihel, B.K.; Chouraqui, S. A Novel Genetic Grey Wolf Optimizer for Global Optimization and Feature Selection. In Proceedings of the 2020 Second International Conference on Embedded & Distributed Systems (EDiS), Oran, Algeria, 3 November 2020. [Google Scholar]
- Laudani, A.; Salvini, A. High Performing Extraction Procedure for the One-Diode Model of a Photovoltaic Panel from Experimental I–V Curves by Using Reduced Forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Rawa, M.; Abusorrah, A.; Bassi, H.; Mekhilef, S.; Ali, Z.M.; Abdel Aleem, S.H.E.; Hasanien, H.M.; Omar, A.I. Economical-technical-environmental operation of power networks with wind-solar-hydropower generation using analytic hierarchy process and improved grey wolf algorithm. Ain Shams Eng. J. 2021, 12, 2717–2734. [Google Scholar] [CrossRef]
- Nishioka, K.; Sakitani, N.; Uraoka, Y.; Fuyuki, T. Analysis of Multicrystal Silicon Solar Cells by Modified 3-Diode Equivalent Circuit Model Taking Leakage Current through Periphery into Consideration. Sol. Energy Mater. Sol. Cells 2007, 91, 1222–1227. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Sera, D.; Teodorescu, R.; Rodriguez, P. PV Panel Model Based on Datasheet Values. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007. [Google Scholar]
- Hasanien, H.M. Performance improvement of photovoltaic power systems using an optimal control strategy based on whale optimization algorithm. Electr. Power Syst. Res. 2018, 157, 168–176. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Mekhilef, S.; Shamsudin, A. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Appl. Energy 2012, 99, 297–308. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Rais, H.; Jadid, S. Feature selection method based on grey wolf optimization for coronary artery disease classification. In Recent Trends in Data Science and Soft Computing; Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2018; pp. 257–266. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Solar Reports. Top 10 PV Module Manufacturers during First Half of 2020, Shipment Scale. Solar Edition. 31 August 2020. Available online: https://solaredition.com/top-10-pv-module-manufacturers-during-first-half-of-2020-shipment-scale/ (accessed on 10 July 2022).
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Identification of electrical parameters for three-diode photovoltaic model using analytical and sunflower optimization algorithm. Appl. Energy 2019, 250, 109–117. [Google Scholar] [CrossRef]
- Zobaa, A.F.; Aleem, S.H.E.A.; Abdelaziz, A.Y. Classical and Recent Aspects of Power System Optimization; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128124413. [Google Scholar]
- Rawa, M.; Al-Turki, Y.; Sindi, H.; Ćalasan, M.; Ali, Z.M.; Abdel Aleem, S.H.E. Current-voltage curves of planar heterojunction perovskite solar cells—Novel expressions based on Lambert W function and Special Trans Function Theory. J. Adv. Res. 2022; in press. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).