Research on the Current Situation of Employment Mobility and Retention Rate Predictions of “Double First-Class” University Graduates Based on the Random Forest and BP Neural Network Models

Abstract

The economic development of various regions is influenced by high-quality population mobility. The research object of this article is the employment mobility data of “Double First-Class” university graduates from 2014 to 2019; the subsequent analysis is based on these data. First, this paper summarizes the current state of university graduates’ employment mobility. Second, this paper employs the fixed-effect model and PCA method to conclude that economic factors are the primary factors influencing university graduates’ employment mobility. Finally, based on the nonlinear, small sample, and high-dimensional characteristics of university graduates’ employment mobility data, this paper employs the random forest and BP neural network methods to build a prediction model for university graduates’ employment retention rate. The results show that the BP neural network model outperforms the random forest model in terms of prediction accuracy. The BP neural network model can accurately predict the employment retention rate of “Double First-Class” university graduates, which can guide the reasonable mobility of university graduates and provide a reference for government universities and individuals to make decisions.

1. Introduction

Since China implemented the university entrance examination policy to increase enrollment, a growing number of people have obtained a higher education. The rapid expansion of higher education, in the context of increasing privatization of education, does not necessarily increase upward mobility in society but rather increases educational inequality. In China, the mismatch between higher education and the labor market, as well as social mobility stagnation, are common [1]. The labor market in China is marked by structural contradictions; supply-side reforms have resulted in a large number of job transfers; scientific and technological progress has influenced the labor market, and rising labor costs have stifled labor demand and employment quality. University graduates are much more mobile than non-university graduates, a difference partly because university graduates are more sensitive to employment opportunities in other fields [2].

Give priority to the development of education, accelerate the construction of first-class universities and first-class disciplines, and realize the connotative development of higher education, according to the report of the Communist Party of China’s 19th National Congress. Simultaneously, it is necessary to eliminate the flaws in the system and mechanisms that impede labor and talent mobility, so that everyone has the opportunity to realize their development through hard work. The disparity in regional labor force quality is a significant factor influencing the uneven development of regional economies [3]. According to the human capital theory, high-quality human capital is the core element that affects the development of the industrial structure, which in turn affects the development of the entire economic level. This paper studies the employment mobility of high-quality human capital, which has guiding significance for economic development.

Push and pull theory is one of the important theories used to study floating population and immigration. It believes that in the case of the market economy and free population mobility, the reason for population migration and immigration relocation is that people can improve their living conditions through relocation. Thus, the factors that improve the living conditions of immigrants in the inmobility areas become the pull force, and the unfavorable socioeconomic conditions in the outmobility areas become the push force. Population migration is accomplished under the combined action of these two forces. What factors will affect the employment migration of university graduates, and what trend will the employment migration of university graduates show in the future: these are all issues worth exploring.

Combined with previous research results, this study further improves the related research in terms of research objects, research methods, and research ideas. First of all, the research object of this study is the employment geographical mobility of graduates from 147 “Double First-Class” universities. Graduates of “Double First-Class” colleges and universities belong to high-quality human capital, and the mobility of high-quality human capital is the core factor affecting economic development. This study further refines the classification of high-end talents, filling the gaps in this research field. Secondly, this paper uses the method of econometrics and the method of PCA to analyze the influencing factors of the employment mobility of “Double First-Class” university graduates and draws consistent conclusions. Finally, in terms of research ideas, this paper first analyzes the characteristics and influencing factors of the employment mobility of “Double First-Class” university graduates, and then uses 22 influencing factors to conduct a comparative study of the prediction methods. The employment retention rate in this paper refers to the proportion of graduates from “Double First-Class” colleges and universities who remain employed in the places where they are studying.

This paper creates a database of university graduates’ employment mobility based on the principle of data availability using the employment quality report data of “Double First-Class” university graduates in 26 provinces from 2014 to 2019. This article attempts to answer the following questions: What is the current status of employment mobility for graduates from “Double-First-Class” universities? What factors affect the employment mobility of graduates from “Double-First-Class” universities? The article normalizes complex data and uses PCA to reduce the dimensionality of multidimensional data. Comparing the random forest and BP neural networks, which method can more accurately predict the retention rate of “Double First-Class” university graduates?

The research results show that there are regional differences in the employment mobility of graduates from “Double First-Class” universities. Graduates from economically developed regions tend to stay in local employment, and graduates mainly move into the eastern regions for employment. Economic factors and educational factors are the main factors affecting the employment mobility of graduates from “Double First-Class” universities. Finally, through a comparative analysis of the prediction models, it was found that the PCA-BP neural network can more accurately predict the employment retention rate of “Double First-Class” university graduates.

The structure of this paper is as follows: Section 2 presents an overview of the related literature. Section 3 describes the current situation of employment mobility of graduates from “Double First-Class” universities. Section 4 discusses the factors that affect the employment mobility of graduates from “Double First-Class” universities. Section 5 uses PCA to reduce the dimensionality of the complex data, and then compares and analyzes the random forest and BP neural network methods to reveal which method can more accurately predict the retention rate of graduates’ employment mobility in “Double First-Class” universities. The final section summarizes the research results and provides policy recommendations.

2. Literature Review

This paper compares and analyzes the random forest and BP neural network methods for predicting the employment retention rate of “Double First-Class” university graduates in 26 provinces and cities.

2.1. The Connotation of “Double First-Class” Construction

“Double first-class” construction is another key construction project implemented by China in the new era of higher education development after the “985 Project” and “211 Project” [4]. First-class universities and disciplines of the world are referred to as “Double First-Class”. There are 137 “Double First-Class” universities in the first batch, including 42 world-class universities (36 in class A and 6 in class B) and 95 world-class discipline universities. The “Double First-Class” construction is predicated on the development of first-class disciplines. The foundation of first-class disciplines is superior discipline knowledge, and the foundation of discipline development is human creativity. First-class disciplines have outstanding academic leaders and teams, adequate academic funding, and advanced scientific research equipment, as well as outstanding academic accomplishments and talent development quality. First-class universities and first-class disciplines are critical drivers of knowledge discovery and scientific and technological innovation, a source of advanced ideas and excellent culture, a foundation for cultivating all types of high-quality talent, and a critical support for economic and social development [5].

In the specific construction tasks, in addition to building a first-class faculty, they also stipulate the cultivation of top-notch innovative talents, the improvement of the scientific research level, the inheritance of excellent culture of innovation, and the promotion of achievement transformation. This is the difference between the “Double First-Class” construction and the “211 Project” and “985 Project”. The “Double First-Class” construction highlights the important task of cultivating top-notch innovative talents [6]. The “Double First-Class” construction aims to implement dynamic monitoring, and the implementation of dynamic management is a good innovation mechanism.

2.2. Graduate Employment Migration

Firstly, domestic and foreign scholars have conducted a lot of research on the characteristics of university graduates’ employment mobility. Generally, individuals with higher levels of human capital are more geographically mobile [7,8]. Most scholars have conducted research on the geographical location of places of study and employment [9,10], and the most important employment locations for graduates are still large and medium-sized cities [11].

Secondly, researchers have analyzed the relevant influencing factors from different perspectives. According to the push and pull theory, the factors that affect the mobility of talents can also be called the factors that attract the mobility of talents. In different eras, different economic development environments, and different political and cultural backgrounds, the influencing factors of talent attraction have gradually shown differentiated characteristics in relation to influencing mechanisms and effects. Generally speaking, income level, per capita GDP, unemployment rate, urban amenities, educational structure and university quality all affect graduate migration [12,13,14,15].

2.3. Forecast Methods

This paper begins by employing a principal component analysis (PCA) to reduce the dimensionality of multiple data sets. A principal component analysis is a multivariate statistical analysis technique that replaces the original variable with a linear combination of the original variables to form an uncorrelated comprehensive variable on the premise of preserving the original variable’s information with the least possible loss [16,17]. This eliminates the correlation between the original variables, reduces the network dimension, and facilitates data sorting and calculation [18,19].

The machine learning method [20], the PDE model [21], system dynamics [22], the exponential smoothing forecasting model [23], the grey model [24], random forest [25,26,27,28], and neural network [29,30,31,32] are the main tools used in population forecasting research. The majority of scholars utilize gray models, random forests, and neural networks [33]. The gray model research object is for unknown information or small samples, with a small sample size requirement [34]. It accomplishes its goal of accurately describing and comprehending the real world by generating, developing, and implementing some known information. Random forest is a statistical learning theory that has a high prediction accuracy, is tolerant of outliers and noise, and can identify abnormal collection points and compare and delete them [35,36]. In addition, it can assess the significance of each predictor’s impact on the classification [37]. Similar to the human brain, the neural network model is capable of approximating a large number of complex nonlinear functions [38,39]. The neural network is one of the machine learning algorithms that imitates the functioning of human neurons to predict various events by continuously fitting nonlinear functions [40].

The BP artificial neural network is a multi-layer forward neural network based on the error back-propagation algorithm (Back-Propagation) developed by Rmenlhart, McClelland, and others [41]. The superiority of BP lies in its high simulation function, which can effectively correct errors through repeated learning of the network and can circumvent the expert scoring link in traditional evaluation, thereby minimizing the impact of subjective factors on the results [42]. Unlike general mathematical regression, the nonlinear operation of BP can better comprehend the relationship between variables and simultaneously incorporate the influence of hidden variables on the overall results into the calculation process [43]. The BP neural network can realize any nonlinear mapping between input and output, so it has the widest range of applications in pattern recognition, risk assessment, and adaptive control, among others [44].

To sum up, there are still two main deficiencies in the previous studies: first, the comprehensive and systematic analysis of the influencing factors of talent attractiveness is not enough; the second is the lack of a quantitative analysis of complex data on the influencing factors of talent attractiveness. This paper examines the factors influencing the employment mobility of university graduates from six main perspectives, tallies 22 relevant data indicators, and examines the factors influencing the employment migration of university graduates comprehensively. This paper primarily uses the random forest and neural networks to predict university graduates’ employment retention rate. These two models are utilized more frequently for population prediction. However, given that the development of population size is affected by many factors, the limitations of using a single model for forecasting are inevitable, and the application of combined models in forecasting has gradually been welcomed by scholars. This paper analyzes the PCA-random forest and PCA-BP neural network models. The improved model has a higher accuracy and a better effect when dealing with uncertain factors.

3. Status Quo of Employment Migration of “Double First-Class” University Graduates

3.1. Regional Differences in Employment Mobility for “Double First-Class” University Graduates Exist

Based on the availability and completeness of data, this study calculated the number of graduates, the number of graduates entering each province, and the number of graduates leaving each province from 2014 to 2019 in 137 “Double First-Class” universities in 26 provinces in China.

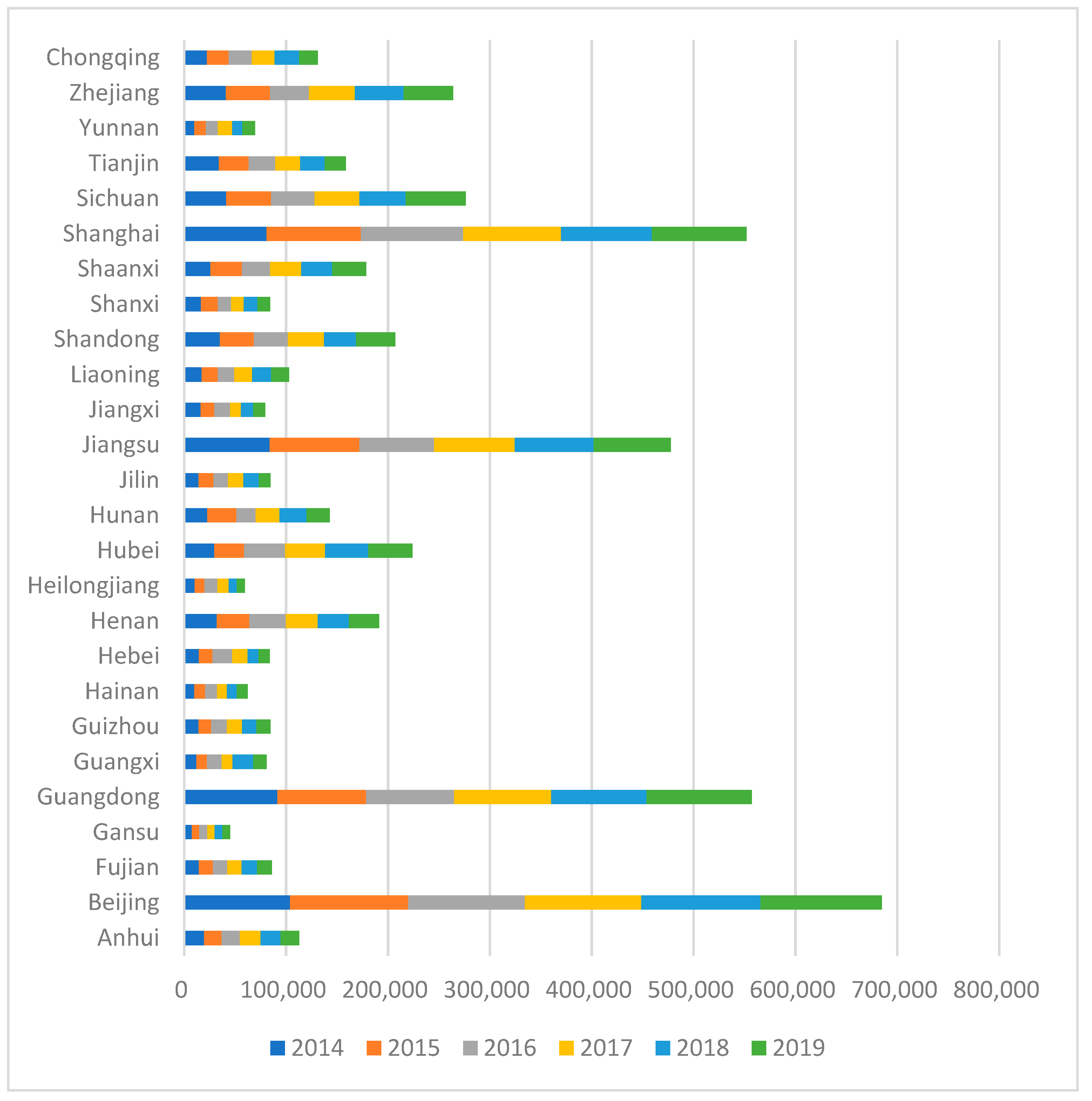
As shown in Figure 1, the number of university graduates in each province increased annually from 2014 to 2019, and the number of university graduates was correlated with the province’s native population and economic growth. Generally speaking, provinces with larger populations have a greater proportion of graduates. There were relatively more graduates from the populous provinces in the eastern and central regions, and relatively few graduates from the western regions. Figure 1 shows that the employment mobility of university graduates presents a clear regional imbalance.

3.2. The Employment Mobility of “Double First-Class” University Graduates Is Sticky

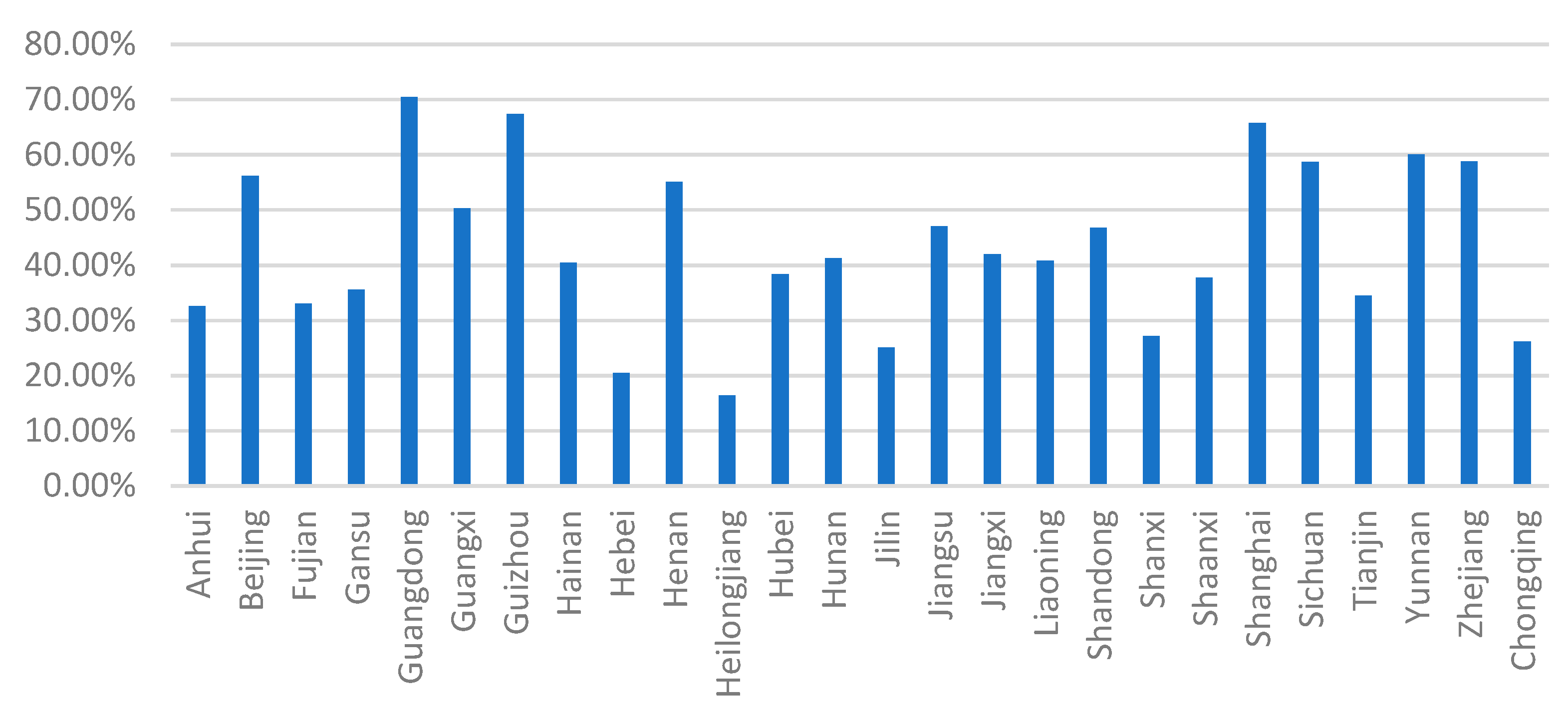
Based on Figure 2, it can be seen that the employment mobility of “Double First-Class” university graduates showed a strong stickiness. Beijing, Guangdong, Guangxi, Henan, Jiangsu, Shandong, Shanghai, Yunnan, and Zhejiang’s “Double First-Class” university graduates were relatively sticky, and the proportion of graduates staying in local employment was more than 50% each year. The proportion of graduates from Heilongjiang, Jilin, Liaoning, and the western regions of “Double First-Class” universities staying in local employment was relatively small. The conclusion is that “dual first-class” university graduates in the central and eastern regions were more sticky when it came to choosing a place of employment, whereas “Double First-Class” university graduates in the west and northeast regions were less sticky.

Guangzhou, Shanghai, Guizhou, Zhejiang, Yunnan, and Henan were the top six provinces where graduates of “Double First-Class” universities stayed employed locally, and the proportions were 72%, 71%, 61%, 60%, and 59%. The proportion of graduates from “Double First-Class” universities staying in employment in this province was closely related to geographic location and climate. The eastern and central plains and the provinces with suitable climates for survival retained more population. The employment rate of “Double First-Class” university graduates in their places of study was also related to the province’s economic development level. In general, economically developed provinces can retain a greater number of graduates for local employment. Due to a lack of educational resources in the western provinces, the “Double First-Class” universities recruited relatively few students from the province and generally attracted more students from other provinces to study. Frequently, a region’s openness is also a factor in determining whether university graduates remain in local employment. Students from less developed areas typically attend school and work in their communities.

3.3. The Employment Mobility of “Double First-Class” University Graduates Exhibits Concentration

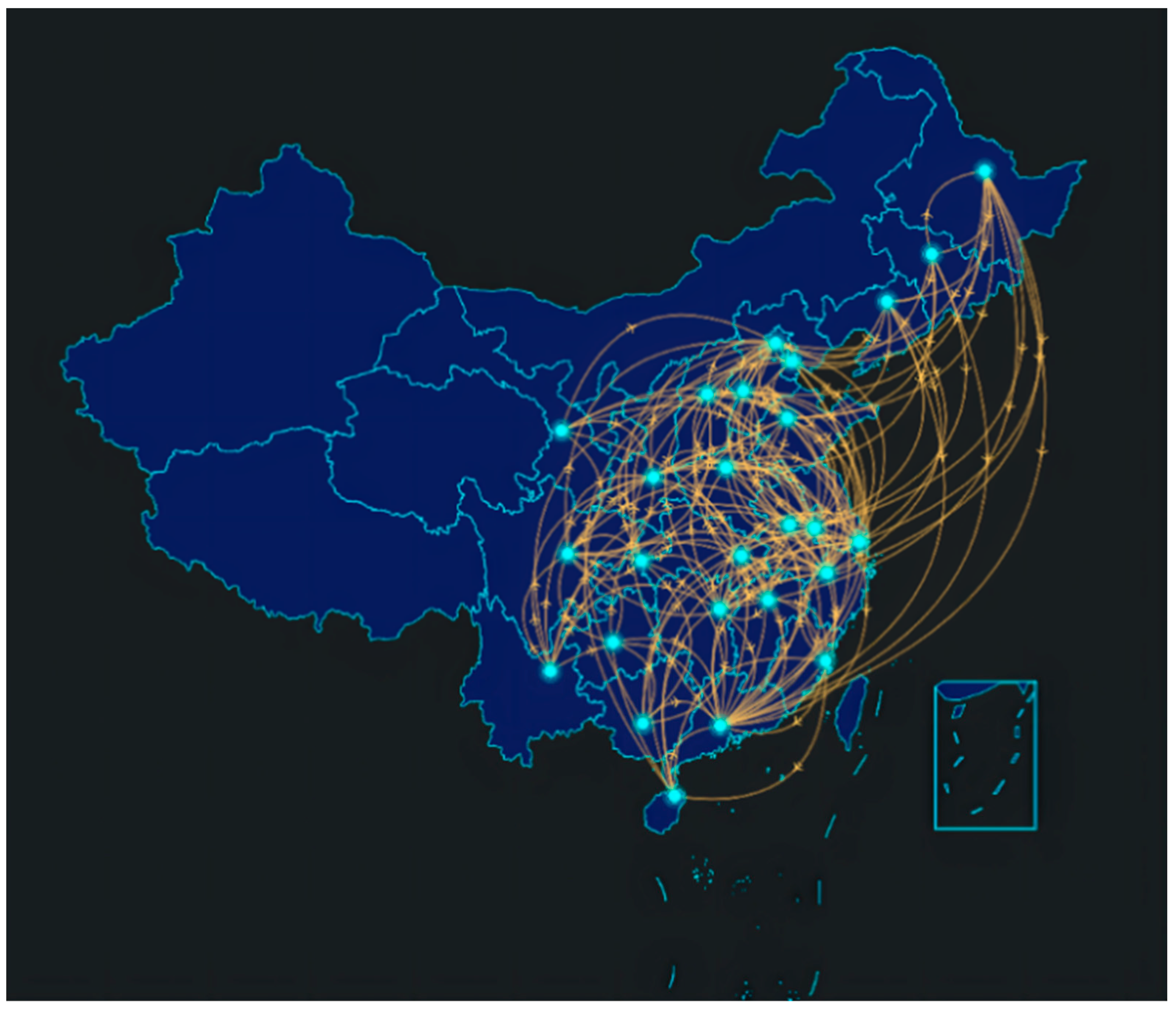
Through the statistics of graduate employment quality reports in universities, we obtained the employment mobility rate and number of migrants from each college province to province. This paper counted a total of 676 province-to-province mobility paths of “Double First-Class” university graduation from 2014 to 2019. Figure 3 is a diagram of the main mobility paths with a graduate employment mobility rate of more than 2% in the “Double First-Class” universities, with a total of 167 routes. This paper used ECHARTS to generate a visualization of graduate employment mobility paths. It can be seen that the employment of “Double First-Class” university graduates was concentrated in Beijing, Guangdong, Shanghai, Zhejiang, and Jiangsu. As one can see, graduates of “dual first-class” universities preferred to work in economically developed provinces. On the one hand, these students possess cutting-edge theoretical knowledge, science, and technology, as well as the ability to find work in economically developed cities. On the other hand, these cities offer graduates a plethora of employment opportunities, relatively high wages, and a broader development platform.

4. Analysis of Influencing Factors of Employment Mobility of “Double First-Class” University Graduates

4.1. Fixed-Effects Model Building

Based on the above data, this paper used panel data from 2014 to 2019 to study the factors influencing the employment mobility of university graduates. Panel data models included a mixed regression model, a random effect model, and a fixed-effect model. In this paper, through the Hausmann test, the fixed-effect model was used to analyze the factors affecting the employment mobility of university graduates.

$$ln{Y}_{it}={\alpha }_0+{\beta }_{1}ln{G}_{it}+{\beta }_{2}ln{W}_{it}+{\beta }_{3}ln{H}_{it}+{\beta }_{4}ln{T}_{it}+{\beta }_{5}ln{S}_{it}+{\beta }_{6}ln{P}_{it}+{\delta }_c+U_{it}$$

(1)

In Equation (1), i denotes the province, t denotes the year, as the constant term; ${\alpha }_0$ is the constant term.$ln{Y}_{it}$ indicates the logarithm of the number of university graduates’ mobility. $ln{G}_{it}$ represents the logarithm of GDP per capita [45]. $ln{W}_{it}$ represents the logarithm of the average wage [46]. $ln{H}_{it}$ represents the logarithm of the average sales price of commercial housing [47,48,49]. $ln{T}_{it}$ represents the logarithm of the local financial expenditure on science and technology [50]. $ln{S}_{it}$ represents the logarithm of the educational level [51], expressed by the number of ordinary primary schools and the number of higher education schools. $ln{P}_{it}$ represents the logarithm of a series of control variables [51,52], expressed in terms of public service level, choice of urban road area per capita, number of beds in medical and health institutions, and Internet broadband access users. $U_{it}$ is the error term. ${\delta }_C$ represents the city’s unobserved fixed effects [52], the city’s customs, history, landscape, and ecological environment. Since it cannot be observed and may be associated with independent variables, the model needed to be processed by first-order difference processing. The latter model was:

$$\mathsf{\Delta }ln{Y}_{it}={\lambda }_1\mathsf{\Delta }ln{G}_{it}+{\lambda }_2\mathsf{\Delta }ln{W}_{it}+{\lambda }_3\mathsf{\Delta }ln{H}_{it}+{\lambda }_4\mathsf{\Delta }ln{T}_{it}+{\lambda }_5\mathsf{\Delta }ln{S}_{it}+{\lambda }_6\mathsf{\Delta }{P}_{it}+\mathsf{\Delta }{U}_{it}$$

(2)

After model processing, the urban fixed effect ${\delta }_c$ was eliminated. In Equation (2), $\Delta ln{G}_{it}$ represents the difference between the logarithmic current period of per capita GDP and the previous period. $\mathsf{\Delta }ln{W}_{it}$ represents the logarithmic current period of the average salary of urban employees and the difference between the previous period. $\mathsf{\Delta }ln{H}_{it}$ represents the average commercial housing sales price of the number of a current phase difference between the previous period. $\mathsf{\Delta }ln{T}_{it}$ represents the difference between the logarithmic current and the previous period of the local fiscal expenditure on science and technology. $\Delta ln{S}_{it}$ represents the difference between the logarithm of the number of ordinary institutions of higher learning and the number of ordinary primary schools in the current period and the previous period. $P_{it}$ represents the variation of per capita urban road area, number of beds in medical and health institutions, and Internet broadband access users. $\Delta U_{it}$ represents the difference of the error term.

4.2. Variable Description

The data used in this study were calculated from the Graduate Employment Quality Report of the “Double First-Class” universities in 26 provinces and cities in Eastern, Central, and Western China from 2014 to 2019, the annual data of university graduates in each province published on the website of the Ministry of Education, and the data of China Statistical Yearbook and statistical yearbook of each province.

Through the statistics of the employment mobility data of graduates from “Double First-Class” universities in each province from 2014 to 2019, the employment mobility database of graduates from “Double First-Class” universities in each province was established. Due to a data shortage for “Double First-Class” universities in some provinces, this article counted the employment mobility of “Double First-Class” university graduates in 26 provinces and cities. This paper selected 22 groups of data that affect the employment mobility of university graduates in six aspects: economic level, industrial structure level, urban development level, science and technology education level, living environment, and quality of life.

Table 1. Variable descriptive statistics.

	Variable Name	Obs	Mean	Std. Dev.	Min	Max
Economic level	GDP	156	29,668	21,393	3449	107,987
	Average wage	156	59,527	29,675	25,202	164,563
	Commodity house price	156	8677	6268	3629	37,420
	Unemployment rate	156	3.173	0.647	1.300	4.500
Industrial structure level	Rationalization of industrial structure	156	1.431	0.789	0.704	5.234
	Advanced industrial structure	156	0.861	0.307	0.251	1.757
	High-tech industrial structure	156	0.147	0.103	0.0222	0.468
	Producer service industry structure	156	2.266	0.726	1.381	5.049
Urban development level	Fixed asset investment	156	14,686	8812	1689	37,664
	Fiscal decentralization	156	6.102	2.602	3.150	14.89
	Urbanization rate	156	0.599	0.119	0.400	0.896
	FDI/GDP	156	0.0217	0.0170	0.000385	0.126
Science and technology education level	R&D full-time equivalent	156	106,560	131,806	1779	642,490
	Science and Technology Fiscal Expenditure	156	16,061	18,089	1238	116,879
	Number of regular high schools	156	95.15	34.46	17	167
	Number of elementary schools	156	6460	4573	698	25,578
Living environment	Road mileage per square kilometer	156	1.081	0.447	0.304	2.115
	Number of medical and health beds	156	28.07	15.00	3.450	64.01
	Harmless treatment of domestic waste	156	24,740	19,377	3880	134,543
Quality of Life	Internet access users	156	12,066	8371	1203	38,016
	Number of performing arts groups	156	507.8	524.2	39	2859
	Number of people participating in pension insurance	156	1430	1029	224.9	5392

summarizes all the variables used in this paper.

To prevent problems with collinearity and endogeneity, the following variables were picked for fitting when the panel fixed effects model was used. According to the above model, the explained variable was the number of university graduates in each province after the migration; the core explanatory variable was economic factors, including per capita GDP (Pergdp), the average wage of urban employees (Wage), and the average sales price of commercial housing (House); explanatory variables were local financial expenditure on science and technology (Tech), number of ordinary universities (Univer), number of ordinary primary schools (Prim); other control variables were the per capita urban road area (Road), the number of beds in medical and health institutions (Health), and the number of Internet Broadband Access Users (Net). In this paper, the variance expansion factor was used to test the data. The average value of the variance expansion factor VIF of each variable was 6.28, and the VIF of each variable was less than 10. There was no collinearity in the above data.

4.3. Empirical Analysis

Model I–Model VI were the regression results of increasing variables in turn. Model VII was the regression result using the instrumental variable method to test the endogeneity of the model.

According to

Table 2. National regression model.

Dependent Variable	Model I	Model II	Model III	Model IV	Mode V	Model VI	Model VII
	Number of University Graduates after Migration in Each Province
(Pergdp)				1.5550 ***	1.6446 ***	1.6782 ***	2.8055 *
				(3.39)	(3.03)	(3.08)	(1.83)
(Wage)				−0.7835 **	−0.6687	−0.6524	0.4577
				(−2.31)	(−1.45)	(−1.41)	(0.31)
(House)					−0.1435	0.4958	−1.2683
					(−0.38)	(0.21)	(−1.29)
(House_sq)						−0.0345
						(−0.30)
(Tech)			0.2803 **	0.1703	0.1652	0.1642	0.1215
			(2.53)	(1.65)	(1.61)	(1.61)	(0.56)
(Univer)		1.8275 **	1.7631 **	1.5173 ***	1.4563 ***	1.4181 **	2.3227 **
		(2.77)	(2.77)	(2.95)	(3.03)	(2.70)	(2.37)
(Prim)		−0.2154	−0.4432	−0.7075 **	−0.7205 **	−0.7071 *	−1.0944 ***
		(−0.61)	(−1.24)	(−2.15)	(−2.17)	(−2.03)	(−2.70)
(Road)	0.1377	0.1381	−0.0142	−0.3225	−0.3614	−0.3755	−0.3731
	(0.52)	(0.70)	(−0.07)	(−1.22)	(−1.09)	(−1.16)	(−0.74)
(Health)	0.9721 **	0.6609	−0.1039	−0.4356	−0.4046	−0.4598	−1.2901
	(2.16)	(1.19)	(−0.16)	(−0.56)	(−0.53)	(−0.56)	(−0.96)
(Net)	−0.2027 *	−0.3181 **	−0.2888 **	−0.3883 **	−0.4090 **	−0.4176 **	−0.7672 *
	(−1.77)	(−2.38)	(−2.42)	(−3.46)	(−3.18)	(−3.31)	(−1.84)
(Constant)	3.2375	1.0818	9.2633	11.9025 *	11.5202 *	8.8332	8.3677
	(0.92)	(0.17)	(1.40)	(1.84)	(1.87)	(0.77)	(0.80)
Observations	156	156	156	156	156	156	130
Number of provinces	26	26	26	26	26	26	26

Note: *, **, *** mean significant at the levels of 10%, 5%, and 1% respectively, and the number in parentheses is the “t” value of the estimated coefficient.

, it can be seen in Model I that the number of beds in medical institutions and the number of Internet broadband access users were both significant, indicating that medical care and the Internet had a significant impact on the mobility of university graduates. According to Model II, after adding the variable of education level, the result shows that the number of ordinary universities was significantly positive at the 5% level. This shows that the richness of higher education resources affected the employment of university graduates. Higher education resource-rich provinces attract more university graduates.

Model III was the addition of variables related to the level of technological innovation, and the results show that local fiscal expenditures on science and technology and the number of universities were both significantly positive. Among them, for every 1% increase in local financial science and technology expenditures, the number of university graduates’ mobility to the province increased by 0.2803%, which was statistically significant at the 5% level. This proves that the more local finance invests in science and technology, the more university graduates it can attract. The higher the level of technological innovation in a place, the more high-quality talents it attracts. Areas with a high level of technological innovation provide a good employment platform, technical support, and sufficient funds for high-quality talents.

According to Model IV, after adding the relevant variables of economic factors, the results show that per capita GDP, average wages, number of higher education schools, and elementary schools were all significant. This shows that after controlling for other variables, the level of economic development and education have a significant impact on the employment mobility of university graduates. With a higher level of economic development in the region’s living standards, wages are high, which meets the pursuit of high-quality talent to higher economic conditions. However, the number of its primary and secondary schools’ coefficients was negative, indicating that fewer primary schools attract more university graduates instead. The possible reason is that the school districts where there are many elementary schools have relatively more houses, and the age of university graduates ranges from 20 to 30 at the time of employment. Most of them are relatively young and do not have children. Therefore, the attractiveness of basic education to university graduates is insufficient.

According to Model V, after adding the housing price factor, the results show that the average salary and the average housing price were not significant, and the per capita GDP, the number of universities and schools, the number of primary schools, and the number of Internet users were significant. When housing costs were taken into account, the attractiveness of wages for university graduates’ employment diminishes significantly. This demonstrates that housing prices have a “crowding out effect” on university graduates’ mobility. High housing costs increase the cost of living for recent graduates, while high wages detract from their attractiveness. After including the average house price’s square term in Model VI, the average house price’s square term was negative, indicating an inverted U-shaped relationship between the average house price and university students’ employment mobility.

Model VII employed the instrumental variable method to eliminate the model’s endogeneity. The observations were reduced to 130 by making the first-order lags of GDP per capita, the first-order lags of average wages, and the first-order lags of average house prices as instrumental variables. The regression results show that the per capita GDP, the number of universities, the number of primary schools, and the number of netizens were all significant, which was consistent with the original model V.

5. Prediction of the Employment Mobility of Graduates from “Double First-Class” Universities

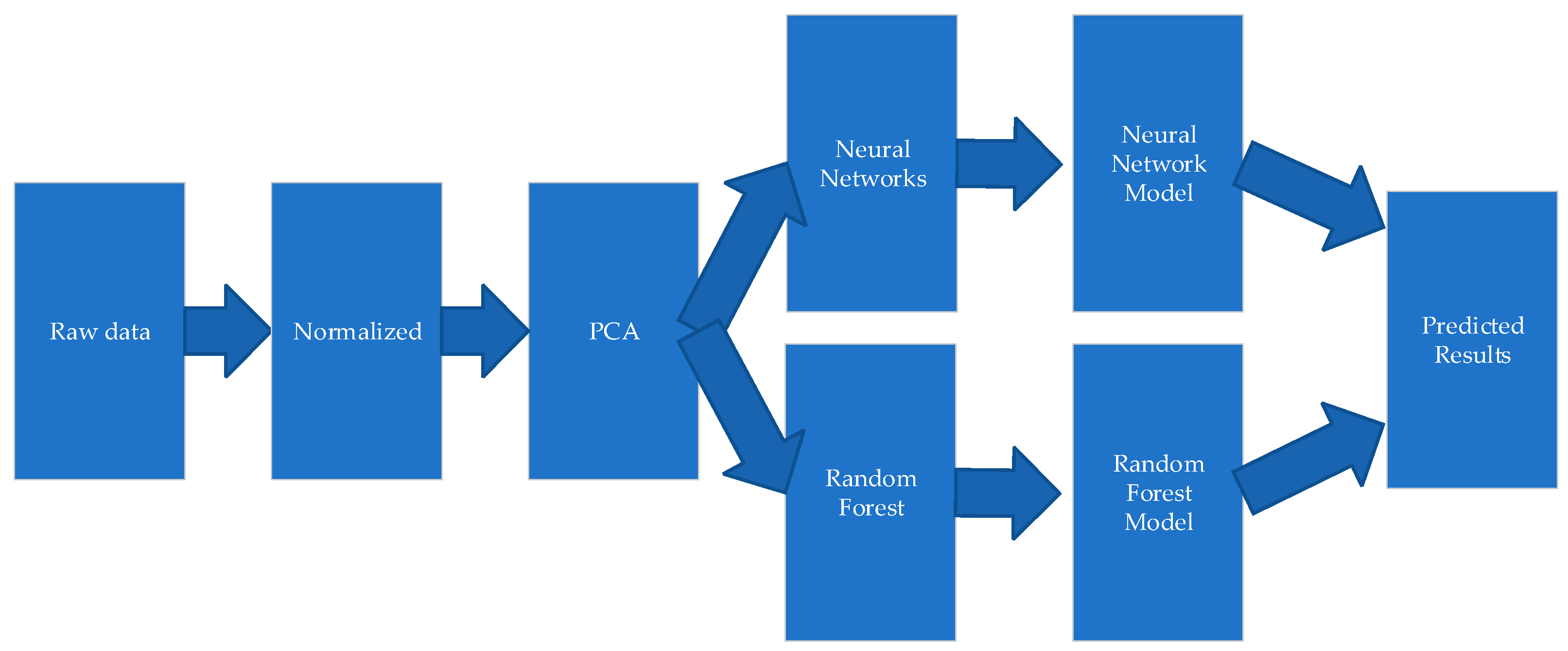
Figure 4 is a mobility chart of the prediction of the retention rate of “double first-class” university graduates. This paper used the following steps to predict the employment retention rate of “Double First-Class” university graduates:

-

Normalization of original data;

-

Use of PCA to reduce the dimension of the data, and reduce the data from 22 dimensions to 9 dimensions;

-

Random forest model prediction results;

-

BP neural network model prediction results;

-

Comparative analysis model and prediction accuracy.

5.1. The Principle of PCA

Through the statistics of the geographical mobility data of the employment of graduates “Double First-Class” universities in each province from 2014 to 2019, this paper established a database of graduate employment mobility of “Double First-Class” universities in each province. Due to the lack of data statistics in individual provinces, this paper counted the employment mobility of graduates from “Double First-Class” universities in 26 provinces and cities, including 22 parameter indicators.

This paper utilized the Z-score standardization method to normalize the data to eliminate the prediction error caused by the various dimensions of the early warning indicator data. This method provides the original data’s mean and standard deviation to standardize the data. The processed data adhere to the normal distribution with a mean of 0 and a standard deviation of 1, and the transformation function is:

$$x^{*}=\frac{x-\mu }{\sigma }$$

(3)

where μ is the mean of all sample data and σ is the standard deviation of all sample data.

Since the input data have too many dimensions, an excessive number of irrelevant x inputs can easily result in the overfitting of the model during training. We used the PCA dimensionality reduction method to reduce the data from 22 dimensions to 9 dimensions to improve the experimental efficiency. PCA (Principal Component Analysis) is a common data analysis method that is frequently used for dimensionality reduction in high-dimensional data and can be used to extract the data’s main feature components [53]. The primary goal of dimensionality reduction is to find a representation of the data with fewer dimensions that retain as much information as possible [54]. PCA is a technique for multivariate statistical analysis [55]. It replaces the original variables with a linear combination of the original variables to form an uncorrelated comprehensive variable under the premise of ensuring the minimum loss of information of the original variables, thus removing the correlation between the original variables [56]. Utilizing the concept of dimensionality reduction, the PCA method can comprehend the primary contradiction of the research problem, simplify the complex problem, and enhance the research efficiency [57].

Assuming that a certain thing is composed of m indicators, which are represented by E₁, E₂, …, E_m, respectively, and the m indicators form an m-dimensional random vector, E = (E₁, E₂, …, E_m)’, let q be mean value of the random vector E. The random vector E can be transformed into a new comprehensive variable by a linear transformation, which is represented by W. Thus, the new comprehensive variable can be linearly represented by the original variable, which satisfies the following formula:

W₁ = q₁₁E₁ + q₁₂E₂ + … + q_1mE_m

(4)

W₂ = q₂₁E₁ + q₂₂E₂ + … + q_2mE_m

(5)

W_n = q_n1E₁ + q_n2E₂ + … + q_nmE_m

(6)

In the equation: The coefficient q_ij is calculable using the following principles:

(1)

q_i1² + q_i2² +… + q_im² = 1 (i = 1, 2, …, m)

(7)

(2)

W_i is linearly independent of W_j (i ≠ j; i, j = 1, 2, …, n);

(3)

W₁ is the one with the largest variance among all linear combinations of E₁, E₂, …, Em; W₂ is the one with the largest variance among all linear combinations of E₁, E₂, …, E_m that are not related to W₁; W_N is the one with the largest variance among all linear combinations when W₁, W₂, … W_N−1 is uncorrelated.

The new variable indexes W₁, W₂, … W_N determined in this way are called the first principal component, the second component, …, and the nth principal component of the original variable indexes E₁, E₂, …, E_m, respectively. Among them, the variance of W₁ accounts for the largest proportion of the total variance, and the variances of W₁, W₂, … W_N decrease in turn. When analyzing practical problems, it is common practice to select the first few largest principal components, which not only reduces the number of variables but also captures the main contradiction of the problem and simplifies the relationship between variables. In this paper, the fit method of PCA was used to train all training data, resulting in the trained PCA model.

Figure 5 depicts the ranking of factors affecting the employment mobility of university graduates after dimension reduction using PCA. It can be seen that economic level factors, including the regional GDP, wages, the average sales price of commercial housing, and the unemployment rate of each province and city, were the primary factors affecting the employment mobility of “Double First-Class” university graduates. The result after PCA for the gross regional product was 0.3178, the result after PCA for wages was 0.2561, and the result after PCA for the average sales price of commercial housing was 0.1088. The level of industrial structure, including the rationalization of industrial structure, the advanced level of industrial structure, the level of high-tech industrial structure, and the level of the industrial structure of producer services, was a secondary factor affecting the employment migration of “Double First-Class” university graduates. The result of PCA after the rationalization of industrial structure was 0.0442, the result after PCA of advanced industrial structure was 0.0400, the result after PCA of high-tech industrial structure level was 0.0343, and the result of industrial structure level of producer service industry after PCA was 0.0321.

The impact of urban development level, scientific and technological education level, living environment, and quality of life on the employment mobility of “Double First-Class” university graduates was relatively small. Therefore, it can be concluded that the ranking of the importance of each principal component after PCA was consistent with the previous results using the fixed effects model. Economic factors were the most important factors affecting the employment mobility of graduates from “Double First-Class” universities.

5.2. Random Forest Prediction Model

Random forest is a statistical learning theory proposed by Breiman in 1996 [58]. It uses the bootstrap resampling method to extract multiple samples from the original sample, models each bootstrap sample as a decision tree, and combines the predictions of multiple decision trees to obtain the final prediction result through voting [59]. The random forest has excellent tolerance for outliers and noise and is not susceptible to overfitting. A random forest is a natural tool for nonlinear modeling. It only requires the continuous training of sample data [60]. It is ideally suited for application problems involving irregular multi-constraint conditions and missing data. This method overcomes the disadvantages of indirect, time-consuming, and inefficient information and knowledge acquisition caused by traditional forecasting methods and lays the groundwork for the practical application of forecasting [61]. It is currently one of the most popular frontier research fields in data mining and bioinformatics, and it has been successfully implemented in medicine, economics, and management, among other fields [62].

The principle of the random forest is as follows.

First, set the original sample set T, where the sample size is N, and use the Bootstrap sampling method to extract K sample sets from the sample set to generate random vector decisions.

Second, a decision tree model {h ($x,{\theta }_i$), i = 1, …, k} is established for evaluating the influencing factors of talent attraction in first-tier cities by using the random vector sequence i distributed independently, where the matrix x is the independent variable.

Finally, after k rounds of training, a regression tree model sequence {h₁(x), h₂($x$) …, h_k ($x$)} is obtained. For any given new sample, its prediction result is the average summary of the results of k rounds, and its formula is:

$$H\left(x\right)=argmax{\displaystyle {{\displaystyle \sum }}_{i=1}^k}I\left(h_i\left(x\right)=Y\right)$$

(8)

In the classification model, $h_i$ represents a single decision tree in the classification model; $H\left(x\right)$ is the random forest combined classification model; Y is the output target variable.

The random forest data processing procedure is as follows:

(1)

In this paper, Bootstrap sampling was used to randomly select N training subsets from the original training set for 22 influencing factors, with the size of each training subset being approximately two-thirds of the original training set. After many repeats, there are always some samples that cannot be drawn; these samples form M out-of-bag data sets, which serve as the test sample set of random forest.

(2)

At each node of each decision tree, randomly select m variables as alternative branch variables, where the number of randomly selected variables is less than the number of original variables, and then select the optimal branch according to the branch goodness criterion.

(3)

Each decision tree begins recursive branching from the top down, and the minimum size of the leaf node is set to five. Based on this as the termination condition for the growth of the regression tree, a random forest model is generated from the generated decision tree.

The final output of the algorithm is implemented by the majority voting method. A test sample will be classified based on the randomly constructed N decision subtrees, the results of each subtree will be summarized, and the classification result with the most votes will be the final output of the classification algorithm [63].

The results from

Table 3. The number and depth results of different tree nodes in random forest.

Number	10	10	10	50	50	50	100	100	100	500	500	500
Depth	10	50	100	10	50	100	10	50	100	10	50	100
MSE	0.1806	0.1799	0.1866	0.1785	0.1761	0.1801	0.1795	0.1794	0.1804	0.1792	0.1782	0.1802
MAE	0.1469	0.1463	0.1523	0.1457	0.1443	0.1468	0.1464	0.1461	0.1469	0.1460	0.1454	0.1467

. show that the number of random forest trees was set to 10, 50, 100, and 500, respectively, and the maximum depth of trees was set to 10, 50, and 100, respectively. When the number of trees in the random forest was 10 and the maximum depth of trees was 50, the value of the loss function MSE was 0.1799 and the value of MAE was 0.1463. When the number of trees in the random forest was 50 and the maximum depth of trees was 50, the value of the loss function MSE was 0.1761 and the value of MAE was 0.1443. When the number of trees in the random forest was 100 and the maximum depth of trees was 50, the loss function MSE was 0.1794 and MAE was 0.1461. When the number of trees in the random forest was 500 and the maximum depth of trees was 50, the metric value of the loss function MSE was 0.1782, and the metric value of MAE was 0.1454. It can be seen that when the number of trees in the random forest was 50 and the maximum depth of the trees was 50, the minimum value of MSE was 0.1761, and the value of MAE was also the minimum 0.1443. At this time, the prediction accuracy of random forest was the best. These values were the results obtained after dimensionality reduction using PCA. The loss function obtained without PCA dimensionality reduction was relatively large.

5.3. BP Neural Network Model

BP neural network is also called an error backpropagation neural network [64]. The BP algorithm’s learning process consists of two parts: forward propagation and backward propagation. The direction of forwarding propagation is the input layer-hidden layer-output layer. Each neuronal layer influences the neurons in the next layer [65]. The error is calculated by subtracting the net-work output from the sample’s expected output. If the error does not meet the threshold, backpropagation is carried out. It propagates forward after returning layer by layer along the original path, adjusting the weights between each neuron. This process is repeatedly looped until the error reaches a predetermined threshold, at which point propagation ceases [66,67]. 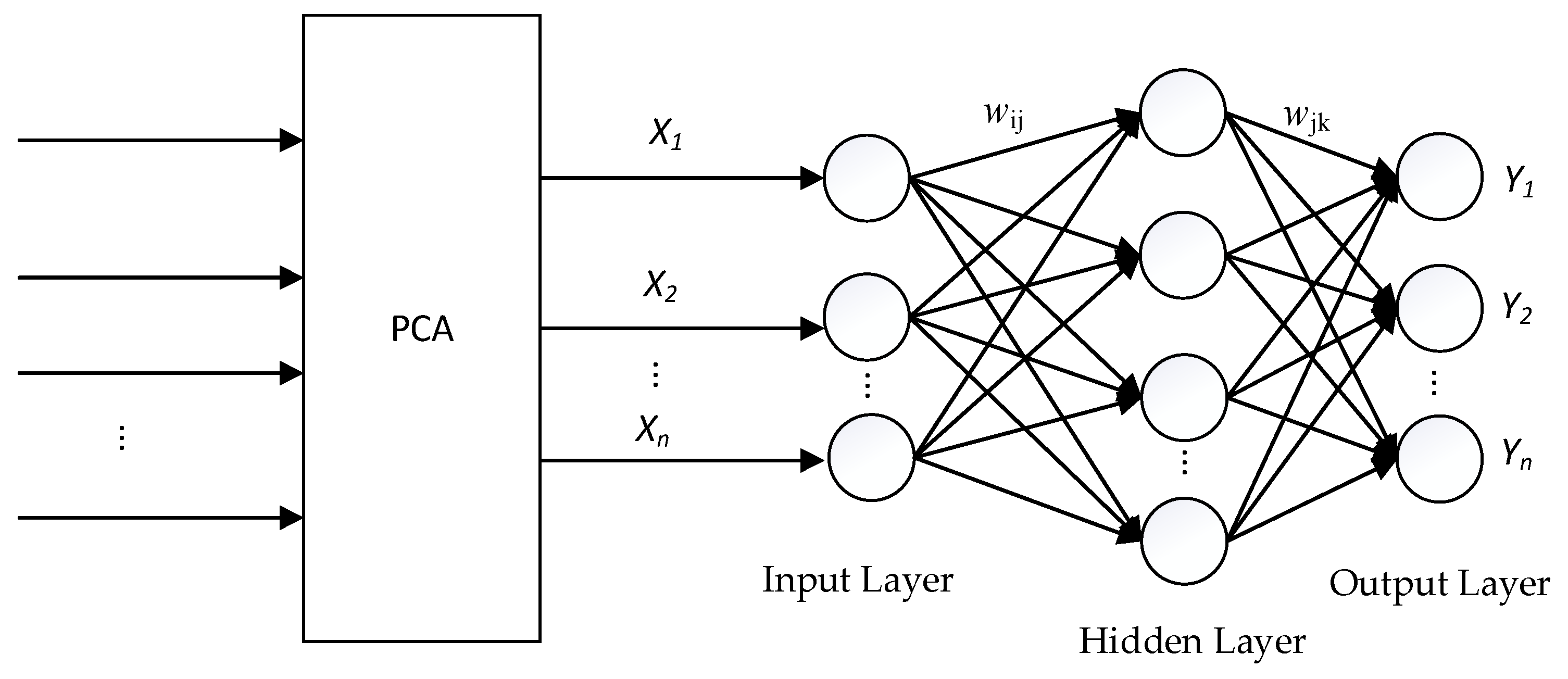Figure 6 shows the structure of the PCA-BP neural network.

General algorithmic operations of the BP neural network:

Let the input vectors be X₁, X₂, X₃, …, X_n; the corresponding expected output vectors are Y₁, Y₂, Y₃, …, Y_n; w_ij and w_jk are the connection weights from the input layer to the hidden layer, and the connection weights are from the hidden layer to the output layer, respectively; n and m are the number of input nodes and the number of output nodes, respectively.

(1)

Assign random values in the interval [−1, +1] to the connection weights w_ij, w_jk and the thresholds a, b;

(2)

According to the input vector X, the connection weight w_ij from the input layer to the hidden layer and the hidden layer threshold a, the hidden layer output T is calculated.

$$T_j=f\left({{\displaystyle \sum }}_{i=1}^n{w}_{ij}{x}_i-a_i\right), j=1,2,3,\dots ,l$$

(9)

In the equation, l represents the number of nodes in the hidden layer; f represents the activation function of the hidden layer, and the activation function is defined as l is the number of nodes in the hidden layer; f is the activation function of the hidden layer, and the activation function is $f\left(x\right)=\frac{1}{1+e^{-x}}$

(3)

According to the hidden layer output T, weight w_ij, and threshold b, through the transfer function, the actual output value C of each unit of the output layer is output;

(4)

According to the expected input Y(Y₁, Y₂, Y₃, …, Y_n) and the actual output value C, the correction error e of each unit of the output layer is calculated;

e_k = Y_k − C_k, k = 1, 2, 3, …, m

(10)

$$W_{ij}=w_{ij}+\mu T_j(1-T_j)x_i$$

(11)

$$W_{jk}=w_{jk}+\mu T_j{e}_k$$

(12)

where: i = 1, 2, 3, …, n; j = 1, 2, 3, …, l; k = 1, 2, 3, …, m; $\mu$ is the learning rate.

$$a_j=a_j+\mu T_j(1-T_j), j=1, 2, 3,\dots ,l$$

(13)

$$b_k=b_k+e_k, k=1, 2, 3,\dots ,m$$

(14)

(5)

Determine whether the global error meets the specified accuracy requirements and whether the number of iteration steps exceeds the specified number of steps. If true, the algorithm terminates; otherwise, it returns.

As shown in

Table 4. Loss function (MSE) and quality metric (MAE) values of the training and validation set.

Epoch	Training Set		Validation Set
	MSE	MAE	MSE	MAE
1	0.6977	0.6777	0.1484	0.1239
2	0.1643	0.1364	0.1411	0.1164
3	0.1595	0.1332	0.1400	0.1160
4	0.1573	0.1314	0.1392	0.1155
5	0.1560	0.1304	0.1385	0.1150
6	0.1549	0.1295	0.1378	0.1146
7	0.1539	0.1288	0.1372	0.1143
8	0.1533	0.1282	0.1367	0.1140
9	0.1527	0.1277	0.1362	0.1137
10	0.1521	0.1272	0.1358	0.1135
…	…	…	…	…
90	0.1301	0.1088	0.1159	0.0930
91	0.1298	0.1085	0.1158	0.0928
92	0.1295	0.1083	0.1158	0.0927
93	0.1292	0.1080	0.1158	0.0926
94	0.1289	0.1078	0.1158	0.0926
95	0.1287	0.1076	0.1158	0.0925
96	0.1284	0.1073	0.1158	0.0924
97	0.1282	0.1071	0.1158	0.0923
98	0.1279	0.1069	0.1158	0.0922
99	0.1277	0.1066	0.1159	0.0922
100	0.1274	0.1064	0.1159	0.0921

and Figure 7, the loss function MSE in the training set had a value of 0.6977 at the 1st epoch and decreased to 0.1274 at the 100th epoch. The value of the MAE metric was 0.6778 and decreased to 0.1064 at the 100th epoch. The lowest MSE and MAE values were recorded at the 100th epoch. In the validation set, the value of the MSE loss function at the 1st epoch was 0.1484 and decreased to 0.1159 at the 100th epoch. The value of the MAE metric was 0.1239 and decreased to 0.0921. The lowest MSE and MAE values were recorded at the 100th epoch.

As shown in

Table 5. Loss function (MSE) and quality metric (MAE) values of the training and validation set after PCA.

Epoch	Training Set		Validation Set
	MSE	MAE	MSE	MAE
1	0.3319	0.2833	0.2085	0.1811
2	0.2097	0.1789	0.1286	0.1015
3	0.1617	0.1315	0.1315	0.1107
4	0.1553	0.1277	0.1255	0.1032
5	0.1534	0.1250	0.1252	0.1047
6	0.1521	0.1239	0.1238	0.1036
7	0.1511	0.1228	0.1233	0.1034
8	0.1503	0.1219	0.1230	0.1031
9	0.1495	0.1212	0.1228	0.1030
10	0.1489	0.1206	0.1227	0.1028
…	…	…	…	…
90	0.1167	0.0890	0.1156	0.0941
91	0.1164	0.0888	0.1155	0.0941
92	0.1161	0.0886	0.1154	0.0941
93	0.1158	0.0883	0.1154	0.0941
94	0.1154	0.0882	0.1152	0.0940
95	0.1151	0.0880	0.1152	0.0940
96	0.1148	0.0878	0.1151	0.0940
97	0.1145	0.0877	0.1152	0.0942
98	0.1142	0.0876	0.1152	0.0942
99	0.1140	0.0874	0.1152	0.0943
100	0.1137	0.0873	0.1152	0.0943

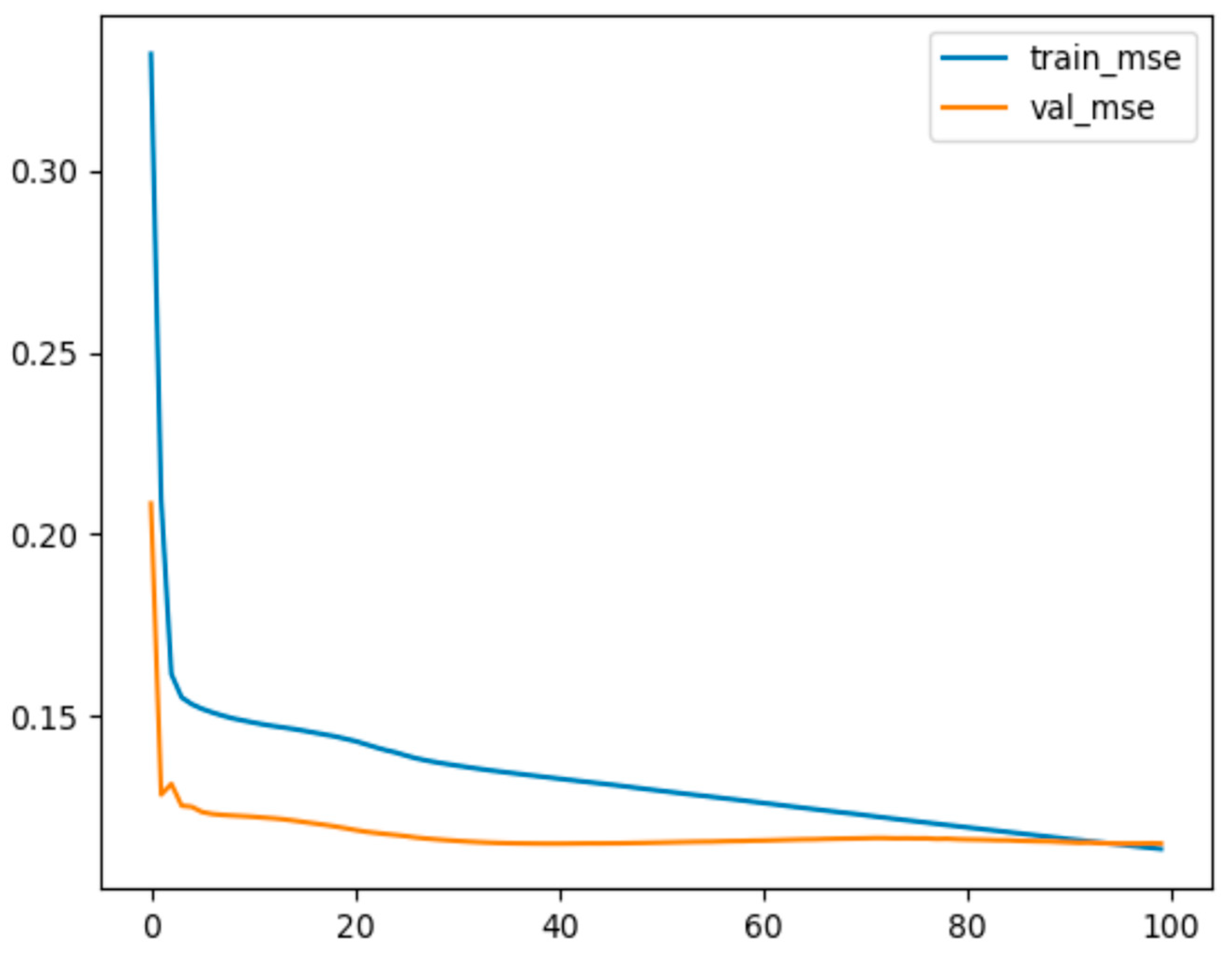
and Figure 8, after dimensionality reduction using PCA, the loss function MSE in the training set had a value of 0.3319 at the 1st epoch and decreased to 0.1137 at the 100th epoch. The value of the MAE metric was 0.2833 and decreased to 0.0873 at the 100th epoch. The lowest MSE and MAE values were recorded at the 100th epoch. In the validation set, the value of the MSE loss function at the 1st epoch was 0.2085 and decreased to 0.1152 at the 100th epoch. The value of the MAE metric was 0.1811 and decreased to 0.0943. The lowest values of MSE and MAE were recorded at the 96th epoch—0.1151 and 0.0940, respectively. The results indicate that the loss function (MSE) and quality indicator (MAE) values of the training and validation sets were not significantly different, and the PCA-BP neural network model can accurately predict the employment retention rate of “Double First-Class” university graduates.

To conclude the above, after dimension reduction via PCA, the minimum loss function (MSE) obtained by the random forest model was 0.1761, whereas the minimum loss function (MSE) obtained by the BP neural network model was 0.1137. The prediction accuracy obtained after using PCA to reduce the dimension was better, and the loss function was relatively small. Comparing random forestry and BP neural network revealed that the BP neural network model provided a more accurate prediction of the employee retention rate of “Double First-Class” university graduates, whereas the relative prediction accuracy of the random forestry model was low.

6. Conclusions and Policy Implications

This paper took the employment mobility data of graduates from “Double First-Class” universities in various provinces from 2014 to 2019 as the research object and counted the panel data on the employment mobility of graduates from “Double First-Class” universities in 26 provinces and cities, with a total of 156 groups. According to the availability of data, this paper counted the employment mobility data of graduates from “Double First-Class” universities for 6 years. There were regional differences in the employment mobility of graduates from “Double-First-Class” universities.

Most graduates stayed in their places of study for employment, and they tended to focus on large cities such as Beijing, Shanghai, and Guangzhou. Economic factors were the main factors affecting the employment mobility of graduates from “Double First-Class” universities. Due to the small number of data years, the large fluctuations in the number of influencing factors, and the existence of certain correlations between indicators, traditional linear prediction methods may not have been able to predict correctly. PCA can effectively remove the correlation between data and reduce the input of indicators, which is conducive to sorting and calculation, but it cannot reflect the nonlinear relationship between indicators, and cannot directly predict the unemployment rate of university graduates.

Through transformation, this method can reduce the dimensionality of the original high-dimensional data without sacrificing much data information, i.e., map it into a low-dimensional space. The experimental results demonstrated that, compared to a random forest, a BP neural network can reduce the number of input nodes while preserving the information’s integrity and avoiding the phenomenon of correlation and information overlap among various influential factors. The accuracy of the BP neural network predictions was greater than that of a random forest prediction model. This method accurately predicted university graduates’ employment retention rate.

This paper gives the following suggestions on how to improve the attractiveness of each province to high-quality talents: First of all, the housing prices in first-tier cities in my country are generally relatively high, and the salary income of university graduates cannot bear the price of high housing prices. Although Beijing, Shanghai, Guangzhou, and Shenzhen have excellent public services and good educational resources, high housing prices are still an important factor for university graduates to consider when choosing a place to work.

Second, strengthen the financial science and technology expenditure, and improve the ability of scientific and technological innovation, especially in the central regions, most of which are located in the plain area, and have had a large population since ancient times. However, rich population resources cannot promote the sustainable development of the economy, and the lack of high-quality talents will lead to insufficient scientific and technological innovation capabilities. Relying on the talent introduction policies formulated by various regions in recent years, at the same time improving the ability of scientific and technological innovation, increasing the employment of high-tech industries, and attracting university graduates to settle down for a long time with the advantage of housing prices, they can effectively deal with the problem of lack of high-quality talents. Enhance scientific and technological innovation capabilities, thereby promoting the development of the entire economic level.

Finally, rationally distribute educational resources and improve education levels. For the central region, the enhancement of basic education is the key to attracting talents. Most of the central regions attract high-quality talents who can settle down for a long time. The improvement of basic education can effectively attract high-quality talents to settle in the region. As for the western region, most of the regions lack higher education resources; therefore, improve the educational equity in the western region, increase the investment in higher education resources, and cultivate more talents to serve the local area.