An Adaptive Multi-Level Quantization-Based Reinforcement Learning Model for Enhancing UAV Landing on Moving Targets
Abstract
:1. Introduction
- A novel RL-based formulation of the problem of autonomous landing based on Q-learning through defining states, actions, and rewards;
- An adaptive quantization of actions relies on a compact type of Q-matrix. It is useful for the fast convergence of training and high gained knowledge while preserving the aimed accuracy;
- A thorough evaluation process has been made by comparing various types of RL-based autonomous landing using several types of mobility scenarios of targets and compares them with classical proportional–integral–derivative (PID)-based control.
2. Methods
2.1. Autonomous Landing
| Algorithm 1 Pseudocode of the Q-learning algorithm |
| Input the states the final state (the termination state) the actions Reward Function Transition Function learning rate discounting factor Output Start Step-1: Initiate with arbitrary Step-2: Check for convergence, if NOT converged continue; otherwise go to 3. Step-2.1: Select Random state from . Step-2.2: Check if the state reached terminated state , if NOT continue; otherwise, Go to 2. Step-2.2.1: Select action based on policy and exploration strategy Step-2.2.2: Find the next state based on the transition . Step-2.2.3: Receive the reward-based . Step-2.2.4: Update the value of using and . Go to Step 2 End |
2.2. Q-Learning
2.2.1. State
2.2.2. Action
2.2.3. Q-Table Representation
2.2.4. Reward
2.2.5. Terminating State
2.2.6. Q-Table Update
2.3. Adaptive Multi-Level Quantization (AMLQ) Model
2.3.1. Learning Phase
| Algorithm 2 Pseudocode of the learning phase in the autonomous landing |
| Input Defined actions and states Rewarding function List of locations of the target the number of episodes number of iterations duration of the heuristic strategy Output Q-matrix Start Initiate Q-matrix For the new location of the target in the list For each episode of the number of episodes For each iteration If (heuristic strategy is on) select random action using the uniform distribution update state and reward update Q-matrix else select actions based on policy derived from the Q-matrix update state and reward update Q-matrix end End |
2.3.2. Operation Phase
| Algorithm 3 Pseudocode of the operation phase |
| Input Q-matrix Final state Output Actions Start While not reaching the final state Measure the target position using the vision Update the state Select the action based on the state using the Q-matrix Enable the action End Perform the landing using a gradual decrease in altitude End |
2.4. Evaluation Metrics
2.4.1. Mean Square Error (MSE)
2.4.2. Root Mean Square Error (RMSE)
2.5. Experimental Design
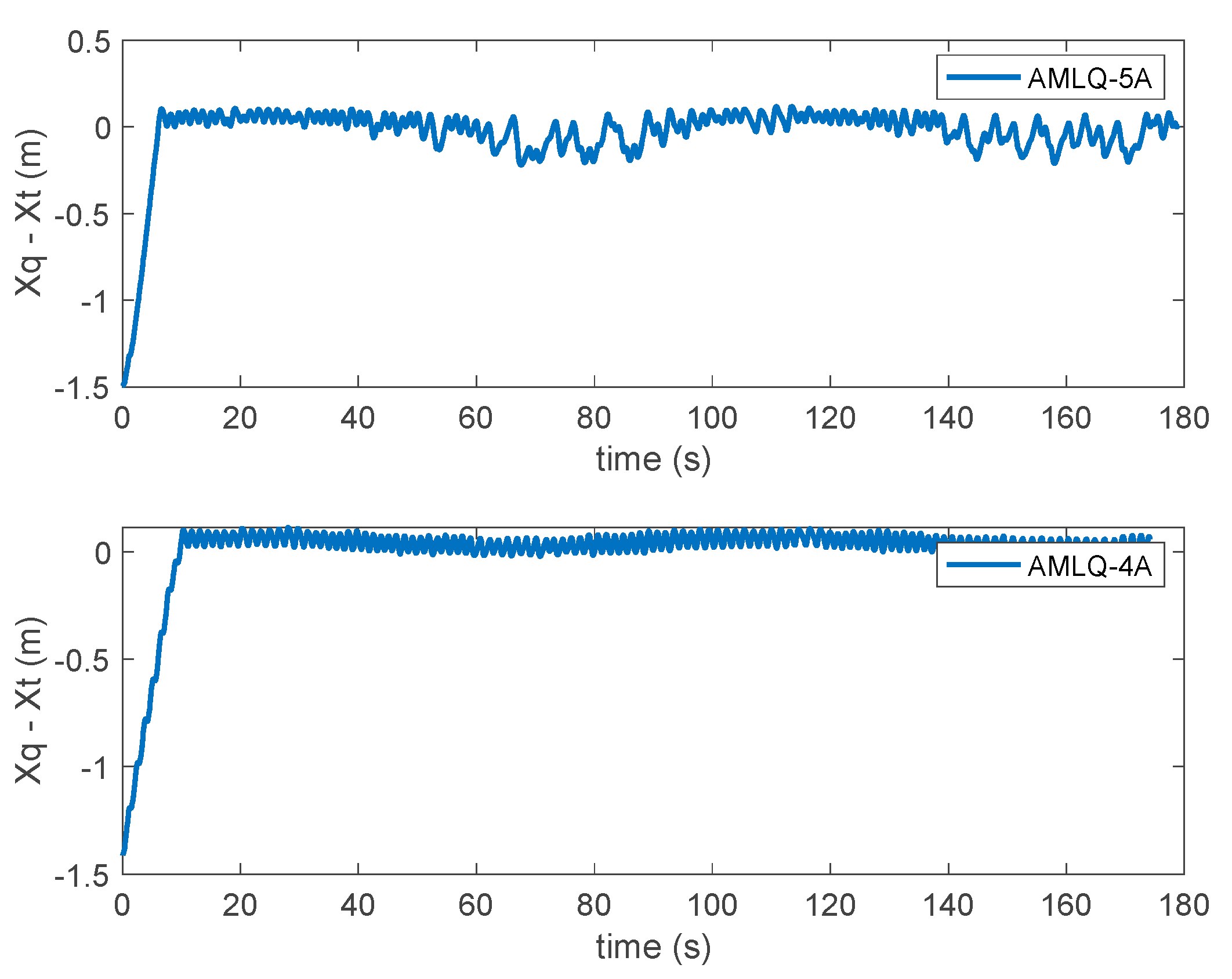
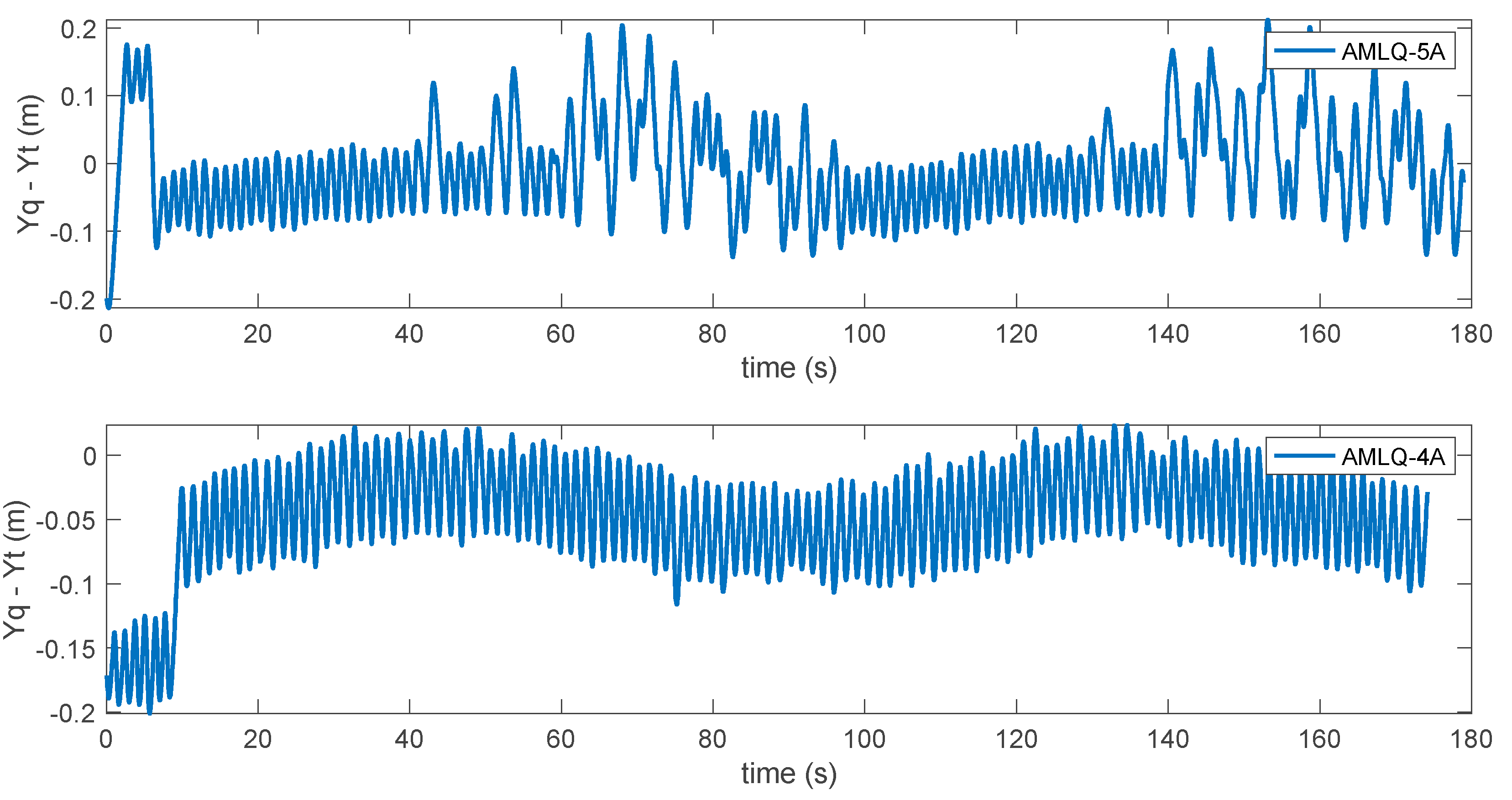
3. Results and Discussion
4. Conclusions and Future Works
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grippa, P.; Behrens, D.A.; Wall, F.; Bettstetter, C. Drone delivery systems: Job assignment and dimensioning. Auton. Robot. 2018, 43, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Mosali, N.A.; Shamsudin, S.S.; Alfandi, O.; Omar, R.; Al-fadhali, N. Twin Delayed Deep Deterministic Policy Gradient-Based Target Tracking for Unmanned Aerial Vehicle with Achievement Rewarding and Multistage Training. IEEE Access 2022, 10, 23545–23559. [Google Scholar] [CrossRef]
- You, H.E. Mission-driven autonomous perception and fusion based on UAV swarm. Chin. J. Aeronaut. 2020, 33, 2831–2834. [Google Scholar]
- Lygouras, E.; Santavas, N.; Taitzoglou, A.; Tarchanidis, K.; Mitropoulos, A.; Gasteratos, A. Unsupervised human detection with an embedded vision system on a fully autonomous uav for search and rescue operations. Sensors 2019, 19, 3542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joshi, G.; Pal, B.; Zafar, I.; Bharadwaj, S.; Biswas, S. Developing Intelligent Fire Alarm System and Need of UAV. In Proceedings of the International Conference on Unmanned Aerial System in Geomatics, Roorkee, India, 6–7 April 2019; pp. 403–414. [Google Scholar]
- Mostafa, S.A.; Mustapha, A.; Gunasekaran, S.S.; Ahmad, M.S.; Mohammed, M.A.; Parwekar, P.; Kadry, S. An agent architecture for autonomous UAV flight control in object classification and recognition missions. Soft Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Li, W.; Chen, S. Automatic power line inspection using UAV images. Remote Sens. 2017, 9, 824. [Google Scholar] [CrossRef] [Green Version]
- Salvo, G.; Caruso, L.; Scordo, A.; Guido, G.; Vitale, A. Traffic data acquirement by unmanned aerial vehicle. Eur. J. Remote Sens. 2017, 50, 343–351. [Google Scholar] [CrossRef]
- Ke, R.; Li, Z.; Tang, J.; Pan, Z.; Wang, Y. Real-time traffic flow parameter estimation from UAV video based on ensemble classifier and optical flow. IEEE Trans. Intell. Transp. Syst. 2019, 20, 54–64. [Google Scholar] [CrossRef]
- Yahia, C.N.; Scott, S.E.; Boyles, S.D.; Claudel, C.G. Unmanned aerial vehicle path planning for traffic estimation and detection of non-recurrent congestion. Transp. Lett. 2021, 1, 1–14. [Google Scholar] [CrossRef]
- Bareiss, D.; Bourne, J.R.; Leang, K.K. On-board model-based automatic collision avoidance: Application in remotely-piloted unmanned aerial vehicles. Auton. Robot. 2017, 41, 1539–1554. [Google Scholar] [CrossRef]
- Aleotti, J.; Micconi, G.; Caselli, S.; Benassi, G.; Zambelli, N.; Bettelli, M.; Zappettini, A. Detection of nuclear sources by UAV teleoperation using a visuo-haptic augmented reality interface. Sensors 2017, 17, 2234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khadka, A.; Fick, B.; Afshar, A.; Tavakoli, M.; Baqersad, J. Non-contact vibration monitoring of rotating wind turbines using a semi-autonomous UAV. Mech. Syst. Signal. Process. 2019, 138, 106446. [Google Scholar] [CrossRef]
- Zhang, D.; Khurshid, R.P. Variable-Scaling Rate Control for Collision-Free Teleoperation of an Unmanned Aerial Vehicle. arXiv 2019, arXiv:1911.04466. [Google Scholar]
- Uryasheva, A.; Kulbeda, M.; Rodichenko, N.; Tsetserukou, D. DroneGraffiti: Autonomous multi-UAV spray painting. In Proceedings of the ACM SIGGRAPH 2019 Studio, Los Angeles, CA, USA, 28 July–1 August 2019; pp. 1–2. [Google Scholar]
- Beul, M.; Houben, S.; Nieuwenhuisen, M.; Behnke, S. Fast autonomous landing on a moving target at MBZIRC. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–6. [Google Scholar]
- Bähnemann, R.; Pantic, M.; Popović, M.; Schindler, D.; Tranzatto, M.; Kamel, M.; Grimm, M.; Widauer, J.; Siegwart, R.; Nieto, J. The ETH-MAV team in the MBZ international robotics challenge. J. Field Robot. 2019, 36, 78–103. [Google Scholar] [CrossRef]
- Lin, S.; Garratt, M.A.; Lambert, A.J. Monocular vision-based real-time target recognition and tracking for autonomously landing an UAV in a cluttered shipboard environment. Auton. Robot. 2017, 41, 881–901. [Google Scholar] [CrossRef]
- Fliess, M. Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. Vol. 2009, 42, 1531–1550. [Google Scholar] [CrossRef] [Green Version]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. IS&T Int. Electron. Imaging 2017, 29, 70–76. [Google Scholar]
- Kersandt, K. Deep Reinforcement Learning as Control Method for Autonomous Uavs. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2018. [Google Scholar]
- Forster, C.; Faessler, M.; Fontana, F.; Werlberger, M.; Scaramuzza, D. Continuous on-board monocular-vision-based elevation mapping applied to autonomous landing of micro aerial vehicles. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 111–118. [Google Scholar]
- Sukkarieh, S.; Nebot, E.; Durrant-Whyte, H. A high integrity IMU/GPS navigation loop for autonomous land vehicle applications. IEEE Trans. Robot. Autom. 1999, 15, 572–578. [Google Scholar] [CrossRef] [Green Version]
- Baca, T.; Stepan, P.; Saska, M. Autonomous landing on a moving car with unmanned aerial vehicle. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–6. [Google Scholar]
- Gui, Y.; Guo, P.; Zhang, H.; Lei, Z.; Zhou, X.; Du, J.; Yu, Q. Airborne vision-based navigation method for UAV accuracy landing using infrared lamps. J. Intell. Robot. Syst. 2013, 72, 197–218. [Google Scholar] [CrossRef]
- Tang, D.; Hu, T.; Shen, L.; Zhang, D.; Kong, W.; Low, K.H. Ground stereo vision-based navigation for autonomous take-off and landing of uavs: A chan-vese model approach. Int. J. Adv. Robot. Syst. 2016, 13, 67. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, S.A.; Mustapha, A.; Shamsudin, A.U.; Ahmad, A.; Ahmad, M.S.; Gunasekaran, S.S. A real-time autonomous flight navigation trajectory assessment for unmanned aerial vehicles. In Proceedings of the 2018 International Symposium on Agent, Multi-Agent Systems and Robotics (ISAMSR), Putrajaya, Malaysia, 27–28 August 2018; pp. 1–6. [Google Scholar]
- Falanga, D.; Zanchettin, A.; Simovic, A.; Delmerico, J.; Scaramuzza, D. Vision-based autonomous quadrotor landing on a moving platform. In Proceedings of the 15th IEEE International Symposium on Safety, Security and Rescue Robotics, Shanghai, China, 11–13 October 2017; pp. 200–207. [Google Scholar]
- Lee, D.; Ryan, T.; Kim, H.J. Autonomous landing of a VTOL UAV on a moving platform using image-based visual servoing. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 971–976. [Google Scholar]
- Xu, Y.; Liu, Z.; Wang, X. Monocular Vision based Autonomous Landing of Quadrotor through Deep Reinforcement Learning. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 10014–10019. [Google Scholar]
- Lee, S.; Shim, T.; Kim, S.; Park, J.; Hong, K.; Bang, H. Vision-based autonomous landing of a multi-copter unmanned aerial vehicle using reinforcement learning. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 108–114. [Google Scholar]
- Araar, O.; Aouf, N.; Vitanov, I. Vision based autonomous landing of multirotor UAV on moving platform. J. Intell. Robot. Syst. 2016, 85, 369–384. [Google Scholar] [CrossRef]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Autonomous Vehicular Landings on the Deck of an Unmanned Surface Vehicle using Deep Reinforcement Learning. Robotica 2019, 37, 1867–1882. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Ramos, A.; Sampedro, C.; Bavle, H.; De La Puente, P.; Campoy, P. A deep reinforcement learning strategy for UAV autonomous landing on a moving platform. J. Intell. Robot. Syst. 2019, 93, 351–366. [Google Scholar] [CrossRef]
- Polvara, R.; Patacchiola, M.; Hanheide, M.; Neumann, G. Sim-to-Real quadrotor landing via sequential deep Q-Networks and domain randomization. Robotics 2020, 9, 8. [Google Scholar] [CrossRef] [Green Version]
- Vankadari, M.B.; Das, K.; Shinde, C.; Kumar, S. A reinforcement learning approach for autonomous control and landing of a quadrotor. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 676–683. [Google Scholar]
- Srivastava, R.; Lima, R.; Das, K.; Maity, A. Least square policy iteration for ibvs based dynamic target tracking. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 1089–1098. [Google Scholar]
- Ling, K. Precision Landing of a Quadrotor UAV on a Moving Target using Low-Cost Sensors. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2014. [Google Scholar]
- Malyuta, D.; Brommer, C.; Hentzen, D.; Stastny, T.; Siegwart, R.; Brockers, R. Long—Duration fully autonomous operation of rotorcraft unmanned aerial systems for remote—Sensing data acquisition. J. Field Robot. 2020, 37, 137–157. [Google Scholar] [CrossRef] [Green Version]

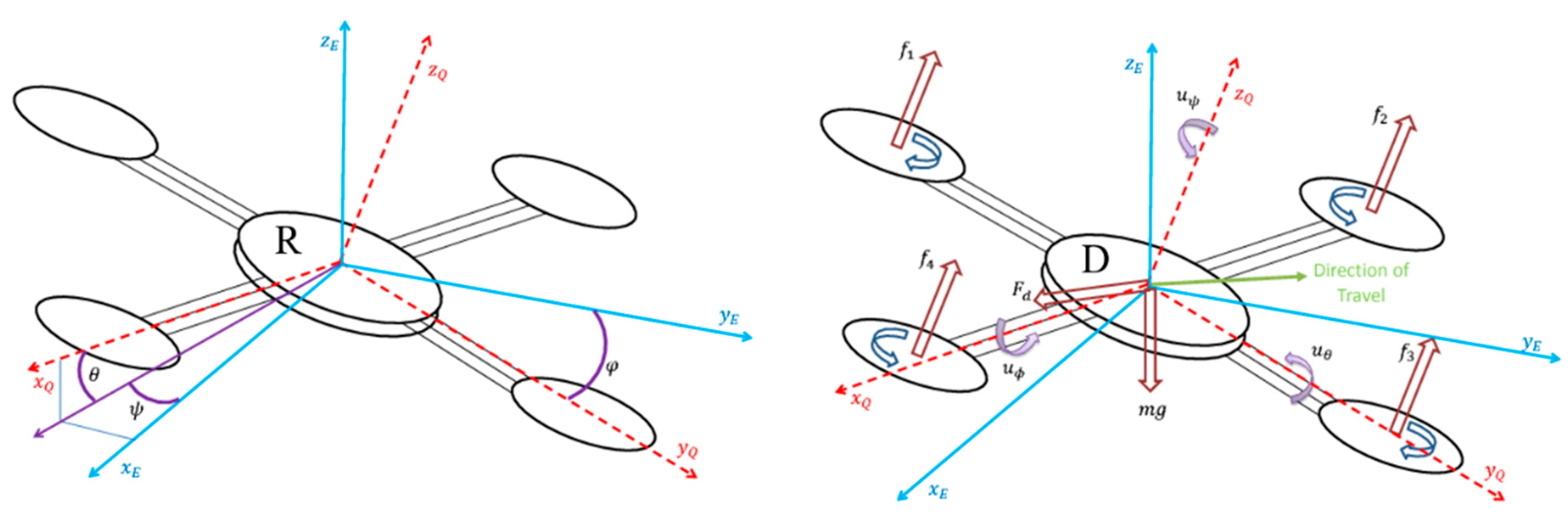


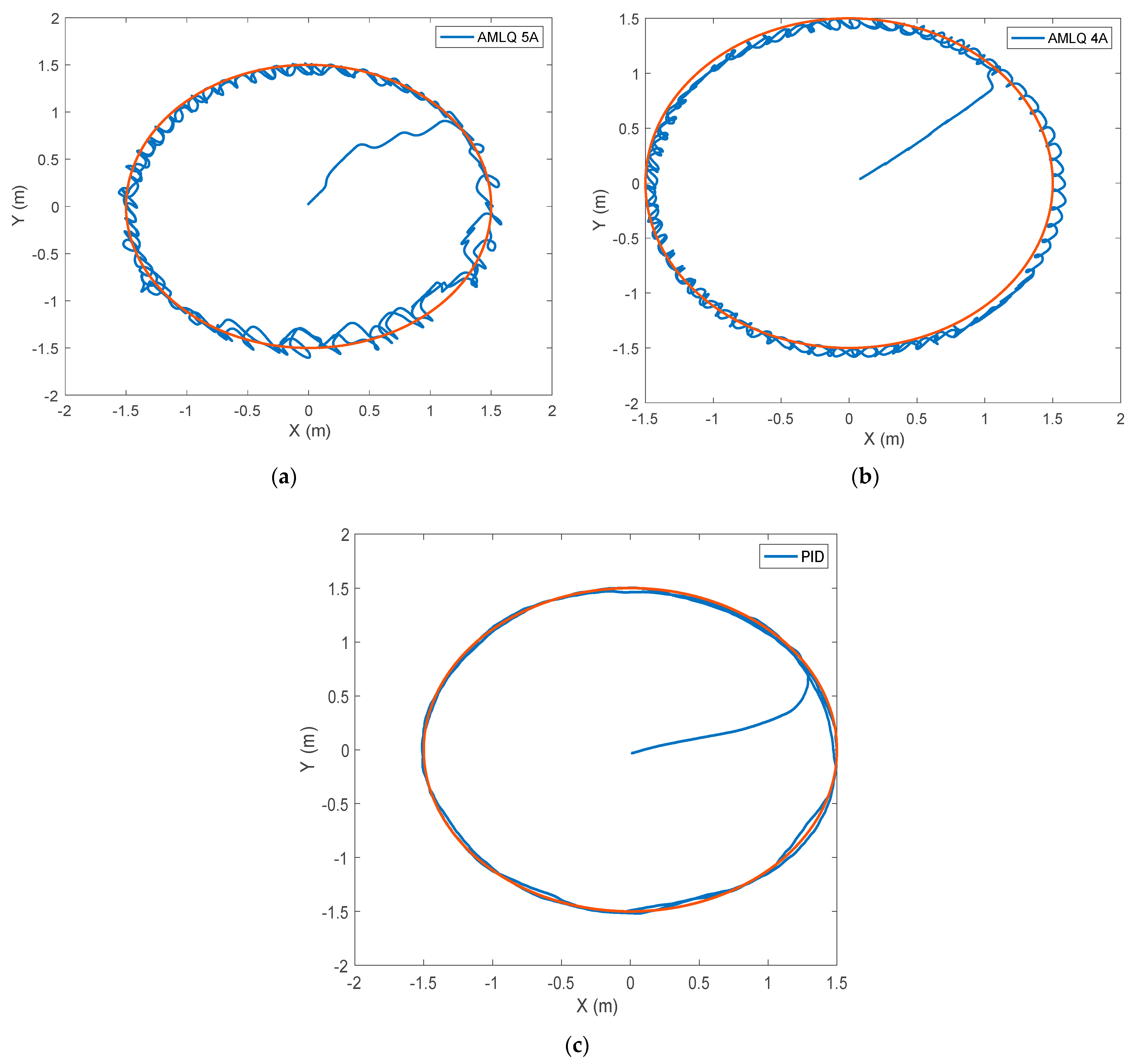
| Symbol | Meaning |
|---|---|
| Reference frame | |
| UAV frame | |
| Pitch angle. This describes the orientation of the UAV with respect to -axis of the reference frame | |
| Roll angle. This describes the orientation of the UAV with respect to -axis of the reference frame | |
| Yaw angle. This describes the orientation of the UAV with respect to -axis of the reference frame | |
| The granularity level of position quantization | |
| The granularity level of velocity quantization | |
| The position of the UAV | |
| The velocity of the UAV | |
| ) | The position of the target |
| The final error of the UAV with respect to the position | |
| The final error of the UAV with respect to the velocity | |
| The relative position of the UAV with respect to the target | |
| The relative velocity of the UAV with respect to the target | |
| The number of actions | |
| The maximum value of the position in the state | |
| The minimum value of the position in the state | |
| The maximum value of velocity in the state | |
| The minimum value of velocity in the state | |
| Decay factor of | |
| Coefficients of the position and velocity rewarding term | |
| Coefficients of the adaptive linear action model | |
| Coefficients of the adaptive exponential action model |
| PID Type | |||
|---|---|---|---|
| −1.0 | −0.05 | −0.005 | |
| −1.0 | −0.05 | −0.005 | |
| 0.8 | 0.1 | 0.1 | |
| 0.8 | 0.1 | 0.1 |
| Parameter Name | Parameter Value |
|---|---|
| 0.8 | |
| 0.9 | |
| 1.0 | |
| 0.01 | |
| 0.001 | |
| 0.5 | |
| 0.5 | |
| 4 | |
| 0.032 | |
| 0.25 |
| Criterion | AMLQ-4A | AMLQ-5A | PID |
|---|---|---|---|
| RMSE | 8.9695 | 8.7052 | 10.0592 |
| MSE | 80.4523 | 75.7811 | 101.1883 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abo Mosali, N.; Shamsudin, S.S.; Mostafa, S.A.; Alfandi, O.; Omar, R.; Al-Fadhali, N.; Mohammed, M.A.; Malik, R.Q.; Jaber, M.M.; Saif, A. An Adaptive Multi-Level Quantization-Based Reinforcement Learning Model for Enhancing UAV Landing on Moving Targets. Sustainability 2022, 14, 8825. https://doi.org/10.3390/su14148825
Abo Mosali N, Shamsudin SS, Mostafa SA, Alfandi O, Omar R, Al-Fadhali N, Mohammed MA, Malik RQ, Jaber MM, Saif A. An Adaptive Multi-Level Quantization-Based Reinforcement Learning Model for Enhancing UAV Landing on Moving Targets. Sustainability. 2022; 14(14):8825. https://doi.org/10.3390/su14148825
Chicago/Turabian StyleAbo Mosali, Najmaddin, Syariful Syafiq Shamsudin, Salama A. Mostafa, Omar Alfandi, Rosli Omar, Najib Al-Fadhali, Mazin Abed Mohammed, R. Q. Malik, Mustafa Musa Jaber, and Abdu Saif. 2022. "An Adaptive Multi-Level Quantization-Based Reinforcement Learning Model for Enhancing UAV Landing on Moving Targets" Sustainability 14, no. 14: 8825. https://doi.org/10.3390/su14148825
APA StyleAbo Mosali, N., Shamsudin, S. S., Mostafa, S. A., Alfandi, O., Omar, R., Al-Fadhali, N., Mohammed, M. A., Malik, R. Q., Jaber, M. M., & Saif, A. (2022). An Adaptive Multi-Level Quantization-Based Reinforcement Learning Model for Enhancing UAV Landing on Moving Targets. Sustainability, 14(14), 8825. https://doi.org/10.3390/su14148825









