1. Introduction
Because of the absence of requirement for DC–AC energy conversion and for extra controller design for frequency and reactive power [
1,
2], DC microgrids are a cost-effective solution [
3,
4] and might also be an attractive technology [
5] that can be easily integrated with Renewable Energy Sources (RES), Energy Storage Systems (ESS), and DC electric loads [
6]. Some of these DC loads, such as railway, telecommunication, and field irrigation with an electrical pump, are located in rural or remote areas where conventional fuels are not convenient for power generation. In fact, the usage of renewable energy sources, solar photovoltaic (PV) units accompanying Battery Energy Storage Systems (BESSs), for power generation will reduce dramatically the fossil fuel dependency. The output power of these sources in direct-current microgrids can be stored in a BESS or used to feed DC loads in the grid both directly and via power electronic converters [
7,
8]. The backbone of the DC microgrid is the common DC bus and all the different interconnected components in the microgrid [
9].
The common DC bus voltage value is an indicator to monitor the DC microgrid, and operational characteristics of any grid is determined based on this voltage level. Loading conditions on the whole system are governed by measuring this voltage [
10,
11,
12]. For this reason, and for any other operating condition, it is necessary to keep the common DC bus voltage at the desired value since voltage variations may negatively affect the electronic loads [
8,
13].
The control approach known as droop control is used often to control the common DC bus voltage to its pre-determined and desired value [
5,
14]. However, the main drawback of the droop control strategy is that it significantly affects the accuracy of the power sharing due to the small voltage differences between the DC bus voltage and the various converters [
15]. The gain-scheduling control method combined with fuzzy logic control has been presented in [
16]. The nonlinear known backstepping approach is introduced as a solution to overcome the limitation of existing model-based linear and nonlinear controllers [
5,
17]. However, the main problem of the adaptive backstepping approach is to require the estimations of all parameters, including some unnecessary parameters. To maintain the overall dynamic stability and efficient operation of the DC microgrids, we need to depend essentially on the capability of the power management of the various components where BESS can be considered as the primary components of the DC microgrids. Moreover, and in order to eliminate the fluctuations in islanded DC microgrids, BESSs are the indispensable solution for storing or releasing energy [
5].
Unlike model-based controllers, model-free intelligent control approaches have also been introduced [
18,
19,
20]. In [
18], in order to obtain a fast response, ideal voltage control, and proper current sharing in the stand-alone shipboard DC–DC converters in the islanded DC microgrids, a novel technique entitled intelligent single-input interval type-2 fuzzy logic controller combined with sliding mode control, is proposed to improve the voltage regulation and current-sharing capability. Another intelligent control method has also been proposed in [
19] where a data-driven optimal control technique for virtual synchronous generator in time in which no expert knowledge or requirement for system model is available. An event-triggered distributed hybrid control technique has been put forward to improve the security and the economic operation for the integrated energy system [
20]. This is done, in order to share the electricity and heat load power accurately without knowing the network parameters for the integrated energy system formed by a cluster of energy hubs. However, huge data requirement for data-driven systems are the main drawbacks of the proposed method-. Additionally, the problems caused by the multiple time scales in the integrated energy system is still an unsolved problem.
By selecting the correct control parameters together with using bidirectional DC–DC converters, only this solution will be available, and BESSs will be controlled effectively [
17]. Such proposed control methods are applied to keep constant voltage level at the common DC bus where the different components of the islanded DC microgrids are connected through converters. Robust operation of DC choppers is essential for various operating values, different loading conditions, and for variable operating points and parameters. Accordingly, some control strategies have been evolved to satisfy the requirements for converter’s output voltage [
21].
Synergetic control is one of the recently developed techniques to solve the aforementioned problems. It is a nonlinear control method, and was developed by Kolesnikov [
22]. This control strategy has been applied with great success to constant power loads, such as shipboard DC power distribution systems, converters with constant power load, etc. [
23,
24]. In this control approach, the nonlinear part of the controlled system is not compensated but only synthesized based on the system model that forces the system sliding onto a manifold. This will be useful for reducing the system order [
25].
The proposed synergetic control technique is not only efficient for nonlinear system control [
26,
27], but is also considered as a very promising robust control techniques. It has the sliding mode control’s invariance principle but with no chattering effect. It is also robust and easy to implement which makes it a promising new control approach. Recently, it has been successfully implemented to various applications such as, the DC–DC power converters [
28], in a battery charging system [
29], and in the design of power system stabilizers [
30]. In these applications, the synergetic control law was developed using an asymptotic stability analysis, and system trajectories reaching the equilibrium at infinity [
21]. Moreover, in [
31] a nonlinear controller for DC-DC converters discrete-time version based synergetic control has been designed and implemented. In [
32], this control technique has been proposed for the integration of photovoltaics and battery energy storage in a DC microgrid.
In this paper we project to design synergetic controllers (SCs) for the various parts in any DC microgrid. Different types of synergetic controllers (SCs), such as simple SC, piecewise linear function form of SC, linear synergetic controller, improved synergetic controller with terminal SC, and fast terminal SC have been designed and applied to an islanded DC microgrid. In order to make the design of the controllers independent from system component values, a generalized mathematical method has been derived for all power electronics-based subsystems of the microgrid system. A small-scale DC microgrid was designed and implemented to experimentally test the effectiveness of the control law from the different synergetic controllers. Moreover, a generalized synergetic controller design approach has been derived in this paper for the islanded DC microgrids. The obtained results from both simulation and experiments have been compared and included in this paper.
2. Outline of DC Microgrids
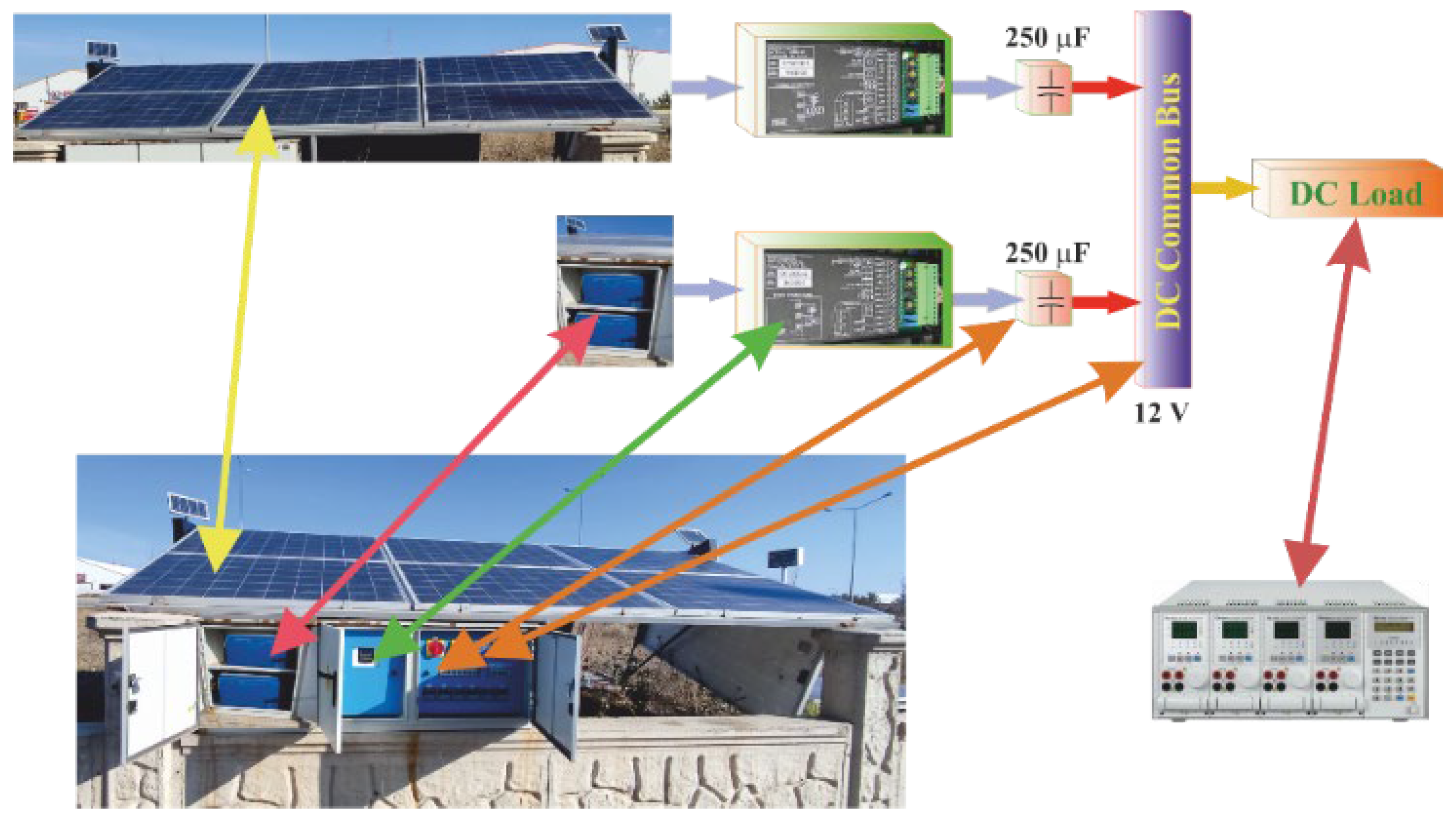
The designed DC small-scale microgrid consists of 6 polycrystalline solar modules in parallel, as a PV unit, and 4 pieces 12 V gel batteries, as a BESS, that are supplying programmable load with different power ratings. The schematic scenario of the DC microgrid system is illustrated in
Figure 1. The solar module’s output voltage is 30.6 V and that of the BESS is 48 V at maximum power value. The primary source of this microgrid is a solar PV unit that delivers power to the DC load through the common DC bus. A DC buck converter is employed to interface with the PV unit whereas a bidirectional buck converter is used to interface the BESS with the common DC bus. This is so, because the output voltages of these sources are higher than those of the common DC bus besides, the load is connected directly to the common DC bus.
One of the objectivesof the paper is to maintain not only the power balance but also a constant voltage at the common DC bus while applying different synergetic control approaches to optimize the solution for this kind of hybrid islanded DC microgrid. This will eventually be accompanied by the effects of external disturbances and parametric uncertainties under any selected operating condition of the DC microgrid.
Dynamical Models of DC Microgrid Components
DC microgrids may consist of different energy resources and the dynamical models used to demonstrate their dynamic performance characteristics. The main work of all the existing components in the DC microgrids is to provide the desired constant common DC bus voltage and power balance by regulating the output voltages values and currents based on appropriate control actions. Considering the voltage and current relationships of the solar PV unit and the BESS, the controllers are modeled accordingly.
DC–DC converters have been used not only to isolate the different power sources from the main DC bus, but also to regulate the variable input voltage level and transfer it to the common DC bus. Despite the similarity of the operating principles of these DC-DC converters, the dynamic behaviors of the power source may be very different from each other. Using simple circuit theory approach, dynamic models of the solar PV unit and BESS can be obtained from their basic equivalent circuit models. The equivalent circuit diagrams for the solar PV unit supplying a DC–DC buck converter input, and the BESS connected to the input of a bidirectional DC–DC converter are illustrated in
Figure 2.
As illustrated in
Figure 2a, the dynamic model for each of the solar PV panels with a DC–DC buck converter can be derived as follows:
Moreover, as shown in
Figure 2b, the dynamic model of the BESS that is connected to the main DC-bus through a bidirectional DC–DC buck converter may be expressed by the following equations:
It can be seen that the dynamic characteristics of the DC–DC converters represented by Equations (1) and (2) are very similar. These equations may be generalized in the following forms:
Although the dynamic model, control objectives, and input of each component are different, the output voltage level and the required conditions are similar due to the common DC-bus voltage. Any controller’s satisfactory performance will depend on not only on the accuracy of the dynamic system model but also on the system parameters. The synergetic control method is a nonlinear control system and its state space method originates from the combination of modern mathematics and synergy; thus, it has intrinsic superiorities, such as global stability and robustness over similar methods, mainly in against modeling inaccuracy and internal parameter disturbances.
Additionally, for complex nonlinear systems, synergetic control may suppress the chattering phenomena. It may also be robust for against the noise or disturbances since it is implemented at a fixed switching frequency. The detailed mathematical proof of this derivation process can be found in [
33]. These features of the synergetic control provide a great advantage in microgrid applications.
3. Synergetic Controller Design
The synergetic controller is modeled using the dynamical model of each component of the small-scale DC microgrid, as described previously. An insight of the proposed control design schemes for the generalized form of the components of the DC microgrid, given in Equation (3), are discussed in the following sections.
A set of nonlinear differential equations is used to describe the system to be controlled using the following form:
In the above equation, denotes the state vector, while is the control input vector and is time.
The design procedure of the synergetic controller is based on a macro-variable as a function of the state variables, .
The nonlinear synergetic controller will compel the system to slide and operate onto the manifold operation.
By defining the dynamic equation correctly, the manifold should approach to the steady point with the described convergence process as:
where
is a design parameter denoting the time of the convergence speed of the system to the manifold specified by the macro-variable. Derivation of the macro variables using chain rule will result in the following:
By substituting Equations (5) and (7) into the Equation (6), that is
The solution of the variable from Equation (8) can be used to synthesize the control variable duty cycle for the case of a switching converter. The control variable duty cycle is sent to a Pulse Width-Modulation (PWM) modulator to generate the switch control variable.
Each manifold will contribute a new constraint on the state space domain which will reduce the system order.
The control law, applied in this paper, will be synthesized by hand for the DC-DC converters that are used in this paper to regulate the output voltage of both the solar PV unit and the BESS in the islanded DC microgrid system.
Solving for the control law
from Equation (8) leads to Equation (9):
State trajectories will be forced by the control law in Equation (9) to satisfy Equation (6). Hence, the order of the system reduced by one with the constraints of Equation (6) while ensuring the controller design to accomplish parameter insensitivity and global stability. Selection of the number of the macro-variable adequately may lead to high performance and secure stability [
34,
35].
The nonlinear system’s state trajectory which is of the nonlinear system under synergetic control reaches the manifold for under the constraint of the dynamic evolution law (6). According to (6), as long as is satisfied, then or assumptions have to be satisfied, and the manifold is reached.
If we assume that the value of at the initial time is , the solution of its dynamic evolution law (6) will result in . According to this result, we noticed that when decays to 0 exponentially. In other words, the system will reach the manifold at any initial state. Thus, the smaller is, the faster decays to 0, that is, the faster the system reaches the manifold .
3.1. Piecewise Linear Function Type Synergetic Controller Design (PLF-SC)
The main objective of this section is to obtain a control law as a function of the state coordinates , which provide the required values of the common DC bus voltage and, therefore, current for various operating modes. condition of the duty cycle must be satisfied.
The first step on the synergetic controller design as a piecewise linear function is to choose a macro-variable. In general, the macro-variable could be any function (including nonlinear functions) of the state of the components of the DC microgrid. As a simple case, piecewise linear function will be chosen as a macro-variable and has the following form:
Substituting Equation (10) into Equation (6) yields:
Substituting the equivalent of
and
from Equation (4) and solving for duty cycle
based on Equation (3), the control law for the chosen macro-variable as piecewise linear function will be:
Based on Equation (12), the trajectory will converge to manifold with a time constant value of and then settles on the manifold for all times. According to this approach, two state variables for the components of the DC microgrid will reach their steady state value such as and , and the errors will reach zero.
3.2. Linear Function of the Tracking Error Type Synergetic Controller Design (LFTE-SC)
Now, let us take a macro-variable
as a linear function of the tracking error expressed as:
where
is a chose constant.
The definition of the error function,
, maybe given as:
Combining Equations (14) and (13) leads to:
Substituting (15) into (6) and solving for duty cycle
based on Equation (4), the control law for the chosen macro-variable as a linear function of the tracking error will be:
The system in Equation (3) under synergetic control of Equation (16) is asymptotically stable and its trajectories converge to equilibrium at infinity. In order to improve its dynamic characteristics and obtain a fast response, another type of a terminal synergetic controller is proposed in the following section.
3.3. Terminal Synergetic Controller Design (TSC)
By reformulating of the macro-variable dynamics in Equation (13) using with a new nonlinear macro-variable as given by Equation (17) will surely reinforce the robustness and tracking ability of the system.
where
and
are positive odd integers satisfying
>
. By substituting Equation (17) into Equation (6) and solving for duty cycle
leads to Equation (18):
Under the control law given in Equation (18), the trajectory of the system defined in Equations (3) and (4) can be driven onto manifold making the tracking fast. To further improve the convergence of the system, another type of controller is proposed in the following section.
3.4. Fast Terminal Synergetic Controller Design (FTSC)
The idea is to design an FTSC which relies on defining macro-variable as given in Equation (19):
Similarly, by substituting Equation (19) into Equation (6) and solving for duty cycle
leads to Equation (20):
The above solution for will also ensure rapid tracking ability and robustness of the system behavior for different operating conditions.
Theorem 1. (Stability analysis of the designed controllers) Under the controller (12), (16), (18), and (20) and with the macro variable (10), (15), (17), and (19), the trajectories of the system (4) can be asymptotically stabilized in an asymptotic way to manifold .
Proof. Choose the Lyapunov candidate as:
which leads, after differentiation then using (6), to
. The proof is completed. □
4. System Simulation and Experimental Verification
Another wayto verify the various derived synergetic control laws, an extended simulation analysis has been conducted. In addition to these synergetic controllers, a sliding mode controller (SMC) and voltage mode controller (VMC) are also designed and compared to synergetic controller results. The reason why SMC has been selected is both SMC and the synergetic control are compelling the system to slide and operate onto a manifold. However, VMC is one of the basic control method derived from PID-like controller design.
For the considered application, the output voltage of the DC-DC converters need to be controlled. SMC and VMC type controllers have been designed for this regulation purpose. To design these type of controllers in a simple manner, the moving averages of converter output have been used. As can be seen from Equation (4), to design SMC for the output voltage regulation,
has been considered as the moving average of the output voltage, and
has been assumed as the desired output voltage value. The sliding surface in the state space is described by the parameter
and according to the sliding-mode control, is shown by,
Thus, a first order path can be selected using the below equation. The convergence speed will have to be controlled accordingly,
where
is a positive real number usually known as the convergence factor.
In continuous conduction mode, voltage mode controller will be obtained as follows:
All of the simulation works have been performed in the MATLAB environment. An experimental prototype setup has been designed and built based on the theoretical analysis, as given in
Figure 1. Since the proposed control fits well for implementation on a Digital Signal Processor (DSP)-based platform, and in order to migrate control laws on the experimental system, a dSpace DS1106 board has been used. Six-piece Telefunken CW Energy CWT250-60P polycrystalline solar modules are used as a PV unit in parallel. Rated maximum power of the panel is 250 Wp, and the solar module’s output voltage is 30.6 V, with 8.17 A at maximum power. To guarantee this maximum power at the output of the PV panels, a classical maximum power point tracking algorithm has been used. Four-piece Orbus 12 V 150 Ah maintenance-free nano carbon gel batteries are used as BESS in the series. A DC 5036-S type step down (buck) converter manufactured by Zahn Electronics, Inc. (Franksville, WI, USA) has been used as an interface unit between the system equipment and common DC bus. Chroma 6310 A series Programmable DC Electronic Load has been used to evaluate the designed controller performances for different operating conditions. An XH-M603 Battery Charge Control Module for 12–24 V gel type batteries is used to charge the Orbus batteries supplying power from bidirectional converter output. Total power supply capacity of the system at the maximum power is 3300 W, approximately. The load in the system has been considered as lumped together and the value of the load assumed as 1000 W at the rated condition.
Initially, the system is assumed at standstill and the predetermined output voltage is taken to be 12 V, the controller parameters have been selected as , , , , and .
The obtained results from FTSC have been compared with Terminal Synergetic Controller (TSC), Linear Function of the Tracking Error-based Synergetic Controller (LFTE-SC), and Piecewise Linear Function based Synergetic Controller (PLF-SC). Different operating conditions have been considered in both simulation study and experimental validation. The scenarios of some the considered cases are described as below.
4.1. Scenario 1: Determination of Reference Tracking Capability of the Designed Controllers
The common DC bus voltage’s reference is set to 12V and step responses of the designed controllers for this case have been investigated.
Figure 3 shows the dynamic responses of the six controllers and their comparative results are given in
Table 1.
In order to determine the best controller in terms of reference tracking capability, both rise time and overshoot values have been considered. Overshoot has only been observed in voltage mode controller (VMC) with the value 10.84%. No overshoot has been observed for the other controllers.
According to the rise time value, the best result has been observed for FTSC with the value 34.5 ms while the worst result 101.3 ms for SMC.
As expressed earlier, the definition of a macro-variable establishes a linear dependence between the selected two-state variables and , thereby reducing by one the order of the system will be reduced by one. For this reason, the system response will be a first-order system. No overshoot has been observed for all four designed synergetic type controllers. However, an overshoot has been observed for VMC, while the settling time of SMC has the biggest value. As a result, the main comparison indicators are settling time and steady-state error. Based on the obtained simulation results, in terms of the settling time, FTSC has shown better performance than the other controllers. While VMC has the worst behavior with an overshoot, SMC has the biggest settling time value without overshoot. For this reason, only synergetic type controllers have been taken into consideration. Because FTSC has shown better performance not only for this scenario but also for the other test cases, only FTSC-based results have been illustrated for evaluation of the shading effect for supplying load demand with BESS. To further test the robustness of the proposed controllers, some disturbances and other cases have been applied to the system and the dynamic performances have been evaluated.
4.2. Scenario 2: Determination of Different Reference Voltage Level Changes Tracking Capability of the Designed Controllers
Reference voltage of common DC bus voltage has been changed from 12 V to 5 V and then from 5 V to 10 V. Similar to the first scenario, FTSC has been found to be effectively more performant than the others. The comparison results for the designed four controllers is illustrated in
Figure 4.
As expected based on the tabulated results in
Table 1 and depicted behaviors in
Figure 3, the fastest and the best response have been seen for FTSC. There is no overshoot in terms of sudden voltage reference changes. Only rise time differences exist.
Based on these two scenarios, FTSC has proven its superiority over the others. For this reason, no more simulations have been performed, since more details can be found in Ref. [
21].
4.3. Scenario 3: Testing Compatibility of the Experiments and Simulation, and Evaluation of Shading Effect for Supplying Load Demand with BESS
A close similarity between simulation and experimental results for the FTSC has been observed. This comparison is illustrated in
Figure 5, where both experimental and simulation behavior of the system for the step response from 0 to 12 V. In
Figure 5a, both simulation and experimental results are drawn within the same figure. As can be seen from
Figure 5a, the two curves almost overlap, except for a very minor difference in the saddle area. In order to show this close similarity between simulation and experimental results, simulation versus experimental results are also illustrated in
Figure 5b. R-squared value, denoted by R
2, measures the proportion of variation in the simulation results that can be attributed to the experimental results and R
2 has been measured as 0.99971. This is another indicator for the overlap degree between simulation and experimental work.
Before initiating the experimentation and to obtain maximum power, we waited until the sun reached its zenith. By doing so, it has been guaranteed that the PV unit should be generating full power, around 1500 W. As illustrated in
Figure 6a, full power conditions for PV unit has been assumed continuous until t = 5 s. During this time, the delivered generation is sufficient enough to supply load demand, as it has been around 1470 W. Since the load can be programmed using a Chroma 6310 A series Programmable DC Electronic Load, the total amount of the load has been constant as 1000 W as given in
Figure 6b, less than the rated load for the system. As shown in
Figure 6c, the remaining power has been used to charge the batteries for future energy generation, around 390 W. The remainder of the generated power, 80 W approximately, has been dissipated as losses within the converters, battery charge unit, and other equipment installed in the small-scale microgrid system that was depicted in
Figure 1.
In order to test the shading effect and BESS support for condition changes that occur suddenly, solar radiation on the PV panel has been reduced from 100% to 50%. For this case, the generated power has been decreased from 1470 W to 780 W by activating a solid-state switch that splits the PV unit by half, approximately, while the load and the temperature remain constant. Switching between the stages has been implemented at t = 5 s. For this case, the generated power of the PV unit is not sufficient for the load demand and BESS has to provide 335 W to compensate the remaining power for load and losses. Activating the second converter on the BESS unit has increased the total power losses of the whole microgrid system. This scenario is described in
Figure 6c. At t = 8 s, the load demand has been changed from 1000 W to 720 W, while generated power at the solar PV unit is still constant as 800 W. For this scenario, supplied power from BESS has reached nearly zero. This is aproof that the power losses are around 80 W. The corresponding common DC bus voltage for the aforementioned experimental tests is shown in
Figure 6d, where disturbances at t = 5 s and t = 8 s have been generated. As expected, disappearance on 50% of prime power generation unit will cause the voltage drop on the common DC bus. In contrast to the previous case, removing load from the microgrid system will increase the voltage level of the common DC bus. For this test situation, the power balance is obtained under both nominal and changing conditions. Swings on the measured power and voltage are based on the atmospheric condition, especially instantaneous wind speed changes and switching factor on the converters. Total fluctuation levels are 28 W for PV unit, 9 W for load, 16 W for BESS, and 0.5 V for common DC bus voltage, respectively. For transient behavior, the common DC bus voltage fluctuations are 0.25 V and 0.38 V for changes on PV unit power and load power, respectively.
5. Conclusions
Different types of synergetic controllers for the different components of the small scale DC microgrid prototype to regulate the output voltages of the existing components, PV unit, and BESS have been designed and implemented in this paper. The main goal was to maintain the power balance as well as a constant voltage at the common bus within the islanded DC microgrid. This paper also presented the theory representing the various components of the DC microgrids together with the controller design approach. Each component of the system was controlled separately in such a way that to match the output voltage with the common DC bus voltage is equal to the voltage output while generating power to meet the desired power for the load demands. Diverse performance evaluation of the designed controllers for different scenarios has been carried out and presented in this paper The simulation tests that were included in the paper show clearly the effectiveness of the various proposed controller schemes by tackling the transients within the DC microgrids such as the power balance and the constant DC bus voltage. Additionally, a generalized mathematical method has been derived for all power electronic-based subsystems of the microgrid system to make the design of the controllers independent from system component values. It has been concluded that the definition of the macro variables is affecting robustness and tracking performance of the designed controllers. Different from the previously presented methods, all of the state variables have been considered during controller design procedures. This approach has increased the accuracy and sensitivity of the designed controllers. According to the obtained results from both simulation and experimental studies, FTSC has confirmed superior performance than the others effectively. In order to compare the synergetic controllers to the classical controller approaches, a sliding mode controller (SMC) and a voltage mode controller (VMC) have been designed and simulated for the same cases. It is observed that while VMC has the worst behavior with an overshoot, SMC has the biggest settling time value without overshoot. For this reason, only synergetic type controllers have been taken into consideration. Among the synergetic based controllers, FTSC has shown better performance for all scenarios, for the evaluation of shading effect for supplying load demand with BESS, as well.
For future works, to improve the performance of the system greatly, the design of the manifolds will be given more attention. For this purpose, a fractional order calculus approach will be considered for the design of the future manifolds. Moreover, with the wide use of observers in various fields, adaptive observers have good application value and prospect and will be investigated by our team in the near future.