A Calculation Model of Carbon Emissions Based on Multi-Scenario Simulation Analysis of Electricity Consumption
Abstract
:1. Introduction
2. Literature Review
2.1. Carbon Emission Calculation Methods Based on Indirect Variables
2.2. Carbon Emission Calculation Methods Based on Direct Variables
3. Calculation Model and Scenario Design
3.1. Calculation Model of Carbon Emissions
3.1.1. Total Carbon Emission Model
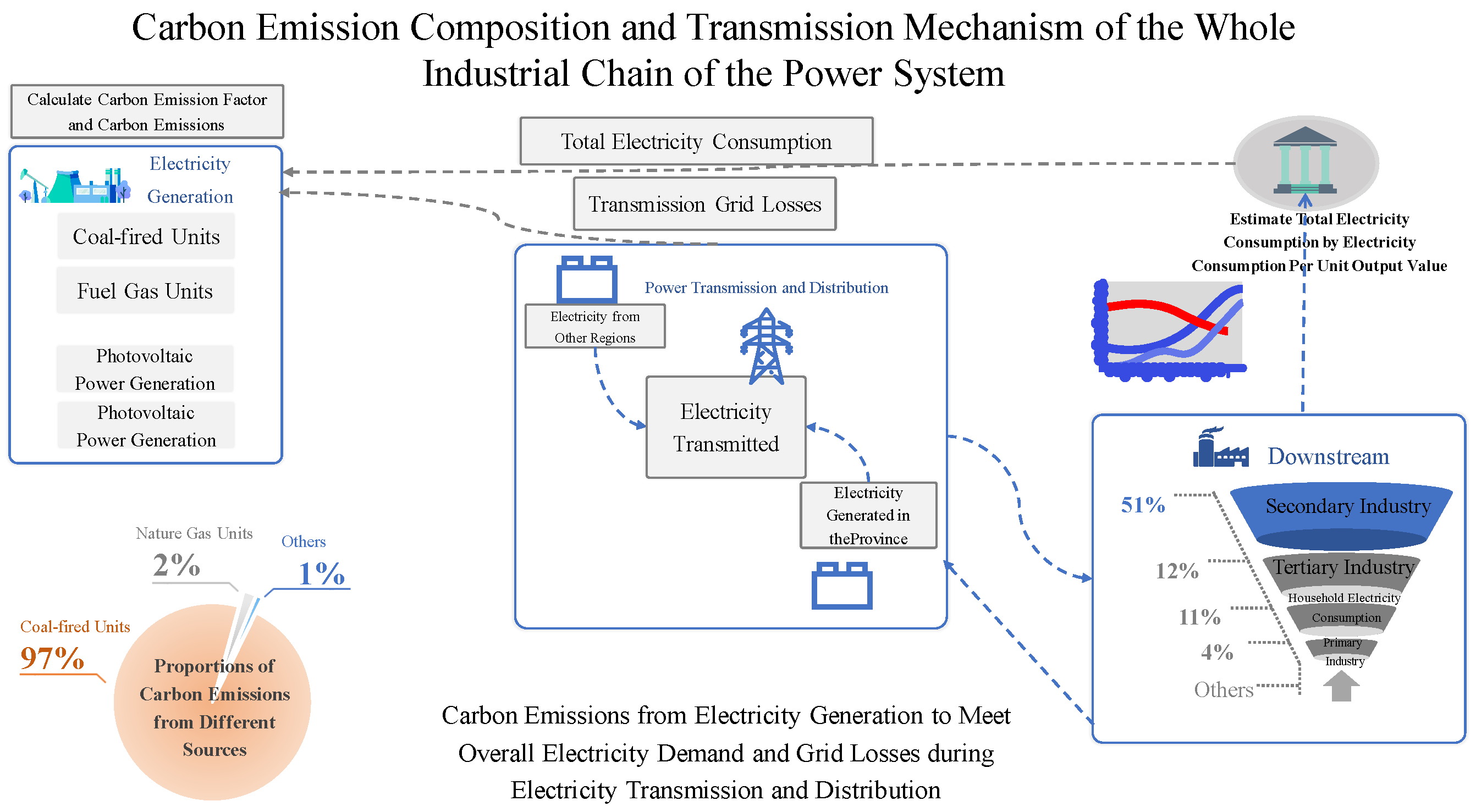
3.1.2. Carbon Emissions from Electricity Generation to Meet Overall Electricity Demand
- Overall Electricity Demand :The overall electricity demand (OED) is a key parameter in predicting carbon emissions. The electricity consumption per unit output value (ECPUOV) method [32] can be used to predict industrial electricity consumption, and PCEC can be used to predict residential electricity consumption. ECPUOV statistically analyzes the ECPUOV of the three major industries (agriculture, industry, and service sector) and determines the ECPUOV of the three industries according to economic development and industrial structure adjustment. Plus annual residential electricity consumption, it predicts the overall electricity demand (OED) in a designated area [33]. The formula is as follows:where represents total electricity consumption in the year t; , the output value of unit consumption of the industry i in the year t; , the output value of the industry i in the year t; , the total population in the region in the year t; , per capita residential electricity consumption in the year t.
- Carbon Emission Factor :According to the results of the Pearson correlation coefficient analysis in Appendix A, and combined with the experience of industry experts and the studies of [34,35,36,37,38,39], this paper defines the carbon emission factor as a parameter that describes the association of the total carbon emissions in the region with the URICFPG, the PFPG and the CRFPG. The calculation formula of the carbon emission factor is as follows:where (explained variable) represents the carbon emission factor in the year t; (key explanatory variable), the URICFPG in the year t; , the PFPG in the year t; , the CRFPG in the year t. is an error, and , , and are variation coefficients.In order to avoid pseudo regression of data, the sequence of each variable must be stable in the regression analysis of explanatory variables and explained variables. This paper uses Eviews to establish an econometric model for the ADF unit root test and cointegration analysis. See Appendix A for specific analysis and results. Firstly, the stationarity of each variable sequence is determined according to the results of the ADF test, and the nonstationary sequence is transformed into a stationary sequence by difference. The test results show that the carbon emission coefficient and its strongly related factors, such as , and , are stable after the first-order difference (FOD). Therefore, the Johansen cointegration test can be performed between these four variables. The results of the cointegration test show that there is at least one cointegration relationship among the four variables at the 5% confidence level, so regression analysis can still be carried out even in the case of non-stationary series.
3.1.3. Carbon Emissions from Electricity Network Losses
3.2. Design of Multi-Scenario
- REF: No climate change measures are adopted. The technology, installed structure, and structure of power generation remain at the same level as that in the year 2021, and the final electricity demand consistent with this emission scenario is met. Coal power has basically realized clean development. The coal consumption rate of generation has a limited reduction space for the generation has basically realized clean development. coal power and new energy power are developing at a low rate. The installed capacity and power generation of thermal power always dominate. According to the current power supply structure, by 2030, the installed capacity of fossil power will account for 61.8%, and electricity generated from fossil energy will account for 64%. Grid losses remain at the current level.
- LC: The latest industrial planning, clean energy goals, and low carbon policies stipulated by the 14th Five-year Plan of G Province have been realized. Coal power gradually decreases after slow growth. New energy power generation develops at a moderate speed. Technical and management measures for reducing grid losses develop at a moderate speed. By 2030, the percentages of the installed capacity of fossil power and power generated from fossil power are expected to fall to 48.7% and 50.4% respectively.
- SC: This scenario considers constraint factors such as rapid growth of electricity consumption and shortages of gas and water based on the low carbon scenario. China’s electricity consumption will grow rapidly and reach 920 billion kWh in 2025, 1050 billion kWh in 2030, and 1130 billion kWh in 2035. There will be a natural gas shortage, and the rise in natural gas prices will lead to an increase in electricity costs. Thus, annual power generation utilization hours are expected to experience a significant decrease. Moreover, the gap in the power supply from western China will widen. It is estimated that 190 billion kWh of electricity will be sent from western China to eastern China during the 14th Five-year Plan period. Under the above security constraints, coal power will compensate for the electricity gap to achieve electricity balance. On the power supply side, the installed capacity of non-fossil energy and power generated by non-fossil energy will gradually play a dominant role after 2025. By 2030, the percentages of the installed capacity of fossil and power generated from fossil energy are expected to drop to 48.7% and 54.6% respectively. On the electric grid side, the electric grid loss reduction level will be constantly optimized. The electric grid loss rate will be reduced to 3.75% beyond expectations and remain relatively stable.
3.3. Data Source
- Source of data for calculating the carbon emission factor. The data of used in the REF are from the Brief Introduction to the Operation of Electric Power Industry of China Electricity Council. The data of and used in the REF are calculated based on electricity generated from different types of energy and unit standard coal consumption specified in the China Energy Statistical Yearbook. The data of , , , and electricity transmitted according to the West-to-East Power Transmission Project used in the LC and the SC are estimated according to the 14th Five-year Plan for Energy Development of G Province.
- Historical output values and ECPUOV of the three major industries of the national economy used to predict electricity consumption are from the G Province Statistical Yearbook. The output values of the three major industries, unit electricity consumption, and per capita household electricity consumption (PCHEC), which are used in the REF, the LC, and the SC, are all reasonably estimated based on historical data.
- The data of grid loss rate of G province power system used in the REF are from the Energy Statistics of G Province Electricity Trade Association, and the data used in the LC and the SC are reasonably estimated according to the 14th Five-year Plan for Energy Development of G Province.
4. Estimated Carbon Emissions of G Province Power System Based on Designed Scenarios
4.1. Calculation of Key Parameters of the Model
4.1.1. Calculation of Carbon Emission Coefficient
4.1.2. Power Consumption Prediction of the Whole Society
4.1.3. Grid Loss Rate
4.2. Quantitative Evaluation Analysis in Different Scenarios
4.2.1. Reference Scenario
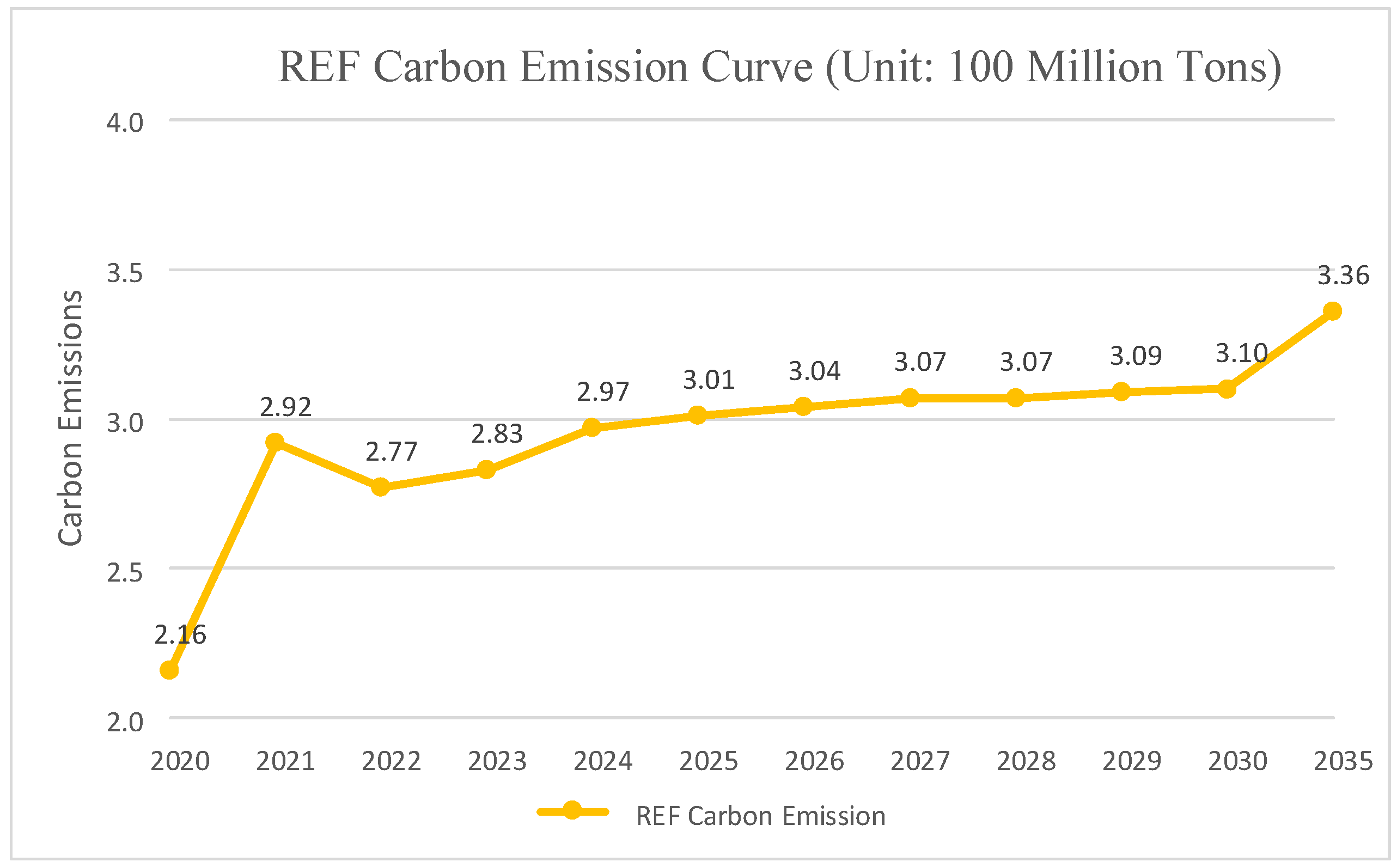
- Estimated Carbon EmissionsCarbon emissions in the REF are shown in Table 5 below.
- Carbon Emission CurveIn the REF, the carbon emission curve of G province’s power system is shown in Figure 2 below. The carbon emissions will gradually increase before 2030, but they will not peak. In 2030, the carbon emissions will stand at 310 million tons, of which 294 million tons are from total electricity consumption and 16 million tons are from grid losses.
4.2.2. Low Carbon Scenario
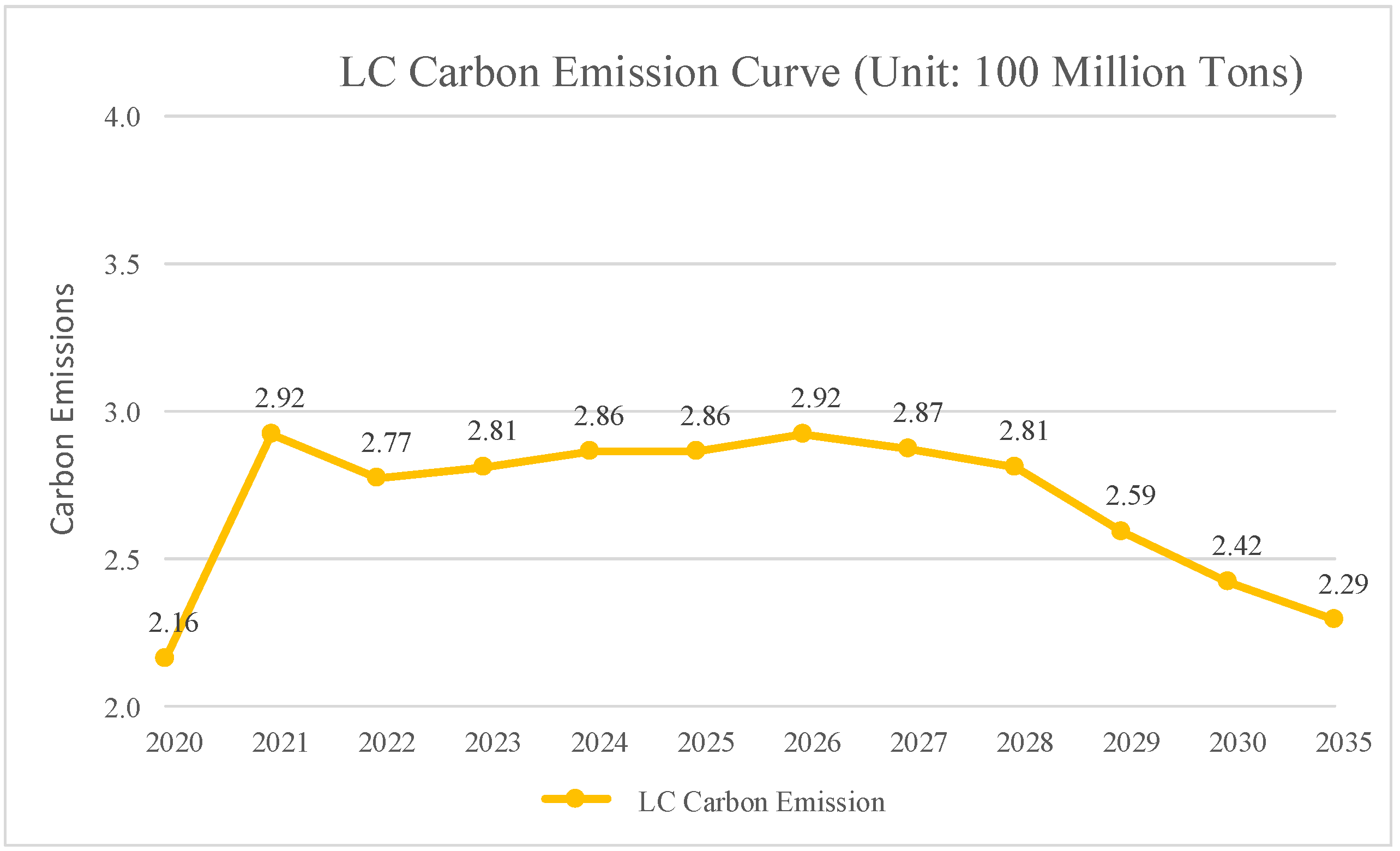
- Estimated Carbon EmissionsAccording to calculation results of the carbon emission factor model and the carbon emission model for the overall electricity demand (OED), estimated carbon emissions under the LC are shown in Table 6 below.
- Carbon Emission CurveIn the LC, the carbon emission curve of G province’s power system is shown in Figure 3 below. In around 2026, G province will peak carbon emissions. In 2030, G province’s power system carbon emissions will stand at 242 million tons, of which 230 million tons are from total electricity consumption and 12 million tons are from grid losses.
4.2.3. Security Constraint Scenario
- Estimated Carbon EmissionsBased on the hypothesized electric quantity and power supply structure in the security constraint scenario, estimated carbon emissions in the SC are shown in Table 7.
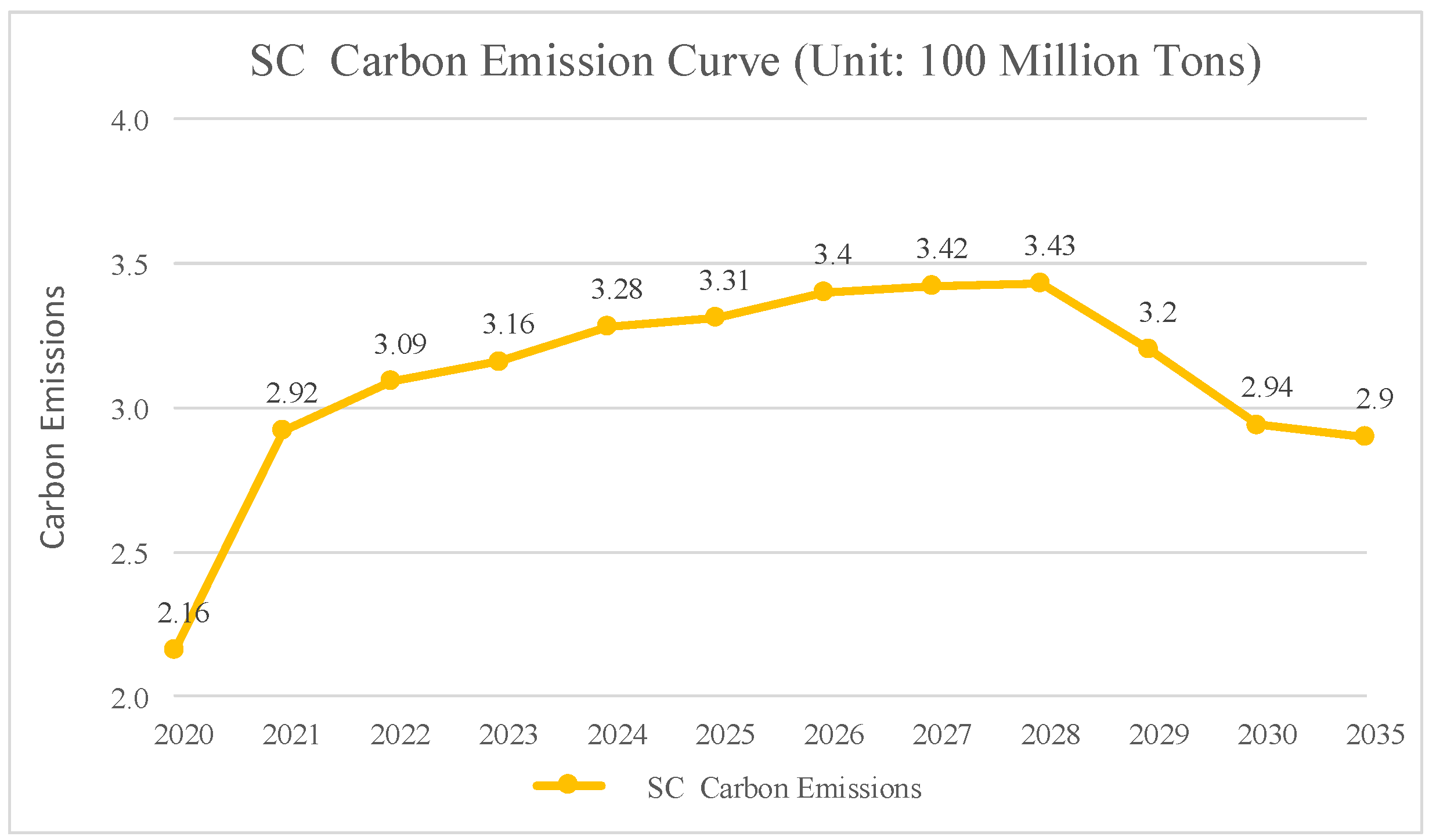
- Carbon Emission CurveIn the SC, the carbon emission curve of G province’s power system is shown in Figure 4 below. carbon emissions from electricity consumption in G province will reach peak carbon emissions in around 2028. In 2025, carbon emissions from electricity consumption in G province will amount to 330 million tons, and in 2030, 294 million tons.
4.2.4. Summary and Discussion of Three Scenarios
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EKC | Environment Kuznets Curve |
| OED | Overall Electricity Demand |
| PCEC | Per Capita Electricity Consumption |
| PCHEC | Per Capita Household Electricity Consumption |
| URICFPG | Utilization Rate of the Installed Capacity of Fossil Power Generation |
| PFPG | Proportion of Fossil Power Generation |
| CRFPG | Conversion Rate of Fossil Power Generation |
| FOD | First-Order Differential |
| SOD | Second-Order Differential |
| TOD | Third-Order Differential |
| REF | Reference Scenario |
| LC | Low Carbon Scenario |
| SC | Security Constraint Scenario |
| CPUOV | Consumption per Unit Output Value |
| ECPUOV | Electricity Consumption per Unit Output Value |
Appendix A. Introduction to Fitting of Carbon Emission Factor
Appendix A.1. Correlation Analysis of Driving Factors
| Type of Variable | (X,Y) |
|---|---|
| URICFPG | 0.9029 |
| PFPG | 0.9839 |
| CRFPG | −0.8542 |
| Electricity Consumption Elasticity Coefficient | −0.4308 |
| Energy Consumption Elasticity Coefficient | −0.1581 |
| Natural Population Growth Rate (%) | −0.7436 |
| Contribution Rate of Tertiary Industry to Regional GDP | −0.8509 |
| Growth Rate of Electricity Consumption Per Unit GDP (%) | −0.3342 |
| Type of Variable | Variables | Correlation | Type |
|---|---|---|---|
| Explained Variable | Carbon Emission Factor | ||
| URICFPG | Strong Positive Correlation | Direct | |
| PFPG | Strong Positive Correlation | Direct | |
| CRFPG | Strong Negative Correlation | Direct | |
| Explanatory Variable | Electricity Consumption Elasticity Coefficient | Negative Correlation | Indirect |
| Energy Consumption Elasticity Coefficient | Weak Negative Correlation | Indirect | |
| Natural Population Growth Rate (%) | Negative Correlation | Indirect | |
| Contribution Rate of Tertiary Industry to Regional GDP | Negative Correlation | Indirect | |
| Growth Rate of Electricity Consumption Per Unit GDP (%) | Negative Correlation | Indirect |
| Variable | t-Statistic | 5%-Level | P | Conclusion |
|---|---|---|---|---|
| Carbon Emission Factor | −0.2098 | −3.25981 | 0.9043 | Non-stationary |
| Carbon Emission Factor (FOD) | −6.0512 | −3.2598 | 0.0014 | Stationary |
| URICFPG | −0.6642 | −3.2127 | 0.8123 | Non-stationary |
| URICFPG (FOD) | −3.8076 | −3.2598 | 0.0231 | Stationary |
| PFPG | −0.6509 | −3.2127 | 0.8157 | Non-stationary |
| PFPG (FOD) | −5.3281 | −3.3209 | 0.0043 | Stationary |
| CRFPG | −0.7831 | −3.2598 | 0.7738 | Non-stationary |
| CRFPG (FOD) | −5.3894 | −3.2598 | 0.003 | Stationary |
| Hypothesized No. of CE(s) | t-Statistic | 5%-Level | P |
|---|---|---|---|
| None | 69.333 | 47.856 | 0.0002 |
| At most 1 | 31.191 | 29.797 | 0.0343 |
| At most 2 | 14.751 | 15.4995 | 0.0645 |
| At most 3 | 2.423 | 3.841 | 0.1196 |
Appendix A.2. Hypothesized Method to Estimate Carbon Emission Factor
Appendix A.3. Calculation of Carbon Emission Factor
| Year | -Model | 1 | ||||
|---|---|---|---|---|---|---|
| 2010 | 68.50% | 80.58% | 40.32% | 0.5672 | 0.5714 | 0.967 |
| 2011 | 77.22% | 82.41% | 40.86% | 0.5793 | 0.5903 | |
| 2012 | 70.73% | 78.16% | 41.13% | 0.5552 | 0.5515 | |
| 2013 | 65.07% | 78.42% | 41.27% | 0.5538 | 0.5418 | |
| 2014 | 61.05% | 77.08% | 41.69% | 0.514 | 0.5222 | |
| 2015 | 55.68% | 75.32% | 41.00% | 0.5058 | 0.5113 | |
| 2016 | 52.73% | 70.61% | 41.69% | 0.4569 | 0.4708 | |
| 2017 | 58.21% | 72.79% | 42.41% | 0.4646 | 0.484 | |
| 2018 | 57.66% | 71.79% | 43.61% | 0.4552 | 0.4629 | |
| 2019 | 53.77% | 66.58% | 43.00% | 0.411 | 0.4337 | |
| 2020 | 51.25% | 67.87% | 42.70% | 0.4338 | 0.4403 |
| Coefficients | Regression Statistics | ||
|---|---|---|---|
| 0.4765 | Multiple R | 0.977 | |
| 0.1703 | R Square | 0.967 | |
| 0.5747 | Standard Error | 0.0097 | |
| −1.2024 |
| Item | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|
| REF | 0.4497 | 0.4302 | 0.4204 | 0.4227 | 0.4138 | 0.3958 | 0.3993 |
| LC | 0.4497 | 0.4307 | 0.4168 | 0.4081 | 0.394 | 0.309 | 0.2727 |
| SC | 0.4497 | 0.4515 | 0.4382 | 0.4325 | 0.4207 | 0.3446 | 0.315 |
Appendix B. Introduction to Estimation of Total Electricity Consumption
Appendix B.1. ECPUOV Method
| Item | 2025 | 2030 | 2035 |
|---|---|---|---|
| ECPUOV of Primary Industry | 0.033 | 0.034 | 0.035 |
| ECPUOV of Secondary Industry | 0.103 | 0.09 | 0.078 |
| ECPUOV of Tertiary Industry | 0.025 | 0.022 | 0.018 |
Appendix B.2. Estimated PCHEC
| Year | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|
| PCEC (kWh) | 359 | 393 | 432 | 471 | 517 | 529 | 593 | 651 |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
| PCEC (kWh) | 672 | 756 | 780 | 822 | 845 | 873 | 937 |
| Coefficients | Regression Statistics | ||
|---|---|---|---|
| Intercept | 307.06 | Multiple R | 0.997 |
| 41.855 | R Square | 0.994 | |
| Standard Error | 15.089 |
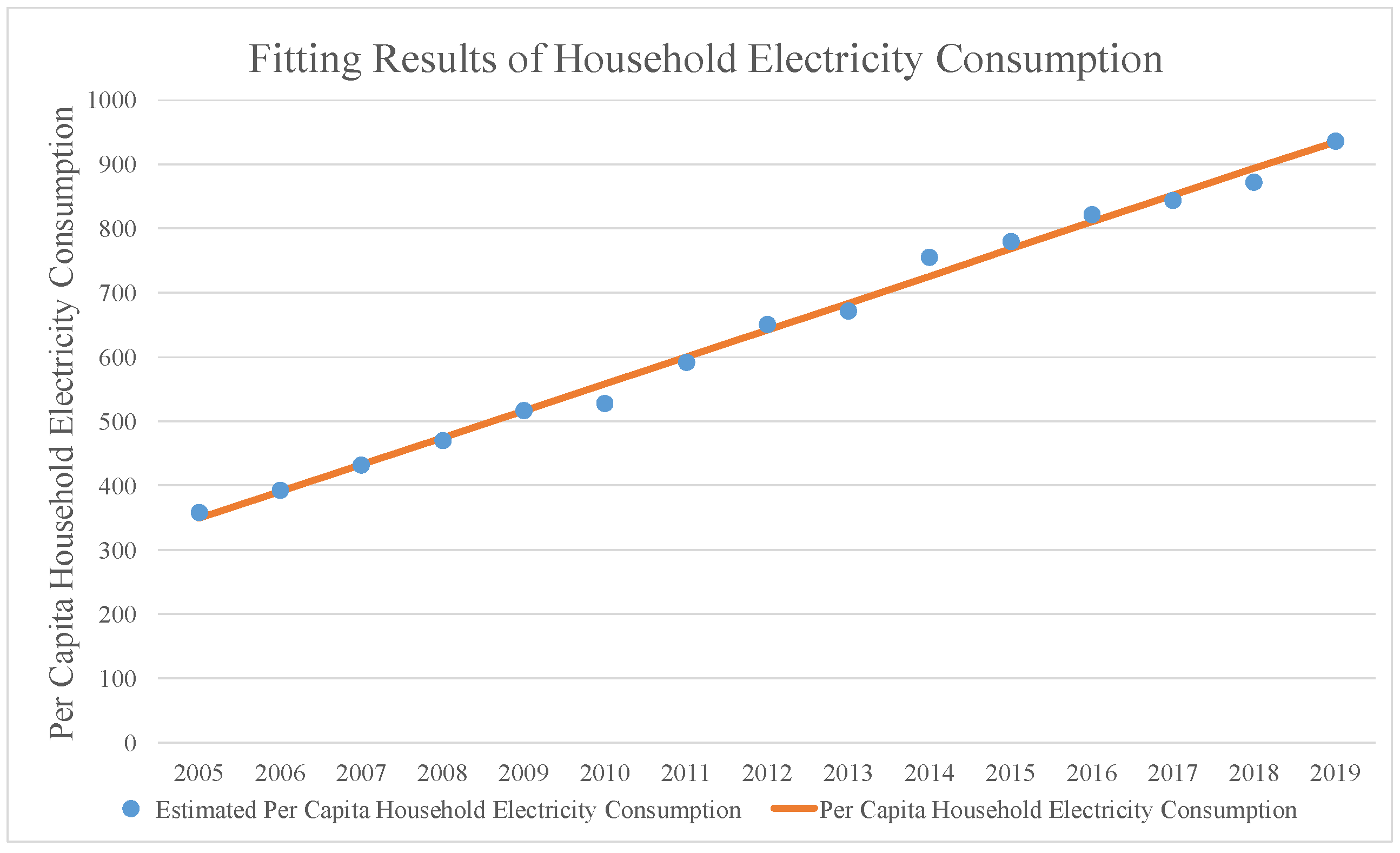
Appendix B.3. Estimated Total Electricity Consumption
| Item | 2025 (Estimated) | 2030 (Estimated) | 2035 (Estimated) |
|---|---|---|---|
| G province’s GDP (CNY 100 Million) 1 | 126,182 | 161,043 | 195,934 |
| Population (10,000 Persons) | 12,240 | 12,700 | 13,000 |
| ECPUOV of Primary Industry (kWh/CNY) | 0.033 | 0.034 | 0.035 |
| ECPUOV of Secondary Industry (kWh/CNY) | 0.103 | 0.09 | 0.078 |
| ECPUOV of Tertiary Industry (kWh/CNY) | 0.025 | 0.022 | 0.018 |
| PCHEC (kWh/Person/Year) | 1186 | 1396 | 1605 |
| Total Electricity Consumption | 9200 | 10,500 | 11,300 |
References
- International Energy Agency. Global Energy Review: CO2 Emissions in 2021. Available online: https://www.iea.org/reports/global-energy-review-CO2-emissions-in-2021-2 (accessed on 20 May 2022).
- International Energy Agency. Enhancing China’s ETS for Carbon Neutrality: Focus on Power Sector. Available online: https://www.iea.org/reports/enhancing-chinas-ets-for-carbon-neutrality-focus-on-power-sector (accessed on 20 May 2022).
- International Energy Agency. An Energy Sector Roadmap to Carbon Neutrality in China. Available online: https://www.iea.org/reports/an-energy-sector-roadmap-to-carbon-neutrality-in-china (accessed on 20 May 2022).
- Zheng, B.; Wang, S.; Xu, J.X. A Review on the CO2 Emission Reduction Scheme and Countermeasures in China’s Energy and Power Industry under the Background of Carbon Peak. Sustainability 2022, 14, 879. [Google Scholar] [CrossRef]
- International Energy Agency. Net Zero by 2050: A Roadmap for the Global Energy Sector. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 20 May 2022).
- McKinsey & Company. Pathways to a Low-carbon Economy: Version 2 of the Global Greenhouse Gas Abatement Cost Curve. Available online: https://www.mckinsey.com/business-functions/sustainability/our-insights/pathways-to-a-low-carbon-economy (accessed on 20 May 2022).
- Fan, Z.G.; Hu, Q. Research on influencing factors and countermeasures of industrial carbon emission in Hebei province based on Kaya model. IOP Conf. Ser.-Earth Environ. Sci. 2020, 450, 012068. [Google Scholar] [CrossRef]
- Tao, Y.; Wen, Z.G.; Xu, L.; Zhang, X.; Tan, Q.L.; Li, H.F.; Evans, S. Technology options: Can Chinese power industry reach the CO2 emission peak before 2030? Resour. Conserv. Recycl. 2019, 147, 85–94. [Google Scholar] [CrossRef]
- Zoundi, Z. CO2 emissions, renewable energy and the Environmental Kuznets Curve, a panel cointegration approach. Renew. Sustain. Energy Rev. 2017, 72, 1067–1075. [Google Scholar] [CrossRef]
- Chang, K.; Chen, G.J.; Du, Z.F.; Hou, F.J.; Li, J.Q.; Chen, F. Decomposition and decoupling research of Chinese power sector carbon emissions through the consumption accounting principle. Environ. Sci. Pollut. Res. 2022, 29, 9080–9096. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.P.; Wei, D.L. Analysis and Measurement of Carbon Emission Aggregation and Spillover Effects in China: Based on a Sectoral Perspective. Sustainability 2020, 12, 8966. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Wang, P.; Wu, W.S.; Zhu, B.Z.; Wei, Y.M. Examining the impact factors of energy-related CO2 emissions using the STIRPAT model in Guangdong Province, China. Appl. Energy 2013, 106, 65–71. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Decomposition of energy-related CO2 emissions in China: An empirical analysis based on provincial panel data of three sectors. Appl. Energy 2017, 190, 772–787. [Google Scholar] [CrossRef]
- Liu, Z.; Guan, D.B.; Wei, W.; Davis, S.J.; Ciais, P.; Bai, J.; Peng, S.S.; Zhang, Q.; Hubacek, K.; Marland, G.; et al. Reduced carbon emission estimates from fossil fuel combustion and cement production in China. Nature 2017, 524, 335–338. [Google Scholar] [CrossRef] [Green Version]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Available online: https://www.ipcc.ch/report/2006-ipcc-guidelines-for-national-greenhouse-gas-inventories (accessed on 20 May 2022).
- Wang, W.X.; Kuang, Y.Q.; Huang, N.S. Study on the decomposition of factors affecting energy-related carbon emissions in Guangdong province, China. Energies 2011, 4, 2249–2272. [Google Scholar] [CrossRef] [Green Version]
- Peter, C.; Fiore, A.; Hagemann, U.; Nendel, C.; Xiloyannis, C. Improving the accounting of field emissions in the carbon footprint of agricultural products: A comparison of default IPCC methods with readily available medium-effort modeling approaches. Int. J. Life Cycle Assess. 2016, 21, 791–805. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.J.; Zhou, C.S.; Li, G.D.; Feng, K.S. CO2, economic growth, and energy consumption in China’s provinces: Investigating the spatiotemporal and econometric characteristics of China’s CO2 emissions. Ecol. Indic. 2016, 69, 184–195. [Google Scholar] [CrossRef]
- Jian, J.H.; Fan, X.J.; He, P.L.; Xiong, H.; Shen, H.Y. The Effects of Energy Consumption, Economic Growth and Financial Development on CO2 Emissions in China: A VECM Approach. Sustainability 2019, 11, 4850. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, M.; Sahoo, J. Effects of renewable and non-renewable energy consumption on CO2 emissions in India: Empirical evidence from disaggregated data analysis. J. Public Aff. 2020, 22, e2307. [Google Scholar] [CrossRef]
- Sahoo, M.; Gupta, M.; Srivastava, P. Does information and communication technology and financial development lead to environmental sustainability in India? An empirical insight. Telemat. Inform. 2021, 60, 101598. [Google Scholar] [CrossRef]
- Mohini, G.; Seema, S.; Malayaranjan, S. Determinants of ecological footprint and PM2.5: Role of urbanization, natural resources and technological innovation. Environ. Chall. 2022, 7, 100467. [Google Scholar] [CrossRef]
- Ali, H.S.; Sahoo, M.; Alam, M.M.; Tijjani, I.I.; Al-Amin, A.; Ahmed, A. Structural transformations and conventional energy-based power utilization on carbon emissions: Empirical evidence from Pakistan. Environ. Dev. Sustain. 2022. [Google Scholar] [CrossRef]
- Villanthenkodath, M.A.; Gupta, M.; Saini, S.; Sahoo, M. Impact of Economic Structure on the Environmental Kuznets Curve (EKC)hypothesis in India. Econ. Struct. 2021, 10, 28. [Google Scholar] [CrossRef]
- Zhou, L.Y. Study on the influence of urban construction land expansion on carbon emission based on VAR Model—A case study of Nanchang City. IOP Conf. Ser. Earth Environ. Sci. 2021, 769, 022071. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Zhang, Z.X.; Zhang, F.F.; Liu, Z.Y. How might Shandong achieve the 2030 CO2 emissions target? A system dynamics analysis from the perspective of energy supply-side structural reform in China. Int. J. Glob. Warm. 2019, 17, 357–372. [Google Scholar] [CrossRef]
- Leitao, J.; Ferreira, J.; Santibanez-Gonzalez, E. New insights into decoupling economic growth, technological progress and carbon dioxide emissions: Evidence from 40 countries. Technol. Forecast. Soc. Chang. 2022, 174, 121250. [Google Scholar] [CrossRef]
- Huang, Y.S.; Xu, J. Research on Carbon Emission Measurement of Electricity Sector Based on Scenario Analysis Method. Appl. Mech. Mater. 2013, 367, 327–332. [Google Scholar] [CrossRef]
- Song, C.; Zhao, T.; Wang, J. Analyzing driving forces of China’s carbon emissions from 1997 to 2040 and the potential emission reduction path: Through decomposition and scenario analysis. Clean Technol. Environ. Policy 2021, 24, 1219–1240. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Su, B.; Zhou, K.L.; Yang, S.L. Decomposition analysis of China’s CO2 emissions (2000–2016) and scenario analysis of its carbon intensity targets in 2020 and 2030. Sci. Total Environ. 2019, 668, 432–442. [Google Scholar] [CrossRef]
- Li, L.C.; Meinrenken, C.J.; Modi, V.; Culligan, P.J. Short-term apartment-level load forecasting using a modified neural network with selected auto-regressive features. Appl. Energy 2021, 287, 116509. [Google Scholar] [CrossRef]
- Seker, M. Long term electricity load forecasting based on regional load model using optimization techniques: A case study. Appl. Energy 2021, 44, 21–43. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, P.; Xie, B.C.; Zhang, N. Assessing drivers of CO2 emissions in China’s electricity sector: A metafrontier production-theoretical decomposition analysis. Eur. J. Oper. Res. 2018, 275, 1096–1107. [Google Scholar] [CrossRef]
- Jiang, H.J.; Geng, Y.; Tian, X.; Zhang, X.; Chen, W.; Gao, Z.Y. Uncovering CO2 emission drivers under regional industrial transfer in China’s Yangtze River Economic Belt: A multi-layer LMDI decomposition analysis. Front. Energy 2020, 15, 292–307. [Google Scholar] [CrossRef]
- Harrathi, N.; Almohaimeed, A. Determinants of Carbon Dioxide Emissions: New Empirical Evidence from MENA Countries. Int. J. Energy Econ. Policy 2022, 12, 469–482. [Google Scholar] [CrossRef]
- Sadr, N.R.; Bahrdo, T.; Taghizadeh, R. Impacts of Paris agreement, fossil fuel consumption, and net energy imports on CO2 emissions: A panel data approach for three West European countries. Clean Technol. Environ. Policy 2022, 24, 1521–1534. [Google Scholar] [CrossRef]
- Shi, H.T.; Chai, J.; Lu, Q.Y.; Zheng, J.L.; Wang, S.Y. The impact of China’s low-carbon transition on economy, society and energy in 2030 based on CO2 emissions drivers. Energy 2021, 239, 122336. [Google Scholar] [CrossRef]
- Li, A.J.; Zhang, A.Z.; Zhou, Y.X.; Yao, X. Decomposition analysis of factors affecting carbon dioxide emissions across provinces in China. J. Clean. Prod. 2017, 141, 1428–1444. [Google Scholar] [CrossRef]
| Year | -Model | 1 | ||||
|---|---|---|---|---|---|---|
| 2010 | 68.50% | 80.58% | 40.32% | 0.5672 | 0.5714 | 0.967 |
| 2011 | 77.22% | 82.41% | 40.86% | 0.5793 | 0.5903 | |
| 2012 | 70.73% | 78.16% | 41.13% | 0.5552 | 0.5515 | |
| 2013 | 65.07% | 78.42% | 41.27% | 0.5538 | 0.5418 | |
| 2014 | 61.05% | 77.08% | 41.69% | 0.514 | 0.5222 | |
| 2015 | 55.68% | 75.32% | 41.00% | 0.5058 | 0.5113 | |
| 2016 | 52.73% | 70.61% | 41.69% | 0.4569 | 0.4708 | |
| 2017 | 58.21% | 72.79% | 42.41% | 0.4646 | 0.484 | |
| 2018 | 57.66% | 71.79% | 43.61% | 0.4552 | 0.4629 | |
| 2019 | 53.77% | 66.58% | 43.00% | 0.411 | 0.4337 | |
| 2020 | 51.25% | 67.87% | 42.70% | 0.4338 | 0.4403 |
| Item | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|
| REF | 0.4497 | 0.4302 | 0.4204 | 0.4227 | 0.4138 | 0.3958 | 0.3993 |
| LC | 0.4497 | 0.4307 | 0.4168 | 0.4081 | 0.394 | 0.309 | 0.2727 |
| SC | 0.4497 | 0.4515 | 0.4382 | 0.4325 | 0.4207 | 0.3446 | 0.315 |
| Item | 2019 | 2020 | 2025 | 2030 | 2035 | |
|---|---|---|---|---|---|---|
| Total Population (10,000 Persons) | 11,521 | 11,640 | 12,240 | 12,700 | 13,000 | |
| PCHEC (kWh/Person) | 937 | 972 | 1200 | 1400 | 1600 | |
| Primary Industry | 3664 | 3772 | 4416 | 4847 | 5310 | |
| Economy (CNY 100 Million) | Secondary Industry | 36,668 | 37,716 | 48,958 | 59,683 | 69,106 |
| Tertiary Industry | 50,332 | 52,803 | 73,059 | 96,465 | 12,1518 | |
| Primary Industry | 0.032 | 0.033 | 0.033 | 0.034 | 0.035 | |
| CPUOV (kWh/CNY) | Secondary Industry | 0.112 | 0.112 | 0.103 | 0.090 | 0.078 |
| Tertiary Industry | 0.027 | 0.027 | 0.025 | 0.022 | 0.018 | |
| Primary Industry | 117 | 124 | 146 | 165 | 186 | |
| Electricity Consumption (100 Million kWh) | Secondary Industry | 4120 | 4209 | 5043 | 5371 | 5390 |
| Tertiary Industry | 1380 | 1435 | 1826 | 2122 | 2187 | |
| Residents | 1079 | 1132 | 1469 | 1778 | 2080 | |
| Total Electricity Consumption (100 Million kWh) | 6696 | 6926 | 9200 | 10,500 | 11,300 |
| Item | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|
| REF | 3.98% | 3.98% | 3.98% | 3.98% | 3.98% | 3.98% | 3.98% |
| LC | 3.96% | 3.95% | 3.94% | 3.90% | 3.80% | 3.80% | 3.80% |
| SC | 3.96% | 3.95% | 3.94% | 3.90% | 3.80% | 3.75% | 3.75% |
| Variable | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|---|
| (100 Million Tons) | 2.16 | 2.92 | 2.77 | 2.83 | 2.97 | 3.01 | 3.10 | 3.36 |
| (100 Million Tons) | 2.04 | 2.77 | 2.63 | 2.69 | 2.82 | 2.86 | 2.94 | 3.18 |
| (100 Million Tons) | 0.12 | 0.15 | 0.14 | 0.14 | 0.15 | 0.15 | 0.16 | 0.18 |
| Variable | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|---|
| (100 Million Tons) | 2.16 | 2.92 | 2.77 | 2.81 | 2.86 | 2.86 | 2.42 | 2.29 |
| (100 Million Tons) | 2.04 | 2.77 | 2.63 | 2.67 | 2.72 | 2.72 | 2.30 | 2.17 |
| (100 Million Tons) | 0.12 | 0.15 | 0.14 | 0.14 | 0.14 | 0.14 | 0.12 | 0.12 |
| Variable | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2030 | 2035 |
|---|---|---|---|---|---|---|---|---|
| (100 Million Tons) | 2.16 | 2.92 | 3.09 | 3.16 | 3.28 | 3.31 | 2.94 | 2.90 |
| (100 Million Tons) | 2.04 | 2.77 | 2.94 | 3.01 | 3.12 | 3.16 | 2.80 | 2.76 |
| (100 Million Tons) | 0.12 | 0.15 | 0.15 | 0.15 | 0.16 | 0.15 | 0.14 | 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liao, Z.; Gao, Z.; Li, Q.; Lv, P.; Zheng, G.; Yang, K. A Calculation Model of Carbon Emissions Based on Multi-Scenario Simulation Analysis of Electricity Consumption. Sustainability 2022, 14, 8765. https://doi.org/10.3390/su14148765
Chen X, Liao Z, Gao Z, Li Q, Lv P, Zheng G, Yang K. A Calculation Model of Carbon Emissions Based on Multi-Scenario Simulation Analysis of Electricity Consumption. Sustainability. 2022; 14(14):8765. https://doi.org/10.3390/su14148765
Chicago/Turabian StyleChen, Xiaoli, Zhiwei Liao, Zhihua Gao, Qian Li, Peng Lv, Guangyu Zheng, and Kun Yang. 2022. "A Calculation Model of Carbon Emissions Based on Multi-Scenario Simulation Analysis of Electricity Consumption" Sustainability 14, no. 14: 8765. https://doi.org/10.3390/su14148765
APA StyleChen, X., Liao, Z., Gao, Z., Li, Q., Lv, P., Zheng, G., & Yang, K. (2022). A Calculation Model of Carbon Emissions Based on Multi-Scenario Simulation Analysis of Electricity Consumption. Sustainability, 14(14), 8765. https://doi.org/10.3390/su14148765






