A Multi-Objective Optimization Model for the Intercity Railway Train Operation Plan: The Case of Beijing-Xiong’an ICR

Abstract

For intercity railway transportation enterprises, a reasonable intercity train operation plan is not only the foundation of the intercity railway operation organization, but also the key to the sustainable development of the intercity railway (ICR). In this paper, taking into account the economic benefits of railway transportation enterprises and the social benefits of passenger travel, an optimization model is established with the intercity railway train operation plan as the research object. The model aims to minimize the operating cost of railway transportation enterprises and minimize the travel time of passengers, and considers constraints such as passenger seat utilization, passenger flow, train frequency, and stops. It is a multi-objective optimization model that accumulates two objectives by introducing the passenger time value coefficient. According to the characteristics of the model, a genetic algorithm is designed to solve the model. Taking the Beijing-Xiong’an Intercity Railway (BXICR) as an example, the “smart business card” of China’s high-speed railway, two scenarios of passenger time value are designed, and the optimized train operation plan is obtained according to the existing OD passenger flow data, which verifies the effectiveness of the model and algorithm. The results show that compared with the original train operation plan, the number of stops per train of the optimized train operation plan under the two passenger time value scenarios decreased by 8.8% and 14.9%, the operating cost of the enterprise decreased by 7.7% and 1.6%, the travel time of passengers decreased by 0.7% and 1.5%, respectively. Under the condition of meeting the demand of passenger flow, the optimized train operation plan can effectively reduce the operating cost of enterprises and save the travel time of passengers, which is conducive to the sustainable development of intercity railways.

1. Introduction

With the continuous improvement of social and economic level, people have put forward higher requirements for intercity railway transportation. How to provide more convenient, efficient and comfortable intercity railway transportation products for the general public is an issue that intercity railway enterprises need to consider. It is worth noting that the planning and construction of intercity railway are of national public interest, with huge investment in project construction, long passenger flow cultivation period, low fares, and weak comprehensive profitability of a single intercity railway transportation service product. In the initial stage of operation, the newly built intercity railway (ICR) not only needs to pay the operation management, depreciation and other expenses, but also needs to pay huge bank loan interest. In addition, affected by coronavirus disease 2019 (COVID-19), the reduction in trains due to insufficient passenger flow also occurs from time to time, which is not conducive to the sustainable development of intercity railway enterprises. How to take active and effective measures to improve the operation of internal funds and ensure the sustainable development of intercity railway enterprises is a major problem to be solved urgently by local governments and business operators at this stage.

Intercity railway trains have relatively short running distances, relatively fixed operating sections, and the distance between stations is generally between 10 km and 50 km. The main service objects are short-distance passengers such as intercity commuting and commuting to school, which have higher requirements on the speed and convenience of transportation tools. The ICR generally adopts the “small group, high-density” operation mode, which shortens the interval time between trains and can provide travelers with more choices of travel time periods. The shorter running distance can better adapt to the transportation task undertaken by the ICR. The passenger train operation plan is the foundation of the intercity railway transportation organization; in view of this, it is necessary to deeply study the intercity railway transportation organization method, optimize the existing train operation plan, and make it better, to improve the surrounding area transportation and promote social and economic development.

This rest of this paper is organized as follows. Section 2 reviews the related existing practical situations and academic research. Section 3 describes the problem tackled in this article and introduces the modeling work. Section 4 proposes a heuristic iterative algorithm. A case study is detailed in Section 5. Section 6 concludes this paper and suggests directions for future work.

2. Literature Review

2.1. Railway Train Operation Plan

The optimization of the train operation plan of the intercity railway and the optimization of the passenger train operation plan are consistent in basic theory. They are based on the passenger flow, and they optimize the operation section, train type, number of trains, operation frequency of passenger trains, etc.

In the preparation of the train operation plan, the line planning problem (LPP) has been widely and deeply studied in the literature. In line planning, a line pool is usually generated in advance, which includes some potential train routes and train running frequencies, e.g., [1,2]. The main purpose of LPP is to select suitable lines and corresponding train frequency from the line pool. In most studies of line planning, train stop plans are given and specified beforehand. Chang et al. [3] developed a multi-objective programming model for the optimal allocation of passenger train services on an intercity high-speed rail line without branches. Fu et al. [4] introduced a two-stage approach for train stop scheduling with a goal of efficiently organizing passenger traffic. Han et al. [5] developed a multi-objective integer programming model to produce a balanced cross-track line plan by combining individual-track high-speed trains into cross-track high-speed trains.

A stop planning problem (SPP) is also part of the train operation plan. Recently, SPP has primarily been investigated based on the method of passenger flow assignment and station classification. Wang et al. [6] proposed a two-layer optimization model within the simulation framework for the high-speed railway line planning problem. Zhang et al. [7,8] developed a train stop optimization method with the goal of minimizing the total seat-kilometers of unoccupied train-set seats, and proposed a line plan optimization method. Lin et al. [9] proposed an integer program approach to determine the optimal service plan for a rail company. Yang et al. [10] used the stop planning indicators as an important decision variable, and formalized the problem of train operation into a multi-objective mixed-integer linear programming model. Lai et al. [11] developed two binary integer programming models and an optimization process to address complex stop planning problems for high-speed rail systems. Tatsuki et al. [12] presented an efficient local search algorithm to optimize stopping patterns. A customer-oriented dynamic cyclical adjustment approach is applied by Huang et al. [13] to optimize a high-speed railway train stop plan. Ehab et al. [14] established a nonlinear integer mathematical model to solve the problem of finding the best skip-stop arrangement that minimize the average travel time of passengers.

Moreover, some researchers have studied the stop planning with given train frequency, e.g., Jong et al. [15], Chen et al. [16], and Qi et al. [17]. Some integrated optimizations of stop planning and other scheduling processes have been presented as well, e.g., Yue et al. [18], Qi et al. [19,20], and Dong et al. [21]. In a study of timetable planning, Roberto et al. [22] proposed a mixed-integer nonlinear model in order to solve the problem of variable demand cyclic railway timetable. Through a case study, Tomas et al. [23] found that integrating the passenger centric train timetabling problem with a ticket pricing problem can significantly increase revenue. Milan et al. [24] used a variety of methods to optimize the timetable to solve the problem of passenger frequency decline.

2.2. Research Ideas

By summarizing the literature on railway train operation planning, it is found that the existing research on railway train operation plan generally focused on long trunk high-speed railway, while there are few studies on intercity railway train operation planning. The ICR is different from long trunk high-speed railway in terms of train stop mode, and limitations of the starting and terminal station are as follows: (1) ICR mainly serves the travel of intercity passengers, and the train stop mode is diversified, including no-stop, big-station-stop, select-station-stop and all-stop mode. However, in the stop mode of long trunk high-speed railway, there are only big-station-stop and select-station-stop, and generally, there is no no-stop and all-stop mode. (2) The ICR section is short, the intermediate station is generally a low-grade station, and the stations at both ends of the line must be used as the starting and terminal of the train. However, for the long trunk high-speed railway, there are many high-grade stations in the channel, which meet the conditions of being starting and terminal station; when compiling the train operation plan, there is no restriction that the stations at both ends of the line are fixed as the starting and terminal station of the train. Therefore, the constraints of the existing method model do not apply to the intercity railway.

With the continuous improvement of social and economic level, people have put forward higher requirements for intercity railway transportation. There is currently a need for a method for compiling train operation plan that is suitable for the characteristics of ICR.

The contributions of this paper are as follows: (1) a multi-objective programming model for the intercity railway train operation plan is presented, (2) a heuristic iterative algorithm is proposed, and (3) we test the proposed model using China’s ICR case; the results verify the effectiveness of our model and algorithm.

3. Mathematical Model

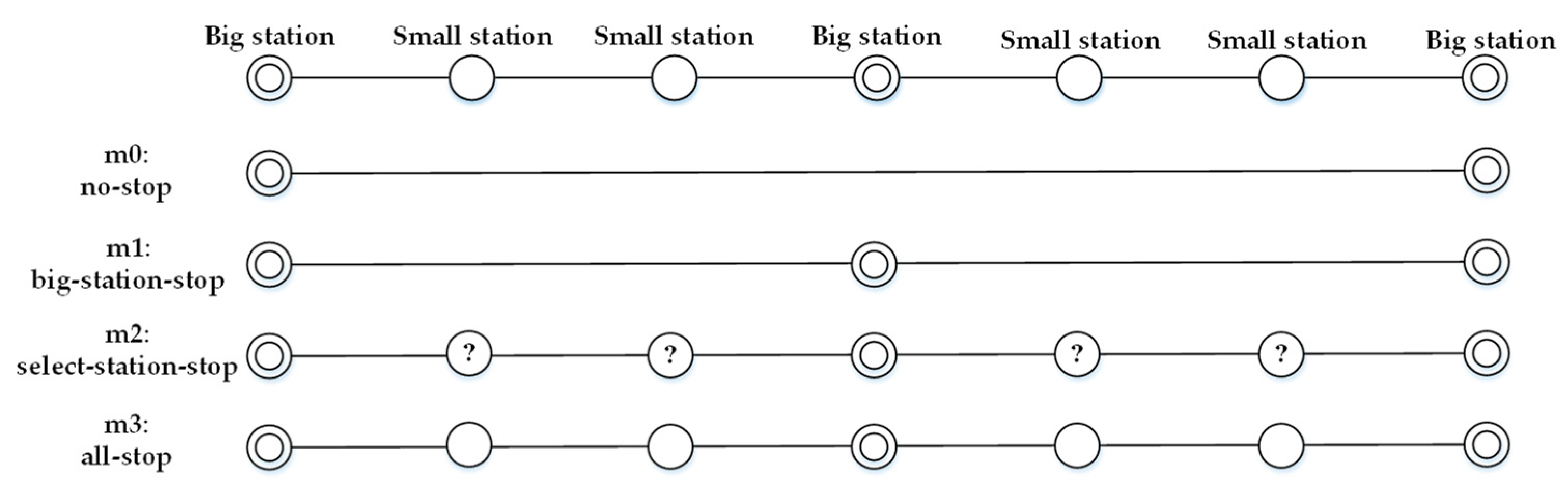
3.1. Problem Description

According to the transportation organization method of “high density, small group and public transportation” of ICR, China’s ICR train formation generally adopts the method of eight carriages. There are four modes of train stop in the ICR transportation organization: no-stop (m₀), big-station-stop (m₁), selected-station-stop (m₂) and all-stop (m₃) modes, as shown in Figure 1. There is only one stop plan for the modes of no-stop, big-station stop and all-stop, while the mode of select-station-stop has a combination of multiple stop plans.

Different stop modes have a great impact on the operating cost of the enterprise and the travel time of passengers, because these two indicators are conflicting. Increasing the times of train stops can achieve better accessibility between ODs, but it will increase the time spent by passengers who do not get off the train, due to the train stopping at the intermediate station; reducing the times of train stops can save a lot of travel time for passengers, but it also means that additional trains need to be run between ODs. Running high frequency trains can make the travel time of passengers more flexible, but at the same time, it will greatly increase the operating costs of railway transportation enterprise. In other words, railway transportation enterprise running high frequency all-stop trains can increase the accessibility of OD, but passengers will consume a lot of travel time; running high frequency no-stop trains can greatly reduce the travel time of passengers, but the operating costs of railway enterprise will also increase.

To summarize, it is necessary to coordinate the operating costs of enterprises and the time consumption of passengers at the same time, while meeting the needs of passenger transportation, finding the optimal combination of four intercity railway train stop modes that can not only ensure corporate benefits but also save travel time for passengers, and establishing a train operating plan corresponding to the operating frequency. The final implementation plan is obtained by comparing with the existing operation plan, which can meet the passenger flow needs of different levels of the ICR while ensuring the reasonable utilization of transportation capacity. That is to say, the essence of the optimization of the train operation plan of the ICR is to analyze the characteristics of passenger flow and the operation situation from different angles. Based on the actual passenger flow data, the optimization model of the intercity railway train operation plan that satisfies the relevant constraints is solved, so that the relevant important indicators of the intercity railway train operation plan can be optimized.

3.2. Model Assumptions

The operating cost of the enterprise and the travel time of passengers need to be effectively coordinated. Before formulating the model, we firstly propose the following assumptions.

(1)

Closed assumption

It is assumed that the system state of the study corresponds to the parameter state, the ICR is not affected by other railway networks, and only the state of main-line trains and passenger flow are considered.

(2)

Deterministic assumption

The optimization model established in this paper is suitable for the ICR that have been operated. Therefore, regardless of the passenger’s preference for travel time and arrival time when purchasing tickets, the passenger flow in one day is constant.

(3)

No transfer assumption

Due to the short operating mileage of intercity railways, it is assumed that all passengers choose trains that can reach their destinations directly, and all passengers do not transfer.

(4)

Capability assumption

China’s ICRs are basically new lines, and high technical standards are adopted in the design and construction. Assuming that the line capacity is not disturbed by external factors, it is the maximum value under idealized conditions.

(5)

Passenger time value assumption

The time value of passengers discussed in this paper refers to the value naturally manifested by passengers choosing a certain means of transportation as a travel mode. For the convenience of research, this paper assumes that the time value of passengers who choose ICR travel is the same.

3.3. Model Notations

Some model notations used in this paper are defined as follows, as shown in

Table 1. Notion in this model.

Notations	Definition
$G$	Intercity railway line, G = (S, E)
$S$	Intercity railway station, s, i, j ∈ S
$E$	Train running sections
$L$	Line length
$l_{ij}$	Distances between i and j
m	Train stop mode, m ∈ M = {m0, m1, m2, m3}
$k^m$	Stop plan for m stop mode, km ∈ Km
$C_0$	The fixed cost of all trains
$C_1$	The stop cost of all trains
$C_2$	The running cost of all trains
$C_3$	The time consumption with train stops
$C_4$	The time consumption with train running
$D$	Train capacity
$t_s$	The stop time of station s, s ∈ S
$R_s$	The stop cost of station s, s ∈ S
$h$	Running cost, CNY per train per kilometer
$p$	Fixed cost of an intercity train
$v_{ij}^{k^m}$	Average running speed between i and j by train with the stop plan km
$q_{ij}^{k^m}$	The passenger flow transported by train with the stop plan km
$Q_{ij}$	The total passenger flow that needs to be transported between i and j
$\delta$	Average passenger time value
$\overline{\theta }$	Maximum occupancy rate
$\underset{\_}{\theta }$	Minimum occupancy rate
$\overline{{\partial }_{}^m}$	Maximum number of trains of m stop mode
$\underset{\_}{{\partial }_{}^m}$	Minimum number of trains of m stop mode
$\overline{{\phi }_{}^m}$	Maximum number of trains stops of m stop mode
$\underset{\_}{{\phi }_{}^m}$	Minimum number of trains stops of m stop mode
$N$	Maximum starting capacity

.

The following are the decision variables for the model, shown in

Table 2. Decision variables in this model.

Decision Variables	Definition
$x_s^{k^m}$	0–1 variable; 1 means train running with stop plan km stops at station s; 0 means otherwise
$f_{}^{k^m}$	The frequency of train running with stop plan km

.

3.4. Mathematical Model

3.4.1. Objective Functions

Intercity railway enterprises need to protect their own economic benefits and consider the interests of passengers when compiling train operation plan. From the perspective of intercity railway transportation enterprise, when formulating the train operation plan of ICR, it is necessary to consider the minimum operating cost of the enterprise; from the perspective of passengers, the main service objects of ICRs pay more attention to travel time. When compiling train operation plans, railway transportation companies need to minimize the travel time of passengers, thereby attracting passenger flow and enhancing market competitiveness. This paper establishes a multi-objective optimization model for the train operation plan of the ICR:

(1)

Minimize the operating cost of intercity railway enterprises

The fixed cost of all trains C₀ can be expressed as Equation (1).

$$C_0={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{f}_{}^{k^m}p}}$$

(1)

The cost of train stops C₁ can be expressed as Equation (2).

$$C_1={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}^{}{\displaystyle \sum _{s=2}^{n-1}{x}_s^{k^m}{f}_{}^{k^m}}}{R}_s}$$

(2)

The running cost of all trains C₂ can be expressed as Equation (3).

$$C_2={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{f}^{k^m}}}hL$$

(3)

In summary, Minimizing the operating cost of ICR enterprise can be expressed as Equation (4).

$$Min{Z}_1=C_0+C_1+C_2={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}(f_{}^{k^m}p+{\displaystyle \sum _{s=2}^{n-1}{x}_s^{k^m}{f}_{}^{k^m}}{R}_s+f_{}^{k^m}hL)}}$$

(4)

(2)

Minimize the travel time of passengers

The time consumption of passengers due to the trains stopping at the intermediate station C₃ can be expressed as Equation (5).

$$C_3={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{\displaystyle \sum _{s=2}^{n-1}{t}_s}}}({\displaystyle \sum _{i=1}^{s-1}{\displaystyle \sum _{j=s+1}^n{q}_{ij}^{k^m}}})x_s^{k^m}$$

(5)

The time consumption of passengers with the train running C₄ can be expressed as Equation (6).

$$C_4={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}^{}{\displaystyle \sum _{i=1}^{n-1}{\displaystyle \sum _{j=2}^n{q}_{ij}^{k^m}}}}}\cdot \frac{l_{ij}}{v_{ij}^{k^m}}$$

(6)

In summary, Minimizing the travel time consumed by passengers can be expressed as Equation (7).

$$Min{Z}_2=C_3+C_4={\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}\{{\displaystyle \sum _{s=2}^{n-1}{t}_s}({\displaystyle \sum _{i=1}^{s-1}{\displaystyle \sum _{j=s+1}^n{q}_{ij}^{k^m}}})x_{ij}^{k^m}+{\displaystyle \sum _{i=1}^{n-1}{\displaystyle \sum _{j=2}^n{q}_{ij}^{k^m}}}\frac{l_{ij}}{v_{ij}^{k^m}}\}}}$$

(7)

3.4.2. Constraint Conditions

The constraints of the model are as follows:

$$\underset{\_}{\theta }\le \frac{q_{ij}^{k^m}}{f_{}^{k^m}D}\le \overline{\theta }$$

(8)

$${\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{q}_{ij}^{k^m}\ge Q_{ij}}}$$

(9)

$${\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{f}^{k^m}}}\le N$$

(10)

$$\underset{\_}{{\partial }_{}^m}\le {\displaystyle \sum _{k^m\in K^m}{f}_{}^{k^m}}\le \overline{{\partial }_{}^m}$$

(11)

$$\underset{\_}{{\phi }_{}^m}\le {\displaystyle \sum _{m\in M}{\displaystyle \sum _{k^m\in K^m}{x}_s^{k^m}}}\le \overline{{\phi }_{}^m}$$

(12)

$$x_1^{k^m}=x_n^{k^m}=1$$

(13)

$${\displaystyle \sum _{s=1}^n{x}_s^{k^m}}\le n$$

(14)

$$x_n^{k^m}\in \{0,1\}$$

(15)

$$f_{}^{k^m}\in N^{*}$$

(16)

Equation (8) indicates that the occupancy rate of intercity railway train meets a certain range; Equation (9) indicates that the passenger flow carried by ICR trains must meet the OD passenger flow; Equation (10) indicates that the number of trains cannot be greater than the maximum departure capacity of the intercity railway; Equation (11) indicates a reasonable limit on the frequency of the trains of m stop mode; Equation (12) indicates that the number of trains stops of m stop mode (including the starting and terminal at the station) needs to meet the conditions; Equation (13) mandatory trains must stop at starting and terminal station; Equations (14)–(16) are used to ensure that the logic of the model is correct.

3.5. Processing of Multi-Objective

The model constructed in this paper is a multi-objective programming model. Before solving the multi-model, it is usually necessary to convert the multi-objective into a single-objective through a certain method. The two objectives of the model are in different dimensions, and the values of different dimensions cannot be directly added. To solve the problem, we introduce the concept of value of travel time (VTT), which uses price to measure the value of travel time.

VTT can be said to be the most important number in transport economics, and its estimation has been the topic of extensive academic and applied work. Andrew Daly et al. [25] pointed out that the primary application of VTT is in the appraisal of transport policy, including infrastructure investment. For estimating VTT, researchers (Hensher, 2006 [26]; Tseng, 2008 [27]; Fezzi, 2014 [28]; Athiria, 2016 [29] and Ashim [30]) generally employed logit model to estimate the VTT.

Affected by different factors, there is an imbalance between supply and demand in the operation of intercity railways. It is necessary to adjust the train operation plan in a timely manner according to the change in the time value of passengers to adapt to the transportation needs and avoid the waste of transportation resources. According to the different travel purposes of passengers, the intercity passenger flow can be divided into business passenger flow, commuter passenger flow and general passenger flow. For business, commuting and other passenger flows, the payment method of time value is complex, and the time value of passengers is relatively high; for general passenger flows, the time value of passengers is paid by individuals, and the time value of passengers is relatively low. In order to easily distinguish the difference in passenger time value, we directly divide passenger time into high time value and low time value. The time value of passengers is related to many factors. For the convenience of calculation, regardless of the difference in the time value of individual passengers, $\delta$ is used to represent the average travel time value of passengers. When affected by COVID-19, the general passenger flow occupies a large proportion, and the average travel time value of passengers is low (${\delta }^{low}$). Normal or holiday business, commuting, and family visits account for a large proportion, and the average travel time value of passengers is high (${\delta }^{high}$). In this way, we convert the consumption time of passengers into costs.

The objective function of the optimization model of the intercity railway train operation plan considering the time value of passengers can be expressed as Equation (17).

$$MinZ=Z_1+Z_2\delta$$

(17)

4. Methods

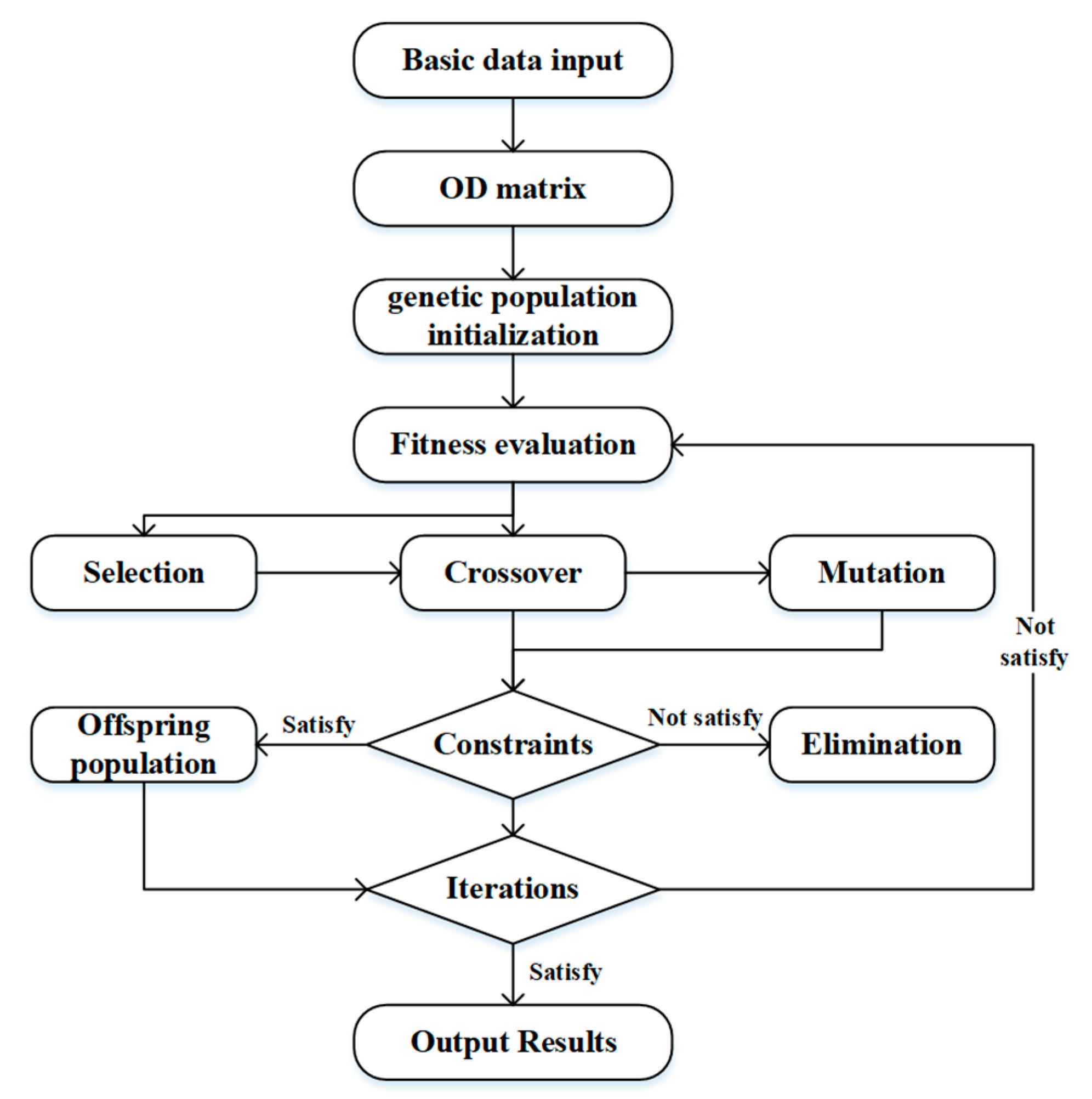
4.1. Genetic Algorithm Design

The model built in this paper has the characteristics of non-linear, multi-constraints, and easy for binary coding of decision variables. In this section, according to the characteristics of the model, the genetic algorithm is used to solve the optimization model of the train operation plan of the ICR, and the reasons are as follows. Genetic algorithm starts from the string set of problem solutions, which has large coverage and is conducive to global optimization; The genetic algorithm uses the probability search method to obtain the optimal solution, which can deal with the constraints of the model well. It has the advantages of good accuracy and fast speed for solving nonlinear problems, and avoids local optimal solutions to a large extent; genetic algorithm itself is easy to implement and optimize. Specific steps are as follows:

(1)

Chromosome Coding

There are many kinds of coding methods for genetic algorithm chromosomes. According to the model and characteristics, this paper adopts the 0–1 coding method.

Because the optimization model of the intercity railway train operation plan constructed in this paper has two decision variables, the train stop plan and the train frequency, each gene segment of the chromosome consists of two parts:

Use the 0–1 variable $x_s^{k^m}$ to indicates whether the train running with stop plan k^m stops at station s. If $x_s^{k^m}=1$, it means stop; if $x_s^{k^m}=0$, it means no stop.

Use $f_{}^{k^m}$ to represent the frequency of train running with stop plan k^m; $f_k^m$ is a non-negative integer. Choose a binary code with a code string length of 8 bits to represent the departure frequency of intercity trains. When encoding, it is necessary to convert the departure frequency of the train from decimal to binary. Considering the actual passing capacity of China’s ICRs, the maximum departure frequency that can be represented by this code is 256 trains, which can fully cover the possible situation of the current departure frequency of intercity trains. The two codes are combined to obtain a gene fragment of the chromosome, as shown in Figure 2.

(2)

Fitness Evaluation

Fitness is mainly used to describe the correspondence between individual traits and fitness in the genetic algorithm, and to measure whether the individual is approximate or has reached the optimum in the iterative process. The fitness function is usually non-negative, and it is generally considered that the greater the fitness, the better the individual, so the inverse of the objective function is used as the fitness function:

$$fitness=\frac{1}{Z}$$

(18)

In this paper, the competition method was used to screen out the individuals with excellent traits in the population. A certain number of individuals are extracted from the population each time, and then the individuals with the best traits are selected to enter the offspring population. Repeat this operation until the new population size reaches the originally set population size.

(3)

Crossover and Mutation Operation

In order to ensure the validity of the algorithm, in the process of genetic algorithm iteration, it is necessary to detect and correct the chromosome code of the offspring chromosome in each iteration process.

Genetic algorithm generates new individuals through crossover operation. The quality of crossover operator determines the global search ability of genetic algorithm, and the global search ability plays a crucial role in the operation of genetic algorithm. In this paper, the crossover operator adopts the method of multi-point crossover, multiple gene sites are randomly set as crossover points in the chromosome gene string, and two individuals are selected for crossover according to a certain crossover probability. To maximize the inheritance of the excellent traits of the parental chromosomes to the next generation.

The mutation operation adopts the method of multi-point mutation. By randomly selecting multiple gene sites in an individual in the current population, gene mutation occurs with a small probability, thereby generating a new individual. To a certain extent, the algorithm can be prevented from falling into a local optimum, and a variety of possibilities can be added to the plan.

4.2. Computing Procedure

The genetic algorithm solution process is divided into 5 steps:

Step 1: Set the chromosome population size M, the crossover probability is P_c, the mutation probability is P_m, the maximum number of iterations of evolution is T, and the current iteration number t = 0.

Step 2: Initialize the population, and randomly generate a population $m_0$ composed of M chromosomes in the feasible solution.

Step 3: Calculate the fitness of each individual in the population $m_t$ according to Formula (17).

Step 4: Perform selection, crossover, and mutation operations on population $m_t$ to generate the next generation population $m_{t+1}$.

Step 5: Determine the stop condition. If the stopping condition of the algorithm is met, stop the iteration and output the optimal solution; if the stopping condition is not met, set t = t + 1, return to Step 3, and continue the iteration.

The flow chart of the genetic algorithm is shown in Figure 3:

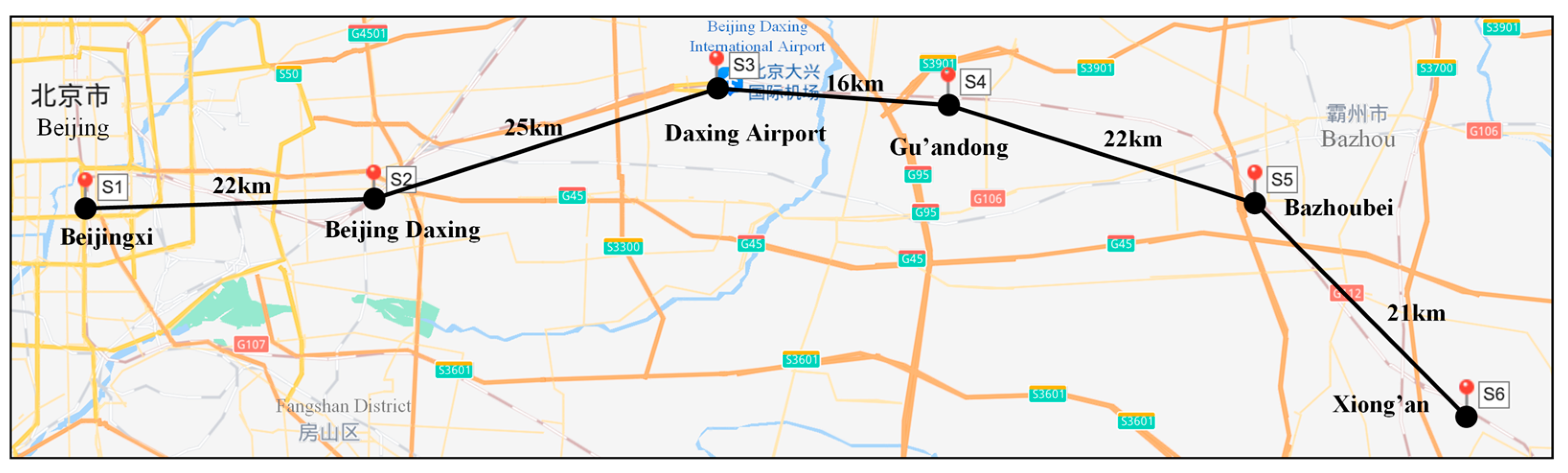
5. Case Study

5.1. Data

The Beijing-Xiong’an Intercity Railway (BXICR) has a total length of 106 km, connecting Beijing and Xiong’an New Area, with a total of six stations. The direction from Beijing to Xiong’an is the down direction. The BXICR is shown in Figure 4, and the related data are shown in

Table 3. Main parameter table of Beijing-Xiong’an intercity railway.

Parameter	Value
Train type	CR400AF EMU
Starting/terminal station	Beijingxi/Xiong’an
Running speed	250~350 km/h
Stop time	3 min (Including start and stop additional time)
Train formation	8 carriages
Seating capacity	576 seats
$\mathrm{VVT}({\delta }^{low}$$/{\delta }^{high}$)	0.5/0.75 ¥/min
Fixed cost	8000 ¥
Stop cost	500 ¥
Running cost	60 ¥/km
Departure capacity	100 trans/day

.

In this paper, by sorting out the passenger ticket data obtained from China Railway Beijing Group Corporation, the daily average OD passenger flow of the BXICR is obtained. The stations along the line from Beijingxi to Xiong’an are represented by S₁–S₆, and the OD passenger flow data is shown in

Table 4. BXICR average daily OD passenger flow data.

Stations	S1	S2	S3	S4	S5	S6
S1	—	15	1696	430	1404	3351
S2	50	—	12	8	24	29
S3	1411	31	—	77	216	767
S4	573	16	124	—	7	28
S5	1302	16	266	11	—	40
S6	3178	77	833	41	38	—

.

Two different scenarios are set up to simulate the change in the time value of passengers in the BXICR.

Scenario 1 refers to situations such as COVID-19, where business, commuting, and other passenger flows have dropped sharply, general passenger flows account for a large proportion, the time value of which is paid by individuals, and the time value of passengers is low. According to the relevant data on China’s ICR in the existing literature, this paper takes the average time value of passengers in this scenario is taken as 0.5 ¥/min. While meeting the needs of passenger flow transportation, intercity railway enterprises should reduce the operating costs and avoid waste of transportation resources.

Scenario 2 means that during normal or holidays, business, commuting, family visits and other passenger flows account for a large proportion, potential payers of passenger time value are complex, the time value of passengers is high. In this paper, the average time value of passengers in this scenario is taken as 0.75 ¥/min, to minimize the travel time cost of passengers, reduce travel time, and meet diverse passenger transportation needs.

5.2. Results

In this paper, the solution model is programmed in MATLAB R2020a software. The operation parameters of the genetic algorithm are mainly determined according to the actual situation of the optimization of the train operation plan of the ICR and the experience of many experiments. In this paper, the initial population size M = 50, the crossover probability pc = 0.6, the mutation probability pm = 0.05, and the maximum number of iterations is 100 generations. The number of up-direction and down-direction trains set to be output must be symmetrical, and the passenger flow data and various parameters are imported to solve the problem. 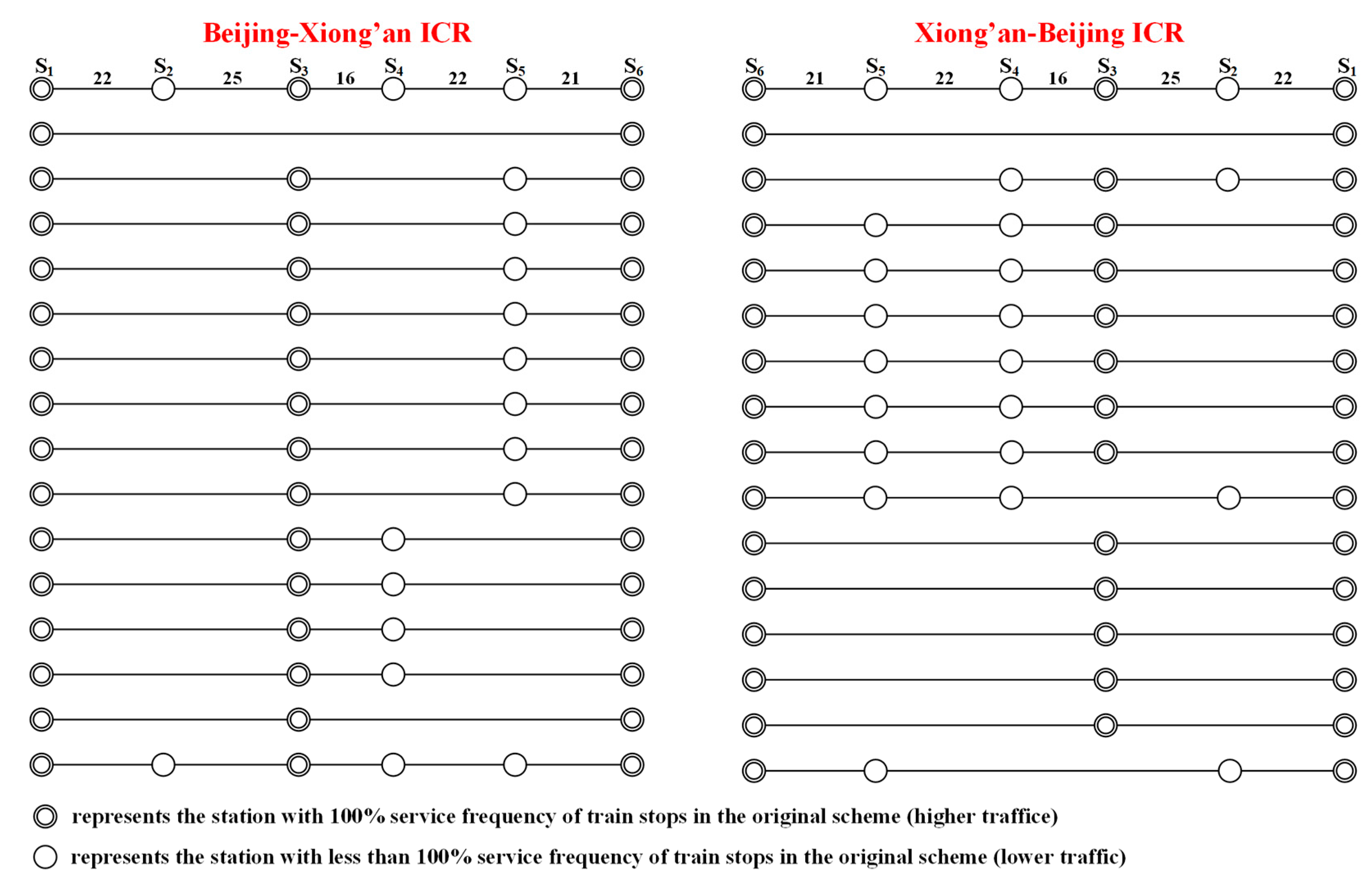The final solution is as follows:

(1)

Scenario 1 optimization plan

Figure 5 shows that when the iteration reaches 58 generations, the objective function reaches the optimum, and the optimization plan is shown in Figure 6.

(2)

Scenario 2 optimization plan

Figure 7 shows that when the iteration reaches 30 generations, the objective function reaches the optimum, and the optimization plan is shown in Figure 8.

5.3. Discussion

In order to verify the effectiveness of the optimization model and algorithm, this section compares the relevant important indicators of the BXICR train operation plan after optimization and the original plan. The original plan refers to the train operation plan currently adopted by BXICR.

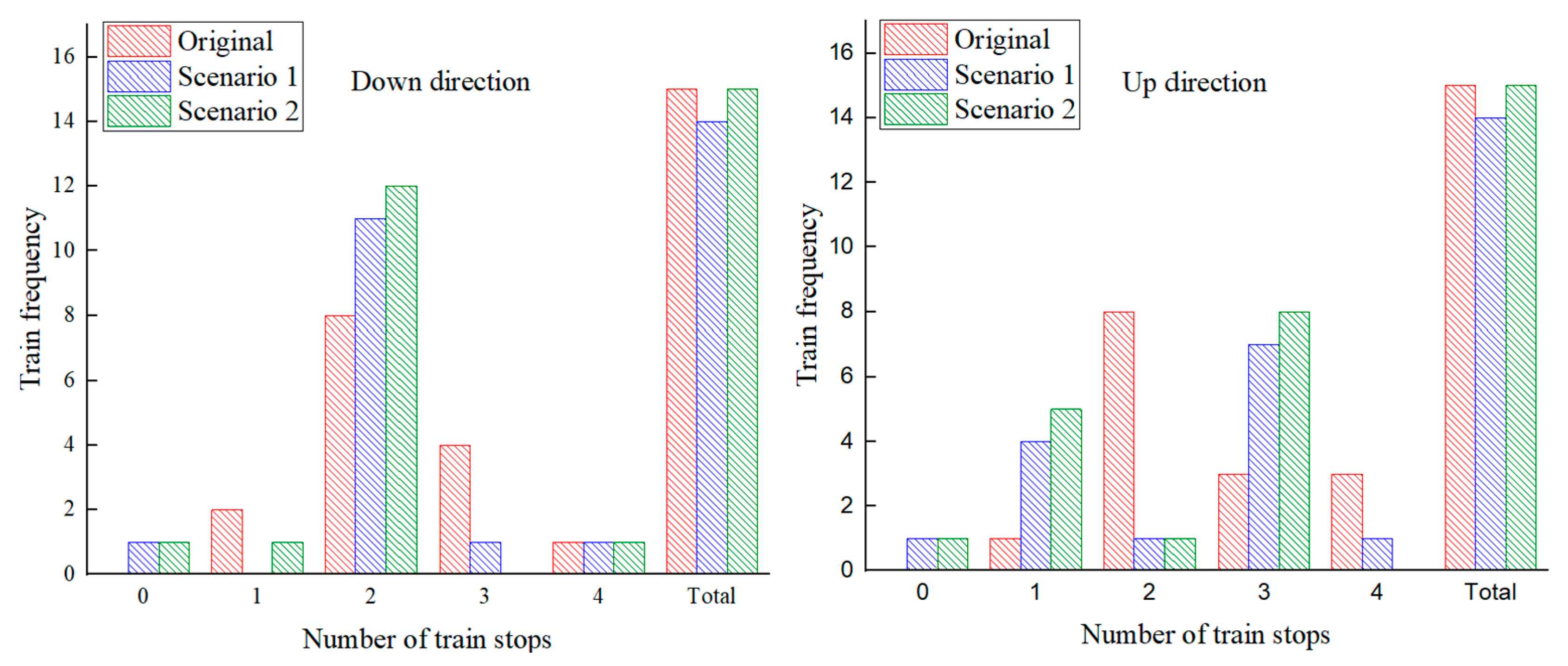
5.3.1. Number of Train Stops

Table 5. Correspondence between the number of train stops and train frequency after optimization.

Direction	Scenarios	Number of Train Stops					Total Frequency	Average Stop Times (per Train)
		0	1	2	3	4
Up direction	Original/freq	0	2	8	4	1	15	2.27
	Scenario 1/freq	1	0	11	1	1	14	2.07
	Scenario 2/freq	1	1	12	0	1	15	1.93
Down direction	Original/freq	0	1	1	8	3	15	2.53
	Scenario 1/freq	1	4	1	7	1	14	2.21
	Scenario 2/freq	1	5	1	8	0	15	2.07

and Figure 9 show the corresponding relationship between the number of stops at the intermediate station of the train and the train frequency after the optimization of the train operation plan. It can be seen that the number of train stops in the downward direction is mainly concentrated in 2 times. Compared with the original plan, both Scenarios 1 and 2 add 1 no-stop train; a total of 14 trains were operated in Scenario 1, and the total number of trains in Scenario 2 remained unchanged; the average number of stops per train in the two optimized plans decreased by 8.8% and 14.9%, respectively.

The number of train stops in the upward direction is mainly concentrated in 1 and 3 times. Compared with the original plan, both Scenarios 1 and 2 add 1 no-stop train, and without all-stop train runs in Scenario 2; a total of 14 trains run in Scenario 1, and the total number of trains in Scenario 2 remains unchanged; the average number of stops per train in the two optimized plans decreased by 12.6% and 18.2%, respectively.

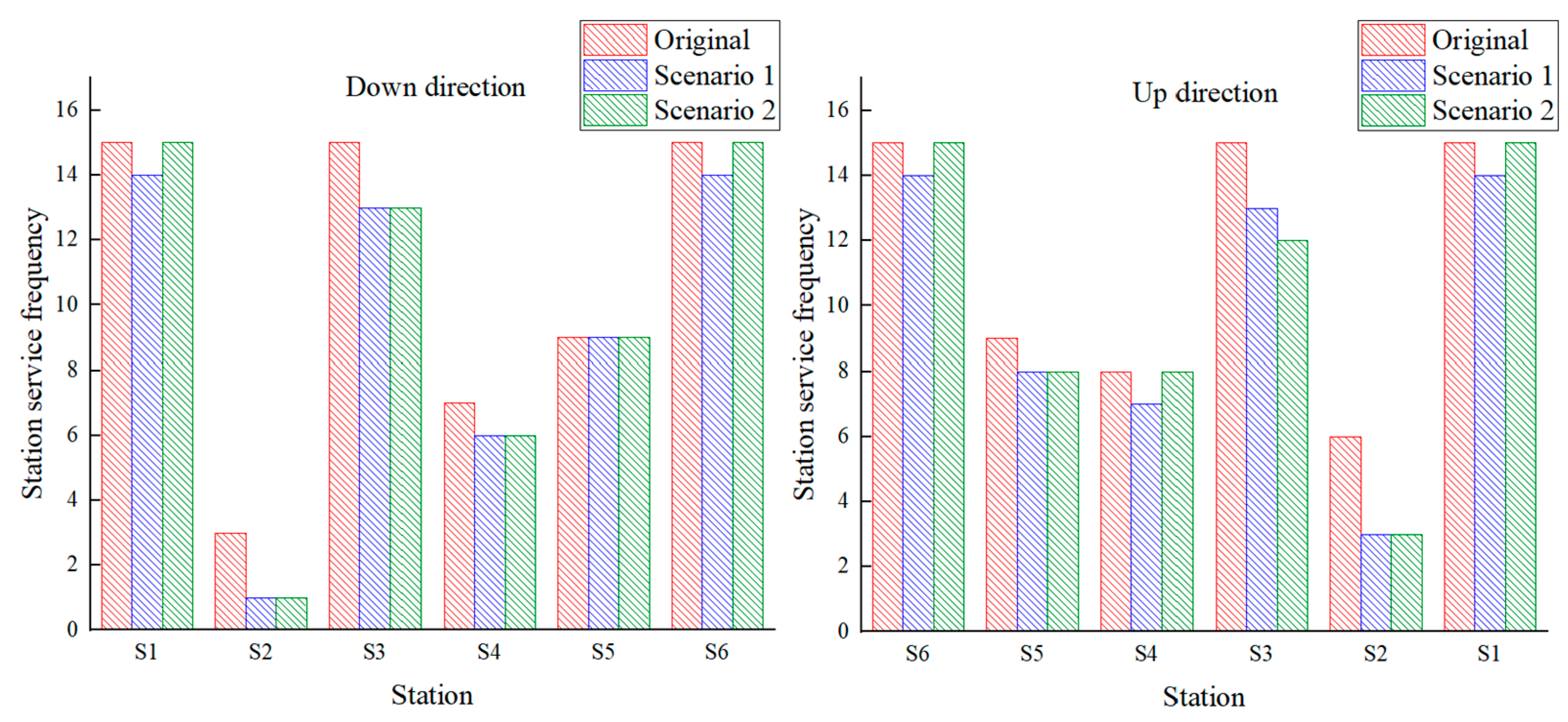
5.3.2. Station Service Frequency

The service frequency of the station after optimization is shown in

Table 6. Station service frequency after optimization.

Direction	Scenarios	Stations						Total
		Beijingxi	Beijing Daxing	Daxing Airport	Gu’an dong	Bazhou bei	Xiong’an
Up direction	Original	15	3	15	7	9	15	64
	Scenario 1	14	1	13	6	9	14	57
	Scenario 2	15	1	13	6	9	15	59
Down direction	Original	15	6	15	8	9	15	68
	Scenario 1	14	3	13	7	8	14	59
	Scenario 2	15	3	12	8	8	15	61

and Figure 10. It can be seen from the figure that in different plans, the station service frequencies of Daxing Airport station in the downward direction are 100%, 93% and 87%, respectively, and the upward direction is 100%, 93% and 87%, respectively, which is much higher than other stations. The reason is that large passenger flow stations need more stop services. The optimized station service frequency conforms to the passenger flow characteristics of each station.

Compared with the original plan, the service frequency of the stations in both Scenarios 1 and 2 decreased or remained the same. The reason is that under the premise of meeting the service frequency and passenger flow transportation requirements of the station, the solution of the optimization plan is relatively optimal under the constraints of the model, and the number of stops of the intercity railway trains at the intermediate station is controlled to the maximum extent, so that the service frequency of some stations is lower than the original plan, but at the same time, it can meet the needs of passenger flow.

5.3.3. Comparison of Important Indicators

(1)

Down direction

The optimized indicators in the down direction are shown in

Table 7. Optimal results of optimization model (down direction).

Indicators	Original	Scenario 1	Scenario 2
Fixed cost/¥	120,000	112,000	120,000
Running cost/¥	81,900	76,440	81,900
Stop cost/¥	17,000	14,500	14,500
Total cost/¥	218,900	202,940	216,400
Stop time/min	37,421	32,612	30,224
Running time/min	393,477	393,477	393,477
Total time/min	430,898	426,089	423,701
Number of stops at intermediate stations	34	29	29
Station service frequency	64	57	59
OD service frequency	106	92	91

.

It can be seen from the table that in cases such as COVID-19, the time value of passengers is low. The fixed cost of Scenario 1 is 112,000 ¥, which is 8000 ¥ lower than the original plan; the train running cost is 76,440 ¥, which is 5460 ¥ lower than the original plan. The cost of train stops is 14,500 ¥, which is 2500 ¥ lower than that of the original plan. The stop time in Scenario 1 is 32,612 min, which is 4809 min lower than the original plan.

In normal or holiday situations, the value of passenger time is higher. The fixed cost and train running cost of Scenario 2 remain unchanged. The cost of train stops is the same as Scenario 1. The stop time in Scenario 2 is 30,224 min, which is 7197 min lower than that of the original plan. The business operating costs of Scenario 1 and Scenario 2 decreased by 7.3% and 1.1%, respectively, and the total travel time decreased by 1.1% and 1.7%, respectively.

(2)

Up direction

The optimized indicators in the up direction are shown in

Table 8. Optimal results of optimization model (up direction).

Indicators	Original	Scenario 1	Scenario 2
Fixed cost/¥	120,000	112,000	120,000
Running cost/¥	81,900	76,440	81,900
Stop cost/¥	19,000	15,500	15,500
Total cost/¥	220,900	203,940	217,400
Stop time/min	39,512	36,637	33,389
Running time/min	370,199	370,199	370,199
Total time/min	409,711	406,836	403,588
Number of stops at intermediate stations	38	31	31
Station service frequency	68	59	61
OD service frequency	132	104	102

.

It can be seen from the table that in the cases such as COVID-19, the fixed cost of the intercity railway train operation plan in Scenario 1 is 112,000 ¥, which is 8000 ¥ lower than the original plan, the train running cost is 76,440 ¥, which is 5460 ¥ lower than the original plan, the cost of train stops is 15,500 ¥, which is 3500 ¥ lower than the original plan. The stop time in Scenario 1 is 36,637 min, which is 2875 min lower than the original plan.

Under normal or holiday conditions, the fixed costs and train running costs of Scenario 2 remain unchanged, the cost of train stops is the same as Scenario 1. The stop time in Scenario 2 is 33,389 min, which is 6123 min lower than the original plan. The business operating costs of Scenario 1 and Scenario 2 decreased by 7.7% and 1.6%, respectively, and the total travel time decreased by 0.7% and 1.5%, respectively.

In summary, both plans are better than the original plan. Under the influence of factors such as COVID-19, the use of the intercity railway train operation plan of Scenario 1 can reduce the operating cost of enterprises and avoid the waste of transportation resources while meeting the needs of passenger flow. Under normal or holiday circumstances, the use of the intercity railway train operation plan of Scenario 2 can reduce the travel time of passengers as much as possible.

After the optimization and adjustment of the train operation plan of BXICR, the ways of train stops are more diverse, and the station service frequency is more matched with the passenger flow of the station. In addition, the total number of train stops in the optimized plan has decreased compared with original plan, operating costs and travel time consumption will be reduced accordingly. In a word, relatively satisfactory results have been obtained on the optimization of the train operation plan of BXICR, which verifies the validity of the optimization model and algorithm of the train operation plan of the ICR established in this paper.

6. Conclusions

This paper mainly studies the optimization problem of the train operation plan of the intercity railway. The objective function is to minimize the operating cost of the enterprise and the time consumption of passengers. A genetic algorithm is designed to solve this problem. The main conclusions are as follows:

• The influence of the change in passenger travel time value on the train operation plan is considered. A multi-objective optimization model aiming at the minimum operating cost of the enterprise and the minimum consumption time of passengers is constructed.
• According to the characteristics of the model, a genetic algorithm is designed to solve the model. The algorithm is calculated on the MATLAB platform, and the optimal solution can be obtained quickly.
• Taking BXICR as a research case, two types of intercity railway train operation plan under different travel time values of passengers are obtained. Scenario 1 runs 14 pairs of trains, which saves a lot of operating costs for the company; Scenario 2 runs 15 pairs of trains, which saves a lot of travel time for passengers.
• Comparing and analyzing different train operation plans, the results show that both optimization plans are better than the original plan. In the down direction, operating costs in Scenario 1 and Scenario 2 decreased by 7.3% and 1.1%, total time consumption decreased by 1.1% and 1.7%, and the number of stops per train for two scenarios decreased by 8.8% and 14.9%, respectively. In the up direction, operating costs in Scenario 1 and Scenario 2 decreased by 7.7% and 1.6%, total time consumption decreased by 0.7% and 1.5%, and the number of stops per train for two scenarios decreased by 12.6% and 18.2%, respectively. The optimized plan reduces the operating cost of the enterprise, attracts more passenger flow, and realizes the sustainable development of the intercity railway enterprise.
• The model established in this paper is a general model suitable for the optimization of the train operation plan of the ICR, taking the Beijing-Xiong‘an Intercity Railway as a case study. ICRs similar to BXICR include Beijing-Tianjin ICR, Nanchang-Jiujiang ICR, Guangzhou-Zhuhai ICR and Wuhan-Huangshi ICR, etc. After investigation, the length and average daily passenger flow of these lines are at the same level as the BXICR. The optimization model established in this paper can be applied to the above-mentioned similar lines, and similar conclusions can be obtained, including the reduction in the total operating costs, the reduction in the number of stops per train, and the reduction in the total time consumption.
• Due to the limited data collection capacity, this paper studies the ICR passenger flow under the condition of fixed demand. In the actual operation process, the passenger flow has strong uncertainty, and the change in the passenger flow law in different periods will also affect the preparation of the train operation plan. In future research, it is necessary to combine passenger flow forecasting and other information, and consider factors other than the train operation plan as comprehensively as possible, so as to strengthen the applicability of the model.