Time-Dependent Behavior of Callovo-Oxfordian Claystone for Nuclear Waste Disposal: Uncertainty Quantification from In-Situ Convergence Measurements
Abstract
:1. Introduction
2. Uncertainty Quantification by Bayesian Inference
2.1. Classical Bayesian Inference
2.2. Hierarchical Bayesian Inference
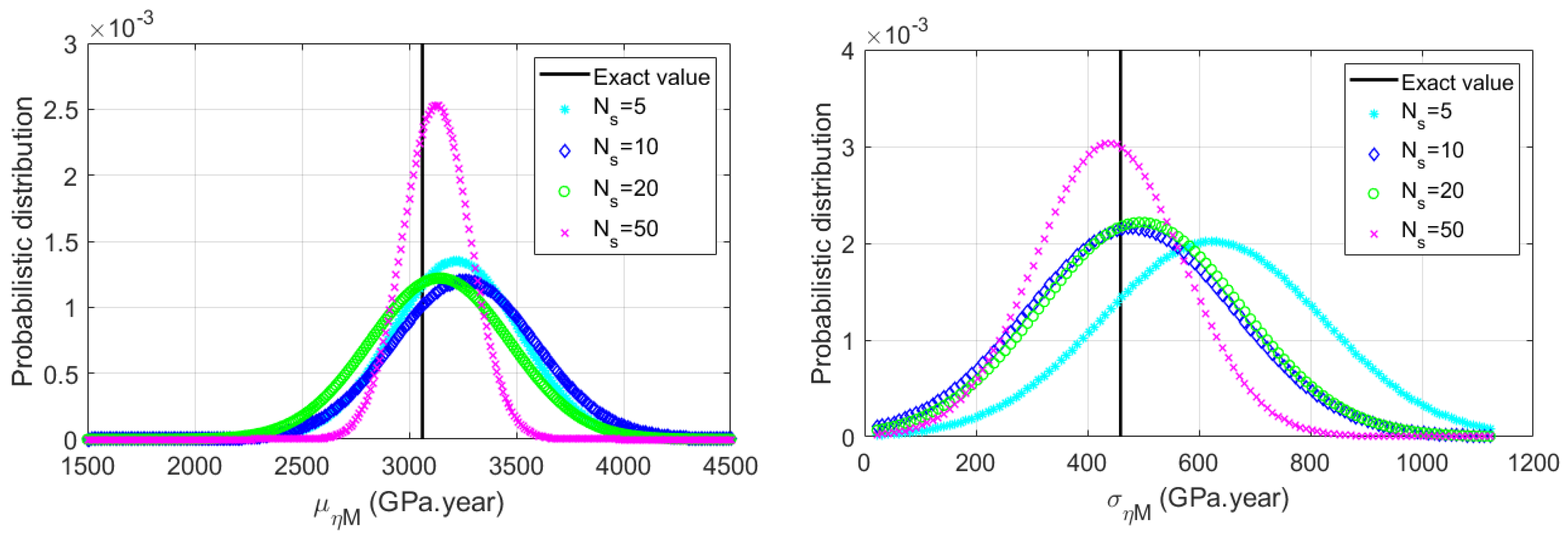
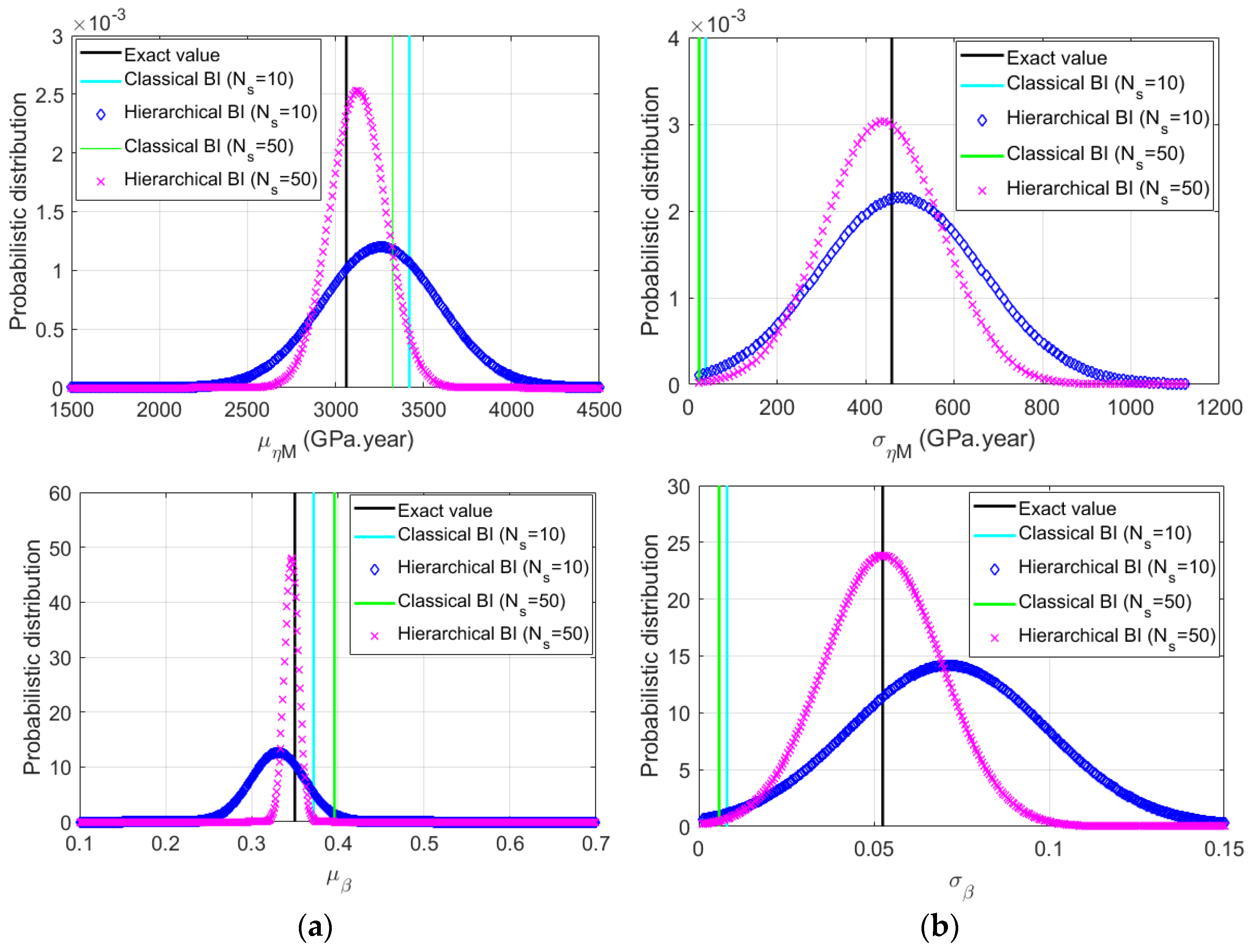
3. Numerical Applications Using Synthetic Data
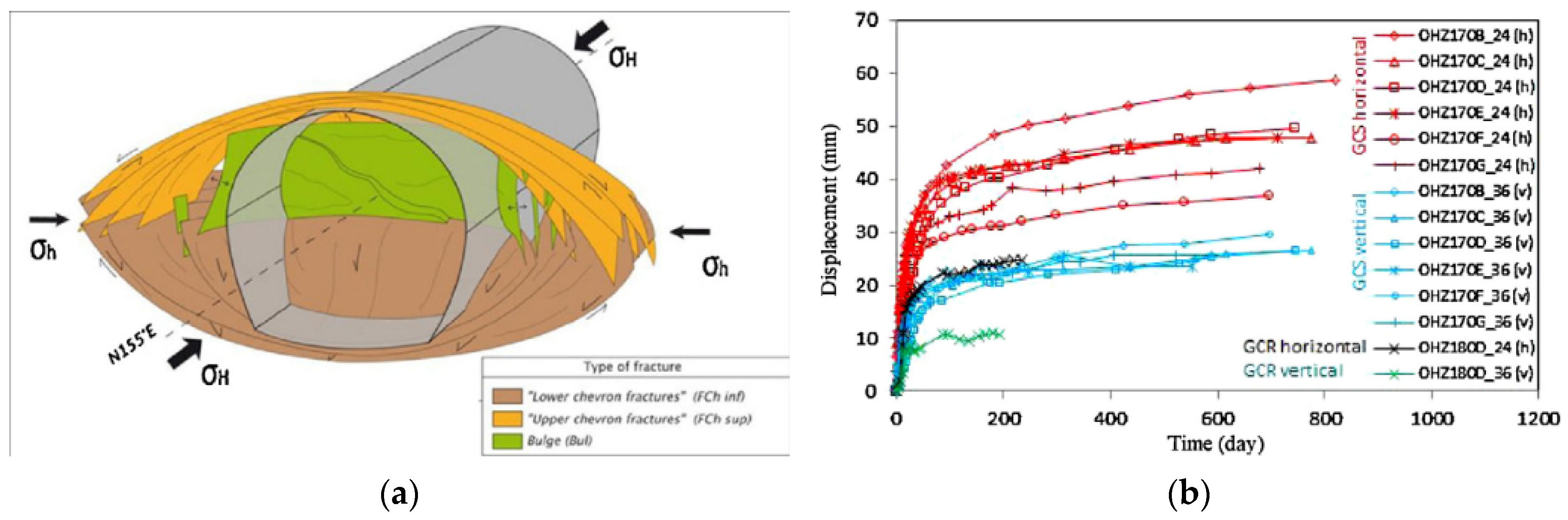
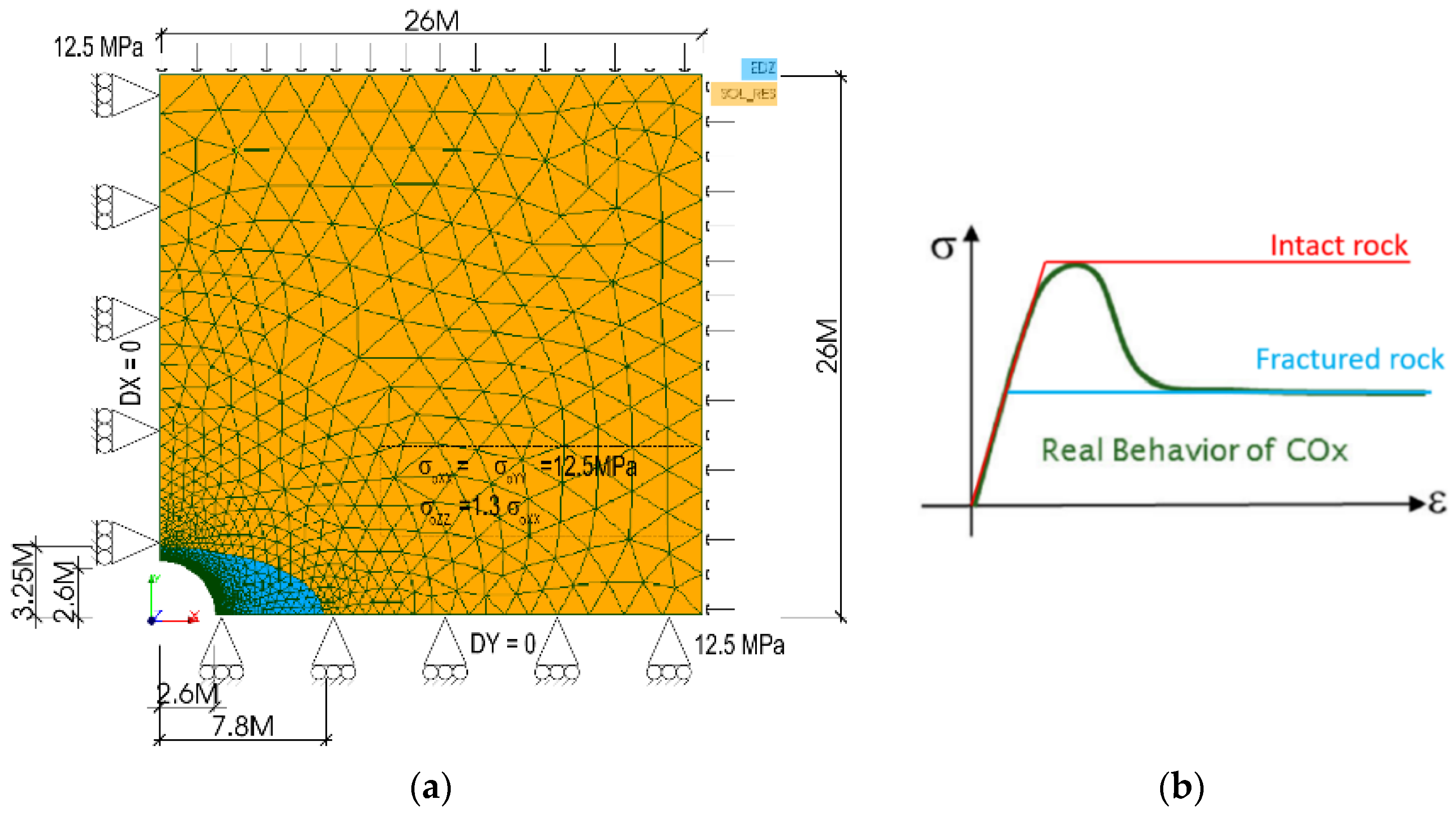
4. Uncertainty of Time-Dependent Behavior of COx Claystone
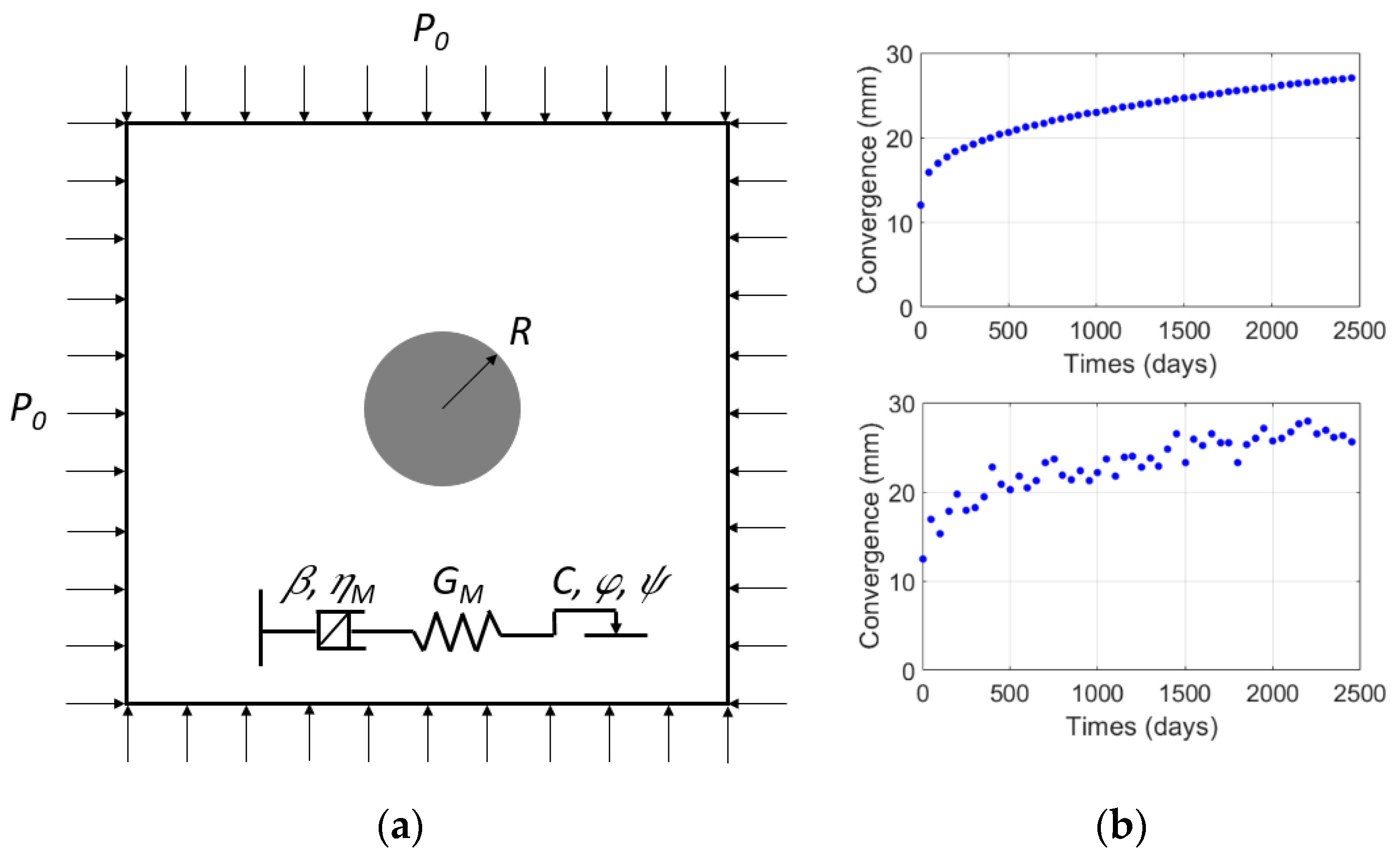
4.1. Description of the Numerical Model
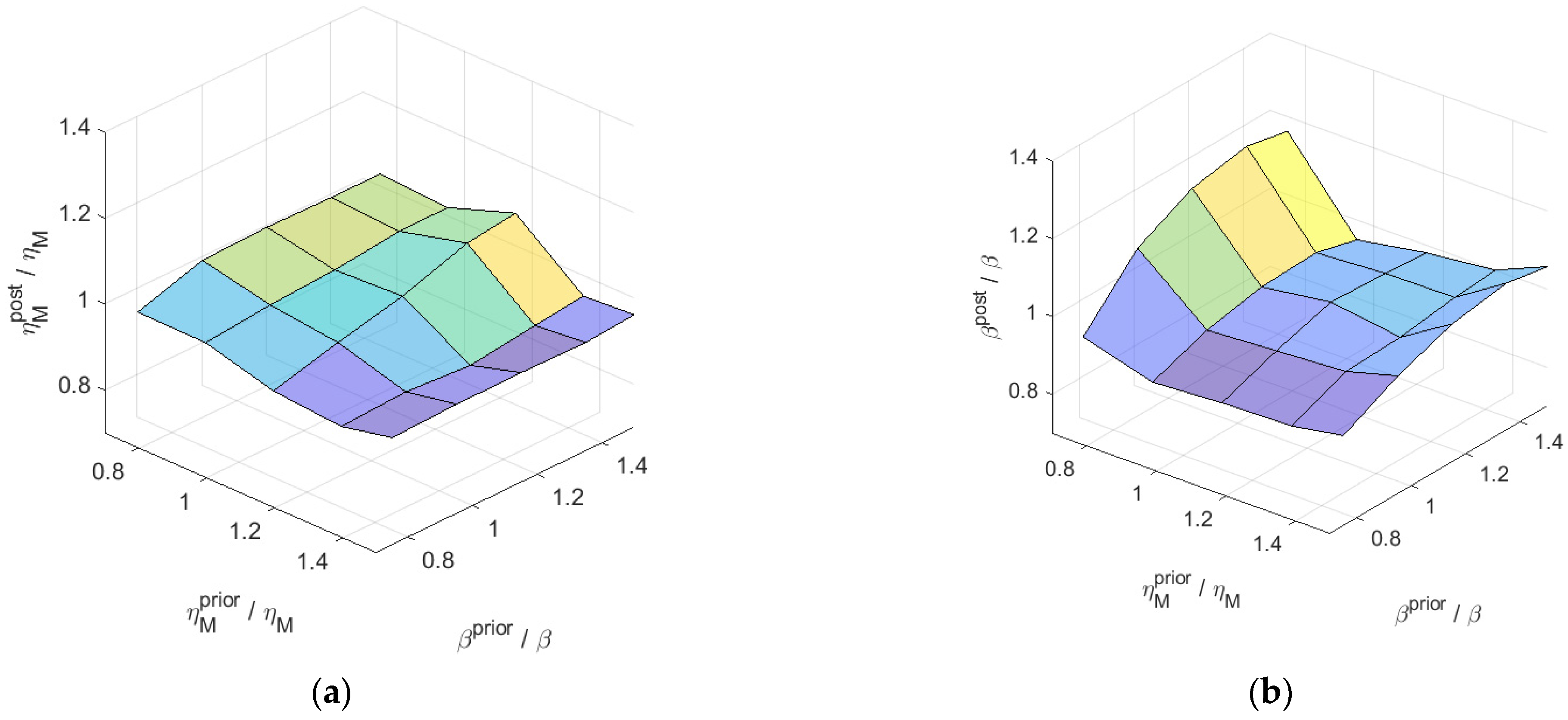
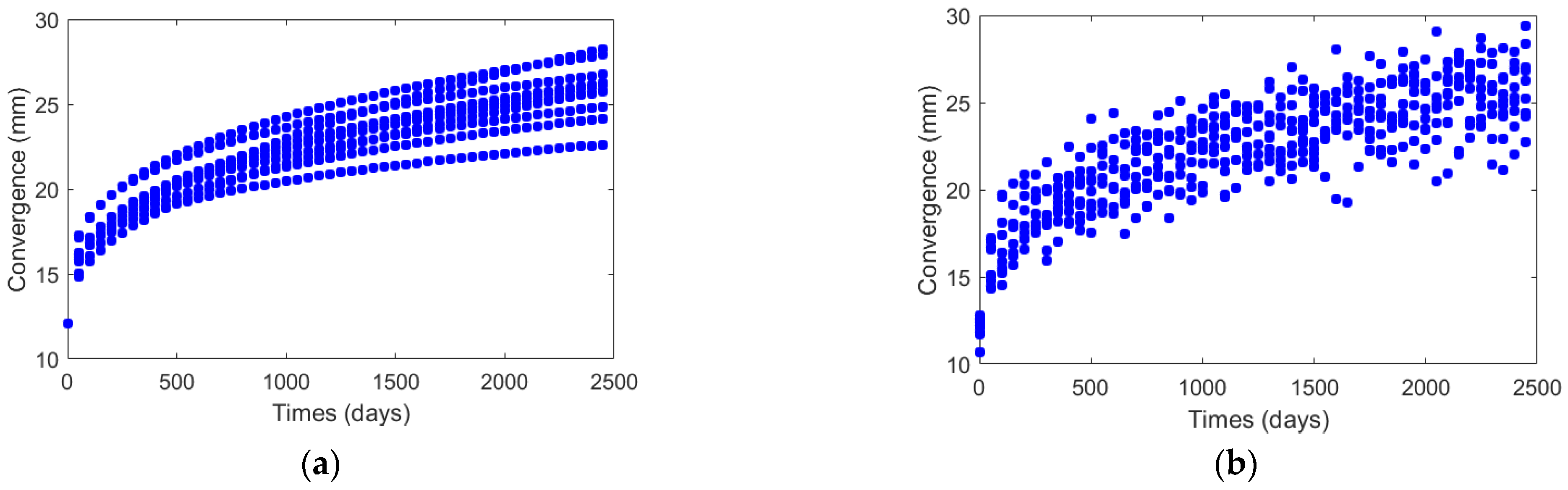
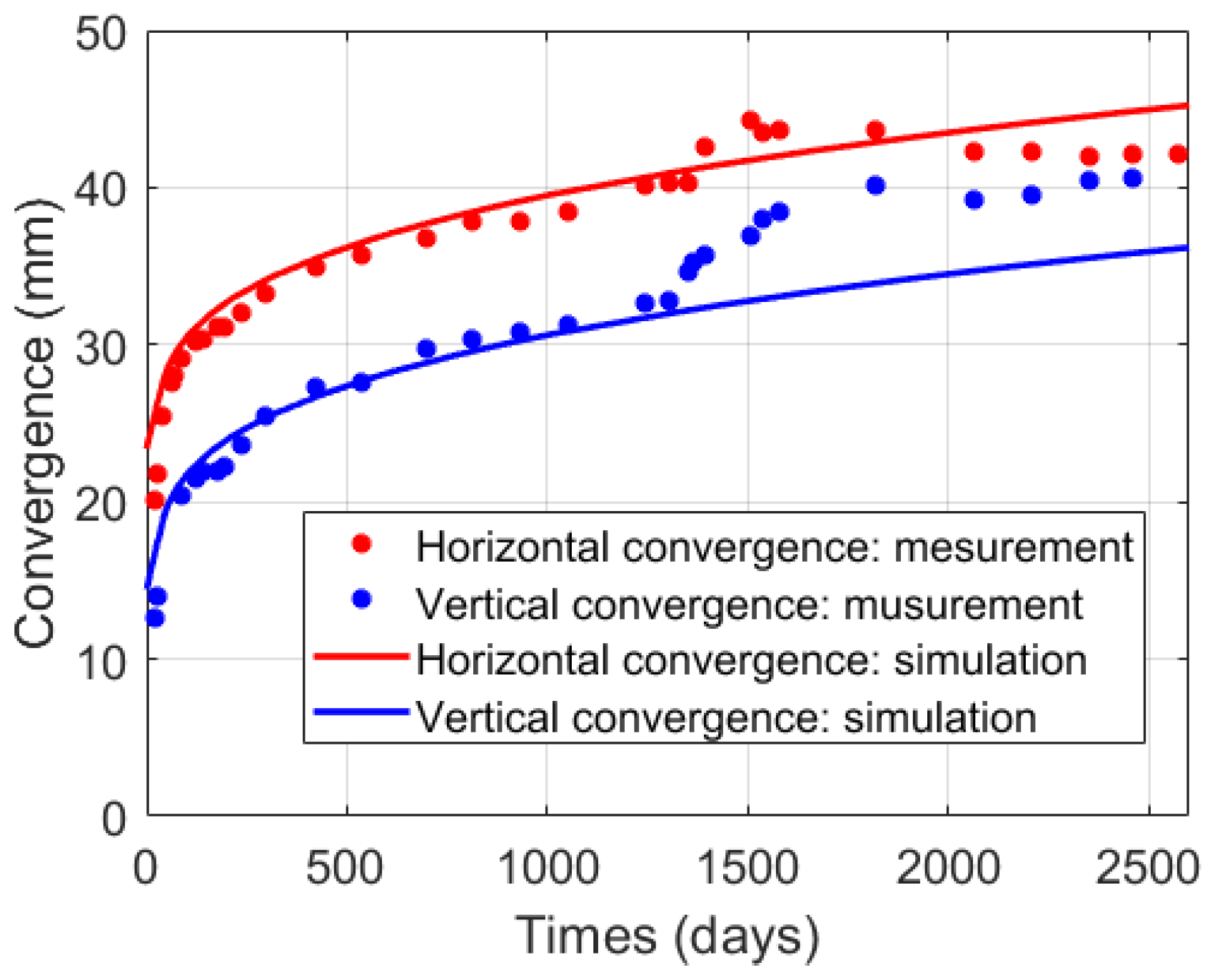
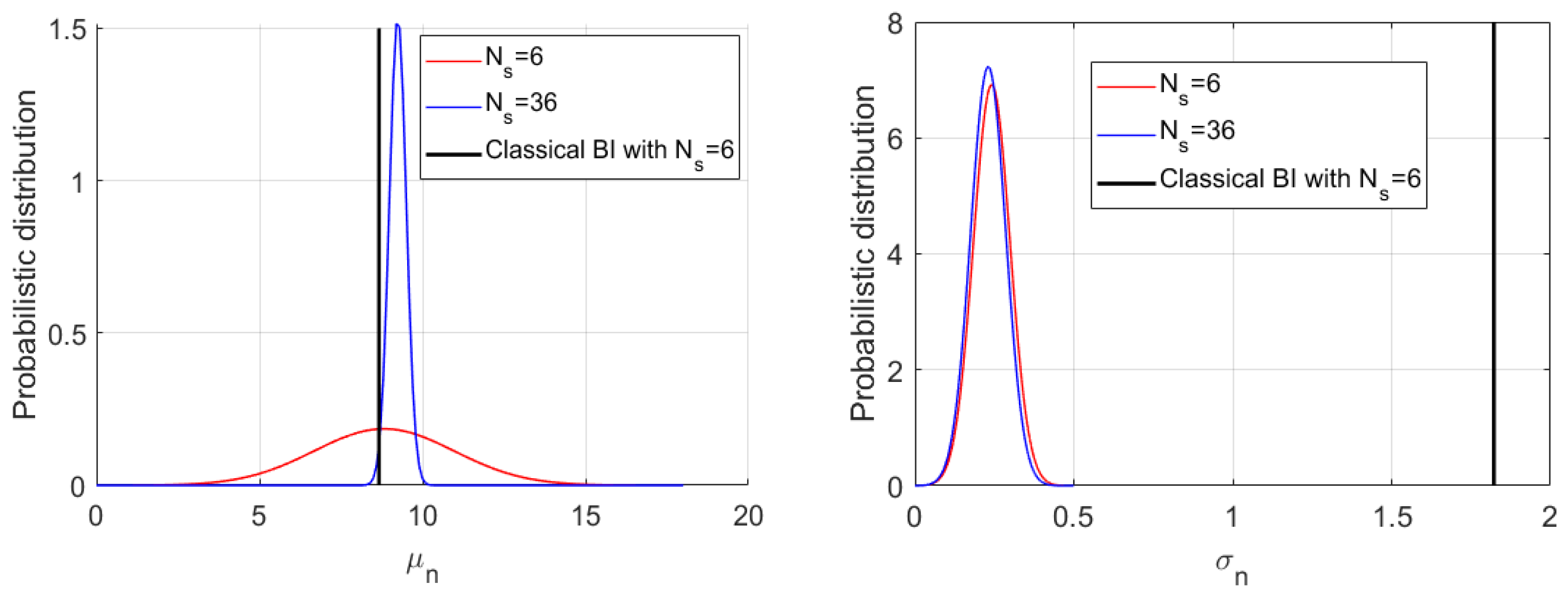
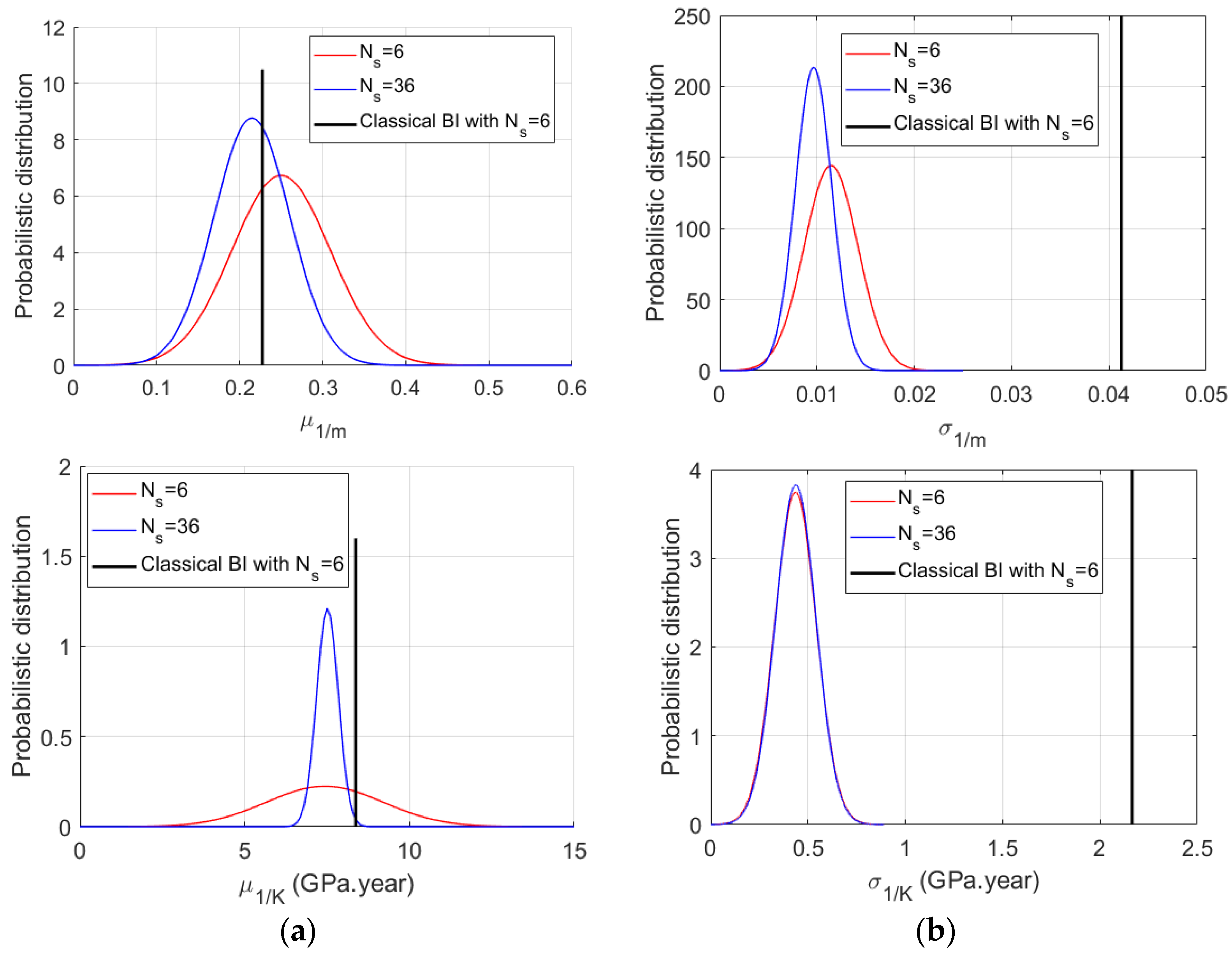
4.2. Results of the Bayesian Inversion and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC Special Report “Global Warming 1.5 °C”. 2018. Available online: https://www.ipcc.ch/sr15/ (accessed on 20 April 2022).
- Armand, G.; Noiret, A.; Zghondi, J.; Seyedi, D.M. Short-and long-term behaviors of drifts in the Callovo Oxfordian claystone at the Meuse/Haute-Marne Underground Research Laboratory. J. Rock Mech. Geotech. Eng. 2013, 5, 221–230. [Google Scholar] [CrossRef] [Green Version]
- Armand, G.; Leveau, F.; Nussbaum, C.; de la Vaissiere, R.; Noiret, A.; Jaeggi, D.; Landrein, P.; Righini, C. Geometry and properties of the excavation induced fractures at the Meuse/Haute-Marne URL drifts. Rock Mech. Rock. Eng. 2014, 47, 21–41. [Google Scholar] [CrossRef]
- Armand, G.; Conil, N.; Talandier, J.; Seyedi, D.M. Fundamental aspects of the hydromechanical behavior of Callovo-Oxfordian claystone: From experimental studies to model calibration and validation. Comput. Geotech. 2017, 85, 277–286. [Google Scholar] [CrossRef]
- Alonso, M.; Vu, M.N.; Vaunat, J.; Armand, G.; Gens, A.; Plua, C. Effect of thermohydro-mechanical coupling on the evolution of stress in the concrete liner of an underground drift in the Cigéo project. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012200. [Google Scholar] [CrossRef]
- Souley, M.; Vu, M.N.; Armand, G. 3D Modelling of Excavation-Induced Anisotropic Responses of Deep Drifts at the Meuse/Haute-Marne URL. Rock Mech. Rock Eng. 2022, 55, 4183–4207. [Google Scholar] [CrossRef]
- Mánica, M.A.; Gens, A.; Vaunat, J.; Armand, G.; Vu, M.N. Numerical simulation of underground excavations in an indurated clay using non-local regularisation. Part 1: Formulation and base case. Géotechnique 2021, 1–21. [Google Scholar] [CrossRef]
- Yu, Z.; Shao, J.; Duveau, G.; Vu, M.N.; Armand, G. Numerical modeling of deformation and damage around underground excavation by phase-field method with hydromechanical coupling. Comput. Geotech. 2021, 138, 104369. [Google Scholar] [CrossRef]
- Zhao, J.J.; Shen, W.Q.; Shao, J.F.; Liu, Z.B.; Vu, M.N. A constitutive model for anisotropic clay-rich rocks considering micro-structural composition. Int. J. Rock Mech. Min. Sci. 2022, 151, 105029. [Google Scholar] [CrossRef]
- Saitta, A.; Lopard, G.; Petizon, T.; Armand, G. Projet Cigéo (France)—Modélisation du comportement des argilites de la galerie GRD du laboratoire souterrain de Meuse/Haute-Marne. In Proceedings of the Congrès AFTES 2017, Paris, France, 13–15 November 2017. [Google Scholar]
- Vu, M.N.; Guayacan-Carrillo, L.M.; Armand, G. Excavation induced over pore pressure around drifts in the Callovo-Oxfordian claystone. Eur. J. Environ. Civil Eng. 2020, 1–16. [Google Scholar] [CrossRef]
- Tran, N.T.; Do, D.P.; Hoxha, D.; Vu, M.N.; Armand, G. Kriging-based reliability analysis of the long-term stability of a deep drift constructed in the Callovo-Oxfordian claystone. J. Rock Mech. Geotech. Eng. 2021, 13, 1033–1046. [Google Scholar] [CrossRef]
- Tran, N.T.; Do, D.P.; Hoxha, D.; Vu, M.N.; Armand, G. Modified AK-MCS method and its application on the reliability analysis of underground structures in the rock mass. J. Sci. Tech. Civil Eng. (STCE)-HUCE 2022, 16, 38–54. [Google Scholar] [CrossRef]
- Fortsakis, P.; Kavvadas, M. Estimation of time dependent ground parameters in tunnelling using back analyses of convergence data. In Proceedings of the Euro:Tun 2009, Bochum, Germany, 9–11 September 2009. [Google Scholar]
- Lecampion, B.; Constantinescu, A.; Nguyen, D.M. Parameter identification for lined tunnels in a viscoplastic medium. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 1191–1211. [Google Scholar] [CrossRef] [Green Version]
- Do, D.P.; Vu, M.N.; Tran, N.T.; Armand, G. Closed-form solution and reliability analysis of deep tunnel supported by a concrete liner and a covered compressible layer within the viscoelastic Burger rock. Rock Mech. Rock Eng. 2021, 54, 2311–2334. [Google Scholar] [CrossRef]
- Do, D.P.; Tran, N.T.; Hoxha, D.; Vu, M.N.; Armand, G. Kriging-based optimization design of deep drift in the rheological Burger rock. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012155. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, J.; Wang, R. Basic framework and main methods of uncertainty quantification. Math. Probl. Eng. 2020, 2020, 6068203. [Google Scholar] [CrossRef]
- Rappel, H.; Bee, L.A.A.; Hale, J.S.; Bordas, S.P.A. Beyasian inference for the stochastic identification of elastoplastic material parameters: Introduction, misconceptions, and additional insight. arXiv 2016, arXiv:1606.02422. [Google Scholar]
- Wagner, P.R.; Nagel, J.; Marelli, S.; Sudret, B. UQLab User Manuel—Bayesian Inference for Model Calibration and Inverse Problem; Report # UQLab-V1.4-113; Risk, Safety and Uncertainty Quantification: Zurich, Switzerland, 2021. [Google Scholar]
- Sedehi, O.; Papadimitriou, C.; Katafygiotis, L.S. Probabilistic Hierarchical Bayesian framework for time-domain model updating and robust predictions. Mech. Sys. Sig. Proc. 2019, 123, 648–673. [Google Scholar] [CrossRef]
- Nagel, J.B.; Sudret, B. A unified framework for multilevel uncertainty quantification in Bayesian inverse problems. Probabilistic Eng. Mech. 2016, 43, 68–84. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Angelikopoulos, P.; Beck, J.L.; Koumoutsakos, P. Hierarchical stochastic model in Bayesian inference for engineering applications: Theoretical implications and efficient approximation. ASCE-ASME J. Risk Uncert. Eng. Sys. Part B. Mech. Eng. 2019, 5, 011006. [Google Scholar] [CrossRef] [Green Version]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in Matlab. In Proceedings of the 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM2014), Liverpool, UK, 13–16 July 2014. [Google Scholar]
- Li, C.; Jiang, S.H.; Li, J.; Huang, J. Bayesian approach for sequential probabilistic back analysis of uncertain geomechanical parameters and reliability updating of tunneling-induced ground settlements. Adv. Civil Eng. 2020, 2020, 8528304. [Google Scholar] [CrossRef]
- Miro, S.; König, M.; Hartmann, D.; Schanz, R. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study. Comput. Geotech. 2015, 68, 38–53. [Google Scholar] [CrossRef]
- Rappel, H.; Bee, L.A.A.; Bordas, S.P.A. Beyasian inference to identify parameters in viscoelasticity. Mech. Time Depend. Mater. 2018, 22, 221–258. [Google Scholar] [CrossRef]
- Kabwe, E.; Karakus, M.; Chanda, E.K. Time-dependent solution for non-circular tunnels considering the elasto-viscoplastic rockmass. Int. J. Rock Mech. Min. Sci. 2020, 133, 104395. [Google Scholar] [CrossRef]




| GM (GPa) | ηM (GPa.year) | C (MPa) | φ (°) | ψ (°) | β | P0 (MPa) | R (m) | λ |
|---|---|---|---|---|---|---|---|---|
| 1.73 | 3.06 | 6 | 20 | 0 | 0.35 | 12.5 | 2.6 | 1 |
| Method | ηM (GPa.year) | β | ||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| Exact | 2.16 | 3.96 | 0.25 | 0.45 |
| Classical BI (Ns = 10) | 3.34 | 3.50 | 0.35 | 0.39 |
| Classical BI (Ns = 50) | 3.28 | 3.37 | 0.38 | 0.41 |
| Hierarchical BI (Ns = 10) | 0.95 | 5.56 | 0.25 | 0.46 |
| Hierarchical BI (Ns = 50) | 1.45 | 4.80 | 0.16 | 0.53 |
| E (GPa) | υ | Ci (MPa) | φi (°) | ψi (°) | Cf (MPa) | φf (°) | ψf (°) |
|---|---|---|---|---|---|---|---|
| 6.6 | 0.3 | 6 | 20 | 0 | 1 | 25 | 5 |
| Section | n | 1/m | 1/K (GPa−1) | |||
|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | |
| OHZ170B | 9.22 | 1.78 | 0.26 | 0.040 | 8.25 | 1.95 |
| OHZ170C | 8.97 | 1.72 | 0.25 | 0.039 | 7.19 | 1.79 |
| OHZ170D | 8.94 | 1.69 | 0.24 | 0.038 | 7.15 | 1.78 |
| OHZ170E | 8.92 | 1.70 | 0.25 | 0.038 | 7.35 | 1.83 |
| OHZ170F | 8.48 | 1.55 | 0.23 | 0.035 | 7.07 | 1.78 |
| OHZ170G | 8.95 | 1.63 | 0.25 | 0.037 | 7.49 | 1.88 |
| Six sections | 8.66 | 1.82 | 0.23 | 0.041 | 8.36 | 2.16 |
| Method | n | 1/m | 1/K (GPa−1) | |||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | |
| Classical BI | 5.09 | 12.24 | 0.15 | 0.31 | 4.12 | 12.60 |
| Hierarchical BI (Ns = 6) | 3.91 | 13.74 | 0.10 | 0.40 | 2.68 | 12.17 |
| Hierarchical BI (Ns = 36) | 8.07 | 10.42 | 0.18 | 0.26 | 5.63 | 9.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, D.-P.; Tran, N.-T.; Hoxha, D.; Vu, M.-N.; Armand, G. Time-Dependent Behavior of Callovo-Oxfordian Claystone for Nuclear Waste Disposal: Uncertainty Quantification from In-Situ Convergence Measurements. Sustainability 2022, 14, 8465. https://doi.org/10.3390/su14148465
Do D-P, Tran N-T, Hoxha D, Vu M-N, Armand G. Time-Dependent Behavior of Callovo-Oxfordian Claystone for Nuclear Waste Disposal: Uncertainty Quantification from In-Situ Convergence Measurements. Sustainability. 2022; 14(14):8465. https://doi.org/10.3390/su14148465
Chicago/Turabian StyleDo, Duc-Phi, Ngoc-Tuyen Tran, Dashnor Hoxha, Minh-Ngoc Vu, and Gilles Armand. 2022. "Time-Dependent Behavior of Callovo-Oxfordian Claystone for Nuclear Waste Disposal: Uncertainty Quantification from In-Situ Convergence Measurements" Sustainability 14, no. 14: 8465. https://doi.org/10.3390/su14148465
APA StyleDo, D.-P., Tran, N.-T., Hoxha, D., Vu, M.-N., & Armand, G. (2022). Time-Dependent Behavior of Callovo-Oxfordian Claystone for Nuclear Waste Disposal: Uncertainty Quantification from In-Situ Convergence Measurements. Sustainability, 14(14), 8465. https://doi.org/10.3390/su14148465







