The Analysis of Carbon Emission’s Characteristics and Dynamic Evolution Based on the Strategy of Unbalanced Regional Economic Development in China
Abstract
:1. Introduction
2. Literature Review
3. Model and Data
3.1. Carbon Emission Measurement
3.2. The Coordination Evaluation and Assessment Model of Energy, Economy and Environment (3E)
3.3. Spatial Econometric Models
3.4. Data Source
- (1)
- The data of China’s energy consumption in 2007–2020 are from the China Energy Statistics Yearbook. The rest of China’s data are mainly from the China Statistical Yearbook, China Labor Statistics Yearbook, China Science and Technology Statistics Yearbook, China Population and Employment Statistics Yearbook, China Foreign Economic Statistics Yearbook and statistical yearbooks of corresponding years in 30 provinces, municipalities, and autonomous regions.
- (2)
- The conversion that is coefficient of various types of energy consumed is determined by the industry in tons of coal equivalent (TCE) and the physical quantities are calculated by referring to the Energy Balance Sheet. The industry’s carbon emission, that is the coefficient of energy consumed, is determined by referring to the IPCC Guidelines for National Greenhouse Gas Inventories 2006 (Appendix A). The carbon emission coefficient of various types of fossil energy is released on the IPCC Guideline (2006). Despite those changes in the carbon emission coefficient in recent years, they are insignificant and, therefore, can be ignored owing to the macro changes studied in this paper.
- (3)
- The regional development strategy of China is divided into three zones in this paper: ① Eastern: Beijing, Fujian, Guangdong, Hainan, Hebei, Jiangsu, Liaoning, Shandong, Shanghai, Tianjin, Zhejiang, and Guangxi; ② Central: Heilongjiang, Anhui, Henan, Jilin, Hubei, Hunan, Jiangxi, Inner Mongolia, and Shanxi; ③ Western: Gansu, Guizhou, Ningxia, Qinghai, Shaanxi, Sichuan, Xinjiang, Yunnan, and Chongqing.
4. Analysis and Discussion
4.1. Basis for Zoning
- (1)
- The establishment of 3E coordination evaluation and assessment system
- (2)
- 3E coordination analysis
4.2. Regional Carbon Emissions Status
- (1)
- Theil index
- (2)
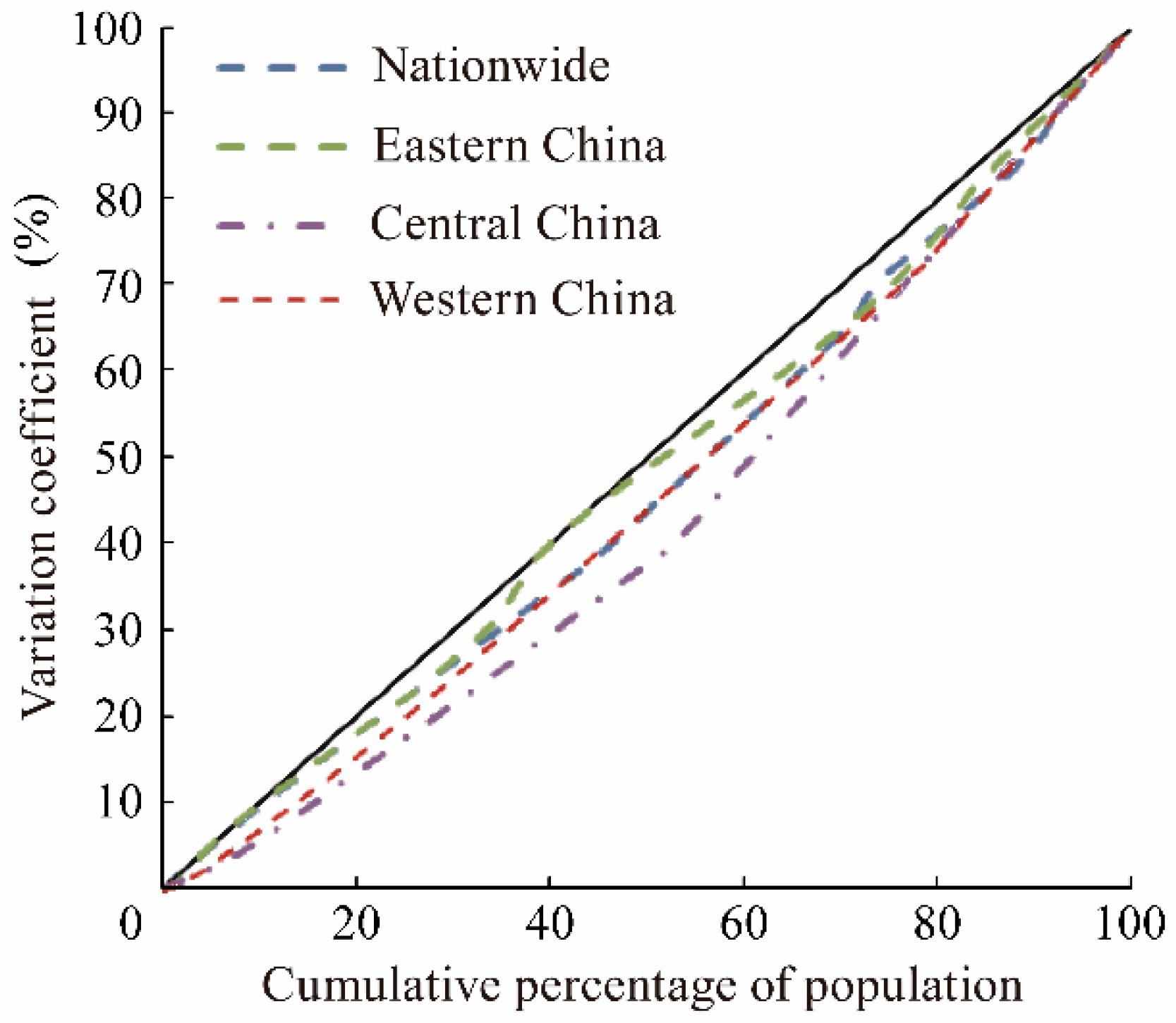
- Variation coefficient and Gini coefficient
- (3)
- Loss deviation coefficient
4.3. Causes for the Cross-Regional Difference in Carbon Emission Level
- (1)
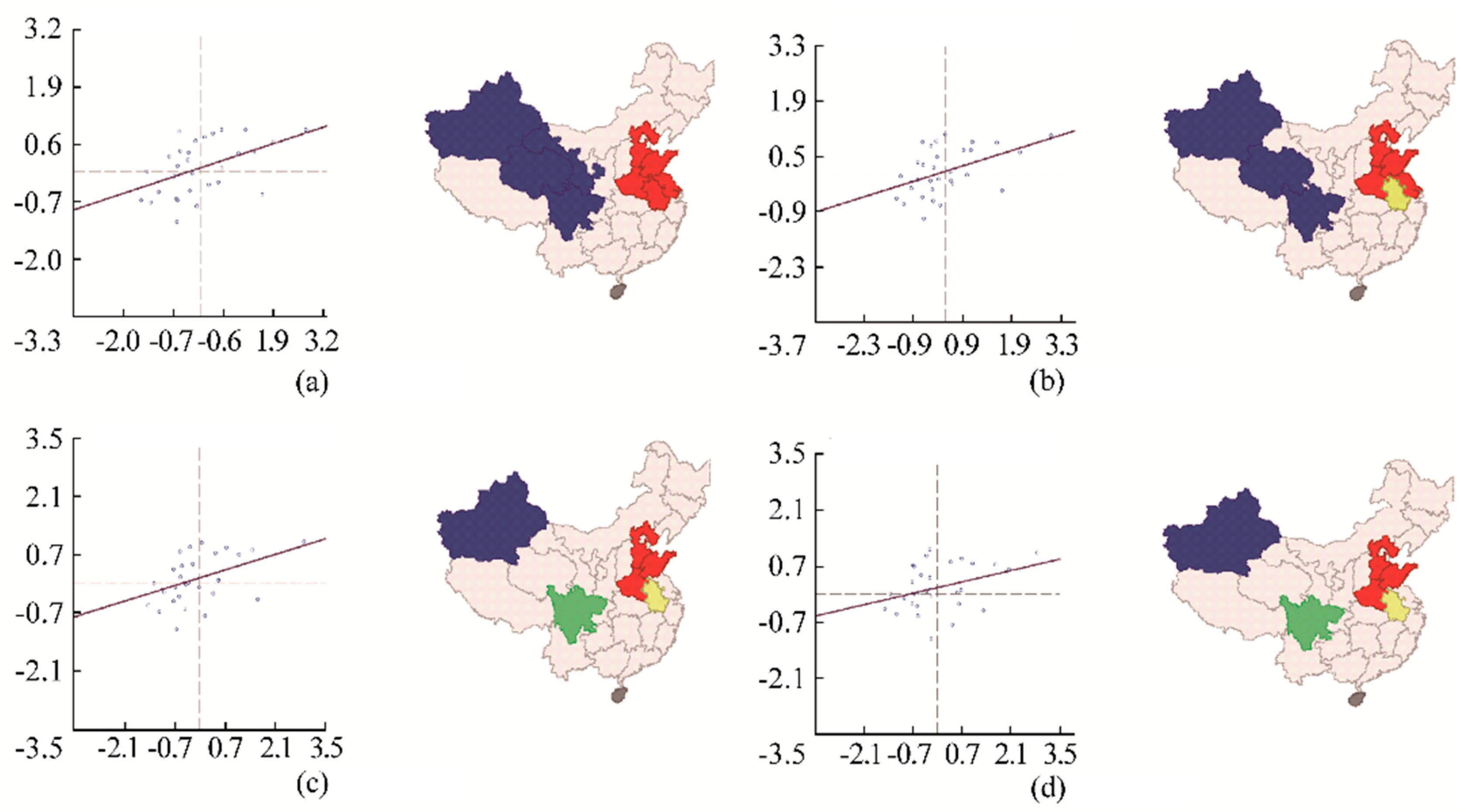
- Spatial dependence characteristics of carbon emission
- (2)
- Test findings of spatial econometric models
4.4. Studies on Influential Factors
- (1)
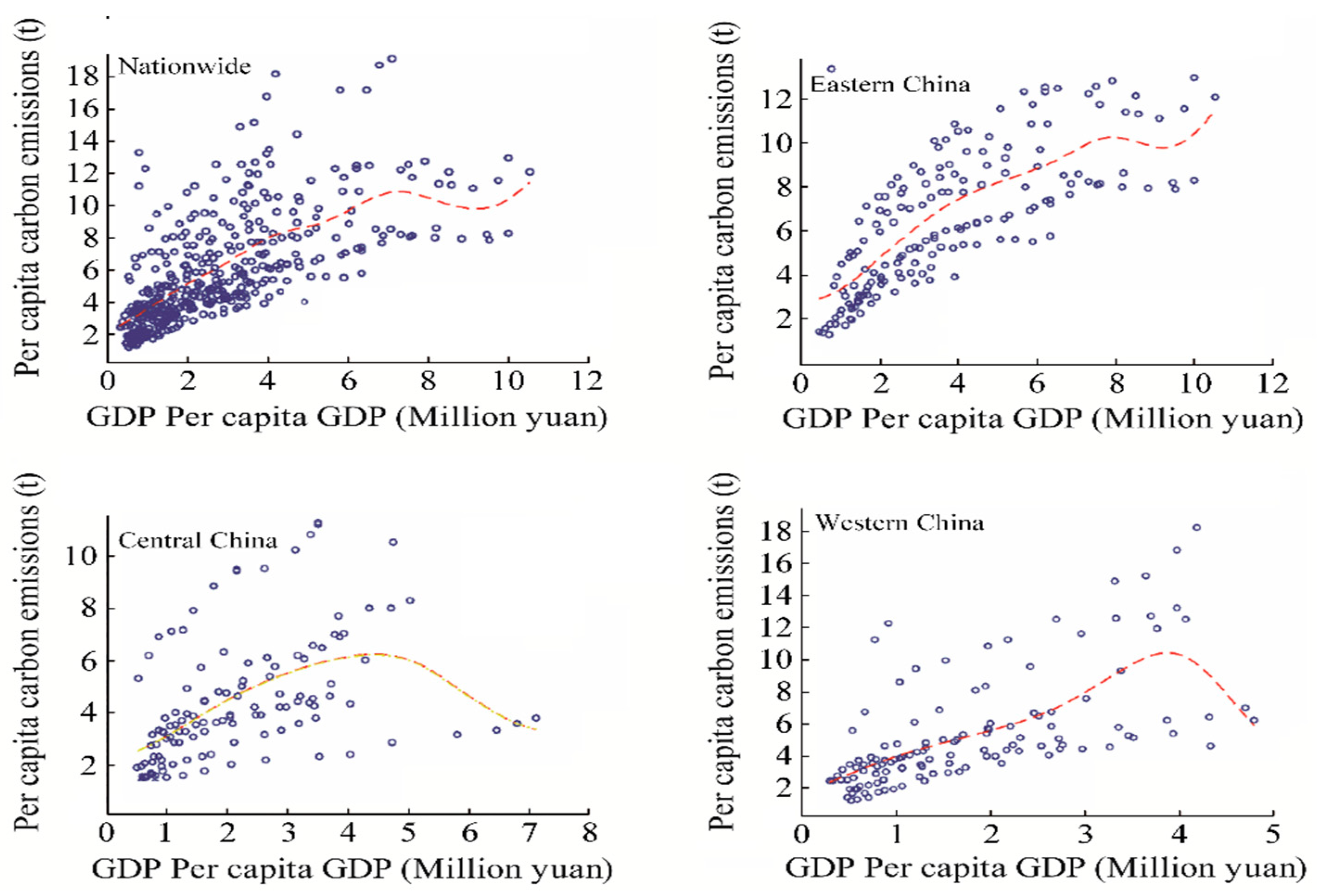
- Economic level
- (2)
- Energy structure
- (3)
- Industrial structure
- (4)
- Population
- (5)
- Energy efficiency
5. Conclusions and Policy Suggestions
5.1. Conclusions
- (1)
- The environmental subsystem has the lowest degree of coordination, reflecting that the deteriorating environmental conditions are not yet controlled from the root and that some regions are still damaging the environment in pursuit of regional economic development. Based on the study of the 3E coordination degree, it is easy to find that the provinces have demonstrated apparent regional (eastern, central and western) features, with most of the poorly coordinated provinces located in the western region. The primary causes lie in outdated economic growth patterns, unbalanced distribution of production factors, backward technology levels and low knowledge popularization, resulting in regional environmental deterioration.
- (2)
- The regression of the spatial econometric model shows that: ① The direct and general effects of the industrial structure are significant at 10%, suggesting the emergence of some trends of deterioration in industrial structure, reflected explicitly by the rising rather than dropping of weights of industries with high energy consumption. However, the indirect effects are positive but insignificant, showing that the cross-regional difference in industrial structure is narrowing down in the evolution of industrial structures and that the regional characteristics are not that significant. On the basis of increasingly integral industrial categories in each region, a more complete system ad a balanced spatial distribution of major industries and product production, as well as a decline in concentration, has gradually been formed. ② Population growth will influence the increase of CO2 emission, caused by the increased population, improved quality and expanded demands, which, specifically, are reflected by the expanded consumption desires, upgraded requirements on quality and the expanding city size.
- (3)
- The increase in population, age structure and quantity of households also function as positive contributors to the increase in CO2 emission. Education level plays a significantly inhibitory role in this process. Although the improvement of education level stimulates people’s desire for a better life, it also leads to the overall improvement of living standards. However, advanced concepts on consumption have increased the awareness of environmental protection. Furthermore, the knowledge and skills of managers in production activities have indirectly contributed to the improvement of productivity and the reduction of carbon dioxide emissions.
5.2. Policy Suggestions
- (1)
- Firstly, China should hold on to its strategy of developing green energy so as to build up an administration mechanism that suits and matches the energy strategies. Furthermore, modes of highly efficient utilization of energy, research systems that facilitate clean and renewable energy production, and advantageous policies for the environment should be created to maintain a stable and safe energy supply. Secondly, actions should be taken to strengthen target management by virtue of total quantity control. For this purpose, yearly goals of energy conservation and consumption reduction should be established stage-by-stage. The intensity of energy market openness should be determined in view of environment carrying capacity, and a comprehensive energy–environment decision-making mechanism be established to ensure the coordinated development of energy and the environment. Thirdly, efforts should be made to push forward the supply-side reform so as to promote the adjustment of energy consumption structure. Furthermore, active actions should be made to develop renewable energies and replace conventional energies with clean energy. Investments in related technological development should be further strengthened, and some privileged policies be enacted to introduce advanced technologies globally to realize diversified energy structure.
- (2)
- As for the demand, China should work actively to adjust and optimize its existing industrial structure to facilitate reasonable energy utilization in good order. In the eastern region, based on the advantages in capital and technologies, China should seek opportunities to build up its post-industrialization and emerging industrial systems. In the central region, the conditional industrial transfer may be encouraged to combine the improvement of energy efficiency and industrial application. In the western region, the second-mover advantages should be made best use of so as to work out reasonable industrial layout, strengthen source control and improve industrialization quality. It is noteworthy to mention that a cross-regional coordination mechanism should be established in response to the needs for cross-regional industrial flows, especially in industries with high CO2 emission levels, and, moreover, overall planning should be done to transfer industries with high CO2 emission levels. Apart from these, to promote coordinated development and environment and quality improvements across various regions, regions should work out policies that are tailored to their specific conditions.
- (3)
- Based on the roles in society, such as consumers, schools, families, enterprises, and governments, special efforts should be made to foster the awareness of environmental protection. For example, consumers are encouraged to develop sound environmental protection and to resist bad habits; schools to carry out education programs on the environment and foster positive school cultures; and families to establish advanced and environment-friendly consumption concepts. As for enterprises, green product awareness should be built up so as to transform the operating strategies to actively take their social responsibilities and strengthen the innovation of green technologies. Governments should lead and guide the environment-friendly conditions for consumers, and establish green quality inspection systems and green consumption mechanisms, and strengthen the construction of green infrastructures.
- (4)
- For western provinces with great potentiality, more elasticity, together with more emission quotas, should be given to the emission reduction policies. Despite the outdated infrastructure, poor worker quality, unbalanced population and resources, and restrictions from conventional industrial paths that resulted in the massive pressure on energy conservation and emission reduction, the top priority in the regional development strategies is still maintained by the West Development Strategy. In the excellent background of the smooth development of industrialization, the “Belt and Road” strategy has revealed new directions and blueprints for economic development in western regions. It is suggested that Chinese governments should, while actively guiding their regional development, give sufficient preferences of materials and time to the western regions. More importance should be attached to the western regions when facing the largest challenges in realizing a well-off society. To achieve this goal, a low-emission and recyclable economy should be stressed to promote their industrialization, urbanization and modern development with local characteristics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Types of Energy | Standard Coal Conversion Coefficient | CO2 Emission Index | Types of Energy | Standard Coal Conversion Coefficient | CO2 Emission Index |
|---|---|---|---|---|---|
| Raw coal | 0.712 kgce/kg | 2.69 CO2kg/kg | Gasoline | 1.471 kgce/kg | 2.76 CO2kg/L |
| Fuel coal | 0.899 kgce/kg | 2.53 CO2kg/kg | Kerosene | 1.471 kgce/kg | 2.56 CO2kg/L |
| Coking coal | 0.971 kgce/kg | 2.69 CO2kg/kg | Diesel oil | 1.457 kgce/kg | 2.73 CO2kg/L |
| Coke oven gas | 0.614 kgce/m3 | 0.93 CO2kg/m3 | Fuel oil | 1.457 kgce/kg | 2.98 CO2kg/L |
| Other coke products | 1.153 kgce/kg | 3.35 CO2kg/kg | Natural gas | 1.330 kgce/m3 | 2.09 CO2kg/m3 |
| Crude oil | 1.428 kgce/kg | 2.76 CO2kg/L | Coke oven gas | 0.613 kgce/m3 | 0.93 CO2kg/m3 |
References
- Anwar, A.; Malik, S. Cogitating the role of technological innovation and institutional quality on environmental degradation in G-7 countries. Int. J. Green Econ. 2021, 15, 213–232. [Google Scholar] [CrossRef]
- Chien, F.; Anwar, A.; Hsu, C.C.; Sharif, A.; Razzaq, A.; Sinha, A. The role of information and communication technology in encountering environmental degradation: Proposing an SDG framework for the BRICS countries. Technol. Soc. 2021, 65, 101587. [Google Scholar] [CrossRef]
- Mengis, N.; Partanen, A.L.; Jalbert, J.; Matthews, H.D. 1.5 °C carbon budget dependent on carbon cycle uncertainty and future non-CO2 forcing. Nature 2018, 8, 5831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naqi, A.; Jang, J.G. Recent progress in green cement technology utilizing low-carbon emission fuels and raw materials: A review. Sustainability 2019, 11, 537. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Huang, C.C. Predictions of carbon emission intensity based on factor analysis and an improved extreme learning machine from the perspective of carbon emission efficiency. J. Clean. Prod. 2022, 338, 130414. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Li, F.; Wu, J.; Zhou, D. Energy and environmental efficiency of China’s transportation sectors under the constraints of energy consumption and environmental pollutions. Energy Econ. 2020, 89, 104817. [Google Scholar] [CrossRef]
- Xi, J. Xi Jinping’s Speech at the Climate Ambition Summit. 2020. Available online: http://www.gov.cn/xinwen/2020-12/13/content_5569138.htm (accessed on 25 March 2021).
- Xi, J. Building a Community of Life between People and Nature. People’s Daily 2021, 004267. [Google Scholar] [CrossRef]
- Safi, A.; Chen, Y.; Wahab, S.; Ali, S.; Yi, X.; Imran, M. Financial instability and consumption-based carbon emission in E-7 countries: The role of trade and economic growth. Sustain. Prod. Consum. 2021, 27, 383–391. [Google Scholar] [CrossRef]
- Liu, L.; Anwar, A.; Irmak, E.; Pelit, I. Asymmetric linkages between public-private partnership, environmental innovation, and transport emissions. Econ. Res. Ekon. Istraživanja 2022, 1–22. [Google Scholar] [CrossRef]
- Den Elzen, M.G.; Beltran, A.M.; Hof, A.F.; van Ruijven, B.; van Vliet, J. Reduction targets and abatement costs of developing countries resulting from global and developed countries’ reduction targets by 2050. Mitig. Adapt. Strateg. Glob. Chang. 2013, 18, 491–512. [Google Scholar] [CrossRef]
- Cutlip, L.; Fath, B.D. Relationship between carbon emissions and economic development: Case study of six countries. Environ. Dev. Sustain. 2012, 14, 433–453. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, M.M.; Li, R.R.; Su, M. Decomposition and decoupling analysis of carbon emission from economic growth: A comparative study of China and United States. J. Clean. Prod. 2018, 197, 178–184. [Google Scholar] [CrossRef]
- Li, J.B.; Huang, X.J.; Kwan, M.P.; Yang, H.; Chuai, X.W. The effect of urbanization on carbon dioxide emissions efficiency in the Yangtze River Delta, China. J. Clean. Prod. 2018, 188, 38–48. [Google Scholar] [CrossRef]
- Dai, H.C.; Zhang, H.B.; Wang, W.T. The impacts of U.S. withdrawal from the Paris Agreement on carbon emission space and mitigation cost of China, E.U., and Japan under the constraints of global carbon emission space. Adv. Clim. Chang. Res. 2017, 8, 226–234. [Google Scholar] [CrossRef]
- Pan, W.; Pan, W.; Shi, Y.; Liu, S.; He, B.; Hu, C.; Tu, H.; Xiong, J.; Yu, D. China’s inter-regional carbon emissions: A input-output analysis under considering national economic strategy. J. Clean. Prod. 2018, 197, 794–803. [Google Scholar] [CrossRef]
- Wu, Y.; Chau, K.W.; Lu, W.S.; Shen, L.Y.; Shuai, C.Y.; Chen, J.D. Decoupling relationship between economic output and carbon emission in the Chinese construction industry. Environ. Impact Assess. Rev. 2017, 71, 6060. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.F. The impacts of GDP, trade structure, exchange rate and FDI inflows on China’s carbon emission. Energy Policy 2018, 120, 347–353. [Google Scholar] [CrossRef]
- Jorgenson, A.; Schor, J.; Huang, X.R. Income inequality and carbon emission in the United States: A state-level analysis, 1997–2012. Ecol. Econ. 2017, 134, 40–48. [Google Scholar] [CrossRef]
- Cohen, G.; Jalles, J.T.; Loungani, P.; Marto, R.; Wang, G.W. Decoupling of emissions and GDP: Evidence from aggregate and provincial Chinese data. Energy Econ. 2019, 77, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Li, J.S.; Zhou, H.W.; Meng, J.; Yang, Q.; Chen, B.; Zhang, Y.Y. Carbon emissions and their drivers for a typical urban economy from multiple perspectives: A case analysis for Beijing city. Appl. Energy 2018, 226, 1076–1086. [Google Scholar] [CrossRef]
- Long, Y.; Yoshida, Y. Quantifying city-scale emission responsibility based on input-output analysis-inside from Tokyo, Japan. Appl. Energy 2018, 218, 349–360. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Zhou, X.Y.; Xu, Q.; Wu, F.; Wang, Q.W.; Zha, D.L. Regional embodied carbon emission and their transfer characteristics in China. J. Clean. Prod. 2018, 197, 178–184. [Google Scholar] [CrossRef]
- Narayan, P.K.; Saboori, B.; Soleymani, A. Economic growth and carbon emissions. Econ. Model. 2016, 53, 388–397. [Google Scholar] [CrossRef]
- Ulucak, R.; Bilgili, F. A reinvestigation of EKC model by ecological footprint measurement for high, middle and low income countries. J. Clean. Prod. 2018, 188, 144–157. [Google Scholar] [CrossRef]
- Dong, F.; Yu, B.L.; Hadachin, T.; Dai, Y.J.; Long, R.Y. Drivers of carbon emission intensity changes in China. Resour. Conserv. Recycl. 2018, 129, 187–201. [Google Scholar] [CrossRef]
- Ang, B.W.; Zhang, F.Q.; Choi, K. Factorizing changes in energy and environmental indicators through decomposition. Energy 1998, 23, 489–495. [Google Scholar] [CrossRef]
- Lin, B.Q.; Long, H.Y. Emissions reduction in China’s chemical industry-Based LMDI. Renew. Sustain. Energy Rev. 2018, 35, 1348–1355. [Google Scholar]
- Jiang, Y.; Bai, H.T.; Feng, X.Y.; Luo, W.; Huang, Y.Y.; Xu, H. How do geographical factors affect energy-related carbon emissions? A Chinese panel analysis. Ecol. Indic. 2018, 93, 1226–1235. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, Y.T.; Zhang, X.; Tang, K. Whether China’s industrial sectors make efforts to reduce CO2 emissions from production? -A decomposed decoupling analysis. Energy 2018, 160, 796–809. [Google Scholar]
- Cai, B.F.; Li, W.X.; Dhakal, S.; Wang, J.H. Source data supported high resolution carbon emissions inventory for urban areas of the Beijing-Tianjin-Hebei region: Spatial patterns, decomposition and policy implications. J. Environ. Manag. 2018, 206, 786–799. [Google Scholar] [CrossRef]
- Anwar, A.; Sinha, A.; Sharif, A.; Siddique, M.; Irshad, S.; Anwar, W.; Malik, S. The nexus between urbanization, renewable energy consumption, financial development, and CO2 emissions: Evidence from selected Asian countries. Environ. Dev. Sustain. 2022, 24, 6556–6576. [Google Scholar] [CrossRef]
- Sun, Y.; Anwar, A.; Razzaq, A.; Liang, X.; Siddique, M. Asymmetric role of renewable energy, green innovation, and globalization in deriving environmental sustainability: Evidence from top-10 polluted countries. Renew. Energy 2022, 185, 280–290. [Google Scholar] [CrossRef]
- Mao, G.; Dai, X.; Wang, Y.; Guo, J.; Cheng, X.; Fang, D.; Song, X.; He, Y.; Zhao, P. Reducing carbon emissions in China: Industrial structural upgrade based on system dynamics. Energy Strategy Rev. 2013, 2, 199–204. [Google Scholar] [CrossRef]
- Lin, B.Q.; Jia, Z.J. Impact of quota decline scheme of emission trading in China: A dynamic recursive CGE model. Energy 2018, 149, 190–203. [Google Scholar] [CrossRef]
- Xiao, B.W.; Niu, D.X.; Wu, H. Exploring the impact of determining factors behind CO2 emissions in China: A CGE appraisal. Sci. Total Environ. 2017, 518, 559–572. [Google Scholar] [CrossRef]
- Sharif, A.; Raza, S.A.; Ozturk, I.; Afshan, S. The dynamic relationship of renewable and nonrenewable energy consumption with carbon emission: A global study with the application of heterogeneous panel estimations. Renew. Energy 2019, 133, 685–691. [Google Scholar] [CrossRef]
- Grübler, A.; Nakicenovic, N. International Burden Sharing in Greenhouse Gas Reduction; International Institute for Applied Systems Analysis: Laxenburg, Austria, 1994. [Google Scholar]
- Yu, S.W.; Wei, Y.M.; Fan, J.L.; Zhang, X.; Wang, K. Exploring the regional characteristics of inter-provincial CO2 emissions in China: An improved fuzzy clustering analysis based on particle swarm optimization. Appl. Energy 2012, 92, 522–562. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, M.H.; Zhang, M. Contrastive Analyses of the Influence Factors of Inter-provincial Carbon Emission Induced by Industry Energy in China. Nat. Hazards 2016, 3, 1405–1433. [Google Scholar] [CrossRef]
- Li, Z.Z.; Li RY, M.; Malik, M.Y.; Murshed, M.; Khan, Z.; Umar, M. Determinants of carbon emission in China: How good is green investment? Sustain. Prod. Consum. 2021, 27, 392–401. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Zhang, J.C.; Zhu, Z.S.; Zhao, G.H. Impacts of the 3E (economy, energy and environment) coordinated development on energy mix in China: The multi-objective optimisation perspective. Struct. Chang. Econ. Dyn. 2019, 50, 56–64. [Google Scholar] [CrossRef]
- Yi, Q.; Feng, J.; Wu, Y.L.; Li, W.Y. 3E (energy, environmental, and economy) evaluation and assessment to an innovative dual-gas polygene ration system. Energy 2014, 66, 285–294. [Google Scholar] [CrossRef]
- Fujita, M. Spatial Development Planning: A Dynamic Convex Programming Approach; North-Holland Publishing Company: Amsterdam, The Netherlands, 1979; pp. 501–503. [Google Scholar]
- Cliff, A.D. Evaluating the percentage points of a spatial autocorrelation coefficient. Geogr. Anal. 1971, 3, 51–62. [Google Scholar] [CrossRef]
- Wang, X.W.; Wang, S.; Zhang, Y.S. The impact of environmental regulation and carbon emissions on green technology innovation from the perspective of spatial interaction: Empirical evidence from urban agglomeration in China. Sustainability 2022, 14, 5381. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.M.; Zhang, M.; Ouyang, J.M.; Shi, W.T. Regional differences in carbon emission of China’s industries and its decomposition effects. J. Clean. Prod. 2020, 270, 122528. [Google Scholar] [CrossRef]
- Barro, R.B. Technological diffusion, convergence, and growth. J. Econ. Growth 1997, 2, 1–27. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, T.L. The impact of cross-region industrial structure optimization on economy, carbon emissions and energy consumption: A case of the Yangtze River Delta. Sci. Total Environ. 2021, 778, 146089. [Google Scholar] [CrossRef]
- Tao, A.X. Research on the realization path of carbon emission reduction in Zhejiang Province. Energy Rep. 2022, 8, 501–506. [Google Scholar] [CrossRef]
- Chiu, Y.B. Carbon dioxide, income and energy: Evidence from a non-linear model. Energy Econ. 2017, 61, 279–288. [Google Scholar] [CrossRef]
- Shao, M.X.; Xue, M.G. Decomposition analysis of carbon emissions: Considering China’s energy efficiency. Energy Rep. 2022, 8, 630–635. [Google Scholar] [CrossRef]
- Zou, W.J.; Zhang, L.Q.; Xu, J.Y.; Xie, Y.F.; Chen, H.X. Spatial–Temporal Evolution Characteristics and Influencing Factors of Industrial Pollution Control Efficiency in China. Sustainability 2022, 14, 5152. [Google Scholar] [CrossRef]
| First Class Indicator | Criterion | Second Class Indicator | Indicator Property |
|---|---|---|---|
| Energy system | Energy scale | Investment in fixed assets in the energy industry (Q1) | + |
| Energy generation capacity (Q2) | + | ||
| Investment ration of fixed assets in energy industry (Q3) | + | ||
| Energy consumption | Energy consumption (Q4) | − | |
| Coal consumption (Q5) | − | ||
| Gas consumption (Q6) | − | ||
| Per capita energy consumption (Q7) | − | ||
| Energy consumption elasticity coefficient (Q8) | − | ||
| Energy efficiency | Energy intensity (Q9) | − | |
| Economic system | Economic scale | GDP per capita (Q10) | + |
| Investment in social fixed assets (Q11) | + | ||
| Import–export volume (Q12) | + | ||
| Economic structure | Proportion of second industry increment in GDP (Q13) | − | |
| Proportion of tertiary industry increment in GDP (Q14) | + | ||
| Economic benefit | Total retail of sales of per capita consumer goods (Q15) | + | |
| Per capita disposable income (Q16) | + | ||
| Economic quality | GDP growth rate (Q17) | + | |
| Revenue growth rate (Q18) | + | ||
| Resident income growth rate (Q19) | + | ||
| Growth rate of investment in fixed assets (Q20) | + | ||
| Industrial of output growth rate (Q21) | + | ||
| Environmental system | Environmental quality | Per capita park green area (Q22) | + |
| Forest cover rate (Q23) | + | ||
| Environmental pollution | Industrial solid waste (Q24) | − | |
| Industrial dust (Q25) | − | ||
| Carbon emissions (Q26) | − | ||
| Environmental protection | Industrial waste disposal rate (Q27) | + | |
| Investment in industrial pollution control (Q28) | + | ||
| Investment in environmental pollution control (Q29) | + | ||
| Proportion of investment in environmental pollution control (Q30) | + |
| Province | Energy Coordination Degree | Economic Coordination Degree | Environment Coordination Degree | 3E Coordination Degree | Coordination State |
|---|---|---|---|---|---|
| Guangdong | 0.7652 | 0.8299 | 0.7041 | 0.7683 | Well coordination |
| Zhejiang | 0.6269 | 0.8027 | 0.7240 | 0.7148 | Well coordination |
| Shandong | 0.6125 | 0.8104 | 0.7352 | 0.7271 | Well coordination |
| Jiangsu | 0.6689 | 0.7501 | 0.7437 | 0.7213 | Well coordination |
| Tianjin | 0.7712 | 0.6848 | 0.6852 | 0.7147 | Well coordination |
| Fujian | 0.6477 | 0.7841 | 0.7082 | 0.7132 | Well coordination |
| Beijing | 0.6739 | 0.7501 | 0.6859 | 0.7073 | Well coordination |
| Shanghai | 0.6457 | 0.7302 | 0.7144 | 0.7018 | Well coordination |
| Chongqing | 0.6748 | 0.7803 | 0.6367 | 0.6894 | Basic maladjustment |
| Hubei | 0.6301 | 0.8412 | 0.5774 | 0.6801 | Basic maladjustment |
| Anhui | 0.7403 | 0.5622 | 0.6401 | 0.6508 | Basic maladjustment |
| Hunan | 0.6818 | 0.5723 | 0.6713 | 0.6494 | Basic maladjustment |
| Inner Mongolia | 0.7271 | 0.6943 | 0.5249 | 0.6482 | Basic maladjustment |
| Heilongjiang | 0.6133 | 0.5051 | 0.7126 | 0.6331 | Basic maladjustment |
| Guangxi | 0.6780 | 0.7371 | 0.4938 | 0.6291 | Basic maladjustment |
| Jilin | 0.6216 | 0.5493 | 0.6654 | 0.6121 | Basic maladjustment |
| Shanxi | 0.6910 | 0.5845 | 0.5376 | 0.5957 | Mild maladjustment |
| Jiangxi | 0.7857 | 0.4979 | 0.5482 | 0.5914 | Mild maladjustment |
| Shaanxi | 0.7436 | 0.5521 | 0.4893 | 0.5845 | Mild maladjustment |
| Liaoning | 0.6914 | 0.6636 | 0.4012 | 0.5716 | Mild maladjustment |
| Henan | 0.6358 | 0.4718 | 0.5352 | 0.5638 | Mild maladjustment |
| Hebei | 0.6233 | 0.4692 | 0.5831 | 0.5699 | Mild maladjustment |
| Sichuan | 0.7007 | 0.4132 | 0.5451 | 0.5570 | Mild maladjustment |
| Yunnan | 0.6579 | 0.5693 | 0.3960 | 0.5491 | Mild maladjustment |
| Hainan | 0.5833 | 0.4512 | 0.5067 | 0.5399 | Mild maladjustment |
| Guizhou | 0.6132 | 0.4479 | 0.5145 | 0.5382 | Mild maladjustment |
| Hainan | 0.5833 | 0.4512 | 0.5067 | 0.5399 | Mild maladjustment |
| Gansu | 0.6669 | 0.4985 | 0.3992 | 0.5236 | Mild maladjustment |
| Xinjiang | 0.6210 | 0.4107 | 0.4114 | 0.4911 | Major maladjustment |
| Qinghai | 0.3481 | 0.4591 | 0.4553 | 0.3981 | Major maladjustment |
| Ningxia | 0.3749 | 0.3672 | 0.3935 | 0.3827 | Major maladjustment |
| Time | Overall National Differences (T) | Inter-Regional Differences (TBR) | Intra-Regional Differences (TWR) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Values | Contribution Rate | Values | Contribution Rate | ||||||
| East Region | Central Region | West Region | East Region | Central Region | West Region | ||||
| 2007 | 0.0275 | 0.0046 | 16.61% | 0.0121 | 0.0058 | 0.0051 | 46.54% | 22.31% | 19.62% |
| 2008 | 0.0251 | 0.0041 | 16.44% | 0.0115 | 0.0059 | 0.0035 | 44.23% | 22.69% | 13.46% |
| 2009 | 0.0257 | 0.0045 | 17.34% | 0.0116 | 0.0062 | 0.0035 | 44.62% | 23.85% | 13.46% |
| 2010 | 0.0251 | 0.0033 | 13.25% | 0.0126 | 0.0056 | 0.0036 | 48.46% | 21.54% | 13.85% |
| 2011 | 0.0268 | 0.0035 | 13.03% | 0.0133 | 0.006 | 0.0039 | 51.15% | 23.08% | 15.00% |
| 2012 | 0.0288 | 0.0039 | 13.71% | 0.0139 | 0.0064 | 0.0045 | 53.46% | 24.62% | 17.31% |
| 2013 | 0.0317 | 0.0043 | 13.68% | 0.0131 | 0.0082 | 0.0061 | 50.38% | 31.54% | 23.46% |
| 2014 | 0.0305 | 0.0044 | 14.50% | 0.0128 | 0.0081 | 0.0052 | 49.23% | 31.15% | 20.00% |
| 2015 | 0.0313 | 0.0047 | 14.38% | 0.0118 | 0.0074 | 0.0033 | 45.38% | 28.46% | 12.69% |
| 2016 | 0.0322 | 0.0038 | 13.15% | 0.0127 | 0.0063 | 0.0031 | 48.85% | 24.23% | 11.92% |
| 2017 | 0.0309 | 0.0036 | 13.07% | 0.0134 | 0.0059 | 0.0041 | 51.54% | 22.69% | 15.77% |
| 2018 | 0.0321 | 0.0041 | 13.91% | 0.0137 | 0.0061 | 0.0044 | 52.69% | 23.46% | 16.92% |
| 2019 | 0.0337 | 0.0044 | 13.62% | 0.0129 | 0.0083 | 0.0062 | 49.62% | 31.92% | 23.85% |
| 2020 | 0.0349 | 0.0045 | 13.19% | 0.0122 | 0.0079 | 0.0059 | 46.92% | 30.38% | 22.69% |
| Regions | Carbon Emission Variation Coefficient | Coefficient of Variation of per Capita Carbon Emission | Coefficient of Variation of Carbon Emission Intensity |
|---|---|---|---|
| Nationwide | 63.43% | 47.10% | 49.23% |
| Eastern China | 66.17% | 34.87% | 37.29% |
| Central China | 36.22% | 60.19% | 40.49% |
| Western China | 45.59% | 54.33% | 42.74% |
| Time | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eastern China EC | 1.17 | 1.17 | 1.19 | 1.19 | 1.16 | 1.16 | 1.14 | 1.13 | 1.14 | 1.12 | 1.13 | 1.13 | 1.14 | 1.14 |
| Eastern China EDC | 2.64 | 2.61 | 2.45 | 2.32 | 2.38 | 2.25 | 2.09 | 1.88 | 1.81 | 1.68 | 1.55 | 1.45 | 1.36 | 1.33 |
| Eastern China LDP | 0.45 | 0.46 | 0.49 | 0.52 | 0.49 | 0.52 | 0.55 | 0.61 | 0.64 | 0.67 | 0.73 | 0.79 | 0.85 | 0.87 |
| Central China EC | 0.85 | 0.85 | 0.84 | 0.85 | 0.86 | 0.84 | 0.85 | 0.89 | 0.89 | 0.91 | 0.91 | 0.92 | 0.9 | 0.91 |
| Central China EDC | 3.62 | 3.63 | 3.48 | 3.26 | 3.2 | 3.12 | 2.8 | 2.41 | 2.34 | 2.07 | 1.92 | 1.79 | 1.73 | 1.66 |
| Central China LDP | 0.24 | 0.24 | 0.25 | 0.27 | 0.28 | 0.28 | 0.31 | 0.37 | 0.39 | 0.45 | 0.48 | 0.52 | 0.53 | 0.56 |
| Western China EC | 0.8 | 0.8 | 0.76 | 0.75 | 0.79 | 0.83 | 0.86 | 0.83 | 0.82 | 0.83 | 0.83 | 0.81 | 0.82 | 0.81 |
| Western China EDC | 3.84 | 3.82 | 3.85 | 3.68 | 3.49 | 3.15 | 2.79 | 2.58 | 2.54 | 2.28 | 2.1 | 2.03 | 1.88 | 1.89 |
| Western China LDP | 0.22 | 0.22 | 0.21 | 0.21 | 0.23 | 0.27 | 0.31 | 0.33 | 0.33 | 0.37 | 0.4 | 0.41 | 0.44 | 0.43 |
| Time | Moran’s I | p Values | Z Values | Time | Moran’s I | p Values | Z Values |
|---|---|---|---|---|---|---|---|
| 2007 | 0.296750 | 0.009 | 2.6919 | 2014 | 0.274120 | 0.011 | 2.9013 |
| 2008 | 0.303145 | 0.003 | 3.0308 | 2015 | 0.274059 | 0.008 | 2.8004 |
| 2009 | 0.253658 | 0.018 | 2.2928 | 2016 | 0.261229 | 0.021 | 2.2197 |
| 2010 | 0.254956 | 0.022 | 2.5713 | 2017 | 0.259345 | 0.010 | 2.2674 |
| 2011 | 0.285425 | 0.010 | 2.7891 | 2018 | 0.229661 | 0.021 | 2.3521 |
| 2012 | 0.309343 | 0.007 | 3.0251 | 2019 | 0.236845 | 0.011 | 2.4521 |
| 2013 | 0.305852 | 0.009 | 3.0167 | 2020 | 0.209347 | 0.014 | 2.2314 |
| Variables | Unfixed Effect | Spatial Fixed Effect | Time Fixed Effect | Double Fixation Effect |
|---|---|---|---|---|
| LnGDP | 0.024013 (0.759231) | 0.011397 (0.074382) | 0.492311 ** (1.898370) | 0.077638 (0.294184) |
| LnUR | 0.137228 ** (2.413623) | 0.167891 (0.963302) | 0.048231 ** (0.578302) | 0.003147 (0.016182) |
| LnEG | 0.948724 *** (54.330901) | 0.875313 *** (0.085213) | 1.508718 *** (5.982374) | 0.886412 *** (0.073591) |
| LnES | 0.153379 *** (5.213401) | 0.074432 (1.286675) | 0.147243 *** (4.716293) | 0.073417 (1.193884) |
| LnIS | 0.123602 ** (1.874413) | −0.079316 (−0.868634) | 0.078362 (1.313449) | 0.180752 ** (2.147083) |
| LnP | 0.023152 (1.236739) | 0.004823 (−0.50132) | 0.493361 ** (2.318647) | −0.304318 (−0.793216) |
| LnEI | −0.044208 * (−1.308731) | −0.136592 (−1.314572) | −0.647382 ** (−2.156182) | −0.069818 (−0.203787) |
| C | −0.581376 (−1.786231) | |||
| σ2 | 0.0312 | 0.0287 | 0.0432 | 0.0158 |
| R2 | 0.9513 | 0.7659 | 0.9348 | 0.2836 |
| Logl | 190.2847 | 253.1713 | 201.5346 | 268.1129 |
| LM text no Spatial lag | 6.40261 p = 0.008 | 1.0633 p = 0.283 | 11.5981 p = 0.000 | 1.1277 p = 0.084 |
| Robust LM text no spatial lag | 8.5913 p = 0.004 | 2.7212 p = 0.089 | 14.5370 p = 0.000 | 0.0762 p = 0.086 |
| LM text no spatial error | 0.0749 p = 0.763 | 0.0037 p = 0.061 | 1.8852 p = 0.183 | 1.0836 p = 0.284 |
| Robust LM text no spatial error | 0.2931 p = 0.439 | 1.8372 p = 0.068 | 6.0558 p = 0.015 | 0.0223 p = 0.871 |
| Test | Spatial Fixed Effect | Time Fixed Effect | Double Fixation Effect |
|---|---|---|---|
| Wald test spatial lag | 56.8102 (0.00000) | 66.3319 (0.52364) | 34.5718 (0.0149) |
| LR test spatial lag | 77.3329 (0.00000) | 64.8421 (0.368819) | 37.5821 (0.0449) |
| Wald test spatial error | 25.6385 (0.4269) | 70.0872 (0.00000) | 42.3813 (0.00169) |
| LR test spatial error | 44.8210 (0.26583) | 31.4798 (0.00103) | 38.6847 (0.00228) |
| Variables | Unfixed Effect | Spatial Fixed Effect | Time Fixed Effect | Double Fixation Effect |
|---|---|---|---|---|
| LnGDP | 0.001823 (0.045732) | 0.007151 (0.045452) | 0.519121 *** (1.783632) | −0.070503 (−0.237428) |
| LnUR | 0.139869 * (2.58153) | 0.152173 (0.957813) | 0.018362 (0.212584) | −0.0163461 (0.124423) |
| LnEG | 0.958717 * (58.2335468) | 0.914841 * (6.125914) | 1.521312 ** (0.198114) | 0.884682 * (2.979816) |
| LnES | 0.133419 * (3.928346) | 0.082712 (1.421851) | 0.113829 ** (3.302852) | 0.081183 (1.247853) |
| LnIS | 0.129421 ** (2.245718) | −0.074281 (−0.721971) | 0.117218 *** (1.723541) | −0.258321 ** (−2.175321) |
| LnP | 0.011437 (1.324815) | 0.238264 (−1.473587) | 0.553921 ** (2.263420) | −0.242594 (−1.125251) |
| LnEI | −0.035383 (−0.998462) | −0.072835 (−1.245331) | −0.591623 ** (−2.385211) | −0.044353 (−0.181453) |
| W × dep.var. | 0.064854 * (2.662913) | −0.070361 (−1.269343) | 0.080973 (4.457573) | −0.097987 (−1.543103) |
| σ2 | 0.0235 | 0.0182 | 0.0213 | 0.017 |
| R2 | 0.9655 | 0.9539 | 0.9632 | 0.9841 |
| Logl | 213.4015 | 260.2193 | 239.1145 | 274.3019 |
| Variables | Direct Effect | T Values | p Values | Indirect Effect | T Values | p Values | Total Effect | T Values | p Values |
|---|---|---|---|---|---|---|---|---|---|
| LnGDP | 0.4831 | 1.9932 | 0.0221 | 0.0416 | 1.8392 | 0.0847 | 0.5247 | 1.8336 | 0.0470 |
| LnUR | 0.0311 | 0.2579 | 0.7112 | 0.0021 | 0.3832 | 0.9159 | 0.0323 | 0.2761 | 0.7432 |
| LnEG | 1.4132 | 5.1343 | 0.0019 | 0.1408 | 4.2803 | 0.0024 | 1.5540 | 5.7423 | 0.0086 |
| LnES | 0.1253 | 4.1784 | 0.0031 | 0.0072 | 3.7902 | 0.0032 | 0.1325 | 4.1238 | 0.0014 |
| LnIS | 0.1048 | 1.6832 | 0.0715 | 0.0337 | 1.5022 | 0.1085 | 0.1385 | 1.6962 | 0.0958 |
| LnP | 0.4319 | 2.2479 | 0.0338 | 0.0878 | 1.8382 | 0.0597 | 0.5193 | 2.2403 | 0.0287 |
| LnEI | −0.5970 | −2.2413 | 0.0273 | −0.0376 | −2.1874 | 0.0519 | −0.6346 | −2.2374 | 0.0316 |
| Fixed Effect | Random Effect | |||
|---|---|---|---|---|
| m(x) | β(x) | m(x) | β(x) | |
| 1 | 2.8307 | 0.2539 | 2.7315 | 0.2553 |
| 2 | 3.9195 | 0.0615 | 3.7184 | 0.0601 |
| 3 | 4.7832 | 0.2582 | 4.5341 | 0.2483 |
| 4 | 5.9188 | 0.1832 | 5.9233 | 0.1834 |
| 5 | 5.2413 | 0.1901 | 5.2636 | 0.1853 |
| 6 | 7.9013 | −0.0021 | 7.9348 | −0.0026 |
| 7 | 12.1992 | −0.8431 | 12.1307 | −0.7838 |
| 8 | 9.3959 | −0.0894 | 9.2945 | −0.0868 |
| 9 | 5.9174 | 0.4913 | 5.8141 | 0.4746 |
| 10 | 10.1431 | 0.0512 | 9.9447 | 0.0521 |
| 11 | 5.8491 | 0.6993 | 6.1592 | 0.6993 |
| 12 | 14.4643 | −0.4310 | 15.2142 | −0.3327 |
| 13 | 3.1823 | 0.9387 | 3.2701 | 0.9841 |
| 14 | 3.9971 | 0.9264 | 2.9148 | 0.8215 |
| 15 | 1.8128 | 0.8919 | 1.7120 | 0.9314 |
| 16 | 1.9235 | 0.7593 | 1.8591 | 0.7849 |
| 17 | 4.3475 | 0.6974 | 4.2547 | 0.6937 |
| Time Periods | Variables | East Region | Central China | West Region |
|---|---|---|---|---|
| 2007–2011 | CI | 1448.37 | −154.14 | 5641.70 |
| ES | −7224.01 | −2481.95 | 328.96 | |
| EI | −24,647.70 | −12,012.00 | −14,599.90 | |
| S | 6809.12 | 2219.22 | 1673.08 | |
| L | 141,620.00 | 69,504.30 | 36,196.00 | |
| 2012–2016 | CI | 3320.79 | 3564.05 | −239.43 |
| ES | −1412.46 | 2233.45 | −2300.97 | |
| EI | −99,419.30 | −96,461.80 | −45,086.70 | |
| S | −7352.16 | 8922.25 | 5039.26 | |
| L | 201,128.00 | 144,540.00 | 78,401.40 | |
| 2017–2020 | CI | 59,672.10 | 21,511.60 | −46,599.80 |
| ES | −9471.15 | 16.72 | −6653.94 | |
| EI | −89,990.40 | −52,319.60 | 40,284.10 | |
| S | −17,111.10 | −10,140.30 | −5213.56 | |
| L | 98,628.30 | 59,887.20 | 49,173.80 |
| Regions | Variables | Correlation Matrix | VIF | F | R2 | Characteristic Root | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | Lnps | Lnpc | Lnph | Lnpe | ||||||
| East region | C | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 110.60 | 0.977 | 4.971 | |
| Lnps | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 | 295.367 | 0.019 | |||
| Lnpc | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 4.395 | 0.004 | |||
| Lnph | 0.01 | 0.00 | 0.39 | 0.06 | 0.05 | 118.023 | 0.000 | |||
| Lnpe | 0.97 | 1.00 | 0.34 | 0.92 | 0.94 | 75.192 | 0.002 | |||
| Central China | C | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 138.41 | 0.954 | 4.591 | |
| Lnps | 0.00 | 0.00 | 0.03 | 0.00 | 0.14 | 7.781 | 0.019 | |||
| Lnpc | 0.00 | 0.00 | 0.17 | 0.00 | 0.71 | 6.884 | 0.003 | |||
| Lnph | 0.04 | 0.01 | 0.78 | 0.96 | 0.08 | 1.913 | 0.000 | |||
| Lnpe | 0.96 | 0.99 | 0.14 | 0.05 | 0.09 | 1.281 | 0.000 | |||
| West region | C | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 202.148 | 0.981 | 4.665 | |
| Lnps | 0.00 | 0.00 | 0.04 | 0.00 | 0.16 | 1.522 | 0.025 | |||
| Lnpc | 0.00 | 0.00 | 0.18 | 0.00 | 0.75 | 8.547 | 0.007 | |||
| Lnph | 0.05 | 0.01 | 0.74 | 0.85 | 0.00 | 8.923 | 0.000 | |||
| Lnpe | 0.95 | 0.99 | 0.05 | 0.17 | 0.12 | 1.904 | 0.000 | |||
| Eastern China | Central China | Western China | Nationwide | ||
|---|---|---|---|---|---|
| β | coefficient | −1.0656 | −1.1221 | −1.0177 | −1.0767 |
| t | −11.59 | −9.72 | −7.68 | −17.17 | |
| Sig. | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Constant | coefficient | 5.3277 | 5.3461 | 4.6593 | 5.1864 |
| t | 11.57 | 9.5900 | 7.68 | 17.08 | |
| Sig. | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| R2 | 0.6808 | 0.6117 | 0.6036 | 0.6761 | |
| F | coefficient | 134.4 | 94.53 | 58.92 | 294.91 |
| p | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Regions | Variables | B var | T | Sig. |
|---|---|---|---|---|
| Eastern China | C | −25.7251 | −8.1974 | 0.0000 |
| Lnps | 2.2318 | 13.6182 | 0.0000 | |
| Lnpc | 5.2381 | 1.9313 | 0.0703 | |
| Lnph | 1.5293 | 9.4852 | 0.0000 | |
| Lnpe | −0.2434 | −3.6803 | 0.0584 | |
| Central China | C | −9.8639 | −7.4595 | 0.0215 |
| Lnps | 0.2694 | 0.1176 | 0.4738 | |
| Lnpc | 12.3349 | 4.3325 | 0.0000 | |
| Lnph | 2.1648 | 4.8215 | 0.0000 | |
| Lnpe | −0.5384 | −4.7633 | 0.0000 | |
| Western China | C | −17.3843 | −6.8419 | 0.0283 |
| Lnps | 0.9812 | 0.7975 | 0.7346 | |
| Lnpc | 10.0674 | 7.3923 | 0.0021 | |
| Lnph | 2.2114 | 8.9563 | 0.0000 | |
| Lnpe | −0. 4729 | −9.8204 | 0.0000 |
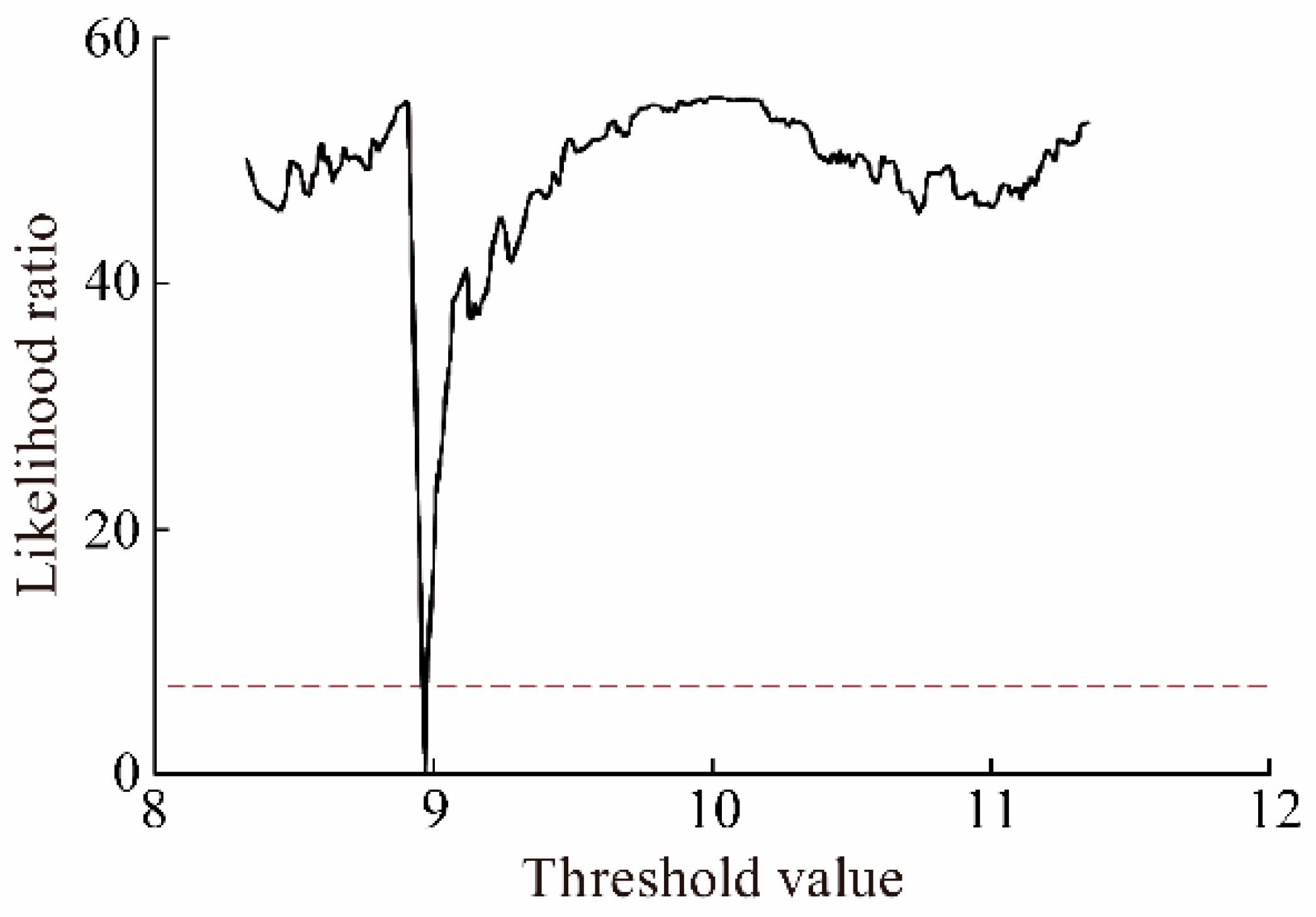
| Variables | Linear Regression Individual Fixed Effect | Threshold Regression | |
|---|---|---|---|
| GDP | TI | ||
| GDP | 0.8779 *** | \ | 0.8417 *** |
| −21.83 | −21.62 | ||
| ES | 0.0434 * | 0.0394 * | 0.0639 * |
| −0.71 | −0.52 | −1.13 | |
| IS | −0.089 | −0.0921 | 0.0051 |
| (−0.19) | (−0.86) | −0.47 | |
| OP | 0.0034 | 0.0139 | 0.004 |
| −0.34 | −0.88 | −0.22 | |
| TI | −0.0162 ** | −0.0153 * | \ |
| (−0.44) | (−0.47) | ||
| 0 (EI) | −0.5713 *** | −0.6487 *** | −0.4781 *** |
| (−7.53) | (−8.42) | (−5.71) | |
| 1 (EI) | −0.7481 ** | −0.6234 * | |
| (−9.15) | (−8.62) | ||
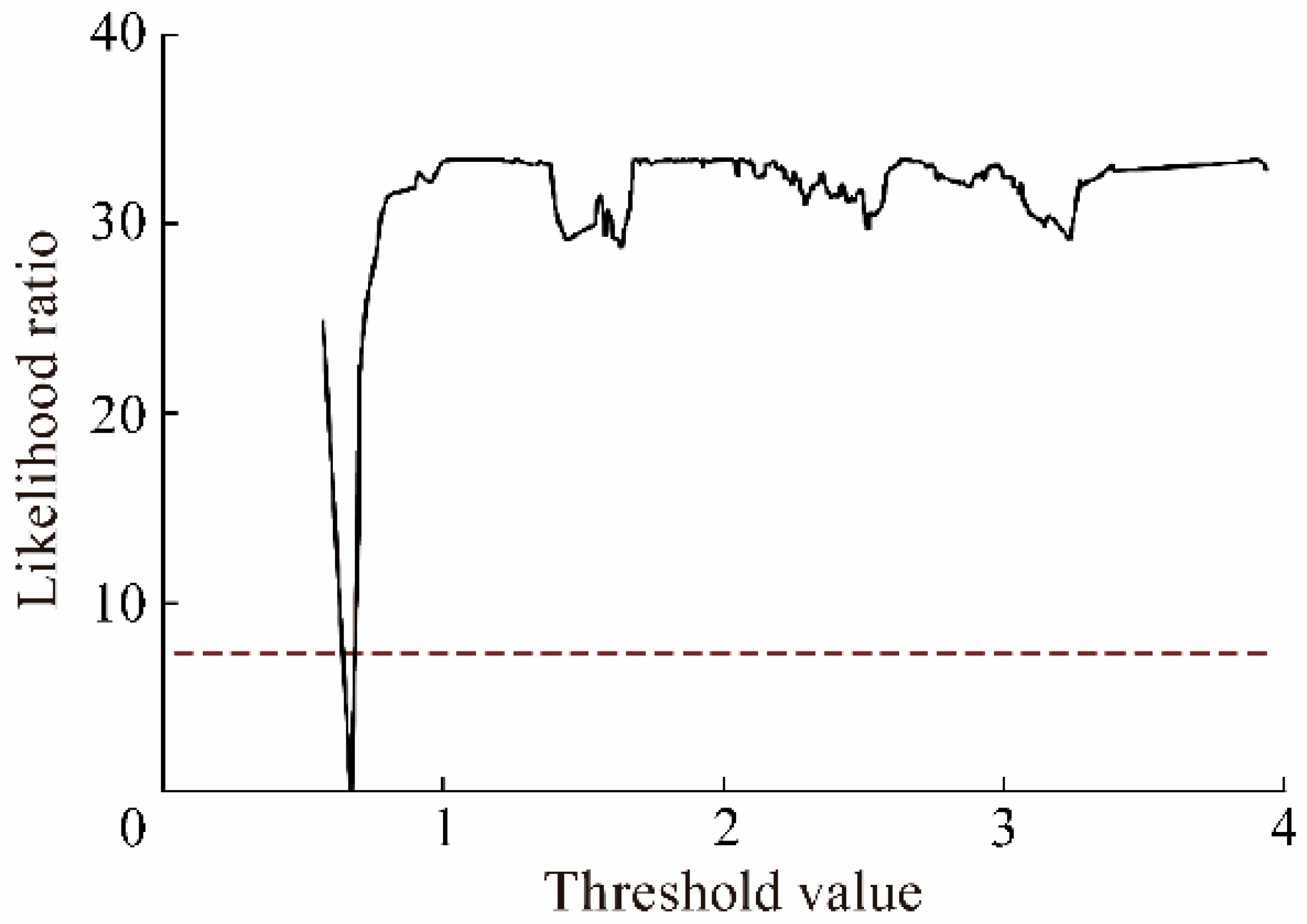
| TH-1 | 8.97 | 0.672 | |
| Lower | 8.955 | 0.574 | |
| Upper | 8.98 | 0.699 | |
| P | 0.0221 | 0.0607 | |
| F | −26.49 | −28.41 | |
| Time | High Location | Low Location |
|---|---|---|
| 2007 | Beijing, Shanghai | Other provinces |
| 2012 | Beijing, Shanghai, Tianjin | Other provinces |
| 2017 | Beijing, Shanghai, Tianjin, Guangdong, Jiangsu, Shandong, Zhejiang | Other provinces |
| 2020 | Anhui, Beijing, Guangdong, Hubei, Jiangsu, Shandong, Shanghai, Tianjin, Zhejiang | Other provinces |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Liang, Z.; Bai, X.; Lv, M.; Zhang, A. The Analysis of Carbon Emission’s Characteristics and Dynamic Evolution Based on the Strategy of Unbalanced Regional Economic Development in China. Sustainability 2022, 14, 8417. https://doi.org/10.3390/su14148417
Guo Q, Liang Z, Bai X, Lv M, Zhang A. The Analysis of Carbon Emission’s Characteristics and Dynamic Evolution Based on the Strategy of Unbalanced Regional Economic Development in China. Sustainability. 2022; 14(14):8417. https://doi.org/10.3390/su14148417
Chicago/Turabian StyleGuo, Quan, Zijing Liang, Xiang Bai, Mengnan Lv, and Anying Zhang. 2022. "The Analysis of Carbon Emission’s Characteristics and Dynamic Evolution Based on the Strategy of Unbalanced Regional Economic Development in China" Sustainability 14, no. 14: 8417. https://doi.org/10.3390/su14148417
APA StyleGuo, Q., Liang, Z., Bai, X., Lv, M., & Zhang, A. (2022). The Analysis of Carbon Emission’s Characteristics and Dynamic Evolution Based on the Strategy of Unbalanced Regional Economic Development in China. Sustainability, 14(14), 8417. https://doi.org/10.3390/su14148417




