A Comparison of Simple Closed-Form Solutions for the EOQ Problem for Exponentially Deteriorating Items
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
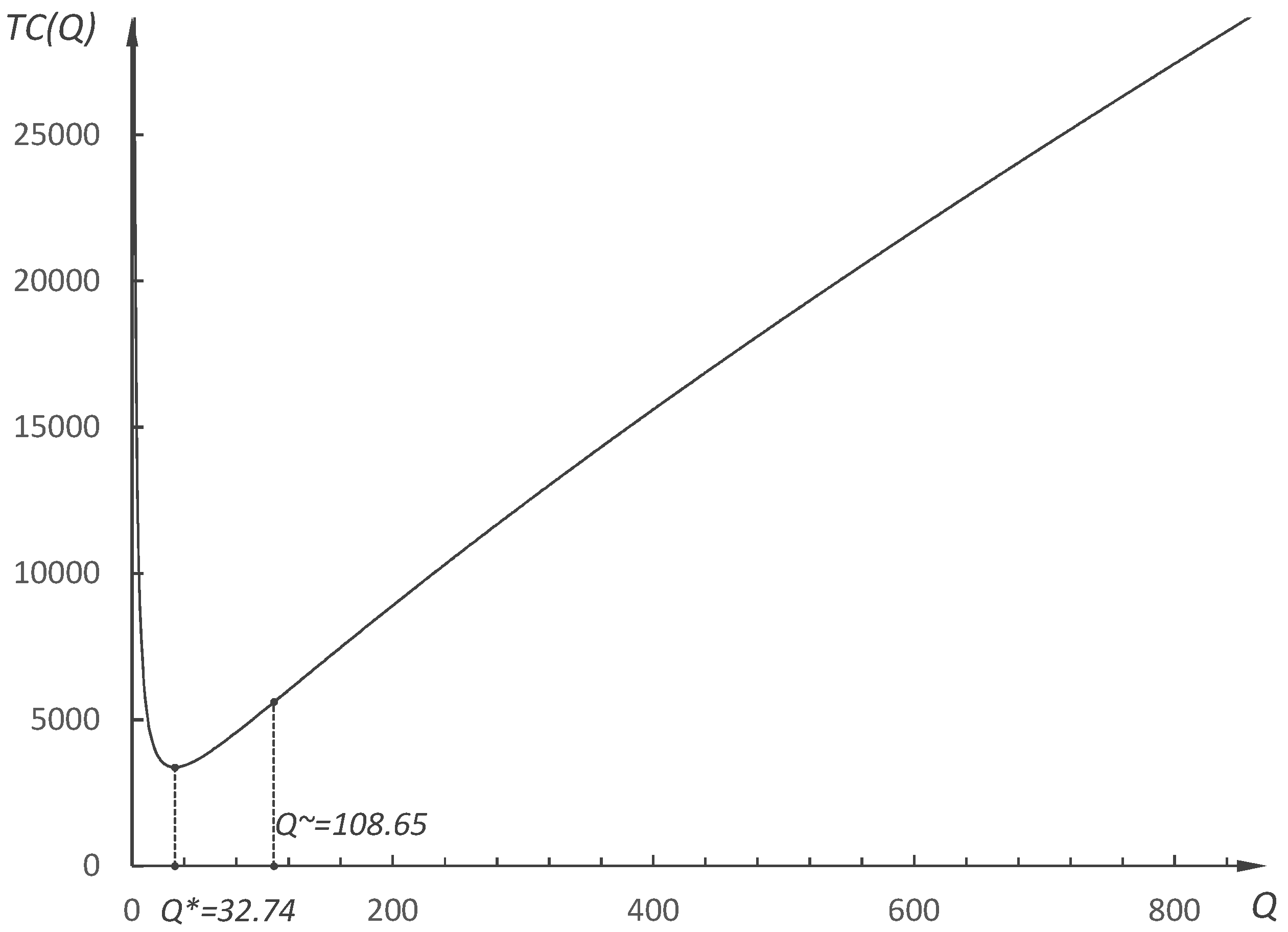
4. The Basic Model
- if
- ○
- and is monotone increasing and approaches from below.
- If
- ○
- for all ;
- ○
- there is an asymptote at ;
- ○
- ;
- ○
- ;
- ○
- is monotone decreasing for and approaches from above.
- If
- ○
- the asymptote is at ;
- ○
- ;
- ○
- (which is of no interest to us);
- ○
- is monotone decreasing.
- If , is monotone decreasing and approaches from above.
- If , is monotone increasing and approaches from below.
- If , for all x, i.e., is constant.
4.1. Existing Closed-Form Solutions
4.2. New Closed-Form Solutions
4.2.1. Closed-Form Solution 1
4.2.2. Closed-Form Solution 2
4.2.3. Closed-Form Solution 3
4.2.4. Closed-Form Solution 4
4.2.5. Closed-Form Solution 5
4.2.6. Closed-Form Solution 6
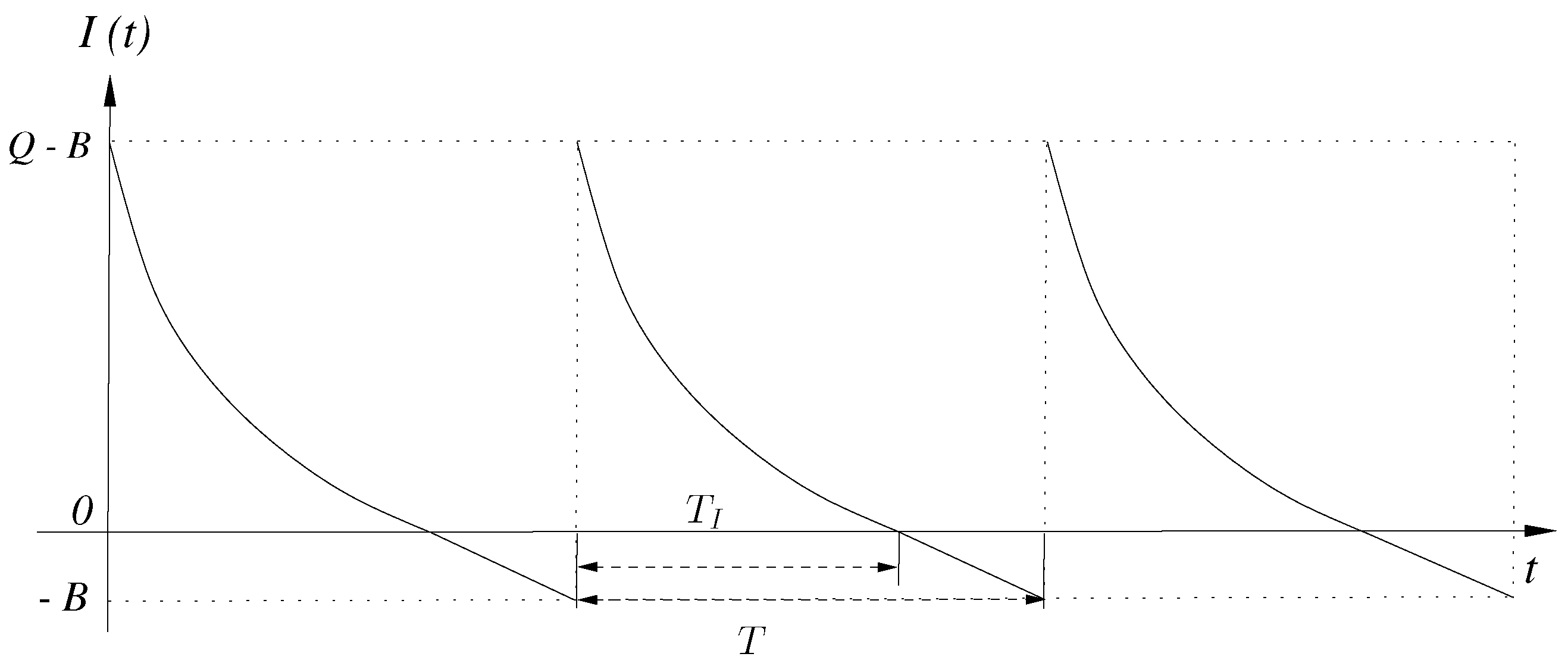
5. The Planned Backorders Model
5.1. Existing Closed-Form Solutions
5.2. New Closed-Form Solutions
5.2.1. Closed-Form Solution 1
The Optimal Inventory Interval ()
The Optimal Order Interval (T)
5.2.2. Closed-Form Solution 2
The Optimal Backorder Quantity (B)
The Optimal Order Quantity (Q)
5.2.3. Closed-Form Solution 3
5.2.4. Closed-Form Solution 4
6. Results
6.1. The Basic Model
| GRG: | The exact optimal solution obtained by the GRG algorithm |
| E1: | The closed-form solution of Ghare and Schrader [9] |
| E2: | The closed-form solution of Chung and Ting [21] |
| E3: | The closed-form solution of Widyadana et al. [36] |
| Ni: | The proposed closed-form solution i in this paper where i = 1, 2, 3, 4, 5, 6 |
6.2. The Planned Backorders Model
| GRG: | The exact optimal solution obtained by the GRG algorithm |
| E3: | The closed-form solution of Widyadana et al. [36] |
| Ni: | The proposed closed-form solution i in this paper where i = 1, 2, 3, 4 |
7. Conclusions
8. Limitations and Future Research
Funding
Conflicts of Interest
References
- Kaur, J.; Rani, G.; Yogalakshmi, K. Chapter 16—Problems and Issues of Food Waste-Based Biorefineries. In Food Waste to Valuable Resources; Banu, J.R., Kumar, G., Gunasekaran, M., Kavitha, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 343–357. [Google Scholar]
- Huang, C.H.; Liu, S.M.; Hsu, N.Y. Understanding Global Food Surplus and Food Waste to Tackle Economic and Environmental Sustainability. Sustainability 2020, 12, 2892. [Google Scholar] [CrossRef] [Green Version]
- Zamri, G.B.; Azizal, N.K.A.; Nakamura, S.; Okada, K.; Nordin, N.H.; Othman, N.; MD Akhir, F.N.; Sobian, A.; Kaida, N.; Hara, H. Delivery, impact and approach of household food waste reduction campaigns. J. Clean. Prod. 2020, 246, 118969. [Google Scholar] [CrossRef]
- Moraes, N.V.; Lermen, F.H.; Echeveste, M.E.S. A systematic literature review on food waste/loss prevention and minimization methods. J. Environ. Manag. 2021, 286, 112268. [Google Scholar] [CrossRef]
- Gustavsson, J.; Cederberg, C.; Sonesson, U.; van Otterdijk, R.; Meybeck, A. Global Food Losses and Food Waste—Extent, Causes and Prevention. In SAVE FOOD: An Initiative on Food Loss and Waste Reduction; Interpack2011, FAO, International Congress: Düsseldorf, Germany, 2011. [Google Scholar]
- Silver, E.A.; Pyke, D.F.; Peterson, R. Inventory Management and Production Planning and Scheduling, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Erlenkotter, D. Ford Whitman Harris and the Economic Order Quantity Model. Oper. Res. 1990, 38, 937–946. [Google Scholar] [CrossRef] [Green Version]
- Harris, F. How Many Parts to Make at Once. Fact. Mag. Manag. 1913, 10, 135–136, 152. [Google Scholar] [CrossRef]
- Ghare, P.M.; Schrader, G.F. A Model for an Exponentially Decaying Inventory. J. Ind. Eng. 1963, 14, 238–243. [Google Scholar]
- Çalışkan, C. A derivation of the optimal solution for exponentially deteriorating items without derivatives. Comput. Ind. Eng. 2020, 148, 106675. [Google Scholar] [CrossRef]
- Nahmias, S. Perishable Inventory Theory: A Review. Oper. Res. 1982, 30, 680–708. [Google Scholar] [CrossRef]
- Raafat, F. Survey of Literature on Continuously Deteriorating Inventory Models. J. Oper. Res. Soc. 1991, 42, 27–37. [Google Scholar] [CrossRef]
- Goyal, S.; Giri, B. Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 2001, 134, 1–16. [Google Scholar] [CrossRef]
- Li, R.; Lan, H.; Mawhinney, J.R. A Review on Deteriorating Inventory Study. J. Serv. Sci. Manag. 2010, 3, 117–129. [Google Scholar] [CrossRef] [Green Version]
- Bakker, M.; Riezebos, J.; Teunter, R.H. Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 2012, 221, 275–284. [Google Scholar] [CrossRef]
- Elsayed, E.; Teresi, C. Analysis of inventory systems with deteriorating items. Int. J. Prod. Res. 1983, 21, 449–460. [Google Scholar] [CrossRef]
- Schmidt, C.P.; Nahmias, S. (S-1,S) Policies for Perishable Inventory. Manag. Sci. 1985, 31, 719–728. [Google Scholar] [CrossRef]
- Dave, U.; Patel, L.K. (T, Si) Policy Inventory Model for Deteriorating Items with Time Proportional Demand. J. Oper. Res. Soc. 1981, 32, 137–142. [Google Scholar] [CrossRef]
- Bahari-Kashani, H. Replenishment Schedule for Deteriorating Items with Time-Proportional Demand. J. Oper. Res. Soc. 1989, 40, 75–81. [Google Scholar] [CrossRef]
- Chung, K.J.; Ting, P.S. A Heuristic for Replenishment of Deteriorating Items with a Linear Trend in Demand. J. Oper. Res. Soc. 1993, 44, 1235–1241. [Google Scholar] [CrossRef]
- Chung, K.J.; Ting, P.S. On replenishment schedule for deteriorating items with time-proportional demand. Prod. Plan. Control 1994, 5, 392–396. [Google Scholar] [CrossRef]
- Kim, D. A heuristic for replenishment of deteriorating items with a linear trend in demand. Int. J. Prod. Econ. 1995, 39, 265–270. [Google Scholar] [CrossRef]
- Çalışkan, C. A note about ‘on replenishment schedule for deteriorating items with time-proportional demand’. Prod. Plan. Control 2021, 32, 1158–1161. [Google Scholar] [CrossRef]
- Çalışkan, C. EOQ Model for Exponentially Deteriorating Items with Planned Backorders without Differential Calculus. Am. J. Math. Manag. Sci. 2022, 41, 223–243. [Google Scholar] [CrossRef]
- Sachan, R.S. On (T, Si) Policy Inventory Model for Deteriorating Items with Time Proportional Demand. J. Oper. Res. Soc. 1984, 35, 1013–1019. [Google Scholar] [CrossRef]
- Wee, H.M. Economic production lot size model for deteriorating items with partial backordering. Comput. Ind. Eng. 1993, 24, 449–458. [Google Scholar] [CrossRef]
- Wee, H.M. A deterministic lot-size inventory model for deteriorating items with shortages and a declining market. Comput. Oper. Res. 1995, 22, 345–356. [Google Scholar]
- Hariga, M.; Benkherouf, L. Optimal and heuristic inventory replenishment models for deteriorating items with exponential time-varying demand. Eur. J. Oper. Res. 1994, 79, 123–137. [Google Scholar] [CrossRef]
- Benkherouf, L. On an inventory model with deteriorating items and decreasing time-varying demand and shortages. Eur. J. Oper. Res. 1995, 86, 293–299. [Google Scholar] [CrossRef]
- Benkherouf, L.; Mahmoud, M.G. On an Inventory Model for Deteriorating Items with Increasing Time-varying Demand and Shortages. J. Oper. Res. Soc. 1996, 47, 188–200. [Google Scholar] [CrossRef]
- Balkhi, Z.T.; Benkherouf, L. A production lot size inventory model for deteriorating items and arbitrary production and demand rates. Eur. J. Oper. Res. 1996, 92, 302–309. [Google Scholar] [CrossRef]
- Giri, B.; Jalan, A.; Chaudhuri, K. Economic Order Quantity model with Weibull deterioration distribution, shortage and ramp-type demand. Int. J. Syst. Sci. 2003, 34, 237–243. [Google Scholar] [CrossRef]
- Chang, H.J.; Dye, C.Y. An EOQ model for deteriorating items with time varying demand and partial backlogging. J. Oper. Res. Soc. 1999, 50, 1176–1182. [Google Scholar] [CrossRef]
- Wang, S.P. A note on Chang H-J and Dye C-Y (1999). An EOQ model for deteriorating items with time varying demand and partial backlogging. J. Oper. Res. Soc. 2001, 52, 597–598. [Google Scholar] [CrossRef]
- Goyal, S.K.; Giri, B.C. A comment on Chang and Dye (1999): EOQ model for deteriorating items with time-varying demand and partial backlogging. J. Oper. Res. Soc. 2001, 52, 238–239. [Google Scholar] [CrossRef]
- Widyadana, G.A.; Cárdenas-Barrón, L.E.; Wee, H.M. Economic order quantity model for deteriorating items with planned backorder level. Math. Comput. Model. 2011, 54, 1569–1575. [Google Scholar] [CrossRef]
- Çalışkan, C. A Simple Derivation of the Optimal Solution for the EOQ Model for Deteriorating Items with Planned Backorders. Appl. Math. Model. 2021, 89, 1373–1381. [Google Scholar] [CrossRef]
- Haijema, R. A new class of stock-level dependent ordering policies for perishables with a short maximum shelf life. Int. J. Prod. Econ. 2013, 143, 434–439. [Google Scholar] [CrossRef]
- Mishra, V.K.; Singh, L.S.; Kumar, R. An inventory model for deteriorating items with time-dependent demand and time-varying holding cost under partial backlogging. J. Ind. Eng. Int. 2013, 9, 4. [Google Scholar] [CrossRef] [Green Version]
- Mahajan, S.; Diatha, K. Minimizing the Discounted Average Cost Under Continuous Compounding in the EOQ Models with a Regular Product and a Perishable Product. Am. J. Oper. Manag. Inf. Syst. 2018, 3, 52–60. [Google Scholar] [CrossRef] [Green Version]
- Çalışkan, C. An Inventory Ordering Model for Deteriorating Items with Compounding and Backordering. Symmetry 2021, 13, 1078. [Google Scholar] [CrossRef]
- Shelbey, S. CRC Standard Mathematical Tables, 23rd ed.; CRC Press: Boca Raton, FL, USA, 1975. [Google Scholar]
- Zucker, I. The cubic equation—A new look at the irreducible case. Math. Gaz. 2008, 92, 264–268. [Google Scholar] [CrossRef]
- Nickalls, R. Viète, Descartes and the cubic equation. Math. Gaz. 2006, 90, 203–208. [Google Scholar] [CrossRef] [Green Version]
- Zipkin, P.H. Foundations of Inventory Management, 1st ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
| D | the demand of the item in number of units per unit time |
| S | the cost of ordering per order |
| c | the unit price of the item |
| the rate of deterioration for one unit of the item per unit time | |
| h | the inventory holding cost per unit of the item per unit time |
| b | the cost of backordering per unit per unit time |
| T | the length of an inventory ordering cycle (order interval) |
| Q | the order quantity |
| the length of time the demand is fulfilled from the inventory | |
| in a cycle (fulfillment interval) | |
| B | the number of units to backorder in each ordering cycle |
| t | the elapsed time since the beginning of an ordering cycle |
| the number of units in the inventory at time t |
| Optimal Order Quantity | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Existing Solutions | New Solutions | |||||||||||
| GRG | E1 | E2 | E3 | N1 | N2 | N3 | N4 | N5 | N6 | ||||
| 500 | 100 | 3.5 | 0.1 | 149.81 | 149.57 | 149.06 | 169.05 | 151.32 | 149.07 | 146.87 | 149.81 | 150.18 | 150.19 |
| 500 | 100 | 3.5 | 1.25 | 81.62 | 85.40 | 78.82 | 169.24 | 87.41 | 79.06 | 71.63 | 81.66 | 82.96 | 83.10 |
| 500 | 100 | 3.5 | 2.5 | 62.09 | 67.53 | 58.86 | 169.45 | 68.94 | 59.23 | 51.11 | 62.17 | 63.62 | 63.85 |
| 500 | 100 | 3.5 | 3.75 | 52.35 | 58.67 | 48.92 | 169.66 | 59.77 | 49.39 | 41.08 | 52.44 | 53.96 | 54.27 |
| 500 | 100 | 3.5 | 5 | 46.25 | 53.17 | 42.69 | 169.87 | 54.09 | 43.23 | 34.89 | 46.36 | 47.91 | 48.28 |
| 500 | 10 | 3.5 | 1 | 27.46 | 27.77 | 27.21 | 53.51 | 27.97 | 27.22 | 26.49 | 27.46 | 27.59 | 27.59 |
| 500 | 60 | 3.5 | 1 | 68.13 | 70.03 | 66.57 | 131.06 | 71.32 | 66.67 | 62.37 | 68.15 | 68.89 | 68.94 |
| 500 | 110 | 3.5 | 1 | 92.94 | 96.49 | 90.04 | 177.46 | 98.93 | 90.27 | 82.49 | 92.99 | 94.34 | 94.47 |
| 500 | 160 | 3.5 | 1 | 112.75 | 117.97 | 108.48 | 214.02 | 121.63 | 108.87 | 97.66 | 112.82 | 114.79 | 115.02 |
| 500 | 210 | 3.5 | 1 | 129.81 | 136.74 | 124.15 | 245.19 | 141.66 | 124.72 | 110.13 | 129.92 | 132.50 | 132.84 |
| 1000 | 50 | 3.5 | 5 | 44.76 | 47.89 | 43.08 | 169.45 | 48.26 | 43.23 | 38.81 | 44.79 | 45.57 | 45.66 |
| 2000 | 50 | 3.5 | 5 | 62.68 | 65.71 | 61.03 | 239.34 | 66.06 | 61.14 | 56.65 | 62.70 | 63.48 | 63.54 |
| 4500 | 50 | 3.5 | 5 | 93.26 | 96.21 | 91.64 | 358.77 | 96.55 | 91.71 | 87.16 | 93.27 | 94.05 | 94.09 |
| 9000 | 50 | 3.5 | 5 | 131.25 | 134.16 | 129.65 | 507.23 | 134.49 | 129.70 | 125.11 | 131.26 | 132.04 | 132.07 |
| 100,000 | 50 | 3.5 | 5 | 433.89 | 436.73 | 432.32 | 1690.35 | 437.04 | 432.34 | 427.69 | 433.90 | 434.67 | 434.68 |
| 10,000 | 50 | 0.3 | 1 | 313.20 | 316.35 | 311.56 | 1825.83 | 316.49 | 311.59 | 306.77 | 313.21 | 314.02 | 314.03 |
| 10,000 | 50 | 0.8 | 1 | 305.83 | 308.61 | 304.27 | 1118.09 | 308.97 | 304.29 | 299.70 | 305.83 | 306.61 | 306.62 |
| 10,000 | 50 | 2.5 | 1 | 284.17 | 286.06 | 282.82 | 632.49 | 286.88 | 282.84 | 278.87 | 284.18 | 284.84 | 284.85 |
| 10,000 | 50 | 5 | 1 | 259.31 | 260.43 | 258.18 | 447.24 | 261.56 | 258.20 | 254.89 | 259.31 | 259.87 | 259.87 |
| 10,000 | 50 | 7.5 | 1 | 240.00 | 240.68 | 239.03 | 365.17 | 241.93 | 239.05 | 236.21 | 240.00 | 240.47 | 240.48 |
| % Difference ofvs. GRG | |||||||||||||
| Parameters | Existing Solutions | New Solutions | |||||||||||
| GRG | E1 | E2 | E3 | N1 | N2 | N3 | N4 | N5 | N6 | ||||
| 500 | 100 | 3.5 | 0.1 | 0.00 | −0.16 | −0.50 | 12.84 | 1.01 | −0.49 | −1.96 | 0.00 | 0.25 | 0.25 |
| 500 | 100 | 3.5 | 1.25 | 0.00 | 4.63 | −3.43 | 107.35 | 7.09 | −3.14 | −12.24 | 0.05 | 1.64 | 1.81 |
| 500 | 100 | 3.5 | 2.5 | 0.00 | 8.76 | −5.20 | 172.91 | 11.03 | −4.61 | −17.68 | 0.13 | 2.46 | 2.83 |
| 500 | 100 | 3.5 | 3.75 | 0.00 | 12.07 | −6.55 | 224.09 | 14.17 | −5.65 | −21.53 | 0.17 | 3.08 | 3.67 |
| 500 | 100 | 3.5 | 5 | 0.00 | 14.96 | −7.70 | 267.29 | 16.95 | −6.53 | −24.56 | 0.24 | 3.59 | 4.39 |
| 500 | 10 | 3.5 | 1 | 0.00 | 1.13 | −0.91 | 94.87 | 1.86 | −0.87 | −3.53 | 0.00 | 0.47 | 0.47 |
| 500 | 60 | 3.5 | 1 | 0.00 | 2.79 | −2.29 | 92.37 | 4.68 | −2.14 | −8.45 | 0.03 | 1.12 | 1.19 |
| 500 | 110 | 3.5 | 1 | 0.00 | 3.82 | −3.12 | 90.94 | 6.45 | −2.87 | −11.24 | 0.05 | 1.51 | 1.65 |
| 500 | 160 | 3.5 | 1 | 0.00 | 4.63 | −3.79 | 89.82 | 7.88 | −3.44 | −13.38 | 0.06 | 1.81 | 2.01 |
| 500 | 210 | 3.5 | 1 | 0.00 | 5.34 | −4.36 | 88.88 | 9.13 | −3.92 | −15.16 | 0.08 | 2.07 | 2.33 |
| 1000 | 50 | 3.5 | 5 | 0.00 | 6.99 | −3.75 | 278.57 | 7.82 | −3.42 | −-13.29 | 0.07 | 1.81 | 2.01 |
| 2000 | 50 | 3.5 | 5 | 0.00 | 4.83 | −2.63 | 281.84 | 5.39 | −2.46 | −9.62 | 0.03 | 1.28 | 1.37 |
| 4500 | 50 | 3.5 | 5 | 0.00 | 3.16 | −1.74 | 284.70 | 3.53 | −1.66 | −6.54 | 0.01 | 0.85 | 0.89 |
| 9000 | 50 | 3.5 | 5 | 0.00 | 2.22 | −1.22 | 286.46 | 2.47 | −1.18 | −4.68 | 0.01 | 0.60 | 0.62 |
| 100,000 | 50 | 3.5 | 5 | 0.00 | 0.65 | −0.36 | 289.58 | 0.73 | −0.36 | −1.43 | 0.00 | 0.18 | 0.18 |
| 10,000 | 50 | 0.3 | 1 | 0.00 | 1.01 | −0.52 | 482.96 | 1.05 | −0.51 | −2.05 | 0.00 | 0.26 | 0.27 |
| 10,000 | 50 | 0.8 | 1 | 0.00 | 0.91 | −0.51 | 265.59 | 1.03 | −0.50 | −2.00 | 0.00 | 0.26 | 0.26 |
| 10,000 | 50 | 2.5 | 1 | 0.00 | 0.67 | −0.48 | 122.57 | 0.95 | −0.47 | −1.87 | 0.00 | 0.24 | 0.24 |
| 10,000 | 50 | 5 | 1 | 0.00 | 0.43 | −0.44 | 72.47 | 0.87 | −0.43 | −1.70 | 0.00 | 0.22 | 0.22 |
| 10,000 | 50 | 7.5 | 1 | 0.00 | 0.28 | −0.40 | 52.15 | 0.80 | −0.40 | −1.58 | 0.00 | 0.20 | 0.20 |
| Optimal Total Cost or | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Existing Solutions | New Solutions | |||||||||||
| GRG | E1 | E2 | E3 | N1 | N2 | N3 | N4 | N5 | N6 | ||||
| 500 | 100 | 3.5 | 0.1 | 674.15 | 674.15 | 674.15 | 679.00 | 674.18 | 674.15 | 674.28 | 674.15 | 674.15 | 674.15 |
| 500 | 100 | 3.5 | 1.25 | 1305.93 | 1307.14 | 1306.65 | 1628.75 | 1308.72 | 1306.53 | 1316.13 | 1305.93 | 1306.08 | 1306.12 |
| 500 | 100 | 3.5 | 2.5 | 1769.62 | 1775.08 | 1771.84 | 2576.62 | 1778.08 | 1771.34 | 1799.27 | 1769.62 | 1770.08 | 1770.22 |
| 500 | 100 | 3.5 | 3.75 | 2146.32 | 2158.16 | 2150.54 | 3464.35 | 2162.33 | 2149.43 | 2200.74 | 2146.33 | 2147.16 | 2147.50 |
| 500 | 100 | 3.5 | 5 | 2474.27 | 2494.17 | 2480.90 | 4307.94 | 2499.36 | 2478.96 | 2557.50 | 2474.28 | 2475.55 | 2476.16 |
| 500 | 10 | 3.5 | 1 | 370.74 | 370.76 | 370.76 | 453.41 | 370.80 | 370.76 | 370.98 | 370.74 | 370.75 | 370.75 |
| 500 | 60 | 3.5 | 1 | 919.79 | 920.11 | 920.02 | 1108.11 | 920.68 | 919.99 | 923.16 | 919.79 | 919.84 | 919.85 |
| 500 | 110 | 3.5 | 1 | 1254.75 | 1255.55 | 1255.33 | 1499.45 | 1256.99 | 1255.24 | 1263.00 | 1254.75 | 1254.87 | 1254.90 |
| 500 | 160 | 3.5 | 1 | 1522.11 | 1523.52 | 1523.14 | 1808.10 | 1526.06 | 1522.96 | 1536.41 | 1522.11 | 1522.33 | 1522.38 |
| 500 | 210 | 3.5 | 1 | 1752.38 | 1754.49 | 1753.93 | 2071.55 | 1758.34 | 1753.63 | 1773.66 | 1752.38 | 1752.71 | 1752.80 |
| 1000 | 50 | 3.5 | 5 | 2394.92 | 2399.84 | 2396.51 | 4479.47 | 2401.05 | 2396.23 | 2417.11 | 2394.92 | 2395.26 | 2395.34 |
| 2000 | 50 | 3.5 | 5 | 3353.40 | 3356.87 | 3354.51 | 6436.92 | 3357.70 | 3354.36 | 3369.43 | 3353.40 | 3353.65 | 3353.69 |
| 4500 | 50 | 3.5 | 5 | 4989.27 | 4991.58 | 4990.00 | 9806.59 | 4992.13 | 4989.94 | 5000.15 | 4989.27 | 4989.44 | 4989.46 |
| 9000 | 50 | 3.5 | 5 | 7021.86 | 7023.49 | 7022.37 | 14,014.64 | 7023.88 | 7022.34 | 7029.64 | 7021.86 | 7021.98 | 7021.99 |
| 100,000 | 50 | 3.5 | 5 | 23,213.25 | 23,213.74 | 23,213.40 | 47,686.78 | 23,213.85 | 23,213.40 | 23,215.63 | 23,213.25 | 23,213.29 | 23,213.29 |
| 10,000 | 50 | 0.3 | 1 | 3225.99 | 3226.14 | 3226.03 | 9438.50 | 3226.16 | 3226.03 | 3226.67 | 3225.99 | 3226.00 | 3226.00 |
| 10,000 | 50 | 0.8 | 1 | 3302.96 | 3303.09 | 3303.00 | 6402.80 | 3303.13 | 3303.00 | 3303.63 | 3302.96 | 3302.97 | 3302.97 |
| 10,000 | 50 | 2.5 | 1 | 3552.16 | 3552.24 | 3552.20 | 4727.92 | 3552.32 | 3552.20 | 3552.78 | 3552.16 | 3552.17 | 3552.17 |
| 10,000 | 50 | 5 | 1 | 3889.61 | 3889.65 | 3889.65 | 4472.61 | 3889.76 | 3889.65 | 3890.18 | 3889.61 | 3889.62 | 3889.62 |
| 10,000 | 50 | 7.5 | 1 | 4199.93 | 4199.95 | 4199.97 | 4570.20 | 4200.07 | 4199.97 | 4200.46 | 4199.93 | 4199.94 | 4199.94 |
| % Difference oforvs. GRG | |||||||||||||
| Parameters | Existing Solutions | New Solutions | |||||||||||
| GRG | E1 | E2 | E3 | N1 | N2 | N3 | N4 | N5 | N6 | ||||
| 500 | 100 | 3.5 | 0.1 | 0.00 | 0.00 | 0.00 | 0.72 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 |
| 500 | 100 | 3.5 | 1.25 | 0.00 | 0.09 | 0.06 | 24.72 | 0.21 | 0.05 | 0.78 | 0.00 | 0.01 | 0.01 |
| 500 | 100 | 3.5 | 2.5 | 0.00 | 0.31 | 0.13 | 45.60 | 0.48 | 0.10 | 1.68 | 0.00 | 0.03 | 0.03 |
| 500 | 100 | 3.5 | 3.75 | 0.00 | 0.55 | 0.20 | 61.41 | 0.75 | 0.14 | 2.54 | 0.00 | 0.04 | 0.05 |
| 500 | 100 | 3.5 | 5 | 0.00 | 0.80 | 0.27 | 74.11 | 1.01 | 0.19 | 3.36 | 0.00 | 0.05 | 0.08 |
| 500 | 10 | 3.5 | 1 | 0.00 | 0.01 | 0.00 | 22.30 | 0.02 | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 |
| 500 | 60 | 3.5 | 1 | 0.00 | 0.04 | 0.03 | 20.47 | 0.10 | 0.02 | 0.37 | 0.00 | 0.01 | 0.01 |
| 500 | 110 | 3.5 | 1 | 0.00 | 0.06 | 0.05 | 19.50 | 0.18 | 0.04 | 0.66 | 0.00 | 0.01 | 0.01 |
| 500 | 160 | 3.5 | 1 | 0.00 | 0.09 | 0.07 | 18.79 | 0.26 | 0.06 | 0.94 | 0.00 | 0.01 | 0.02 |
| 500 | 210 | 3.5 | 1 | 0.00 | 0.12 | 0.09 | 18.21 | 0.34 | 0.07 | 1.21 | 0.00 | 0.02 | 0.02 |
| 1000 | 50 | 3.5 | 5 | 0.00 | 0.21 | 0.07 | 87.04 | 0.26 | 0.05 | 0.93 | 0.00 | 0.01 | 0.02 |
| 2000 | 50 | 3.5 | 5 | 0.00 | 0.10 | 0.03 | 91.95 | 0.13 | 0.03 | 0.48 | 0.00 | 0.01 | 0.01 |
| 4500 | 50 | 3.5 | 5 | 0.00 | 0.05 | 0.01 | 96.55 | 0.06 | 0.01 | 0.22 | 0.00 | 0.00 | 0.00 |
| 9000 | 50 | 3.5 | 5 | 0.00 | 0.02 | 0.01 | 99.59 | 0.03 | 0.01 | 0.11 | 0.00 | 0.00 | 0.00 |
| 100,000 | 50 | 3.5 | 5 | 0.00 | 0.00 | 0.00 | 105.43 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 0.3 | 1 | 0.00 | 0.00 | 0.00 | 192.58 | 0.01 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 0.8 | 1 | 0.00 | 0.00 | 0.00 | 93.85 | 0.01 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 2.5 | 1 | 0.00 | 0.00 | 0.00 | 33.10 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 5 | 1 | 0.00 | 0.00 | 0.00 | 14.99 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 7.5 | 1 | 0.00 | 0.00 | 0.00 | 8.82 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| Optimal Order Quantity | Optimal Backorder Quantity | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Existing | New Solutions | Existing | New Solutions | ||||||||||||
| GRG | E3 | N1 | N2 | N3 | N4 | GRG | E3 | N1 | N2 | N3 | N4 | |||||
| 500 | 100 | 3.5 | 0.1 | 20 | 165.59 | 170.52 | 166.82 | 164.99 | 165.91 | 165.91 | 30.42 | 25.40 | 30.30 | 30.30 | 30.30 | 30.47 |
| 500 | 100 | 3.5 | 1.25 | 20 | 107.46 | 170.68 | 110.63 | 106.07 | 108.35 | 108.34 | 47.76 | 25.42 | 47.14 | 47.14 | 47.14 | 48.15 |
| 500 | 100 | 3.5 | 2.5 | 20 | 93.38 | 170.86 | 96.10 | 92.24 | 94.17 | 94.16 | 54.87 | 25.45 | 54.20 | 54.20 | 54.20 | 55.33 |
| 500 | 100 | 3.5 | 3.75 | 20 | 87.18 | 171.03 | 89.47 | 86.25 | 87.86 | 87.85 | 58.60 | 25.47 | 57.97 | 57.97 | 57.97 | 59.05 |
| 500 | 100 | 3.5 | 5 | 20 | 83.66 | 171.21 | 85.63 | 82.88 | 84.25 | 84.25 | 60.90 | 25.50 | 60.33 | 60.33 | 60.33 | 61.32 |
| 500 | 10 | 3.5 | 1 | 20 | 35.37 | 53.96 | 35.67 | 35.22 | 35.45 | 35.45 | 14.25 | 8.04 | 14.19 | 14.19 | 14.19 | 14.29 |
| 500 | 60 | 3.5 | 1 | 20 | 87.14 | 132.18 | 89.03 | 86.28 | 87.65 | 87.65 | 35.12 | 19.69 | 34.77 | 34.77 | 34.77 | 35.32 |
| 500 | 110 | 3.5 | 1 | 20 | 118.39 | 178.97 | 121.92 | 116.83 | 119.37 | 119.37 | 47.71 | 26.66 | 47.08 | 47.08 | 47.08 | 48.10 |
| 500 | 160 | 3.5 | 1 | 20 | 143.16 | 215.85 | 148.39 | 140.90 | 144.64 | 144.63 | 57.69 | 32.15 | 56.78 | 56.78 | 56.78 | 58.28 |
| 500 | 210 | 3.5 | 1 | 20 | 164.37 | 247.29 | 171.33 | 161.42 | 166.37 | 166.35 | 66.24 | 36.83 | 65.05 | 65.05 | 65.05 | 67.04 |
| 1000 | 50 | 3.5 | 5 | 500 | 46.86 | 169.51 | 50.01 | 45.49 | 47.75 | 47.74 | 4.53 | 1.18 | 4.40 | 4.40 | 4.40 | 4.40 |
| 2000 | 50 | 3.5 | 5 | 500 | 65.71 | 239.43 | 68.76 | 64.33 | 66.55 | 66.54 | 6.35 | 1.66 | 6.22 | 6.22 | 6.22 | 6.22 |
| 4500 | 50 | 3.5 | 5 | 500 | 97.88 | 358.89 | 100.86 | 96.49 | 98.68 | 98.67 | 9.46 | 2.49 | 9.33 | 9.33 | 9.33 | 9.33 |
| 9000 | 50 | 3.5 | 5 | 500 | 137.86 | 507.41 | 140.78 | 136.46 | 138.62 | 138.62 | 13.33 | 3.53 | 13.19 | 13.19 | 13.19 | 13.19 |
| 100,000 | 50 | 3.5 | 5 | 500 | 456.28 | 1690.94 | 459.13 | 454.88 | 457.01 | 457.01 | 44.10 | 11.75 | 43.97 | 43.97 | 43.97 | 43.97 |
| 10,000 | 50 | 0.3 | 1 | 20 | 384.58 | 1827.20 | 386.75 | 383.52 | 385.14 | 385.14 | 130.73 | 27.00 | 130.37 | 130.37 | 130.37 | 130.92 |
| 10,000 | 50 | 0.8 | 1 | 20 | 378.61 | 1120.32 | 380.65 | 377.61 | 379.13 | 379.13 | 132.76 | 43.09 | 132.41 | 132.41 | 132.41 | 132.94 |
| 10,000 | 50 | 2.5 | 1 | 20 | 361.37 | 636.42 | 363.03 | 360.56 | 361.80 | 361.79 | 138.99 | 70.71 | 138.68 | 138.68 | 138.68 | 139.15 |
| 10,000 | 50 | 5 | 1 | 20 | 342.20 | 452.79 | 343.48 | 341.57 | 342.52 | 342.52 | 146.66 | 90.56 | 146.39 | 146.39 | 146.39 | 146.80 |
| 10,000 | 50 | 7.5 | 1 | 20 | 327.83 | 371.94 | 328.86 | 327.33 | 328.09 | 328.09 | 152.99 | 101.44 | 152.75 | 152.75 | 152.75 | 153.11 |
| % Difference ofandvs. GRG | ||||||||||||||||
| Optimal Order Quantity | Optimal Backorder Quantity | |||||||||||||||
| Parameters | Existing | New Solutions | Existing | New Solutions | ||||||||||||
| GRG | E3 | N1 | N2 | N3 | N4 | GRG | E3 | N1 | N2 | N3 | N4 | |||||
| 500 | 100 | 3.5 | 0.1 | 20 | 0.00 | 2.98 | 0.74 | −0.36 | 0.19 | 0.19 | 0.00 | −16.50 | −0.39 | −0.39 | −0.39 | 0.16 |
| 500 | 100 | 3.5 | 1.25 | 20 | 0.00 | 58.83 | 2.95 | −1.29 | 0.83 | 0.82 | 0.00 | −46.78 | −1.30 | −1.30 | −1.30 | 0.82 |
| 500 | 100 | 3.5 | 2.5 | 20 | 0.00 | 82.97 | 2.91 | −1.22 | 0.85 | 0.84 | 0.00 | −53.62 | −1.22 | −1.22 | −1.22 | 0.84 |
| 500 | 100 | 3.5 | 3.75 | 20 | 0.00 | 96.18 | 2.63 | −1.07 | 0.78 | 0.77 | 0.00 | −56.54 | −1.08 | −1.08 | −1.08 | 0.77 |
| 500 | 100 | 3.5 | 5 | 20 | 0.00 | 104.65 | 2.35 | −0.93 | 0.71 | 0.71 | 0.00 | −58.13 | −0.94 | −0.94 | −0.94 | 0.69 |
| 500 | 10 | 3.5 | 1 | 20 | 0.00 | 52.56 | 0.85 | −0.42 | 0.23 | 0.23 | 0.00 | −43.58 | −0.42 | −0.42 | −0.42 | 0.28 |
| 500 | 60 | 3.5 | 1 | 20 | 0.00 | 51.69 | 2.17 | −0.99 | 0.59 | 0.59 | 0.00 | −43.94 | −1.00 | −1.00 | −1.00 | 0.57 |
| 500 | 110 | 3.5 | 1 | 20 | 0.00 | 51.17 | 2.98 | −1.32 | 0.83 | 0.83 | 0.00 | −44.12 | −1.32 | −1.32 | −1.32 | 0.82 |
| 500 | 160 | 3.5 | 1 | 20 | 0.00 | 50.78 | 3.65 | −1.58 | 1.03 | 1.03 | 0.00 | −44.27 | −1.58 | −1.58 | −1.58 | 1.02 |
| 500 | 210 | 3.5 | 1 | 20 | 0.00 | 50.45 | 4.23 | −1.79 | 1.22 | 1.20 | 0.00 | −44.40 | −1.80 | −1.80 | −1.80 | 1.21 |
| 1000 | 50 | 3.5 | 5 | 500 | 0.00 | 261.74 | 6.72 | −2.92 | 1.90 | 1.88 | 0.00 | −73.95 | −2.87 | −2.87 | −2.87 | −2.87 |
| 2000 | 50 | 3.5 | 5 | 500 | 0.00 | 264.37 | 4.64 | −2.10 | 1.28 | 1.26 | 0.00 | −73.86 | −2.05 | −2.05 | −2.05 | −2.05 |
| 4500 | 50 | 3.5 | 5 | 500 | 0.00 | 266.66 | 3.04 | −1.42 | 0.82 | 0.81 | 0.00 | −73.68 | −1.37 | −1.37 | −1.37 | −1.37 |
| 9000 | 50 | 3.5 | 5 | 500 | 0.00 | 268.06 | 2.12 | −1.02 | 0.55 | 0.55 | 0.00 | −73.52 | −1.05 | −1.05 | −1.05 | −1.05 |
| 100,000 | 50 | 3.5 | 5 | 500 | 0.00 | 270.59 | 0.62 | −0.31 | 0.16 | 0.16 | 0.00 | −73.36 | −0.29 | −0.29 | −0.29 | −0.29 |
| 10,000 | 50 | 0.3 | 1 | 20 | 0.00 | 375.12 | 0.56 | −0.28 | 0.15 | 0.15 | 0.00 | −79.35 | −0.28 | −0.28 | −0.28 | 0.15 |
| 10,000 | 50 | 0.8 | 1 | 20 | 0.00 | 195.90 | 0.54 | −0.26 | 0.14 | 0.14 | 0.00 | −67.54 | −0.26 | −0.26 | −0.26 | 0.14 |
| 10,000 | 50 | 2.5 | 1 | 20 | 0.00 | 76.11 | 0.46 | −0.22 | 0.12 | 0.12 | 0.00 | −49.13 | −0.22 | −0.22 | −0.22 | 0.12 |
| 10,000 | 50 | 5 | 1 | 20 | 0.00 | 32.32 | 0.37 | −0.18 | 0.09 | 0.09 | 0.00 | −38.25 | −0.18 | −0.18 | −0.18 | 0.10 |
| 10,000 | 50 | 7.5 | 1 | 20 | 0.00 | 13.46 | 0.31 | −0.15 | 0.08 | 0.08 | 0.00 | −33.70 | −0.16 | −0.16 | −0.16 | 0.08 |
| Optimal Total Cost or | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Existing | New Solutions | ||||||||
| GRG | E3 | N1 | N2 | N3 | N4 | |||||
| 500 | 100 | 3.5 | 0.1 | 20 | 608.30 | 611.08 | 608.33 | 608.31 | 608.30 | 608.31 |
| 500 | 100 | 3.5 | 1.25 | 20 | 955.18 | 1292.64 | 956.16 | 955.26 | 955.22 | 955.37 |
| 500 | 100 | 3.5 | 2.5 | 20 | 1097.44 | 1947.59 | 1098.96 | 1097.52 | 1097.48 | 1097.77 |
| 500 | 100 | 3.5 | 3.75 | 20 | 1171.91 | 2537.43 | 1173.60 | 1171.98 | 1171.95 | 1172.29 |
| 500 | 100 | 3.5 | 5 | 20 | 1217.92 | 3077.12 | 1219.63 | 1217.98 | 1217.95 | 1218.32 |
| 500 | 10 | 3.5 | 1 | 20 | 285.07 | 366.85 | 285.10 | 285.07 | 285.08 | 285.08 |
| 500 | 60 | 3.5 | 1 | 20 | 702.35 | 894.07 | 702.72 | 702.38 | 702.42 | 702.42 |
| 500 | 110 | 3.5 | 1 | 20 | 954.21 | 1207.62 | 955.11 | 954.29 | 954.38 | 954.38 |
| 500 | 160 | 3.5 | 1 | 20 | 1153.83 | 1454.04 | 1155.42 | 1153.97 | 1154.13 | 1154.13 |
| 500 | 210 | 3.5 | 1 | 20 | 1324.79 | 1663.74 | 1327.18 | 1324.99 | 1325.24 | 1325.24 |
| 1000 | 50 | 3.5 | 5 | 500 | 2264.74 | 4417.00 | 2270.03 | 2265.66 | 2265.36 | 2265.35 |
| 2000 | 50 | 3.5 | 5 | 500 | 3175.80 | 6350.39 | 3179.53 | 3176.48 | 3176.22 | 3176.22 |
| 4500 | 50 | 3.5 | 5 | 500 | 4730.68 | 9678.66 | 4733.15 | 4731.14 | 4730.95 | 4730.94 |
| 9000 | 50 | 3.5 | 5 | 500 | 6662.58 | 13,835.06 | 6664.33 | 6662.92 | 6662.76 | 6662.76 |
| 100,000 | 50 | 3.5 | 5 | 500 | 22,051.65 | 47,093.84 | 22,052.17 | 22,051.75 | 22,051.70 | 22,051.70 |
| 10,000 | 50 | 0.3 | 1 | 20 | 2614.65 | 9172.20 | 2614.74 | 2614.66 | 2614.66 | 2614.66 |
| 10,000 | 50 | 0.8 | 1 | 20 | 2655.19 | 5973.18 | 2655.28 | 2655.20 | 2655.21 | 2655.21 |
| 10,000 | 50 | 2.5 | 1 | 20 | 2779.78 | 3990.02 | 2779.85 | 2779.79 | 2779.79 | 2779.79 |
| 10,000 | 50 | 5 | 1 | 20 | 2933.11 | 3456.57 | 2933.17 | 2933.12 | 2933.12 | 2933.12 |
| 10,000 | 50 | 7.5 | 1 | 20 | 3059.77 | 3344.22 | 3059.81 | 3059.77 | 3059.78 | 3059.78 |
| % Difference oforvs. GRG | ||||||||||
| Parameters | Existing | New Solutions | ||||||||
| GRG | E3 | N1 | N2 | N3 | N4 | |||||
| 500 | 100 | 3.5 | 0.1 | 20 | 0.00 | 0.46 | 0.00 | 0.00 | 0.00 | 0.00 |
| 500 | 100 | 3.5 | 1.25 | 20 | 0.00 | 35.33 | 0.10 | 0.01 | 0.00 | 0.02 |
| 500 | 100 | 3.5 | 2.5 | 20 | 0.00 | 77.47 | 0.14 | 0.01 | 0.00 | 0.03 |
| 500 | 100 | 3.5 | 3.75 | 20 | 0.00 | 116.52 | 0.14 | 0.01 | 0.00 | 0.03 |
| 500 | 100 | 3.5 | 5 | 20 | 0.00 | 152.65 | 0.14 | 0.00 | 0.00 | 0.03 |
| 500 | 10 | 3.5 | 1 | 20 | 0.00 | 28.69 | 0.01 | 0.00 | 0.00 | 0.00 |
| 500 | 60 | 3.5 | 1 | 20 | 0.00 | 27.30 | 0.05 | 0.00 | 0.01 | 0.01 |
| 500 | 110 | 3.5 | 1 | 20 | 0.00 | 26.56 | 0.10 | 0.01 | 0.02 | 0.02 |
| 500 | 160 | 3.5 | 1 | 20 | 0.00 | 26.02 | 0.14 | 0.01 | 0.03 | 0.03 |
| 500 | 210 | 3.5 | 1 | 20 | 0.00 | 25.59 | 0.18 | 0.02 | 0.03 | 0.03 |
| 1000 | 50 | 3.5 | 5 | 500 | 0.00 | 95.03 | 0.23 | 0.04 | 0.03 | 0.03 |
| 2000 | 50 | 3.5 | 5 | 500 | 0.00 | 99.96 | 0.12 | 0.02 | 0.01 | 0.01 |
| 4500 | 50 | 3.5 | 5 | 500 | 0.00 | 104.59 | 0.05 | 0.01 | 0.01 | 0.01 |
| 9000 | 50 | 3.5 | 5 | 500 | 0.00 | 107.65 | 0.03 | 0.01 | 0.00 | 0.00 |
| 100,000 | 50 | 3.5 | 5 | 500 | 0.00 | 113.56 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 0.3 | 1 | 20 | 0.00 | 250.80 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 0.8 | 1 | 20 | 0.00 | 124.96 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 2.5 | 1 | 20 | 0.00 | 43.54 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 5 | 1 | 20 | 0.00 | 17.85 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10,000 | 50 | 7.5 | 1 | 20 | 0.00 | 9.30 | 0.00 | 0.00 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çalışkan, C. A Comparison of Simple Closed-Form Solutions for the EOQ Problem for Exponentially Deteriorating Items. Sustainability 2022, 14, 8389. https://doi.org/10.3390/su14148389
Çalışkan C. A Comparison of Simple Closed-Form Solutions for the EOQ Problem for Exponentially Deteriorating Items. Sustainability. 2022; 14(14):8389. https://doi.org/10.3390/su14148389
Chicago/Turabian StyleÇalışkan, Cenk. 2022. "A Comparison of Simple Closed-Form Solutions for the EOQ Problem for Exponentially Deteriorating Items" Sustainability 14, no. 14: 8389. https://doi.org/10.3390/su14148389
APA StyleÇalışkan, C. (2022). A Comparison of Simple Closed-Form Solutions for the EOQ Problem for Exponentially Deteriorating Items. Sustainability, 14(14), 8389. https://doi.org/10.3390/su14148389






