Causes and Evolution Characteristics of Green Innovation Efficiency Loss: The Perspective of Factor Mismatch under Local Government Competition
Abstract
1. Introduction
2. Literature Review
3. Theoretical Framework
3.1. Local Government Competition and Innovation Elements Mismatch
3.2. Mismatching of Innovation Elements and Loss of Green Innovation Efficiency
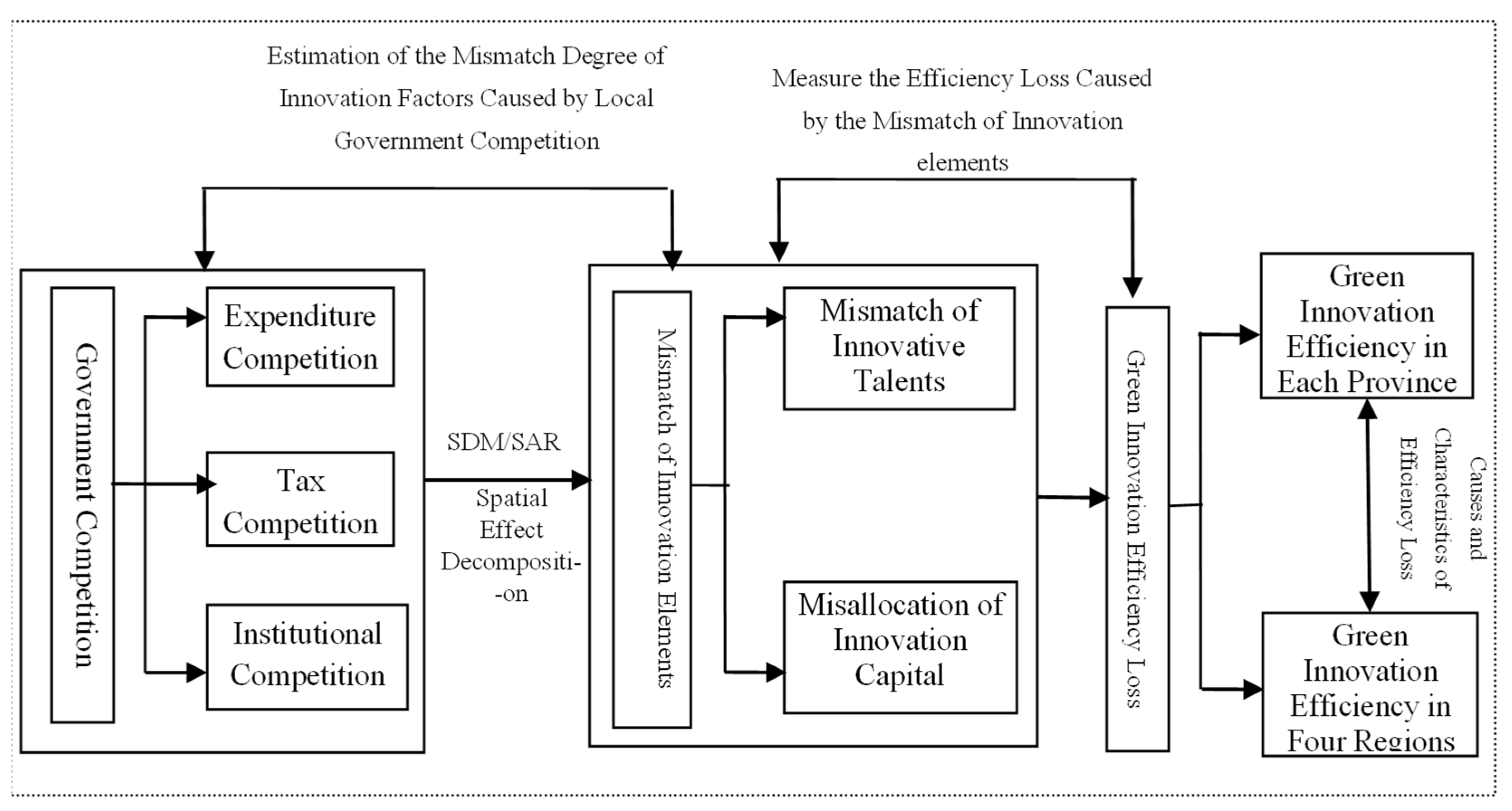
4. Research Design
4.1. Local Government Competition and Innovation Factor Mismatch
4.1.1. Model Construction of Local Government Competition
- (1)
- Benchmark model
- (2)
- Spatial effect decomposition model
4.1.2. Variable Measurement and Data Description
- (1)
- Mismatch coefficient of innovation elements
- (2)
- Local government competition
- ①
- Expenditure Competition (excom): Based on Zhong et al. [43], the total expenditure of local public finance is measured as the proportion of GDP, and the measurement results reflect the influence of regional public service supply level caused by expenditure competition on the spatial allocation of innovation elements.
- ②
- Tax Competition (taxcom): Based on Xiao et al. [44], is used to measure tax competition, in which and represent the total tax revenue of China in year and the total tax revenue of region in year , respectively. and represent the gross domestic product of China in year and the gross domestic product of region in year , respectively.
- ③
- Institutional Competition (inscom): Based on Zhang et al. [45], the ratio of registered population to permanent population is used to measure the level of household registration system competition.
- (3)
- Other variables
4.2. Calculation of Loss of Green Innovation Efficiency Caused by Mismatching of Innovation Elements
5. Analysis of the Mismatch of Innovation Factors Due to Local Government Competition
6. Analysis of the Measurement Results of Green Innovation Efficiency Loss Due to Local Government Competition
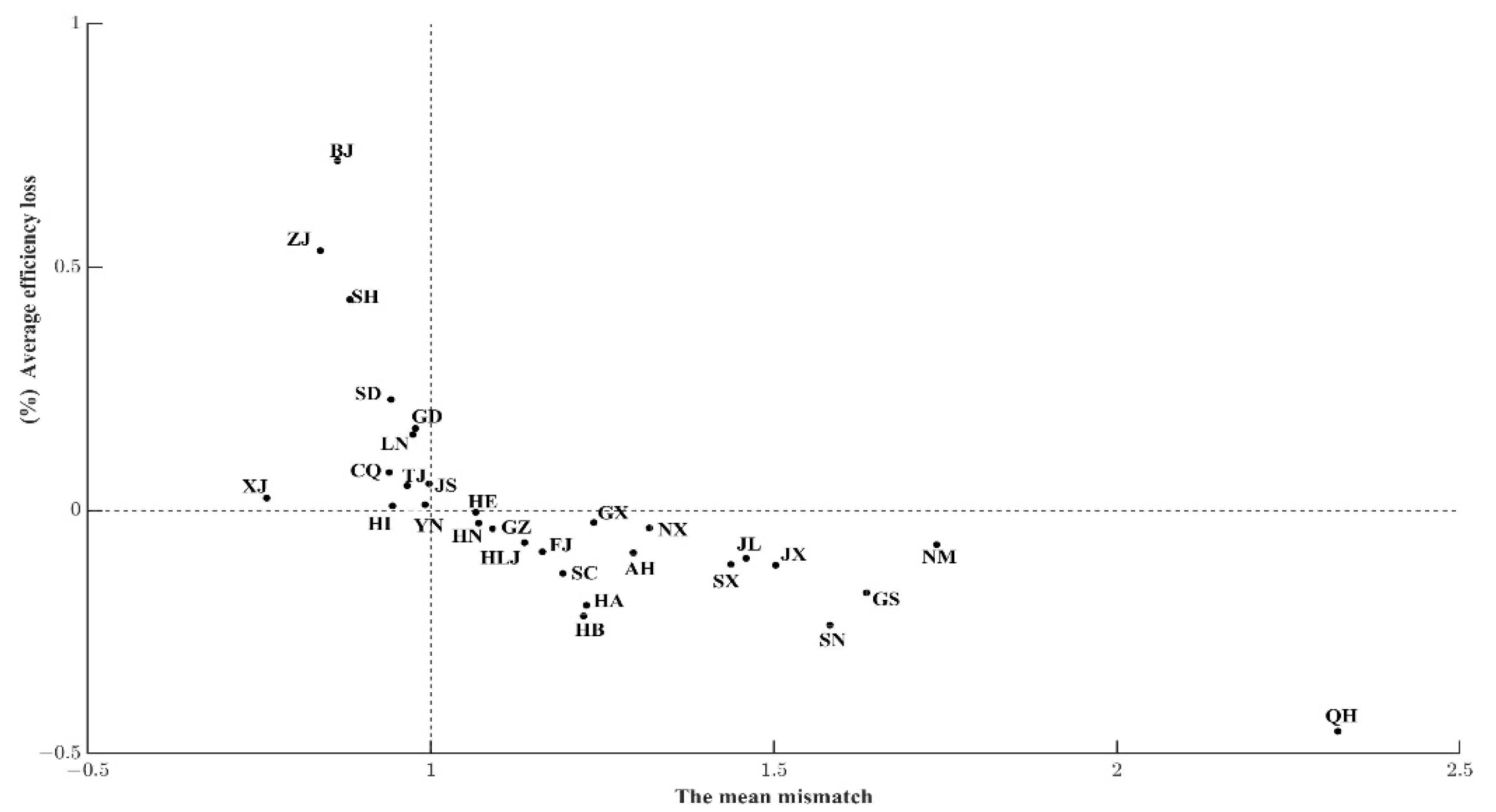
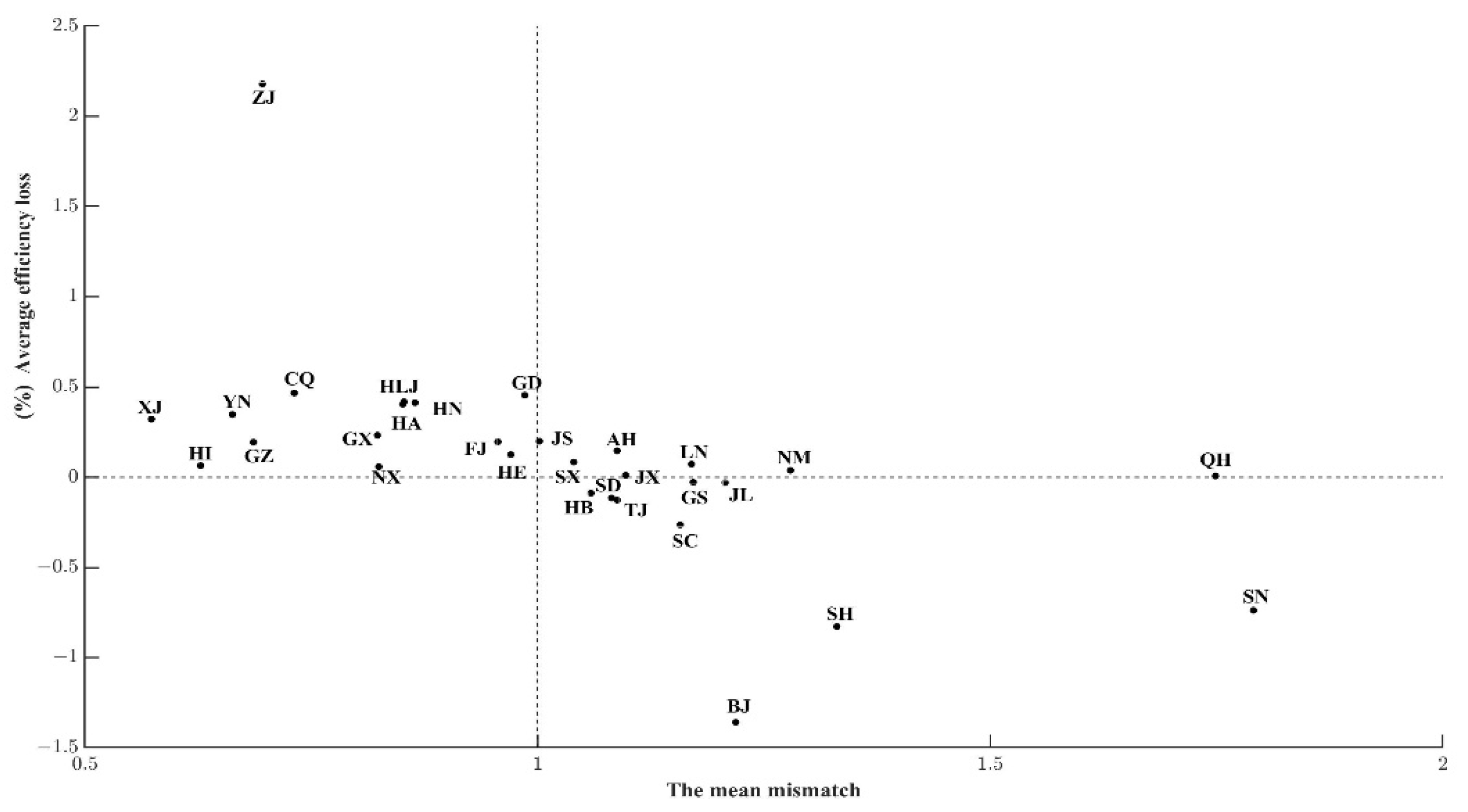
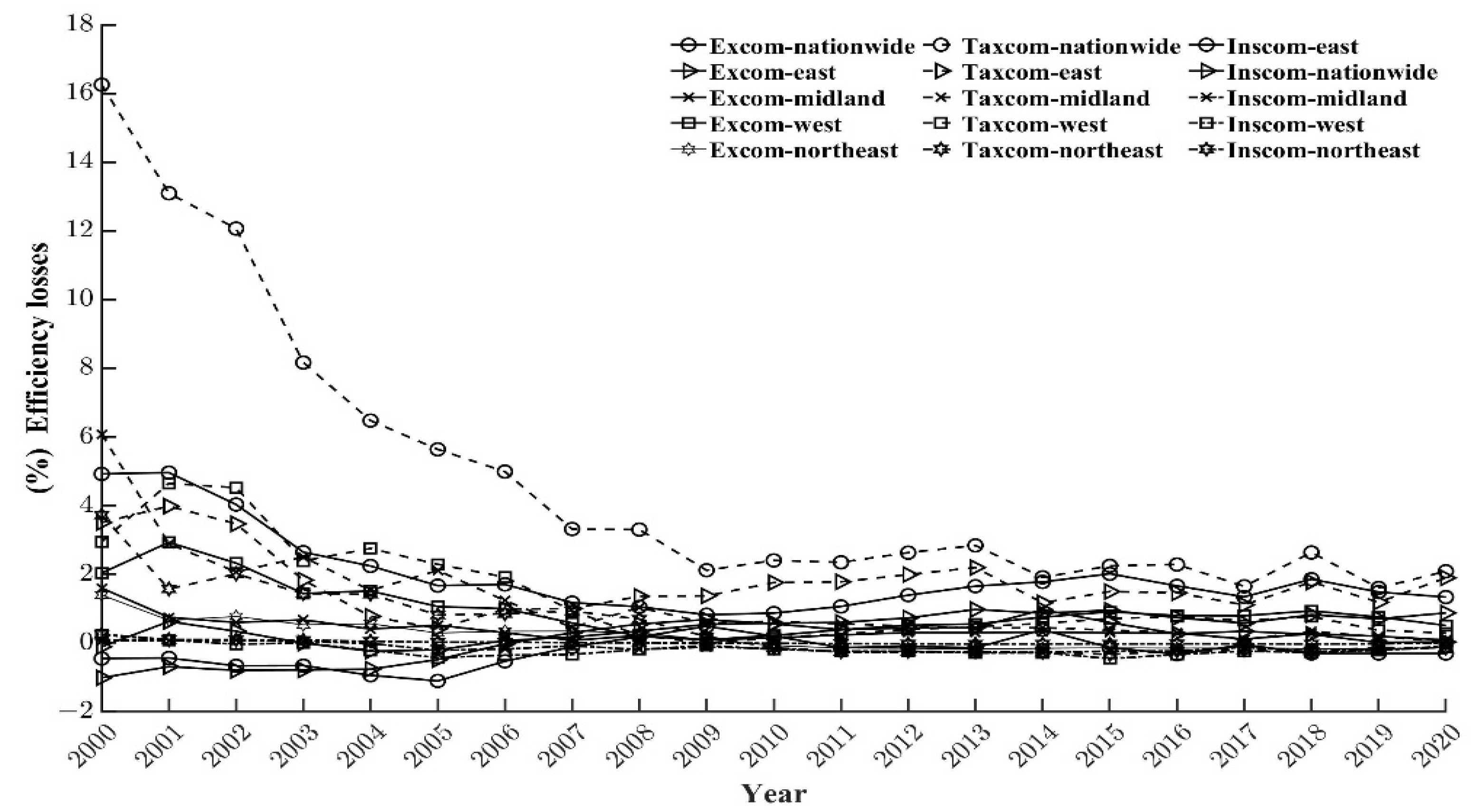
6.1. Measurement Results and Difference Analysis of Provincial Green Innovation Efficiency Loss
6.1.1. Calculation Result of Regional Green Innovation Efficiency Loss Caused
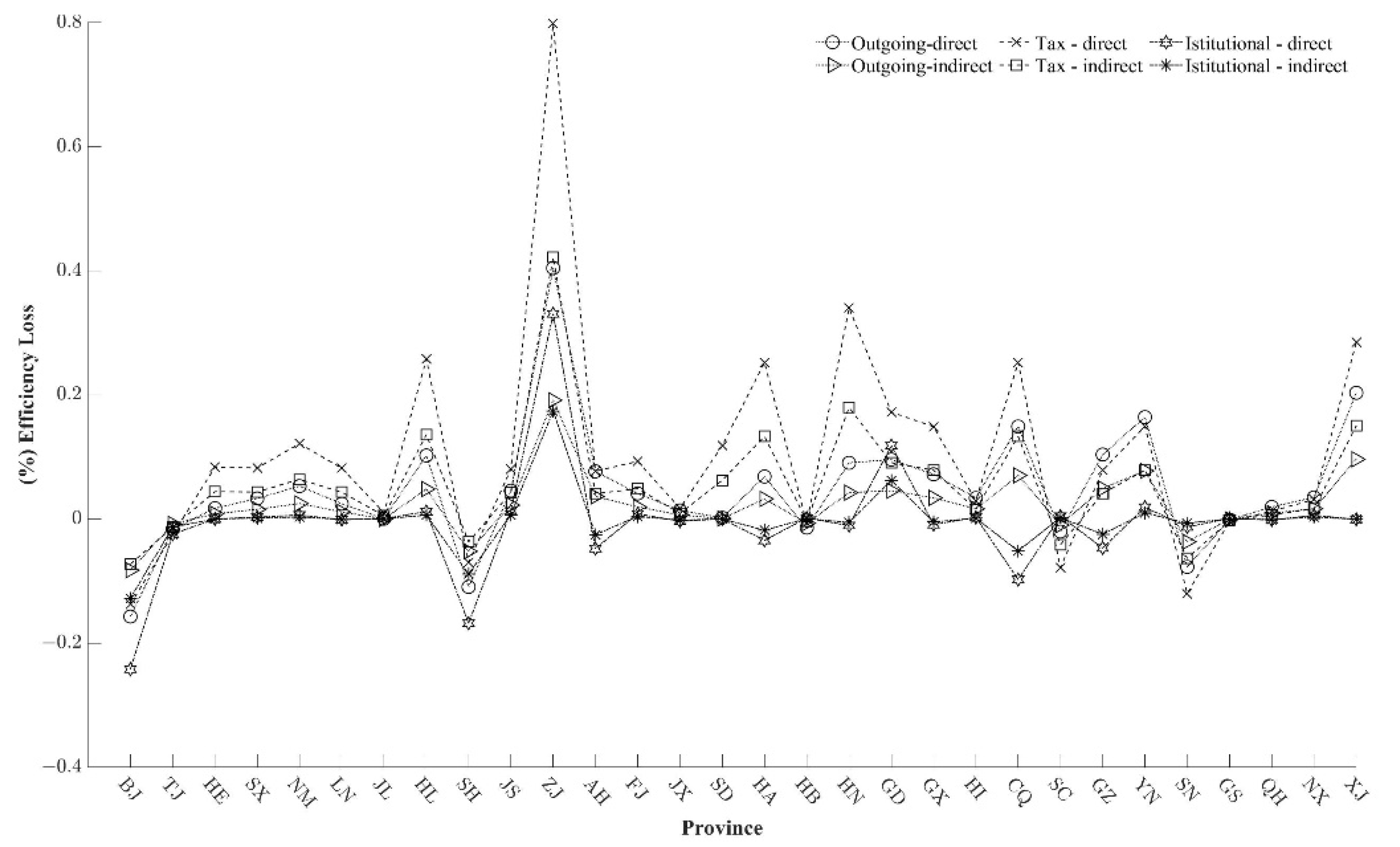
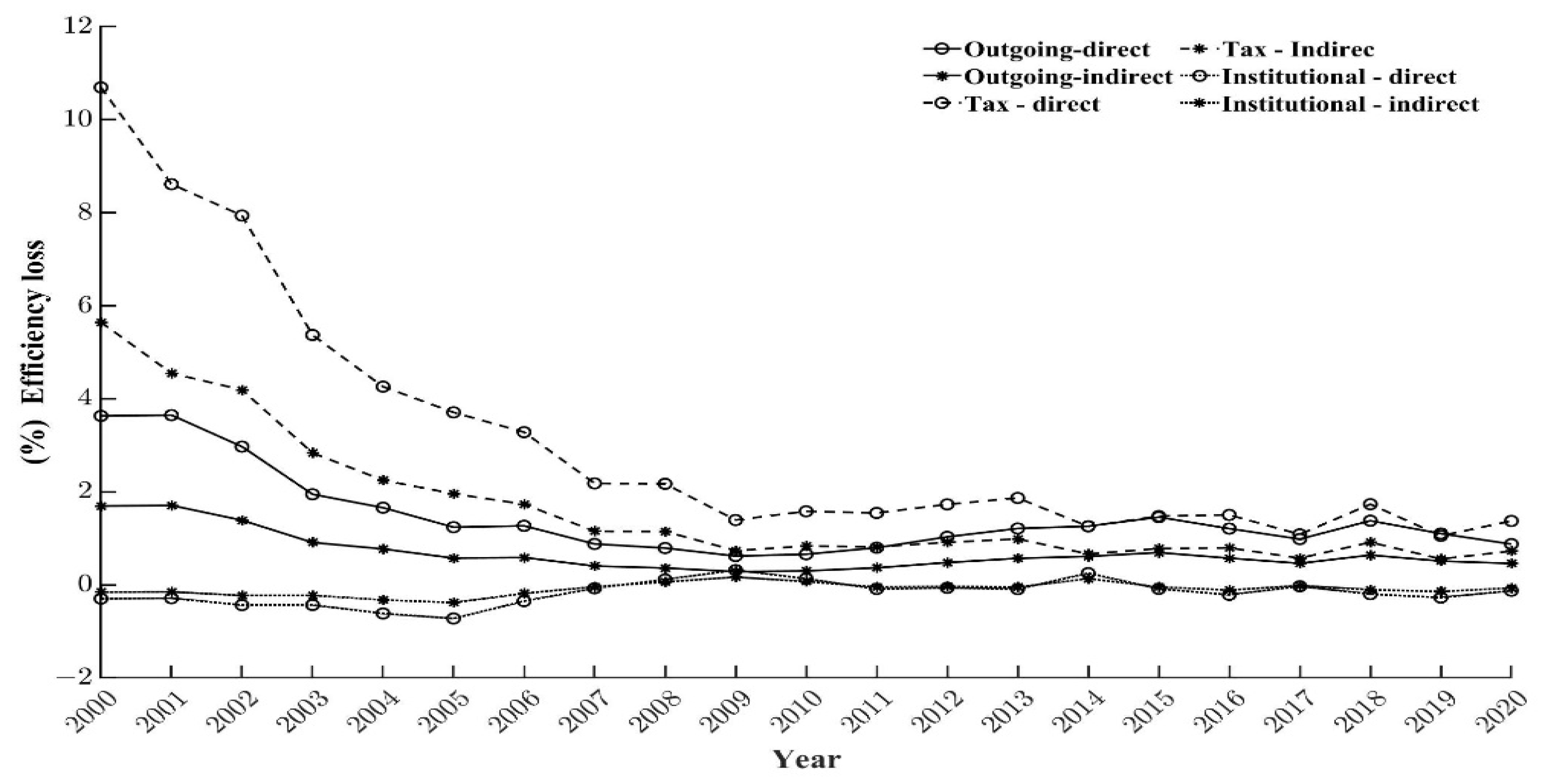
6.1.2. Analysis of Loss Difference Caused by Three Means of Competition among Provinces
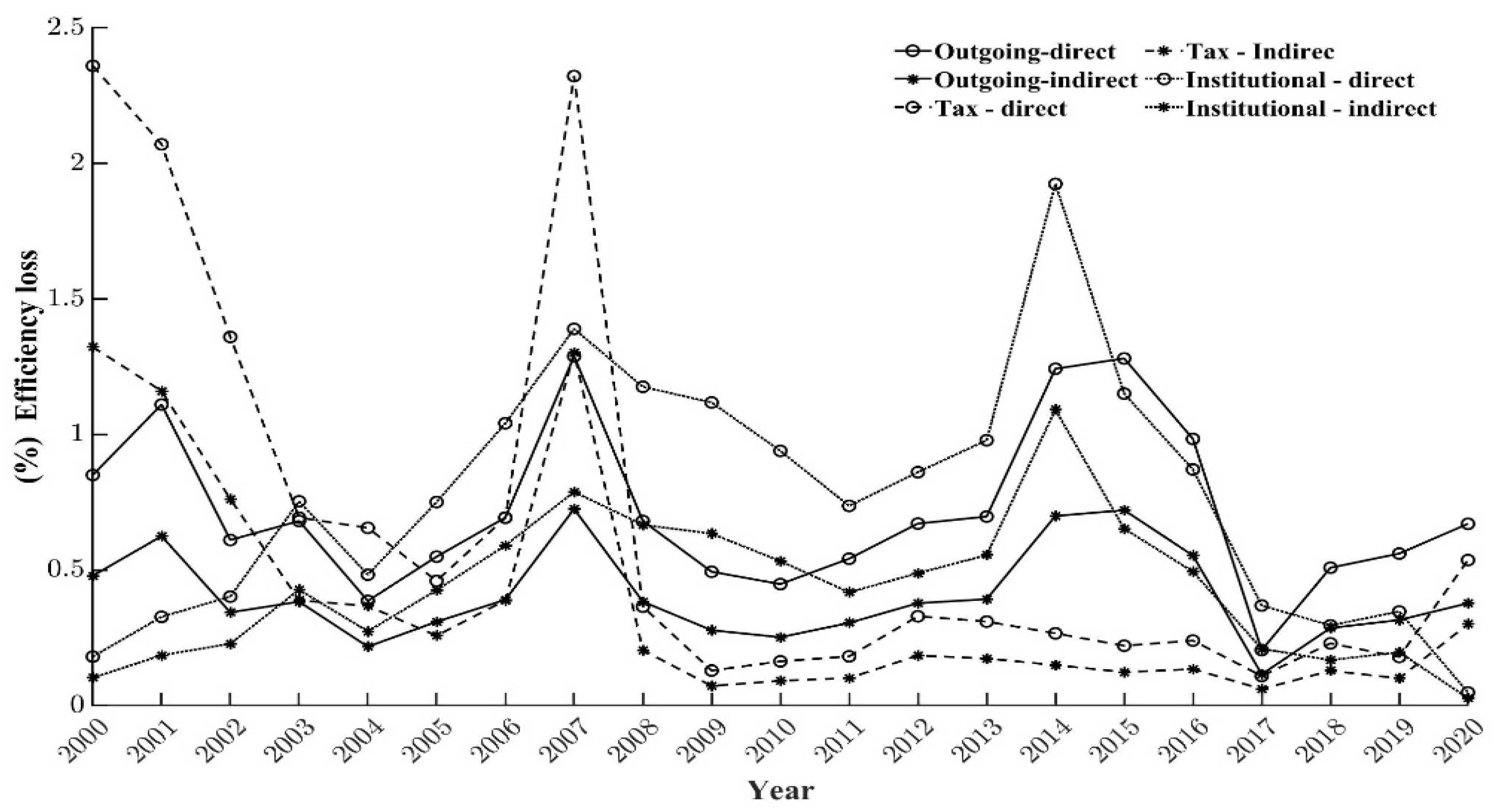
6.1.3. Analysis of the Difference in Losses Caused by the Three Competitive Means over Time
6.2. Dynamic Difference Analysis of Green Innovation Efficiency Loss Caused by Local Government Competition in Four Sectors
6.2.1. Trend Difference Analysis
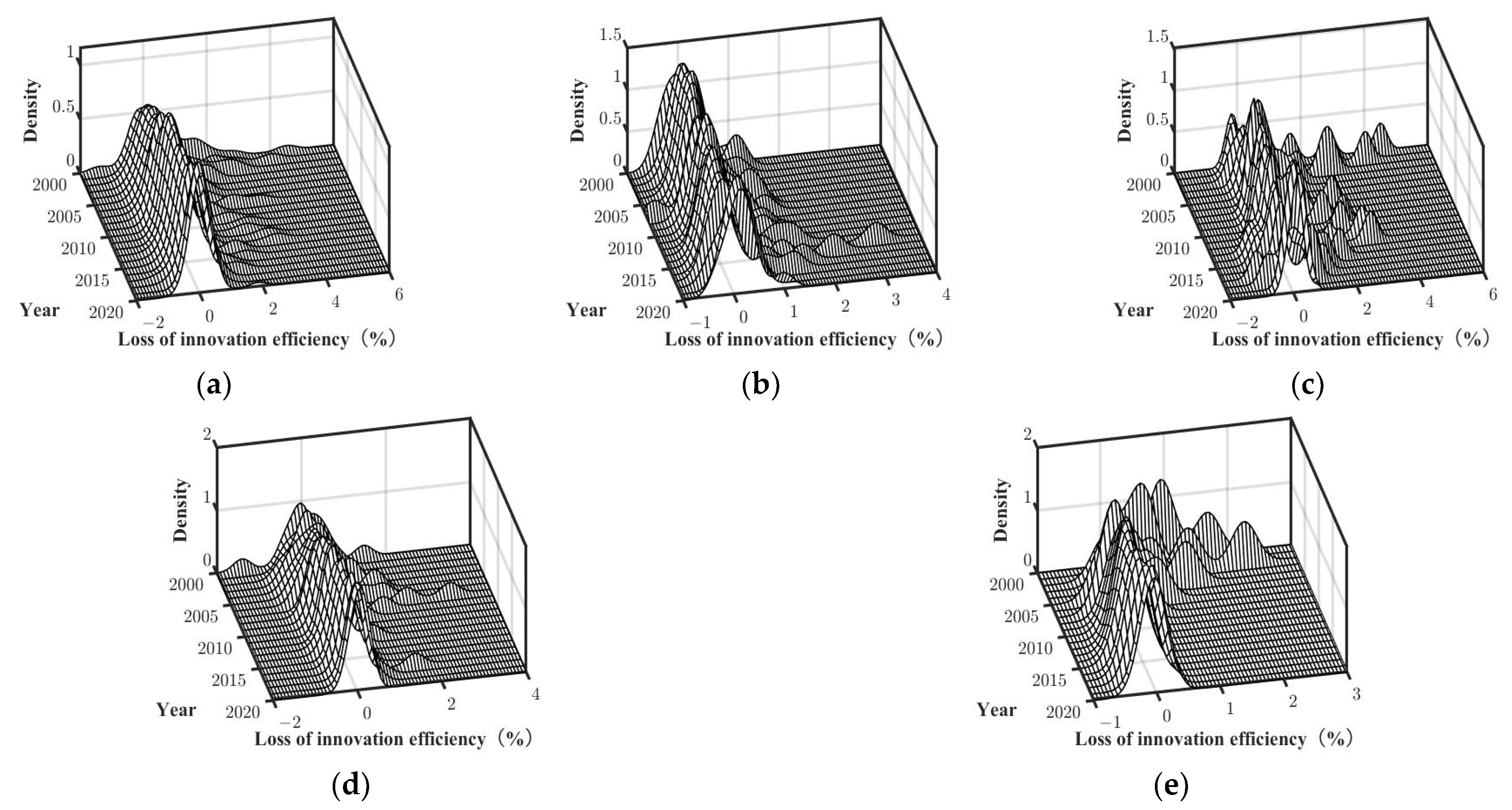
6.2.2. Analysis of Dynamic Distribution Differences
7. Conclusions
- (1)
- Guide local governments to establish cooperative relationships and prevent excessive competition from hurting the green innovation efficiency.
- (2)
- Formulate “tax reduction and fee reduction” in light of local conditions to prevent the loss of green innovation efficiency caused by “race to the bottom” tax cuts.
- (3)
- Cultivate and attract innovative talents and prevent further loss of green innovation efficiency in Beijing, Shanghai, and Tianjin.
- (4)
- Prevent the loss of green innovation efficiency caused by institutional competition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, J.; Teo, T. Will China’s R&D Investment Improve Green Innovation Performance? An Empirical Study. Environ. Sci. Pollut. Res. 2022, 29, 39331–39344. [Google Scholar] [CrossRef]
- Rogge, K.S.; Schleich, J. Do Policy Mix Characteristics Matter for Low-Carbon Innovation? A Survey-Based Exploration of Renewable Power Generation Technologies in Germany. Res. Policy 2018, 47, 1639–1654. [Google Scholar] [CrossRef]
- Brandt, L.; Tombe, T.; Zhu, X. Factor Market Distortions Across Time, Space and Sectors in China. Rev. Econ. Dyn. 2013, 16, 39–58. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Klenow, P.J. Misallocation and Manufacturing TFP in China and India. Q. J. Econ. 2009, 124, 1403–1448. [Google Scholar] [CrossRef]
- Sun, X.; Loh, L.; Chen, Z.; Zhou, X. Factor Price Distortion and Ecological Efficiency: The role of institutional quality. Environ. Sci. Pollut. Res. 2020, 27, 5293–5304. [Google Scholar] [CrossRef]
- Tiebout, C.M. A Pure Theory of Local Expenditures. J. Political Econ. 1956, 64, 416–424. [Google Scholar] [CrossRef]
- Hayashi, M.; Boadway, R. An Empirical Analysis of Intergovernmental Tax Interaction: The case of business income taxes in Canada. Can. J. Econ./Rev. Can. D’économique 2001, 34, 481–503. [Google Scholar] [CrossRef]
- Rosário, C.; Varum, C.; Botelho, A. Impact of Public Support for Innovation on Company Performance: Review and Meta-Analysis. Sustainability 2022, 14, 4718–4731. [Google Scholar]
- Li, H.B.; Zhou, L.A. Political Turnover and Economic Performance: The incentive role of personnel control in China. J. Public Econ. 2005, 89, 1743–1762. [Google Scholar] [CrossRef]
- Zhou, X.G. Reverse Soft Budget Constraint: An organizational analysis of government behavior. Chin. Soc. Sci. 2005, 2, 132–143. [Google Scholar]
- Poncet, S. Measuring Chinese Domestic and International Integration. China Econ. Rev. 2003, 14, 1–21. [Google Scholar] [CrossRef]
- Tang, J.; Qin, F. Analyzing the Impact of Local Government Competition on Green Total Factor Productivity from the Factor Market Distortion Perspective: Based on the three stage DEA model. Environ. Dev. Sustain. 2022, 1–29. [Google Scholar] [CrossRef]
- Mingran, W. Measurement and Spatial Statistical Analysis of Green Science and Technology Innovation Efficiency among Chinese Provinces. Environ. Ecol. Stat. 2021, 28, 423–444. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X.; Zhang, F. Industrial Co-Agglomeration, Green Technological Innovation, and Total Factor Energy Efficiency. Environ. Sci. Pollut. Res. 2022, 1–20. [Google Scholar] [CrossRef]
- Zhou, J.W.; Zhang, Y.; Jiang, Z.Y. Influence of the Innovation Cluster to Green Economy Efficiency: Empirical Analysis Based on Spatial Econometric Model. Ecol. Econ. 2018, 34, 57–62. [Google Scholar]
- Delgado-Verde, M.; Amores-Salvadó, J.; Martín-de Castro, G.; Navas-López, J.E. Green Intellectual Capital and Environmental Product Innovation: The mediating role of green social capital. Knowl. Manag. Res. Pract. 2014, 12, 261–275. [Google Scholar] [CrossRef]
- Iqbal, S.; Akhtar, S.; Anwar, F.; Kayani, A.J.; Sohu, J.M.; Khan, A.S. Linking Green Innovation Performance and Green Innovative Human Resource Practices in SMEs; a moderation and mediation analysis using PLS-SEM. Curr. Psychol. 2021, 1–18. [Google Scholar] [CrossRef]
- Yumei, H.; Iqbal, W.; Irfan, M.; Fatima, A. The Dynamics of Public Spending on Sustainable Green Economy: Role of technological innovation and industrial structure effects. Environ. Sci. Pollut. Res. 2022, 29, 22970–22988. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, D.; Xu, M.; Yang, M.; Zou, W. Capital Misallocation, Technological Innovation, and Green Development Efficiency: Empirical Analysis Based on China Provincial Panel Data. Environ. Sci. Pollut. Res. 2022, 1–14. [Google Scholar] [CrossRef]
- Cai, W.; Ye, P. Local-neighborhood Effects of Different Environmental Regulations on Green Innovation: Evidence from Prefecture Level Cities of China. Environ. Dev. Sustain. 2022, 24, 4810–4834. [Google Scholar] [CrossRef]
- Bucovetsky, S.; Haufler, A. Tax Competition When Firms Choose Their Organizational Form: Should Tax Loopholes for Multinationals be Closed? J. Int. Econ. 2008, 74, 188–201. [Google Scholar] [CrossRef]
- Holmstrom, B.; Milgrom, P. Multitask Principal–Agent Analyses: Incentive Contracts, Asset Ownership, and Job Design. J. Law Econ. Organ. 1991, 7, 24. [Google Scholar] [CrossRef]
- Zhang, W.; Li, G. Environmental Decentralization, Environmental Protection Investment, and Green Technology Innovation. Environ. Sci. Pollut. Res. 2022, 29, 12740–12755. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Wang, S.; Ahmad, F.; Chandio, A.A.; Ahmad, M.; Xue, D. The Nexus Between Misallocation of Land Resources and Green Technological Innovation: A Novel Investigation of Chinese Cities. Clean Technol. Environ. Policy 2021, 23, 2101–2115. [Google Scholar] [CrossRef]
- Nie, Y.; Wan, K.; Wu, F.; Zou, W.; Chang, T. Local Government Competition, Development Zones and Urban Green Innovation: An Empirical Study of Chinese Cities. Appl. Econ. Lett. 2021, 1–6. [Google Scholar] [CrossRef]
- Deng, Y.; You, D.; Wang, J. Optimal Strategy for Enterprises’ Green Technology Innovation from the Perspective of Political Competition. J. Clean. Prod. 2019, 235, 930–942. [Google Scholar] [CrossRef]
- Zhang, N.; Deng, J.; Ahmad, F.; Draz, M.U. Local Government Competition and Regional Green Development in China: The Mediating Role of Environmental Regulation. Int. J. Environ. Res. Public Health 2020, 17, 3485. [Google Scholar] [CrossRef]
- Young, A. The Razor’s Edge: Distortions and Incremental Reform in the People’s Republic of China. Q. J. Econ. 2000, 115, 1091–1135. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Yang, X.; Ren, S.; Ran, Q.; Hao, Y. Does Local Government Competition Aggravate Haze Pollution? A New Perspective of Factor Market Distortion. Socio-Econ. Plan. Sci. 2021, 76, 100959. [Google Scholar] [CrossRef]
- Krugman, P. Increasing Returns and Economic Geography. J. Political Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab Software for Spatial Panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Elhorst, J.P. Applied Spatial Econometrics: Raising the Bar. Spat. Econ. Anal. 2010, 5, 9–28. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Z.Y.; Li, K. Business Environment Optimization, Group Preference and Technological Innovation. Econ. Rev. 2019, 6, 17–30. [Google Scholar]
- Lesage, J.P.; Pace, R.K. Spatial Econometric Modeling of Origin-Destination Flows. J. Reg. Sci. 2010, 48, 941–967. [Google Scholar] [CrossRef]
- Corrado, L.; Fingleton, B. Where is the Economics in Spatial Econometrics? J. Reg. Sci. 2012, 52, 210–239. [Google Scholar] [CrossRef]
- Aoki, S.A. Simple Accounting Framework for the Effect of Resource Misallocation on Aggregate Productivity. J. Jpn. Int. Econ. 2012, 26, 473–494. [Google Scholar] [CrossRef]
- Chari, V.V.; Kehoe, P.J.; McGrattan, E.R. Accounting for the Great Depression. Am. Econ. Rev. 2002, 92, 22–27. [Google Scholar] [CrossRef][Green Version]
- Jin, L.Q.; Hu, S.C.; Zhang, B.C. Research on the Structural Mismatch Degree of Innovation Resources in China. Sci. Res. 2019, 37, 545–555. [Google Scholar]
- Wang, W.; Sun, Z. Measurement of R&D Resource Mismatch among Regions in China and Analysis of Influencing Factors. Financ. Trade Econ. 2020, 5, 67–83. [Google Scholar]
- Carvache-Franco, O.; Carvache-Franco, M.; Carvache-Franco, W.; Bustamante-Ubilla, M.A. The Relationship between Human-Capital Variables and Innovative Performance: Evidence from Colombia. Sustainability 2022, 14, 3294. [Google Scholar] [CrossRef]
- Bai, J.H.; Bian, Y.C. Market Distortion and Efficiency Loss of China’s Innovative Production. Chin. Ind. Econ. 2016, 11, 39–55. [Google Scholar]
- Hall, B.H.; Mairesse, J. Exploring the Relationship between R&D and Productivity in French Manufacturing Firms. J. Econom. 1995, 65, 263–293. [Google Scholar]
- Zhang, J.W.; Lin, Y.R. Local Government Competition, Capital Flow and Spatial Balance of Regional Economy. J. Yunnan Univ. Financ. Econ. 2018, 34, 23–33. [Google Scholar]
- Xiao, Y.; Liu, X.B. Does Tax Competition Promote the Transformation and Upgrading of Industrial Structures? —Based on the Dual Perspective of Total Amount and Structure. Financ. Res. 2018, 5, 60–74. [Google Scholar]
- Zhang, K.L.; Liu, Q.J. Household Registration System Competition and Its Economic Development Effect—An Empirical Test Based on Dynamic Spatial Durbin Model. J. Zhongnan Univ. Econ. Law 2019, 4, 78–88. [Google Scholar]
- Adikari, A.; Liu, H.; Marasinghe, M. Inward Foreign Direct Investment-Induced Technological Innovation in Sri Lanka? Empirical Evidence Using ARDL Approach. Sustainability 2021, 13, 7334. [Google Scholar] [CrossRef]
- Lee, L.F. Asymptotic Distributions of Quasi-Maximum Likelihood Estimators for Spatial Autoregressive Models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Deng, Y.; You, D.; Wang, J. Research on the Nonlinear Mechanism Underlying the Effect of Tax Competition on Green Technology Innovation-An Analysis Based on the Dynamic Spatial Durbin Model and the Threshold Panel Model. Resour. Policy 2022, 76, 102545. [Google Scholar] [CrossRef]
- Nakada, M. Environmental Tax Reform and Growth: Income Tax Cuts or Profits Tax Reduction. Environ. Resour. Econ. 2010, 47, 549–565. [Google Scholar] [CrossRef]
- Deng, J.; Zhang, N.; Ahmad, F.; Draz, M.U. Local Government Competition, Environmental Regulation Intensity and Regional Innovation Performance: An Empirical Investigation of Chinese Provinces. Int. J. Environ. Res. Public Health 2019, 16, 2130. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhang, L. Entrepreneurial Urban Governance and Talent Policy: The Case of Shanghai. China Popul. Dev. Stud. 2020, 4, 25–44. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, H.; Jiang, J.; Yan, W. Impact of Green Finance and Environmental Regulations on the Green Innovation Efficiency in China. Sustainability 2022, 14, 3026. [Google Scholar] [CrossRef]
- Ruan, J.Y. An Empirical Study on the Efficiency of Green Innovation of Industrial Enterprises in China. In Proceedings of the 14th International Conference on Innovation and Management, Tokyo, Japan, 7–10 February 2017; pp. 554–559. [Google Scholar]
- Yin, J.H.; Wang, S.; Gong, L.D. The Effects of Factor Market Distortion and Technical Innovation on China’s Electricity Consumption. J. Clean. Prod. 2018, 188, 195–202. [Google Scholar] [CrossRef]





| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|---|
| 0.118 ** (1.702) | −0.007 (0.335) | 0.087 * (1.34) | 0.083 ** (1.96) | 0.204 *** (2.945) | 0.083 *** (2.67) | 0.144 ** (2.124) | |
| −0.017 (0.201) | −0.067 (−0.385) | −0.072 (−0.428) | −0.061 (−0.349) | 0.035 (0.781) | −0.003 (0.558) | 0.056 (1.045) | |
| Year | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 0.181 ** (2.3) | 0.168 ** (2.12) | 0.144 ** (2.12) | 0.244 *** (3.13) | 0.138 ** (2.08) | 0.133 ** (1.862) | 0.068 (1.19) | |
| 0.160 ** (2.109) | 0.164 ** (2.100) | 0.056 (1.045) | 0.241 *** (3.03) | 0.150 ** (2.226) | 0.133 ** (1.89) | 0.118 ** (1.68) | |
| Year | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| 0.111 ** (1.69) | 0.045 (0.91)0.905 | 0.079 * (1.31) | 0.08 (1.26) | 0.22 *** (2.73) | 0.204 *** (2.51) | 0.158 ** (2.04) | |
| 0.084 * (1.35) | 0.140 ** (1.87) | 0.135 ** (1.82) | 0.104 * (1.47) | 0.132 ** (1.75) | 0.121 * (1.63) | 0.109 * (1.52) |
| Excom | Taxcom | Inscom | LMerr | LMlag | R2 | Individual | Time | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.494 *** (4.056) | 0.154 *** (3.321) | 0.903 ** (2.481) | Y | 0.377 *** (6.306) | [0.345] | [0.009] | 0.2797 | N | Y | |
| 0.899 *** (2.596) | 0.123 *** (2.791) | 0.906 *** (2.595) | Y | 0.361 *** (6.027) | [0.343] | [0.023] | 0.1286 | N | Y |
| Direct Effect | Indirect Effect | Total Effect | ||||
|---|---|---|---|---|---|---|
| Effect Category Variable | ||||||
| excom | 1.549 *** (4.015) | 0.935 ** (2.571) | 0.872 *** (3.083) | 0.491 ** (2.219) | 2.421 *** (3.984) | 1.426 ** (2.558) |
| taxcom | 0.157 *** (3.429) | 0.125 *** (2.875) | 0.088 *** (2.697) | 0.066 ** (2.366) | 0.245 *** (3.354) | 0.190 *** (2.828) |
| inscom | 0.959 *** (2.655) | 0.958 *** (2.774) | 0.544 ** (2.274) | 0.505 ** (2.396) | 1.503 *** (2.612) | 1.464 *** (2.757) |
| Province | Innovative Talents | Innovation Capital | ||||
|---|---|---|---|---|---|---|
| Excome | Taxcom | Inscom | Excome | Taxcom | Inscom | |
| Beijing | 0.599 | 0.312 | 0.605 | −0.239 | −0.209 | −0.370 |
| Tianjin | 0.044 | 0.033 | 0.033 | −0.022 | −0.038 | −0.037 |
| Hebei | −0.005 | −0.008 | 0.001 | 0.024 | 0.127 | 0.000 |
| Shanxi | −0.029 | −0.029 | −0.002 | 0.046 | 0.125 | 0.005 |
| Inner Mongolia | −0.009 | −0.017 | −0.001 | 0.073 | 0.185 | 0.010 |
| Liaoning | 0.072 | 0.126 | 0.004 | 0.033 | 0.125 | −0.002 |
| Jilin | −0.030 | −0.045 | −0.001 | 0.001 | 0.016 | 0.001 |
| Heilongjiang | −0.021 | −0.030 | 0.000 | 0.141 | 0.392 | 0.019 |
| Shanghai | 0.307 | 0.181 | 0.351 | −0.151 | −0.106 | −0.257 |
| Jiangsu | 0.029 | 0.042 | 0.008 | 0.065 | 0.122 | 0.020 |
| Zhejiang | 0.200 | 0.411 | 0.101 | 0.556 | 1.215 | 0.505 |
| Anhui | −0.006 | −0.031 | −0.001 | 0.106 | 0.117 | −0.073 |
| Fujian | −0.012 | −0.032 | −0.004 | 0.057 | 0.141 | 0.013 |
| Jiangxi | −0.027 | −0.048 | 0.004 | 0.019 | 0.027 | −0.005 |
| Shandong | 0.071 | 0.259 | 0.001 | 0.002 | 0.180 | 0.001 |
| Henan | −0.052 | −0.128 | 0.029 | 0.094 | 0.383 | −0.052 |
| Hubei | −0.059 | −0.127 | 0.014 | −0.019 | −0.009 | 0.003 |
| Hunan | −0.008 | 0.015 | 0.007 | 0.124 | 0.517 | −0.016 |
| Guangdong | 0.085 | 0.207 | 0.076 | 0.133 | 0.262 | 0.181 |
| Guangxi | 0.000 | 0.000 | 0.005 | 0.099 | 0.226 | −0.014 |
| Hainan | 0.012 | 0.010 | 0.001 | 0.048 | 0.045 | 0.004 |
| Chongqing | 0.073 | 0.073 | −0.027 | 0.204 | 0.383 | −0.149 |
| Sichuan | 0.013 | −0.052 | −0.008 | −0.028 | −0.119 | 0.007 |
| Guizhou | 0.007 | 0.002 | −0.005 | 0.143 | 0.119 | −0.071 |
| Yunnan | 0.014 | 0.009 | 0.001 | 0.226 | 0.227 | 0.029 |
| Shaanxi | 0.011 | 0.024 | 0.005 | −0.106 | −0.183 | −0.019 |
| Gansu | −0.052 | −0.061 | 0.001 | −0.001 | −0.006 | 0.001 |
| Qinghai | −0.128 | −0.081 | 0.008 | 0.028 | 0.020 | −0.002 |
| Ningxia | −0.008 | −0.007 | −0.001 | 0.048 | 0.048 | 0.009 |
| Xinjiang | 0.036 | 0.025 | 0.001 | 0.280 | 0.433 | −0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Nan, T.; Wang, X. Causes and Evolution Characteristics of Green Innovation Efficiency Loss: The Perspective of Factor Mismatch under Local Government Competition. Sustainability 2022, 14, 8338. https://doi.org/10.3390/su14148338
Liu F, Nan T, Wang X. Causes and Evolution Characteristics of Green Innovation Efficiency Loss: The Perspective of Factor Mismatch under Local Government Competition. Sustainability. 2022; 14(14):8338. https://doi.org/10.3390/su14148338
Chicago/Turabian StyleLiu, Fei, Ting Nan, and Xinliang Wang. 2022. "Causes and Evolution Characteristics of Green Innovation Efficiency Loss: The Perspective of Factor Mismatch under Local Government Competition" Sustainability 14, no. 14: 8338. https://doi.org/10.3390/su14148338
APA StyleLiu, F., Nan, T., & Wang, X. (2022). Causes and Evolution Characteristics of Green Innovation Efficiency Loss: The Perspective of Factor Mismatch under Local Government Competition. Sustainability, 14(14), 8338. https://doi.org/10.3390/su14148338








