TRNSYS Simulation and Experimental Validation of Internal Temperature and Heating Demand in a Glass Greenhouse
Abstract
1. Introduction
Scope of the Study
2. Materials and Methods
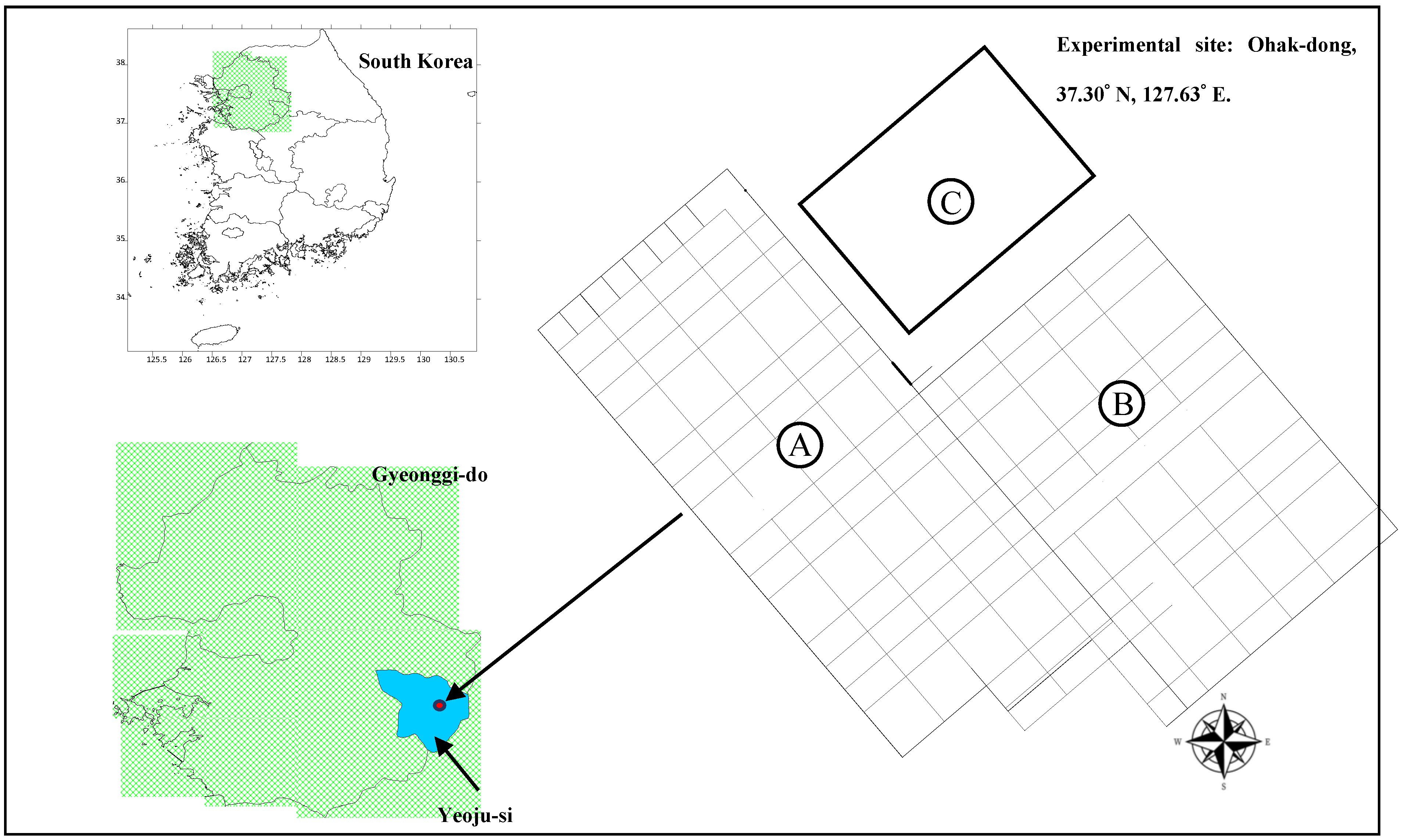
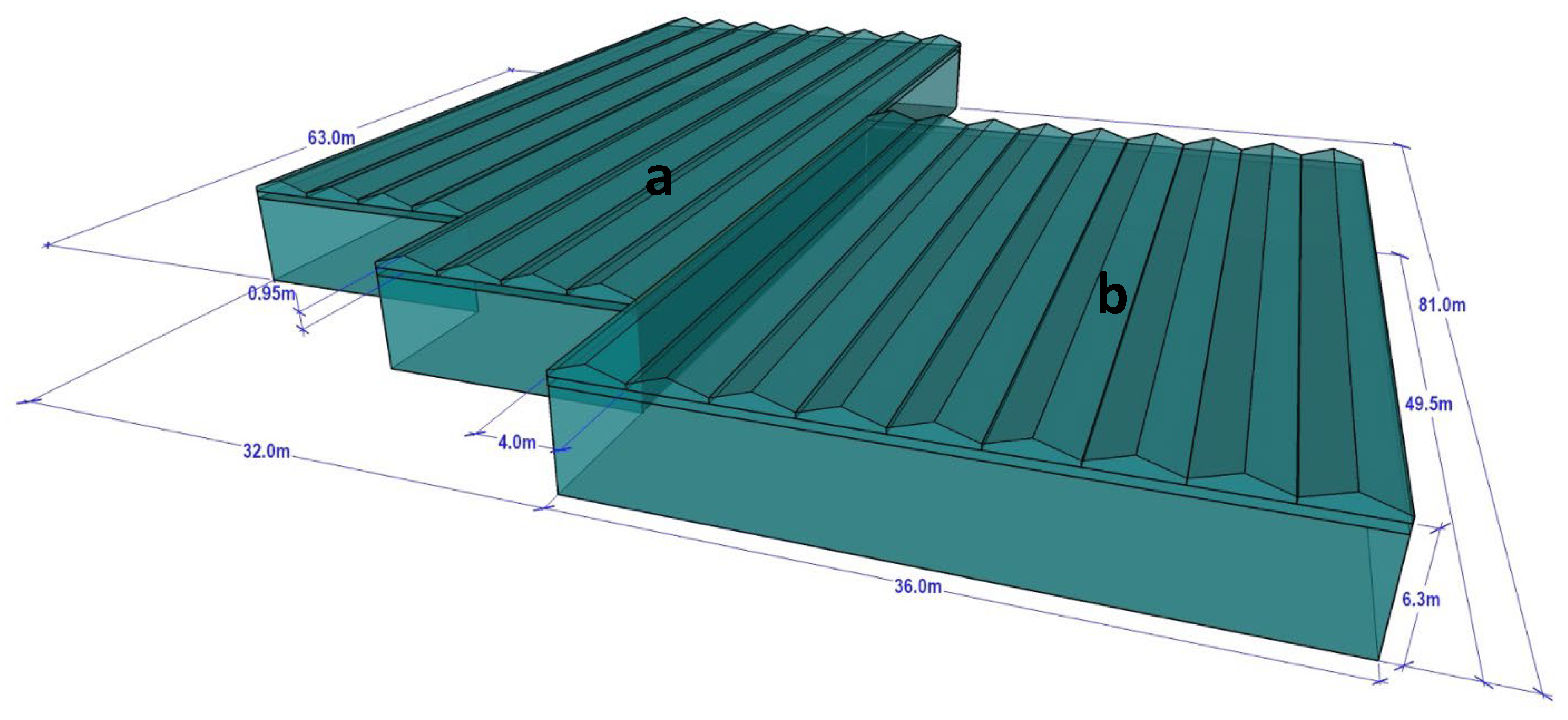
2.1. Description of the Experimental Site
2.2. Greenhouse Material Properties
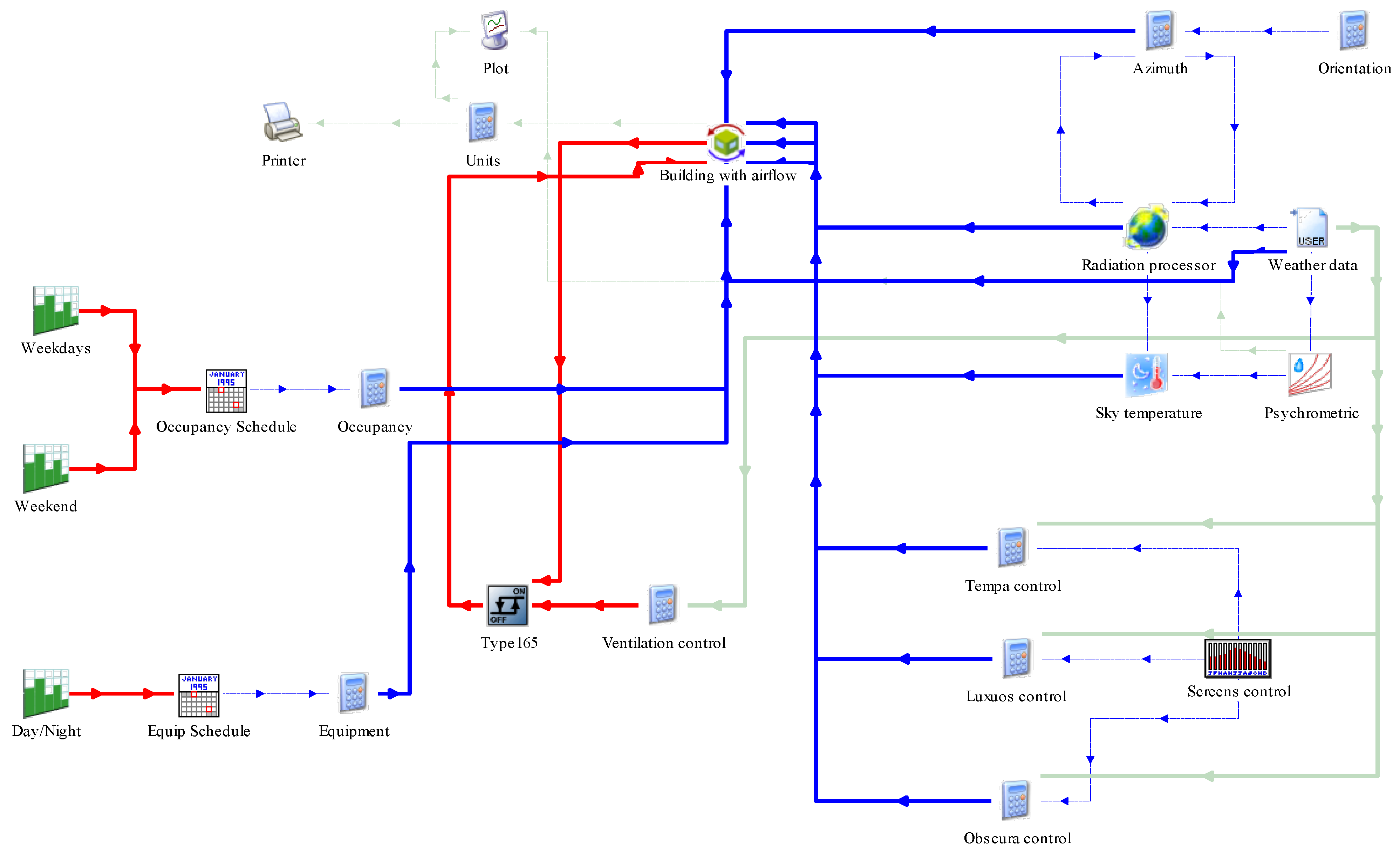
2.3. Greenhouse Simulation Modelling in TRNSYS 18
2.3.1. Beam Radiation Distribution
2.3.2. Diffuse Radiation Distribution
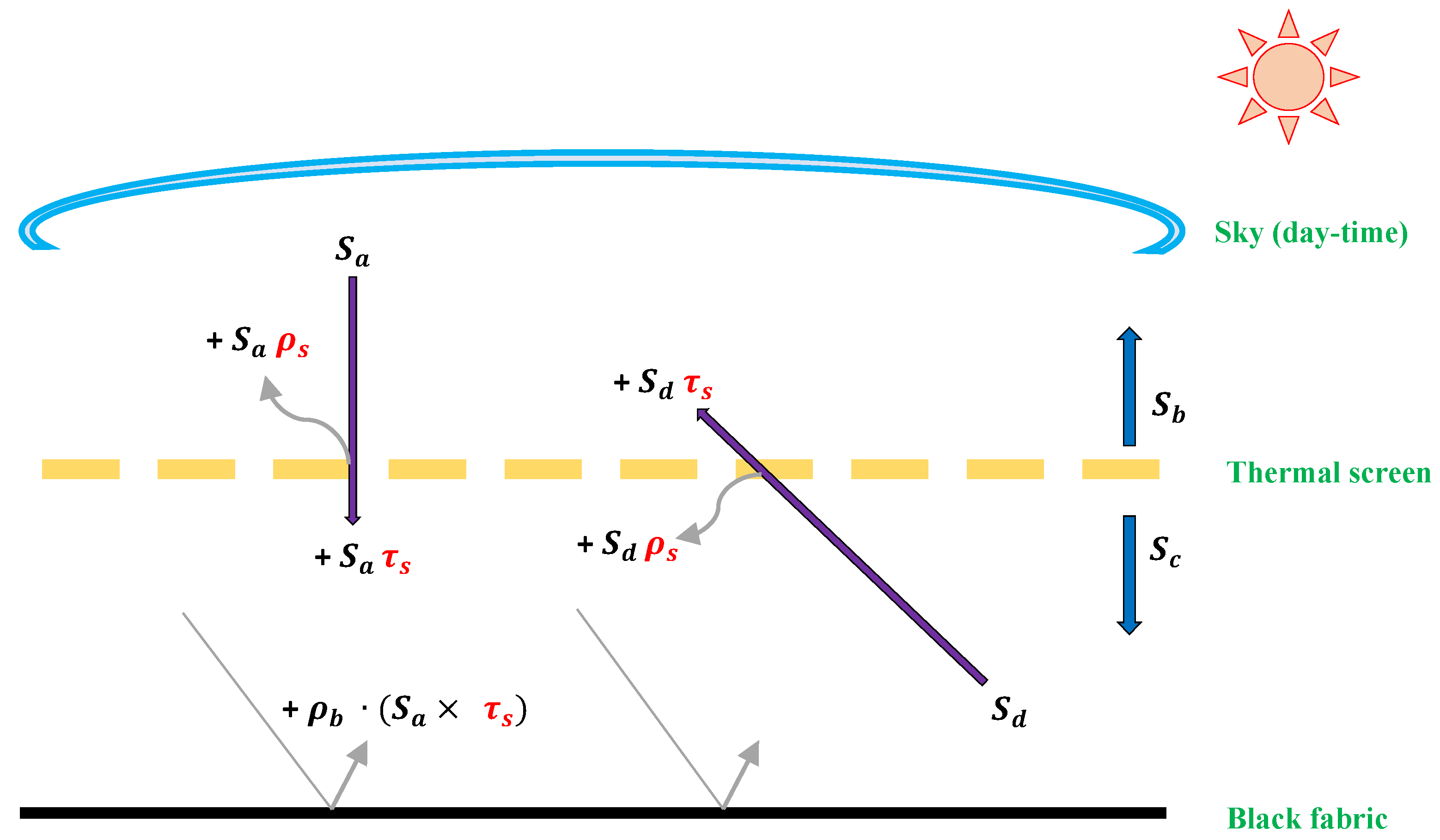
2.3.3. Longwave Radiation Distribution
2.4. BES Model Validation
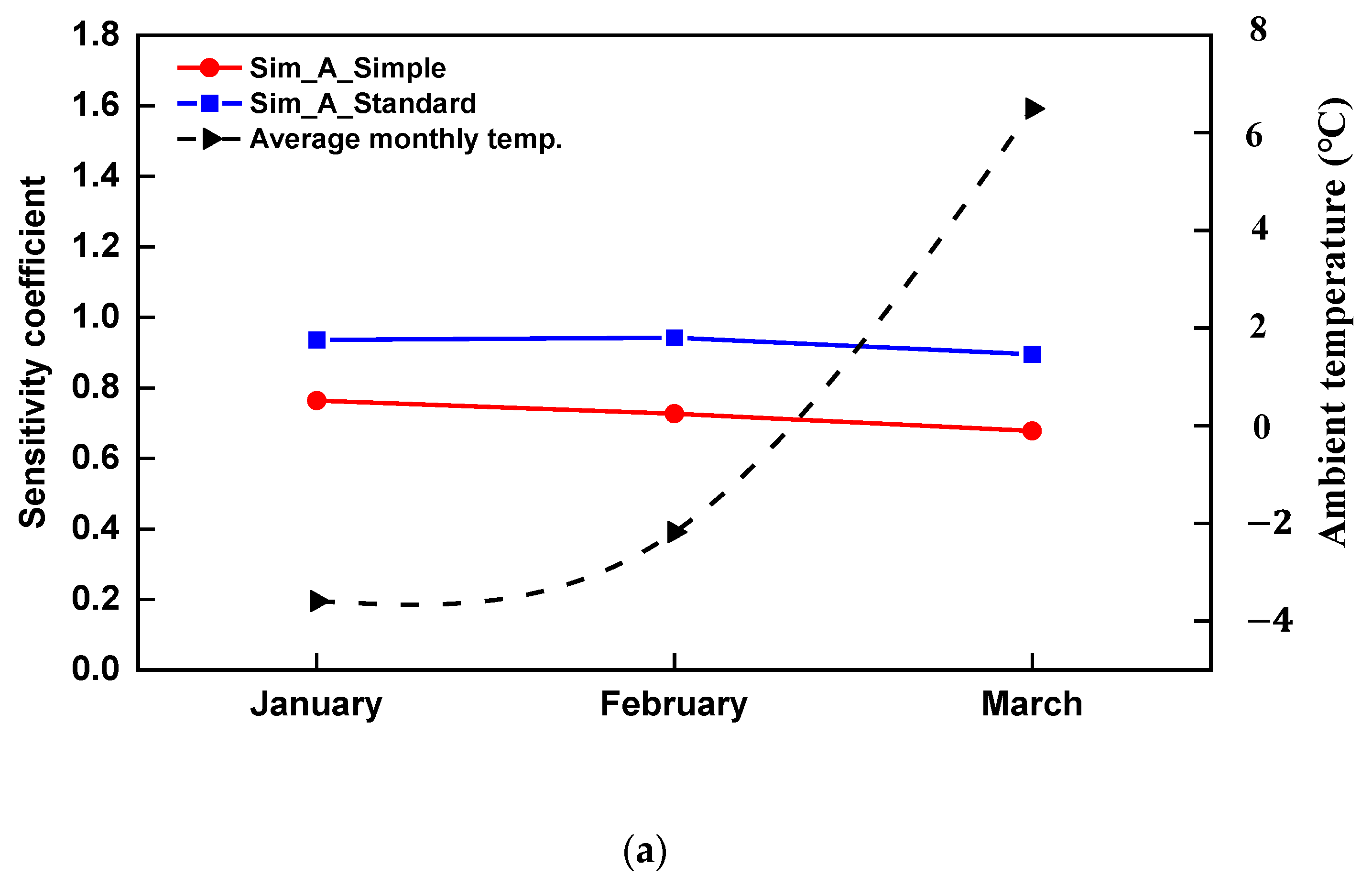
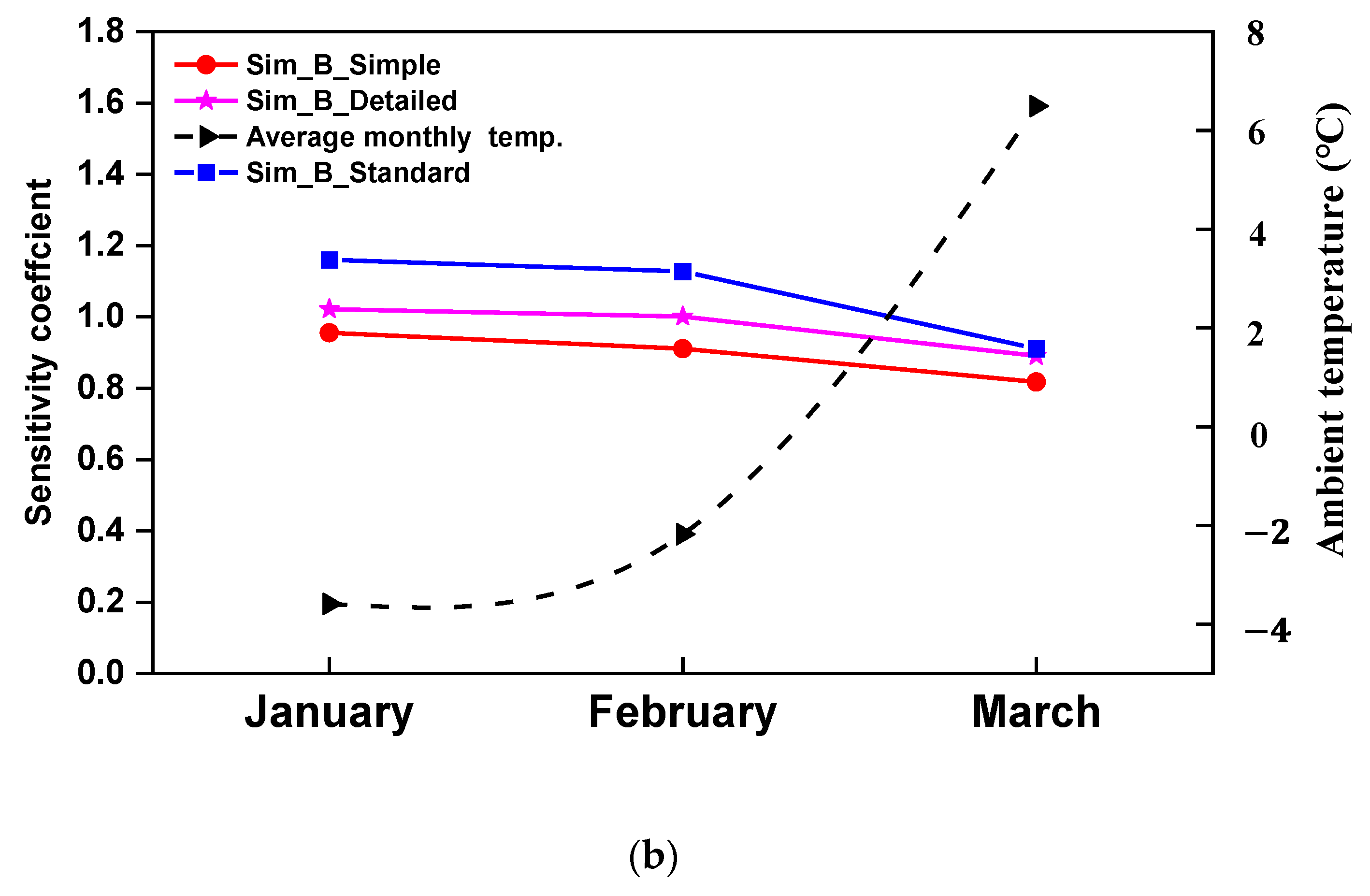
2.5. Sensitivity Analysis
3. Results and Discussion
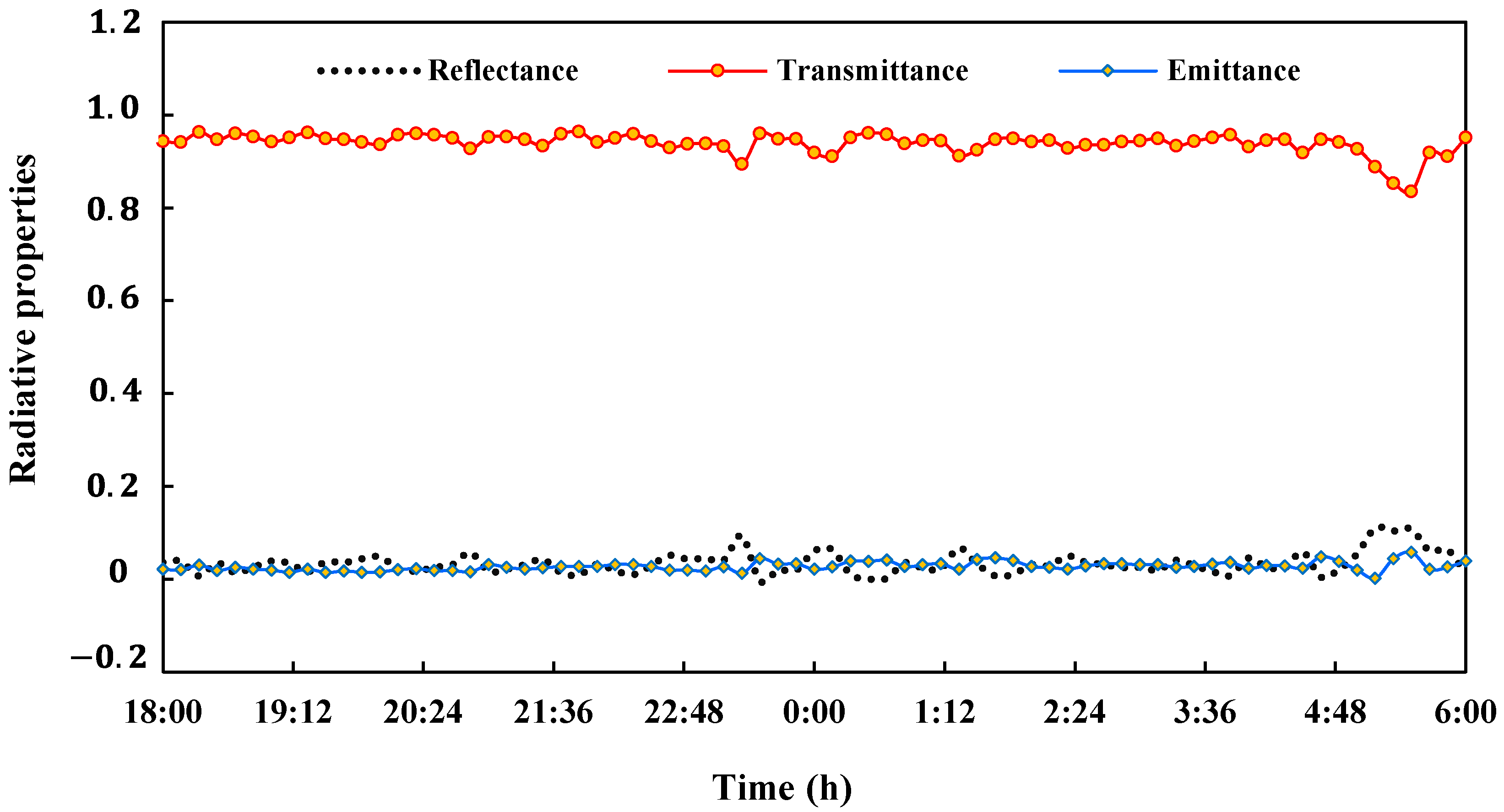
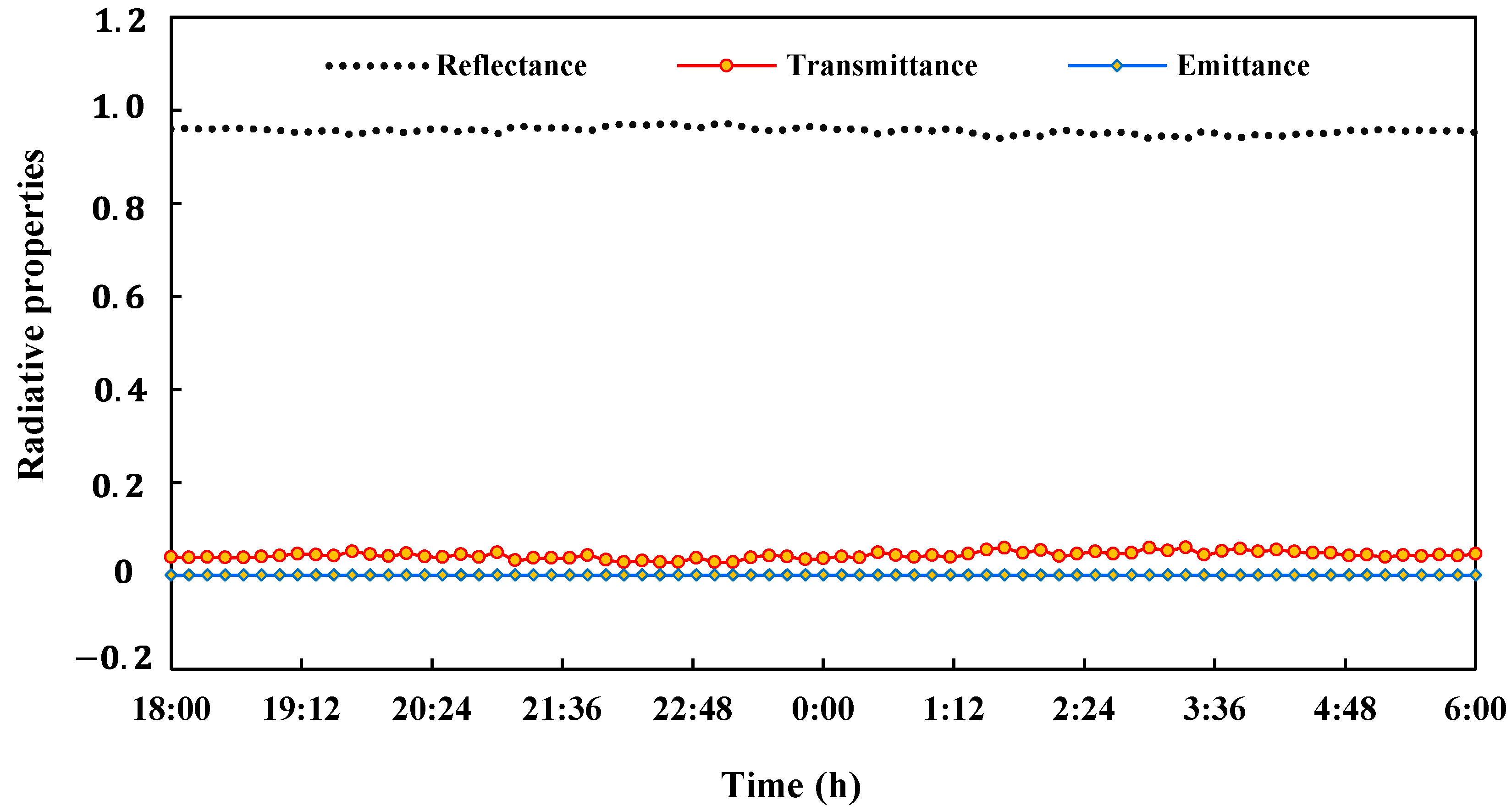
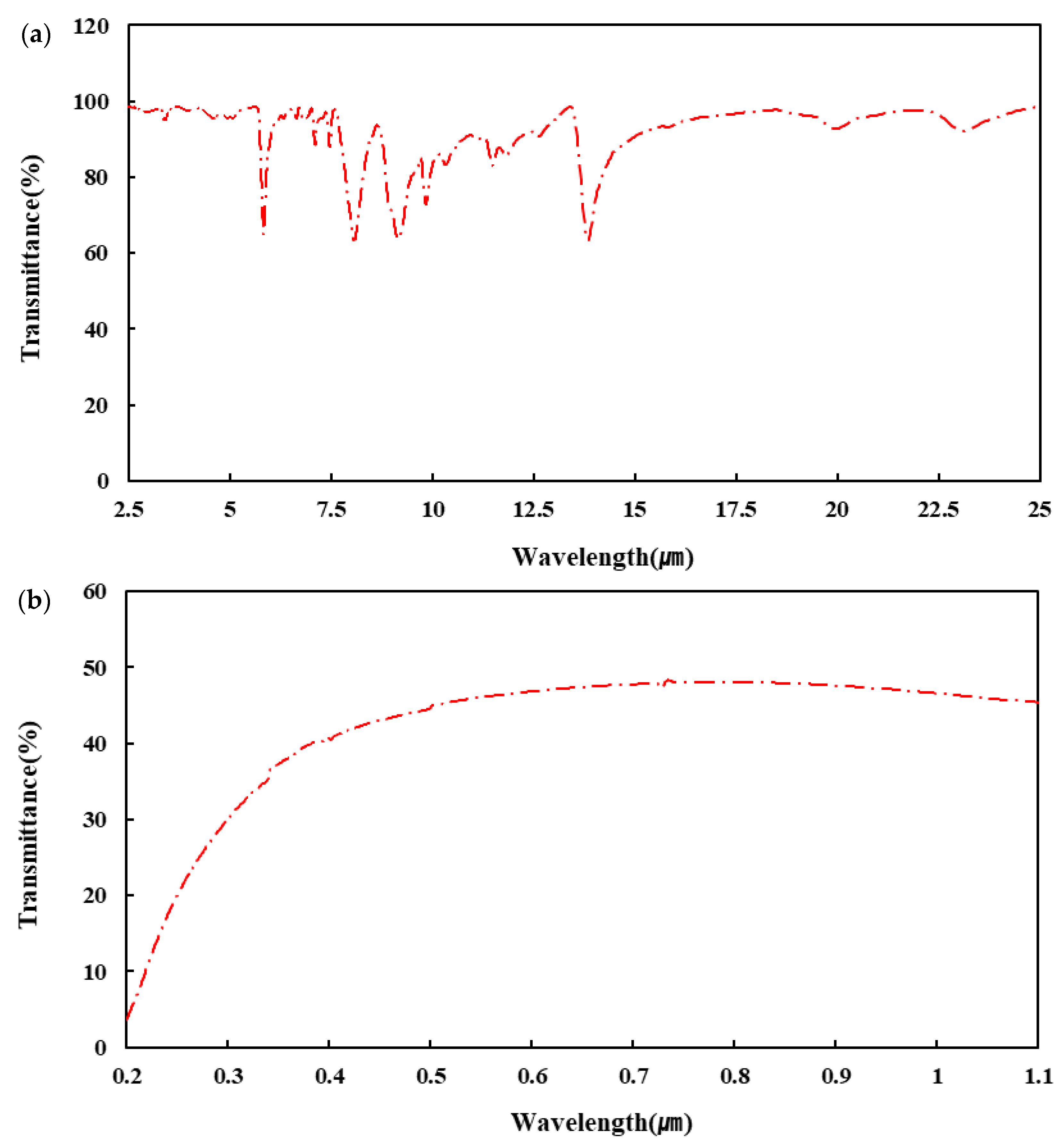
3.1. Radiometric Properties of the Novel Greenhouse Materials
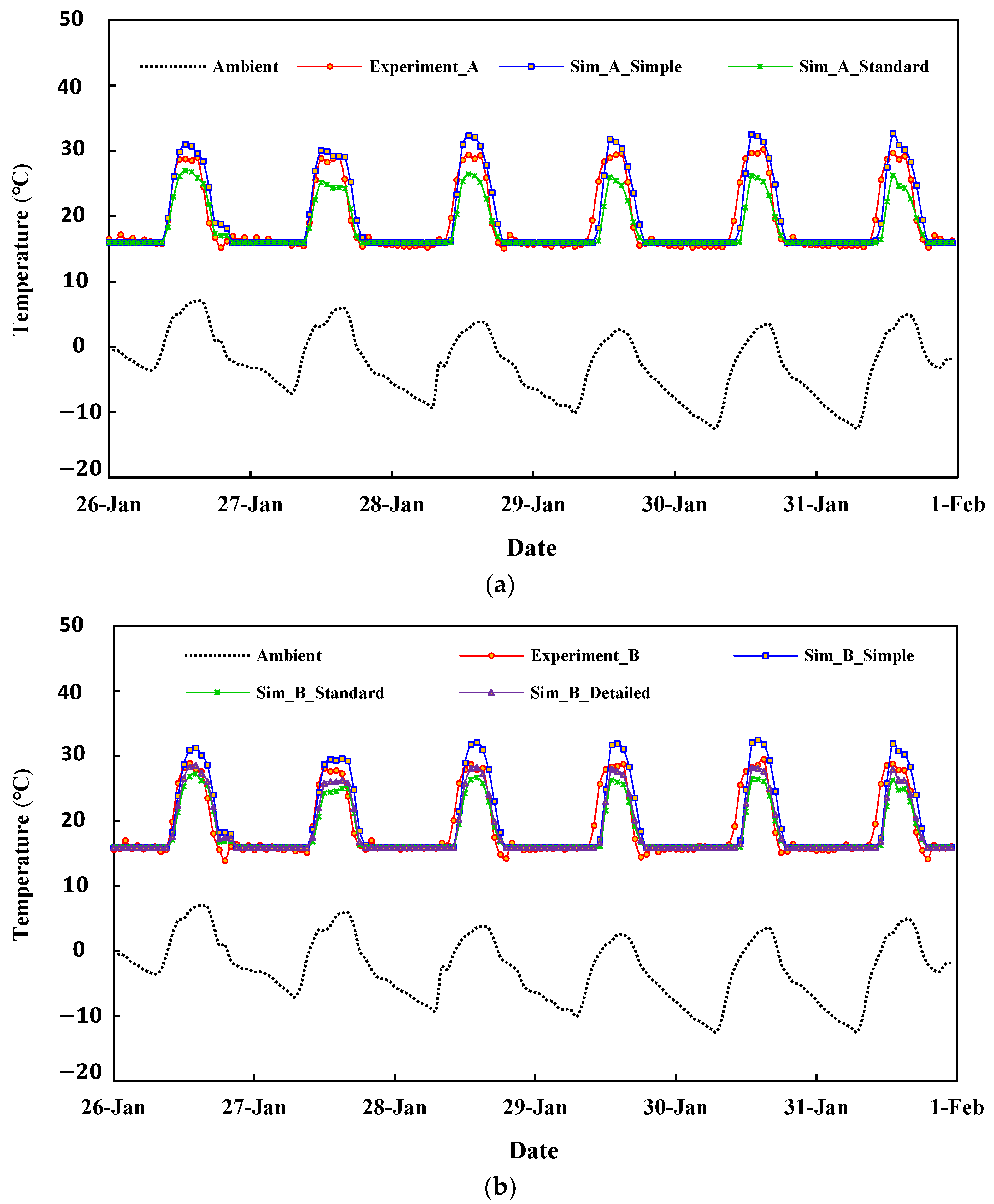
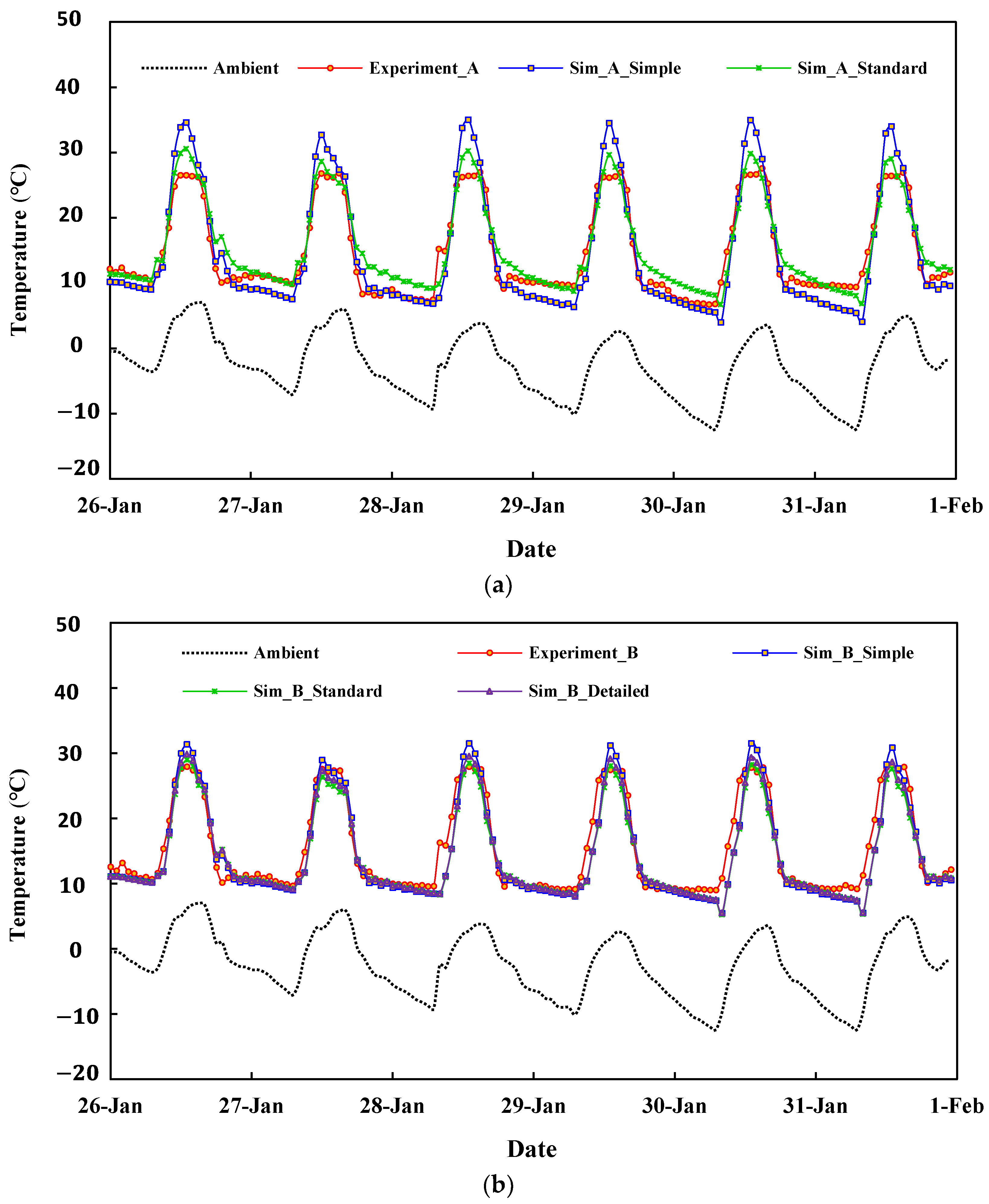
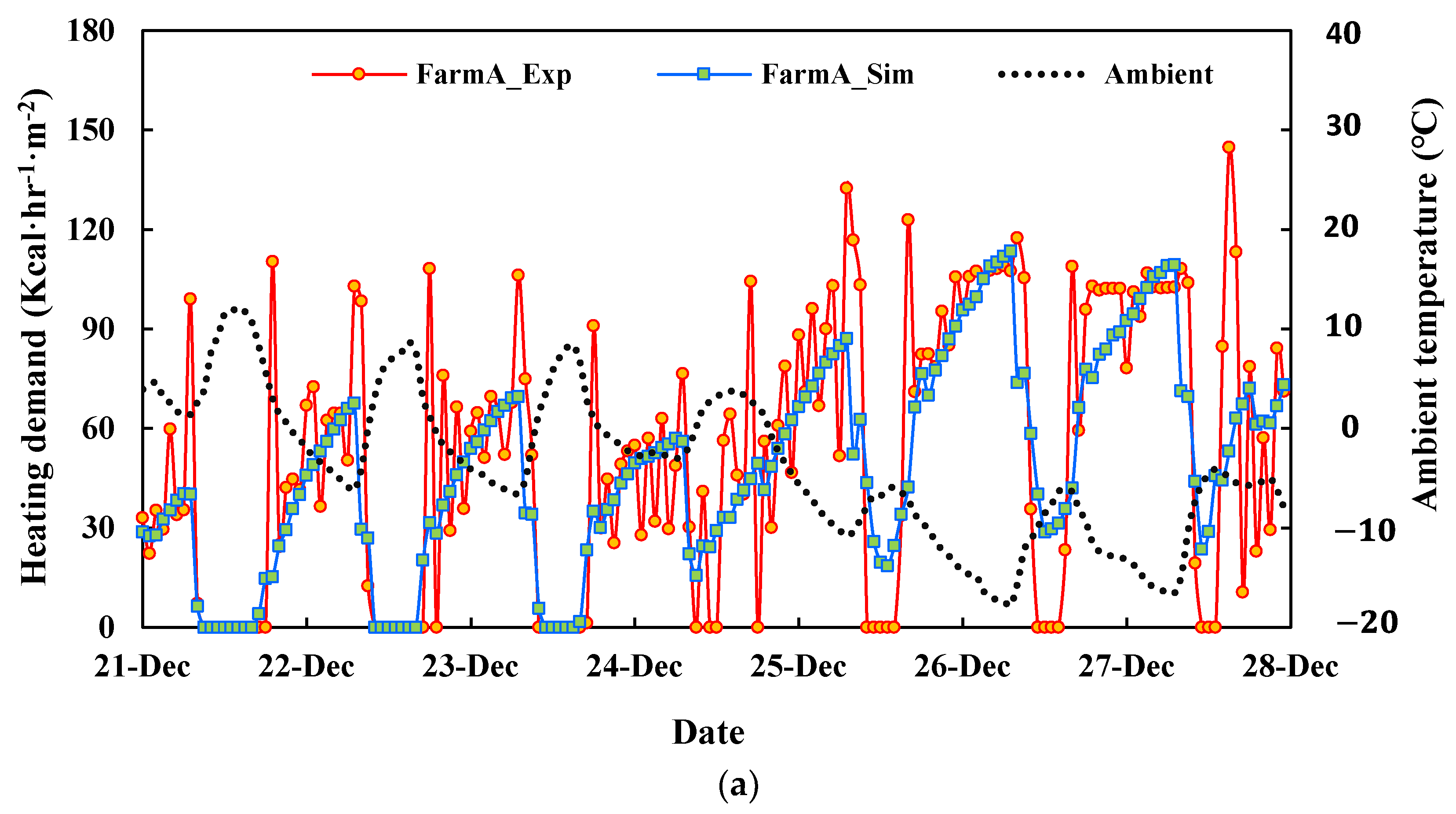
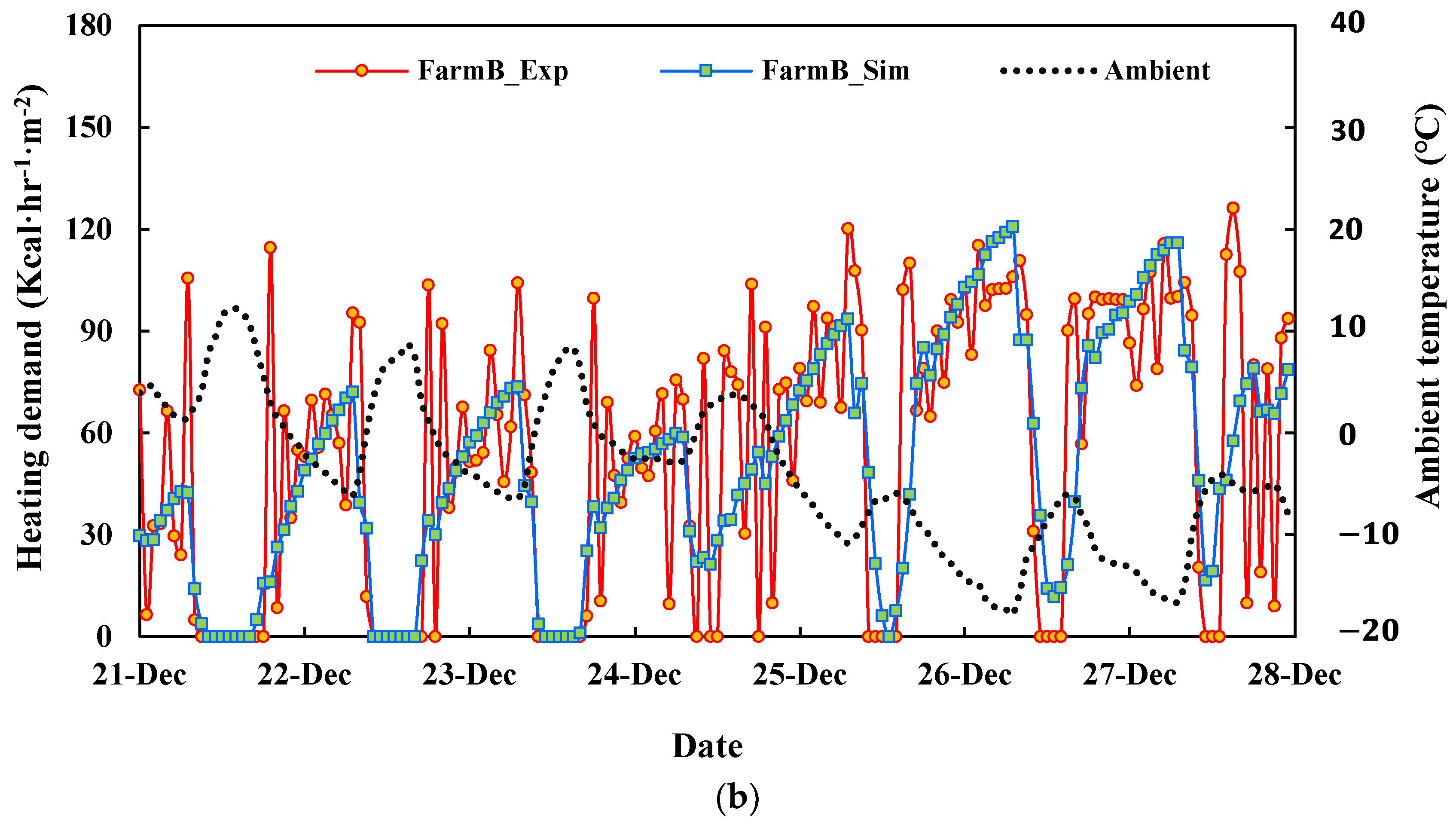
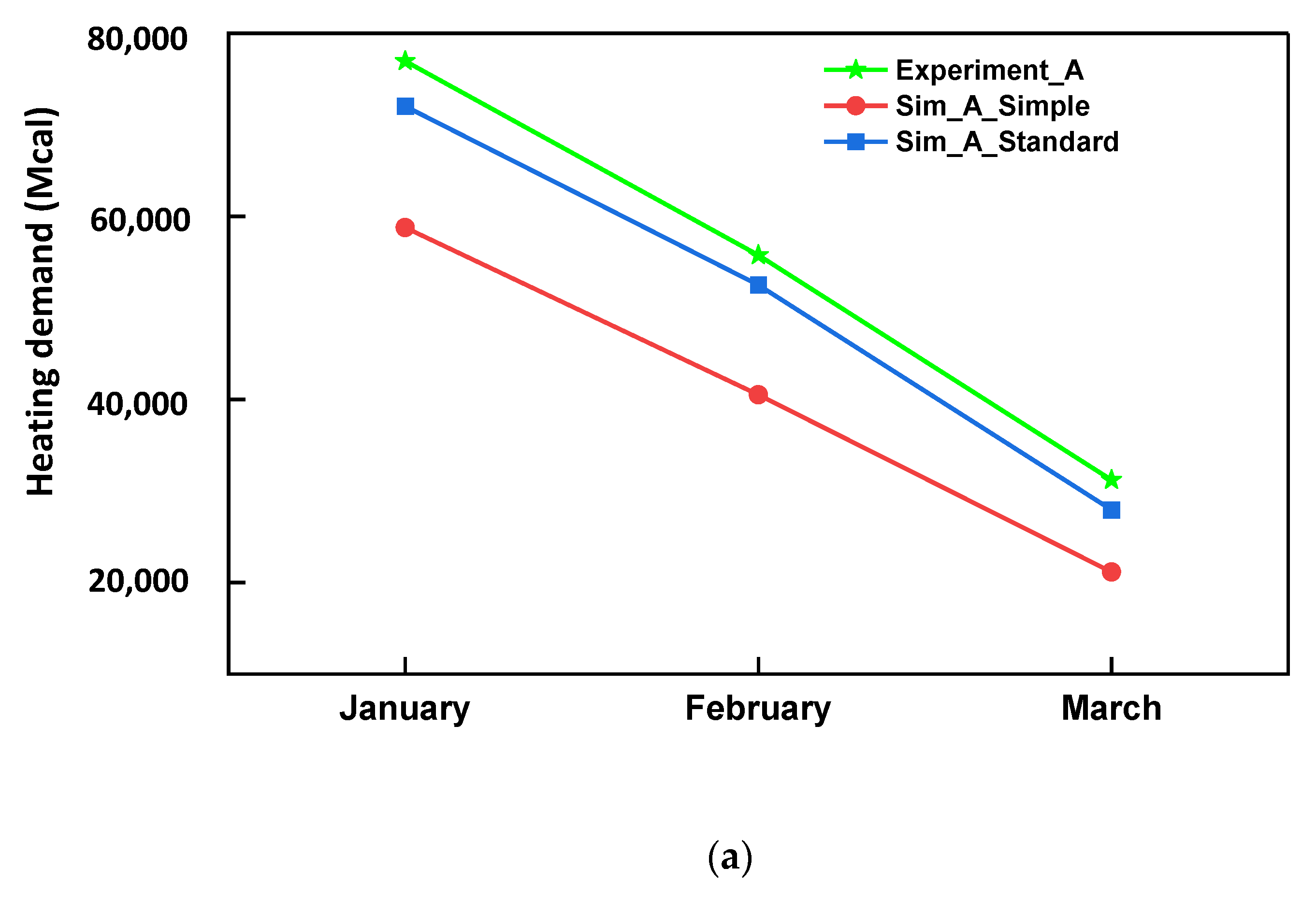
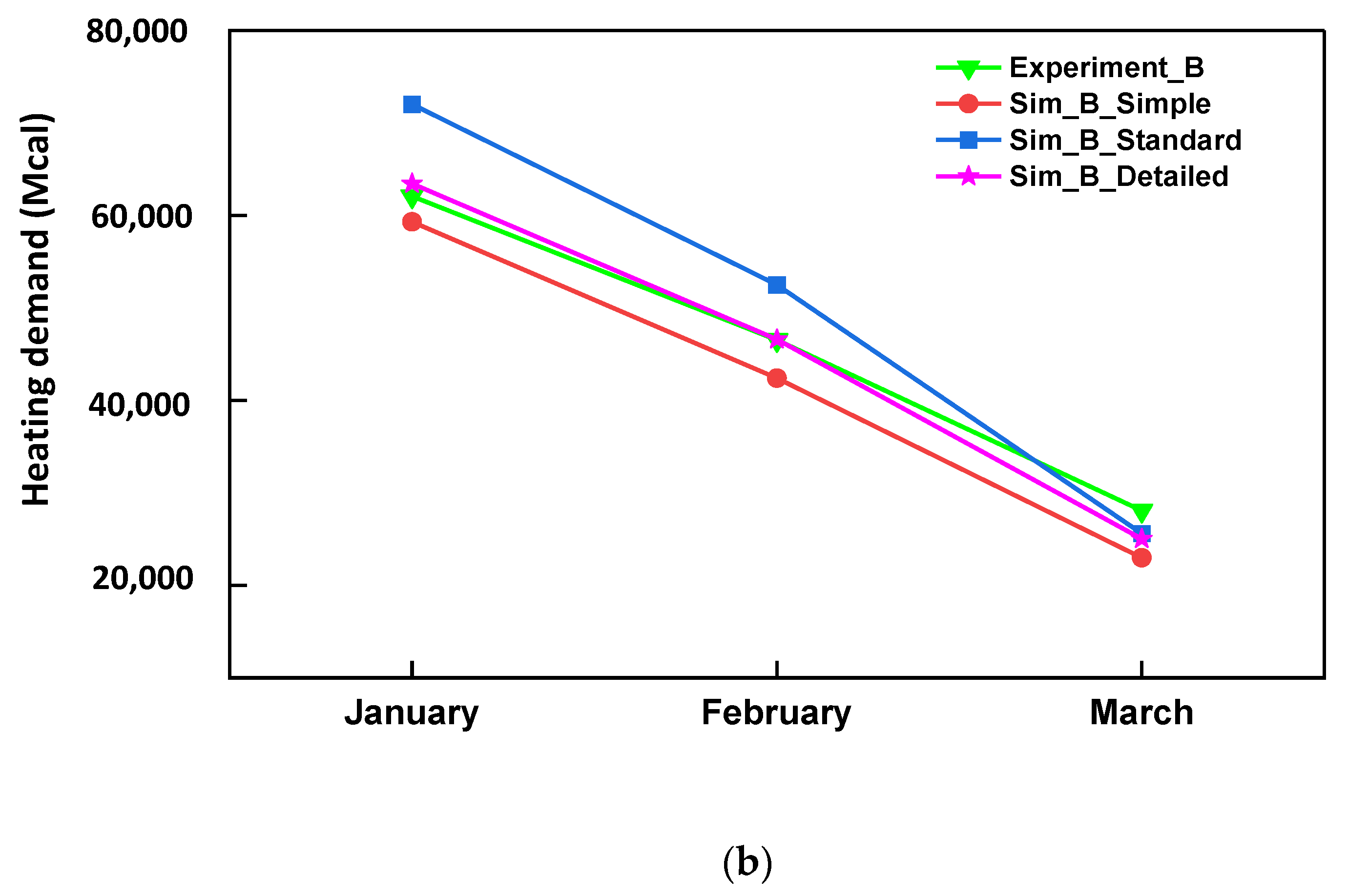
3.2. Comparison of Results of the TRNSYS Model with the Experimental Measurements
3.3. Limitation of the Study and Future Work
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Inside surface area, m2 | |
| Thermal capacitance of the zone masses, kJ | |
| Specific heat capacity of water, kcalkg−1−1 | |
| Es | Emissive power of the material, Wm−2 |
| View factor of the sky | |
| Gebhart factor | |
| Auxiliary matrix | |
| Transpose of | |
| Greenhouse height, m | |
| Convective heat transfer coefficient at the outside surface, Wm−2K−1 | |
| Reference height, m | |
| Heat of vaporisation of water, kJ | |
| Mass flow rate of water, kgh−1 | |
| Mass flow rate due to couplings of two zones, kg | |
| Mass flow rate of infiltration air, kg | |
| Mass flow rate of ventilation air, kg | |
| Effective moisture capacitance, kg | |
| Combined convective and radiative heat flux in the inner surface, kJ | |
| Combined convective and radiative heat flux to the outside surface, kJ | |
| Convective heat flux to the outside surface, kJ | |
| Radiative heat flux to the outside surface, kJ | |
| Q | Energy consumed, kcalh−1 |
| Qa | Inward sky radiation toward the material, Wm−2 |
| Qb | Upward longwave radiation from the material to the sky, Wm−2 |
| Qc | Upward longwave radiation from the material to the black fabric during the night, Wm−2 |
| Heat conduction through the building envelope, kJ | |
| Convective heat flux between the zone and the inner surface, kJ | |
| Convective heat flux between the external surface and ambient, kJ | |
| Gains due to inter-connected air nodes kJ | |
| Internal convective gains, kJ | |
| Qd | Inward longwave radiation from the black fabric toward the material, Wm−2 |
| Radiative heat flux, kJ | |
| Infiltration heat flux, kJ | |
| Solar radiation absorbed on all internal shading devices of the zone, kJ | |
| Latent energy flux of the zone, kJ | |
| Longwave radiation exchange between two inner surfaces, kJ | |
| Longwave radiation emitted by the outside surfaces to the Surroundings, kJ | |
| Sensible heat flux of the zone, kJ | |
| Solar radiation entering an air node through external windows, kJ | |
| Absorbed solar gain on the outside opaque surfaces, kJ | |
| Convective gain from surfaces, kJ | |
| Ventilation heat flux, kJ | |
| Resistance of each surface, Ohms | |
| Equivalent resistance of all the surfaces, Ohms | |
| Sa | Downward shortwave radiation from the sky, Wm−2 |
| Sb | Outward shortwave radiation from the material toward the sky, Wm−2 |
| Sc | Outward shortwave radiation from the material toward the black material, Wm−2 |
| Sd | Radiation from the black fabric toward the material, Wm−2 |
| Temperature difference, | |
| Change in simulation time step | |
| T | Temperature vector of the enclosure |
| Outside surface temperature, | |
| Surface temperature, | |
| Fictive temperature difference between the ground and sky, | |
| Equivalent air node temperatures, | |
| Temperature of the zone masses, | |
| Fictive ground temperature, | |
| Fictive sky temperature, | |
| Surface air node temperatures, | |
| Ambient temperature, | |
| Tstar | Artificial temperature of the air node, |
| Calculated wind speed, ms−1 | |
| Reference wind speed, ms−1 | |
| Ambient humidity ratio, | |
| Adjacent air node humidity ratio, | |
| Air node humidity ratio, | |
| Humidity ratio of ventilation air | |
| Internal humidity gain, | |
| Experimentally measured data | |
| Simulated data and | |
| Mean of the experimentally measured data | |
| Greek symbols | |
| ∝ | Power law exponent |
| ρL | Longwave reflectance of the material |
| τL | Longwave transmittance of the material |
| Stefan–Boltzmann constant | |
| Emissivity of the black fabric | |
| ρs | Reflectance of the material |
| τS | Transmittance of the material |
| Longwave emissivity of the outside surface from the WINDOW library | |
| Diagonal matrices describing reflectivity | |
| Diagonal matrices describing emissivity | |
| Abbreviations | |
| A | Diagonal matrix describing the surface areas |
| I | Identity matrix |
| F | View factor |
| ir | Longwave range of the radiation spectrum (infrared) |
| BES | Building Energy Simulations |
| TRNSYS | Transient System Simulation |
| NSE | Nash–Sutcliffe Efficiency Coefficient |
| CSG | Chinese-style Solar Greenhouse |
| HG | Horticultural Glass |
| KMA | Korean Meteorological Administration |
| QTM | Quick Thermal Meter |
| RBM | Radiation Balance Method |
| SC | Sensitivity Coefficient |
| OP | Output |
| IP | Input |
References
- Baudoin, W.; Nono-Womdim, R.; Lutaladio, N.; Hodder, A.; Castilla, N.; Leonardi, C.; De Pascale, S.; Qaryouti, M. Cultural Practices and Environment. In Hobby Hydroponics; CRC Press: Boca Raton, FL, USA, 2013; pp. 42–55. ISBN 9789251076491. [Google Scholar]
- Akpenpuun, T.D.; Na, W.H.; Ogunlowo, Q.O.; Rabiu, A.; Adesanya, M.A.; Addae, K.S.; Kim, H.T.; Lee, H.-W. Effect of Glazing Configuration as an Energy-Saving Strategy in Naturally Ventilated Greenhouses for Strawberry (Seolhyang Sp.) Cultivation. J. Agric. Eng. 2021, 52, 1177. [Google Scholar] [CrossRef]
- Ogunlowo, Q.O.; Akpenpuun, T.D.; Na, W.H.; Rabiu, A.; Adesanya, M.A.; Addae, K.S.; Kim, H.T.; Lee, H.W. Analysis of Heat and Mass Distribution in a Single-and Multi-Span Greenhouse Microclimate. Agriculture 2021, 11, 891. [Google Scholar] [CrossRef]
- Banakar, A.; Montazeri, M.; Ghobadian, B.; Pasdarshahri, H.; Kamrani, F. Energy Analysis and Assessing Heating and Cooling Demands of Closed Greenhouse in Iran. Therm. Sci. Eng. Prog. 2021, 25, 101042. [Google Scholar] [CrossRef]
- Mazzeo, D.; Baglivo, C.; Panico, S.; Congedo, P.M. Solar Greenhouses: Climates, Glass Selection, and Plant Well-Being. Sol. Energy 2021, 230, 222–241. [Google Scholar] [CrossRef]
- Akpenpuun, T.D.; Na, W.H.; Ogunlowo, Q.O.; Rabiu, A.; Adesanya, M.A.; Addae, K.S.; Kim, H.T.; Lee, H.W. Effect of Greenhouse Cladding Materials and Thermal Screen Configuration on Heating Energy and Strawberry (Fragaria Ananassa Var. “Seolhyang”) Yield in Winter. Agronomy 2021, 11, 2498. [Google Scholar] [CrossRef]
- Baglivo, C.; Mazzeo, D.; Panico, S.; Bonuso, S.; Matera, N.; Congedo, P.M.; Oliveti, G. Complete Greenhouse Dynamic Simulation Tool to Assess the Crop Thermal Well-Being and Energy Needs. Appl. Therm. Eng. 2020, 179, 115698. [Google Scholar] [CrossRef]
- Zhang, Y.; Gauthier, L.; De Halleux, D.; Dansereau, B.; Gosselin, A. Effect of Covering Materials on Energy Consumption and Greenhouse Microclimate. Agric. For. Meteorol. 1996, 82, 227–244. [Google Scholar] [CrossRef]
- Rasheed, A.; Na, W.H.; Lee, J.W.; Kim, H.T.; Lee, H.W. Optimization of Greenhouse Thermal Screens for Maximized Energy Conservation. Energies 2019, 12, 3592. [Google Scholar] [CrossRef]
- Shukla, A.; Tiwari, G.N.; Sodha, M.S. Thermal Modeling for Greenhouse Heating by Using Thermal Curtain and an Earth-Air Heat Exchanger. Build. Environ. 2006, 41, 843–850. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. Energy Saving Techniques for Reducing the Heating Cost of Conventional Greenhouses. Biosyst. Eng. 2019, 178, 9–33. [Google Scholar] [CrossRef]
- Rasheed, A.; Lee, J.W.; Lee, H.W. Development of a Model to Calculate the Overall Heat Transfer Coefficient of Greenhouse Covers. Spanish J. Agric. Res. 2017, 15, e0208. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, H.; Zhang, S.; Wang, Y.; Chow, D. Modeling and Optimization of Environment in Agricultural Greenhouses for Improving Cleaner and Sustainable Crop Production. J. Clean. Prod. 2021, 285, 124843. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, I.B.; Lee, S.N.; Yeo, U.H.; Kim, J.G.; Kim, R.W.; Decano-Valentin, C. Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant. Agronomy 2021, 11, 1461. [Google Scholar] [CrossRef]
- Zhang, G.; Ding, X.; Li, T.; Pu, W.; Lou, W.; Hou, J. Dynamic Energy Balance Model of a Glass Greenhouse: An Experimental Validation and Solar Energy Analysis. Energy 2020, 198, 117281. [Google Scholar] [CrossRef]
- Baneshi, M.; Gonome, H.; Maruyama, S. Wide-Range Spectral Measurement of Radiative Properties of Commercial Greenhouse Covering Plastics and Their Impacts into the Energy Management in a Greenhouse. Energy 2020, 210, 118535. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. A Quasi-Steady State Model for Predicting the Heating Requirements of Conventional Greenhouses in Cold Regions. Inf. Process. Agric. 2018, 5, 33–46. [Google Scholar] [CrossRef]
- Katzin, D.; van Henten, E.J.; van Mourik, S. Process-Based Greenhouse Climate Models: Genealogy, Current Status, and Future Directions. Agric. Syst. 2022, 198, 103388. [Google Scholar] [CrossRef]
- Fabrizio, E. Energy Reduction Measures in Agricultural Greenhouses Heating: Envelope, Systems and Solar Energy Collection. Energy Build. 2012, 53, 57–63. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. Development of a Thermal Model for Simulation of Supplemental Heating Requirements in Chinese-Style Solar Greenhouses. Comput. Electron. Agric. 2018, 150, 235–244. [Google Scholar] [CrossRef]
- Mashonjowa, E.; Ronsse, F.; Milford, J.R.; Pieters, J.G. Modelling the Thermal Performance of a Naturally Ventilated Greenhouse in Zimbabwe Using a Dynamic Greenhouse Climate Model. Sol. Energy 2013, 91, 381–393. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. Modeling Heating Demands in a Chinese-Style Solar Greenhouse Using the Transient Building Energy Simulation Model TRNSYS. J. Build. Eng. 2020, 29, 101114. [Google Scholar] [CrossRef]
- Rasheed, A.; Kwak, C.S.; Na, W.H.; Lee, J.W.; Kim, H.T.; Lee, H.W. Development of a Building Energy Simulation Model for Control of Multi-Span Greenhouse Microclimate. Agronomy 2020, 10, 1236. [Google Scholar] [CrossRef]
- Sharma, P.K.; Tiwari, G.N.; Sorayan, V.P.S. Temperature Distribution in Different Zones of the Micro-Climate of a Greenhouse: A Dynamic Model. Energy Convers. Manag. 1999, 40, 335–348. [Google Scholar] [CrossRef]
- Asa’d, O.; Ugursal, V.I.; Ben-Abdallah, N. Investigation of the Energetic Performance of an Attached Solar Greenhouse through Monitoring and Simulation. Energy Sustain. Dev. 2019, 53, 15–29. [Google Scholar] [CrossRef]
- Rabiu, A.; Na, W.; Denen, T.; Rasheed, A.; Aderemi, M. ScienceDirect Determination of Overall Heat Transfer Coefficient for Greenhouse Energy-Saving Screen Using Trnsys and Hotbox. Biosyst. Eng. 2022, 217, 83–101. [Google Scholar] [CrossRef]
- Castellucci, S.; Carlini, M. Modelling and Simulation for Energy Production Parametric Dependence in Greenhouses. Math. Probl. Eng. 2010, 2010, 590943. [Google Scholar] [CrossRef]
- Choab, N.; Allouhi, A.; El Maakoul, A.; Kousksou, T.; Saadeddine, S.; Jamil, A. Effect of Greenhouse Design Parameters on the Heating and Cooling Requirement of Greenhouses in Moroccan Climatic Conditions. IEEE Access 2020, 9, 2986–3003. [Google Scholar] [CrossRef]
- Rasheed, A.; Kim, H.T.; Lee, H.W. Modeling-Based Energy Performance Assessment and Validation of Air-To-Water Heat Pump System Integrated with Multi-Span Greenhouse on Cooling Mode. Agronomy 2022, 12, 1374. [Google Scholar] [CrossRef]
- Yeoju Climate, Weather by Month, Average Temperature (South Korea)—Weather Spark. Available online: https://weatherspark.com/y/142307/Average-Weather-in-Yeoju-South-Korea-Year-Round (accessed on 4 March 2022).
- Weather Data Opening Portal. Available online: https://data.kma.go.kr/data/grnd/selectAsosRltmList.do?pgmNo=36 (accessed on 18 June 2022).
- Jung, S.-H.; Lee, J.-W.; Lee, S.-Y.; Lee, H.-W. Analysis of Wind Velocity Profile for Calculation of Wind Pressure on Greenhouse. Prot. Hortic. Plant Fact. 2015, 24, 135–146. [Google Scholar] [CrossRef]
- Valera, M.D.; Molina, A.F.; Alvarez, M. Protocolo de Auditoría Energética En Invernaderos Auditoría Energética de Un Invernadero Para Cultivo de Flor Cortada; Instituto para la diversificacion y ahorro de la Energia: Madrid, Spain, 2008; ISBN 9788496680265. [Google Scholar]
- Rafiq, A.; Na, W.H.; Rasheed, A.; Lee, J.W.; Kim, H.T.; Lee, H.W. Measurement of Longwave Radiative Properties of Energy-Saving Greenhouse Screens. J. Agric. Eng. 2021, 52. [Google Scholar] [CrossRef]
- Nijskens, J.; Deltour, J.; Coutisse, S.; Nisen, A. Radiometric and thermal properties of the new plastic films for greenhouse covering. Acta Hortic. 1989, 77, 7–38. [Google Scholar] [CrossRef]
- Rasheed, A.; Lee, J.W.; Lee, H.W. Development and Optimization of a Building Energy Simulation Model to Study the Effect of Greenhouse Design Parameters. Energies 2018, 11, 2001. [Google Scholar] [CrossRef]
- Solar Energy Laboratory. TRNSYS 18 Manual Documentation; University of Wisconsin: Madison, WI, USA, 2018; Volume 5, Available online: http://www.trnsys.com (accessed on 4 March 2022).
- Transsolar. TRNSYS 18 Manual Documentation (TRNFLOW Manual). 2009. Available online: http://www.transsolar.com (accessed on 4 March 2022).
- Lim, A. A Comparative Study between TRNSYS and RC Thermal Models to Simulate a District Thermal Demand. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2020. Available online: https://research.tue.nl/en/studentTheses/a-comparative-study-between-trnsys-and-rc-thermal-models-to-simul (accessed on 4 March 2022).
- Seem, J.E. Modeling of Heat in Buildings. Ph.D. Thesis, Solar Energy Laboratory, University of Wisconsin Madison, Madison, WI, USA, 2011. [Google Scholar]
- Lam, J.C.; Hui, S.C.M. Sensitivity Analysis of Energy Performance of Office Buildings. Build. Environ. 1996, 31, 27–39. [Google Scholar] [CrossRef]
- Choab, N.; Allouhi, A.; El Maakoul, A.; Kousksou, T.; Saadeddine, S.; Jamil, A. Review on Greenhouse Microclimate and Application: Design Parameters, Thermal Modeling and Simulation, Climate Controlling Technologies. Sol. Energy 2019, 191, 109–137. [Google Scholar] [CrossRef]
- Jeon, J.G.; Lee, D.G.; Paek, Y.; Kim, H.G. Study on Heating Performance of Hybrid Heat Pump System Using Geothermal Source and Solar Heat for Protected Horticulture. J. Korean Sol. Energy Soc. 2015, 35, 49–56. [Google Scholar] [CrossRef][Green Version]
- Rasheed, A.; Na, W.H.; Lee, J.W.; Kim, H.T.; Lee, H.W. Development and Validation of Air-to-Water Heat Pump Model for Greenhouse Heating. Energies 2021, 14, 4714. [Google Scholar] [CrossRef]
- Adjustment, A.H. Long-Term Trend of Surface Wind Speed in Korea: Anemometer Height Adjustment. Atmosphere 2021, 31, 101–112. [Google Scholar]
- Kim, M.H.; Kim, D.; Heo, J.; Lee, D.W. Techno-Economic Analysis of Hybrid Renewable Energy System with Solar District Heating for Net Zero Energy Community. Energy 2019, 187, 115916. [Google Scholar] [CrossRef]
- Cooper, P.I.; Fuller, R.J. A Transient Model of the Interaction between Crop, Environment and Greenhouse Structure for Predicting Crop Yield and Energy Consumption. J. Agric. Eng. Res. 1983, 28, 401–417. [Google Scholar] [CrossRef]

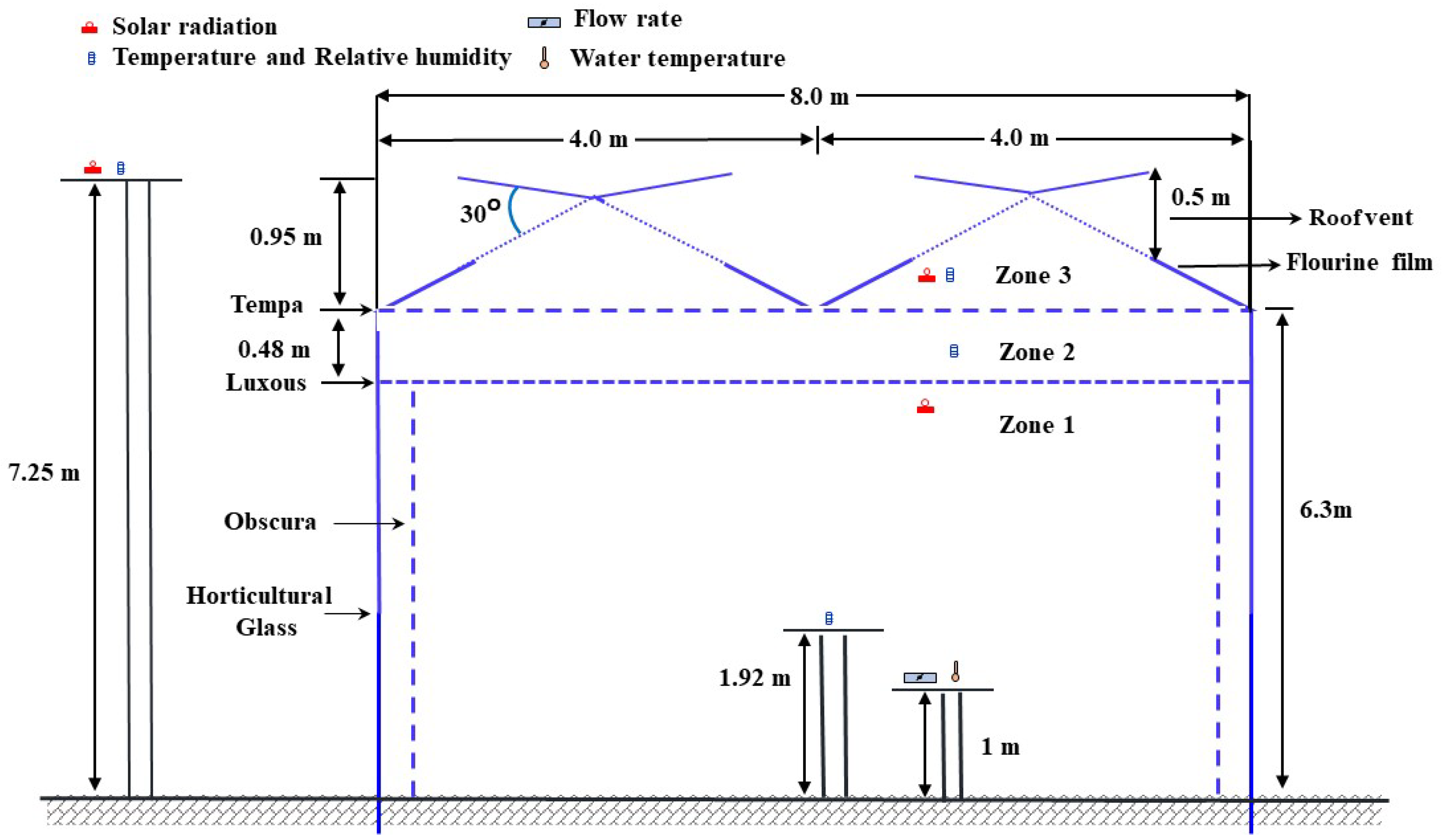






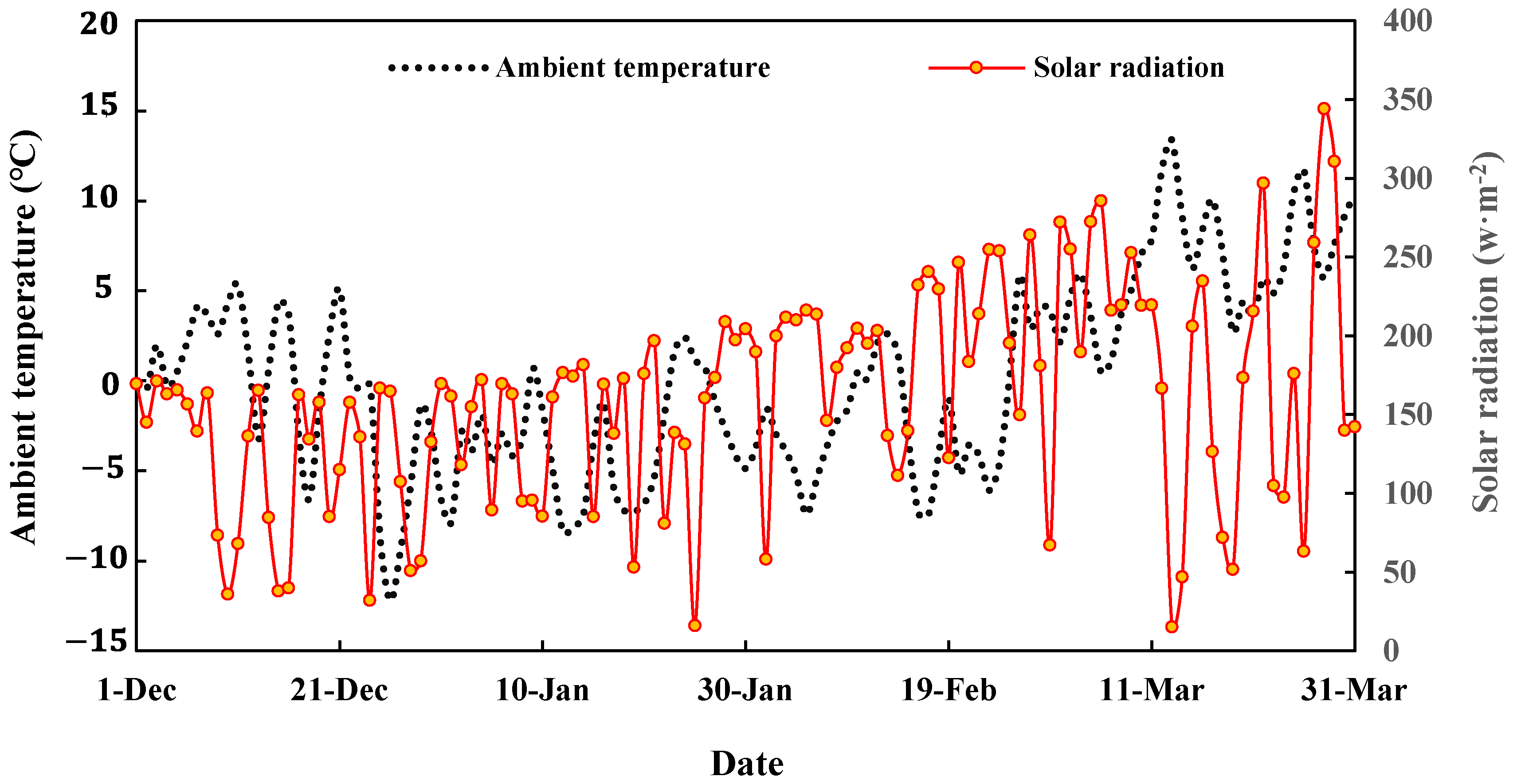

| Parameter | Measurement Method | Sensor | Precision of Sensor | Characteristics |
|---|---|---|---|---|
| Ambient temperature (°C) | 9 places at 1.92 m above the ground (zone 1) and 1 place at the centre of zone 2 and 3 | HOBO MX1102A | ±0.5% | Field recorded |
| Relative humidity (%) | 9 places at 1.92 m above the ground (zone 1) and 1 place at the centre of zone 2 and 3 | HOBO MX1102A | ±0.5% | Field recorded |
| Solar radiation (Wm−2) | 7.25 m above the ground (outside the greenhouse) | CMP3 pyranometer | ±2% | Field recorded |
| Water temperature (°C) | 1 m above the ground (zone 1) | I-Sensor, PT 100 | ±0.3 °C | Field recorded |
| Flow rate (LPM) | 1 m above the ground (zone 1) | KFCM-1000 K-2101083-2 | ±5% | Field recorded |
| Wind speed (ms−1) | 10 m above the ground (at the weather station) | Clima sensor, US, Thies Clima | ±5% | KMA |
| Wind direction (degree) | 10 m above the ground (at the weather station) | Clima sensor, US, Thies Clima | ±5% | KMA |
| Ambient pressure (hPa) | 10 m above the ground (at the weather station) | PTB-220TS, VAISALA | ±5 hPa | KMA |
| Cover Characteristics | Covering Material | Thermal Screens | |
|---|---|---|---|
| HG | Tempa | Luxous | |
| Thickness (mm) | 4 | 0.31 | 0.30 |
| Solar transmittance (front) | 0.89 | 0.10 | 0.58 |
| Solar transmittance (back) | 0.89 | 0.12 | 0.57 |
| Solar reflectance (front) | 0.08 | 0.65 | 0.30 |
| Solar reflectance (back) | 0.08 | 0.51 | 0.25 |
| Visible radiation transmittance (front) | 0.91 | 0.10 | 0.58 |
| Visible radiation transmittance (back) | 0.91 | 0.12 | 0.57 |
| Visible radiation reflection (front) | 0.08 | 0.65 | 0.30 |
| Visible radiation reflection (back) | 0.08 | 0.51 | 0.25 |
| Thermal radiation transmittance | 0.1 | 0.05 | 0.38 |
| Thermal radiation emission (front) | 0.90 | 0.20 | 0.44 |
| Thermal radiation emission (back) | 0.90 | 0.33 | 0.44 |
| Thermal conductivity (Wm−1K−1) | 0.10 | 0.52 | 0.06 |
| Infiltration (m3h−1m2) | - | 3.62 | 6.45 |
| Materials | Thickness (m) | Thermal Conductivity (kJh−1m−1K−1) | Thermal Capacity (kJkg−1K−1) | Density (kgm−3) | Convective Heat Transfer Coefficient (kJh−1m−2K−1) | |
|---|---|---|---|---|---|---|
| Front | Back | |||||
| Ground | 0.1000 | 0.97 | 0.75 | 2900 | 11 | 0.001 |
| Steel | 0.05 | 54 | 1.8 | 7800 | 11 | 64 |
| Cover Characteristics | Fluorine Film | Obscura |
|---|---|---|
| Thickness (mm) | 0.08 | 0.34 |
| Solar transmittance (front) | 0.92 | 0.01 |
| Solar transmittance (back) | 0.92 | 0.01 |
| Solar reflectance (front) | 0.06 | 0.64 |
| Solar reflectance (back) | 0.06 | 0.64 |
| Visible radiation transmittance (front) | 0.92 | 0.01 |
| Visible radiation transmittance (back) | 0.92 | 0.01 |
| Visible radiation reflection (front) | 0.06 | 0.64 |
| Visible radiation reflection (back) | 0.06 | 0.64 |
| Thermal radiation transmittance | 0.94 | 0.001 |
| Thermal radiation emission (front) | 0.02 | 0.045 |
| Thermal radiation emission (back) | 0.03 | 0.045 |
| Thermal conductivity (Wm−1K−1) | 0.15 | 0.35 |
| Infiltration (m3h−1m2) | - | - |
| Farm | Greenhouse Set Point Temperature (°C) | Maximum Outside Temperature (°C) | Greenhouse Heating Area (m2) | Radiation Mode | Maximum Heating Load (kcal/hm2) |
|---|---|---|---|---|---|
| A | 15 | −17.8 | 2160 | Simple | 101.3 |
| Standard | 113.5 | ||||
| B | 15 | −17.8 | 1782 | Simple | 116.4 |
| Standard | 123.4 | ||||
| Detailed | 120.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adesanya, M.A.; Na, W.-H.; Rabiu, A.; Ogunlowo, Q.O.; Akpenpuun, T.D.; Rasheed, A.; Yoon, Y.-C.; Lee, H.-W. TRNSYS Simulation and Experimental Validation of Internal Temperature and Heating Demand in a Glass Greenhouse. Sustainability 2022, 14, 8283. https://doi.org/10.3390/su14148283
Adesanya MA, Na W-H, Rabiu A, Ogunlowo QO, Akpenpuun TD, Rasheed A, Yoon Y-C, Lee H-W. TRNSYS Simulation and Experimental Validation of Internal Temperature and Heating Demand in a Glass Greenhouse. Sustainability. 2022; 14(14):8283. https://doi.org/10.3390/su14148283
Chicago/Turabian StyleAdesanya, Misbaudeen Aderemi, Wook-Ho Na, Anis Rabiu, Qazeem Opeyemi Ogunlowo, Timothy Denen Akpenpuun, Adnan Rasheed, Yong-Cheol Yoon, and Hyun-Woo Lee. 2022. "TRNSYS Simulation and Experimental Validation of Internal Temperature and Heating Demand in a Glass Greenhouse" Sustainability 14, no. 14: 8283. https://doi.org/10.3390/su14148283
APA StyleAdesanya, M. A., Na, W.-H., Rabiu, A., Ogunlowo, Q. O., Akpenpuun, T. D., Rasheed, A., Yoon, Y.-C., & Lee, H.-W. (2022). TRNSYS Simulation and Experimental Validation of Internal Temperature and Heating Demand in a Glass Greenhouse. Sustainability, 14(14), 8283. https://doi.org/10.3390/su14148283










