A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System
Abstract
:1. Introduction
- The importance of incorporating FACTS devices in a regulated and deregulated system was studied in terms of system economy, locational marginal pricing (LMP), and system voltage profile;
- The system risk was calculated by considering several abnormalities in the system (i.e., bus failure, line outage, system load increment, etc.). The worst condition was chosen based on the risk assessment parameter (i.e., VaR, CVaR) values;
- Placement of a wind farm within the system while checking the system risk;
- The optimal operation of FACTS devices was performed along with the wind farm while checking the system risk;
- Comparative studies of system risk and system economy were completed using three different optimization techniques, i.e., Artificial Gorilla Troops Optimizer Algorithm (AGTO), Honey Badger Algorithm (HBA), and Sequential Quadratic Programming (SQP);
- The artificial gorilla troops optimizer algorithm (AGTO) was utilized for the first time concerning this kind of risk mitigation problem, which constitutes the uniqueness of this paper.
2. System Modeling
2.1. Thyristor Controlled Series Compensator (TCSC)
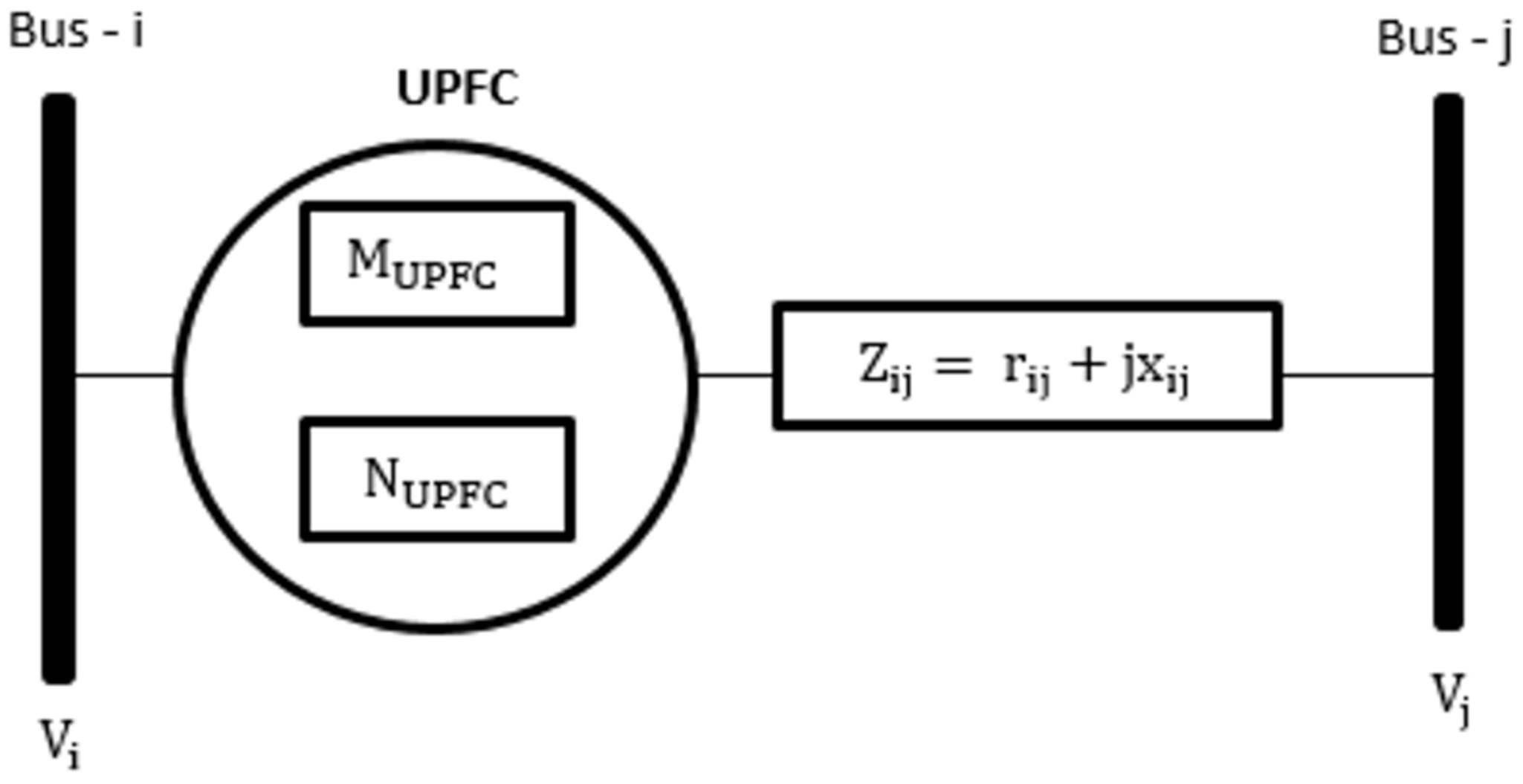
2.2. Unified Power Flow Controller (UPFC)
2.3. Investment Cost of TCSC & UPFC
2.4. Bus Loading Sensitivity Factor (BLSF)
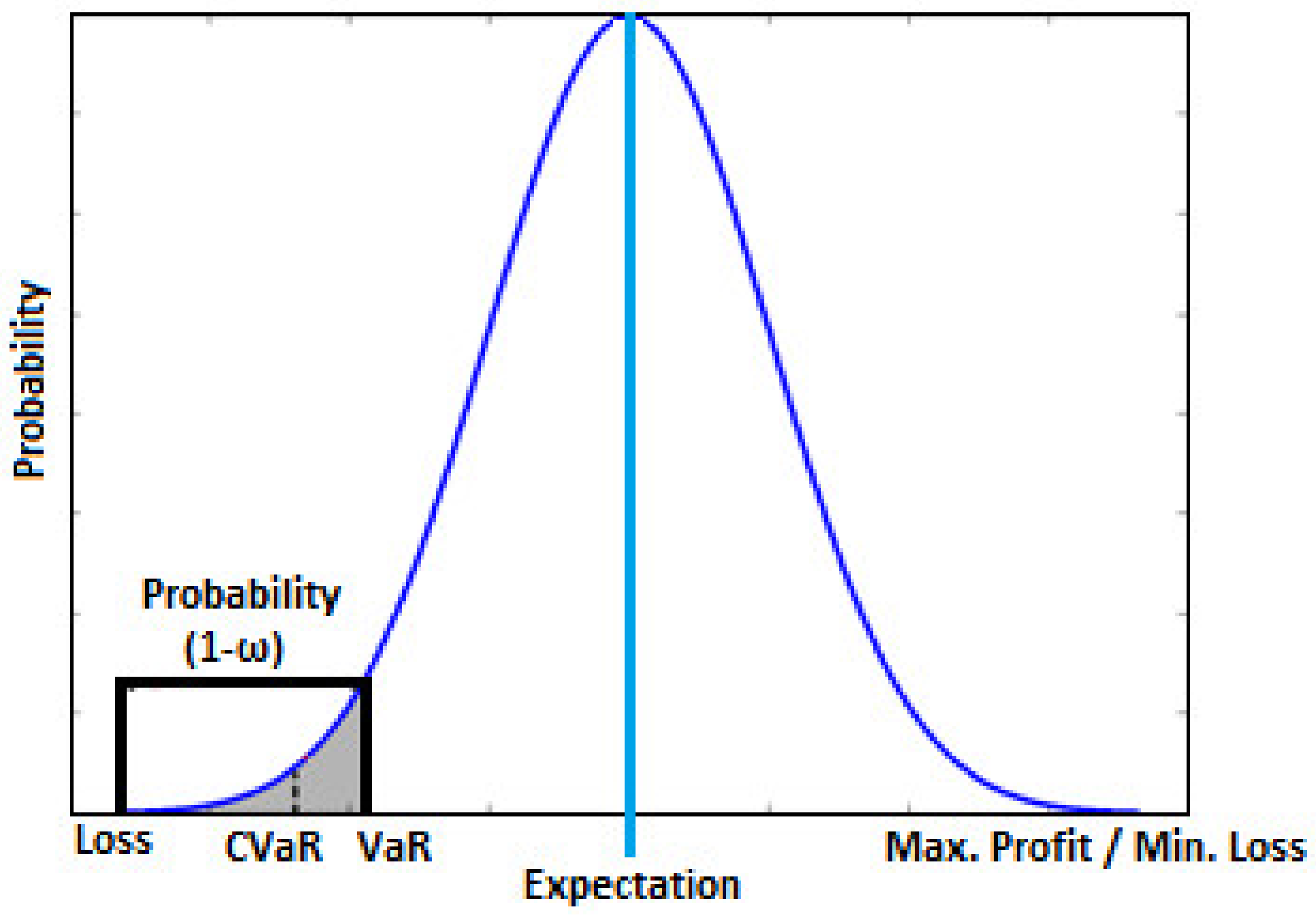
2.5. VaR and CVaR
3. Optimization Techniques
3.1. Artificial Gorilla Troops Optimizer Algorithm (AGTO)
- Migration to unknown areas increases the exploration of AGTO.
- Moving to other gorillas increases the balance between exploration and exploitation.
- Migration towards a known place increases the searching capability in different optimization spaces.
- Follow the silverback (leader for a group that makes decisions and guides others), which maintains the systematic and continued exploration in individual groups to ease exploitation.
- Competition for adult females explains or mimics the group’s expansion fight process by puberty/adult gorillas after choosing adult females.
3.2. Honey Badger Algorithm (HBA)
3.3. Sequential Quadratic Programming (SQP)
4. Objective Function
- (i)
- Minimization of system risk by improving the values of VaR and CVaR.
- (ii)
- Minimization of system generation cost.
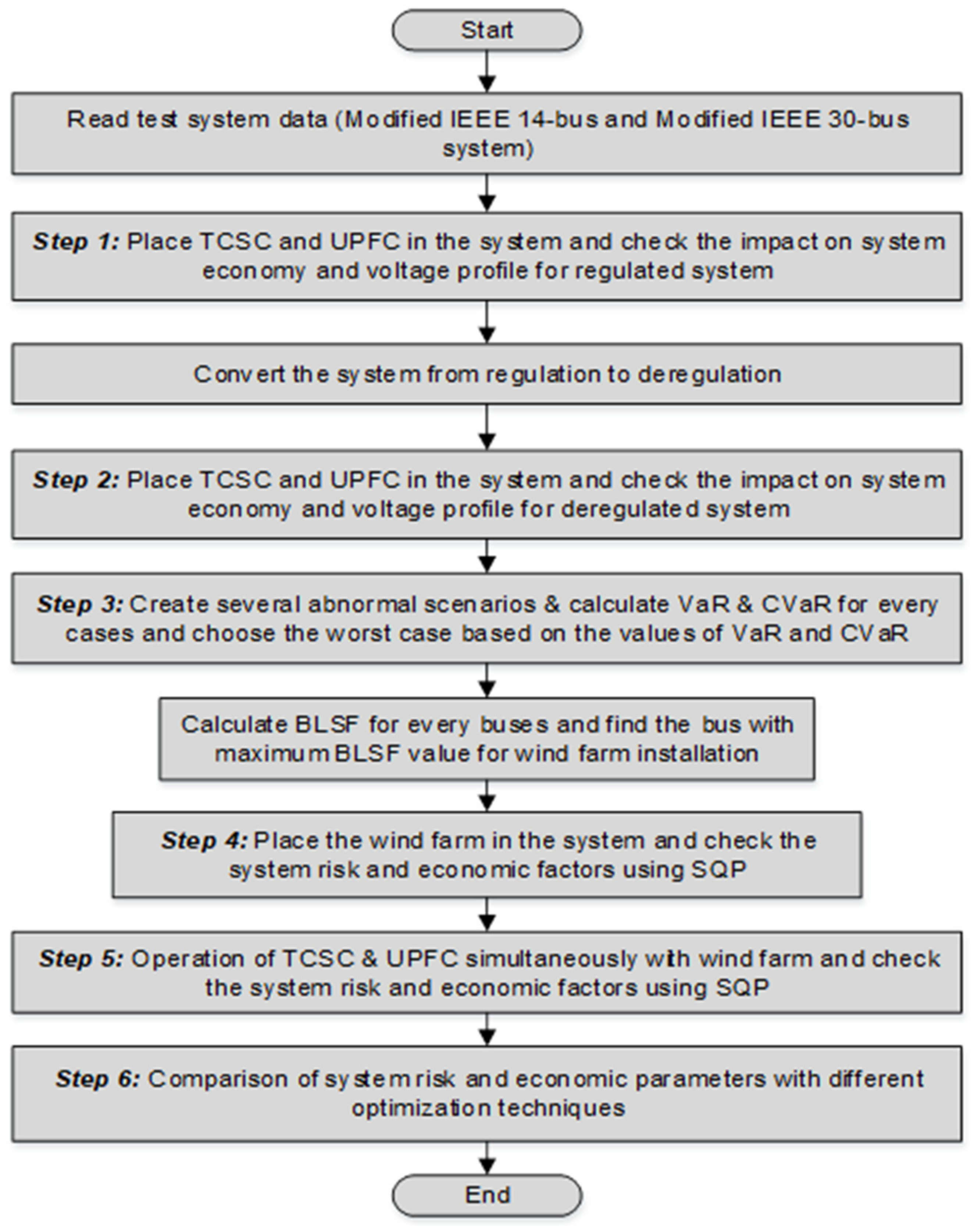
5. Results and Discussions
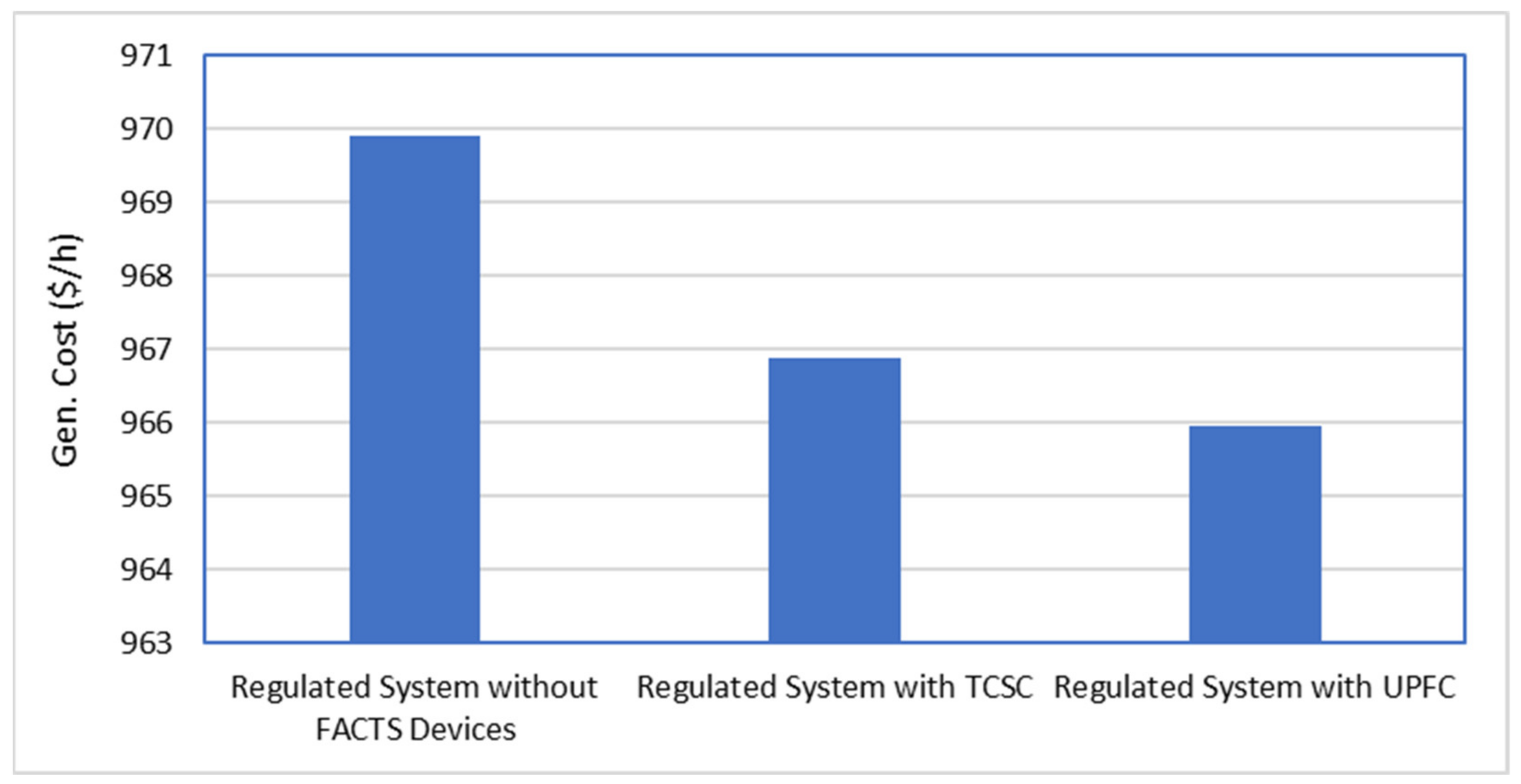
5.1. Impact of FACTS Devices in a Regulated System for the Modified IEEE 14-Bus System
5.2. Impact of FACTS Devices in a Regulated System for Modified IEEE 30-Bus System
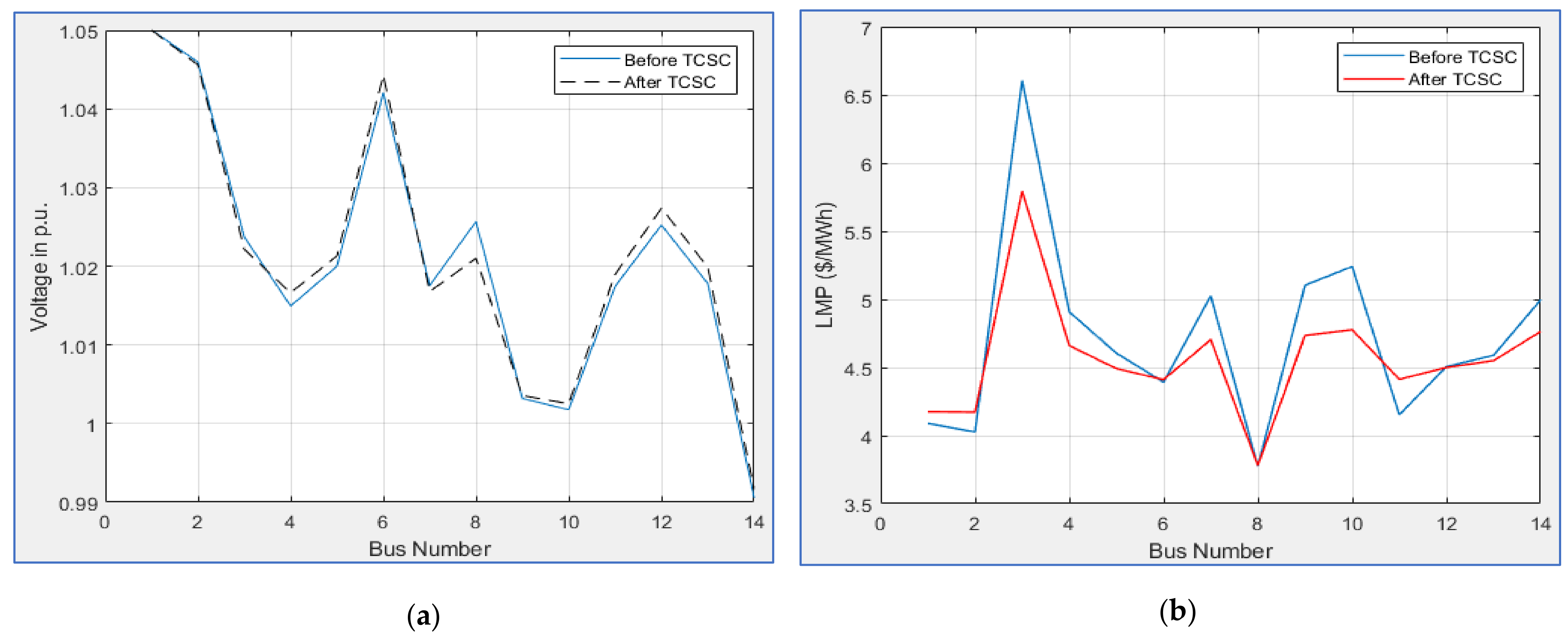
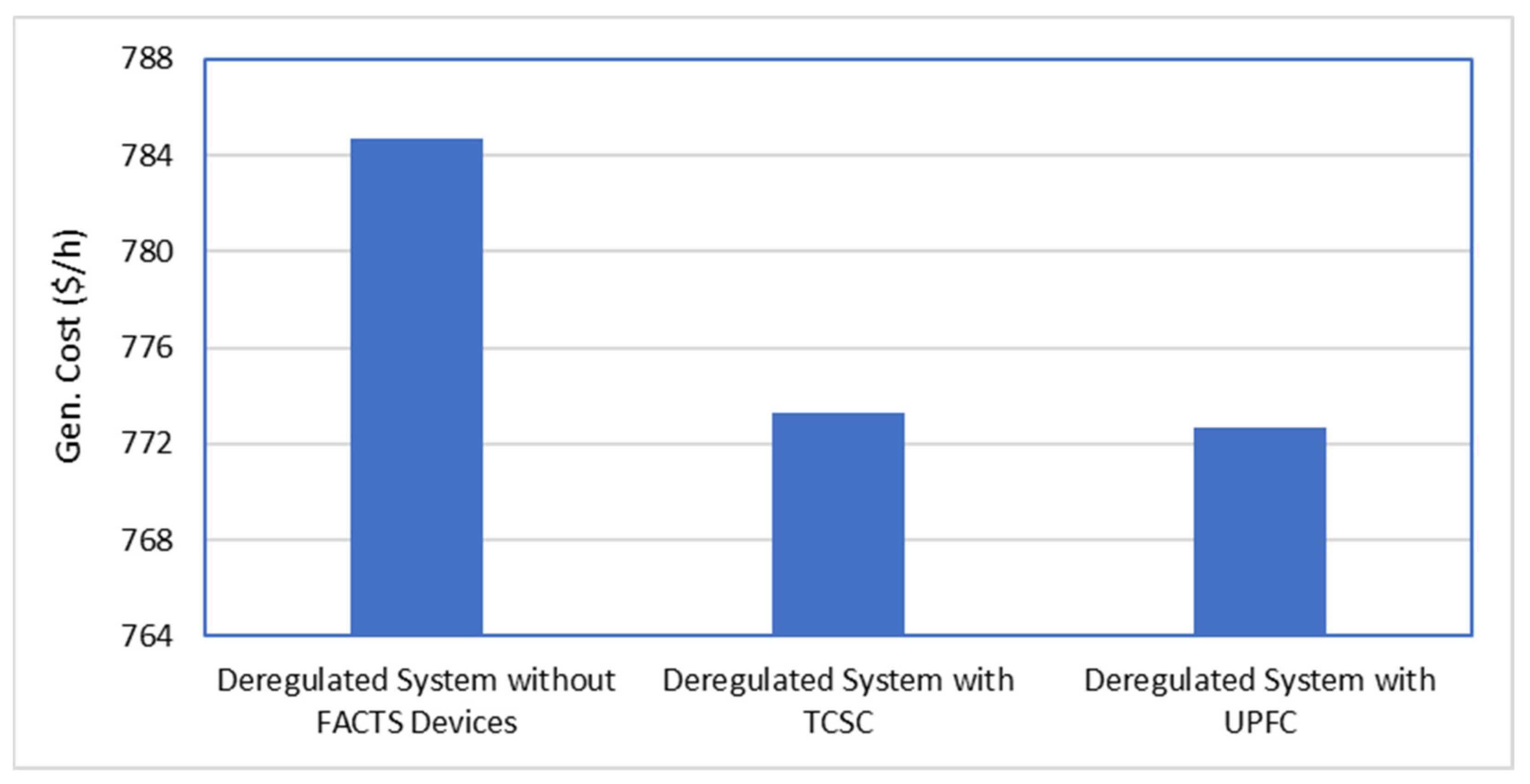
5.3. Impact of FACTS Devices in a Deregulated System for Modified IEEE 14-Bus System
5.4. Impact of FACTS Devices in a Deregulated System for Modified IEEE 30-Bus System
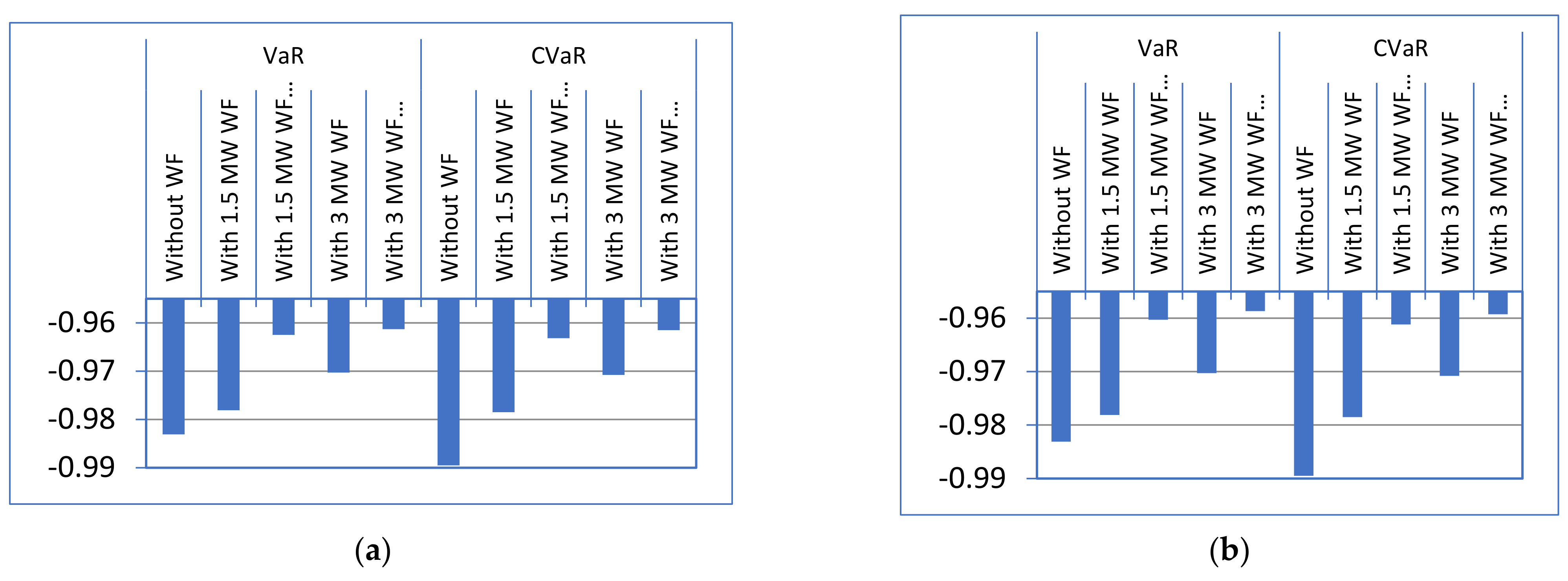
5.5. Calculate the System Risk in Terms of VaR and CVaR
5.6. Placement of Wind Farm and Check the System Risk and Economic Factors Using SQP
5.7. Operation of FACTS Devices along with Wind Farm and Check the System Risk and Economic Factors Using SQP for Deregulated System
5.8. Comparison of Economic Parameters with Different Optimization Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hussain, S.M.S.; Nadeem, F.; Aftab, M.A.; Ali, I.; Ustun, T.S. The Emerging Energy Internet: Architecture, Benefits, Challenges, and Future Prospects. Electronics 2019, 8, 1037. [Google Scholar] [CrossRef] [Green Version]
- Ustun, T.S.; Aoto, Y. Analysis of Smart Inverter’s Impact on the Distribution Network Operation. IEEE Access 2019, 7, 9790–9804. [Google Scholar] [CrossRef]
- Elmitwally, A.; Eladl, A. Planning of multi-type FACTS devices in restructured power systems with wind generation. Int. J. Electr. Power Energy Syst. 2016, 77, 33–42. [Google Scholar] [CrossRef]
- Arango-Aramburo, S.; Bernal-García, S.; Larsen, E.R. Renewable energy sources and the cycles in deregulated electricity markets. Energy 2021, 223, 120058. [Google Scholar] [CrossRef]
- Dawn, S.; Tiwari, P.K. Improvement of economic profit by optimal allocation of TCSC & UPFC with wind power generators in double auction competitive power market. Int. J. Electr. Power Energy Syst. 2016, 80, 190–201. [Google Scholar]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system. Appl. Energy 2021, 282, 116–171. [Google Scholar] [CrossRef]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Optimum Synthesis of a BOA Optimized Novel Dual-Stage PI − (1 + ID) Controller for Frequency Response of a Microgrid. Energies 2020, 13, 3446. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Aftab, M.A.; Ali, I.; Hussain, S.M.S.; Ustun, T.S. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. [Google Scholar] [CrossRef] [Green Version]
- Dey, P.P.; Das, D.C.; Latif, A.; Hussain, S.M.S.; Ustun, T.S. Active Power Management of Virtual Power Plant under Penetration of Central Receiver Solar Thermal-Wind Using Butterfly Optimization Technique. Sustainability 2020, 12, 6979. [Google Scholar] [CrossRef]
- Chauhan, A.; Upadhyay, S.; Khan, M.T.; Hussain, S.M.S.; Ustun, T.S. Performance Investigation of a Solar Photovoltaic/Diesel Generator Based Hybrid System with Cycle Charging Strategy Using BBO Algorithm. Sustainability 2021, 13, 8048. [Google Scholar] [CrossRef]
- Hussain, I.; Das, D.C.; Sinha, N.; Latif, A.; Hussain, S.M.S.; Ustun, T.S. Performance Assessment of an Islanded Hybrid Power System with Different Storage Combinations Using an FPA-Tuned Two-Degree-of-Freedom (2DOF) Controller. Energies 2020, 13, 5610. [Google Scholar] [CrossRef]
- Esfahani, M.M.; Sheikh, A.; Mohammed, O. Adaptive real-time congestion management in smart power systems using a real-time hybrid optimization algorithm. Electr. Power Syst. Res. 2017, 150, 118–128. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Jiang, Y.; Bie, P.; Li, H. Chance-constrained stochastic congestion management of power systems considering uncertainty of wind power and demand side response. Int. J. Electr. Power Energy Syst. 2019, 107, 703–714. [Google Scholar] [CrossRef]
- Biplab, B.; Sanjay, K. Loadability enhancement with FACTS devices using gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 470–479. [Google Scholar]
- Kavitha, K.; Neela, R. Optimal allocation of multi-type FACTS devices and its effect in enhancing system security using BBO, WIPSO & PSO. J. Electr. Syst. Inf. Technol. 2018, 5, 777–793. [Google Scholar]
- Packiasudha, M.; Suja, S.; Jerome, J. A new Cumulative Gravitational Search algorithm for optimal placement of FACT device to minimize system loss in the deregulated electrical power environment. Int. J. Electr. Power Energy Syst. 2017, 84, 34–46. [Google Scholar] [CrossRef]
- Biplab, B.; Sanjay, K. Approach for the solution of transmission congestion with multi-type FACTS devices. IET Gener. Transm. Distrib. 2016, 10, 2802–2809. [Google Scholar]
- Necoechea-Porras, P.D.; López, A.; Salazar-Elena, J.C. Deregulation in the Energy Sector and Its Economic Effects on the Power Sector: A Literature Review. Sustainability 2021, 13, 3429. [Google Scholar] [CrossRef]
- Dawn, S.; Tiwari, P.K.; Goswami, A.K. An approach for efficient assessment of the performance of double auction competitive power market under variable imbalance cost due to high uncertain wind penetration. Renew. Energy 2017, 108, 230–243. [Google Scholar] [CrossRef]
- Dawn, S.; Tiwari, P.K.; Goswami, A.K. An approach for long term economic operations of competitive power market by optimal combined scheduling of wind turbines and FACTS controllers. Energy 2019, 181, 709–723. [Google Scholar] [CrossRef]
- Lakshmi, C.; Iniyan, S.; Ranko, G. Modeling wind power investments, policies and social benefits for deregulated electricity market—A review. Appl. Energy 2019, 242, 364–377. [Google Scholar]
- Wang, Y.; Dong, W.; Yang, Q. Multi-stage optimal energy management of multi-energy microgrid in deregulated electricity markets. Appl. Energy 2022, 310, 118528. [Google Scholar] [CrossRef]
- Sahoo, A.; Hota, P.K. Impact of energy storage system and distributed energy resources on bidding strategy of micro-grid in deregulated environment. J. Energy Storage 2021, 43, 103230. [Google Scholar] [CrossRef]
- Yao, X.; Yi, B.; Yu, Y.; Fan, Y.; Zhu, L. Economic analysis of grid integration of variable solar and wind power with conventional power system. Appl. Energy 2020, 264, 114706. [Google Scholar] [CrossRef]
- Dorotić, H.; Ban, M.; Pukšec, T.; Duić, N. Impact of wind penetration in electricity market on optimal power-to-heat capacities in a local district heating system. Renew. Sustain. Energy Rev. 2020, 132, 110095. [Google Scholar] [CrossRef]
- Bashir, N.; Irwin, D.; Shenoy, P. A probabilistic approach to committing solar energy in day-ahead electricity markets. Sustain. Comput. Inform. Syst. 2021, 29, 100477. [Google Scholar] [CrossRef]
- Gencer, B.; Larsen, E.R.; van Ackere, A. Understanding the coevolution of electricity markets and regulation. Energy Policy 2020, 143, 111585. [Google Scholar] [CrossRef]
- Das, S.S.; Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Joint Scheduling Strategy for Wind and Solar Photovoltaic Systems to Grasp Imbalance Cost in Competitive Market. Sustainability 2022, 14, 5005. [Google Scholar] [CrossRef]
- Singh, N.K.; Koley, C.; Gope, S.; Dawn, S.; Ustun, T.S. An Economic Risk Analysis in Wind and Pumped Hydro Energy Storage Integrated Power System Using Meta-Heuristic Algorithm. Sustainability 2021, 13, 13542. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Ao, J.; Wang, Z.; Dong, H.; Zeng, M. Profit Allocation Strategy of Virtual Power Plant Based on Multi-Objective Optimization in Electricity Market. Sustainability 2022, 14, 6229. [Google Scholar] [CrossRef]
- Albogamy, F.R.; Khan, S.A.; Hafeez, G.; Murawwat, S.; Khan, S.; Haider, S.I.; Basit, A.; Thoben, K.D. Real-Time Energy Management and Load Scheduling with Renewable Energy Integration in Smart Grid. Sustainability 2022, 14, 1792. [Google Scholar] [CrossRef]
- Corona, L.; Mochon, A.; Saez, Y. Electricity market integration and impact of renewable energy sources in the Central Western Europe region: Evolution since the implementation of the Flow-Based Market Coupling mechanism. Energy Rep. 2022, 8, 1768–1788. [Google Scholar] [CrossRef]
- Soofi, A.F.; Manshadi, S.D. Strategic bidding in electricity markets with convexified AC market-clearing process. Int. J. Electr. Power Energy Syst. 2022, 141, 108096. [Google Scholar] [CrossRef]
- Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Risk Curtailment Strategy for Solar PV-Battery Integrated Competitive Power System. Electronics 2022, 11, 1251. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new Nature-inspired Metaheuristic Algorithm for Global Optimization Problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]







| Base Case [20] | with TCSC | ||||||
|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of TCSC at Line No. | LTCSC | Thermal Gen. Cost ($/h) | TCSC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 899.09 | 1226.182 | 4 | −0.55 | 887.121898 | 0.933067 | 888.05496 | 1292.774 |
| Base Case [20] | with UPFC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of UPFC at Line No. | Opt. Loc. of Ninj at Bus No. | LUPFC | NUPFC | Thermal Gen. Cost ($/h) | UPFC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 899.09 | 1226.182 | 4 | 2 | −0.7 | 2 | 884.50665 | 3.087367 | 887.5940 | 1294.476 |
| Base Case [20] | with TCSC | ||||||
|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of TCSC at Line No. | LTCSC | Thermal Gen. Cost ($/h) | TCSC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 969.91 | 1312.604 | 41 | −0.7 | 966.875852 | 0.007570 | 966.883422 | 1320.524 |
| Base Case [20] | with UPFC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of UPFC at Line No. | Opt. Loc. of Ninj at Bus No. | LUPFC | NUPFC | Thermal Gen. Cost ($/h) | UPFC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 969.91 | 1312.604 | 28 | 10 | 0.2 | −10 | 965.90837 | 0.046346 | 965.9547 | 1322.605 |
| without TCSC | with TCSC | ||||||
|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of TCSC at Line No. | LTCSC | Thermal Gen. Cost ($/h) | TCSC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 784.73 | 1158.069 | 4 | −0.55 | 772.843737 | 0.482298 | 773.326035 | 1228.083 |
| without UPFC | with UPFC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of UPFC at Line No. | Opt. Loc. of Ninj at Bus No. | LUPFC | NUPFC | Thermal Gen. Cost ($/h) | UPFC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 784.73 | 1158.069 | 4 | 2 | −0.7 | 2 | 769.31535 | 3.343308 | 772.6586 | 1230.131 |
| without TCSC | with TCSC | ||||||
|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of TCSC at Line No. | LTCSC | Thermal Gen. Cost ($/h) | TCSC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 731.39 | 1172.377 | 24 | −0.7 | 727.357248 | 0.002102 | 727.359350 | 1182.321 |
| without UPFC | with UPFC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Gen. Cost ($/h) | Revenue ($/h) | Opt. Loc. of UPFC at Line No. | Opt. Loc. of Ninj at Bus No. | LUPFC | NUPFC | Thermal Gen. Cost ($/h) | UPFC Investment Cost ($/h) | Total Gen. Cost ($/h) | Revenue ($/h) |
| 731.39 | 1172.377 | 41 | 6 | −0.7 | −6 | 726.33555 | 0.197623 | 726.5331 | 1186.325 |
| Sl. No. | Transmission Line Outage | Risk Assessment Parameters | Rank | |
|---|---|---|---|---|
| VaR | CVaR | |||
| 1 | 05–06 | −0.9825 | −1.0917 | 1 |
| 2 | 04–09 | −0.9741 | −1.0823 | 2 |
| 3 | 06–11 | −0.9676 | −1.075 | 3 |
| 4 | 06–13 | −0.9669 | −1.0743 | 4 |
| 5 | 13–14 | −0.9665 | −1.074 | 5 |
| Sl. No. | Transmission Line Outage | Risk Assessment Parameters | Rank | |
|---|---|---|---|---|
| VaR | CVaR | |||
| 1 | 01–02 | −0.9831 | −0.9895 | 1 |
| 2 | 09–10 | −0.9817 | −0.9820 | 2 |
| 3 | 01–03 | −0.9752 | −0.9768 | 3 |
| 4 | 10–20 | −0.9738 | −0.9741 | 4 |
| 5 | 06–10 | −0.9726 | −0.9732 | 5 |
| Bus No. | Bus Loading Sensitivity Factor (BLSF) | Bus No. | Bus Loading Sensitivity Factor (BLSF) | Bus No. | Bus Loading Sensitivity Factor (BLSF) |
|---|---|---|---|---|---|
| 1 | 0.1 | 6 | 0.2 | 11 | 0.1 |
| 2 | 0.2 | 7 | 0.15 | 12 | 0.1 |
| 3 | 0.05 | 8 | 0.05 | 13 | 0.15 |
| 4 | 0.25 | 9 | 0.2 | 14 | 0.1 |
| 5 | 0.2 | 10 | 0.1 |
| Bus No. | Bus Loading Sensitivity Factor (BLSF) | Bus No. | Bus Loading Sensitivity Factor (BLSF) | Bus No. | Bus Loading Sensitivity Factor (BLSF) |
|---|---|---|---|---|---|
| 1 | 0.049 | 11 | 0.024 | 21 | 0.049 |
| 2 | 0.098 | 12 | 0.122 | 22 | 0.073 |
| 3 | 0.024 | 13 | 0.024 | 23 | 0.049 |
| 4 | 0.098 | 14 | 0.049 | 24 | 0.073 |
| 5 | 0.049 | 15 | 0.098 | 25 | 0.073 |
| 6 | 0.171 | 16 | 0.049 | 26 | 0.024 |
| 7 | 0.049 | 17 | 0.049 | 27 | 0.098 |
| 8 | 0.049 | 18 | 0.049 | 28 | 0.073 |
| 9 | 0.073 | 19 | 0.049 | 29 | 0.049 |
| 10 | 0.146 | 20 | 0.049 | 30 | 0.049 |
| Case | Outage Line | Wind Farm Placed at Bus No. | Wind Power Quantity (MW) | System Generation Cost before Placement of Wind Farm ($/h) | System Generation Cost after Placement of Wind Farm ($/h) | Risk Parameter before Wind Farm Placement | Risk Parameter after Wind Farm Placement | ||
|---|---|---|---|---|---|---|---|---|---|
| VaR | CVaR | VaR | CVaR | ||||||
| IEEE 14-bus system | 05–06 | 4 | 1.5 | 785.23 | 781.485 | −0.9825 | −1.0917 | −0.9778 | −0.9965 |
| 3 | 779.79 | −0.9712 | −0.9907 | ||||||
| IEEE 30-bus system | 01–02 | 6 | 1.5 | 733.94 | 732.45 | −0.9831 | −0.9895 | −0.9781 | −0.9785 |
| 3 | 731.01 | −0.9703 | −0.9708 | ||||||
| FACTS Device | Outage Line | Wind Farm Placed at Bus No. | Wind Power Quantity (MW) | FACTS Device Placed at Line No. | System Generation Cost after Wind Farm Placement but without FACTS Devices ($/h) | System Generation Cost after Wind Farm and FACTS Devices Placement ($/h) | Risk Parameter after Wind Farm Placement but without FACTS Devices | Risk Parameter after Wind Farm and FACTS Devices Placement | ||
|---|---|---|---|---|---|---|---|---|---|---|
| VaR | CVaR | VaR | CVaR | |||||||
| TCSC | 05–06 | 4 | 1.5 | 4 | 781.485 | 780.259 | −0.9778 | −0.9965 | −0.9695 | −0.9857 |
| 3 | 779.79 | 778.354 | −0.9712 | −0.9907 | −0.9656 | −0.9836 | ||||
| UPFC | 1.5 | 4 | 781.485 | 780.038 | −0.9778 | −0.9965 | −0.9587 | −0.9783 | ||
| 3 | 779.79 | 777.962 | −0.9712 | −0.9907 | −0.9603 | −0.9792 | ||||
| FACTS Device | Outage Line | Wind Farm Placed at Bus No. | Wind Power Quantity (MW) | FACTS Device Placed at Line No. | System Generation Cost after Wind Farm Placement but without FACTS Devices ($/h) | System Generation Cost after Wind Farm and FACTS Devices Placement ($/h) | Risk Parameter after Wind Farm Placement but without FACTS Devices | Risk Parameter after Wind Farm and FACTS Devices Placement | ||
|---|---|---|---|---|---|---|---|---|---|---|
| VaR | CVaR | VaR | CVaR | |||||||
| TCSC | 01–02 | 6 | 1.5 | 24 | 732.45 | 731.135 | −0.9781 | −0.9785 | −0.9625 | −0.9632 |
| 3 | 731.01 | 729.934 | −0.9703 | −0.9708 | −0.9613 | −0.9615 | ||||
| UPFC | 1.5 | 41 | 732.45 | 730.952 | −0.9781 | −0.9785 | −0.9603 | −0.9612 | ||
| 3 | 731.01 | 729.264 | −0.9703 | −0.9708 | −0.9587 | −0.9593 | ||||
| System Details | Wind Farm Placed at Bus No. and Wind Power Quantity | Generation Cost after WF Placement but without FACTS ($/h) Using SQP | Generation Cost after WF Placement but without FACTS ($/h) Using AGTO | Generation Cost after WF Placement but without FACTS ($/h) Using HBA | System Generation Cost after Wind Farm and TCSC ($/h) Using SQP | System Generation Cost after Wind Farm and TCSC ($/h) Using AGTO | System Generation Cost after Wind Farm and TCSC ($/h) Using HBA | System Generation Cost after Wind Farm and UPFC ($/h) Using SQP | System Generation Cost after Wind Farm and UPFC ($/h) Using AGTO | System Generation Cost after Wind Farm and UPFC ($/h) Using HBA |
|---|---|---|---|---|---|---|---|---|---|---|
| IEEE 14-bus system | Bus No. 4 with 3 MW | 779.79 | 760.24 | 761.26 | 778.354 | 759.05 | 760.24 | 777.962 | 758.53 | 759.62 |
| IEEE 30-bus system | Bus No. 6 with 3 MW | 731.01 | 711.56 | 712.43 | 729.934 | 709.95 | 710.86 | 729.264 | 708.65 | 709.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System. Sustainability 2022, 14, 8069. https://doi.org/10.3390/su14138069
Das A, Dawn S, Gope S, Ustun TS. A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System. Sustainability. 2022; 14(13):8069. https://doi.org/10.3390/su14138069
Chicago/Turabian StyleDas, Arup, Subhojit Dawn, Sadhan Gope, and Taha Selim Ustun. 2022. "A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System" Sustainability 14, no. 13: 8069. https://doi.org/10.3390/su14138069
APA StyleDas, A., Dawn, S., Gope, S., & Ustun, T. S. (2022). A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System. Sustainability, 14(13), 8069. https://doi.org/10.3390/su14138069







