Parameter Identification and Sliding Pressure Control of a Supercritical Power Plant Using Whale Optimizer
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review and Paper Contributions
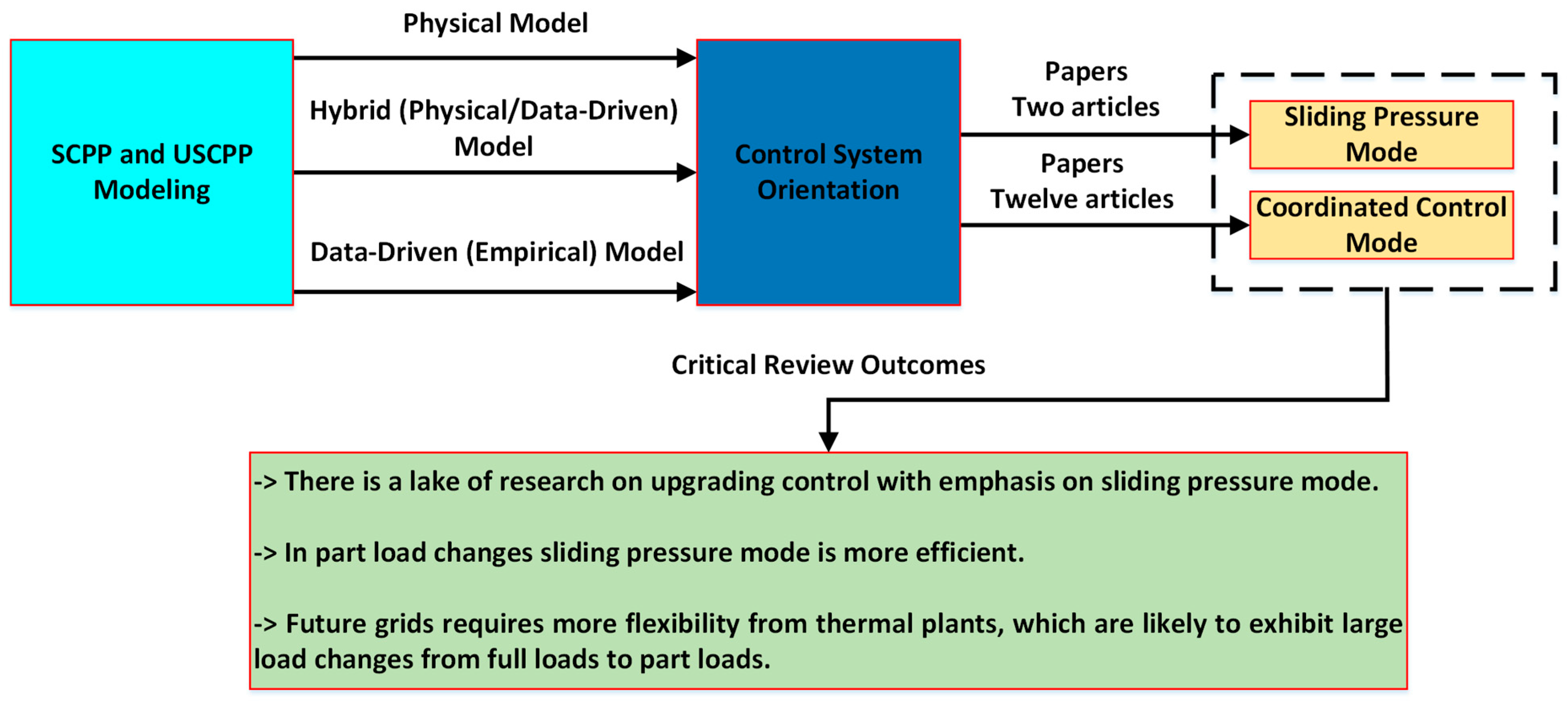
1.2.1. Review on Modeling
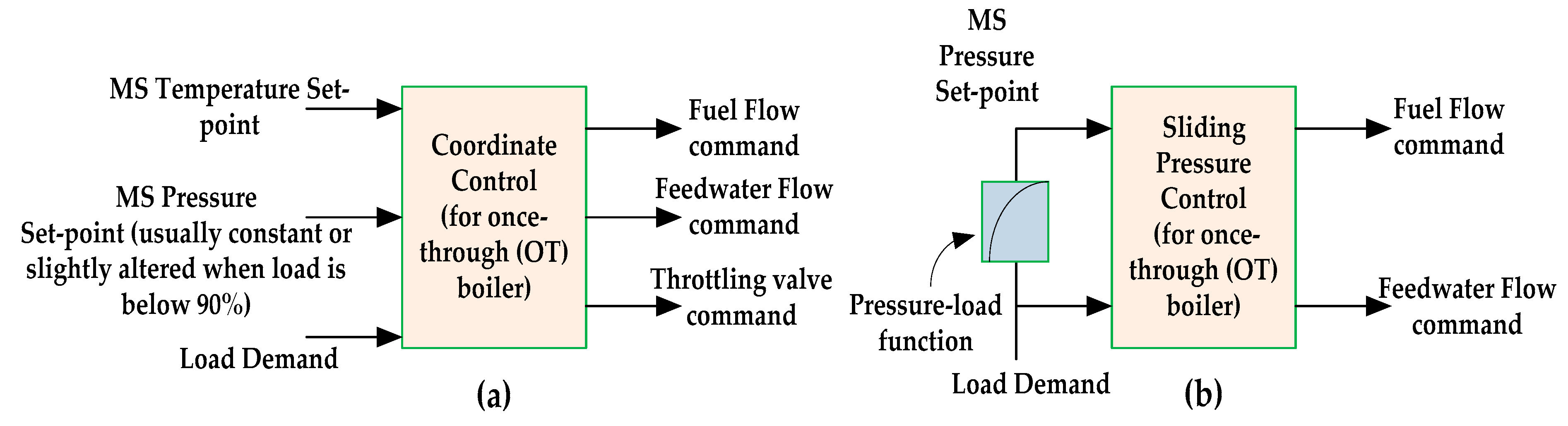
1.2.2. Control System Review
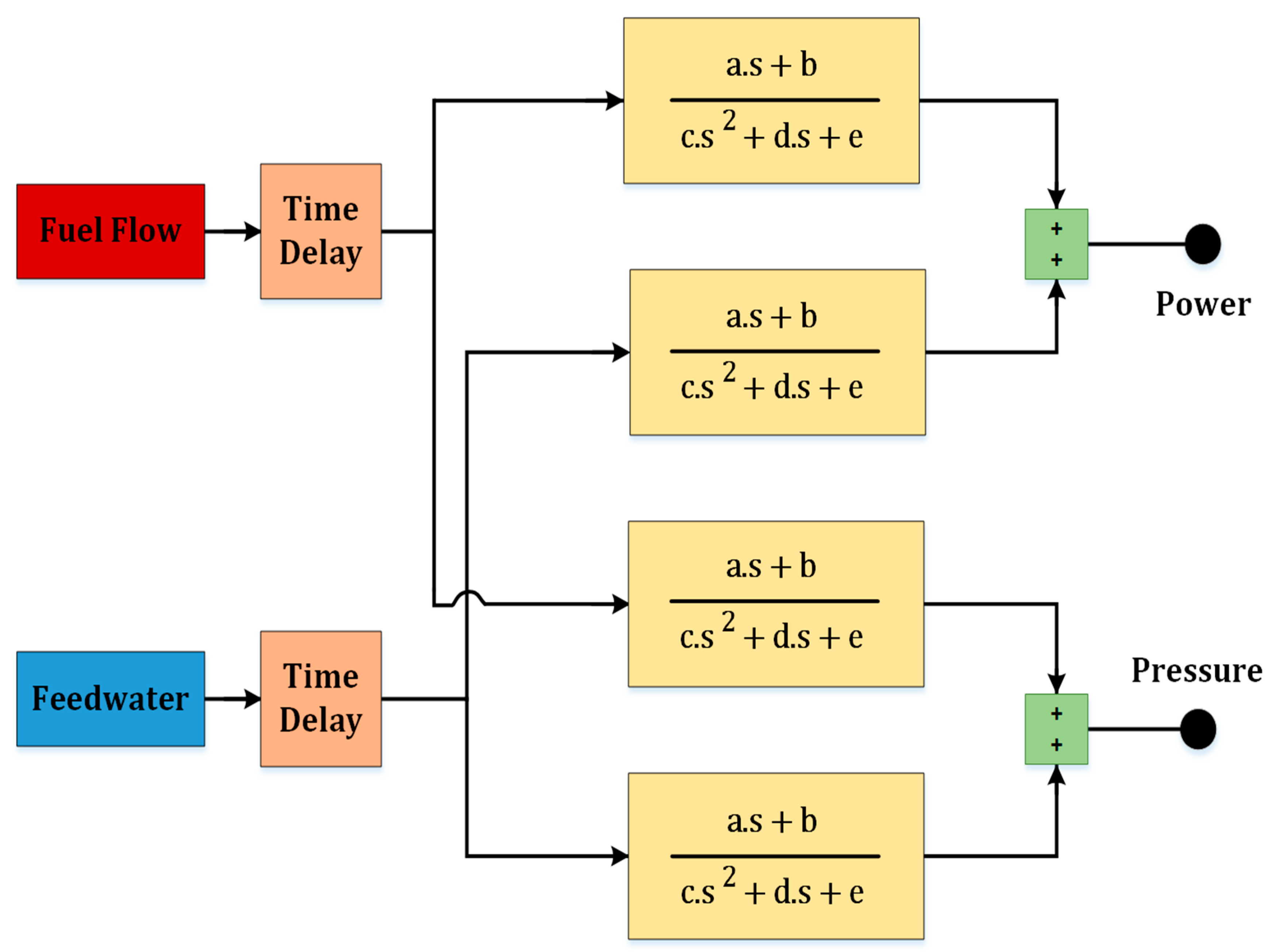
- A simplified MIMO Transfer matrix model for the sliding pressure operation mode of the supercritical power plant has been built. This model is validated for the entire OT operational characteristic.
- The second potential addition is that state-of-the-art optimization techniques will be applied to identify the parameters, which are the Whale Optimizer (WO) and Grey-Wolf Optimizer (GWO). It would be fascinating to compare these techniques against commonly used techniques, such as Genetic Algorithms, to see which one is truly more accurate for SC plants and control systems. It can be newly argued that the WO is more accurate in modeling and control than other techniques in both objectives concerned with system dynamics, energy efficiency, and cleaner operation.
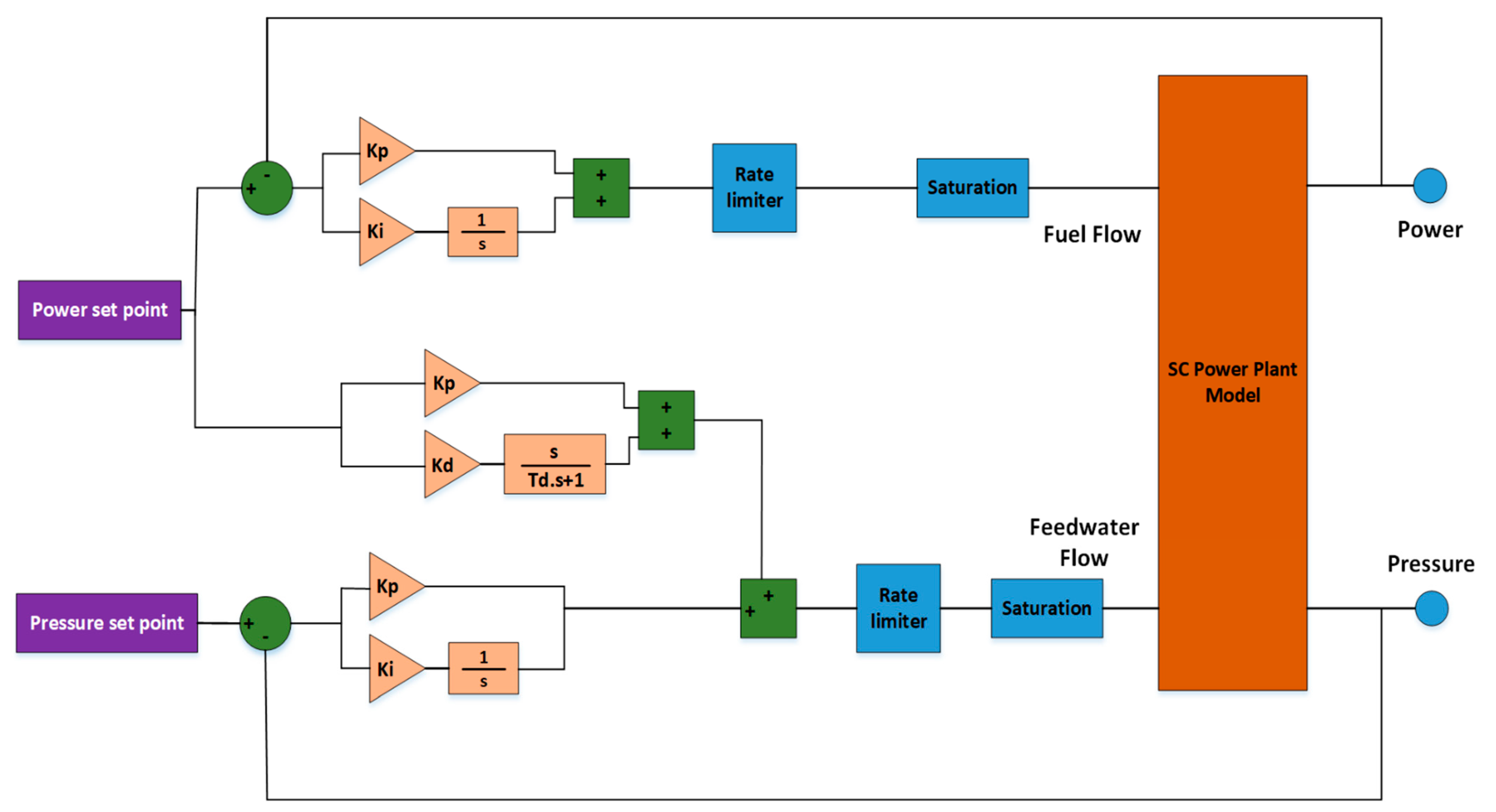
- The third feasible contribution is that the study presents the design of a practically adequate multivariable PI/PD control system that is compatible with sliding pressure operation and integrates into the previously mentioned model for system dynamics and sudden load changes. This control system is capable of increasing the speed of load demand response while simultaneously lowering the plant’s fuel and feedwater consumption.
2. An Overview of the Whale Optimizer (WO)
2.1. Inspiration
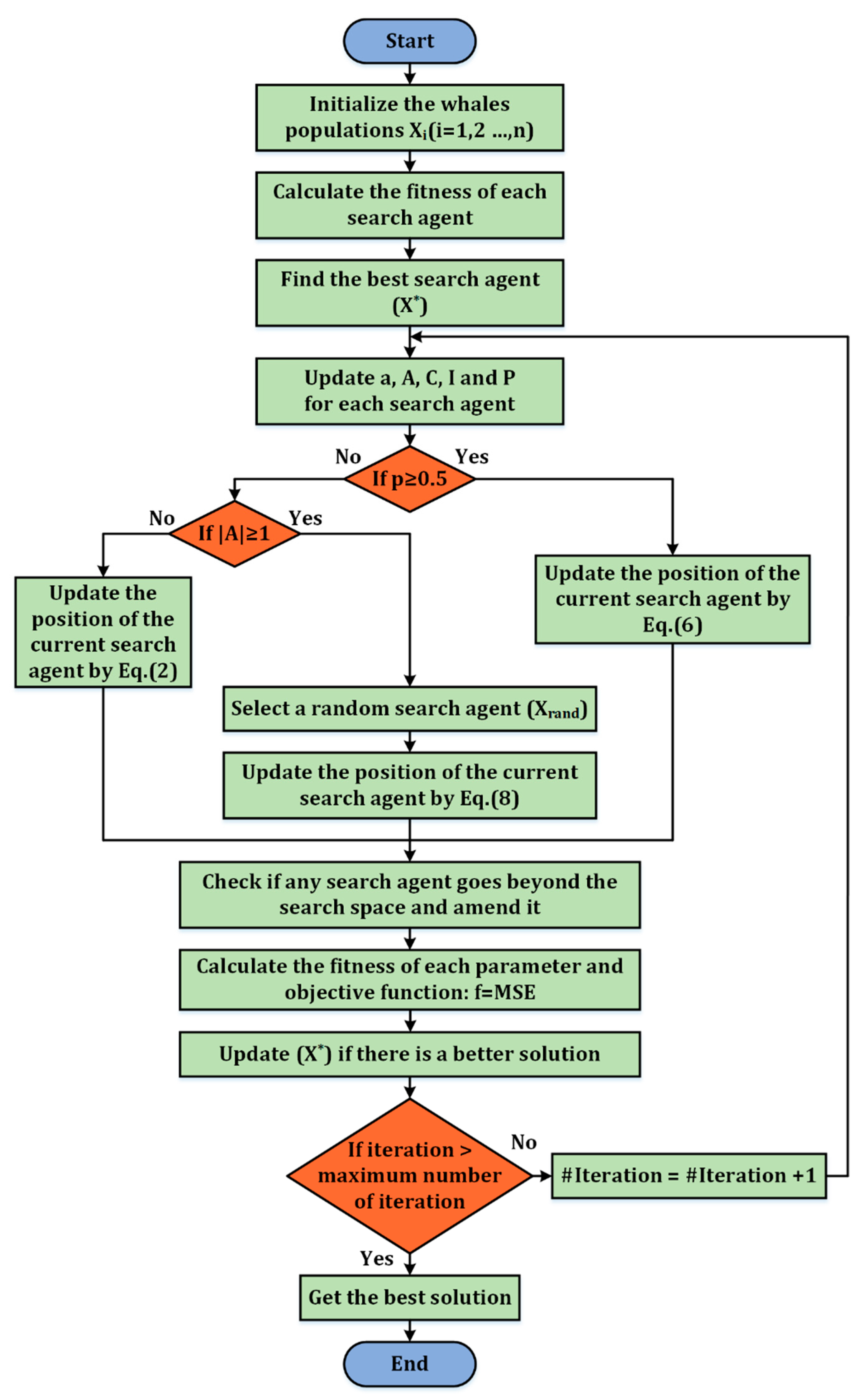
2.2. Modeling and Optimization of the Algorithm
2.2.1. Encircling Prey
2.2.2. Hunting Technique
- 1.
- Shrinking encircling technique:
- 2.
- Spiral updating position:
2.2.3. Searching for Prey
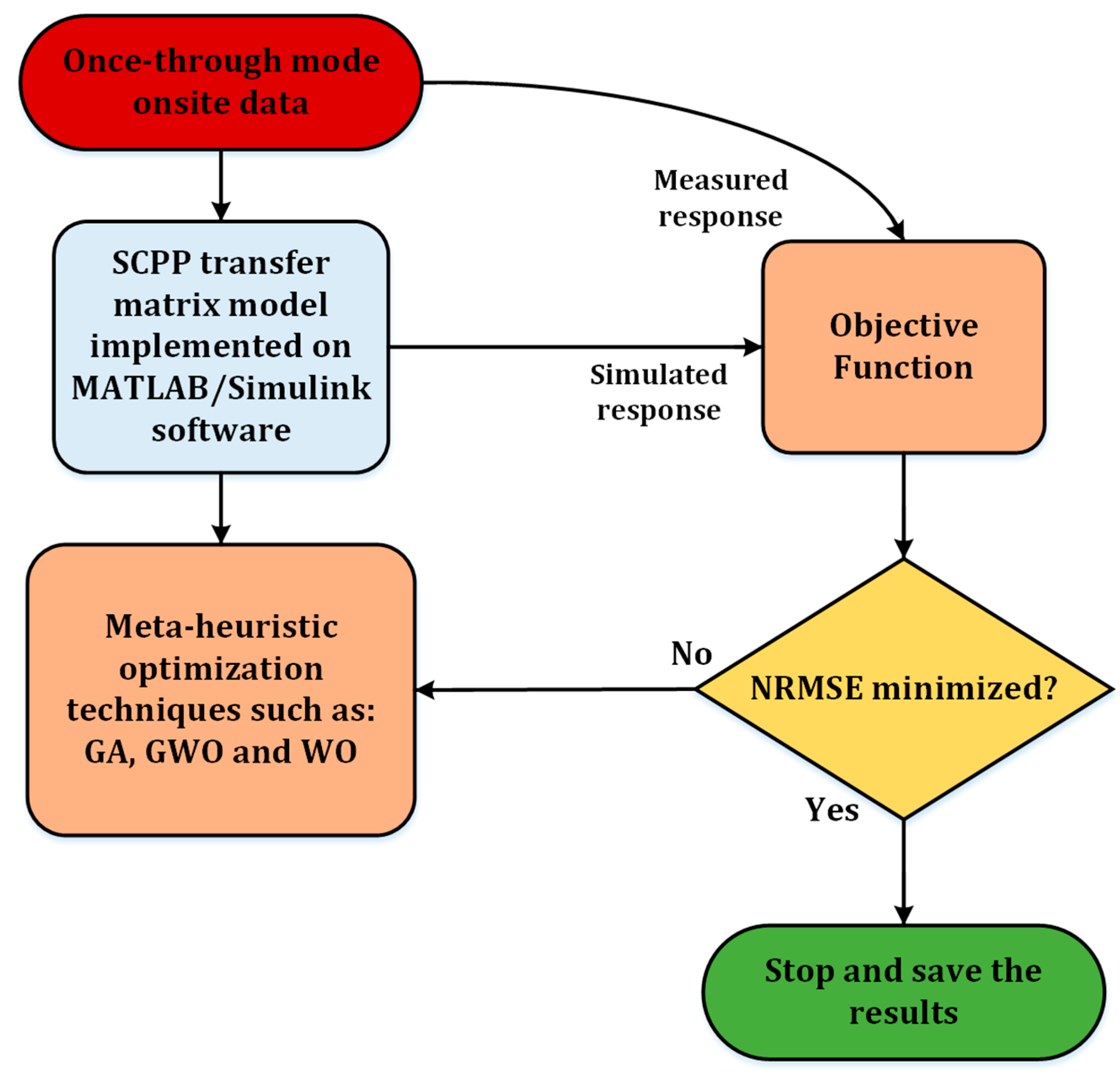
3. Model Structure and Parameter Identification
3.1. MIMO Transfer Matrix for Sliding Pressure Mode
3.2. Parameter Identification
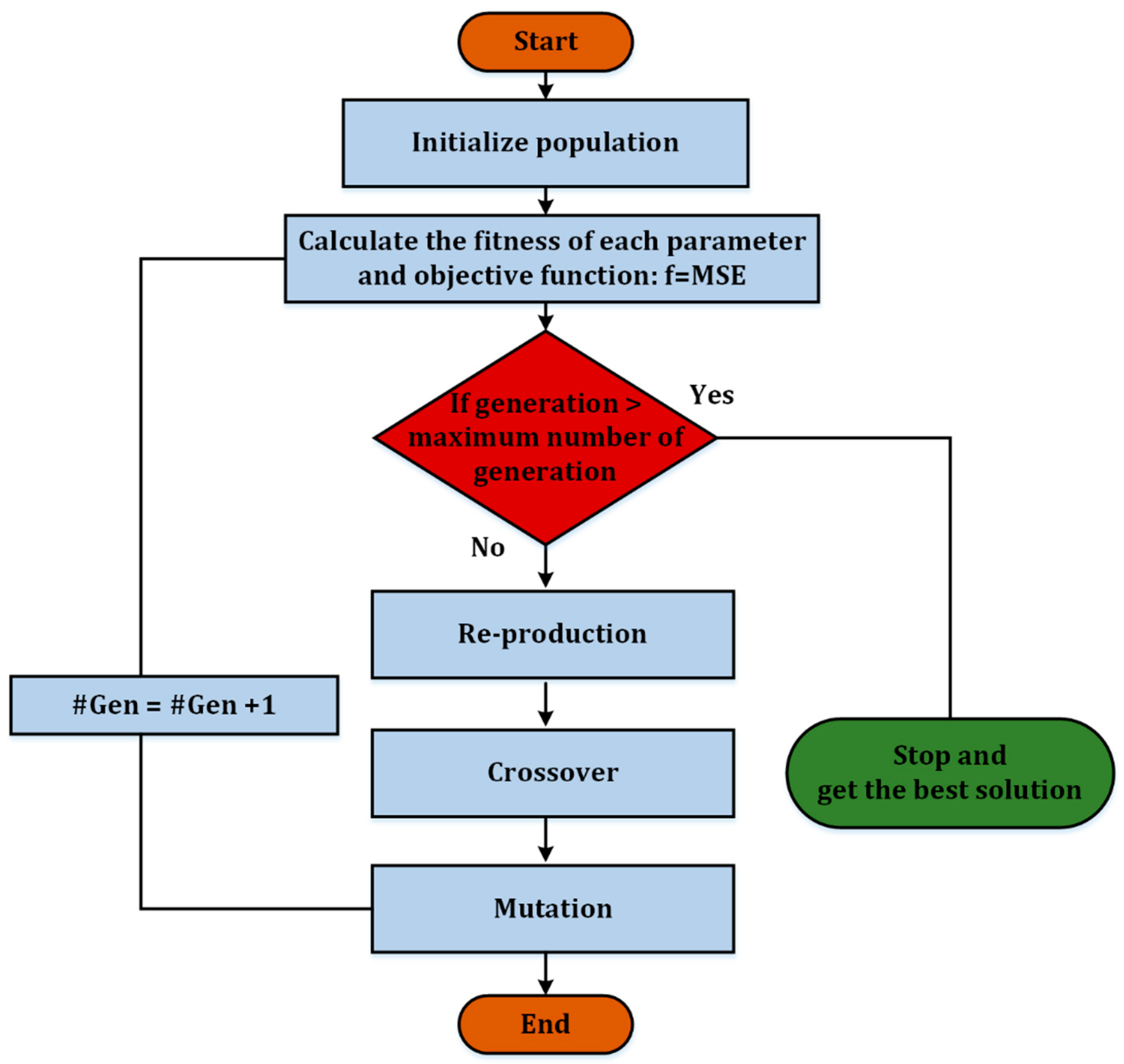
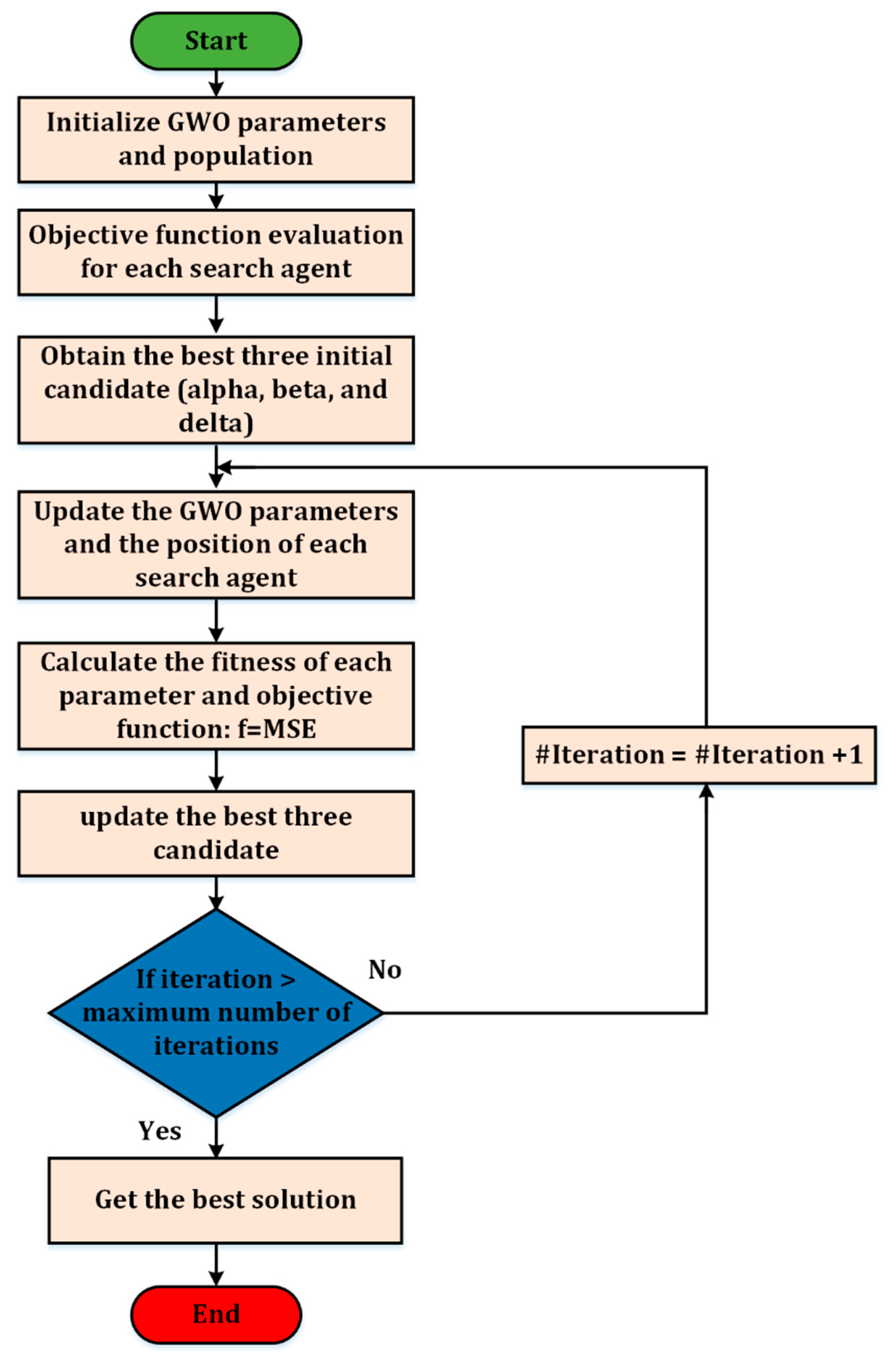
3.2.1. Genetic Algorithm
3.2.2. Grey-Wolf Optimizer
3.2.3. Whale Optimizer
4. Control Tuning and Testing
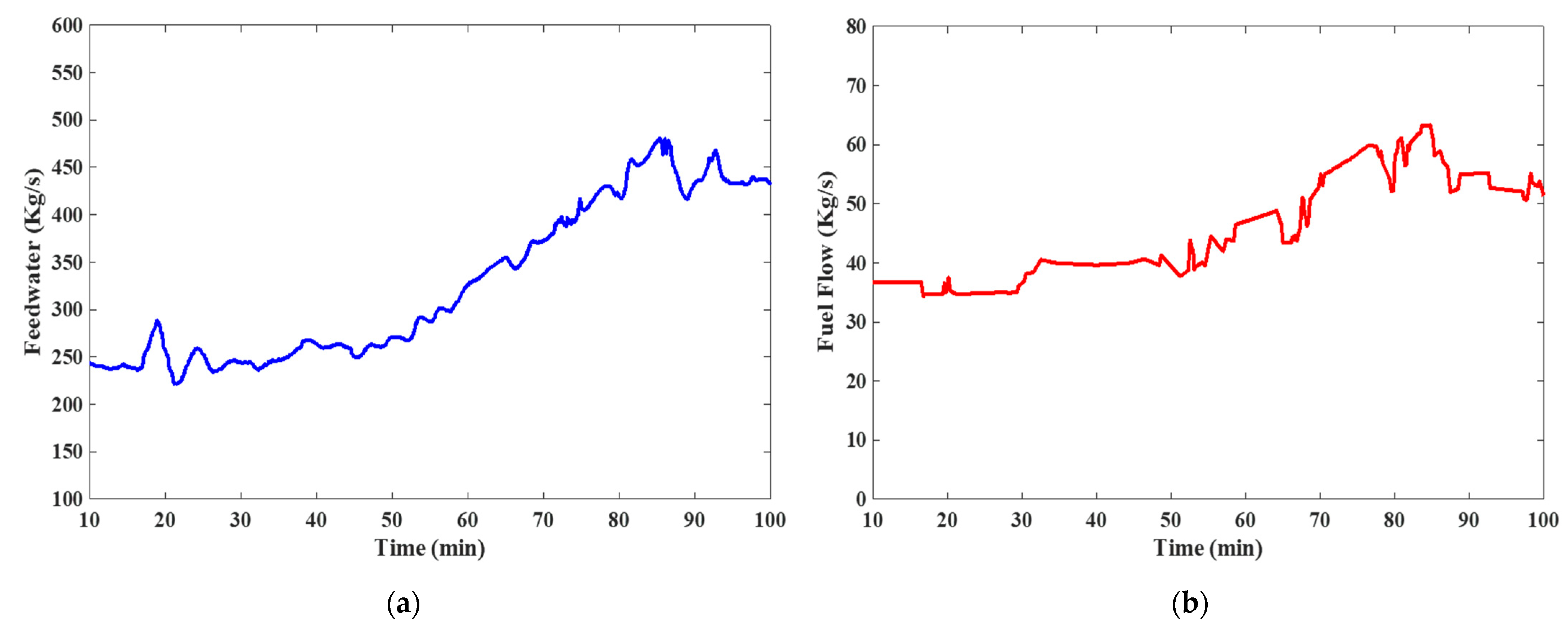
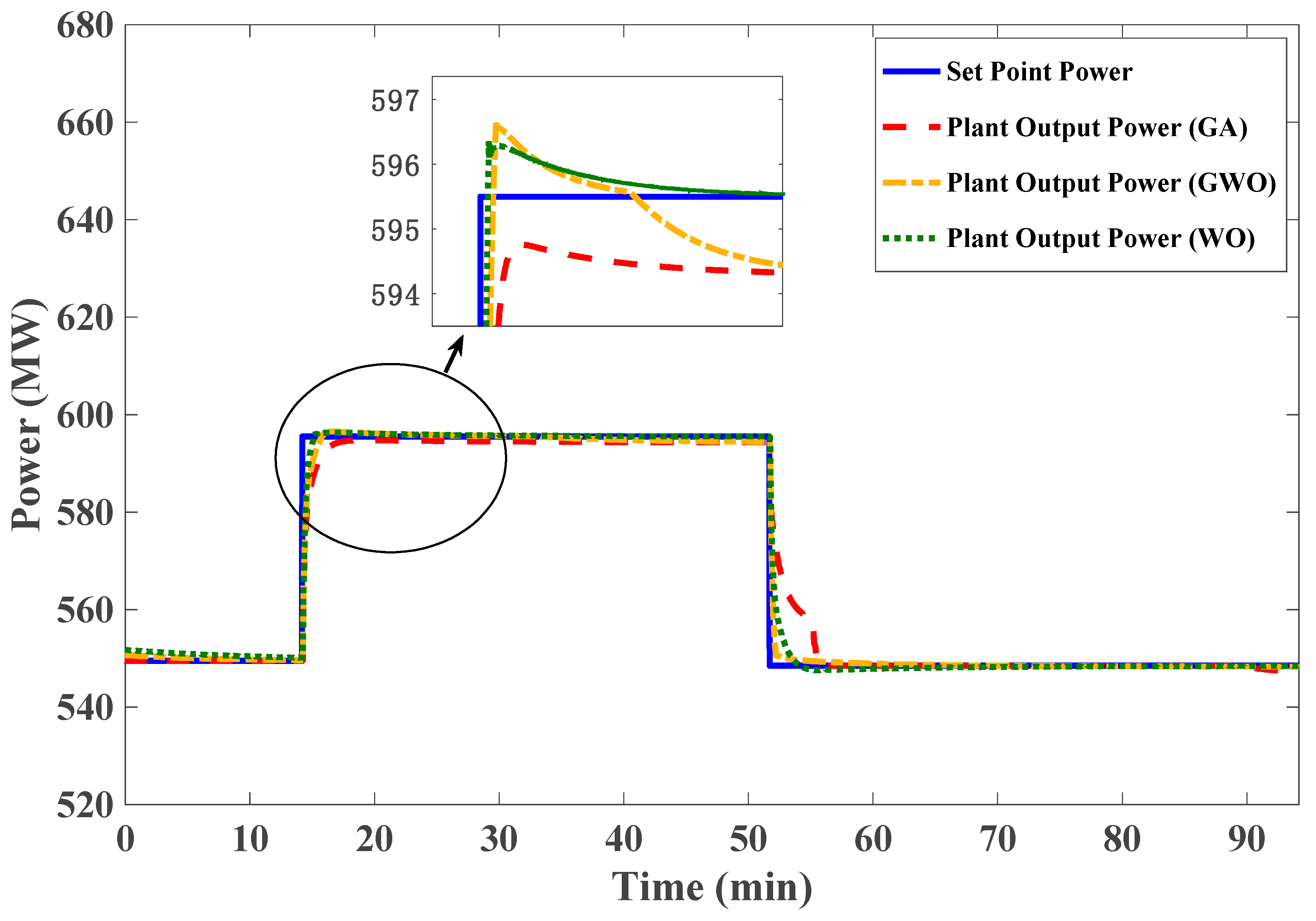
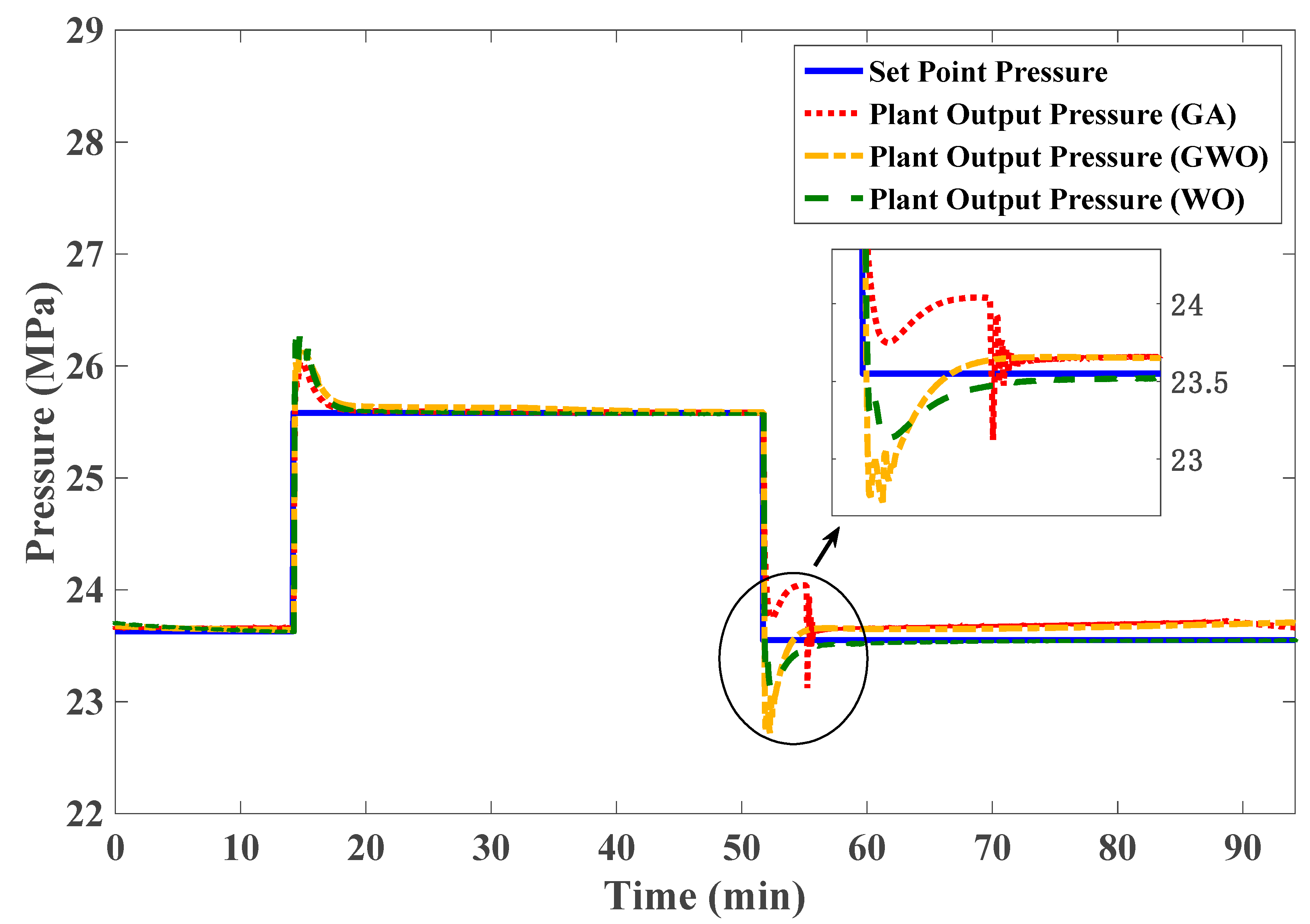
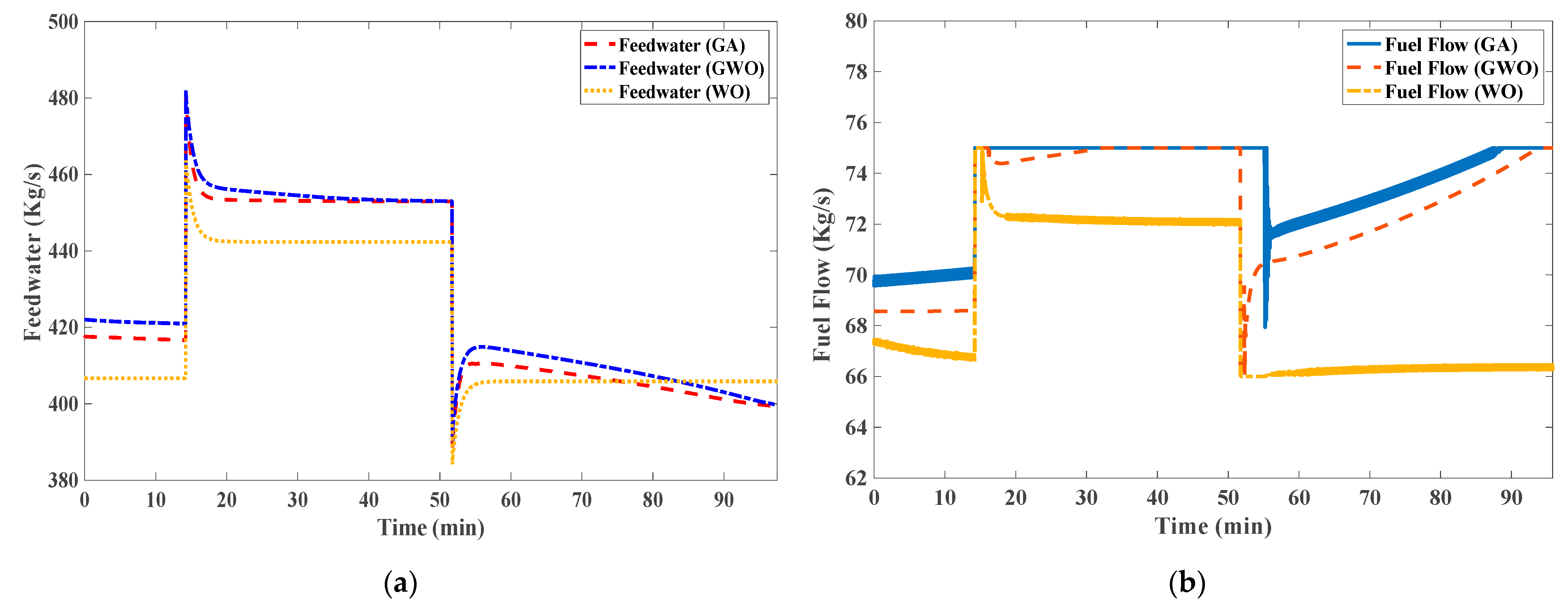
5. Control System Performance Results
6. Conclusions
- -
- A simplified transfer matrix model for supercritical generation units has been developed with some additional blocks to capture the system nonlinearities and delays in the fuel preparation system. This structure is more suitable from a control point of view in sliding pressure operational modes.
- -
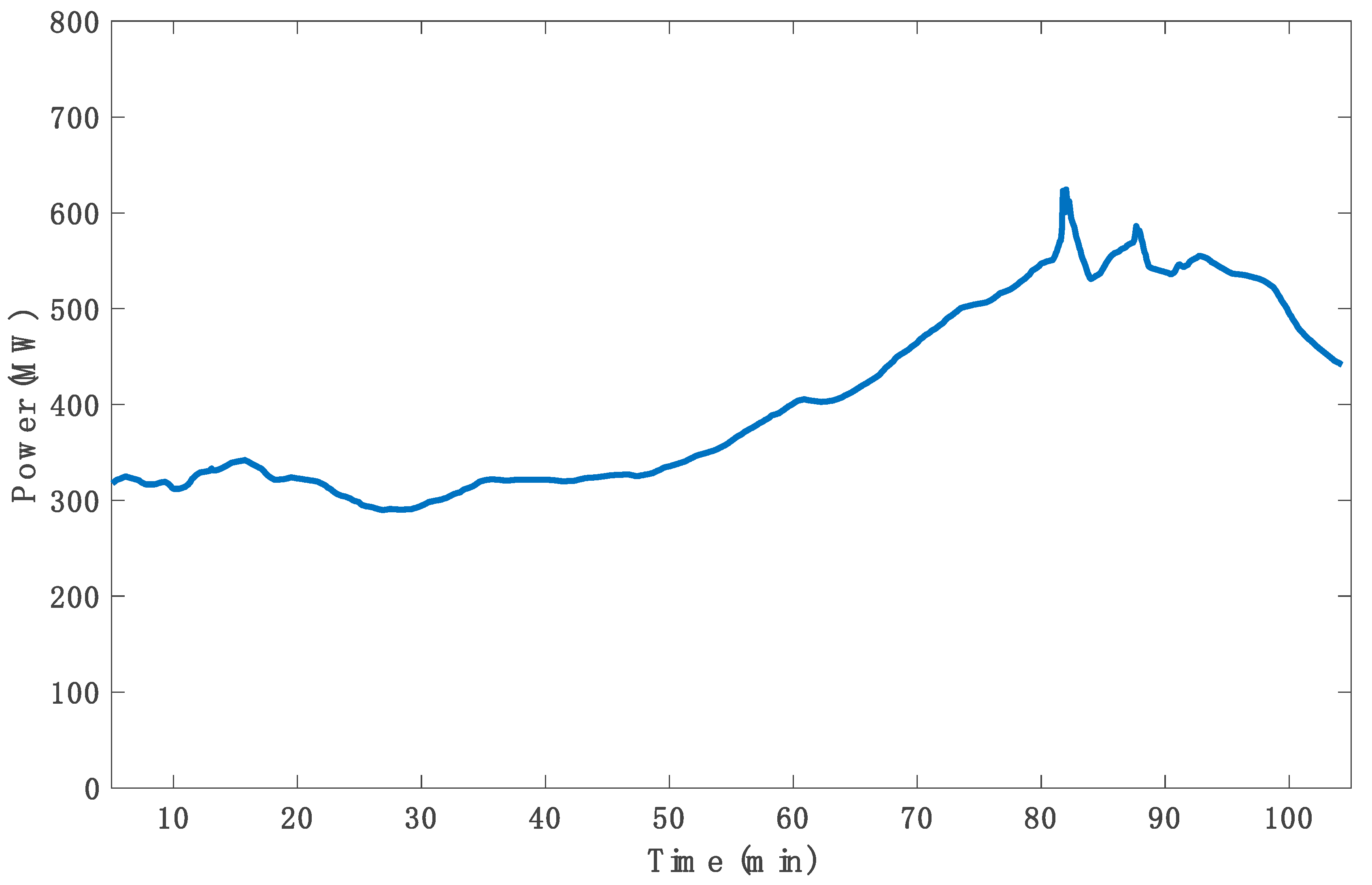
- The parameters of the transfer matrix are identified to fit a practical 600 MW SCPP via three different metaheuristic optimization techniques, which are the Whale Optimizer, Grey-Wolf Optimizer, and Genetic Algorithms. Considerable effort has been made to adjust the settings of the various optimization methods to yield the best possible results for all chosen techniques.
- -
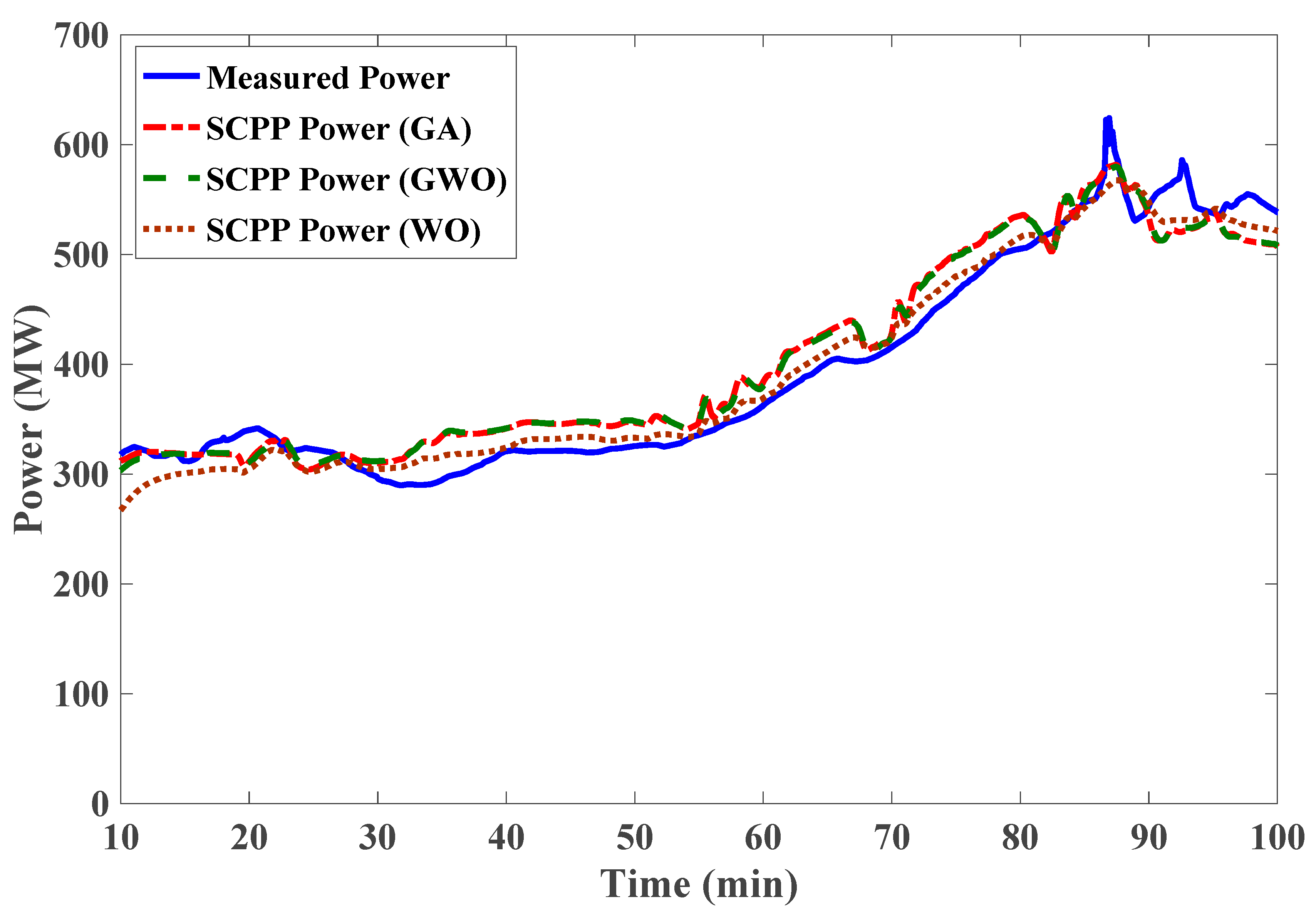
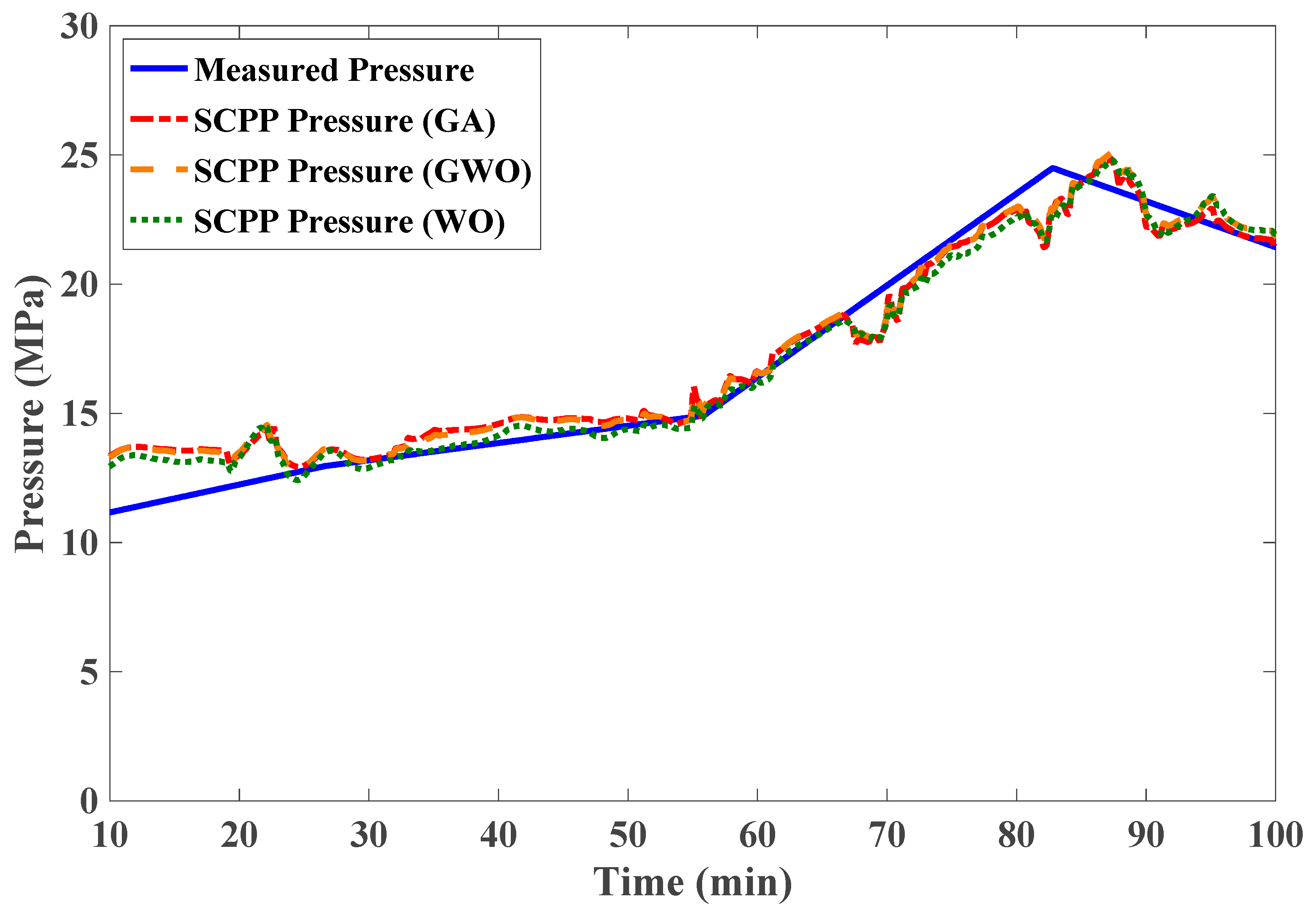
- The Whale Optimizer has proven to be more robust and accurate than the Grey-Wolf Optimizer and Genetic Algorithms for parameter estimation. The criterion chosen for the modeling part is the NRMSE of the pressure and power responses and through a basic inspection of the depicted responses.
- -
- A robust controller has been designed and successfully implemented to govern part-load operation changes. Again, the three techniques of Whale Optimizer, Grey-Wolf Optimizer, and Genetic Algorithms have been evaluated against tuning the parameters for optimum control performance. The Whale Optimizer technique of parameter tuning is found to be better than other techniques in terms of lower fuel consumption and better output responses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CFP | Coal-fired Plant |
| DEH | Digital Electro-Hydraulic |
| FWF | Feedwater Flow |
| GA | Genetic Algorithm |
| GWO | Grey-wolf Optimizer |
| MIMO | Multi-input Multi-output |
| MSE | Mean-squared Error |
| NRMSE | Normalized Mean-squared Error |
| OT | Once-Through |
| PID | Proportion integration differentiation |
| SCPP | Supercritical Power Plant |
| SLO | Sliding Pressure Operation |
| DMC | Dynamic Matrix Control |
| CCS | Coordinated Control System |
| MST | Main Steam Temperature |
| WO | Wolf Optimizer |
| AGC | Automatic Generation Control |
| MPC | Model Predictive Control |
| ADRC | Active Disturbance Rejection Control |
| SI | Swarm Intelligence |
References
- Heard, B.P.; Brook, B.W.; Wigley, T.M.; Bradshaw, C.J. Burden of proof: A comprehensive review of the feasibility of 100% renewable-electricity systems. Renew. Sustain. Energy Rev. 2017, 76, 1122–1133. [Google Scholar] [CrossRef]
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Pudasainee, D.; Kurian, V.; Gupta, R. Coal: Past, present, and future sustainable use. In Future Energy; Elsevier: Amsterdam, The Netherlands, 2020; pp. 21–48. [Google Scholar]
- Wu, Z.; He, T.; Liu, Y.; Li, D.; Chen, Y. Physics-informed energy-balanced modeling and active disturbance rejection control for circulating fluidized bed units. Control Eng. Pract. 2021, 116, 104934. [Google Scholar] [CrossRef]
- Rayaprolu, K. Boilers for Power and Process; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Basu, S.; Debnath, A.K. Power Plant Instrumentation and Control Handbook: A Guide to Thermal Power Plants; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw Hill: Columbus, OH, USA, 1994. [Google Scholar]
- Mohamed, O.; Wang, J.; Guo, S.; Wei, J.; Al-Duri, B.; Lv, J.; Gao, Q. Mathematical modelling for coal fired supercritical power plants and model parameter identification using genetic algorithms. In Electrical Engineering and Applied Computing; Springer: Dordrecht, The Netherlands, 2011; pp. 1–13. [Google Scholar]
- Haddad, A.; Mohamed, O.; Zahlan, M.; Wang, J. Parameter identification of a highly promising cleaner coal power station. J. Clean. Prod. 2021, 326, 129323. [Google Scholar] [CrossRef]
- Liu, J.Z.; Yan, S.; Zeng, D.L.; Hu, Y.; Lv, Y. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit. Energy 2015, 93, 2069–2078. [Google Scholar] [CrossRef]
- Huang, C.; Sheng, X. Data-driven model identification of boiler-turbine coupled process in 1000 MW ultra-supercritical unit by improved bird swarm algorithm. Energy 2020, 205, 118009. [Google Scholar] [CrossRef]
- Fan, H.; Su, Z.G.; Wang, P.H.; Lee, K.Y. A dynamic mathematical model for once-through boiler-turbine units with superheated steam temperature. Appl. Therm. Eng. 2020, 170, 114912. [Google Scholar] [CrossRef]
- Al-Momani, A.; Mohamed, O.; Elhaija, W.A. Multiple processes modeling and identification for a cleaner supercritical power plant via Grey Wolf Optimizer. Energy 2022, 252, 124090. [Google Scholar] [CrossRef]
- Mohamed, O.; Al-Duri, B.; Wang, J. Predictive control strategy for a supercritical power plant and study of influences of coal mills control on its dynamic responses. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 918–923. [Google Scholar]
- Chen, C.; Zhou, Z.; Bollas, G.M. Dynamic modeling, simulation and optimization of a subcritical steam power plant. Part I: Plant model and regulatory control. Energy Convers. Manag. 2017, 145, 324–334. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zhao, Y.; Liu, M.; Qiao, Y.; Chong, D.; Yan, J. Peak shaving operational optimization of supercritical coal-fired power plants by revising control strategy for water-fuel ratio. Appl. Energy 2018, 216, 212–223. [Google Scholar] [CrossRef]
- Sarda, P.; Hedrick, E.; Reynolds, K.; Bhattacharyya, D.; Zitney, S.E.; Omell, B. Development of a dynamic model and control system for load-following studies of supercritical pulverized coal power plants. Processes 2018, 6, 226. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Li, Y.; Wu, X.; Shen, J. Nonlinear modeling and inferential multi-model predictive control of a pulverizing system in a coal-fired power plant based on moving horizon estimation. Energies 2018, 11, 589. [Google Scholar] [CrossRef] [Green Version]
- Zeng, D.; Gao, Y.; Hu, Y.; Liu, J. Optimization control for the coordinated system of an ultra-supercritical unit based on stair-like predictive control algorithm. Control Eng. Pract. 2019, 82, 185–200. [Google Scholar] [CrossRef]
- Wu, Z.; He, T.; Li, D.; Xue, Y.; Sun, L.; Sun, L. Superheated steam temperature control based on modified active disturbance rejection control. Control Eng. Pract. 2019, 83, 83–97. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, M.; Hong, F.; Liu, J.; Wang, X. Control-oriented modelling and investigation on quick load change control of subcritical circulating fluidized bed unit. Appl. Therm. Eng. 2019, 163, 114420. [Google Scholar] [CrossRef]
- Shi, G.; Wu, Z.; Guo, J.; Li, D.; Ding, Y. Superheated steam temperature control based on a hybrid active disturbance rejection control. Energies 2020, 13, 1757. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Peng, C.; Zhang, T. Fuzzy K-means cluster based generalized predictive control of ultra supercritical power plant. IEEE Trans. Ind. Inform. 2020, 17, 4575–4583. [Google Scholar] [CrossRef]
- Arastou, A.; Rabieyan, H.; Karrari, M. Inclusive modelling and parameter estimation of a steam power plant using an LMI-based unknown input reconstruction algorithm. IET Gener. Transm. Distrib. 2021, 16, 1425–1437. [Google Scholar] [CrossRef]
- Lee, T.; Han, E.; Moon, U.C.; Lee, K.Y. Supplementary control of air–fuel ratio using dynamic matrix control for thermal power plant emission. Energies 2020, 13, 226. [Google Scholar] [CrossRef] [Green Version]
- Znad, O.A.; Mohamed, O.; Elhaija, W.A. Speeding-up Startup Process of a Clean Coal Supercritical Power Generation Station via Classical Model Predictive Control. Process Integr. Optim. Sustain. 2022, 1–14. [Google Scholar] [CrossRef]
- Hou, G.; Gong, L.; Yang, Z.; Zhang, J. Multi-objective economic model predictive control for gas turbine system based on quantum simultaneous whale optimization algorithm. Energy Convers. Manag. 2020, 207, 112498. [Google Scholar] [CrossRef]
- Bhatt, R.; Parmar, G.; Gupta, R. Whale optimized PID controllers for LFC of two area interconnected thermal power plants. ICTACT J. Microelectr. 2018, 3, 467–472. [Google Scholar]
- Mohamed, O.; Khalil, A.; Wang, J. Modeling and control of supercritical and ultra-supercritical power plants: A review. Energies 2020, 13, 2935. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mohamed, O.; Wang, J.; Guo, S.; Al-Duri, B.; Wei, J. Modelling study of supercritical power plant and parameter identification using genetic algorithms. In Proceedings of the World Congress on Engineering ; Springer: Berlin/Heidelberg, Germany, 2010; Volume 2. [Google Scholar]
- Mohamed, O.R.I. Study of Energy Efficient Supercritical Coal-Fired Power Plant Dynamic Responses and Control Strategies. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2012. [Google Scholar]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5. [Google Scholar]
- Zhao, Y.; Wang, C.; Liu, M.; Chong, D.; Yan, J. Improving operational flexibility by regulating extraction steam of high-pressure heaters on a 660 MW supercritical coal-fired power plant: A dynamic simulation. Appl. Energy 2018, 212, 1295–1309. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
| Recent Studies | Plant Modeling | Algorithm | Control Strategy | Mode Coordinated/Sliding | Control System Objectives |
|---|---|---|---|---|---|
| Mohamed et al. (2012) | Physical model | GA | MPC | Coordinated | Enhance the overall dynamic responses |
| Chen et al. (2017) | Software-based model | - | Conventional PID | Coordinated | Maintain the fluid level under load changes |
| Sarda et al. (2018) | Steady-state model | - | Conventional PID | Coordinated | Maintain main and reheater steam temperature |
| Liang et al. (2018) | Physical model | GA | Multi MPC | Coordinated | improve the pulverizing system performance |
| Shi et al. (2020) | Transfer function model | GA | Hybrid ADRC | Coordinated | Maintain the super-heated steam temperature |
| Wu et al. (2021) | Physical model | MOGA | ADRC & PID | Coordinated | Improve the load demand following responses |
| Abu Znad et al. (2022) | State-space model | - | Classical MPC | Sliding | Speed up the starting process |
| This work | Data-driven model | GWO * & WO * | Multivariable PI/PD | Sliding | Enhance the load demand following responses and reduce fuel and feedwater flow usage |
| GA Option | Setting |
|---|---|
| Population size | 30 |
| Number of generations | 50 |
| Crossover function | Heuristic |
| Mutation function | Adaptive feasible |
| Selection function | Tournament |
| Migration direction | Forward |
| GWO Option | Setting |
|---|---|
| Population size (Number ofsearch agents) | 30 |
| Number of iterations | 50 |
| WO Option | Setting |
|---|---|
| Population size (Number of search agents) | 30 |
| Number of iterations | 50 |
| Unknown Parameter | GA | GWO | WO |
|---|---|---|---|
| a11 | 0.77 | 0.3465 | 0.2615 |
| b11 | 0.369 | 0.3 | 0.2297 |
| c11 | 1.548 | 2.5 | 3.0653 |
| d11 | 2.952 | 2.2 | 1.9263 |
| e11 | 1.861 | 1.8 | 1.8844 |
| a12 | 0.536 | 0.7378 | 0.7006 |
| b12 | 0.168 | 0.201 | 0.2702 |
| c12 | 2.804 | 1.8 | 1.9268 |
| d12 | 68.48 | 60 | 52.1208 |
| e12 | 6.382 | 6.5 | 7.4443 |
| a21 | 1.942 | 1.0448 | 1 |
| b21 | 3.967 | 2.9705 | 2.5 |
| c21 | 6.102 | 7.5 | 6.034 |
| d21 | 1.724 | 2.0092 | 4 |
| e21 | 0.849 | 0.6124 | 0.998 |
| a22 | 5.787 | 4.6825 | 4 |
| b22 | 1.317 | 0.7091 | 0.5392 |
| c22 | 9.434 | 8.1908 | 9.5 |
| d22 | 30.574 | 30 | 20.8656 |
| e22 | 2.147 | 1.2 | 0.6003 |
| Response | NRMSE/GA | NRMSE/GWO | NRMSE/WO |
|---|---|---|---|
| Power | 0.088 | 0.0868 | 0.0561 |
| Pressure | 0.0765 | 0.0735 | 0.0409 |
| Parameter/Technique | GA | GWO | WO |
|---|---|---|---|
| Kp1 | 7.5433 | 5.6564 | 8.0019 |
| Ki1 | 1.5321 | 0.0331 | 0.0312 |
| Kp2 | 0.2770 | 0.6726 | 3 × 10−6 |
| Ki2 | 0.0870 | 0.1315 | 4 × 10−7 |
| Kp3 | 0.8270 | 0.8404 | 0.7765 |
| Kd | 11.4520 | 11.5471 | 11.6 |
| Td | 20.0010 | 24.1048 | 24.1048 |
| Input/Technique | GA | GWO | WO |
|---|---|---|---|
| Fuel flow (Kg/s) | 73.4991 | 72.2625 | 68.8226 |
| Feedwater flow (Kg/s) | 425.7973 | 428.5004 | 418.4478 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasem, M.; Mohamed, O.; Abu Elhaija, W. Parameter Identification and Sliding Pressure Control of a Supercritical Power Plant Using Whale Optimizer. Sustainability 2022, 14, 8039. https://doi.org/10.3390/su14138039
Qasem M, Mohamed O, Abu Elhaija W. Parameter Identification and Sliding Pressure Control of a Supercritical Power Plant Using Whale Optimizer. Sustainability. 2022; 14(13):8039. https://doi.org/10.3390/su14138039
Chicago/Turabian StyleQasem, Mohammad, Omar Mohamed, and Wejdan Abu Elhaija. 2022. "Parameter Identification and Sliding Pressure Control of a Supercritical Power Plant Using Whale Optimizer" Sustainability 14, no. 13: 8039. https://doi.org/10.3390/su14138039
APA StyleQasem, M., Mohamed, O., & Abu Elhaija, W. (2022). Parameter Identification and Sliding Pressure Control of a Supercritical Power Plant Using Whale Optimizer. Sustainability, 14(13), 8039. https://doi.org/10.3390/su14138039








