2.1. Measurement, Collection, and Pretreatment of Data
Figure 2 shows cylindrical samples of both the surface and intermediate layers of the asphalt pavement that were cored from 66 random locations on the No. 25 expressway route (Nonsan-Cheonan Expressway). We conducted an indirect tensile strength test according to KS F 2382 for the 50 mm thick upper part of the intermediate layer cut from the core samples. We measured the deformation of the core samples at 25 °C based on the load at a loading velocity of 50 mm/min.
Figure 3 shows how the FT—defined as the area surrounded by the load–deformation curve and deformation axis—was calculated for each core sample.
We collected HPMS data for 66 unit sections with lengths of 100 m, where the samples were cored. The HPMS database includes general information—such as the route, direction, lane, distance from the origin, and management branch—as well as pavement conditions, including IRI, RD, SD, and annual average daily traffic (AADT) by vehicle type. In this study, we assumed that the IRI, RD, SD, and AADT—commonly measured for entire expressway asphalt pavement sections—influence the FT and collected them to develop an ANN model for predicting the FT of entire expressway asphalt pavement sections.
Distress, such as cracks that develop in the intermediate layer, reduces the FT at the location and can propagate up to the surface layer [
13]. When the FT of the intermediate layer is reduced due to distress, the unrecoverable deformation at the pavement surface caused by the repetitive passing of heavy vehicles might worsen [
13]. The repetitive passing of heavy vehicles also reduces the FT of the intermediate layer [
14]. In this study, we used the ESAL, which sums up the multiplication of the ESAL factor and traffic volume by vehicle type and quantifies the effect of heavy vehicles on pavement conditions as an independent variable in the FT prediction model.
The regression models, including the ANN model, should use variables whose normality is verified [
15]. Therefore, in this study, we verified the normality of the dependent variable, FT, and independent variables (IRI, RD, SD, and ESAL) of the ANN model by calculating their skewness and kurtosis. We used Equation (1) to calculate the skewness, representing the asymmetry of the data of a variable. The distribution of data leans to the right if the skewness is negative and to the left if the skewness is positive [
16].
We calculated the kurtosis, which represents the degree of concentration of the data of a variable, using Equation (2). The distribution of the data approaches a normal distribution if the kurtosis approaches an absolute value of 3. The degree of concentration increases if the kurtosis becomes smaller than the absolute value of 3 and decreases if the kurtosis becomes larger than the absolute value of 3 [
17]. Although data with skewness close to zero and kurtosis close to the absolute value of three shows high normality, ordinary data cannot satisfy the criteria. Therefore, data with skewness less than the absolute value of 3 and kurtosis less than the absolute value of 10 were set as the criteria for normality, as suggested by Kline [
18].
In Equations (1) and (2), represents skewness, represents kurtosis, is the number of data elements, is the data element, and is the average of the data elements.
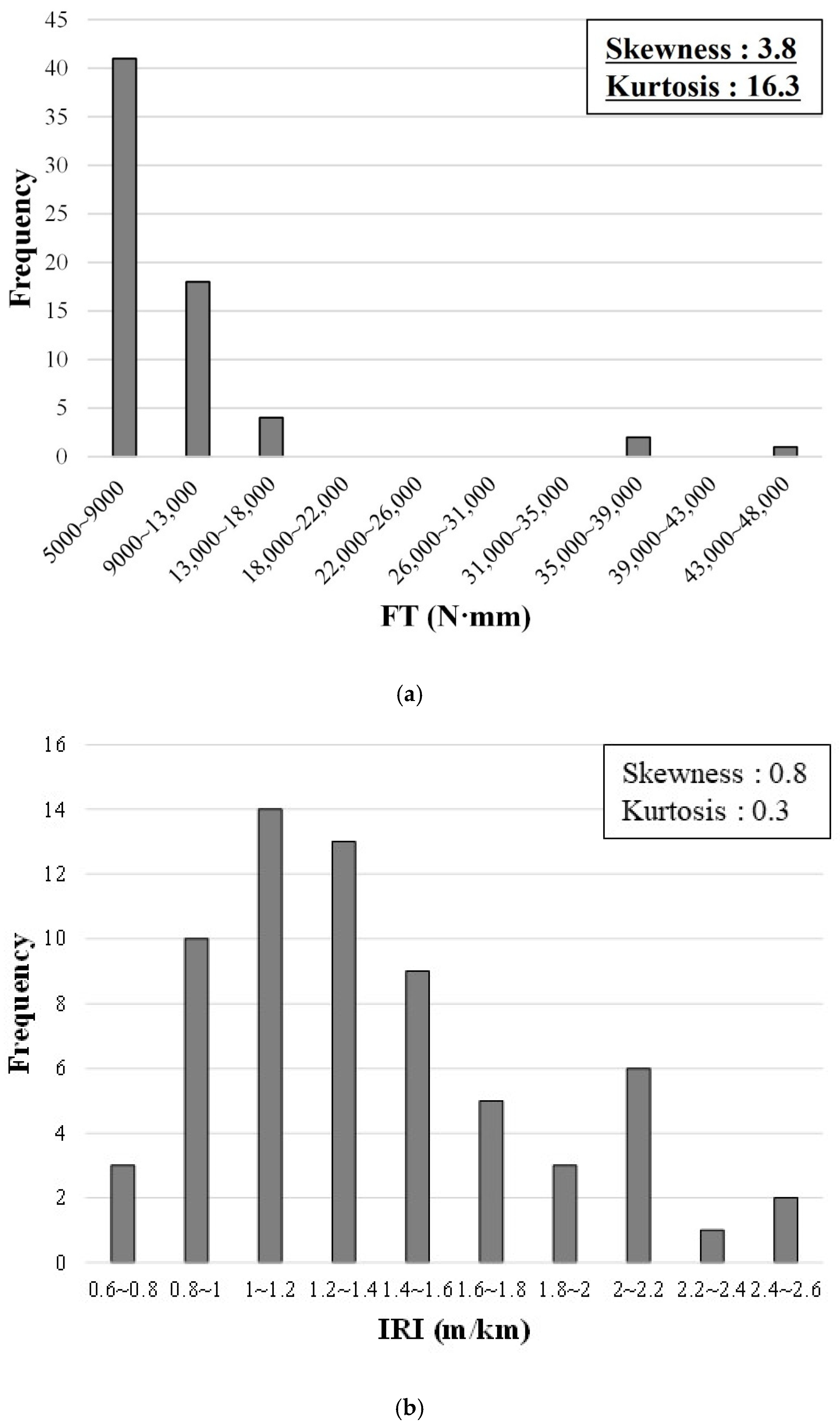
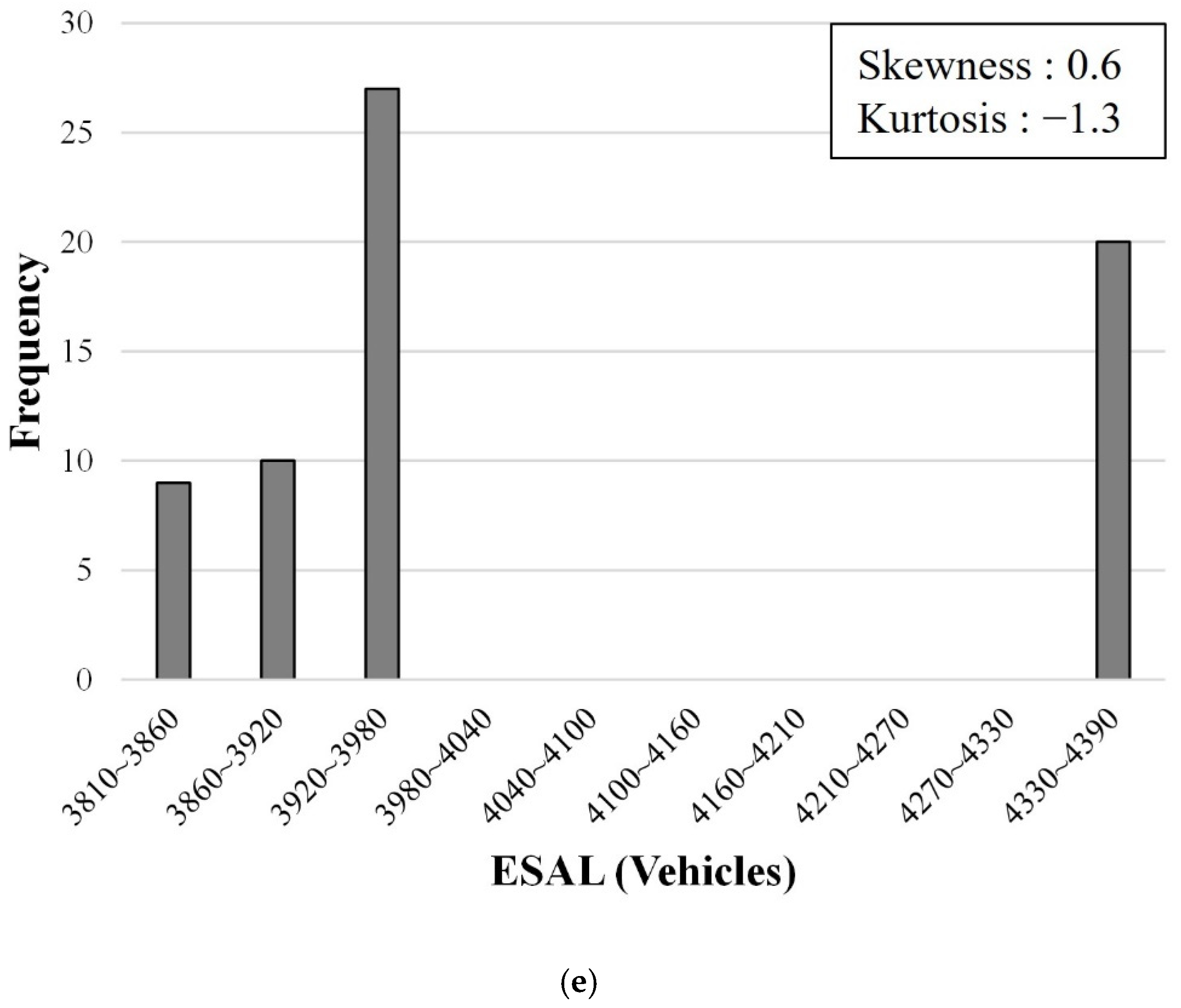
Figure 4 shows the distribution of the dependent variable (FT) and independent variables (IRI, RD, SD, and ESAL), and their respective skewness and kurtosis. The distribution of IRI (skewness: 0.8; kurtosis: 0.3) and RD (skewness: 0.5; kurtosis: −0.5) satisfied the normality visually, and their skewness and kurtosis satisfied the normality criteria. The distribution of ESAL dissatisfied the normality visually because there was relatively little data in the middle part. However, the skewness and kurtosis of ESAL were 0.6 and −1.3, respectively, satisfying both criteria of normality. Meanwhile, FT and SD showed a distribution with the data concentrated on small numbers. Their skewness was 3.8 and 4.4, and their kurtosis values were 16.3 and 22.6, respectively; thus, they did not meet the normality criteria.
If the data do not satisfy the criteria for normality, they can be adjusted to achieve normality by applying square roots, cube roots, or logarithms [
19,
20]. We visually verified the distributions of FT and SD after applying the square root, cube root, and logarithm, as shown in
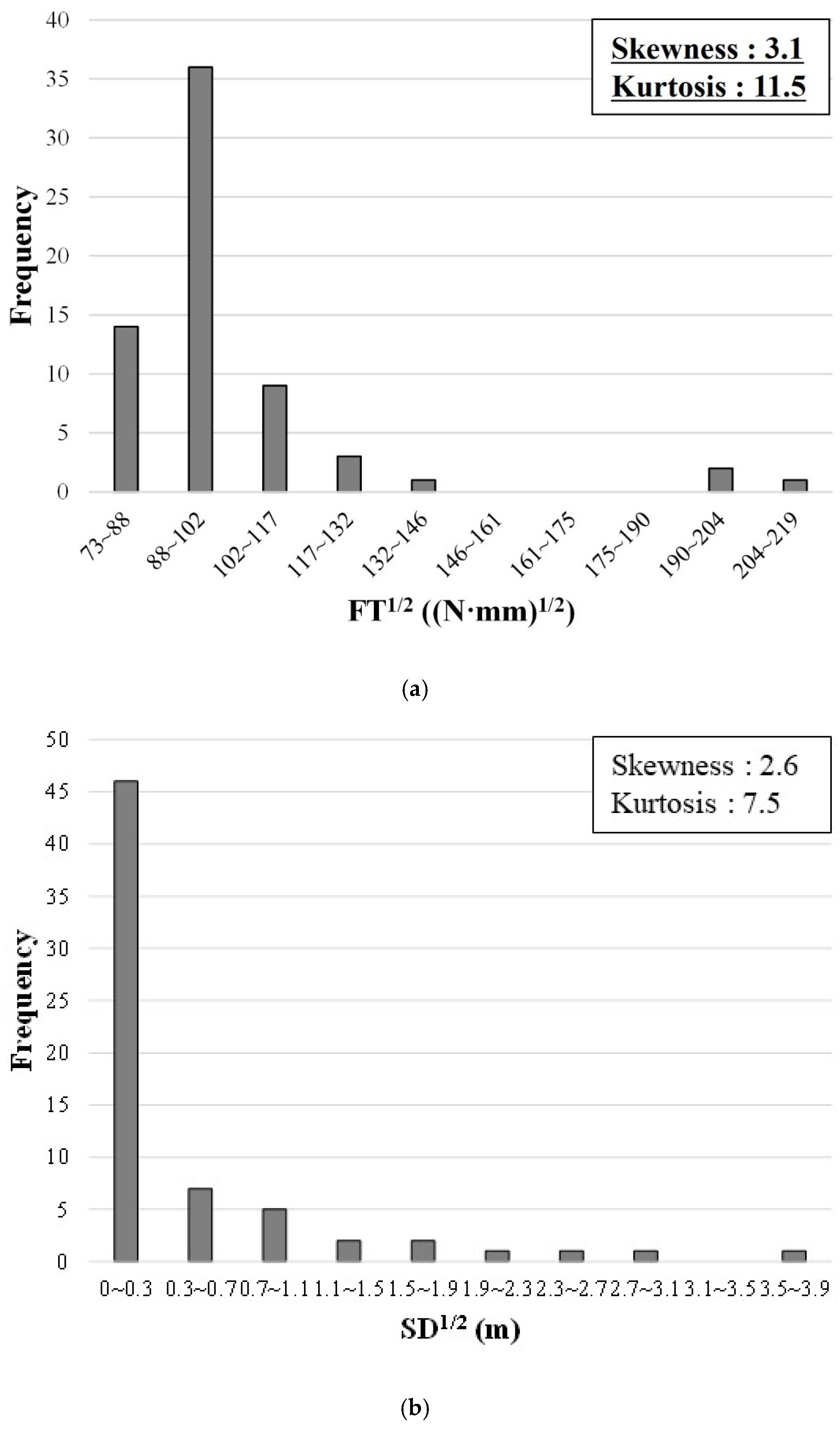
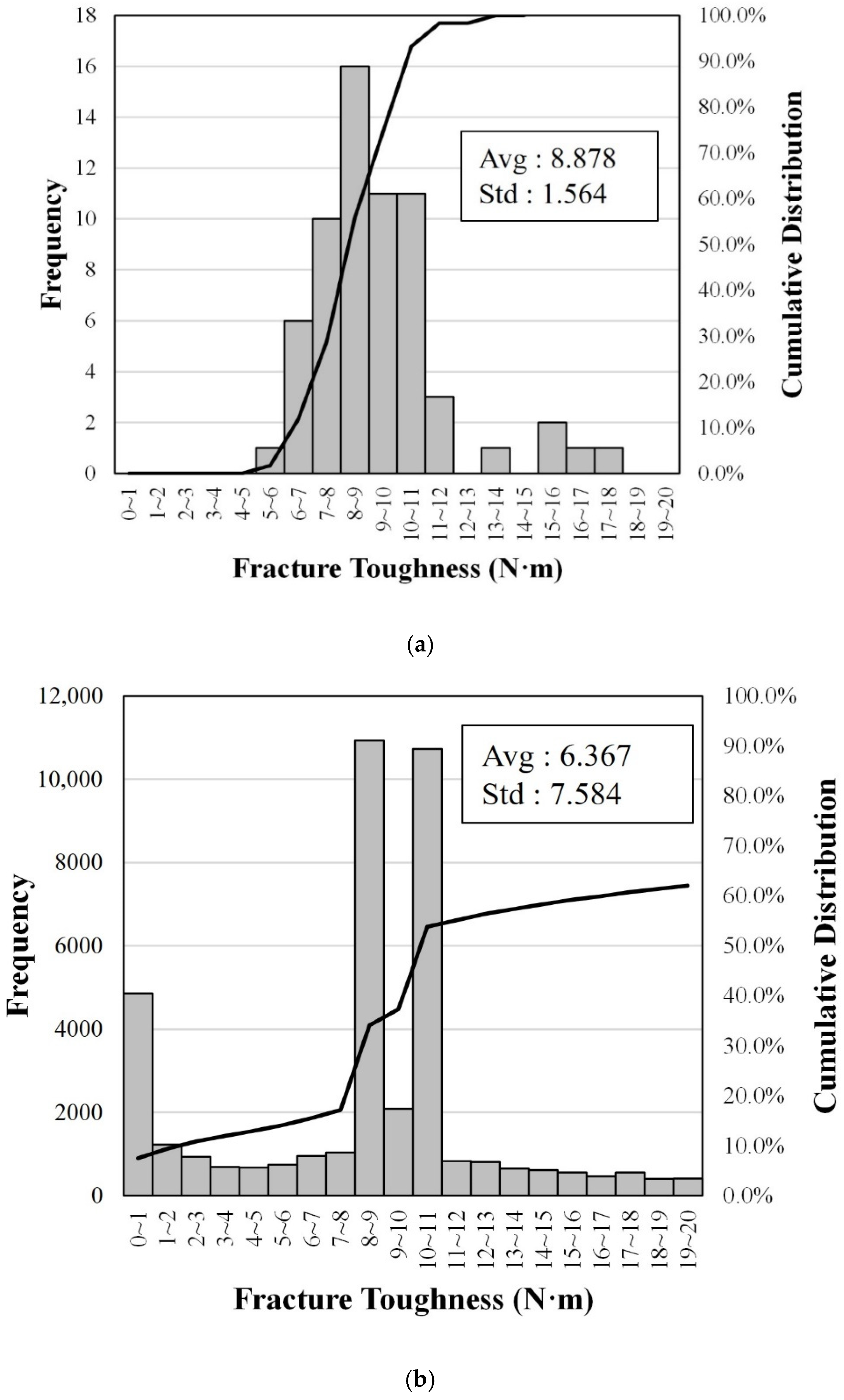
Figure 5, and examined their skewness and kurtosis. The distribution of the square root of FT in
Figure 5a shows skewness and kurtosis of 3.1 and 11.5, respectively; thus, the criteria for normality were not met. However, the square root of SD in
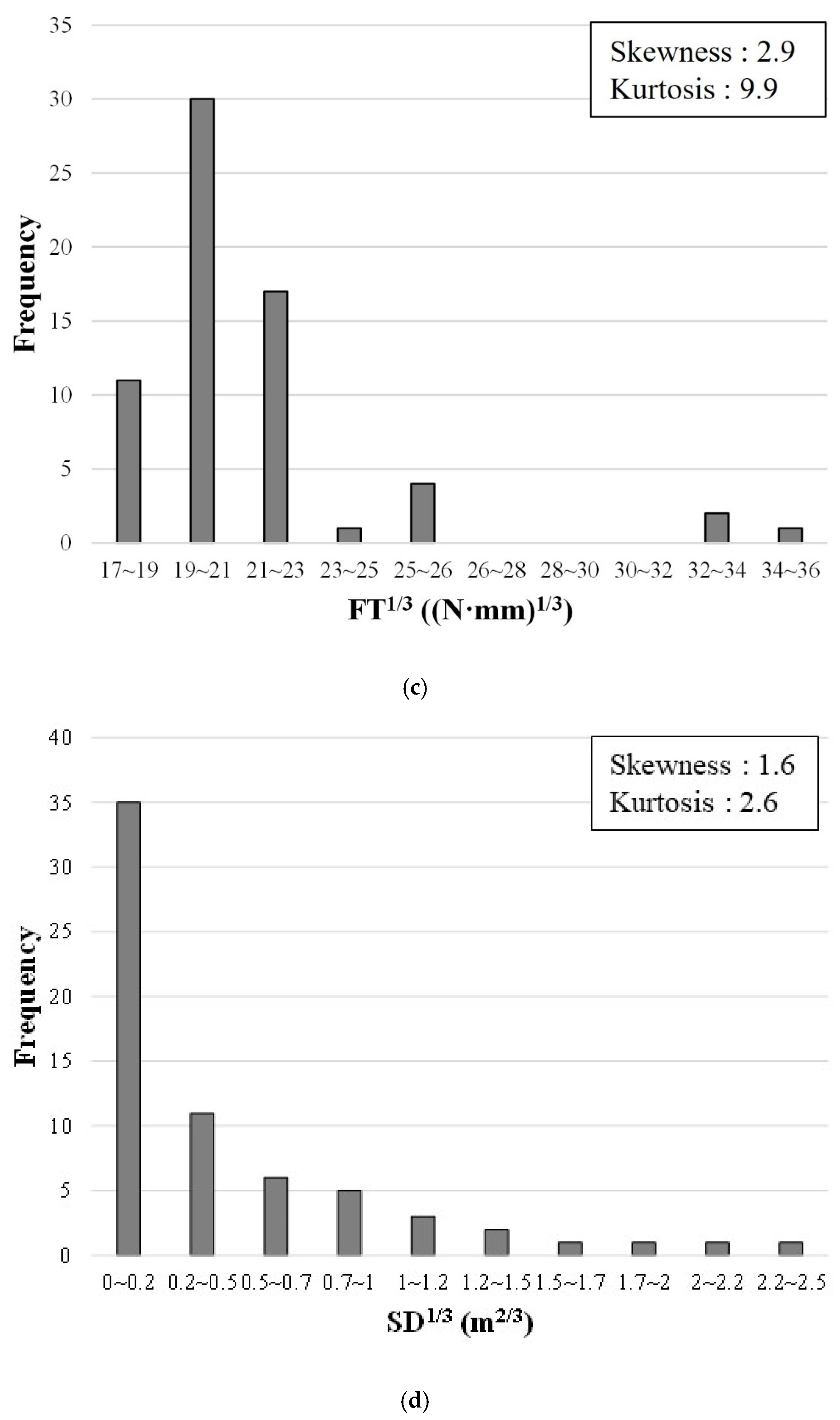
Figure 5b shows skewness and kurtosis of 2.6 and 7.5, respectively, both of which satisfy the normality criteria. The cube root of the FT (in
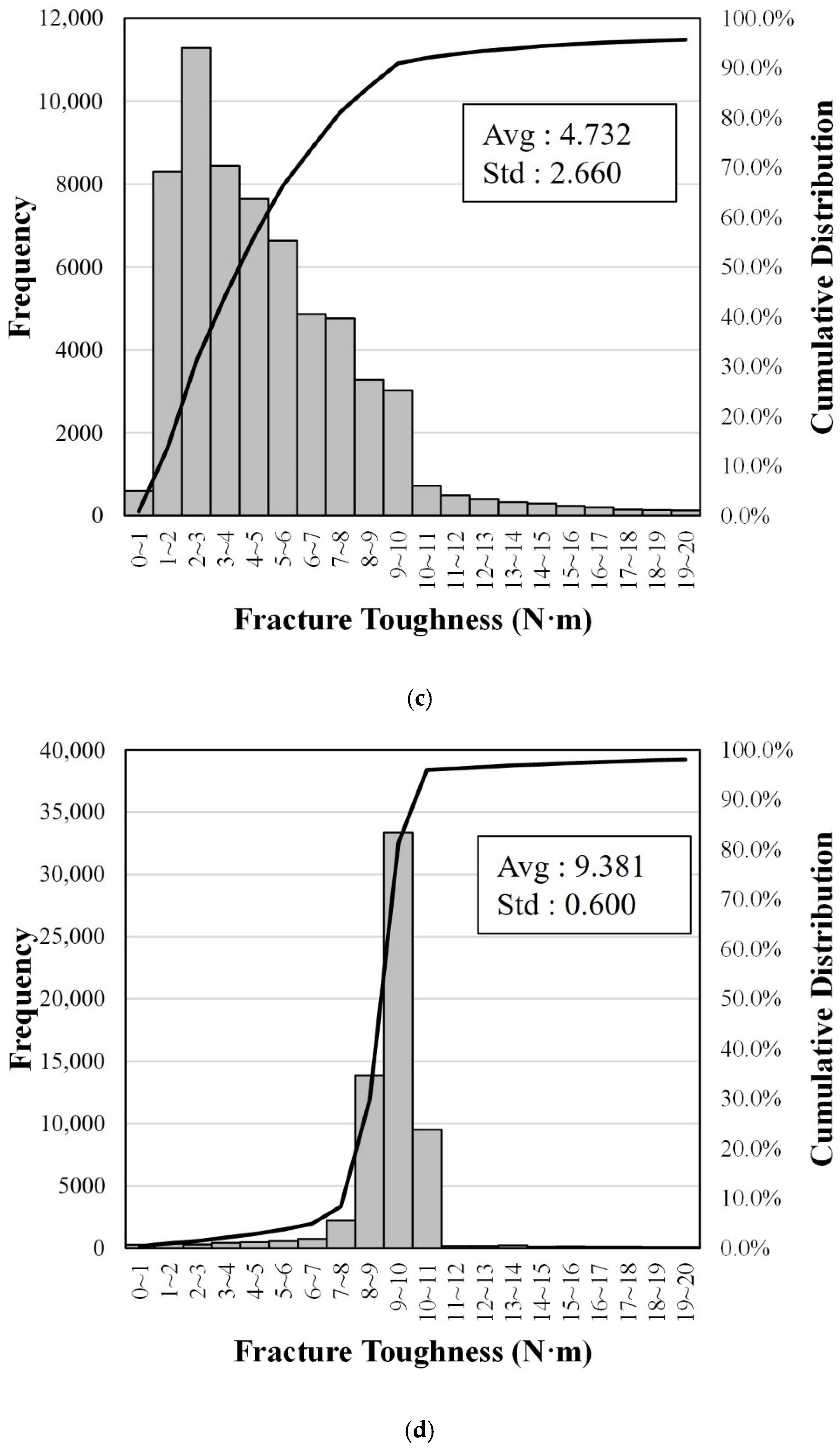
Figure 5c) and SD (in
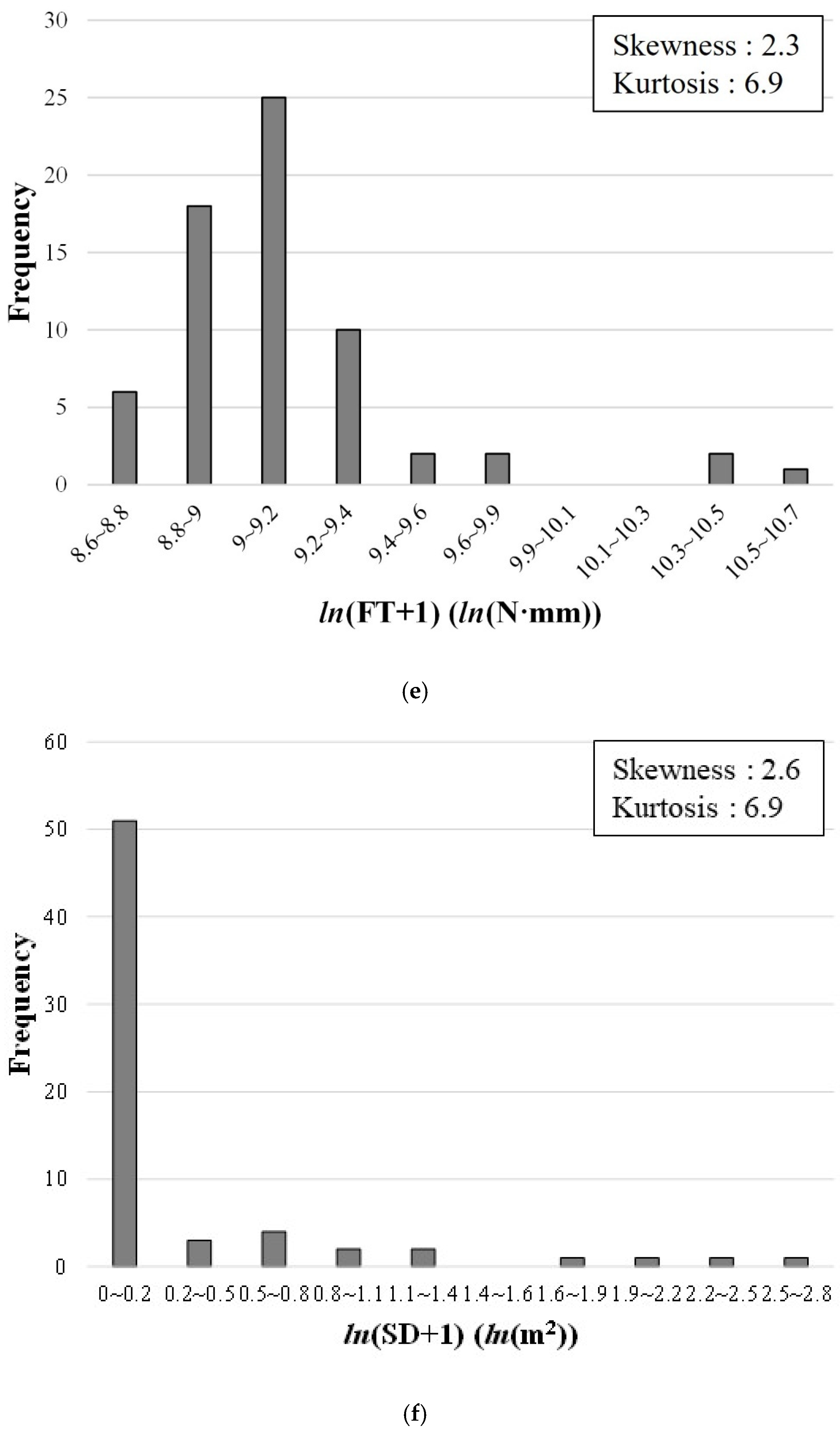
Figure 5d) and the logarithm of the FT (in
Figure 5e) and SD (in
Figure 5f) satisfied the criteria for normality. Consequently, we developed the FT prediction models by using dataset 1, comprising the actual values of IRI, RD, and ESAL, the cube root of FT, and the cube root of SD. We also used dataset 2, comprising the actual values of IRI, RD, and ESAL, the logarithm of FT, and the logarithm of SD, as shown in
Table 1.
Accurately reflecting the weight of each variable in the regression models, including the ANN model, requires standardization matching of the average and standard deviation of the data for each variable [
21].
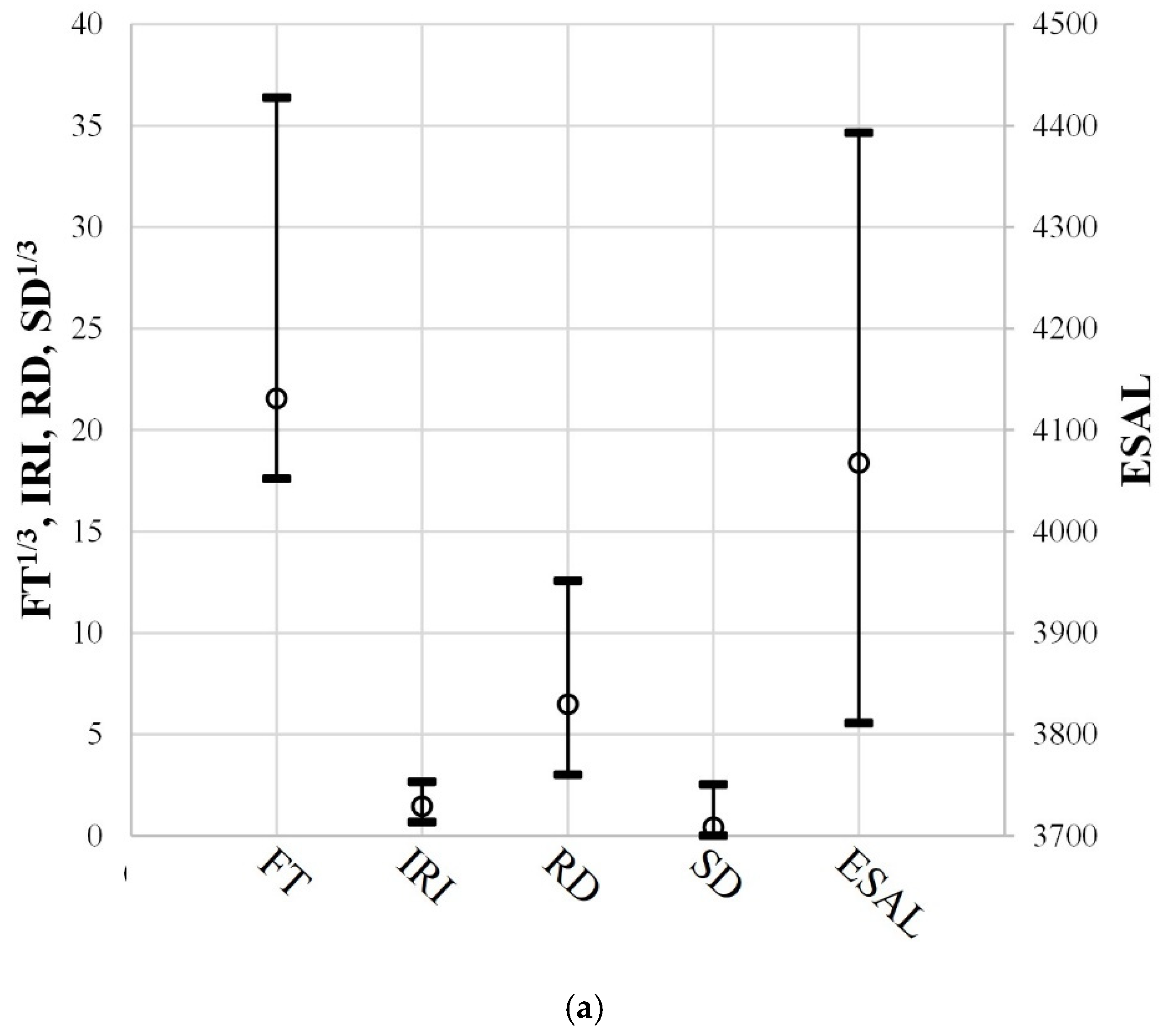
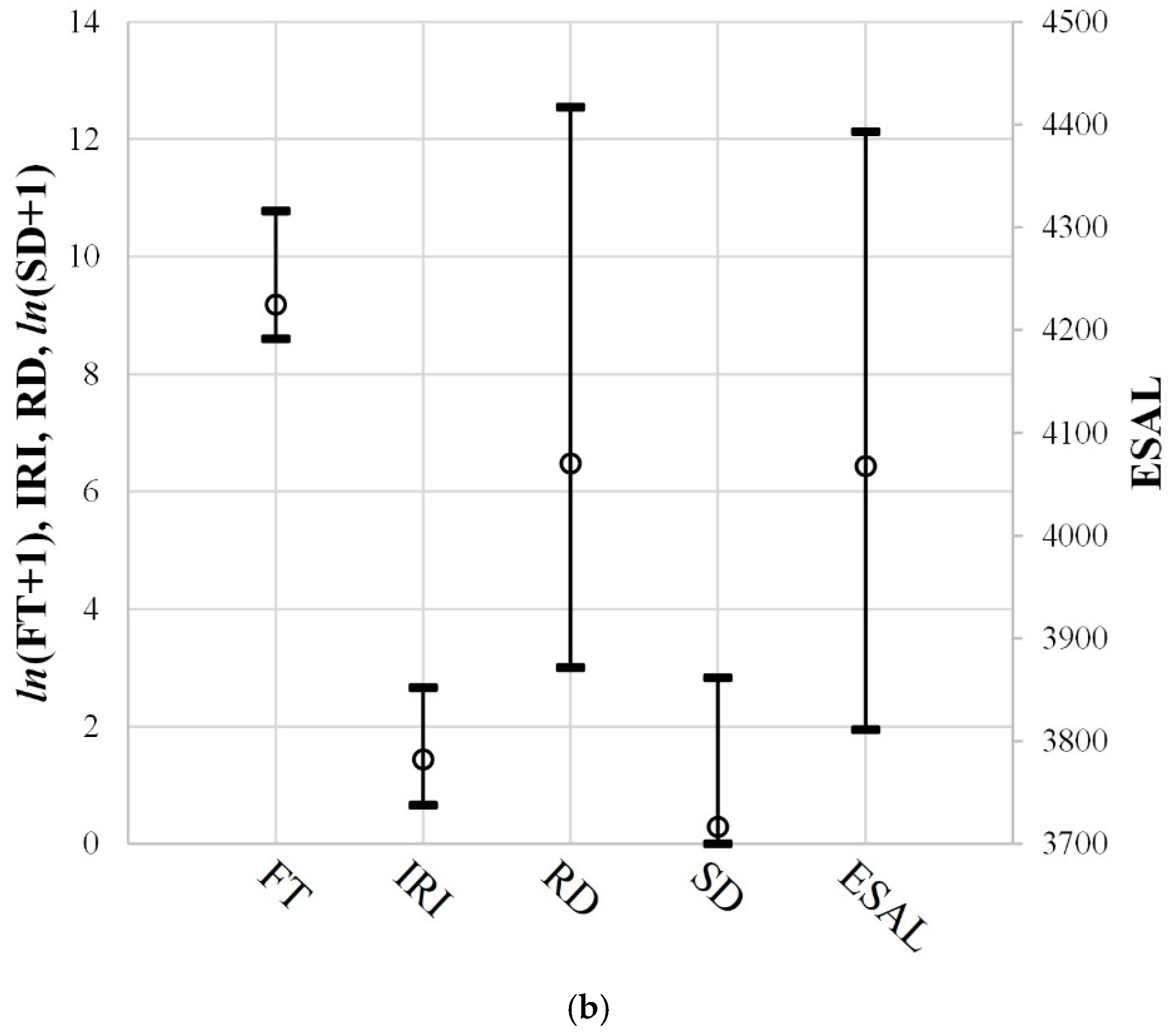
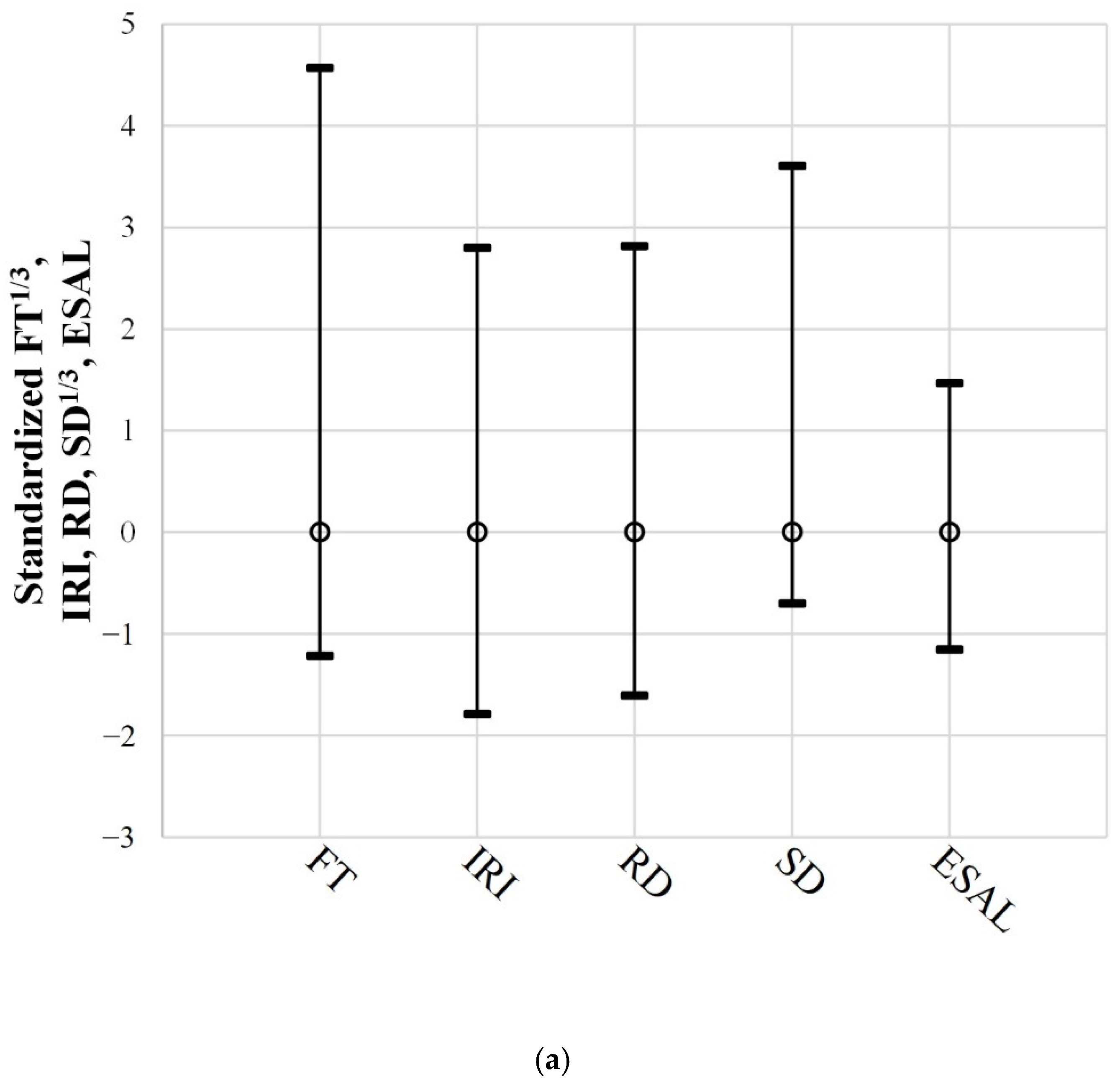
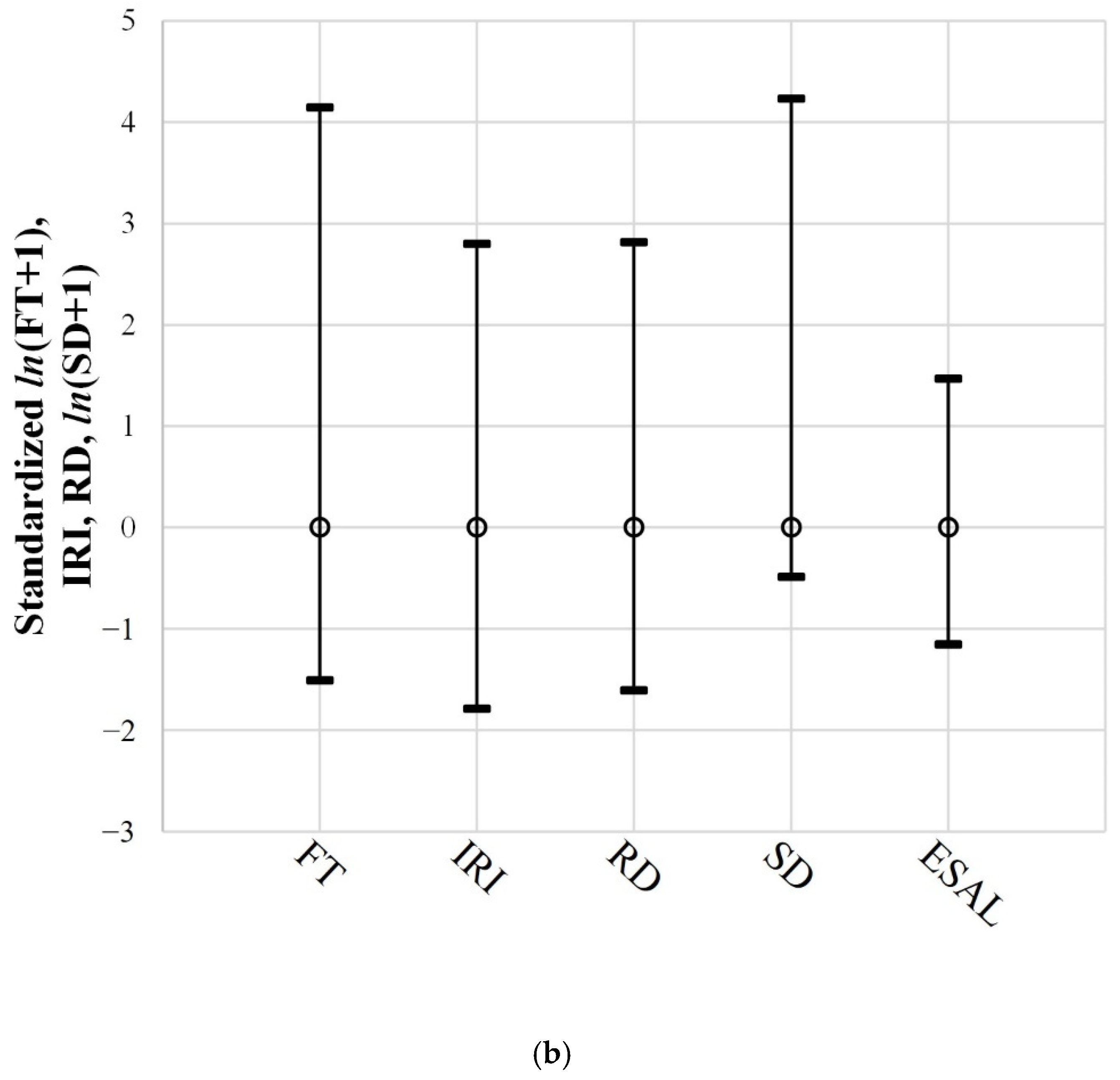
Figure 6 shows the maximum, minimum, and average values of the data for each variable included in datasets 1 and 2. All variables excluding IRI and SD showed different ranges of data distribution. In particular, ESAL was distributed across a much wider range, with tens to thousands of larger values than those of the other variables. Therefore, we used Equations (3)–(5) to standardize the data elements for each variable to obtain the average and standard deviation of 0 and 1, respectively. Consequently, the distribution of data for all variables included in datasets 1 and 2 became more similar, as shown in
Figure 7.
In Equations (3)–(5), represents the standardized data element, is the data element, is the average of the data elements, and is the standard deviation of the data element.
2.2. ANN Modeling for FT Prediction
The ANN model is a prediction method that uses machine learning to imitate the function of a human neural network [
22]. In the human neural network, a signal is carried from the input neuron, where the stimulus is input, to the hidden neuron based on the coupling strength (line thickness) between the neurons. The response is obtained from the output neuron when the signal is transferred again from the hidden neuron to the output neuron according to the coupling strength.
Figure 8 shows the procedure for constructing the ANN model with the optimal weight and bias, minimizing the error. First, we conducted pretreatment normalizing and standardizing of the data for each variable and determined input layers with input nodes, hidden layers with hidden nodes, output layers with output nodes, and activation functions at each hidden node to construct the ANN structure. Subsequently, we randomly set the weights and biases connecting the nodes in different layers. Using feed-forward processing, the input values are fed into the input nodes to generate results at the output nodes after passing through hidden nodes, weights, and biases. If the errors between the predicted and measured values are larger than the criterion, weights and biases are optimized using an appropriate optimizer and feed-forward processing is repeated until the error became smaller than the criterion.
We fabricated ANN models for predicting the FT of the intermediate layer of expressway asphalt pavements by using the independent variables IRI, RD, SD, and ESAL, as shown in
Table 2. We fabricated 100 ANN models by combining five types of optimizers, two types of data, and ten combinations of hidden layers and hidden nodes to compare their prediction performance. To determine the label of each model, we combined the abbreviations of the optimizer type (Adagrad: Ag; Adam: Ad; Adamax: Am; Nadam: Nd; and RMSprop: Rp), data type (dataset 1: 1 and dataset 2: 2), and the number of nodes in the first and second hidden layers (first and second numbers are the number of nodes in the first and second hidden layers, respectively). For example, if we determined the label of the model as Ad245, it means that Adam is used as the optimizer with dataset 2, and the numbers of the nodes in the first and second hidden layers are 4 and 5, respectively.
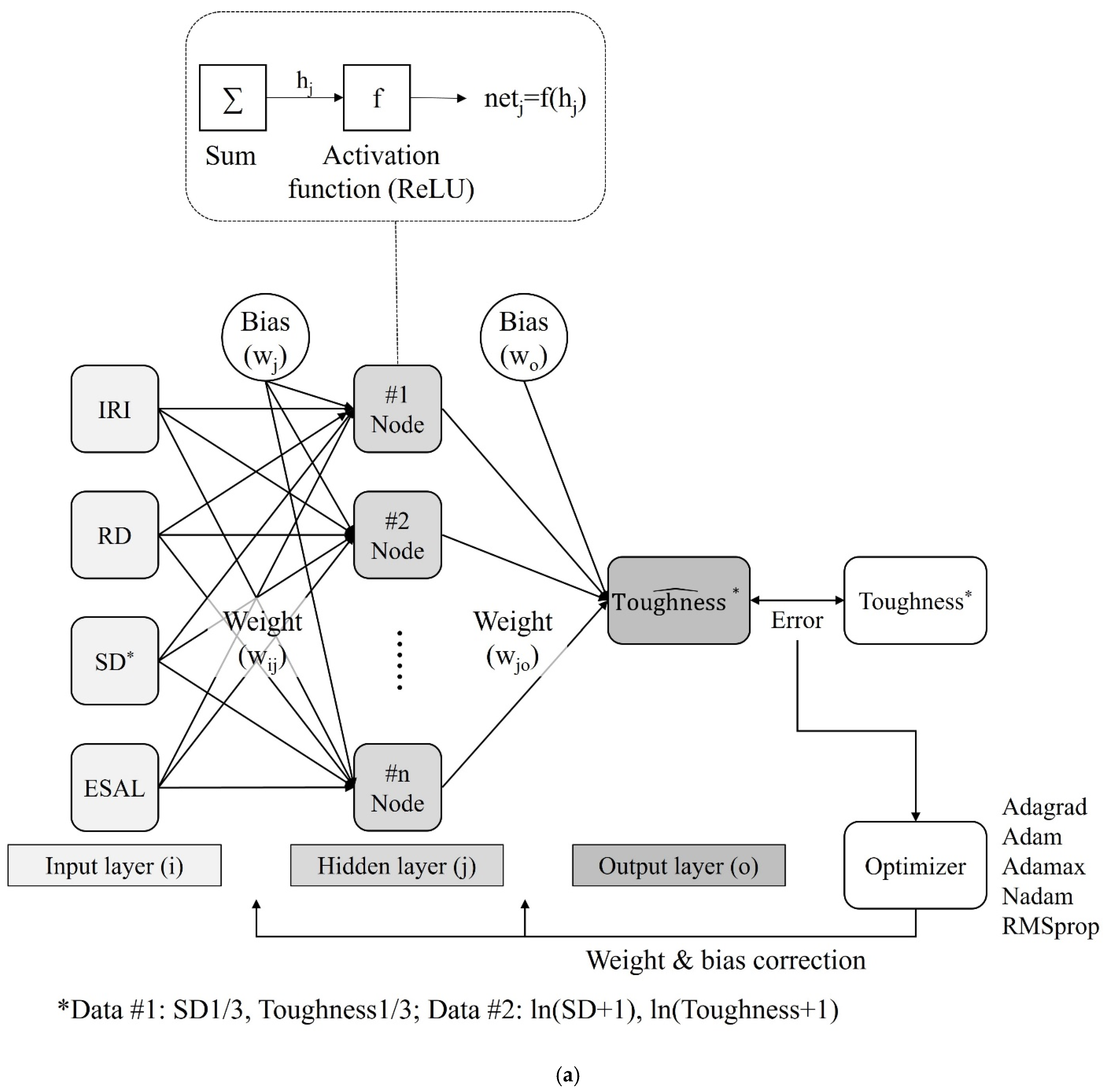
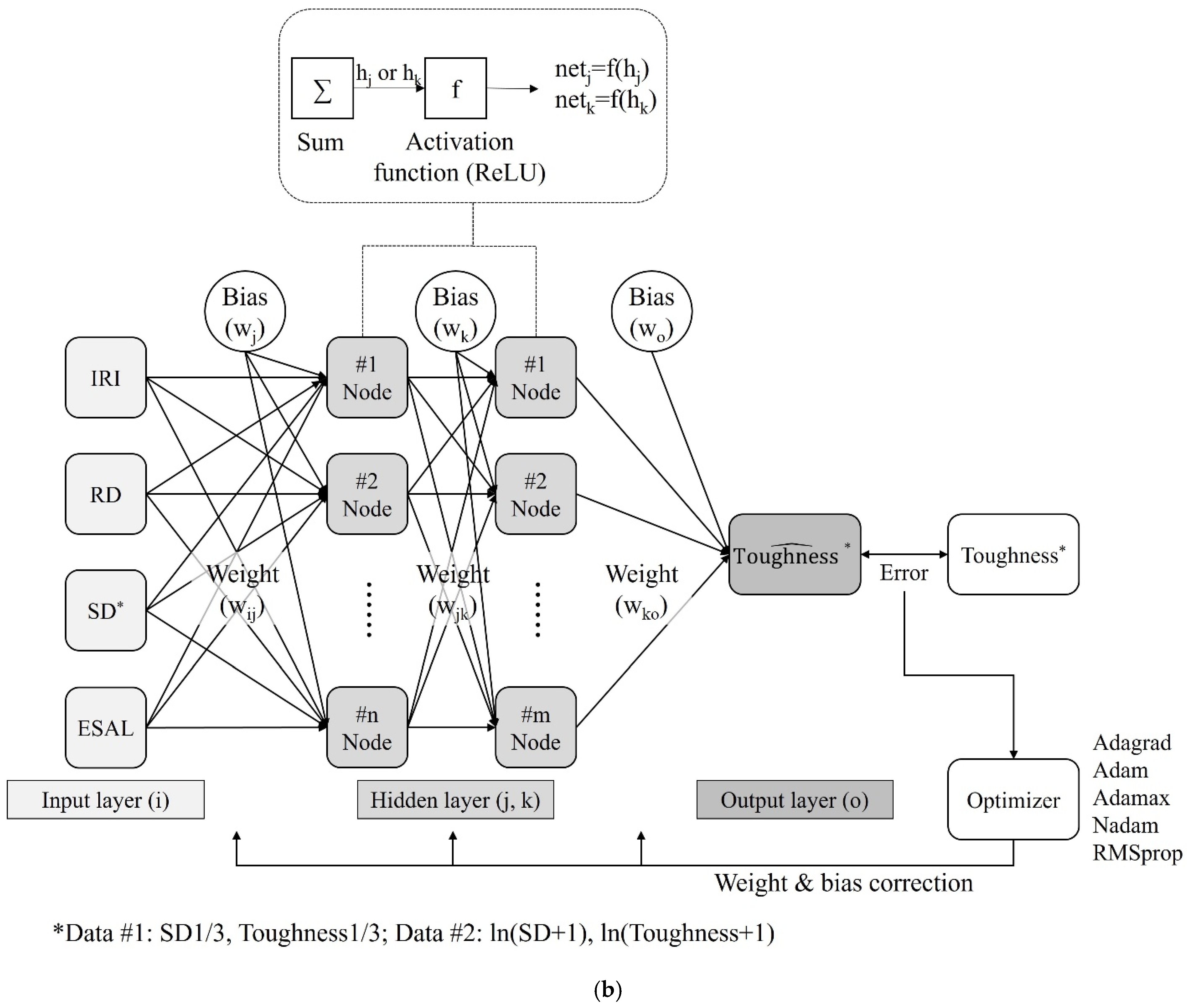
Figure 9 shows the constructed ANN model. The input layer comprises four nodes for IRI, RD, SD, and ESAL, and the hidden layer comprises one or two layers, as shown in
Figure 9a,b). The activation function at each node in the hidden layers assigns a nonlinearity to the model. In the ANN model with multiple layers, the sigmoid function—the most basic activation function—can cause a gradient vanishing problem, in which the adjusted values of the weights and biases converge to zero [
23]. The proposed ANN model comprises multiple layers. Therefore, we used a rectified linear unit (ReLU) based on Equation (6) as the activation function because it does not cause the vanishing gradient problem and has been used in the most extensive scope of research [
24]. The output layer consists of one node that outputs the predicted FT. The model could correct the weights and biases by using an appropriate optimizer when the error between the predicted and measured values is larger than the criterion.
We categorized datasets 1 and 2—normalized and standardized by pretreatment—into training and test datasets at an 8:2 ratio. We also assigned 20% of the training dataset to the validation dataset to verify the errors resulting from the training dataset for each training session. Equation (7) determines the number of hyperparameters according to the number of hidden layers and nodes.
In Equation (7), is the number of hyperparameters between two layers from n − 1 to n and is the number of nodes in the hidden layer k.
The hyperparameter, adjusted by training, is the weight and bias between each layer in the ANN model [
25]. The prediction performance of the ANN model using the training dataset improves, whereas the one using the validation dataset deteriorates, causing overfitting when the hyperparameter is too large. However, errors caused by both the training and validation datasets increase when the hyperparameter is too small. Therefore, an appropriate number of hyperparameters should be used to limit the number of hidden layers and nodes [
26].
In this study, we limited the number of hyperparameters to 53, corresponding to the number of training datasets—that is, 80% of the total data (66). Accordingly, we constructed 100 models by using five combinations of nodes for one hidden layer and five combinations of nodes for two hidden layers. First, we constructed five ANN models with four, five, six, seven, and eight nodes, respectively, with each model having one hidden layer. We also constructed five ANN models with two hidden layers, in which the layers had combinations of three and six nodes, three and seven nodes, four and four nodes, four and five nodes, and five and three nodes, respectively.
We used each of the five optimizers—Adagrad (adaptive gradient), Adam (adaptive moment estimation), Adamax (Adam max), Nadam (Nesterov momentum to Adam), and RMSprop (root mean square propagation)—to optimize the weights and biases of the ANN model:
Adagrad, based on Equation (8), optimizes the model less when the adjustment amount for the weights and biases is large, whereas it optimizes the model more when the adjustment amount is small [
27].
Adam, based on Equations (9) and (10), optimizes the model by using an extremely small operational quantity that simplifies the gradient, which determines the adjusted amounts of weights and biases [
28].
Adamax, based on Equations (9) and (11), has a similar function to that of Adam while restricting the maximum adjustment amount [
28].
Nadam, based on Equation (12), is also similar to Adam, but it expands the range of previous errors involved in the determination of the adjustment amount [
29].
RMSprop, based on Equations (13) and (14), is similar to Adagrad, but it reflects more recent learning information than past information [
30]:
In Equations (8)–(14), is the parameter vector, is the step size, is the first-moment vector, is the gradient, is the loss function, is the second-moment vector, is the exponential mean of the square of the loss function gradient, and serve as float values.
2.3. Selection and Evaluation of Candidate ANN Models
To train the models, we optimized the weights and biases a maximum of 2000 times for each model, and the models predicted the FT as the output.
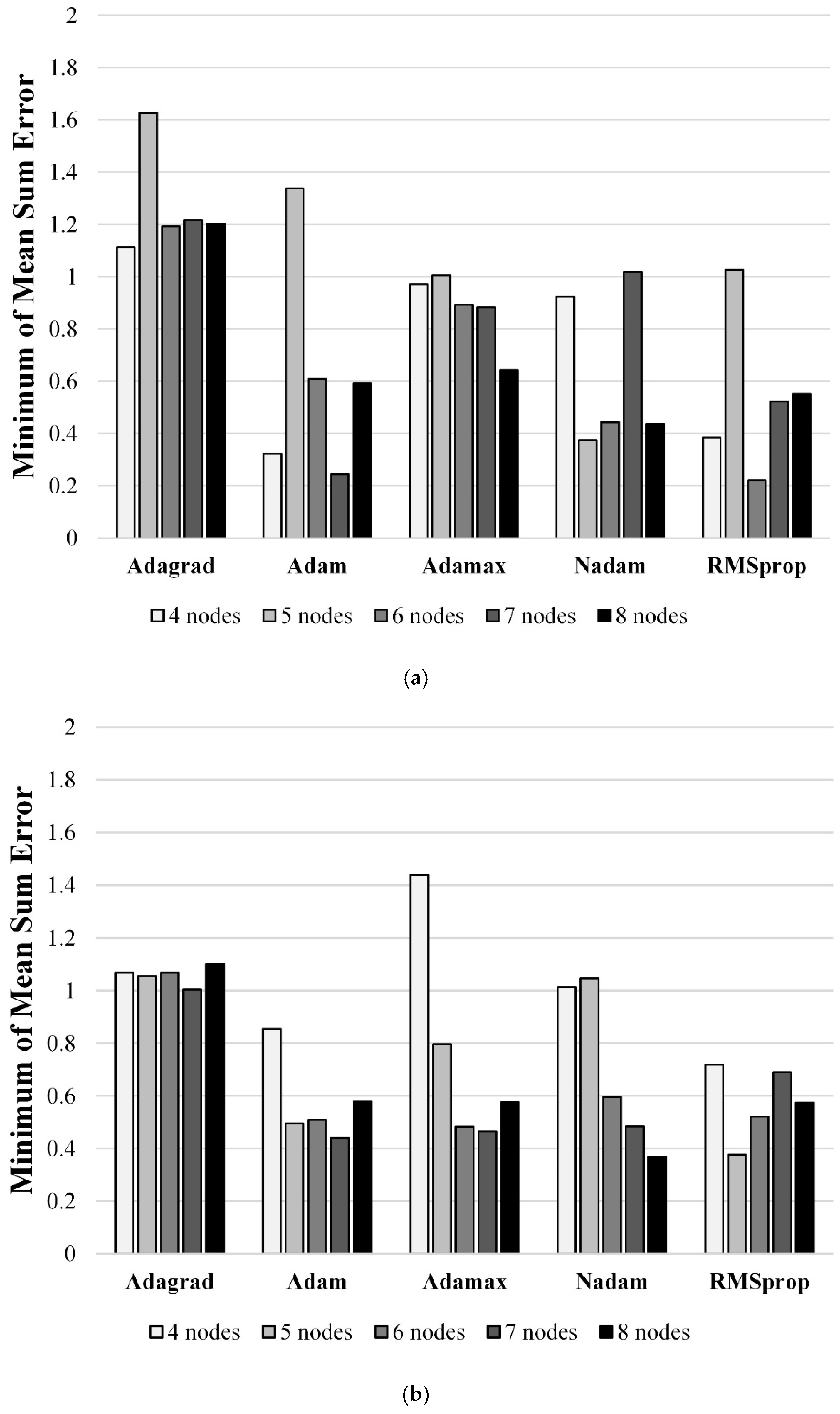
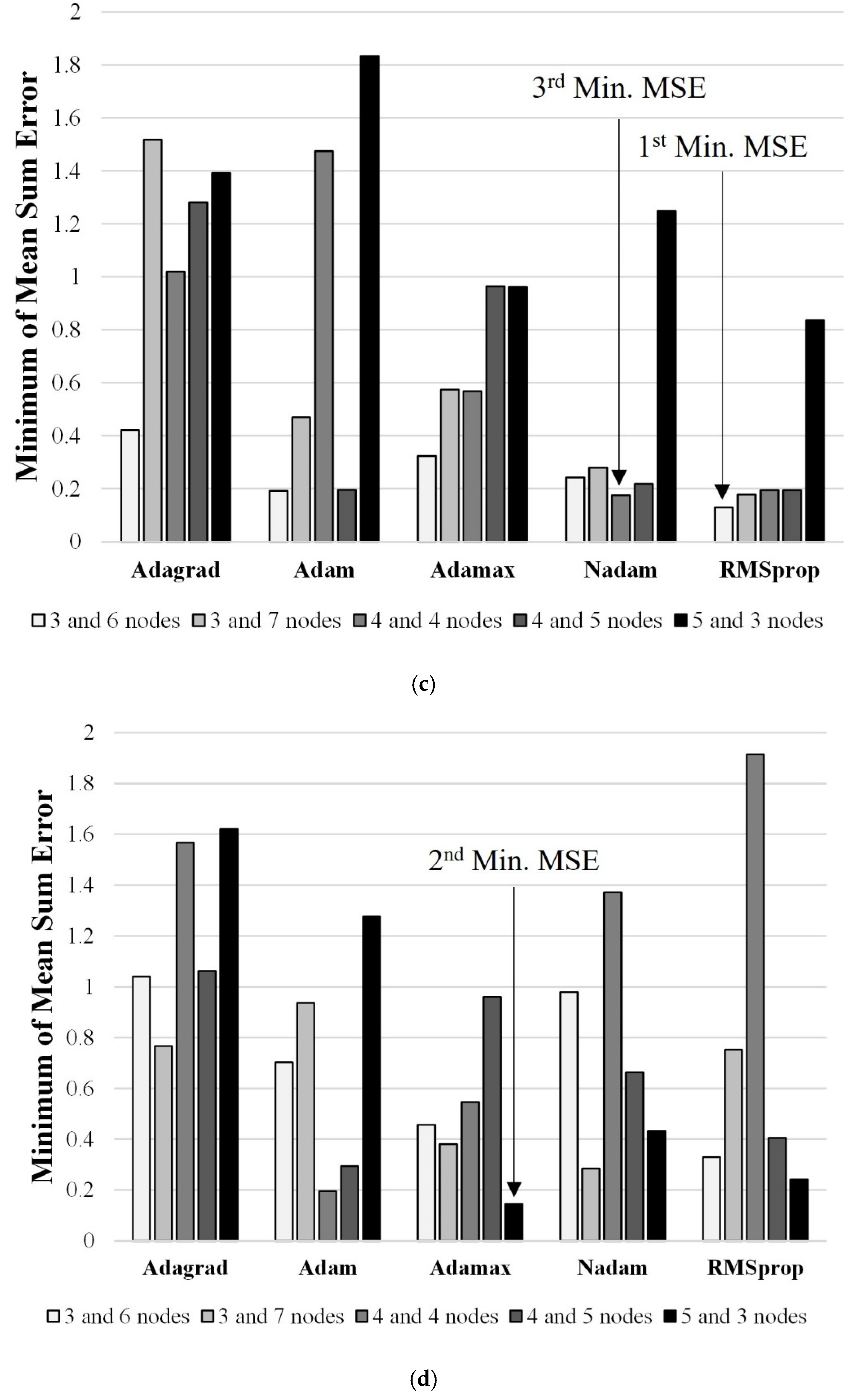
Figure 10 shows the minimum errors recorded between the FT training (dataset) predictions and the measured FTs as a function of the composition of the hidden layers, type of data (dataset), and type of optimizer.
Figure 10a shows the errors for dataset 1 and one hidden layer. The errors for the Adam, Nadam, and RMSprop optimizers were the lowest; in particular, the Rp160 model was the best, with an error of 0.22.
Figure 10b shows the errors for dataset 2 and one hidden layer. The errors for the Adam, Nadam, and RMSprop optimizers were the lowest. In particular, the Nd280 model showed superior performance with an error of 0.37. The errors for dataset 1 and two hidden layers are shown in
Figure 10c. The errors for the Nadam and RMSprop optimizers were the lowest; specifically, the Rp136 model showed superior performance with the lowest error of 0.13, compared to that of all the models. Furthermore, the error for the Nd144 model was 0.18, which was the third-lowest overall error.
Figure 10d shows the errors for dataset 2 and two hidden layers. The errors for the Adamax optimizer were the lowest; specifically, the Am253 model was the best, with an error of 0.15, which was the second lowest, overall.
The models with one hidden layer showed higher errors than those with two hidden layers because they had fewer hyperparameters, resulting in poorer prediction performance. Therefore, we selected the Rp136, Am253, and Nd144 models—all of which contained two hidden layers—as the candidate models with the lowest errors.
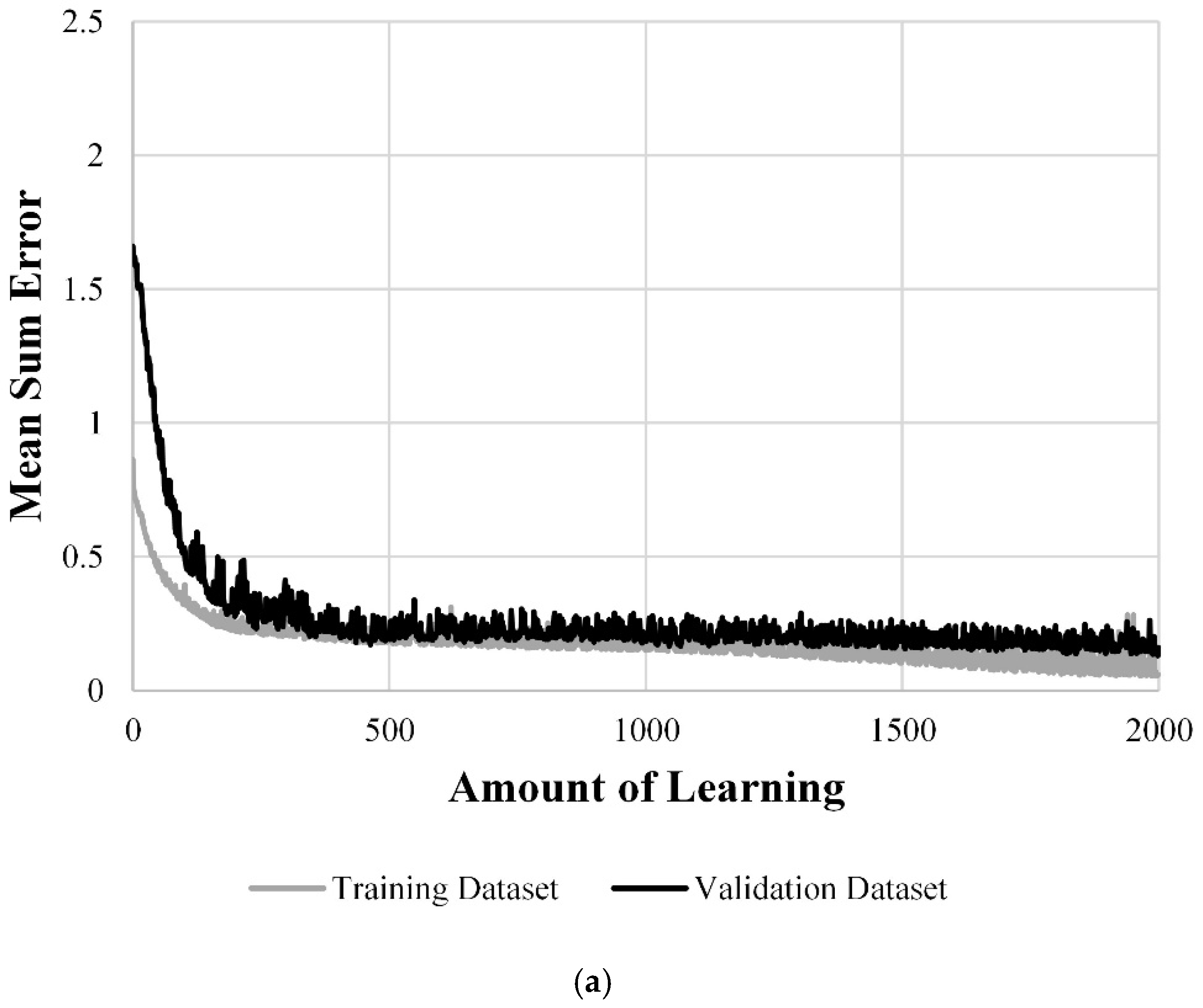
We compared the errors recorded using the training dataset with those recorded using the validation dataset as a function of the amount of learning, as shown in
Figure 11, to investigate the learning generality of the candidate models. We excluded the validation dataset, which occupied 20% of the training dataset, from feed-forward processing to examine the overfitting of the candidate models. The errors of all candidate models decreased with the amount of learning for both the training and validation datasets, reducing the possibility of overfitting.
Figure 11a shows that for the Rp136 model, both datasets have unstable errors with large variations, even with increased amounts of learning. The Am253 model shows stable errors for the validation dataset in
Figure 11b because the errors from the training dataset are sufficiently stable, regardless of the learning amount. The Nd144 model in
Figure 11c shows errors with irregular variation for the validation dataset because the errors of the model for the training dataset are slightly unstable regardless of the learning amount.
We compared the error rates from the training dataset with those from the test dataset. We calculated the error rates by dividing the error between the predicted and measured FTs by the measured FT, as expressed in Equation (15). The average of the entire error rate calculated for each FT is used to represent the error rate of each candidate model.
In Equation (15), is the error rate (%), is the prediction value, is the actual value, and represents the number of data elements.
Figure 12,
Figure 13 and
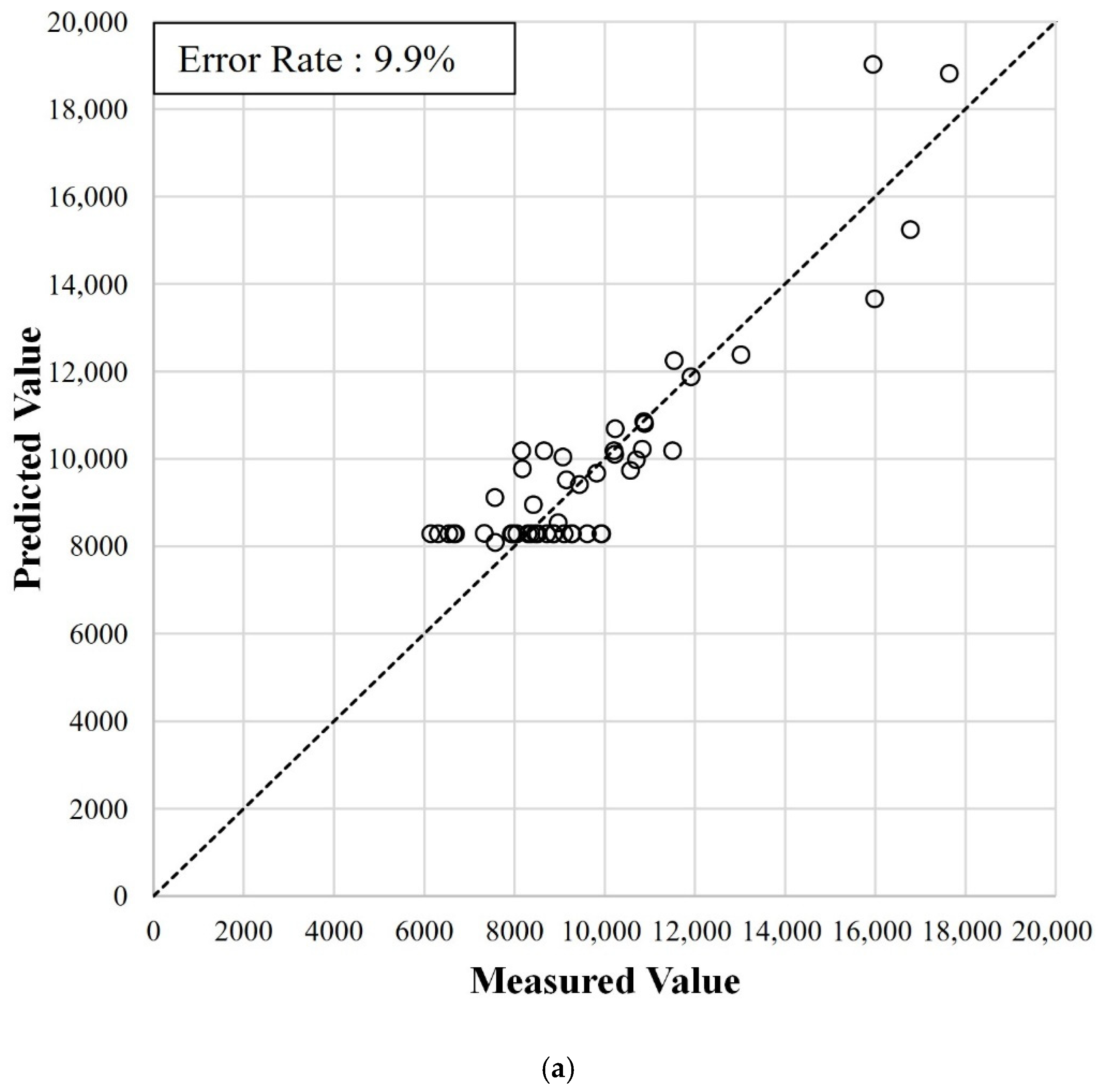
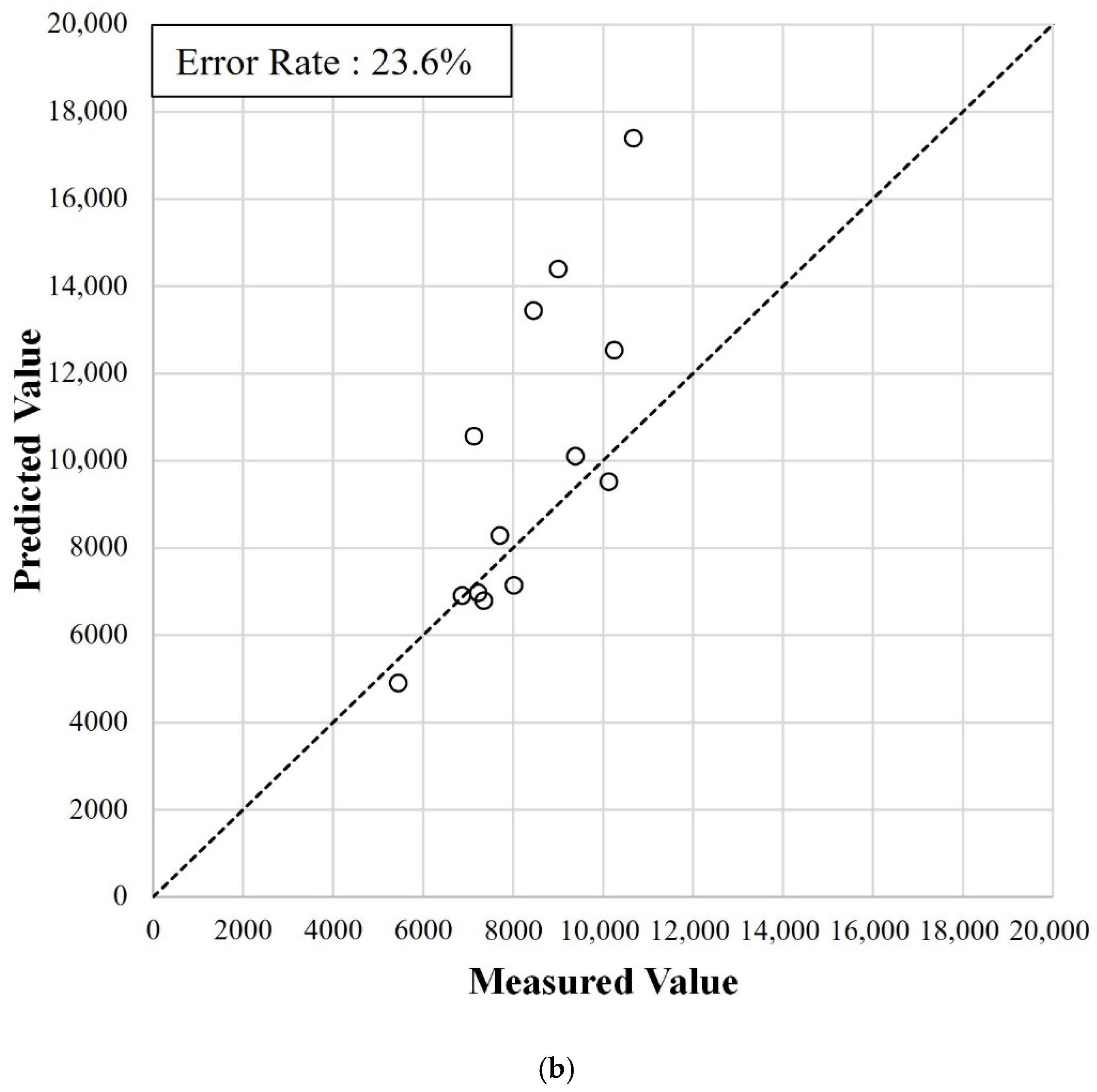
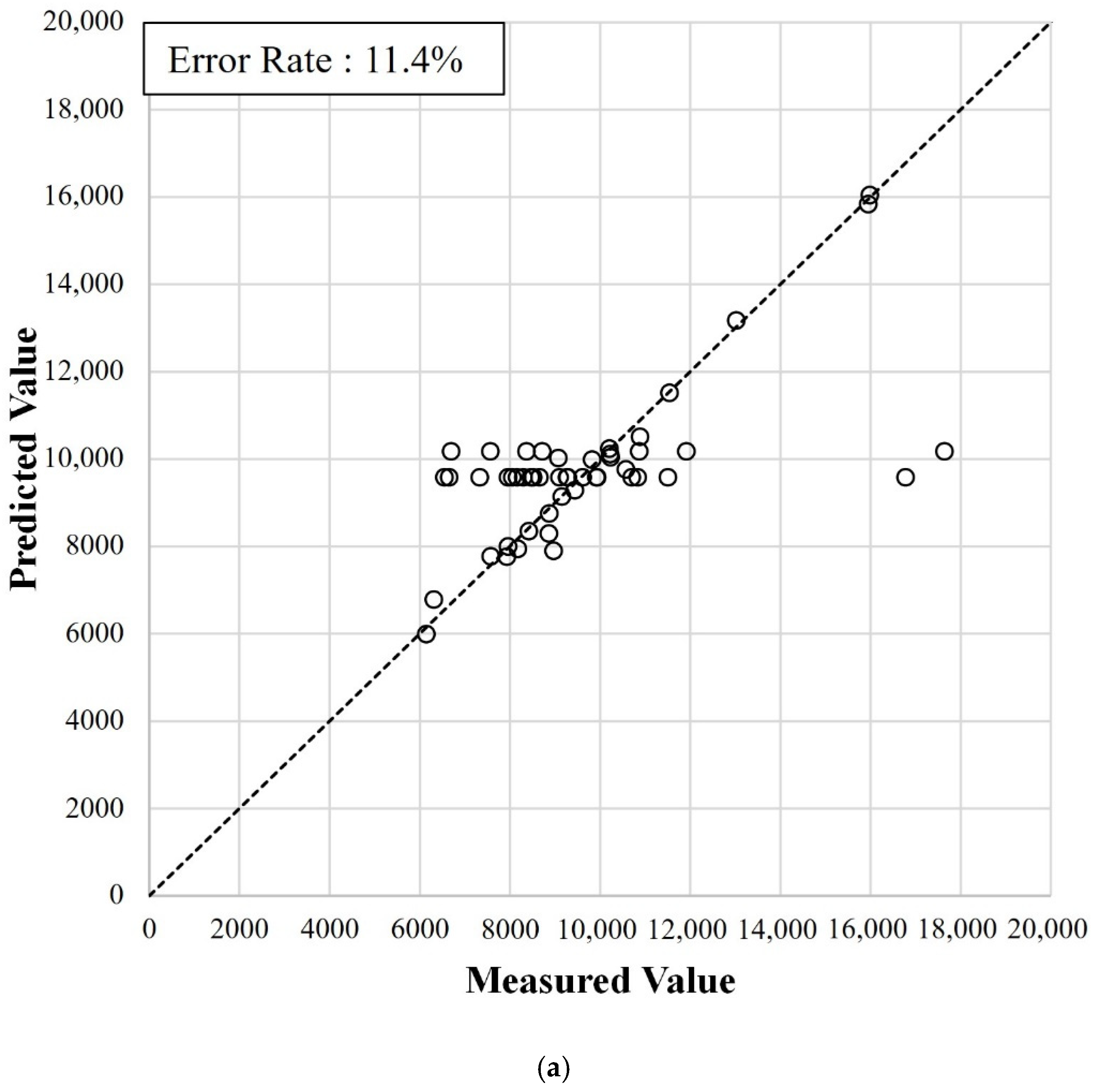
Figure 14 show the FT predictions using both the training and test datasets, as well as the measured FTs, and error rate of the Rp136, Am253, and Nd144 models, respectively. The error rate for the Rp136 model for the training dataset was low (9.9%), whereas the error rate for the test dataset was relatively high (23.6%). This significant difference was most likely caused by the unstable errors observed for both the training and validation datasets, regardless of the learning amount, as shown in
Figure 11a. Similar error rates for the Am253 model for the training and test datasets occurred at 12.2% and 12.4%, respectively, because of the error stability for both datasets, as shown in
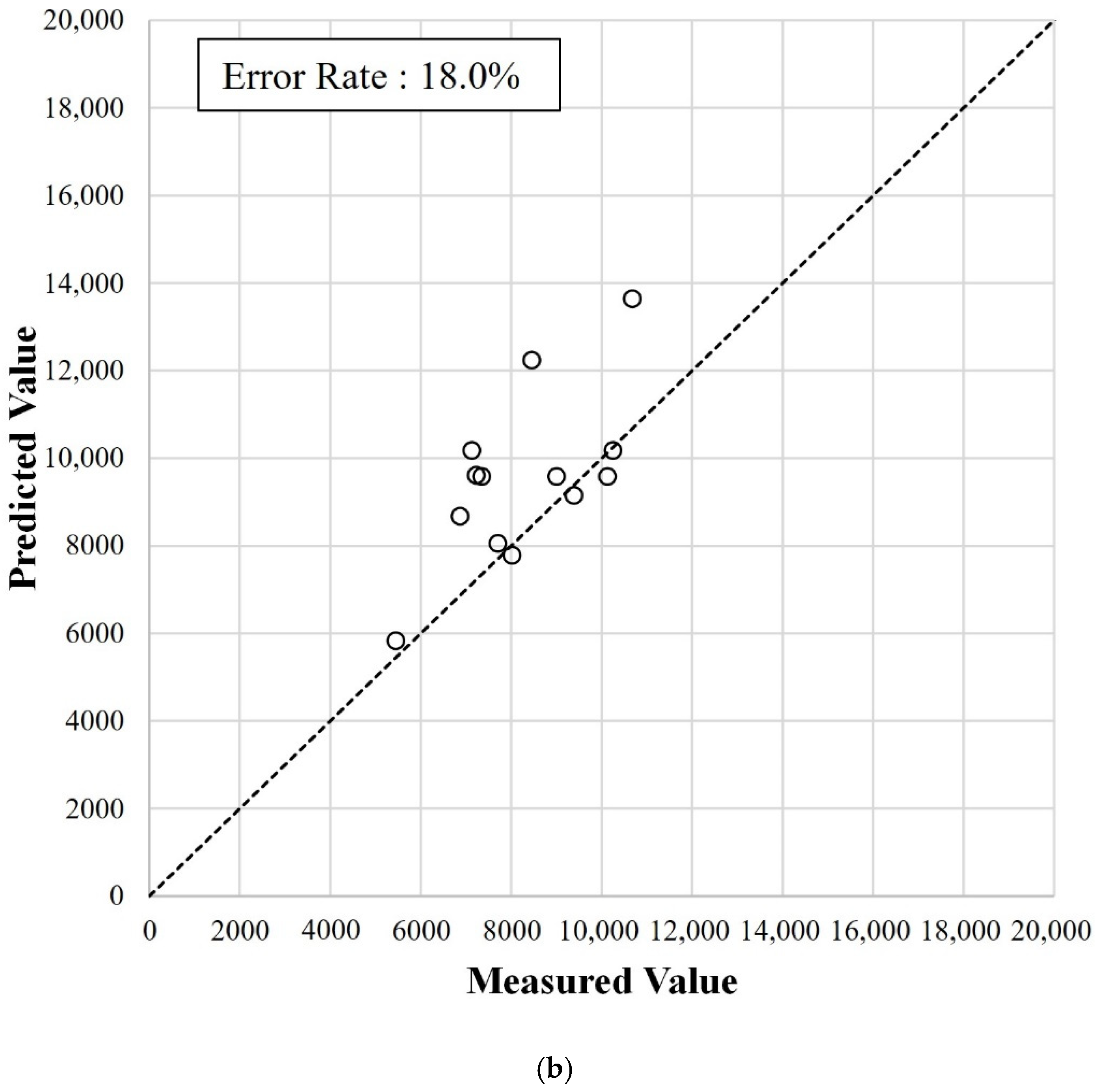
Figure 11b. For the Nd144 model, the error rate of the test dataset was slightly higher (18.0%) than that of the training dataset (11.4%).
Figure 11c shows the slightly increased error rate of the test dataset because of the slightly unstable errors observed for both datasets.