When Offline Stores Reduce Online Returns
Abstract
:1. Introduction
1.1. Omnichannel Retailing and Product Returns
- -
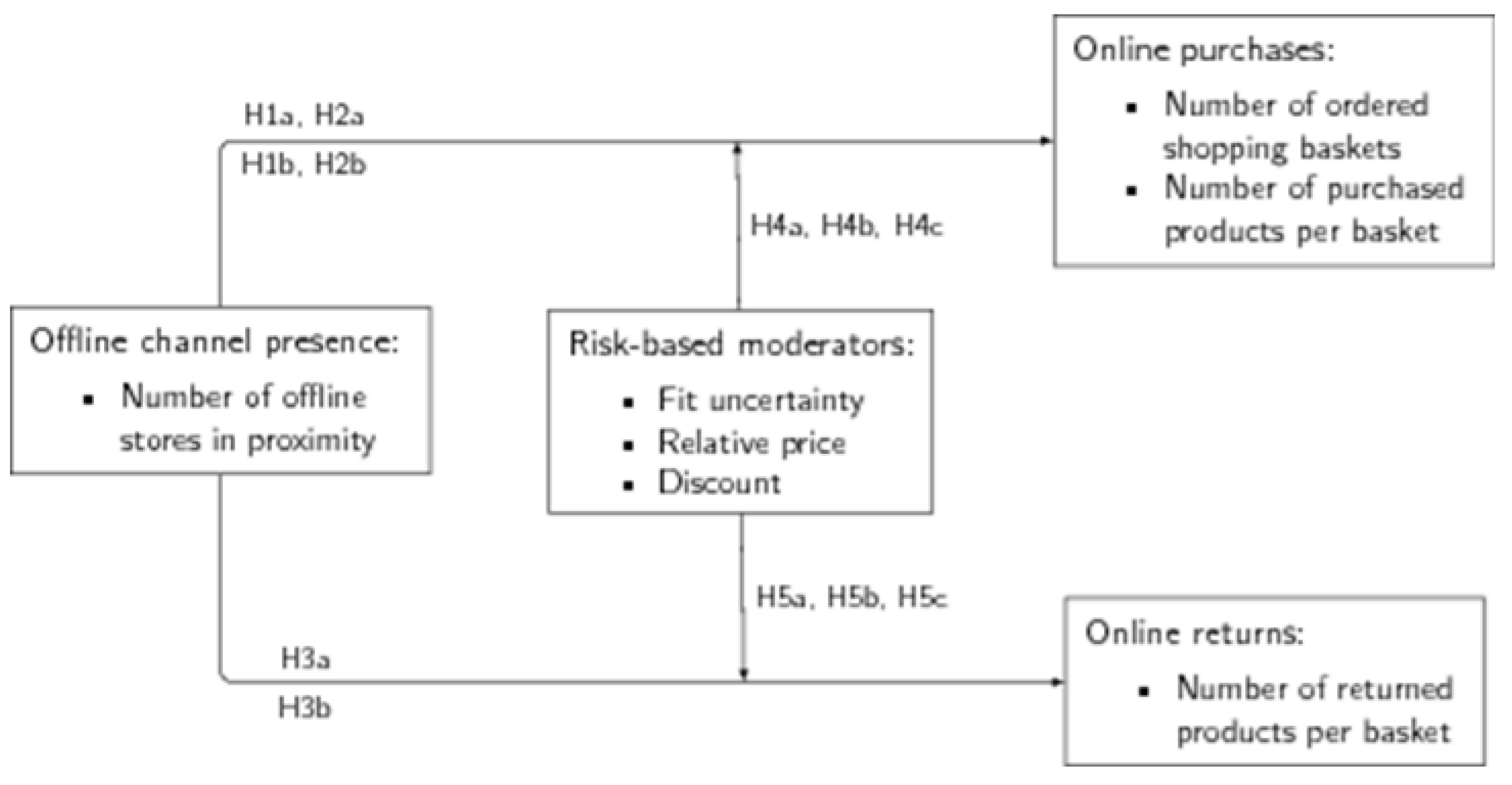
- investigating the influence of offline store presence on online purchases (in terms of how often and how much at a time customers order) and returns,
- -
- integrating how risk-related product characteristics moderate the influence of offline stores presence, and
- -
- proposing a novel spatial model specification to analyze the effect, avoiding regional selection bias and taking account of the spatial structure of the data.
1.2. Theoretical Background
1.2.1. Purchases
1.2.2. Returns
1.2.3. The Role of Risk
2. Materials & Methods
2.1. Data
2.1.1. Sample
2.1.2. Variables
2.1.3. Invalid Cases and Missing Variables
2.1.4. Descriptive Overview
2.2. Methodology
2.2.1. Base Model Specifications
2.2.2. Spatial Durbin Error Model
2.2.3. Estimation
3. Results
3.1. Model-Free Insights
3.2. Ordered Shopping Baskets
| DV | Basketsc | |
|---|---|---|
| Intercept | −0.002 | (−0.061, 0.056) |
| (W × Stores)r | −0.046 | (−0.127, 0.032) |
| Regional control variables | ||
| (W × posts)r | 0.066 | (−0.013, 0.146) |
| welfarer | −0.000 | (−0.038, 0.039) |
| urbanizationr | −0.008 | (−0.048, 0.033) |
| carsr | 0.223 | (0.019, 0.390) * |
| Customer control variables | ||
| gender_manc | −0.065 | (−0.160, 0.027) |
| gender_missingc | −1.215 | (−1.312, −1.113) *** |
| agec | 0.003 | (0.000, 0.007) * |
| age_missingc | −0.250 | (−0.319, −0.180) *** |
| Random effects and spatial autocorrelation | ||
| τ (random effect region) | 0.572 | (0.527, 0.619) *** |
| λ (spatial auto-correlation) | 0.335 | (0.010, 0.857) *** |
3.3. Purchases and Returns per Shopping Basket
3.4. Influence of Risk
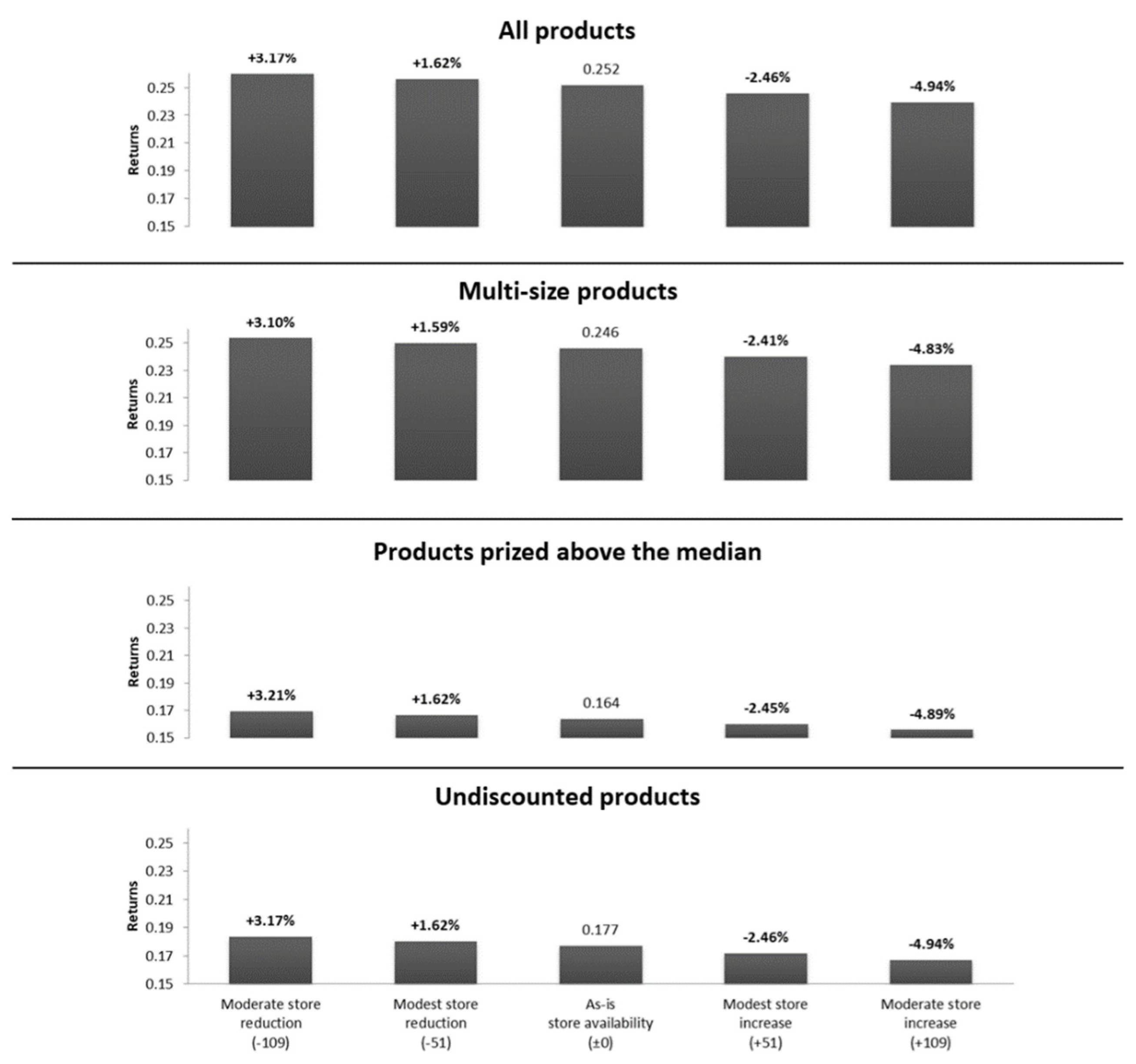
3.5. Simulation of Effect Magnitude
| Uni-Size Products | Multi-Size Products | |||
|---|---|---|---|---|
| DV | Purchasesi | Returnsi | Purchasesi | Returnsi |
| Intercept | −3.572 *** | −8.908 *** | −0.074 | −2.902 *** |
| (W × stores)r | 0.126 | −0.365 | −0.015 | −0.123 ** |
| Regional control variables | ||||
| (W × posts)r | −0.150 * | −0.234 | 0.028 * | −0.060 |
| welfarer | 0.062 | −0.119 | −0.011 | −0.013 |
| urbanisationr | −0.150 *** | 0.141 | 0.010 | −0.068 ** |
| carsr | −0.010 | −0.716 | 0.087 * | −0.475 *** |
| Customer control variables | ||||
| gender_manc | −0.956 *** | −0.893 * | 0.016 | −0.513 *** |
| gender_missingc | −0.010 | −0.082 *** | −0.319 *** | |
| agec | −0.003 | −0.053 * | 0.000 | 0.004 |
| age_missingc | −0.067 | 0.571 | 0.014 | 0.151 * |
| Order control variables | ||||
| purchasesi | n.a. | 3.045 *** | n.a. | 0.596 *** |
| yeari | 0.013 | −0.133 | 0.057 *** | 0.077 *** |
| monthi,2 | 0.243 | −1.701 | −0.022 | −0.124 |
| monthi,3 | −0.105 | 0.577 | 0.111 ** | 0.048 |
| monthi,4 | −0.611 ** | 0.505 | 0.152 *** | 0.007 |
| monthi,5 | 0.087 | 0.502 | 0.127 *** | −0.016 |
| monthi,6 | −0.116 | 0.750 | 0.147 *** | 0.088 |
| monthi,7 | −0.285 | −0.439 | 0.249 *** | −0.285 ** |
| monthi,8 | 0.052 | 0.621 | 0.148 *** | −0.252 * |
| monthi,9 | −0.081 | 0.260 | 0.090 * | −0.460 *** |
| monthi,10 | −0.418 * | −0.005 | 0.124 *** | −0.243 * |
| monthi,11 | 0.321 | 0.070 | 0.019 | −0.077 |
| monthi,12 | 0.711 *** | −0.246 | 0.056 | −0.133 |
| Random effects and spatial autocorrelation | ||||
| σ (random effect customer) | 1.254 *** | 2.149 *** | 0.010 *** | 0.780 *** |
| τ (random effect region) | 0.117 *** | 0.627 *** | 0.010 *** | 0.203 *** |
| λ (spatial auto-correlation) | 0.506 *** | 0.499 *** | 0.500 *** | 0.601 *** |
| Products Priced below Median | Products Priced above Median | |||
|---|---|---|---|---|
| DV | purchasesi | returnsi | purchasesi | returnsi |
| Intercept | −1.034 *** | −4.035 *** | −0.547 *** | −3.414 *** |
| (W × stores)r | −0.018 | −0.127 | −0.006 | −0.132 * |
| Regional control variables | ||||
| (W × posts)r | 0.044 | −0.060 | 0.002 | −0.063 |
| welfarer | 0.019 | −0.029 | −0.029 *** | 0.011 |
| urbanisationr | 0.052 *** | −0.052 | −0.023 ** | −0.055 * |
| carsr | 0.106 | −0.375 | 0.113 ** | −0.557 *** |
| Customer control variables | ||||
| gender_manc | 0.157 *** | −0.476 *** | −0.135 *** | −0.502 *** |
| gender_missingc | −0.094 ** | −0.355 *** | −0.058 * | −0.263 *** |
| agec | −0.005 ** | −0.001 | 0.003 * | 0.004 |
| age_missingc | 0.076 | 0.086 | −0.027 | 0.183 ** |
| Order control variables | ||||
| purchasesi | n.a. | 0.824 *** | n.a. | 0.895 *** |
| yeari | 0.038 ** | 0.044 | 0.065 *** | 0.078 ** |
| monthi,2 | −0.119 | −0.247 | 0.070 | −0.102 |
| monthi,3 | −0.250 *** | 0.116 | 0.294 *** | −0.039 |
| monthi,4 | 0.026 | 0.217 | 0.196 *** | −0.076 |
| monthi,5 | 0.293 *** | 0.413 ** | −0.005 | −0.208 |
| monthi,6 | 0.471 *** | 0.541 *** | −0.174 *** | −0.021 |
| monthi,7 | 0.724 *** | 0.181 | −0.404 *** | −0.434 *** |
| monthi,8 | 0.428 *** | −0.104 | −0.156 *** | −0.244 * |
| monthi,9 | −1.201 *** | −1.816 *** | 0.493 *** | −0.484 *** |
| monthi,10 | −0.994 *** | −1.149 *** | 0.488 *** | −0.245 * |
| monthi,11 | −0.487 *** | −0.272 | 0.294 *** | −0.079 |
| monthi,12 | −0.150 * | −0.185 | 0.243 *** | −0.150 |
| Random effects and spatial autocorrelation | ||||
| σ (random effect customer) | 0.464 *** | 1.088 *** | 0.022 *** | 0.742 *** |
| τ (random effect region) | 0.114 *** | 0.210 *** | 0.025 *** | 0.226 *** |
| λ (spatial auto-correlation) | 0.599 *** | 0.511 *** | 0.516 *** | 0.518 *** |
| Discounted Products | Undiscounted Products | |||
|---|---|---|---|---|
| DV | Purchasesi | Returnsi | Purchasesi | Returnsi |
| Intercept | −4.059 *** | −5.814 *** | 0.354 *** | −3.128 *** |
| (W × stores)r | 0.001 | −0.068 | −0.009 | −0.153 ** |
| Regional control variables | ||||
| (W × posts)r | −0.029 | −0.113 | 0.036 * | −0.042 |
| welfarer | −0.039 * | −0.018 | 0.003 | −0.006 |
| urbanisationr | 0.045 ** | −0.094 * | −0.014 | −0.055 * |
| carsr | 0.092 | −0.607 * | 0.074 | −0.294 |
| Customer control variables | ||||
| gender_manc | −0.245 *** | −0.845 *** | 0.071 * | −0.449 *** |
| gender_missingc | −0.260 *** | −0.440 *** | 0.008 | −0.271 *** |
| agec | 0.001 | 0.008 | −0.000 | 0.002 |
| age_missingc | 0.055 | 0.203 | −0.019 | 0.142 * |
| Order control variables | ||||
| purchasesi | n.a. | 0.940 *** | n.a. | 0.775 *** |
| yeari | 0.405 *** | 0.278 *** | −0.053 *** | 0.055 ** |
| monthi,2 | 0.489 *** | 0.429 | −0.114 * | −0.307 * |
| monthi,3 | 1.210 *** | 0.642 ** | −0.283 *** | 0.009 |
| monthi,4 | 0.980 *** | 0.601 ** | −0.099 * | 0.033 |
| monthi,5 | 1.076 *** | 0.360 | −0.161 *** | −0.047 |
| monthi,6 | 0.493 *** | 0.470 * | 0.052 | 0.021 |
| monthi,7 | 0.532 *** | −0.458 | 0.161 *** | −0.377 *** |
| monthi,8 | 0.378 *** | −0.106 | 0.093 * | −0.287 ** |
| monthi,9 | 1.296 *** | −0.010 | −0.356 *** | −0.406 *** |
| monthi,10 | 1.123 *** | 0.042 | −0.169 *** | −0.158 |
| monthi,11 | 0.924 *** | 0.437 | −0.196 *** | −0.048 |
| monthi,12 | 1.191 *** | 0.295 | −0.212 *** | −0.125 |
| Random effects and spatial autocorrelation | ||||
| σ (random effect customer) | 0.766 *** | 1.200 *** | 0.014 *** | 0.736 *** |
| τ (random effect region) | 0.069 *** | 0.146 *** | 0.013 *** | 0.224 *** |
| λ (spatial auto-correlation) | 0.500 *** | 0.504 *** | 0.501 *** | 0.563 *** |
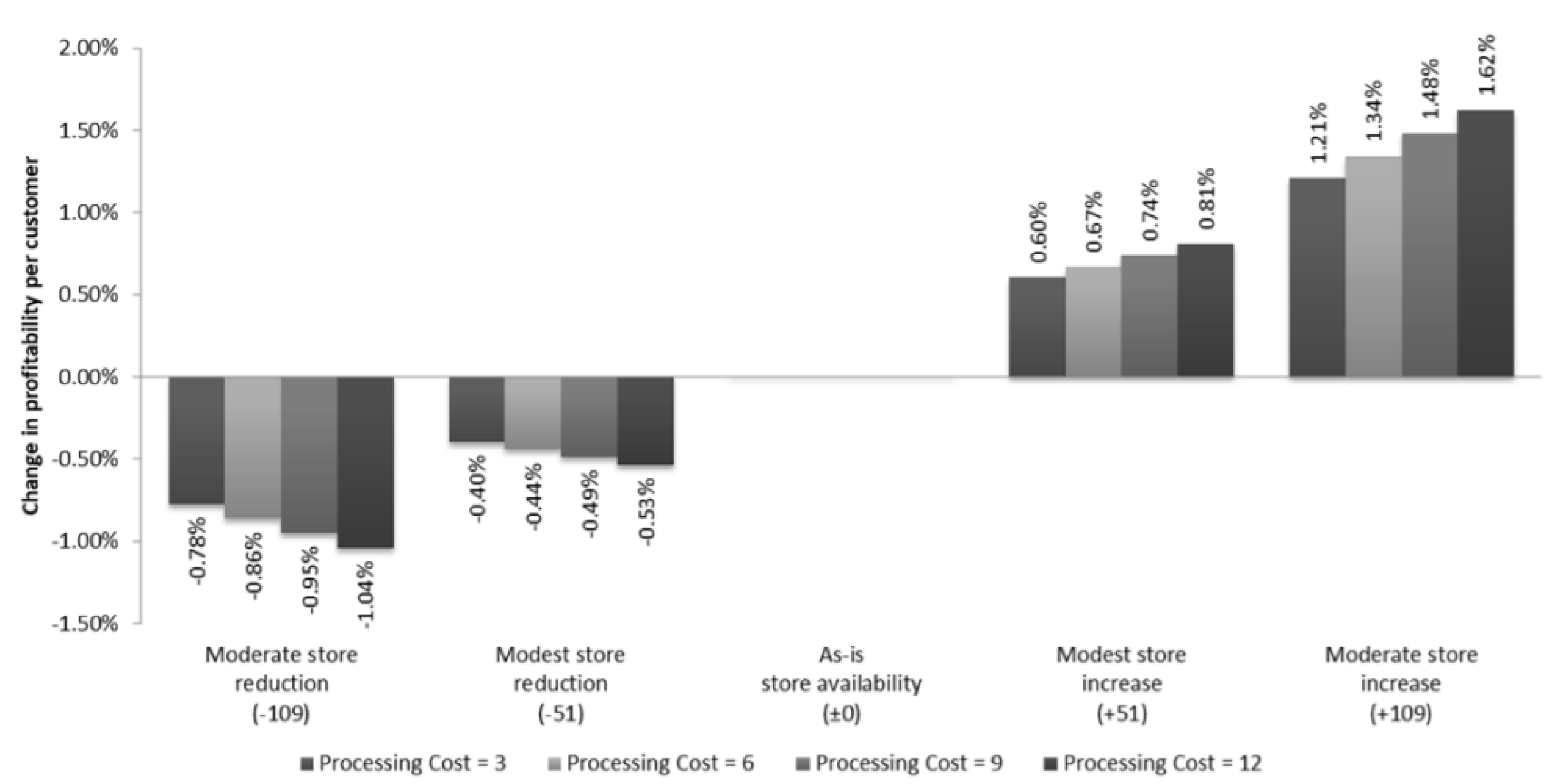
3.6. Profit Implications
- Return cost per basket, defined as (number of returns per basket) × (return processing cost per return).
- Gross profit per basket, defined as (gross margin × price of an ordered product) × (number of ordered products per basket-number of product returns per basket)
- Profit per customer, defined as (gross profit per basket-return cost per basket) × (number of ordered baskets per customer).
4. Discussion
4.1. Summary of Findings
4.2. Managerial Implications
4.3. Limitations and Further Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Approximation of the Spatial Durbin Error Term
Appendix A.2. Model Convergence
Appendix A.3. Simulation
References
- Deloitte. Global Powers of Retailing 2022 Resilience Despite Challenges; Deloitte Touche Tohmatsu Limited: New York, NY, USA, 2022; pp. 1–52. [Google Scholar]
- Coppola, D. Leading Fashion and Apparel Websites Worldwide 2022, Based on Visit Share. Statista. 19 April 2022. Available online: https://www.statista.com/statistics/1255963/most-visited-fashion-and-apparel-websites/ (accessed on 19 May 2022).
- Jolly, J. Zara Owner to Close up to 1200 Fashion Stores around the World. The Guardian. 10 June 2020. Available online: https://www.theguardian.com/business/2020/jun/10/zara-owner-to-close-up-to-1200-fashion-stores-around-the-world (accessed on 19 May 2022).
- Geiger Smith, E. How Online Retailers Predict Your Perfect Outfit. The Wall Street Journal. 5 August 2015. Available online: https://www.wsj.com/articles/how-online-retailers-predict-your-perfect-outfit-1438794462 (accessed on 19 May 2022).
- Zalando. Returns at Zalando. Zalando. 17 June 2022. Available online: https://corporate.zalando.com/en/newsroom/en/stories/returns-zalando (accessed on 19 May 2022).
- National Retail Federation. Customer Returns in the Retail Industry 2021. National Retail Federation. 25 January 2022. Available online: https://cdn.nrf.com/sites/default/files/2022-01/Customer%20Returns%20in%20the%20Retail%20Industry%202021.pdf (accessed on 19 May 2022).
- Mazareanu, E. Costs of Return Deliveries in the United States in 2017 and 2020. Statista. 9 February 2021. Available online: https://www.statista.com/statistics/871365/reverse-logistics-cost-united-states/ (accessed on 19 May 2022).
- Stock, J.H.; Speh, T.; Shear, H. Managing Product Returns for Competitive Advantage. MIT Sloan Manag. Rev. 2006, 48, 57–62. [Google Scholar]
- Anne, K.; Rohrbeck, F.; Salewski, C. Schmutziger Fussabdruck. Zeit.de. 11 November 2021. Available online: https://www.zeit.de/2021/46/nike-sneaker-turnschuhe-recycling-muell-modeindustrie-sneakerjagd (accessed on 19 May 2022).
- Minter, A. Those Amazon Returns? They’re Killing the Environment. Los Angeles Times. 13 November 2019. Available online: https://www.latimes.com/business/story/2019-11-13/amazon-returns-are-killing-the-environment (accessed on 19 May 2022).
- Minnema, A.; Bijmolt, T.H.; Gensler, S.; Wiesel, T. To Keep or Not to Keep: Effects of Online Customer Reviews on Product Returns. J. Retail. 2016, 92, 253–267. [Google Scholar] [CrossRef]
- Rosen, E. Online Brands Try a Traditional Marketing Strategy: Physical Stores. The New York Times. 23 March 2022. Available online: https://www.nytimes.com/2022/03/23/business/direct-consumer-retail-stores.html (accessed on 19 May 2022).
- Dastin, J. Amazon to Shut Its Bookstores and Other Shops as Its Grocery Chain Expands. Reuters. 3 March 2022. Available online: https://www.reuters.com/business/retail-consumer/exclusive-amazon-close-all-its-physical-bookstores-4-star-shops-2022-03-02/ (accessed on 19 May 2022).
- Chen, C. All Kohl’s Stores Are Now Accepting Amazon Returns—Here’s How It’ll Work and What Kohl’s Hopes to Win from This Convenient Service. Business Insider. 2 July 2019. Available online: https://www.businessinsider.com/amazon-returns-at-kohls-how-does-it-work (accessed on 19 May 2022).
- CB Insights. We Analyzed 6 E-Commerce Brands Breaking into Brick-and-Mortar to Understand the Secrets to Their Success—Here’s What We Learned. CB Insights. 14 October 2018. Available online: https://www.cbinsights.com/research/online-offline-retail-ecommerce-brick-and-mortar/ (accessed on 19 May 2022).
- Kapner, S. E-Commerce Needs Real Store Locations Now More than Ever. The Wall Street Journal. 25 November 2021. Available online: https://www.wsj.com/articles/e-commerce-needs-real-store-locations-now-more-than-ever-11637836200 (accessed on 19 May 2022).
- Taylor, K. The Retail Apocalypse Is Far from over as Analysts Predict 75,000 More Store Closures. Business Insider. 9 April 2019. Available online: https://www.businessinsider.com/retail-apocalypse-thousands-store-closures-predicted-2019-4 (accessed on 19 May 2022).
- Minnema, A.; Bijmolt, T.H.A.; Petersen, J.A.; Shulman, J.D. Managing Product Returns Within the Customer Value Framework. In Customer Engagement Marketing; Palmatier, R.W., Kumar, V., Harmeling, C.M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 95–118. [Google Scholar]
- Avery, J.; Steenburgh, T.J.; Deighton, J.; Caravella, M. Adding Bricks to Clicks: Predicting the Patterns of Cross-Channel Elasticities over Time. J. Mark. 2012, 76, 96–111. [Google Scholar] [CrossRef]
- Li, H. Are e-books a different channel? Multichannel management of digital products. Quant. Mark. Econ. 2021, 19, 179–225. [Google Scholar] [CrossRef]
- Pauwels, K.; Neslin, S.A. Building With Bricks and Mortar: The Revenue Impact of Opening Physical Stores in a Multichannel Environment. J. Retail. 2015, 91, 182–197. [Google Scholar] [CrossRef]
- Van Nierop, J.E.M.; Leeflang, P.S.H.; Teerling, M.L.; Huizingh, K.R.E. The Impact of the Introduction and Use of an Informational Website on Offline Customer Buying Behaviour. Int. J. Res. Mark. 2011, 28, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Goldfarb, A. Can Offline Stores Drive Online Sales? J. Mark. Res. 2017, 54, 706–719. [Google Scholar] [CrossRef]
- Weltevreden, J.W.J. Substitution or Complementarity? How the Internet Changes City Centre Shopping. J. Retail. Consum. Serv. 2007, 14, 192–207. [Google Scholar] [CrossRef]
- Eurostat. E-Commerce Statistics for Individuals. Eurostat. (Issue January). 2022. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=E-commerce_statistics_for_individuals (accessed on 19 May 2022).
- Glover, E. Chile’s Atacama Desert Becomes Dumping Ground for Fast Fashion Leftovers. The Independent. 9 November 2021. Available online: https://www.independent.co.uk/climate-change/news/fast-fashion-atacama-desert-chile-b1953722.html (accessed on 19 May 2022).
- Verhoef, P.C.; Kannan, P.K.; Inman, J.J. From Multi-Channel Retailing to Omni-Channel Retailing. Introduction to the Special Issue on Multi-Channel Retailing. J. Retail. 2015, 91, 174–181. [Google Scholar] [CrossRef]
- Bijmolt, T.H.; Broekhuis, M.; De Leeuw, S.; Hirche, C.; Rooderkerk, R.P.; Sousa, R.; Zhu, S.X. Challenges at the marketing–operations interface in omni-channel retail environments. J. Bus. Res. 2019, 122, 864–874. [Google Scholar] [CrossRef]
- Lemon, K.N.; Verhoef, P.C. Understanding Customer Experience Throughout the Customer Journey. J. Mark. 2016, 80, 69–96. [Google Scholar] [CrossRef]
- Rohm, A.J.; Swaminathan, V. A typology of online shoppers based on shopping motivations. J. Bus. Res. 2002, 57, 748–757. [Google Scholar] [CrossRef]
- King, J. Why Shop Online? It’s Easy. EMarketer. 2 April 2018. Available online: https://www.emarketer.com/content/why-shop-online-it-s-easy (accessed on 19 May 2022).
- Rekuc, D. Study: Why 92% of Retail Purchases Still Happen Offline. Ripen. 28 April 2018. Available online: https://ripen.com/blog/ecommerce_survey (accessed on 19 May 2022).
- Neslin, S.A.; Shankar, V. Key Issues in Multichannel Customer Management: Current Knowledge and Future Directions. J. Interact. Mark. 2009, 23, 70–81. [Google Scholar] [CrossRef]
- Mitra, D.; Fay, S. Managing Service Expectations in Online Markets: A Signaling Theory of E-tailer Pricing and Empirical Tests. J. Retail. 2010, 86, 184–199. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.-H.; Han, S.-L.; Jang, Y.-Y.; Shin, Y.-C. The Effects of the Antecedents of “Buy-Online-Pick-Up-in-Store” Service on Consumer’s BOPIS Choice Behaviour. Sustainability 2020, 12, 9989. [Google Scholar] [CrossRef]
- Ketzenberg, M.; Akturk, M.S. How “Buy Online, Pick up In-Store” Gives Retailers an Edge. Harvard Business Review. 25 May 2021. Available online: https://hbr.org/2021/05/how-buy-online-pick-up-in-store-gives-retailers-an-edge (accessed on 19 May 2022).
- Kushwaha, T.; Shankar, V. Are Multichannel Customers Really more Valuable? The Moderating Role of Product Category Characteristics. J. Mark. 2013, 77, 67–85. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, V.W. Understanding Consumers’ Behaviour: Can Perceived Risk Theory Help? Manag. Decis. 1992, 30, 26–31. [Google Scholar] [CrossRef]
- Gu, Z.; Tayi, G.K. Consumer mending and online retailer fit-uncertainty mitigating strategies. Quant. Mark. Econ. 2015, 13, 251–282. [Google Scholar] [CrossRef]
- Anderson, E.T.; Hansen, K.; Simester, D. The Option Value of Returns: Theory and Empirical Evidence. Mark. Sci. 2009, 28, 405–423. [Google Scholar] [CrossRef] [Green Version]
- Janakiraman, N.; Ordóñez, L. Effect of effort and deadlines on consumer product returns. J. Consum. Psychol. 2012, 22, 260–271. [Google Scholar] [CrossRef]
- Kim, J.; Wansink, B. How Retailers’ Recommendation and Return Policies Alter Product Evaluations. J. Retail. 2012, 88, 528–541. [Google Scholar] [CrossRef]
- Petersen, J.A.; Kumar, V. Perceived Risk, Product Returns, and Optimal Resource Allocation: Evidence from a Field Experiment. J. Mark. Res. 2015, 52, 268–285. [Google Scholar] [CrossRef] [Green Version]
- Grewal, D. Product quality expectations: Towards an understanding of their antecedents and consequences. J. Bus. Psychol. 1995, 9, 225–240. [Google Scholar] [CrossRef]
- ESRI. ArcGIS REST API; Environmental Systems Research Institute: Redlands, CA, USA, 2016. [Google Scholar]
- Graham, J.W. Missing Data Analysis: Making It Work in the Real World. Annu. Rev. Psychol. 2009, 60, 549–576. [Google Scholar] [CrossRef] [Green Version]
- Bradlow, E.T.; Bronnenberg, B.; Russell, G.J.; Arora, N.; Bell, D.R.; Duvvuri, S.D.; Ter Hofstede, F.; Sismeiro, C.; Thomadsen, R.; Yang, S. Spatial Models in Marketing. Mark. Lett. 2005, 16, 267–278. [Google Scholar] [CrossRef]
- Halleck, V.S.; Elhorst, J.P. The SLX Model. J. Reg. Sci. 2015, 55, 339–363. [Google Scholar] [CrossRef]
- Lesage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Elhorst, J.P. Spatial Econometrics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- LeSage, J.P. What Regional Scientists Need to Know about Spatial Econometrics. SSRN Electron. J. 2014, 44, 13–32. [Google Scholar]
- Lacombe, D.J.; McIntyre, S.G. Local and global spatial effects in hierarchical models. Appl. Econ. Lett. 2016, 23, 1168–1172. [Google Scholar] [CrossRef] [Green Version]
- Inouye, D.I.; Yang, E.; Allen, G.I.; Ravikumar, P. A Review of Multivariate Distributions for Count Data Derived from the Poisson Distribution: A Review of Multivariate Distributions for Count Data. Wiley Interdiscip. Rev. Comput. Stat. 2017, 9, e1398. [Google Scholar] [CrossRef] [Green Version]
- Stan Development Team. Stan Modeling Language User’s Guide and Reference Manual; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2017; p. 397. [Google Scholar]
- Leeflang, P.S.H.; Wieringa, J.E.; Bijmolt, T.H.A.; Pauwels, K.H. Modeling Markets; Springer: New York, NY, USA, 2016. [Google Scholar]
- Damodaran, A. Margins by Sector (US); NYU Stern School of Business: New York, NY, USA, 2021. [Google Scholar]
- Ofek, E.; Katona, Z.; Sarvary, M. “Bricks and Clicks”: The Impact of Product Returns on the Strategies of Multichannel Retailers. Mark. Sci. 2011, 30, 42–60. [Google Scholar] [CrossRef] [Green Version]
- Bijmolt, T.H.A.; Verhoef, P.C. Loyalty Programs: Current Insights, Research Challenges, and Emerging Trends. In Handbook of Marketing Decision Models; Wierenga, B., van der Lans, R., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 143–165. [Google Scholar]
- Brynjolfsson, E.; Hu, J.Y.; Rahman, M.S. Competing in the Age of Omnichannel Retailing; MIT Sloan Management Review: Cambridge, MA, USA, 2013. [Google Scholar]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, M.-L. Handbook of Markov Chain Monte Carlo. In Handbooks of Modern Statistical Methods; Chapman & Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar]

| k | Variables | Description |
|---|---|---|
| k = 0 | purchasesi,c,r,0 returnsi,c,r,0 | Number of overall purchased/returned products a |
| k = 1 | purchasesi,c,r,1 returnsi,c,r,1 | Number of purchased/returned multi-size products a |
| k = 2 | purchasesi,c,r,2 returnsi,c,r,2 | Number of purchased/returned uni-size products a |
| k = 3 | purchasesi,c,r,3 returnsi,c,r,3 | Number of purchased/returned products priced above the median price in their category a |
| k = 4 | purchasesi,c,r,4 returnsi,c,r,4 | Number of purchased/returned products priced below the median price in their category a |
| k = 5 | purchasesi,c,r,5 returnsi,c,r,5 | Number of purchased/returned products without discount a |
| k = 6 | purchasesi,c,r,6 returnsi,c,r,6 | Number of purchased/returned products with discount a |
| Variable | Description |
|---|---|
| Customer Behavior | |
| basketsc,r | Number of ordered shopping baskets by customer c in region r |
| purchasesi,c,r,k | Number of purchased products in shopping basket i of customer c in region r with product characteristic k |
| returnsi,c,r,k | Number of returned products in shopping basket i of customer c in region r with product characteristic k |
| Regional characteristics | |
| (W × stores)r | Number of stores in region r and its surrounding regions with spatial decay |
| (W × posts)r | Number of post offices in region r and its surrounding regions with spatial decay |
| welfarer | welfare indicator a for region r |
| urbanizationr | urbanization indicator a for region r |
| carsr | cars per capita a in region r |
| Order characteristics | |
| yeari | Year in which the order i was made (0 = 2008, …, 6 = 2014), accounting for a linear trend |
| month2,i, …, month12,i | 11 indicators for the month in which order i was made (baseline: January), accounting for seasonal effects |
| Customer characteristics | |
| agec | Age of customer c in years a |
| genderc | Customer c is female (1) or male (0) |
| Stores in Proximity (W × stores): | [0, 3.33) | [3.33, 6.67) | [6.67, 10) | [10, 13.3) | [13.3, 16.9) | Correlation |
|---|---|---|---|---|---|---|
| Purchases: | ||||||
| Overall | 1.39 | 1.41 | 1.45 | 1.41 | 1.07 | 0.015 |
| Multi-size | 1.33 | 1.36 | 1.41 | 1.34 | 1.07 | 0.022 ** |
| Uni-size | 0.06 | 0.05 | 0.04 | 0.07 | 0.00 | −0.024 ** |
| Price above median | 0.89 | 0.80 | 0.82 | 0.93 | 0.67 | −0.047 *** |
| Price below median | 0.51 | 0.61 | 0.63 | 0.48 | 0.40 | 0.060 *** |
| Undiscounted | 1.00 | 0.99 | 1.04 | 1.13 | 1.00 | 0.015 |
| Discounted | 0.39 | 0.42 | 0.41 | 0.27 | 0.07 | 0.000 |
| Returns: | ||||||
| Overall | 0.28 | 0.21 | 0.19 | 0.16 | 0.00 | −0.064 *** |
| Multi-size | 0.27 | 0.20 | 0.19 | 0.16 | 0.00 | −0.062 *** |
| Uni-size | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | −0.018 * |
| Price above median | 0.18 | 0.13 | 0.11 | 0.12 | 0.00 | −0.063 *** |
| Price below median | 0.10 | 0.07 | 0.08 | 0.04 | 0.00 | −0.025 ** |
| Undiscounted | 0.20 | 0.14 | 0.13 | 0.15 | 0.00 | −0.060 *** |
| Discounted | 0.08 | 0.07 | 0.06 | 0.02 | 0.00 | −0.027 ** |
| Observations | 9688 | 3510 | 1048 | 165 | 15 |
| DV | Purchasesi | Returnsi | ||
|---|---|---|---|---|
| Intercept | −2.000 | (−2.193, −1.817) *** | −2.879 | (−3.111, −2.652) *** |
| (W × stores)r | −0.039 | (−0.101, 0.024) | −0.127 | (−0.216, −0.038) ** |
| Regional control variables | ||||
| (W × posts)r0 | 0.068 | (0.012, 0.126) * | −0.059 | (−0.140, 0.022) |
| welfarer | −0.027 | (−0.058, 0.002) | −0.015 | (−0.056, 0.025) |
| urbanisationr | 0.012 | (−0.021, 0.045) | −0.061 | (−0.106, −0.016) * |
| carsr | 0.222 | (0.065, 0.375) ** | −0.437 | (−0.749, −0.143) ** |
| Customer control variables | ||||
| gender_manc | −0.024 | (−0.136, 0.088) | −0.511 | (−0.682, −0.346) *** |
| gender_missingc | −0.244 | (−0.333, −0.157) *** | −0.320 | (−0.434, −0.206) *** |
| agec | 0.000 | (−0.004, 0.005) | 0.003 | (−0.003, 0.009) |
| age_missingc | 0.033 | (−0.056, 0.128) | 0.158 | (0.040, 0.275) ** |
| Order control variables | ||||
| ordersi | n.a. | 0.572 | (0.543, 0.600) *** | |
| yeari | 0.197 | (0.165, 0.230) *** | 0.075 | (0.034, 0.115) *** |
| monthi,2 | 0.037 | (−0.149, 0.222) | −0.135 | (−0.345, 0.073) |
| monthi,3 | 0.383 | (0.235, 0.536) *** | 0.058 | (−0.128, 0.241) |
| monthi,4 | 0.487 | (0.339, 0.633) *** | 0.028 | (−0.148, 0.201) |
| monthi,5 | 0.459 | (0.316, 0.602) *** | −0.000 | (−0.179, 0.178) |
| monthi,6 | 0.496 | (0.349, 0.645) *** | 0.109 | (−0.073, 0.287) |
| monthi,7 | 0.687 | (0.548, 0.833) *** | −0.271 | (−0.453, −0.082) ** |
| monthi,8 | 0.479 | (0.332, 0.628) *** | −0.233 | (−0.428, −0.041) * |
| monthi,9 | 0.315 | (0.171, 0.464) *** | −0.438 | (−0.628, −0.249) *** |
| monthi,10 | 0.427 | (0.278, 0.575) *** | −0.238 | (−0.429, −0.050) ** |
| monthi,11 | 0.130 | (−0.047, 0.298) | −0.073 | (−0.280, 0.122) |
| monthi,12 | 0.406 | (0.241, 0.562) *** | −0.151 | (−0.356, 0.044) |
| Random effects and spatial autocorrelation | ||||
| σ (random effect customer) | 0.736 | (0.698, 0.776) *** | 0.785 | (0.723, 0.850) *** |
| τ (random effect region) | 0.056 | (0.003, 0.144) *** | 0.196 | (0.034, 0.325) *** |
| λ (spatial auto-correlation) | 0.492 | (0.030, 0.973) *** | 0.585 | (0.041, 0.986) *** |
| Scenario | Change in No. Stores | Description |
|---|---|---|
| Moderate store reduction | −109 | Closure of one store in each region which has a below-median client/store ratio |
| Modest store reduction | −51 | Closure of one store in each region with a client/store ratio in the lowest quartile |
| As-is store availability | ±0 | Actual store availability as observed in the data |
| Modest store increase | +51 | Opening of one store per region, ranked by high to low (prospective) client/store ratio until the same number of stores are opened which were closed in the “Modest store reduction” scenario |
| Moderate store increase | +109 | Opening of one store per region, ranked by high to low (prospective) client/store ratio until the same number of stores are opened which were closed in the “Moderate store reduction” scenario |
| Hypothesis | Findings | |
|---|---|---|
| H1a | Offline channel presence decreases the number of ordered shopping baskets. | Not supported |
| H1b | Offline channel presence increases the number of ordered shopping baskets. | Not supported |
| H2a | Offline channel presence decreases the number of purchased products per shopping basket. | Not supported |
| H2b | Offline channel presence increases the number of purchased products per shopping basket. | Not supported |
| H3a | Offline channel presence decreases the number of returned products per shopping basket. | Supported |
| H3b | Offline channel presence increases the number of returned products per shopping basket. | Not supported |
| H4a | The impact of offline channel presence on the number of purchased products per shopping basket is more negative/less positive for products with higher fit uncertainty compared to products with lower fit uncertainty | Not supported |
| H4b | The impact of offline channel presence on the number of purchased products per shopping basket is more negative/less positive for higher-priced products compared to lower-priced products | Not supported |
| H5a | The impact of offline channel presence on the number of returned products per shopping basket is more negative/less positive for products with higher fit uncertainty compared to products with lower fit uncertainty | Supported |
| H5b | The impact of offline channel presence on the number of returned products per shopping basket is more negative/less positive for higher-priced products compared to lower-priced products | Supported |
| H5c | The impact of offline channel presence on the number of returned products per shopping basket is more negative/less positive for undiscounted products compared to discounted products | Supported |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirche, C.F.; Bijmolt, T.H.A.; Gijsenberg, M.J. When Offline Stores Reduce Online Returns. Sustainability 2022, 14, 7829. https://doi.org/10.3390/su14137829
Hirche CF, Bijmolt THA, Gijsenberg MJ. When Offline Stores Reduce Online Returns. Sustainability. 2022; 14(13):7829. https://doi.org/10.3390/su14137829
Chicago/Turabian StyleHirche, Christian F., Tammo H. A. Bijmolt, and Maarten J. Gijsenberg. 2022. "When Offline Stores Reduce Online Returns" Sustainability 14, no. 13: 7829. https://doi.org/10.3390/su14137829
APA StyleHirche, C. F., Bijmolt, T. H. A., & Gijsenberg, M. J. (2022). When Offline Stores Reduce Online Returns. Sustainability, 14(13), 7829. https://doi.org/10.3390/su14137829






