Efficient Data-Driven Crop Pest Identification Based on Edge Distance-Entropy for Sustainable Agriculture

Abstract

Human agricultural activities are always accompanied by pests and diseases, which have brought great losses to the production of crops. Intelligent algorithms based on deep learning have achieved some achievements in the field of pest control, but relying on a large amount of data to drive consumes a lot of resources, which is not conducive to the sustainable development of smart agriculture. The research in this paper starts with data, and is committed to finding efficient data, solving the data dilemma, and helping sustainable agricultural development. Starting from the data, this paper proposed an Edge Distance-Entropy data evaluation method, which can be used to obtain efficient crop pests, and the data consumption is reduced by 5% to 15% compared with the existing methods. The experimental results demonstrate that this method can obtain efficient crop pest data, and only use about 60% of the data to achieve 100% effect. Compared with other data evaluation methods, the method proposed in this paper achieve state-of-the-art results. The work conducted in this paper solves the dilemma of the existing intelligent algorithms for pest control relying on a large amount of data, and has important practical significance for realizing the sustainable development of modern smart agriculture.

1. Introduction

Agriculture is the backbone of a country’s national economy, and planting is the foundation of agriculture. The healthy development of sustainable planting is of great significance to human society [1]. However, human planting production is always accompanied by pests and diseases [2]. With the advancement of science and technology and the development of society, various modern elements have been introduced and are increased continuously, such as new varieties, chemical fertilizers, pesticides, etc. [3]. In recent decades, the damage of global pests and diseases has become more and more serious [4]. Despite hard work, pests and diseases seem to be getting harder to control. As much as 40% of global crop production is lost annually to pests, which cost at least $70 billion [5]. There is a common problem in the process of pest control. Due to the wide variety of pests, farmers cannot accurately distinguish the class of pests and blindly use pesticides, which cannot achieve the purpose of accurate killing. Instead, plants often die due to the high toxicity of pesticides. In recent years, deep learning [6] technology has been applied to the fields of agriculture and is committed to solving the problem of pests. The intelligent algorithm of automatic pest identification [7] based on deep learning can replace agricultural experts and farmers in the identification of crop pests.

Generally speaking, the existing intelligent algorithms based on deep learning mainly perform image recognition [8] and target detection [9] for pest data, which can help humans obtain information on the category and location of agricultural pests. Image recognition usually uses CNN network [10] architecture to train a large amount of pest data to obtain high-precision image recognition models. With the development of deep neural networks, many excellent CNN network architectures have emerged, such as GoogLeNet [11], ResNet [12] and EfficientNet [13], etc. This has achieved a certain role in pest control. Object detection uses a large number of pest data with location and class label information to train the model. The trained model obtains the location and class information of the pest image through feature extraction, classification and regression positioning. Currently, there are many excellent network structures that have worked in agriculture, such as OverFeat [14], YOLOv5 [15], SSD [16], RetinaNet [17], etc.

Although existing deep learning intelligent algorithm [18] methods have reported satisfactory results in the field of pest identification, they are all driven by massive amounts of data, and the acquisition of large amounts of data and labels relies on numerous human and natural resources. If only efficient data [19] is selected to participate in the training of intelligent algorithms, resources can be greatly saved without reducing the accuracy, which is of great significance for promoting the development of sustainable smart agriculture [20].

This study proposes a data evaluation method for Edge Distance-Entropy that can be used to obtain efficient data, which focuses on finding the samples closest to the decision boundary. The proposed method is validated on a crop pest dataset containing 10 different classs of crop pests that are common in crop-growing regions of China. At the same time, we proposed Anomaly Feature Detection Strategy, abbreviated as AFDS, which can effectively resist the feature bias caused by abnormal data. The results demonstrate that the proposed Edge Distance-Entropy data evaluation method can pick out efficient crop pest data, and in the pest identification task, compared with other existing evaluation methods, it achieves state-of-the-art results in terms of accuracy.

The following points summarize the contributions of this research work: (1) We focus on the data dilemma encountered in the field of smart agriculture, and use the proposed method to effectively solve the task of crop pest identification, which is of great significance for promoting the development of sustainable agriculture. (2) We built a crop pest dataset with 10 categories CP-10 that can be used for pest data assessment. (3) An Edge Distance-Entropy data evaluation method that can be applied to pest identification tasks is proposed. This method can effectively select high-efficiency pest data, and only use a small amount of data to achieve the performance brought by a large amount of data. On our established pest dataset, our proposed method achieves state-of-the-art performance compared to other methods. (4) Furthermore, we have proposed Anomaly Feature Detection Strategy to resist the influence of anomalous pest data by eliminating anomalous feature points that deviate from the feature group.

This paper is organized as follows. The dataset and method used in this paper are reported in Section 2. Experimental results and analysis are reported in Section 3. Finally, the discussion part of this paper is given in Section 4 and the conclusion is given in Section 5.

2. Materials and Methods

2.1. Materials

This subsection explains the relevant datasets used in this study. To meet our research needs, we re-collected a crop pest dataset called CP-10. The dataset includes 10 different classes of crop pests commonly found in agricultural areas: Aleurocanthus Spiniferus, Army Worm, Cicadellidae, Lcerya Purchasi Maskell, Legume blister beetle, Locustoidea, Lycorma delicatula, Miridae, Mole Cricket and Trialeurodes Vaporariorum. These images are obtained by searching keywords on the Internet, and the sizes are not uniform, but they are all in uniform JPEG format. We collected less than 1000 images of each class, to avoid classification imbalance, and we re-filtered the collected data and kept 600 images per type for research use. The dataset we used contains a large amount of insect information and is well suited for data evaluation in pest identification tasks. Figure 1 shows an example of some pest images in the dataset.

2.2. Framework

First, our task goal is to train a model that recognizes 10 classes of pest data under supervision. We divide the complete train set ${\mathcal{D}}_T$ into the labeled set ${\mathcal{D}}_l={\left\{\left(x_i,y_i\right)\right\}}_{j=1}^{M_1}$ and the unlabeled ${\mathcal{D}}_u={\left\{\left(x_j,y_j\right)\right\}}_{j=1}^{M_2}$ two parts, where $x_i\in \mathcal{X}$ represents the input image and $y_i\in \{1,\dots ,N\}$ represents the relevant class label. It is worth noting that these two parts are continuous updated. At the beginning, we will randomly select a small amount of labeled data, denoted as ${\mathcal{D}}_B$, that is, ${\mathcal{D}}_l={\mathcal{D}}_B$ at this time. We use ${\mathcal{D}}_B$ to train the network to obtain the first model, and then use the data evaluation method to evaluate each data in ${\mathcal{D}}_u$, and give each data a score, then rank the scores. Select the $\mathcal{M}$ number of data $\mathcal{C}$ with the highest score from ${\mathcal{D}}_u$. Add it to the candidate set, perform manual annotation, and obtain $Y^{new}=$ Query $\left(\mathcal{C}\right)$. Add the labeled candidate set to ${\mathcal{D}}_l$, and update the model with the new ${\mathcal{D}}_l$. We do many such cycles until ${\mathcal{D}}_u=⌀$. The performance of the model is evaluated on an unseen pest test set. Our use a deep neural network $f=f_e+f_c$ with parameters $\theta =\{\theta e,\theta c\}$ as learner. Here, $f_e:X\to {\mathbb{R}}^D$ is the backbone feature extraction network, which converts the input data into feature vectors in D-dimensional space, that is, $z=f_e\left(x;{\theta }_e\right)$. $f_c:{\mathbb{R}}^D\to {\mathbb{R}}^N$ is a classifier that maps D-dimensional features of the data to corresponding outputs, which can be transformed by $p(y\mid z;\theta )=softmax\left(fc\right(z;\theta c\left)\right)$ as probability distributions. We take the Cross-Entropy loss as the loss and optimize the model parameters by minimizing the loss: $H(q,p)=-{\sum }_x(q\left(y\right)logp\left(y\right)$). Figure 2 presents the complete framework of our approach.

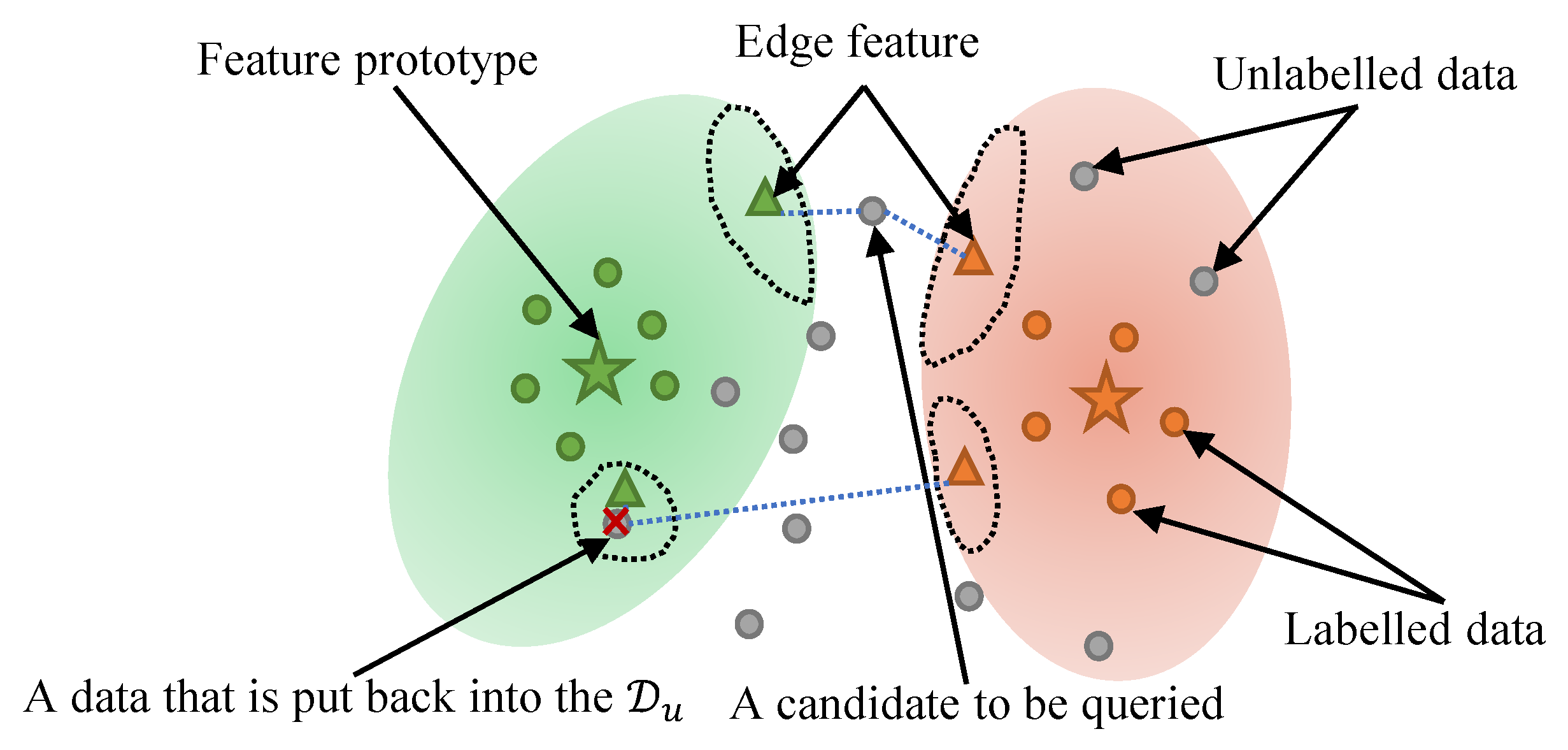
2.3. Edge Distance-Entropy

In the feature distribution of the dataset, samples of the same class have a high degree of similarity and will be clustered in the feature space. However, the data whose feature points are located at the boundary of the feature group are easily confused between the two categories and are not easy to identify. Our intuition is that the model’s mispredictions are mainly due to the inability to accurately judge the data that is ambiguously between the two classes. If more efficient boundary data is added to the train set, it will bring more gains to the model. To find such boundary samples, we proposed a data evaluation method of Edge Distance-Entropy. Figure 3 shows the strategy of Edge Distance-Entropy. Specifically, we first map the labeled train set and unlabeled set to the feature space with the help of the feature extractor $f_e$ trained on the labeled train set, and then obtain the high-dimensional feature vector $f_e\left(x_l\right)$, $x_l\in {\mathcal{D}}_l$ of the labeled train set, and the high-dimensional feature vector $f_e\left(x_u\right)$, $x_u\in {\mathcal{D}}_u$ of the unlabeled set. We sum and average the high-dimensional vectors of each class in the train set to obtain the feature prototypes of each class. The feature prototype [21] of the i-th class is:

$${Proto}_i=\frac{1}{n}\sum _{j=1}^n{f}_e\left(x_j^i\right)$$

(1)

Taking a data $x_u$ of an unlabeled set as an example, its high-dimensional feature vector $f_e\left(x_u\right)$ is measured with prototype of each class by the Euclidean distance, and n distances are obtained:

$$L_p=\left[l_{\mathrm{p}}^1,l_{\mathrm{p}}^2,\dots \dots ,l_p^n\right]$$

(2)

Select the two categories corresponding to the two smallest distances in $L_p$, that is, select the two categories closest to the unlabeled data feature. Next, we need to obtain the edge distance from $x_u$ to the two nearest neighbors. The distance is calculated as follows:

$${\mathrm{d}}_i={∥f_e\left(x_u\right)-f_e\left(x_{edge}^i\right)∥}_2=\sqrt{\sum _{j=1}^n{\left(f_e{\left(x_u\right)}_j-f_e{\left(x_{edge}^i\right)}_j\right)}^2}$$

(3)

Among them, $f_e\left(x_{edge}^i\right)$ is the edge feature of the i-th class, that is, the average value of the k data feature points whose high-dimensional feature is closest to $f_e\left(x_u\right)$. $f_e\left(x_{edge}^i\right)$ is calculated as follows:

$$f_e\left(x_{\mathit{edge}}^i\right)=\overline{f_e\left(x_{\mathit{edge}-k}^i\right)}=\frac{1}{k}\sum _{j=1}^n{f}_l\left(x_{ij}\right),k=\alpha \ast num\left(x_i\right)$$

(4)

A parameter $\alpha$ is mentioned in the formula, it is the proportion of data involved in computing edge features. When $\alpha$ is 1, all high-dimensional features in the class are selected to calculate $f_e\left(x_{edge}^i\right)$; at this time, $k=\mathrm{num}\left(x^i\right)$, $f_e\left(x_{edge}^i\right)$ is the class prototype. In order to accurately calculate edge features, we seek a high-order decay function. When there is less data, the features are scattered, and all data features are selected to calculate edge features. As the data increases, the proportion of data features we select gradually decays. When the amount of data approaches 100%, $\alpha$ is close to 0. We calculate $\alpha$ using the following formula:

$$\alpha ={\left(1-\left(Selec{t}_{ratio}-Bas{e}_{ratio}\right)\right)}^3$$

(5)

Among them, $Bas{e}_{ratio}$ is $D_B/D_T$; it is the proportion of $D_B$ to all train set data, and $Selec{t}_{ratio}$ is $D_l/D_T$; it is the proportion of currently labeled data to all train set data. The edge distance $(d_1,d_2)$ of $x_u$ from the two nearest neighbor classes is obtained by Equation  (3), we use the softmax function:

$$p_i=\frac{e^{-d_i}}{{\sum }_{j=1}^2{e}^{-d_j}}$$

(6)

Convert the two edge distances into probability distribution, and use the entropy calculation formula to obtain the Edge Distance-Entropy of the $x_u$:

$$E\left(x_u\right)=\sum _{i=1}^n{p}_i{log}_2\frac{1}{p_i}$$

(7)

The Edge Distance-Entropy E of each data in ${\mathcal{D}}_u$ is calculated by the above steps, and the Edge Distance-Entropy of the data in ${\mathcal{D}}_u$ is sorted from high to low to obtain $\mathcal{L}$. Select the first $\mathcal{M}$ data from L to a candidate set $\mathcal{C}$, query the labels of the data in $\mathcal{C}$, and perform manual marking. Add the marked $\mathcal{C}$ to ${\mathcal{D}}_l$ to obtain a new ${\mathcal{D}}_l$. At the same time, delete the data in $\mathcal{C}$ from ${\mathcal{D}}_u$.

2.4. Anomaly Feature Detection Strategy

When a sample has noise or label error [22], the feature vector it maps on the high-dimensional feature space will be far away from the feature group of the label class, which we call abnormal feature points. Under the interference of noise samples, the above method may be less effective. In order to resist the interference caused by abnormal feature points, we propose AFDS. Generally speaking, when the data is noisy, the similarity with the data of the class to which it belongs will become lower. Therefore, the abnormal features generated by the noisy data in the high-dimensional feature space will be far away from the feature cluster.

Our proposed AFDS is dedicated to finding anomalous feature points that are far away from feature clusters. Specifically, similar to the method mentioned in Section 2.3, we first obtain the high-dimensional feature vector $f_e\left(x_l\right)$, $x_l\in {\mathcal{D}}_l$ of the labeled train set and the high-dimensional feature vector $f_e\left(x_u\right)$, $x_u\in {\mathcal{D}}_u$ of the unlabeled set with the help of $f_e$. We sum and average the high-dimensional vectors of each class in the train set to obtain feature prototypes for each class. Taking a data $x_u$ in an unlabeled set as an example, its high-dimensional feature vector $f_e\left(x_u\right)$ is measured by Euclidean distance and each class prototype, and n distances are obtained: $L_p=\left[l_{\mathrm{p}}^1,l_{\mathrm{p}}^2,\dots \dots ,l_p^n\right]$. We use the softmax function: $q_i=\frac{e^{l_{\mathrm{p}}^i}}{{\sum }_{j=1}^2{e}^{-l_{\mathrm{p}}^j}}$ to convert n distances into probability distributions, using the calculation formula of entropy to get the outlier of $x_u$:

$$\mathcal{O}\left(x_u\right)=\sum _{i=1}^n{q}_i{log}_2\frac{1}{q_i}$$

(8)

The outlier $\mathcal{O}$ of each data in ${\mathcal{D}}_u$ is calculated by the above steps, and the outlier $\mathcal{O}$ of the data in ${\mathcal{D}}_u$ is sorted from high to low. Select the top $\mathcal{H}$ data with the largest outlier $\mathcal{O}$ from ${\mathcal{D}}_u$, and delete its high-dimensional feature points, thereby eliminating the abnormal features of ${\mathcal{D}}_u$ mapping (Algorithm 1).

Algorithm 1: Our Edge Distance-Entropy algorithm.

3. Results

3.1. Experiment Settings

The experiments we conduct rely on reliable physical and software resources to guarantee the validity and scientific validity of the results. As far as software is concerned, we take the system environment as Ubuntu 18.04 with CUDA 11.3, Python 3.8, Pytorch 1.10.2. As for hardware, we use a high-performance server with NVIDIA RTX 3080Ti GPU.

In the experiments, we conduct comprehensive experiments with a variety of different settings to verify the effect of our method on the pest dataset. Our setup consists of multiple parameters, including the initial labeled train set, the number of cycle, the amount of new data $\mathcal{M}$ = 500 (10%) added at each cycle and the deep neural network structure. First, we took the CP-10 dataset and randomly divided the CP-10 dataset into a train set and a test set according to 5:1. We randomly sample the train set in three groups, each time taking a certain amount of the initial labeled train set. We set three sets of cycle parameters, namely: 10 cycle, initial 500 data, $\mathcal{M}$ = 500 (10%); 5 cycle, initial 1000 data, $\mathcal{M}$ = 1000 (20%); 3 cycle, initial 1000 data, $\mathcal{M}$ = 2000 (40%). The deep neural network structure is fixed as the classic ResNet-18 network. Combining the above different parameters can obtain multiple sets of experimental settings, and we conduct multiple experiments under different experimental settings.

We selected several classical data evaluation methods for comparative experiments, including Entropy [23], Distance-Entropy [24], and Metric [25]. Entropy is an entropy-based method that selects the unlabeled instance with the highest entropy. Distance-Entropy embodies the entropy method in the high-dimensional feature space, and finds data with a uniform distance from various data feature prototypes. Metric is a simple measurement method that finds data in various categories that are far from the prototype of that category. These methods have achieved good results on public datasets.

Based on previous experimental experience, we adopt the following supervised [26] train setting. First, the train set images are preprocessed to a size of 84 × 84 and randomly inverted with a probability of 0.5, and then fed into the network. We use a batchsize of 128 and 100 epochs for network training. At each cycle, the initial learning rate is set to 0.01, which is then decayed by a factor of 10 at the 30th, 60th, and 80th epochs. Meanwhile, we optimize the network using a Cross Entropy loss and a learned SGD optimizer. Momentum and weight decay are set to 0.9 and 0.0005.

3.2. Overall Results

3.2.1. Comparison of Different Methods

Figure 4 shows the experimental results of different methods under three settings of $\mathcal{M}$ = 500, 1000, and 2000. The solid line in the figure represents the average of the results obtained from experiments using three different initial labeled train sets. The shaded area represents the range of results obtained from three experiments. It can be observed from the figure that our proposed Edge Distance-Entropy method achieves the best results under three different $\mathcal{M}$ settings. When $\mathcal{M}$ = 500, we only use 60% of the data to achieve the effect of 100% of the data. Compared with other methods, we use 5% to 15% less data to achieve this effect. This demonstrates that the method we proposed is very effective on the CP-10, and can effectively obtain efficient data, thereby reducing the amount of data and promoting the rational allocation of resources.

3.2.2. Influence of Parameter $\mathcal{M}$

In order to explore the influence of $\mathcal{M}$ on the experimental results, we compare the Edge Distance-Entropy results under different $\mathcal{M}$. Figure 5 shows the experimental results. It can be seen from the figure that when the value of $\mathcal{M}$ is relatively small, the Edge Distance-Entropy data evaluation method is more accurate. This is because the introduction of redundant data [27] can be avoided when only a small amount of data is added each time. However, if the value of $\mathcal{M}$ is too small, the number of cycle will become too much, the time cost will be greatly increased, and the work may become not worth the loss. Therefore, the value of $\mathcal{M}$ is a problem worth exploring. Generally speaking, the value of $\mathcal{M}$ should be reduced as much as possible within the acceptable time cost range.

4. Discussion

4.1. Discussion in the Case of Abnormal Data

This section discusses the presence of noise in crop pest dataset. In the process of data collection or data transmission, due to factors such as the shooting environment or equipment failure, it is inevitable that noisy data will appear in the dataset, and it is a tedious task to manually remove these noise data [28]. A large amount of noisy data will inevitably affect the performance of the model and the effectiveness of the data evaluation method. Is there a strategy that can be adopted to mitigate the effects of noisy data? We put some thought into this.

When there is noise in a certain pest data, if the target is heavily occluded, the model cannot identify the target type, and can only learn some background information, and the background of the pest data is mostly similar, with green as the main color. We believe that the noise data at this time is very similar to each class in the background, but the foreground is very different, and the model’s judgment of the noise data tends to be ambiguous among multiple classes. Therefore, we came up with a strategy to find feature points with relatively uniform distances from each class in the feature space, and this point is also an outlier [29] relative to the center of each class, which we call abnormal feature points. These abnormal feature points are eliminated, and the data corresponding to the remaining feature points are evaluated. We call this strategy AFDS, and use AFDS to conduct related comparative experiments.

When preparing for the experiment, we first randomly sampled 100 pieces of data from each class of ${\mathcal{D}}_T$ in CP-10, added noise, to simulate the situation of a noisy dataset. As shown in Figure 6, these noisy data target subjects are heavily occluded. The test set is the same as the experimental setup in the previous section. We use the Edge Distance-Entropy method, combined with the AFDS, select $\mathcal{M}$ = 500, and conduct experiments. At the same time, we also set up a control group without AFDS for comparison. The experimental results are shown in Figure 7.

As can be observed from Figure 7, when AFDS is used, the effect of noisy samples is obviously mitigated. Especially in the initial evaluation data, using AFDS improves the performance by about 5%. As the amount of data increases, the Edge Distance-Entropy method using AFDS can reach the peak performance first. Because it avoids introducing noisy data when training the neural network.

We only propose a method to solve the simple black block occlusion noise problem, but in practice, the noise is diverse, including Gaussian noise, mosaic, label noise, etc. In addition, there are problems such as image duplication in the dataset. For different kinds of noise problems and image repetition problems, it is necessary to conduct more in-depth research and carry out targeted solutions.

4.2. Application of Data Evaluation

At present, the application of deep learning is mostly driven by a large amount of data. It is a considerable research direction to evaluate the data and find efficient data, which has a wide range of application prospects. In addition to agriculture, there are many data-dependent application scenarios for data quality assessment methods that can be targeted for research. For example, images in the medical field require expert annotation, which is expensive. If intelligent algorithms can be used to find efficient data for labeling, the cost can be greatly reduced. For another example, text classification in many scenarios in text recognition tasks cannot provide so much training data, such as intent recognition in dialogue scenarios. These fields need more efficient data to drive, and finding efficient data has become a way to solve the problem.

5. Conclusions

5.1. Conclusions

In this paper, we propose a data evaluation method based on Edge Distance-Entropy for the problem that smart agriculture relies heavily on data. We effectively apply this method to the recognition task of crop pest datasets and demonstrate its state-of-the-art results in various settings. It is attractive that only about 60% of the data is used to achieve good results. When the amount of data reaches 70%, the performance has exceeded the level of 100% of the data. This is due to the existence of some negative migration data in the dataset. Our results can demonstrate that with efficient data, the input of data can be greatly reduced, which undoubtedly contributes to the sustainable development of smart agriculture. In addition, we also explored the influence of the parameter $\mathcal{M}$ on the method, and found that the value of $\mathcal{M}$ has an adverse effect on the performance. For noisy data, we propose Anomaly Feature Detection Strategy to alleviate the adverse effect of noisy data on the method. Experiments show that our proposed method is effective.

5.2. Future Work

The method proposed in this paper is effective, can effectively solve the data problem in the task of crop pest identification, and provides ideas for the sustainable development of smart agriculture. However, there are still some deficiencies in the work of this paper, and related research needs to be carried out in the future. First of all, the problems of noisy data and $\mathcal{M}$ value strategy are mentioned and analyzed in this paper, and solutions are given. However, the proposed method has certain limitations and needs to be further explored. This paper only conducts relevant experiments on the pest data set, but in the agricultural field, in addition to pest data, there are many other categories of data that also need to be identified, such as picking classification tasks in fruit farming [30], crop identification tasks, etc. This paper conducts experiments on the task of pest image recognition, but as the data dilemma does not only appear in the recognition task, other tasks also need to solve this problem, such as pest target detection, semantic segmentation [31], etc. In future research, we will expand to these fields and combine the proposed method with practical tasks in more agricultural fields to promote the sustainable development of smart agriculture in multiple aspects.