The Dynamic Behaviour of a Binary Adsorbent in a Fixed Bed Column for the Removal of Pb2+ Ions from Contaminated Water Bodies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of the Biosorbents
2.2. Characterisation of the Biosorbents
2.2.1. Fourier Transform Infrared (FTIR) Spectroscopy
2.2.2. Scanning Electron Microscopy (SEM)
2.3. Batch Experiments
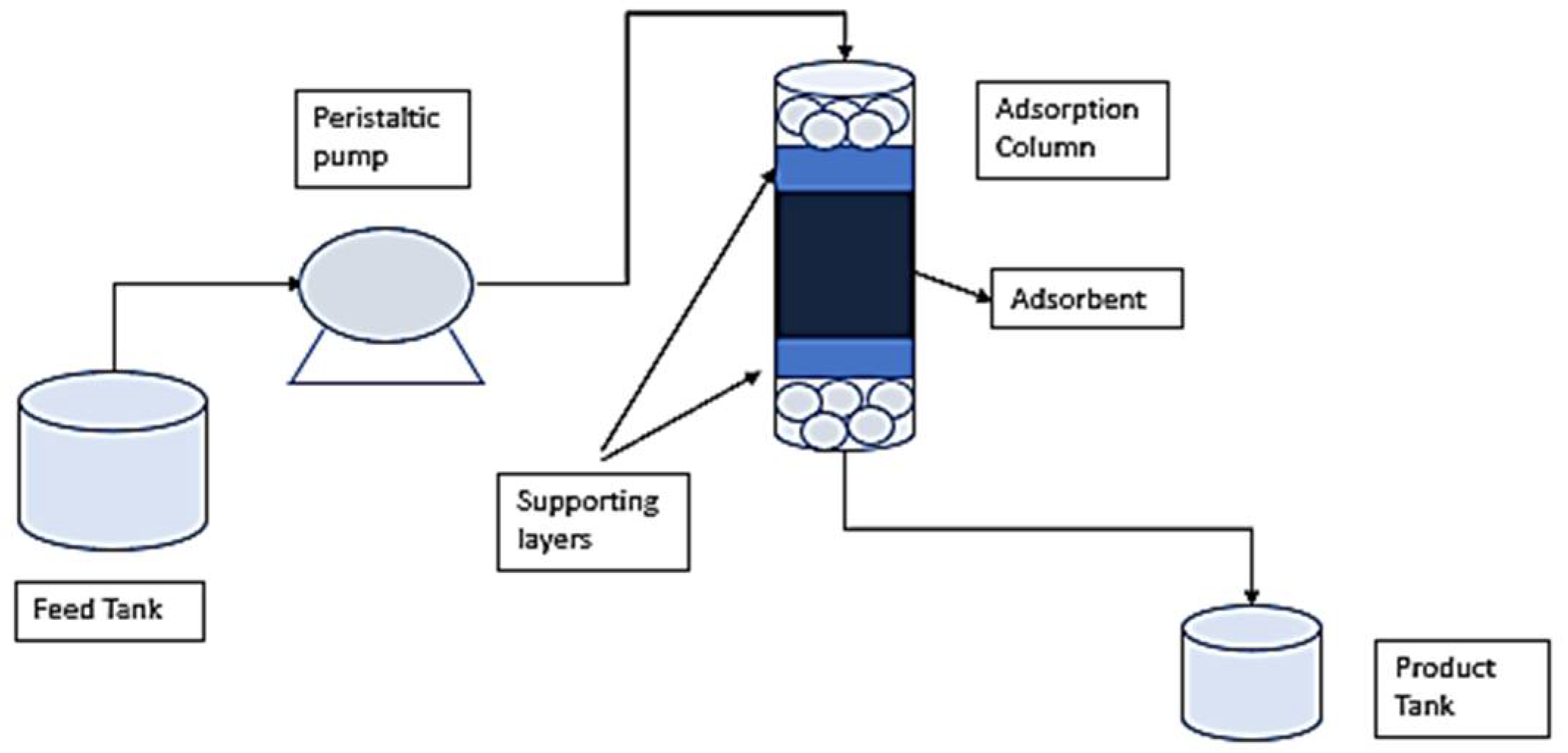
2.4. Fixed Bed Experiments
2.5. Mathematical Modelling
2.5.1. The Thomas Model
2.5.2. The Yoon–Nelson Model
3. Results and Discussion
3.1. Characterisation
3.1.1. Fourier Transform Infrared (FTIR) Spectroscopy Analysis
3.1.2. Scanning Electron Microscopy (SEM)
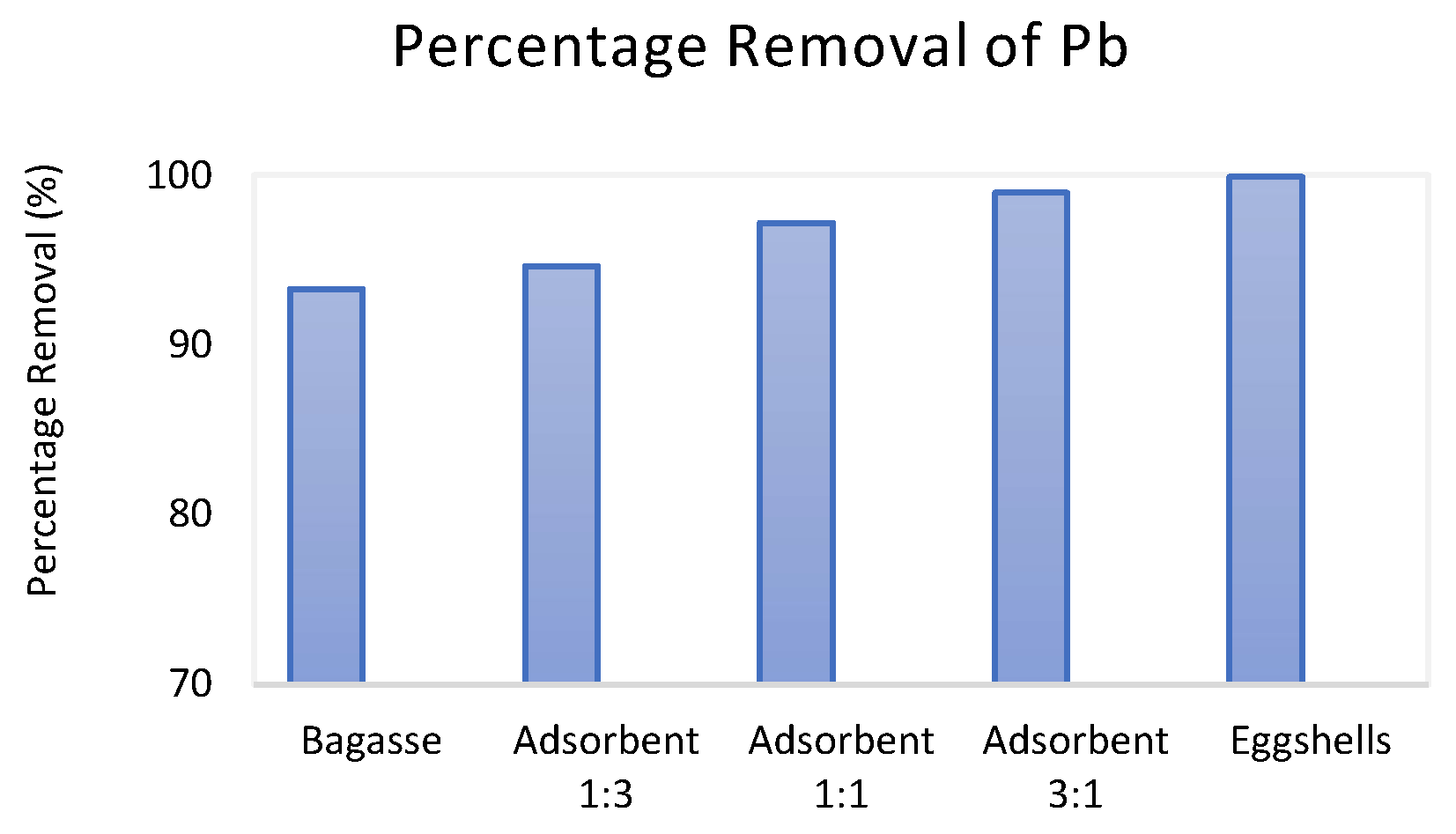
3.2. Comparative Performance of the Adsorbents
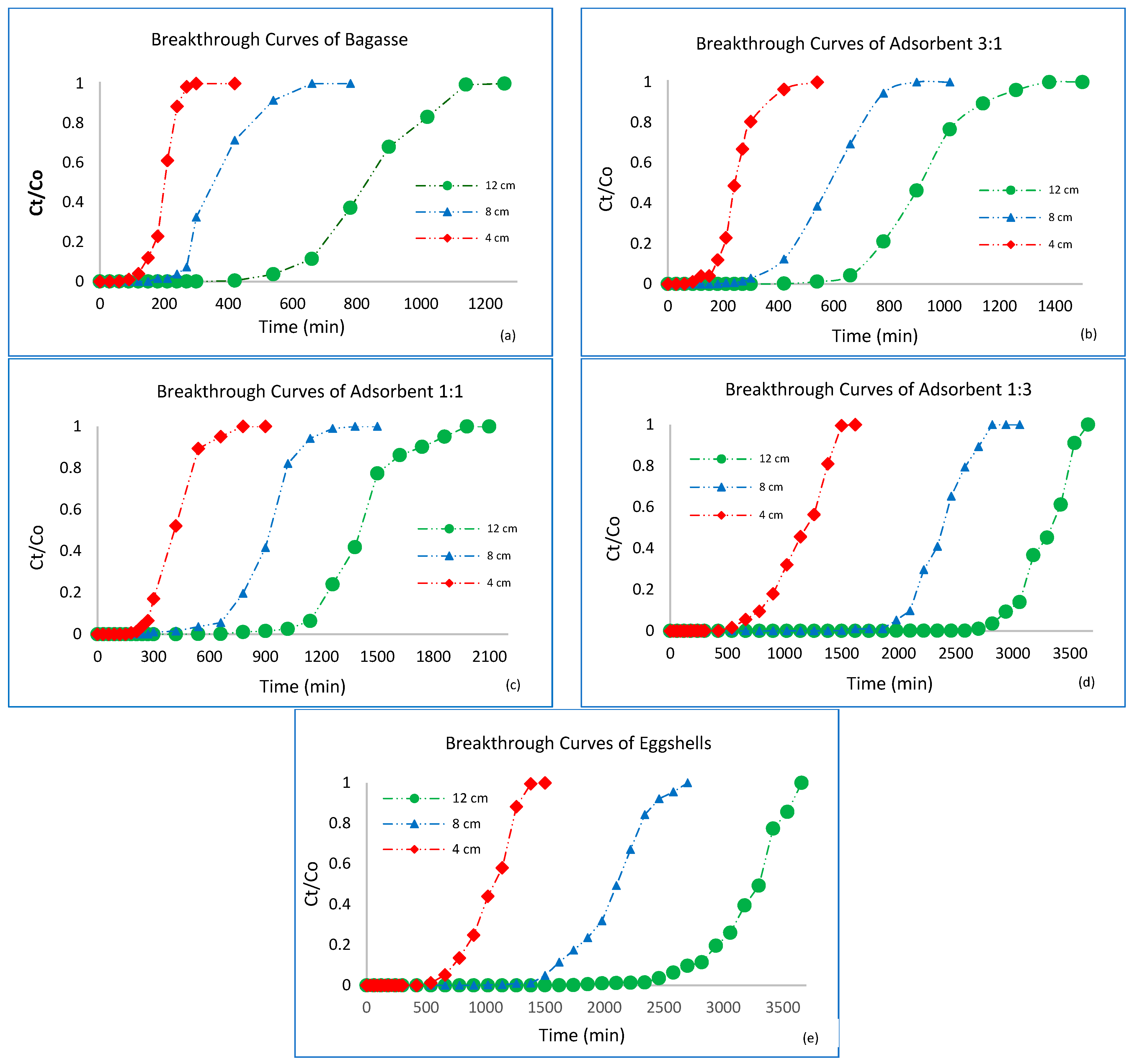
3.3. Breakthrough Curve Analysis
3.4. Effect of Bed Height
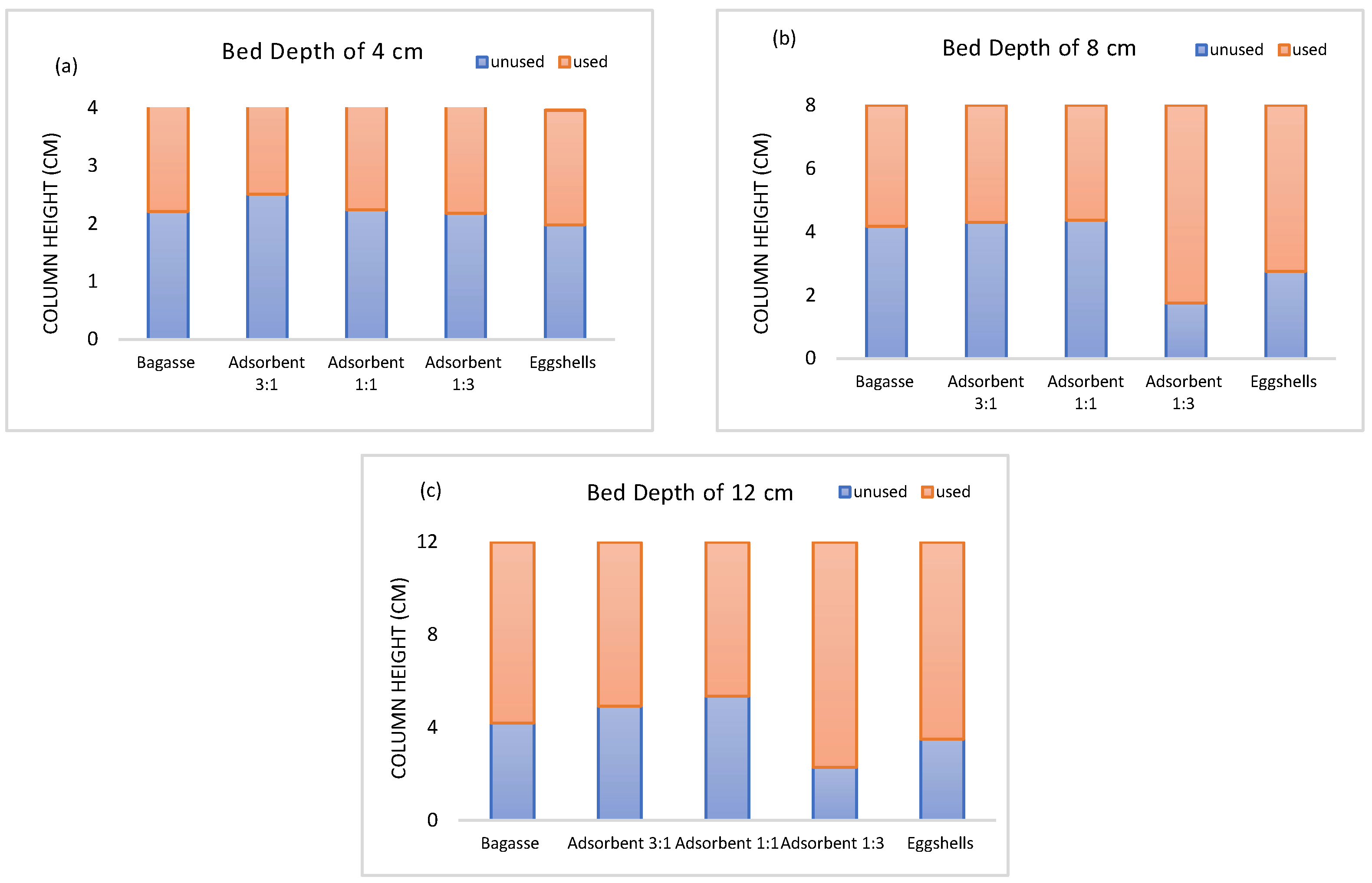
3.5. Bed Volumes (BV)
3.6. Adsorption Exhaustion Rate (AER)
3.7. Mass Transfer Zone (MTZ)
3.8. Breakthrough Curve Modelling
3.8.1. Application of the Thomas Model
3.8.2. Application of the Yoon–Nelson Model
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abdolali, A.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Zhang, J.; Liang, S.; Chang, S.W.; Nguyen, D.D.; Liu, Y. Application of a breakthrough biosorbent for removing heavy metals from synthetic and real wastewaters in a lab-scale continuous fixed-bed column. Bioresour. Technol. 2017, 229, 78–87. [Google Scholar] [CrossRef] [Green Version]
- Jaishankar, M.; Tseten, T.; Anbalagan, N.; Mathew, B.B.; Beeregowda, K.N. Toxicity, mechanism and health effects of some heavy metals. Interdiscip. Toxicol. 2014, 7, 60–72. [Google Scholar] [CrossRef] [Green Version]
- Lakherwal, D. Adsorption of Heavy Metals: A Review. Int. J. Environ. Res. Dev. 2014, 4, 41–48. [Google Scholar]
- Lestari, I. Isotherm and Kinetics of Cd(II) Adsorption by Durian (Durio zibethinus) seed Immobilized into Ca-alginate. In Proceedings of MICoMS; Emerald Reach Proceedings Series; Emerald Publishing Limited: Bradford, UK, 2018; Volume 1, pp. 569–574. [Google Scholar]
- Aldaghi, T.; Javanmard, S. The evaluation of wastewater treatment plant performance: A data mining approach. J. Eng. Des. Technol. 2021. ahead of print. [Google Scholar] [CrossRef]
- Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy metal toxicity and the environment. Mol. Clin. Environ. Toxicol. 2012, 101, 133–164. [Google Scholar] [CrossRef] [Green Version]
- Cruz-Olivares, J.; Perez-Alonso, C.; Barrera-Díaz, C.; Ureña-Nuñez, F.; Chaparro-Mercado, M.; Bilyeu, B. Modeling of lead (II) biosorption by residue of allspice in a fixed-bed column. Chem. Eng. J. 2013, 228, 21–27. [Google Scholar] [CrossRef]
- Morosanu, I.; Teodosiu, C.; Paduraru, C.; Ibanescu, D.; Tofan, L. Biosorption of lead ions from aqueous effluents by rapeseed biomass. New Biotechnol. 2017, 39, 110–124. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Lin, H. Competitive adsorption of Pb(II) and Zn(II) fromaqueous solution by modified beer lees in a fixedbed column. Proc. Saf. Environ. Protect. 2017, 111, 263–269. [Google Scholar] [CrossRef]
- Farouk, A.M.; Rahman, R.A.; Romali, N.S. Economic analysis of rehabilitation approaches for water distribution net-works: Comparative study between Egypt and Malaysia. J. Eng. Des. Technol. 2021. ahead of print. [Google Scholar]
- Okampo, E.J.; Nwulu, N. Optimal energy mix for a reverse osmosis desalination unit considering demand response. J. Eng. Des. Technol. 2020, 18, 1287–1303. [Google Scholar] [CrossRef]
- Chowdhury, Z.Z.; Zain, S.M.; Rashid, A.K.; Rafique, R.F.; Khalid, K. Breakthrough Curve Analysis for Column Dynamics Sorption of Mn(II) Ions from Wastewater by Using Mangostana garcinia Peel-Based Granular-Activated Carbon. J. Chem. 2012, 2013, 959761. [Google Scholar] [CrossRef] [Green Version]
- Mittal, A.; Teotia, M.; Soni, R.; Mittal, J. Applications of egg shell and egg shell membrane as adsorbents: A review. J. Mol. Liq. 2016, 223, 376–387. [Google Scholar] [CrossRef]
- De Angelis, G.; Medeghini, L.; Conte, A.M.; Mignardi, S. Recycling of eggshell waste into low-cost adsorbent for Ni removal from wastewater. J. Clean. Prod. 2017, 164, 1497–1506. [Google Scholar] [CrossRef]
- Park, H.J.; Jeong, S.W.; Yang, J.K.; Gil Kim, B.; Lee, S.M. Removal of heavy metals using waste eggshell. J. Environ. Sci. 2007, 19, 1436–1441. [Google Scholar] [CrossRef]
- Masukume, M.; Onyango, M.S.; Maree, J. Sea shell derived adsorbent and its potential for treating acid mine drainage. Int. J. Miner. Process. 2014, 133, 52–59. [Google Scholar] [CrossRef]
- Zaib, Q.; Kyung, D. Optimized removal of hexavalent chromium from water using spent tea leaves treated with ascorbic acid. Sci. Rep. 2022, 12, 1–14. [Google Scholar] [CrossRef]
- Gómez-Aguilar, D.L.; Rodríguez-Miranda, J.P.; Salcedo-Parra, O.J. Fruit Peels as a Sustainable Waste for the Biosorption of Heavy Metals in Wastewater: A Review. Molecules 2022, 27, 2124. [Google Scholar] [CrossRef] [PubMed]
- Hussain, T.; Imran, M.; Mushtaq, Z.; Khan, M.I.; Ahmad, M.H.; Mahr-Un-Nisa; Khan, M.K. Heavy Metal Biosorption by Polyphenol-Free Banana Peel Powder. JAPS J. Anim. Plant Sci. 2022, 32, 2. [Google Scholar]
- Sahu, V.; Attri, R.; Gupta, P.; Yadav, R. Development of eco friendly brick using water treatment plant sludge and processed tea waste. J. Eng. Des. Technol. 2019, 18, 727–738. [Google Scholar] [CrossRef]
- Won, S.W.; Kotte, P.; Wei, W.; Lim, A.; Yun, Y.-S. Biosorbents for recovery of precious metals. Bioresour. Technol. 2014, 160, 203–212. [Google Scholar] [CrossRef]
- Chojnacka, K. Biosorption of Cr(III) ions by eggshells. J. Hazard. Mater. 2005, 121, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Kuppusamy, V.; Man Joshi, U. Chicken Eggshells Remove Pb(II) Ions from Synthetic Wastewater. Environ. Eng. Sci. 2013, 30, 67–73. [Google Scholar]
- Flores-Cano, J.V.; Leyva-Ramos, R.; Mendoza-Barron, J.; Guerrero-Coronado, R.M.; Aragón-Piña, A.; Labrada-Delgado, G.J. Sorption mechanism of Cd(II) from water solution onto chicken eggshell. Appl. Surf. Sci. 2013, 276, 682–690. [Google Scholar] [CrossRef]
- Amar, I.A.; Hassan, S.M.; Aqeela, F.H.; Najem, M.Y.; Altohami, F.A. Removal of methylene blue using balanites ae-gyptiaca bark powder as low-cost and eco-friendly biosorbent. Res. J. Text. Appar. 2021. ahead of print. [Google Scholar]
- Zhang, T.; Tu, Z.; Lu, G.; Duan, X.; Yi, X.; Guo, C.; Dang, Z. Removal of heavy metals from acid mine drainage using chicken eggshells in column mode. J. Environ. Manag. 2017, 188, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gurgel, L.; Freitas, R.; Gil, L.F. Adsorption of Cu(II), Cd(II), and Pb(II) from aqueous single metal solutions by sugarcane bagasse and mercerized sugarcane bagasse chemically modified with succinic anhydride. Carbohydr. Polym. 2008, 74, 922–929. [Google Scholar] [CrossRef] [Green Version]
- Chao, H.P.; Chang, C.C.; Nieva, A. Biosorption of heavy metals on Citrus maxima peel, passion fruit shell, and sugarcane bagasse in a fixed-bed column. J. Ind. Eng. Chem. 2014, 20, 3408–3414. [Google Scholar] [CrossRef]
- Shekhawat, P.; Sharma, G.; Singh, R.M. Durability analysis of eggshell powder–flyash geopolymer composite subjected to wetting–drying cycles. J. Eng. Des. Technol. 2020, 18, 2043–2060. [Google Scholar] [CrossRef]
- Wong, S.Y.; Tan, Y.P.; Abdullah, A.H.; Ong, S.T. Removal of Basic Blue 3 And Reactive Orange 16 By Adsorption Onto Quartenized Sugar Cane Bagasse. Malays. J. Analyt. Sci. 2009, 13, 185–193. [Google Scholar]
- Mao, Y.; Mingming, S.; Xu, C.; Yanfang, F.; Jinzhong, W.; Kuan, L.; Da, T.; Manqiang, L.; Jun, W.; Schwab, A.P.; et al. Feasibility of sulfate-calcined eggshells for removing pathogenic bacteria and antibiotic resistance genes from landfill leachates. Waste Manag. 2017, 63, 275–283. [Google Scholar]
- Hussin, M.H.; Othman, N.H.; Wan Ibrahim, M.H. Carbonation of concrete containing mussel (Perna viridis) shell ash. J. Eng. Des. Technol. 2019, 17, 904–928. [Google Scholar] [CrossRef]
- Luo, X.; Liu, F.; Deng, Z.; Lin, X. Removal of copper(II) from aqueous solution in fixed-bed column by carboxylic acid functionalized deacetylated konjac glucomannan. Carbohydr. Polym. 2011, 86, 753–759. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous Ion Exchange in a Flowing System. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Acheampong, M.A.; Pakshirajan, K.; Annachhatre, A.P.; Lens, P.N. Removal of Cu(II) by biosorption onto coconut shell in fixed-bed column systems. J. Ind. Eng. Chem. 2012, 19, 841–848. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of Gas Adsorption Kinetics—II: A Theoretical Model for Respirator Cartridge Service Life and Its Practical Applications. Am. Ind. Hyg. Assoc. J. 1984, 45, 517–524. [Google Scholar] [CrossRef]
- Putra, W.P.; Kamari, A.; Yusoff, S.N.M.; Ishak, C.F.; Mohamed, A.; Hashim, N.; Isa, I.M. Biosorption of Cu(II), Pb(II) and Zn(II) Ions from Aqueous Solutions Using Selected Waste Materials: Adsorption and Characterisation Studies. J. Encapsulation Adsorpt. Sci. 2014, 4, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Harripersadth, C.; Musonge, P.; Isa, Y.M.; Morales, M.G.; Sayago, A. The application of eggshells and sugarcane bagasse as potential biomaterials in the removal of heavy metals from aqueous solutions. S. Afr. J. Chem. Eng. 2020, 34, 142–150. [Google Scholar] [CrossRef]
- Geankoplis, C.J. Transport Processes and Separation Process Principles: Includes Unit Operations, 4th ed.; Prentice Hall Professional Technical Reference: Hoboken, NJ, USA, 2003. [Google Scholar]
- Du, Z.; Zheng, T.; Wang, P. Experimental and modelling studies on fixed bed adsorption for Cu(II) removal from aqueous solution by carboxyl modified jute fiber. Powder Technol. 2018, 338, 952–959. [Google Scholar] [CrossRef]
- Malkoc, E.; Nuhoglu, Y.; Abali, Y. Cr(VI) adsorption by waste acorn of Quercus ithaburensis in fixed beds: Prediction of breakthrough curves. Chem. Eng. J. 2006, 119, 61–68. [Google Scholar] [CrossRef]
- Luo, X.; Deng, Z.; Lin, X.; Zhang, C. Fixed-bed column study for Cu2+ removal from solution using expanding rice husk. J. Hazard. Mater. 2011, 187, 182–189. [Google Scholar] [CrossRef]
- Nakajima, H. Mass Transfer Advances in Sustainable Energy and Environment Oriented Numerical Modeling; InTech Open: London, UK, 2014. [Google Scholar]
- Naja, G.; Volesky, B. Behavior of the Mass Transfer Zone in a Biosorption Column. Environ. Sci. Technol. 2006, 40, 3996–4003. [Google Scholar] [CrossRef] [PubMed]
- Verduzco-Navarro, I.P.; Rios-Donato, N.; Jasso-Gastinel, C.F.; Martínez-Gómez, D.J.; Mendizábal, E. Removal of Cu(II) by Fixed-Bed Columns Using Alg-Ch and Alg-ChS Hydrogel Beads: Effect of Operating Conditions on the Mass Transfer Zone. Polymers 2020, 12, 2345. [Google Scholar] [CrossRef] [PubMed]
- Aksu, Z.; Gönen, F. Biosorption of phenol by immobilized activated sludge in a continuous packed bed: Prediction of breakthrough curves. Process Biochem. 2004, 39, 599–613. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R. Root mean square error (RMSE) or mean absolute error (MAE)? Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Dong, L.; Yan, H.; Li, H.; Jiang, Z.; Kan, X.; Yang, H.; Li, A.; Cheng, R. Removal of methylene blue from aqueous solutions by straw based adsorbent in a fixed-bed column. Chem. Eng. J. 2011, 173, 429–436. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, J.-G.; Pan, B.-C. Mathematically modeling fixed-bed adsorption in aqueous systems. J. Zhejiang Univ. A 2013, 14, 155–176. [Google Scholar] [CrossRef] [Green Version]


| Bagasse | Adsorbent 1:3 | Adsorbent 1:1 | Adsorbent 3:1 | Eggshells | |
|---|---|---|---|---|---|
| Bagasse | 100% | 75% | 50% | 25% | - |
| Eggshells | - | 25% | 50% | 75% | 100% |
| Bagasse | 90 | 201 | 4 | 1.79 | 2.21 | 48 | 240 | 45 | 0.55 | 21.05 | 4.75 | |
| 210 | 435 | 8 | 3.82 | 4.18 | 56 | 600 | 48 | 0.52 | 22.77 | 25 | 4.39 | |
| 540 | 830 | 12 | 7.81 | 4.19 | 66 | 1200 | 65 | 0.35 | 28.97 | 43 | 3.45 | |
| Adsorbent 3:1 | 90 | 242 | 4 | 1.49 | 2.51 | 45 | 240 | 37 | 0.63 | 12.32 | 21 | 8.12 |
| 270 | 585 | 8 | 3.69 | 4.31 | 65 | 600 | 46 | 0.54 | 14.90 | 31 | 6.70 | |
| 540 | 915 | 12 | 7.08 | 4.92 | 66 | 1200 | 59 | 0.41 | 15.53 | 41 | 6.44 | |
| Adsorbent 1:1 | 210 | 477 | 4 | 1.76 | 2.24 | 61 | 480 | 44 | 1.27 | 15.57 | 48 | 6.22 |
| 420 | 925 | 8 | 3.63 | 4.37 | 67 | 1020 | 45 | 1.20 | 15.80 | 48 | 6.42 | |
| 780 | 1408 | 12 | 6.65 | 5.35 | 71 | 2160 | 55 | 0.80 | 16.06 | 59 | 6.32 | |
| Adsorbent 1:3 | 540 | 1188 | 4 | 1.82 | 2.18 | 73 | 1680 | 45 | 1.20 | 27.95 | 122 | 3.35 |
| 1860 | 2385 | 8 | 6.24 | 1.76 | 78 | 4560 | 78 | 0.28 | 29.85 | 210 | 3.34 | |
| 2700 | 3336 | 12 | 9.71 | 2.29 | 91 | 6960 | 81 | 0.24 | 29.98 | 212 | 3.58 | |
| Eggshells | 540 | 1071 | 4 | 2.02 | 1.98 | 71 | 1680 | 50 | 0.98 | 21.11 | 121 | 4.65 |
| 1380 | 2105 | 8 | 5.24 | 2.76 | 78 | 3120 | 66 | 0.53 | 21.48 | 155 | 4.74 | |
| 2340 | 3303 | 12 | 8.5 | 3.5 | 90 | 5520 | 71 | 0.41 | 22.08 | 175 | 4.53 |
| Adsorbent | Bed Height | R2 | RMSE | MAE | |||
|---|---|---|---|---|---|---|---|
| Bagasse | 4 cm | 5.29 × 10−4 | 20.48 | 21.05 | 0.962 | 0.034 | 0.009 |
| 8 cm | 2.67 × 10−4 | 20.57 | 22.77 | 0.856 | 0.068 | 0.020 | |
| 12 cm | 1.47 × 10−4 | 28.90 | 28.97 | 0.978 | 0.033 | 0.003 | |
| Adsorbent 3:1 | 4 cm | 3.55 × 10−4 | 12.44 | 12.32 | 0.9087 | 0.029 | 0.004 |
| 8 cm | 1.85 × 10−4 | 14.65 | 14.91 | 0.9155 | 0.039 | 0.001 | |
| 12 cm | 1.35 × 10−4 | 16.03 | 15.54 | 0.9486 | 0.037 | 0.010 | |
| Adsorbent 1:1 | 4 cm | 2.42 × 10−4 | 14.99 | 16.06 | 0.890 | 0.047 | 0.019 |
| 8 cm | 1.35 × 10−4 | 15.00 | 15.57 | 0.9108 | 0.028 | 0.005 | |
| 12 cm | 5.29 × 10−4 | 16.06 | 15.80 | 0.9881 | 0.030 | 0.007 | |
| Adsorbent 1:3 | 4 cm | 1.10 × 10−4 | 27.79 | 28.05 | 0.9482 | 0.078 | 0.013 |
| 8 cm | 8.20 × 10−4 | 22.16 | 29.95 | 0.884 | 0.080 | 0.036 | |
| 12 cm | 6.0 × 10−5 | 28.23 | 34.26 | 0.9265 | 0.048 | 0.017 | |
| Eggshells | 4 cm | 1.27 × 10−4 | 21.48 | 20.33 | 0.9676 | 0.065 | 0.010 |
| 8 cm | 6.7 × 10−5 | 21.11 | 20.69 | 0.9828 | 0.021 | 0.000 | |
| 12 cm | 4.5 × 10−5 | 22.08 | 21.51 | 0.9804 | 0.036 | 0.001 |
| Adsorbent | Bed Height | R2 | RMSE | MAE | |||
|---|---|---|---|---|---|---|---|
| Bagasse | 4 cm | 202 | 196 | 1.36 × 10−2 | 0.962 | 0.034 | 0.009 |
| 8 cm | 284 | 366 | 2.73 × 10−2 | 0.769 | 0.058 | 0.002 | |
| 12 cm | 800 | 877 | 5.29 × 10−2 | 0.979 | 0.027 | 0.006 | |
| Adsorbent 3:1 | 4 cm | 242 | 263 | 2.95 × 10−2 | 0.895 | 0.058 | 0.032 |
| 8 cm | 585 | 575 | 1.85 × 10−2 | 0.916 | 0.039 | 0.001 | |
| 12 cm | 915 | 944 | 1.35 × 10−2 | 0.949 | 0.037 | 0.010 | |
| Adsorbent 1:1 | 4 cm | 413 | 445 | 1.92 × 10−2 | 0.890 | 0.047 | 0.019 |
| 8 cm | 925 | 890 | 1.29 × 10−2 | 0.913 | 0.027 | 0.005 | |
| 12 cm | 1408 | 1427 | 8.40 × 10−3 | 0.985 | 0.048 | 0.017 | |
| Adsorbent 1:3 | 4 cm | 1188 | 1106 | 1.10 × 10−2 | 0.948 | 0.078 | 0.013 |
| 8 cm | 2385 | 2246 | 8.20 × 10−3 | 0.884 | 0.08 | 0.036 | |
| 12 cm | 877 | 3374 | 6.00 × 10−3 | 0.927 | 0.048 | 0.017 | |
| Eggshells | 4 cm | 1071 | 1024 | 1.26 × 10−2 | 0.971 | 0.060 | 0.006 |
| 8 cm | 2106 | 2106 | 6.20 × 10−3 | 0.968 | 0.024 | 0.011 | |
| 12 cm | 3304 | 3262 | 4.20 × 10−3 | 0.945 | 0.039 | 0.008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harripersadth, C.; Musonge, P. The Dynamic Behaviour of a Binary Adsorbent in a Fixed Bed Column for the Removal of Pb2+ Ions from Contaminated Water Bodies. Sustainability 2022, 14, 7662. https://doi.org/10.3390/su14137662
Harripersadth C, Musonge P. The Dynamic Behaviour of a Binary Adsorbent in a Fixed Bed Column for the Removal of Pb2+ Ions from Contaminated Water Bodies. Sustainability. 2022; 14(13):7662. https://doi.org/10.3390/su14137662
Chicago/Turabian StyleHarripersadth, Charlene, and Paul Musonge. 2022. "The Dynamic Behaviour of a Binary Adsorbent in a Fixed Bed Column for the Removal of Pb2+ Ions from Contaminated Water Bodies" Sustainability 14, no. 13: 7662. https://doi.org/10.3390/su14137662
APA StyleHarripersadth, C., & Musonge, P. (2022). The Dynamic Behaviour of a Binary Adsorbent in a Fixed Bed Column for the Removal of Pb2+ Ions from Contaminated Water Bodies. Sustainability, 14(13), 7662. https://doi.org/10.3390/su14137662







