Simulation Analysis of a Double Auction-Based Local Energy Market in Socio-Economic Context
Abstract
:1. Introduction
- How may socio-economic outcomes from LEM operation differ from current retail energy market outcomes, under a UDA mechanism? Specifically, can uniform market access be maintained under LEM operation? To what extent may local energy affordability issues be addressed? How may the range of allowed bidding and asking prices impact LEM outcomes?
2. Methodology
2.1. Simulation Environment Modeling
| Algorithm 1: Daily initialization of agent generation quantities. | |
| 1. | For each: |
| 2. | If (): |
| 3. | |
| 4. | Else: |
| Algorithm 2: Overview of modeled double auction, which uses merit-order supply allocation and a uniform, market-clearing price. | |
| 1. | For each : |
| 2. | |
| 3. | |
| 4. | While (): |
| 5. | |
| 6. | If ( of ): |
| 7. | If (): |
| 8. | of |
| 9. | Remove from |
| 10. | Else if ( of ): |
| 11. | If (): |
| 12. | of |
| 13. | Remove from |
| 14. | Calculate and assign transaction costs for time t |
2.2. Consumer Agent Modeling
2.3. Prosumer Agent Modeling
2.4. Agent-Level Parameter Initialization
| Algorithm 3: Initialization of agent types and behavioral parameters | |
| 1. | Randomly select agents (no replacement): |
| 2. | Set // initialize consumer |
| 3. | Set as in Section 2.1 |
| 4. | Set |
| 5. | Set |
| 6. | Set |
| 7. | where: |
| 8. | |
| 9. | |
| 10 | |
| 11. | Randomly select agents (no replacement): |
| 12. | Set // initialize prosumer |
| 13. | Set as in Section 2.1 |
| 14. | Set |
| 15. | Set |
| 16. | where: |
| 17. | such that: |
| 18. | |
| 19. | and |
| 20. | For all agents : |
| 21. | Set |
2.5. Agent Learning & Behavior
| Algorithm 4: Overview of Modified Roth-Erev learning algorithm for double-sided auction behavior representation in energy market. | |
| 1. | For market settlements : |
| 2. | For agents : |
| 3. | Draw |
| 4. | Submit strategy to LEM |
| 5. | Receive LEM settlement results: |
| 6. | Calculate via Equations (7)–(9), such that: |
| 7. | If (): // if agent is “consumer” type |
| 8. | |
| 9. | Else: // if agent is “prosumer” type |
| 10. | |
2.6. Results Analysis Metrics
| Results Analysis Metrics (Per Simulation) | ||
|---|---|---|
| Metric Name | Metric Calculation | |
| Agent Rationality Measurement | (10) | |
| Technical Market Efficiency | ): | |
| (11) | ||
| Else: | ||
| (12) | ||
| Consumer Relative Market Access | (13) | |
| Prosumer Relative Market Access | (14) | |
| Consumer Energy Cost Burden | : | |
| (15) | ||
| Else: | ||
| (16) | ||
| Mean Market Price | (17) | |
3. Experiments
3.1. Experiment Parameters
3.2. Simulated Agent Results Clustering
| Results Clustering by Agent Type | ||||
|---|---|---|---|---|
| Low-Income: | Middle-Income: | High-Income: | ||
| Value Preference: | Con 1 | Con 2 | Con 4 | |
| Con 3 | Con 5 | |||
| Con 6 | ||||
| Value Preference: | Pro 1 | |||
| Pro 2 | ||||
| Pro 3 | ||||
4. Results & Discussion
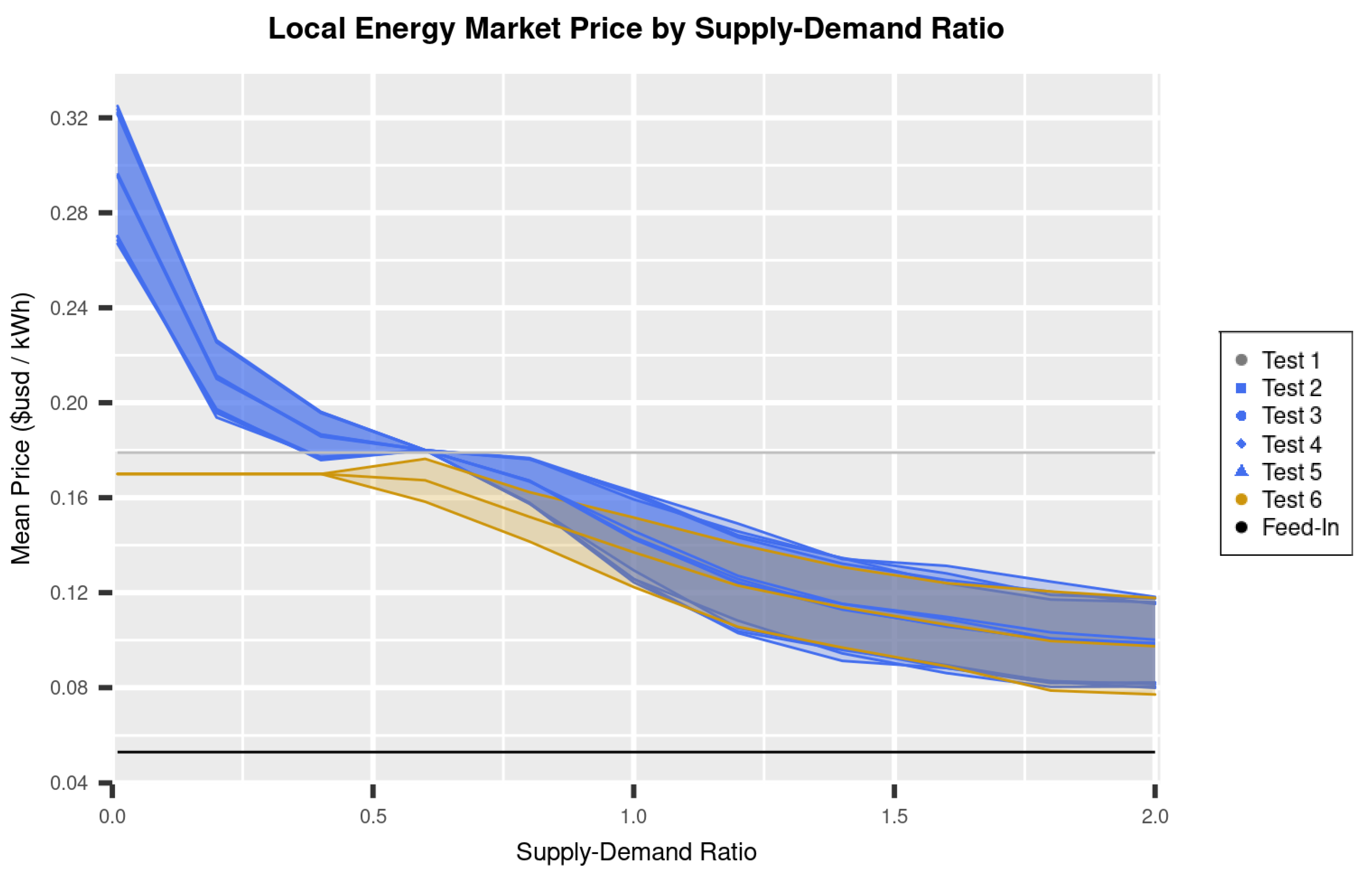
4.1. Local Market Price
4.2. Agent Rationality and Market Efficiency
| Validation Metrics for Simulation Implementation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | Agent Rationality (ARA) | Market Efficiency (TME) | ||||||||||
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Test 6 | Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Test 6 | |
| Low-SDR | <na> | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Target-SDR | <na> | 1 | 1 | 1 | 1 | 1 | 1 | 0.97 | 0.97 | 0.97 | 0.97 | 0.95 |
| High-SDR | <na> | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
4.3. Consumers’ Relative Market Access
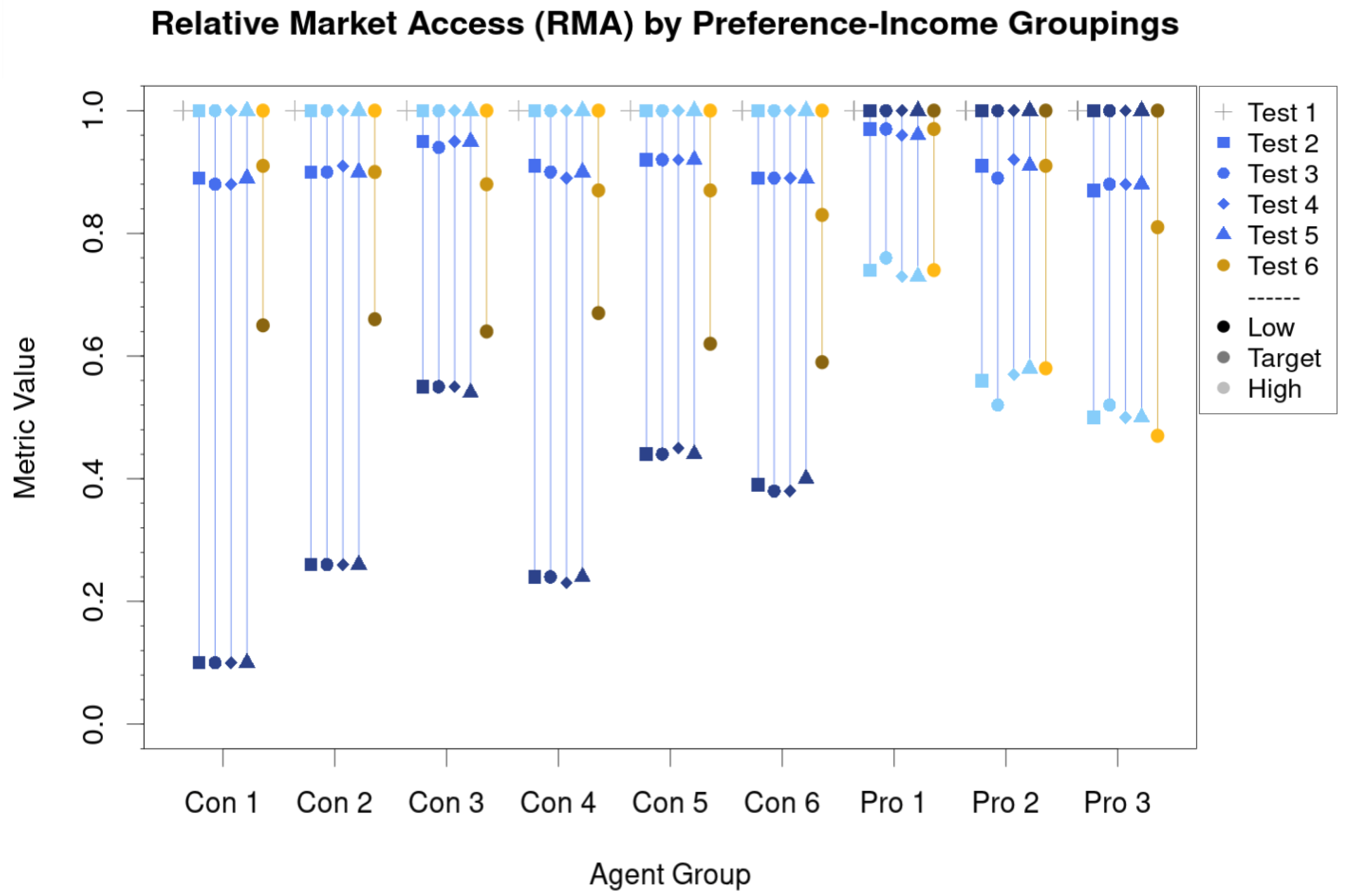
4.4. Prosumers’ Relative Market Access
4.5. Energy Cost Burden
5. Conclusions & Future Work
6. Glossary of Symbols and Abbreviations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drehobl, A.; Ross, L.; Ayala, R. How High Are Household Energy Burdens? An Assessment of National and Metropolitan Energy Burden across the United States; ACEEE: Washington, WA, USA, 2020. [Google Scholar]
- Wang, F.; Harindintwali, J.D.; Yuan, Z.; Wang, M.; Li, S.; Yin, Z.; Huang, L.; Fu, Y.; Li, L.; Chang, S.X.; et al. Technologies and perspectives for achieving carbon neutrality. Innovation 2021, 2, 100180. [Google Scholar] [CrossRef] [PubMed]
- Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D.; Poor, H.V. Peer-to-Peer Trading in Electricity Networks: An Overview. IEEE Trans. Smart Grid 2020, 11, 3185–3200. [Google Scholar] [CrossRef] [Green Version]
- Staudt, P.; Köpje, S.; Weinhardt, C. Market mechanisms for neighbourhood electricity grids: Design and agent-based evaluation. In Proceedings of the 27th European Conference on Information Systems—Information Systems in a Sharing Society ECIS 2019, Stockholm, Sweden, 8 June 2019; pp. 1–16. [Google Scholar]
- Khorasany, M.; Mishra, Y.; Ledwich, G. Market framework for local energy trading: A review of potential designs and market clearing approaches. IET Gener. Transm. Distrib. 2018, 12, 5899–5908. [Google Scholar] [CrossRef] [Green Version]
- Georgarakis, E.; Bauwens, T.; Pronk, A.-M.; AlSkaif, T. Keep it green, simple and socially fair: A choice experiment on prosumers’ preferences for peer-to-peer electricity trading in the Netherlands. Energy Policy 2021, 159, 112615. [Google Scholar] [CrossRef]
- Wörner, A.M.; Ableitner, L.; Meeuw, A.; Wortmann, F.; Tiefenbeck, V. Peer-to-Peer Energy Trading in the Real World: Market Design and Evaluation of the User Value Proposition. In Proceedings of the 40th International Conference on Information Systems ICIS 2019, Munich, Germany, 15–18 December 2019. [Google Scholar] [CrossRef]
- Wilkins, D.J.; Chitchyan, R.; Levine, M. Peer-to-Peer Energy Markets: Understanding the Values of Collective and Community Trading. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, New York, NY, USA, 25 April 2020. [Google Scholar] [CrossRef]
- Wilkinson, S.; Hojckova, K.; Eon, C.; Morrison, G.M.; Sandén, B. Is peer-to-peer electricity trading empowering users? Evidence on motivations and roles in a prosumer business model trial in Australia. Energy Res. Soc. Sci. 2020, 66, 101500. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Staudt, P.; Garttner, J.; Weinhardt, C. Trading on local energy markets: A comparison of market designs and bidding strategies. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017. [Google Scholar] [CrossRef]
- El-Baz, W.; Tzscheutschler, P.; Wagner, U. Evaluation of energy market platforms potential in microgrids: Scenario analysis based on a double-sided auction. Front. Energy Res. 2019, 7, 41. [Google Scholar] [CrossRef]
- Lin, J.; Pipattanasomporn, M.; Rahman, S. Comparative analysis of auction mechanisms and bidding strategies for P2P solar transactive energy markets. Appl. Energy 2019, 255, 113687. [Google Scholar] [CrossRef]
- Parag, Y.; Sovacool, B.K. Electricity market design for the prosumer era. Nat. Energy 2016, 1, 1–6. [Google Scholar] [CrossRef]
- New York City. Understanding and Alleviating Energy Cost Burden in New York City. 2019. Available online: https://www1.nyc.gov/assets/sustainability/downloads/pdf/publications/EnergyCost.pdf (accessed on 8 June 2022).
- Beattie, S.; Chan, W.-K.V. Broadening the Scope of Analysis for Peer-to-Peer Local Energy Markets to Improve Design Evaluations: An Agent-Based Simulation Approach. In Lecture Notes in Operations Research; Springer International Publishing: Cham, Switzerland, 2021; pp. 238–253. [Google Scholar]
- US Census. 2019—New York–Kings County—Brooklyn Borough. Am. Commun. Surv. 2019. Available online: https://data.census.gov/cedsci/table?t=IncomeandPoverty&g=0600000US3604710022&tid=ACSST5Y2019.S1901 (accessed on 7 July 2021).
- Zhou, Y.; Wu, J.; Long, C.; Cheng, M.; Zhang, C. Performance Evaluation of Peer-to-Peer Energy Sharing Models. Energy Procedia 2017, 143, 817–822. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Zhou, Y. Peer-to-Peer Energy Trading in Microgrids and Local Energy Systems; Jenkins, J.W.E.-N., Ed.; IntechOpen: Rijeka, Croatia, 2021; Chapter 3. [Google Scholar]
- Nicolaisen, J.; Petrov, V.; Tesfatsion, L. Market power and efficiency in a computational electricity market with discriminatory double-auction pricing. IEEE Trans. Evol. Comput. 2001, 5, 504–523. [Google Scholar] [CrossRef] [Green Version]
- Ableitner, L.; Tiefenbeck, V.; Meeuw, A.; Wörner, A.; Fleisch, E.; Wortmann, F. User behavior in a real-world peer-to-peer electricity market. Appl. Energy 2020, 270, 115061. [Google Scholar] [CrossRef]
- Ecker, F.; Spada, H.; Hahnel, U.J.J. Independence without control: Autarky outperforms autonomy benefits in the adoption of private energy storage systems. Energy Policy 2018, 122, 214–228. [Google Scholar] [CrossRef]
- Hahnel, U.J.J.; Herberz, M.; Pena-Bello, A.; Parra, D.; Brosch, T. Becoming prosumer: Revealing trading preferences and decision-making strategies in peer-to-peer energy communities. Energy Policy 2020, 137, 111098. [Google Scholar] [CrossRef]
- Frank, M.; Colgrove, M.; Martin, C.; Levin, E.; Palchak, E.; Stephenson, R. Towards Standardized Equity Measurement in the Clean Energy Industry: Work Plan and Literature Reveiws. Available online: https://www.veic.org/Media/default/documents/resources/reports/equity_measurement_clean_energyindustry.pdf (accessed on 7 September 2019).
- McCauley, D.A.; Heffron, R.J.; Stephan, H.; Jenkins, K. Advancing energy justice: The triumvirate of tenets. Int. Energy Law Rev. 2013, 32, 107–110. [Google Scholar]
- Sovacool, B.K.; Dworkin, M.H. Energy justice: Conceptual insights and practical applications. Appl. Energy 2015, 142, 435–444. [Google Scholar] [CrossRef]
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Narahari, Y. Game Theory and Mechanism Design; World Scientific Publishing Company; Indian Institute of Science: Bangalore, India, 2014. [Google Scholar]
- Xu, X.; Chen, C. Energy efficiency and energy justice for US low-income households: An analysis of multifaceted challenges and potential. Energy Policy 2019, 128, 763–774. [Google Scholar] [CrossRef]
- Kontokosta, C.E.; Reina, V.J.; Bonczak, B. Energy cost burdens for low-income and minority households: Evidence from energy benchmarking and audit data in five US cities. J. Am. Plan. Assoc. 2020, 86, 89–105. [Google Scholar] [CrossRef]
- Fisher Sheehan Colton Public Finance General Economics. Home Energy Affordability Gap. 2021. Available online: http://homeenergyaffordabilitygap.com/01_whatIsHEAG2.html (accessed on 20 January 2022).
- New York Energy Ratings, Electricity Rates and Usage for Brooklyn, New York. 2019. Available online: https://www.nyenergyratings.com/electricity-rates/new-york/brooklyn (accessed on 7 July 2021).
- Sharma, R.; Brooklyn Microgrid Gets Approval for Blockchain-based Energy Trading. Energy Central. 2019. Available online: https://energycentral.com/c/iu/brooklyn-microgrid-gets-approval-blockchain-based-energy-trading (accessed on 1 May 2022).
- New York City, Deriving a Poverty Threshold for New York City. 2020. Available online: https://www1.nyc.gov/assets/opportunity/pdf/NYCgovPoverty2020_Appendix_B.pdf (accessed on 7 July 2021).
- Block, C.; Neumann, D.; Weinhardt, C. A market mechanism for energy allocation in micro-CHP grids. In Proceedings of the Annual Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 7–10 January 2008; p. 172. [Google Scholar] [CrossRef]
- Livingston, D.; Sivaram, V.; Freeman, M.; Fiege, M. Applying Blockchain Technology to Decentralized Waste Management. 2018, pp. 2–3. Available online: https://blogs.systweak.com/applying-blockchain-technology-to-waste-management/ (accessed on 20 April 2018).
- LO3 Energy, Brooklyn Microgrid—About. 2019. Available online: https://www.brooklyn.energy/about (accessed on 7 July 2021).


| Other Abbreviated Terms | ||
|---|---|---|
| Acronym | Name | Description |
| DES | Distributed energy system | Energy system which is decentralized, but feature some level of inter-connection; a number of localized microgrids connected to a main, regional energy grid is an example of DES; often characterized by RER |
| RER | Renewable energy resource | Device used for renewable energy generation, storage, etc. These may include, e.g., solar PV panels, wind turbines, battery storage, or electric vehicles. |
| LEM | Local energy market | Virtual platform to coordinate local-scale energy distribution; often a peer-to-peer network or a centralized auction platform for local utility customers |
| UDA | Uniform double-sided auction | A double-sided auction with a uniform market-clearing price, merit-order supply allocation, and a closed order book. Double-sided auctions are a class of auction commonly used to produce efficient allocations of private goods. |
| Agent-Level Income Distribution | ||
|---|---|---|
| Population % | Agents Selected (N = 100) | |
| 8.8 | 9 | |
| 6.4 | 6 | |
| 9.6 | 10 | |
| 8.3 | 8 | |
| 10.5 | 11 | |
| 14.1 | 14 | |
| 11.2 | 11 | |
| 14.0 | 14 | |
| 7.4 | 7 | |
| 9.6 | 10 | |
| Simulation Parameters by Experiment | ||||
|---|---|---|---|---|
| Experiment 0 | Experiment 1 | Experiment 2 | ||
| Test Number(s) | 1 | {2, 3, 4, 5} | 6 | |
| Parameters | (0.33, 0.33, 0.33) | (0.33, 0.33, 0.33), (0.5, 0.25, 0.25), (0.25, 0.5, 0.25), (0.25, 0.25, 0.5) | (0.33, 0.33, 0.33) | |
| K | True | True | False | |
| SDR | {0.01, 0.1, 0.2, …, 2.0} | {0.01, 0.1, 0.2, …, 2.0} | {0.01, 0.1, 0.2, …, 2.0} | |
| M | “Baseline” | “UDA” | “UDA” | |
| Simulation Parameters | ||
|---|---|---|
| Name | Initialization | Description |
| Set of simulation steps | Local and retail markets settled once per step | |
| Agent index numbers | ← Consumer agent indices ← Prosumer agent indices | |
| Number of consumers | 75 consumer agents selected at initialization (Section 2.4) | |
| Number of prosumers | 25 consumer agents selected at initialization (Section 2.4) | |
| Grid feed-in tariff | $0.053 USD/kWh | (Section 2.1) |
| Grid retail price | $0.175 USD/kWh | (Section 2.1) |
| Agent daily demand | (Section 3) | |
| Agent daily generation | Function of variable parameter Set based on current SDR value (Section 3.1) | : ): |
| Equitable supply threshold | (Section 2.6) | |
| Minimum agent income | = $10,000 USD/year | (Section 2.1) |
| Maximum agent income | = $200,000 USD/year | (Section 2.1) |
| Agent incomes | Set by random distribution | (Section 2.1) |
| Locally-defined threshold for affordable energy cost | 6% of income is considered affordable locally (Section 2.4, Section 2.6) | |
| Locally-observed “high” energy cost burden | ) | initialization (Section 2.4) |
| Consumers’ individually affordable energy prices | : | (Section 2.4) |
| Agent is “consumer”? | Set of Boolean values indicating agent “type” (Section 3) | |
| Learning “memory” | (Section 2.5) | |
| Learning “rate” | (Section 2.5) | |
| Agent utility preferences | Consumer: Prosumer: | Consumer: own-economic utility preference Prosumer: utility preference “type” (Section 2.2, Section 2.3 and Section 2.4) |
| Market mechanism | (Section 2.1, Section 3) Experiment 0 Parameter | |
| Prosumer type distribution | Where: | (Section 3.1) Experiment 1 Parameter |
| Local price constraint? | required in the LEM at each time step? | (Section 3.1) Experiment 2 Parameter |
| Market supply-demand ratio (SDR) | Variable parameter for all modeling scenarios tested (Section 3.1) | |
| Market Data Notation | |
|---|---|
| Variable | Description |
holds consumer costs and prosumer sales | |
| . | |
holds agents’ local purchase and sale quantities | |
holds agents’ retail purchase and sale quantities | |
holds agents’ initial demand and supply quantities | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beattie, S.; Chan, W.-K.; Wei, Z.; Zhu, Z. Simulation Analysis of a Double Auction-Based Local Energy Market in Socio-Economic Context. Sustainability 2022, 14, 7642. https://doi.org/10.3390/su14137642
Beattie S, Chan W-K, Wei Z, Zhu Z. Simulation Analysis of a Double Auction-Based Local Energy Market in Socio-Economic Context. Sustainability. 2022; 14(13):7642. https://doi.org/10.3390/su14137642
Chicago/Turabian StyleBeattie, Steven, Wai-Kin (Victor) Chan, Zixuan Wei, and Zhibin Zhu. 2022. "Simulation Analysis of a Double Auction-Based Local Energy Market in Socio-Economic Context" Sustainability 14, no. 13: 7642. https://doi.org/10.3390/su14137642
APA StyleBeattie, S., Chan, W.-K., Wei, Z., & Zhu, Z. (2022). Simulation Analysis of a Double Auction-Based Local Energy Market in Socio-Economic Context. Sustainability, 14(13), 7642. https://doi.org/10.3390/su14137642






