Abstract
This study explores the spatial effect of infrastructure development on real estate prices in the Yangtze River Delta. It constructs an evaluation system of the infrastructure development level across five dimensions (i.e., transportation, water supply and drainage, energy and power, postal communication, and ecological environment), analyzes the development characteristics of urban infrastructure in the Yangtze River Delta, and uses a spatial panel model to explore how urban infrastructure development affects real estate prices. Results indicate that (1) the overall development level of urban infrastructure in the Yangtze River Delta region shows an upward trend. Significant regional differences exist as the development level of urban infrastructure in the eastern region is ahead of that in the central region; (2) Spatial autocorrelation and real estate prices in the Yangtze River Delta region in infrastructure development and overall levels, respectively, are high; (3) Infrastructure directly affects local real estate market demand and improves the vitality of the housing market in adjacent areas; and (4) Infrastructure construction can significantly promote the rise of urban real estate prices in the eastern region, while this driving effect is not significant in the central region. This research will help the government promote the coordinated development of urban infrastructure and formulate relevant policies for the macro-control of the real estate market in urban agglomerations.
1. Introduction
Several government policies have promoted internal circulation and steady economic development in China since the 2008 global financial crisis. Urban infrastructure construction is an important investment direction for governments to expand domestic demand. The Yangtze River Delta region—as the core city cluster of economic development—had a gross domestic product of 219.04 billion yuan (about 25% of the country’s total economic volume) by the end of 2018. With rapid economic development, the Yangtze River Delta region has seen strong infrastructure development. From 2006 to 2018, average annual growth rates in the region were as follows: highway mileage (5.20%), road area (6.15%), bus number (6.12%), drainage pipe length (8.04%), and total mobile phone volume (9.03%). Owing to rapid infrastructure development, a large amount of capital flows into the Yangtze River Delta, accelerating circulation of industrial elements, expanding the economic scale, and increasing the regional population. Housing prices in these regions have increased simultaneous to this. The average selling price of commercial housing in the Yangtze River Delta region rose from 4427.30 yuan per square meter in 2006 to 11,433.76 yuan per square meter in 2018, with an average annual growth rate of 8.24%. Hence, what is the correlation between rapid infrastructural development and increased real estate prices in urban agglomerations during this period? What are the spatial distribution characteristics of urban infrastructure development in the Yangtze River Delta region? What are the links between real estate markets in different cities? Exploring spatial characteristics of cities and studying the relationship between infrastructure development and real estate prices in urban agglomerations are key to the macro-control of the real estate market and the promotion of healthy infrastructure development.
Owing to early development time and the mature development system of the real estate industry, many achievements in related research on the factors affecting real estate prices have been made. On the supply side, factors such as land, real estate investment, mortgage interest rates, and credit scale have always been main variables in studies on real estate prices [1,2,3]. On the demand side, factors such as demographic structure, migration, income, and industrial structure also have a significant impact on housing prices [4,5,6]. Additionally, real estate market speculation, government regulatory policies, and infrastructure service quality are key factors affecting the vitality of the urban real estate market [7,8].
Urban infrastructure is a physical entity that points to the production and distribution sectors and offers public services and production factors for residents [9]. Urban infrastructure includes transportation, water supply and drainage, energy and power, postal communication, and the ecological environment [10]. In recent years, significant progress has been made in infrastructure development. Regarding comprehensive evaluation principles of infrastructure, Lu and Jiang [11] proposed seven evaluation principles of national infrastructure development. In the comprehensive evaluation method, Xiang et al. [12] used the analytic hierarchy process (AHP) to evaluate infrastructure safety in big cities from five dimensions: roads, the environment, energy and power, water supply and drainage, and communication. However, Xu et al. [13] believed that the index weight of AHP was somewhat subjective and that the entropy method could make the results more objective and reasonable. Some attempts have been made to examine urban infrastructure externalities. For example, He et al. [14] comprehensively evaluated the economic, social, and environmental benefits of an urban public transport infrastructure.
The relationship between urban infrastructure development and the real estate market has received theoretical interest. Some scholars believe that urban infrastructure construction is directly related to real estate price. For example, Belke and Keil [15] studied the real estate market in 100 German cities and found that local infrastructure was closely related to real estate prices. Abidoye et al. [16] highlighted that constructing new infrastructure will affect property, economy, the environment and the housing value of the surrounding area. Others believe that infrastructure construction affects the real estate market indirectly through an intermediary effect. For example, Stover [17] argued that urban infrastructure development would reduce land supply and thus increase the price of developable land. This would eventually transfer to the price of new residential real estate through a cost transfer mechanism. Weisbrod et al. [18] suggested that infrastructure construction in urban areas could broaden urban boundaries and influence housing values in surrounding areas. Suen et al. [19] proposed that insufficient real estate development investment would lead to a low density of newly built housing in the region and that the improvement of infrastructure could effectively attract capital investment to increase the housing density in this area.
Several empirical studies have been conducted on the impact of a single type of infrastructure on real estate prices. With regard to transportation infrastructure, impact range, intensity, and mechanism of transportation infrastructure have been examined [20,21,22]. Additionally, Zhang and Jiao [23] studied the correlation between rail transit facilities and housing prices at different stages of their life cycle. Moreover, the initial stage of planning and construction had the greatest effect. Zhang et al. [24] compared the impact of different types of public transport facilities on residential value using a geographically weighted model (GWR). However, some studies demonstrated that transport infrastructure negatively affects housing prices. For example, Szczepanska et al. [25] argued that noise generated by transportation infrastructure can reduce apartment housing prices in nearby areas. Riccioli et al. [26] proposed that being too close to the main road of a rail transit line would lead to serious traffic jams and pollution, which would lower housing prices. In green environmental infrastructure, Jim and Chen [27] believe that green space usability could be more attractive than propinquity. Wu et al. [28] confirmed this view. Some scholars prioritized the capitalization effect of environmental facilities. For example, Zhang and Dong [29] proposed that houses with a high horizontal green view index (HGVI) are more attractive to homebuyers and are of higher economic value. In water supply and drainage facilities, Sohn and Kim [30] studied the capitalization effect of rainwater treatment ponds on real estate prices.
The US National Environmental Protection Agency defines brownfield infrastructure as: “Land and facilities which are abandoned, idle or underutilized for industry and commerce”. With the further development of urbanization and the change of transportation mode, a large number of abandoned railways and industrial plant facilities have been left behind. These abandoned railways and industrial plants occupy a large amount of land resources and separate the spatial connection of urban places. Brownfield will harm not only the environment but also urban economic development and social health. Therefore, the redevelopment of brownfield infrastructure is an area of concern to many scholars. It has been indicated that brownfield redevelopment can bring a wide range of economic, social and environmental benefits to stakeholders, with a total output multiplier of 3.8 [31]. The redevelopment methods of brownfield infrastructure are also diverse. Finger and Yanar proposed three aspects of abandoned railway reuse (i.e., transportation facilities, commercial and tourist places, and public spaces) [32]. Railway brownfield redevelopment can accelerate the realization of urban internal connections [33]. Vias V erdestands, a project in Spain, has transformed a 2700 km railway line into 125 greenways, including 110 stations [34]. Degioanni and Ferretti point out that the restoration of abandoned railways can rebuild urbanized areas [35]. The demolition of abandoned factories stimulates regional economic and social development. The riverside in London has redeveloped abandoned industrial land into high-end residential buildings [36]. The Seattle gas plant park in the United States and the Duisburg North Park in Germany act as typical examples of the transformation from brownfield into industrial landscape parks [37,38]. Brownfield infrastructure reuse can boost the economy, clean up polluted areas and improve city life. Consequently, Bowman et al. believe that brownfield infrastructure transformation will bring new opportunities to urban real estate markets [39].
Various research methods have been developed to determine the correlation between urban infrastructure and real estate price. Hess and Almeida [40] constructed a hedonic model to study the impact of light rail on housing prices. Liang et al. [41] found that the externalities of infrastructure (e.g., parks, lakes, rail transit, and middle schools) have significant spatial unstable influence on housing prices by applying a geo-weighted model (GWT). Lan et al. [42] studied the impact of public service facilities on the housing market using a mixed-method weighted regression model (MGWR) and a geographical detector model (GD). Many scholars prefer spatial econometric models in the related studies. Hadier and Miller [43] found that the spatial lag model (SAR) has a better fitting effect than the nonspatial model. Dorantes and Paez [44] constructed a spatial error model and a spatial lag model to analyze the impact of Madrid Metro Line 12 on real estate prices. Efthymiou and Antoniou [45] constructed a spatial econometric model and found that subways, trams, suburban railways, and bus stations can raise house prices. Conversely, national rail stations, airports, and ports have a negative impact on the rise of house prices owing to externalities such as noise.
The spatial econometric model can comprehensively explain the spatial autocorrelation of both urban infrastructure and the real estate market. However, attention has only focused on analyzing the relationship between a certain type of infrastructure (i.e., transportation, environment, drainage, and other facilities) and real estate prices, and not from the perspective of overall urban infrastructure development [46,47]. Additionally, with rapid development of transportation, communication, and other infrastructure, the integration process of urban agglomerations has accelerated, and there is strong spatial autocorrelation in the real estate market. From the perspective of the Yangtze River Delta urban agglomerations, spatial-temporal evolution characteristics of infrastructure and its spatial effect on real estate prices are necessary. To fill research gaps, this study constructs a relatively comprehensive evaluation index system of urban infrastructure development level to analyze spatial distribution and temporal evolution characteristics of infrastructure development in the Yangtze River Delta urban agglomeration. This study analyzes the impact of urban infrastructure development on real estate prices based on three spatial weight matrices from geographical and economic perspectives and a spatial panel model. After decomposing the total effect, urban infrastructure is demonstrated to affect real estate prices. Finally, this study divides the Yangtze River Delta region into eastern and central regions according to geographical location and explores the spatial effect of infrastructure development in different regions on real estate prices.
The article is divided into four sections. Section 1 introduces the research background, research significance, and literature review. Section 2 provides a full account of the research area, data, and methods. Section 3 elaborates on the results. First, this study reveals the temporal and spatial patterns of infrastructure development of urban agglomeration in the Yangtze River Delta. After careful analysis, we then obtain the results of the spatial autocorrelation test between real estate prices and infrastructure development. Finally, this study measured the spatial effect of infrastructure development on real estate prices in the urban agglomeration in the Yangtze River Delta region. Section 4 discusses the results and proposes future research directions. We present a summary of the research results and corresponding policy suggestions at the end of this paper.
2. Materials and Methods
2.1. Study Area
China’s Cabinet unveiled the outline of the Yangtze River Delta regional integration development plan in 2019, stipulating that the Yangtze River Delta includes 41 cities in Jiangsu, Zhejiang, Anhui, and Shanghai. Conversely, the Yangtze River Delta, a core urban agglomeration of economic development, is the region with the most developed economy and highest degree of urban agglomeration in China. In 2020, there were 218.91 million people (15.5% of the national population) living in Shanghai. Moreover, GDP was at 2.44735 trillion yuan (24.09% of the country’s total GDP). With the vigorous development of transportation and network communication facilities, a two-hour traffic circle has been built in developed cities such as Shanghai, Nanjing, Suzhou, Hangzhou, and Hefei. As a result of the integrated Yangtze River Delta urban agglomeration, the circulation barriers of capital factors, such as population, technology, and information in the regional market, are gradually broken. Moreover, more connections can be found among real estate markets in the Yangtze River Delta. Accordingly, real estate price in the Yangtze River Delta urban agglomeration remains high, although the government has issued many real estate regulation policies (e.g., restrictions on purchases, sales, and loans). In sharp contrast to the year-by-year increase in housing inventory, the affordability of residents is declining. Therefore, high housing prices has become an important issue affecting people’s livelihoods.
2.2. Data Collection and Index System Construction
This study aims to explore the spatial effect of the comprehensive infrastructure development level on real estate prices in the Yangtze River Delta urban agglomeration. To strengthen the conclusion, this should be based on a scientific and objective evaluation index system. According to related references [10,48,49,50], this study considered the characteristics of close regional transportation links and a high degree of integration of cities in the Yangtze River Delta and constructed an evaluation index system reflecting the level of urban infrastructure development (Table 1). The index system contains five primary and 13 secondary indicators, the former of which includes transportation facilities, water supply and drainage facilities, post and telecommunications facilities, energy and power facilities, and ecological and environmental facilities.

Table 1.
The evaluation index system of infrastructure development level.
Among these indicators, railway network density can indicate kilometers of new railways and highways in a city each year, and reflect the impact of urban abandoned railway reuse as well. Some abandoned railways have been transformed into greenways and urban tracks which connect the urban area with the surrounding environment, change city accessibility, and increase the road network area [51]. Another part of the abandoned railway has been transformed into commercial tourism places and public spaces, e.g., New York’s High Line [52], Berlin’s Triangle Park, and the French bus corridor [53]. This reconstruction can lead to the reduction in urban abandoned railways and the expansion in city green areas. Average per capita garden green space area reflecting the scale change of urban park green space comes from not only greening land development in urban construction land, but also from the redevelopment and reconstruction of brownfield sites (e.g., urban abandoned factories and abandoned mines). In the Ruhr district of Germany, most industrial brownfields have been transformed into urban parks and industrial forests, covering an area of more than 50 hm2 in each place [54]. And Xuzhou, China has transformed coal mine brownfields into green infrastructure to expand city green areas [55]. These two indicators reflect the impact of brownfield facilities redevelopment on infrastructure (e.g., urban transportation and green landscape). Accordingly, this paper analyzes the external impact of brownfield facilities transformation on the urban real estate market.
This study examines the spatial effect of urban infrastructure development on urban real estate prices. Hence, the main variables were selected as follows:
- (1)
- Real estate price (RSP): Real estate price is the explained variance obtained by dividing the sales volume of commercial housing in each city by the sales area of commercial housing in the year. To reduce the impact of the model on heteroscedasticity, logarithms were used for processing.
- (2)
- Infrastructure development level (IDL): This is weighted using the improved entropy method.
- (3)
- Other control variables. Industrial structure (IS): As upgrading industrial structure is closely related to urban housing prices [56], this study adopts the ratio of the output value of secondary and tertiary industries to the GDP of the current year to represent the change in industrial structure. City size (CZ): Population density was selected as the measurement index of city size considering two significant characteristics of large differences in urban areas and significant differences in population size. Land transfer price (LTP): This indicator reflects the cost of real-estate land development. It is calculated based on the amount of land concessions and the area of land concessions in each city in the current year and is taken in logarithmic form. Per capita disposable income of urban residents (INC): This variable measures the impact of urban residents’ income on real estate prices from the perspective of demand and reflects residents’ purchasing ability in logarithmic form. Credit scale (CS): Credit means can directly regulate the demand and supply of the real estate market [57]. It is usually measured by the ratio of year-end loans of financial institutions in cities to the GDP of the year.
2.3. Data Source and Processing
2.3.1. Data Source
This study selected the panel data of 41 prefecture-level cities in the Yangtze River Delta region from 2006 to 2018 obtained from the China City Statistical Yearbook, the China City Construction Statistical Yearbook, and the CEIC database. Missing data for some years were supplemented using the moving average method. To eliminate inflation, the consumer price index of each province is deflated based on the base period, as 2006 data are used so that all value variables can be provided appropriately. Additionally, GDP and output values of each industry are processed by the GDP deflator.
2.3.2. Improved Entropy Method
The entropy method is a multi-objective comprehensive evaluation method that assigns weights according to degree of information of each evaluation index, with the characteristics of objectivity in assigning weights and preserving data integrity [48]. Considering temporal changes in each index, the improved entropy value method [58] was used to measure the infrastructure development level of 41 cities in the Yangtze River Delta region from 2006 to 2018. The calculation steps of the entropy method are as follows:
- (1)
- Set r as years, n as cities and m as indicators, and is the j-th index value of city i in the t year.
- (2)
- Index standardization processing: All indexes need to be standardized science different indexes have different dimensions and units.
(i) Positive indicators standardization:
(ii) Negative indicators standardization:
(iii) Index weight determination:
(iv) Calculate the j-th index entropy:
(v) Calculate the information utility value of j-th index:
(vi) Calculate the weight of each index:
(vii) Calculate the comprehensive score of infrastructure development level per city:
2.3.3. Spatial Correlation Test
The first law of geography, proposed by American geographer Waldo R. Tobler, proposes that the closer the distance, the stronger the spatial autocorrelation of things [59]. Hence, this dissertation applies the global Moran’s I and local Moran’s I to measure the spatial autocorrelation of real estate prices and the urban infrastructure development levels of urban agglomeration.
The global Moran’s I measures the existence of a significant spatial autocorrelation of variables. The calculation formula is as follows:
Here, represents the observed value of city i, and denotes the i-line and j-column elements of , which is the n-th spatial weight matrix. The value range of Moran’s I was [−1,1]. When the value is greater than 0, a positive spatial correlation is found. When the value is less than 0, a negative spatial correlation is found. When the value is 0, no spatial correlation of individuals can be found.
The local Moran’s I is mainly used to measure characteristics of individual spatial agglomeration distributions. Hence, the calculation formula is as follows:
Here, and represent the observed values for regions i and j, respectively.
2.3.4. Construction of Spatial Weight Matrices
Owing to the importance of constructing the appropriate spatial matrix of the spatial panel model to ensure the accuracy of the empirical results, this study constructs adjacency, geographic, and nested matrices of geographical and economic relations among cities in urban agglomerations for empirical analysis.
Adjacency matrix. The adjacency matrix is a type of 0–1 matrix. With the hypothesis that the spatial autocorrelation of real estate prices exists only in geographically adjacent cities, the value is 1 if two cities have a common boundary; otherwise, the value is 0.
Geographical matrix. The closer the geographical distance between cities, the more frequent the circulation of industrial elements in two cities and the deeper the mutual influence of the real estate market. Therefore, the distance between cities is calculated using urban longitude and latitude, and an inverse geographical matrix is constructed by taking the square of its reciprocal. It can be expressed as follows:
is the city distance calculated using latitude and longitude compiled by the National Geographic Information Network.
Nested matrix. Real estate prices are closely related to the level of urban economic development, and real estate prices of cities with the same economic level tend to be similar owing to the gradual improvement in urban transportation infrastructure and the expansion of inter-regional trade. Consequently, considering the dual factors of economy and geography, a nested matrix is established, which can be defined as follows:
diag(…) denotes the diagonal matrix. is the distance inverse matrix. is the starting time of the computation period. denotes the deflated real GDP per capita of city i in period t, and is the real GDP per capita of all the cities in the study period.
2.4. Data Model
2.4.1. Spatial Panel Model
Considering the geographic proximity between cities and the integration of regional economic development, there is a close spatial correlation of urban real estate prices, and the closer the geographic distance between cities, the stronger the correlation [60]. Ignoring spatial characteristics will produce errors in the regression results. This paper chooses a spatial panel model to analyze this issue empirically. The model is set as follows.
represents the real estate price of each region at the time of T. represents the real estate price of each region in the lag phase. represents the weight matrix of n-dimensional space. represents the explanatory variable. α is the constant term. θ is the regression coefficient of the lagging housing price in the first stage. ρ is the spatial lag coefficient. and are the regression coefficients of the spatial effect of the explanatory variable and explanatory variable respectively. μ is the individual fixed effect. , represents the unit n-order matrix.
2.4.2. Spatial Total Effect Decomposition
James and Robert [61] proposed that the regression coefficients for estimating spillover effects in the spatial Durbin model are systematically biased when the coefficient of the spatial lag term of the dependent variable is significantly non-zero. Thus, partial differentiation of the dependent variable is carried out to decompose the total effect into direct effect and indirect effect. The direct effect represents the average influence of the control variable on the city, while the indirect effect represents the influence of the control variable on other surrounding cities, so as to obtain:
The elements on the main diagonal of the matrix mean the direct effect, and the sum of each row and column of the non-diagonal elements refer to the indirect effect. represents the unit n-order matrix.
3. Results
3.1. Spatial-Temporal Evolution of Urban Infrastructure Development in the Yangtze River Delta
This study uses Arcgis10.2 software to classify urban infrastructure development into four levels according to the natural breakpoint clustering method: low, medium-low, medium-high, and high. Figure 1 shows spatial distribution of the level of urban infrastructure development in the Yangtze River Delta region in 2006, 2012, and 2018.
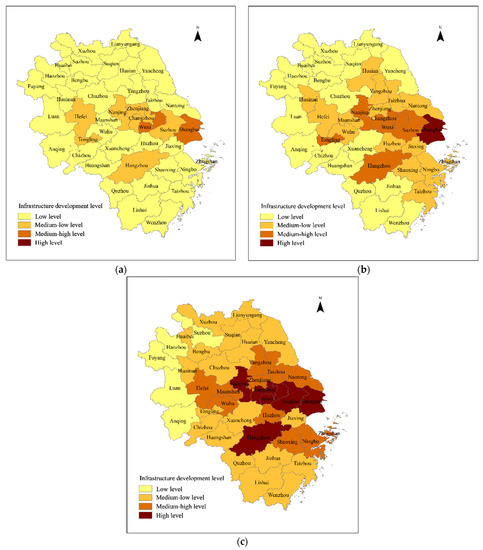
Figure 1.
Distribution map of infrastructure development level in Yangtze River Delta region in (a) 2006, (b) 2012, and (c) 2018.
Overall, urban infrastructure development in the Yangtze River Delta region exhibits an increasing trend, and the distribution structure has changed significantly. The comprehensive infrastructure level in the Yangtze River Delta city cluster increased from 0.154 in 2006 to 0.335 in 2018, with an annual growth rate of 6.20%. From 2006 to 2018, the number of cities with low levels of infrastructure development gradually decreased. Conversely, the number of cities with medium-high levels and high levels gradually increased. In 2006, 32 cities had low infrastructure levels, and this dropped to 19 in 2012 and continued to fall to five. In contrast, the number of cities with medium-high and high levels of infrastructure increased from two (Shanghai and Wuxi) in 2006 to seven (Shanghai, Nanjing, Wuxi, Suzhou, Changzhou, Hangzhou, and Tongling) in 2012 and reached 17 in 2018, accounting for 41.46%. Furthermore, the distribution structure of urban infrastructure in the Yangtze River Delta region has changed significantly. In 2006, most cities had a low level of infrastructure development. The number of cities at low, medium, and high levels declined in that order, showing a “pyramid” structure. In 2018, 46.34% of the cities were at medium-low levels, whereas the percentage of cities at high and low levels was 14.63% and 12.19%, respectively, presenting an overall “olive-shaped” structure. Although the infrastructure development level of the urban agglomerations in the Yangtze River Delta has significantly improved, the overall level remains low. In 2018, the comprehensive average was only 0.335, which is at a medium-low level; hence, overall development needs to be further improved.
At the regional level, there are differences in the development of infrastructure in the Yangtze River Delta region, showing a spatial distribution pattern of high in the east and low in the centre. Cities with medium-high and high levels of infrastructure were mostly in the eastern region (Shanghai, Jiangsu Province, Zhejiang Province). Conversely, cities with low levels were mostly in the central region (Anhui Province). In 2006–2018, the growth rate of infrastructure development in eastern cities was higher than that in the central region. On the one hand, five cities in the central region (Lu’an, Anqing, Fuyang, Maozhou, and Suzhou) have maintained a low level of development, and only two cities, Maanshan and Wuhu, have improved their infrastructure from a low level by two levels to medium-high levels. On the other hand, 11 eastern cities, accounting for 42.31% of all eastern cities, improved their infrastructure development level by two grades. The top five cities in infrastructure development level in 2018 were Wuxi, Shanghai, Nanjing, Changzhou, and Hangzhou, which are all in the eastern region. The findings demonstrate a pattern of infrastructure development level decreasing from the east to the center in the Yangtze River Delta region.
3.2. Spatial Autocorrelation Test
3.2.1. Global Spatial Autocorrelation Test
The global Moran’s I of real estate prices and infrastructure development levels of the 41 prefectures in the Yangtze River Delta region were calculated using Stata 15.0 software. Table 2 presents the results. The Moran’s I of real estate prices in all years was greater than zero in the three spatial weight matrices. This indicates that a significant positive spatial correlation was found among each prefecture’s housing prices. According to the Moran value for each year, overall regional real estate price autocorrelation presents a trend of decreasing and then increasing, with a “U-shaped” distribution, and the lowest value is in 2011. Additionally, the global Moran’s I of urban real estate price is the largest in the adjacency matrix and is followed by the geographical matrix. This indicates that the closer the geographical location of cities, the stronger the degree of mutual influence of real estate markets among cities. The global Moran’s I of the urban infrastructure development level is not only significantly greater than 0 in the three spatial weight matrices but also shows an increasing trend. This indicates that the spatial autocorrelation of each city’s infrastructure development level has gradually increased since the state has increased its investment in urban infrastructure.

Table 2.
The global Moran’s I of real estate price and infrastructure development level in different weight matrices.
3.2.2. Local Spatial Autocorrelation Tests
Figure 2 shows the Moran scatter plot of the real estate prices and infrastructure development levels of prefecture-level cities in the Yangtze River Delta region in 2018 in the adjacency matrix. Cities were mainly distributed in the first and third quadrants. High-priced cities, which are mainly 16 eastern cities (e.g., Shanghai, Hangzhou, and Suzhou clusters) in the first quadrant are called H-H type areas. Similarly, there are five cities, including Nantong and Taizhou, in the second quadrant, which is known as the H-L type area. The third quadrant is an L-L type area, indicating the clustering of low-price cities and low-price cities, including Huaibei, Wuhu, Yancheng, and 17 other cities, which are mainly concentrated in the central region. The fourth quadrant is the L-H type area, representing the clustering of low- and high-priced cities, including Yangzhou, Nanjing, and Hefei. Moreover, urban real estate price has heterogeneity distribution in regional space. Distribution of the infrastructure development level is similar to that of real estate prices, which are mainly concentrated in H-H and L-L type areas. There were 14 cities in the H-H type region (mainly in the eastern region, four cities in Zhejiang, and eight cities in Jiangsu), 18 cities in the L-L type (mainly in the central region, 11 cities in Anhui, and three cities in the northern region of Jiangsu), five cities in the H-L type (Xuancheng, Chuzhou, Quzhou, Yancheng, and Jiaxing), and four cities in the L-H type (Hefei, Wuhu, Hangzhou, and Tongling). The results were indicative of not only significant spatial autocorrelation between real estate price and infrastructure development level of prefecture-level cities but also obvious differences in spatial location distribution in the Yangtze River Delta urban agglomeration. Results show that there is not only significant spatial autocorrelation, but also differences in spatial location distribution between real estate price and infrastructure development level of prefecture-level cities in the Yangtze River Delta urban agglomeration. Therefore, spatial factors must be considered when studying the relationship between urban infrastructure development level and urban real estate prices.
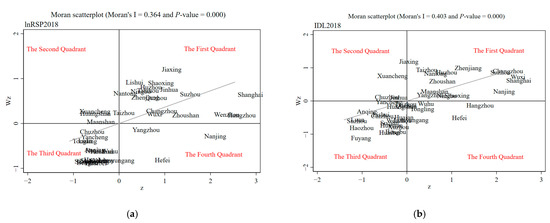
Figure 2.
Moran scatter plot of real estate prices and infrastructure development level in the adjacency matrix in 2018. (a) Real estate price; (b) Infrastructure development level.
3.3. Spatial Effect Test
To evaluate the applicability of the spatial panel model, we conducted the following tests: Lagrange multiplier (LM), robust Lagrange multiplier (Robust LM), and likelihood ratio (LR). Table 3 lists the test results. The results suggest that the Lagrange multiplier-error, Lagrange multiplier-lag, and robust Lagrange multiplier test statistics are all significant at the 1% level. The likelihood ratio test results all reject the original hypothesis at the 1% significance level. This confirms that the spatial panel model is appropriate. Moreover, the Hausman test was used to determine the type of fixed effects. This is because as the number of individuals in the panel data is larger than that of the time periods. Considering the development level disparity of each city within the urban cluster, choosing the individual fixed effects became the final decision.

Table 3.
Model Selection Test Results.
3.4. Analysis of the Model Regression Effect
This study builds an individual fixed spatial panel model to analyze the driving effect of infrastructure development on real estate price increases in the Yangtze River Delta region. Table 4 shows this according to the comparison and analysis of panel data model and difference generalized method of moments (GMM).

Table 4.
Model regression results.
Table 4 presents the following conclusions:
- (1)
- The first column is individual fixed-effect regression and the second column is the difference GMM method that considers dynamic characteristics of real estate prices. No significant difference was found between regression results in the two methods, which indicates that overall regression results qualified. Urban infrastructure development can significantly promote an increase in real estate prices. Among controlled variables, real estate price in the lagging phase has a significant impact on the current housing price. Considering the regression result of difference GMM method as an example, housing prices increase by 1% in the previous period and by 0.407% in the current period.
- (2)
- From regression results of the spatial panel model, the spatial autoregressive coefficients in the adjacency, geographic, and nested matrices are all significant. This confirms that real estate prices within urban agglomerations have evident spatial spillover effects. Additionally, the autocorrelation coefficient in the nested matrix model with the introduction of economic factors was the largest, at 0.530, followed by the geographical matrix. Moreover, the regression coefficient of the adjacency matrix is the smallest. The degree to which real estate prices among cities influence each other will be deeper if geographical and economic factors are fully considered. The close exchange of economic activities among cities with close geographical distance will drive the speed of capital circulation and increase industrial transaction frequency. When coactivity of the real estate market in close areas is enhanced, housing prices of the surrounding cities will promote significant fluctuations in housing prices in the city.
- (3)
- Regression results between the panel data and the spatial panel models contain several differences. By comparing the regression results of the fixed effect and spatial panel models in the geographical matrix, the regression coefficient of the urban infrastructure development level decreased from 0.641 to 0.612, and other variables also decreased to different degrees. Moreover, the panel data model does not consider the spatial spillover of variables, which includes the influence of explanatory variables in the surrounding areas on local housing prices.
- (4)
- When the lag term of the variables was included in the regression equation of the spatial econometric model, the model’s regression coefficient did not accurately reflect the influence of controlled variables on dependent variables. Despite this, correlations can be drawn between urban infrastructure development and housing prices. In both the geographical and nested matrices, the regression coefficients of the infrastructure development level are significantly positive, which indicates that urban infrastructure development can significantly promote the increase of local real estate prices, considering the geographical distance and spatial attributes of economic exchange among cities.
3.5. Direct Effects and Indirect Effects
The spatial lag term of real estate price in the model is significantly non-zero. Therefore, the spatial spillover effect makes the coefficients of each controlled variable unable to fully explain the effects on real estate price fluctuations. Consequently, total spatial effects must be decomposed into direct and indirect effects. Table 5 presents the direct, indirect, and gross effects of each variable in different weight matrices.

Table 5.
Direct and indirect effects in different matrices.
3.5.1. The Analysis of Direct Effects
In direct effects, influence coefficients of urban infrastructure development on real estate prices in the three different weight matrices are all significantly positive at 0.552, 0.635, and 0.616, respectively. This indicates that urban infrastructure construction can raise real estate prices. The direct effect of urban infrastructure development on real estate prices is largest in the geographic matrix, followed by nested weight, and the adjacency weight matrix is smallest. This indicates that the closer the urban space, the stronger the promotion effect owing to infrastructure construction. The reason why direct effects of infrastructure development in different weight matrices (0.552, 0.635, 0.616) are higher than the regression coefficients (0.521, 0.612, 0.596) is the “feedback effects” of direct effects. Essentially, the impact of urban infrastructure development on real estate prices of neighboring cities feeds back the real estate prices of the city [62].
Among the control variables, the direct effects of city size, land transfer price, and credit scale on housing price increases are significantly positive in the three weight matrices. City size has the greatest impact on real estate prices. And city size expansion means that the population has risen sharply. The new population consists of newborns under the two-child policy and net population influx from surrounding backward areas. The large influx of labor has brought a demographic dividend to urban development. Growth in the labour force has changed the age composition of the urban population, reduced the dependency ratio of the urban elderly, and increased the housing demand in the region. Land transfer price is directly related to real estate development cost, and the increase in land price is transferred to real estate price through the cost mechanism. An increase in credit scale can affect the real estate price from the both supply and demand sides. Moreover, real estate developers get more bank loans, but land auction costs are rising under limitations in land supply. Second, consumers can obtain more housing loans with the expansion of bank credit. However, a short-term increase in housing demand eventually leads to imbalance between housing supply and demand and a rise in real estate prices in the region. Additionally, the direct effect of the industrial structure of real estate prices is significant in the nested matrix, indicating that industrial structure changes from the aspect of the economic effect of the real estate market. Because of the transformation of the industrial structure from a secondary industry to a tertiary one, productive forces have been liberated. Regional competitiveness has greatly improved owing to industrial agglomeration and economic growth. This means that many migrants come to work here, increasing the demand for urban housing.
3.5.2. The Analysis of Indirect Effects
In indirect effects, spillover effects of urban infrastructure on real estate prices are significantly positive in three spatial weight matrices. Hence, the rapid construction of urban infrastructure can promote the increase of real estate prices in other regions when considering the spatial correlation of urban geography, economy, and other factors. Constructing transportation and communication infrastructure reduces transaction costs and makes the information flow more complete among cities. The diffusion effect owing to improvement in infrastructure in central cities enables surrounding areas to acquire a large amount of technology and knowledge from the central area. This stimulates economic development of the surrounding areas and improves the vitality of the real estate market in the surrounding areas [63,64].
Among other controlled variables, the city size has the most significant effect on the housing prices in surrounding areas in three spatial weight matrices. With continuous expansion, the central city’s congestion costs will continue to increase. The diffusion effect will promote the flow of industries, funds and other production factors to surrounding cities. This will further stimulate the economies of surrounding cities and activate the housing market in surrounding areas. The indirect effects of land transfer price on housing prices are significantly positive. Rising housing prices in the city will prompt buyers and investors to choose houses in surrounding cities. Meanwhile, real estate developers will intensify the development of the real estate market in the surrounding areas to reduce costs, resulting in rising real estate prices in the surrounding cities. The indirect effects of industrial structure on real estate prices are significantly positive in geographic and nested matrices. The frequent exchange of industrial activities in closed cities promotes the spillover of knowledge, technology, population, and other factors, affecting the economic development of surrounding areas and the vitality of the housing market. Additionally, the indirect effects of per capita disposable income on real estate prices were significantly negative. The higher disposable income of residents indicates the higher happiness of local urban life, which will encourage the population from the surrounding areas to flood into the region, reduce housing demand in surrounding cities, and restrain the rise of real estate prices in surrounding areas.
3.6. Analysis of Regional Heterogeneity
The Yangtze River Delta region is undergoing unbalanced development. The economic development of eastern regions (e.g., Jiangsu, Zhejiang, and Shanghai) is rapid. Conversely, those of central regions (e.g., Anhui) is slow. From 2006 to 2018, the average selling price of real estate was 6408.680 yuan per square meter in the eastern region and 3417.210 yuan per square meter in the central region. Compared with the development index of infrastructure of 0.182 in the central part, 0.276 in the eastern part is obviously higher, according to the entropy method. Therefore, including geographical differences when exploring the spatial effect of infrastructure development on real estate prices is necessary. Moreover, Table 6 presents the regression results for cities in the eastern and central parts of the Yangtze River Delta in three spatial weight matrices.

Table 6.
Regression results of regional heterogeneity.
Table 6 highlights the following conclusions:
- (1)
- In the eastern region, spatial autoregressive coefficients of urban real estate prices are not significant except for the adjacency matrix. In the central region, spatial autoregressive coefficients of the three matrices were significant. In nested matrix, the spatial autoregression coefficient reached its maximum (0.350). This is because spatial distance between cities in the east is relatively greater and housing prices of some cities are too high owing to urban policies. For example, the correlation of the urban real estate market is weak owing to the higher housing price of Wenzhou in Zhejiang Province compared with surrounding cities. Similarly, central region cities, which are geographically closer, belong to the same province. Hence, their real estate market regulation policies are highly consistent, resulting in stronger mutual influence among real estate prices.
- (2)
- The direct and indirect effects of urban infrastructure development on real estate prices in eastern China are significantly positive. The degree of impact is higher than that of the entire Yangtze River Delta’s urban agglomeration. However, this effect is not significant in Central China. The amount of infrastructure investment in eastern China increased, and infrastructure development was rapid from 2006 to 2018, which had a strong driving effect on real estate prices. However, the level of economic development in the central region is low. Low investment in infrastructure leads to slow development, which has little impact on housing prices.
- (3)
- In addition to urban infrastructure, land transfer price, industrial structure, credit scale, and other factors also have a considerable influence on eastern China’s real estate market. Fluctuations in the real estate market in central China mainly depend on the land market. Jiangsu, Zhejiang, and Shanghai, as economic development centers, have gradually transformed their industrial structures into secondary and tertiary industries. Hence, China’s financial market is more developed, and various factors adjust the real estate market. Anhui Province, an important grain-producing area in China, is more inclined to develop industrial structures for agriculture. The local government’s land revenue from finance is so large that the land transfer price has a significant impact on the local real estate market.
4. Discussion
The comprehensive infrastructure development level in the eastern part of the Yangtze River Delta urban agglomeration is higher than that in the central part, according to the spatiotemporal evolution characteristics of infrastructure development. The degree of infrastructure development is closely related to the seriousness of local governments and the environment they face. The infrastructure of eastern provinces is expanding because they consider infrastructure construction as the focus of industrial structure transformation, in addition to upgrading and extensively invest in key projects (e.g., transportation, electric power, communication, water conservancy, and environmental protection). Meanwhile, the central region has issued the “central rise plan”, which has brought new development opportunities to infrastructure construction in the central region. Anhui Province, an important grain production base with low infrastructure stock in China, takes agricultural development as the core of economic development and has great development potential.
The spatial effect test results exhibit a significant spatial autocorrelation in the Yangtze River Delta urban agglomeration real estate market. Previous studies have demonstrated that population migration, spatial arbitrage, and buyers’ psychological expectations are all key factors influencing real estate price correlation among cities [65,66]. When obvious differences in urban real estate prices can be found, some residents will migrate to cities with lower housing prices owing to cost pressure, spatial arbitrage, and other factors. Therefore, cities with low housing prices will have a higher housing demand, while cities with high housing prices will have lower housing demand owing to massive population loss. For regional markets with adjacent geographical locations and integrated economic development, the improvement of infrastructure reduces obstacles to the flow of population, information, and other factors within the urban agglomeration and strengthens the spatial relevance of the real estate market.
Using the spatial panel model to further explore the spatial effect of infrastructure development on real estate prices, we found that there is consistency with previous studies that urban infrastructure construction can significantly affect real estate prices and that this effect is influenced by geographical location. Guo and Su [67] found that the attraction of regional real estate has greatly improved because infrastructure construction improves the accessibility of cities and promotes urban industry development, which increases investors’ willingness to buy commercial housing and speculative demand. Moreover, infrastructure construction can enable real estate developers to reduce housing supply through higher land sales prices and more commercial housing development costs. An imbalance between supply and demand structures in the real estate market leads to an increase in real estate prices in urban agglomerations. Moreover, these studies ignored the autocorrelation of urban spaces. Comparing regression results of the general and spatial panel models, we find that the spatial panel model can accurately measure the impact of infrastructure on real estate prices. This impact would be overestimated if urban spatial correlation was excluded.
On one hand, the abandoned railway is transformed, appropriately enough, into high-speed rail or other rail transit to improve city accessibility and the density of the urban road network [68]. On the other hand, transformation from abandoned railway to non motorized traffic (e.g., greenways and railway footpaths related to business, leisure and tourism) is appropriate [69,70]. Abandoned industrial land has good infrastructure and geographical advantages for historical reasons, and is suitable to be transformed into residential areas, green spaces and urban parks. Location advantages will attract more businesses to settle in and realize industrial transformation and upgrading. Plant demolition and redevelopment may lead to reinvestment of regional capital, social upgrading of high-level regional groups and landscape changes, whereas capital investment and the physical changes of surrounding landscape environment and the sales price of redeveloped houses will rise substantially. The brownfield infrastructure redevelopment has promoted urban infrastructure. Superior subways, green spaces, parks and other infrastructure have led to increased populations and boosted property values [71]. Additionally, the redevelopment of brownfield infrastructure can significantly improve land use efficiency, reduce industrial and mining storage land, and increase construction land supply. Extra residential land supply provides a guarantee for urban expansion and population growth.
The transformation and operation of brownfield infrastructure requires multiple urban participation entities. Public private partnerships are common to urban brownfield infrastructure reuse operations [72]. Government departments entrust the private sector (e.g., real estate developers) to design, build, finance and operate urban development projects. The franchising mode is widely used in Brownfield infrastructure redevelopment projects, including design-build-finance-maintain (DBFM), design-build-finance (DBF), build-operate-transfer (BOT), and other modes. Since land and residential projects are developed by the private sector, the risk and income are also borne by real estate developers. Thanks to good infrastructure conditions, developers can save some infrastructure construction costs. However, real estate developers should face many risks in Brownfield redevelopment. Due to the lack of historical data, the Brownfield pollution degree is difficult to determine. Governance funds demand is high, and the “stigma” of Brownfield will also harm the bank loan amount and consumer confidence. These risks pose great challenges to the Brownfield redevelopment of public-private partnerships. Burinskiene et al. [73] regard environment, society, economy and urban strategy as the most important factors for Brownfield redevelopment. Technical facilities development, sound urban and environmental policies, and good public-private partnerships and standardized approval mechanisms are the key to Brownfield redevelopment [74].
This study not only measures comprehensive development levels of infrastructure for urban agglomeration in the Yangtze River Delta from five dimensions—transportation, water supply and drainage, energy, communication, and environmental protection—but also highlights the spatial effect of the comprehensive development level of infrastructure on real estate prices. In addition to the above infrastructure, the service quality of public facilities (e.g., schools and hospitals) also affects real estate prices. Therefore, studies on the impact of the service quality of social infrastructure, including schools and hospitals on real estate prices, are increasingly needed.
5. Conclusions
Based on data of 41 prefecture-level cities in the Yangtze River Delta region from 2006 to 2018, this study established an evaluation index system of the infrastructure development level and calculated the comprehensive infrastructure development level of each prefecture-level city in the Yangtze River Delta region. Hence, three spatial weight matrices were constructed based on geographical and economic dimensions, and the spatial panel model was used to analyze the spatial effect of urban infrastructure development on real estate prices.
First, the overall infrastructure development level in the Yangtze River Delta region is rising, and significant regional heterogeneity, evidenced by a spatial distribution pattern of high in the east and low in the centre, can be found. In 2006, the development level of infrastructure in the Yangtze River Delta exhibited a pyramid structure, and most of the urban infrastructure was at a low level. In 2018, the level of infrastructure development in the Yangtze River Delta region presented an “olive-shaped” structure, with most cities’ infrastructure at medium-low levels.
Second, spatial autocorrelation is exhibited in the real estate prices and urban infrastructure development levels in the Yangtze River Delta urban agglomeration. During the study period, the Moran’s I value of real estate price exhibited a U-shaped development trend, while the Moran’s I value of the urban infrastructure development level increased yearly. This shows that the spatial autocorrelation of real estate prices in the Yangtze River Delta region first decreases and then increases, while the regional association of infrastructure development level gradually strengthens. Most cities in the H-H cluster are located in the eastern region; conversely, most cities in the L-L cluster are located in the central region.
Third, regression results of both the panel and spatial panel models verify that urban infrastructure construction can positively promote real estate price increases. If the spatial effect is not considered, the driving effect of urban infrastructure development on real estate prices will be overestimated, which is a result of the regression result of the panel data model including the spatial effect brought by the development of adjacent urban infrastructure.
Fourth, after further calculations of the direct and indirect spatial effects of urban infrastructure development on the real estate price, both the significant and direct effects are higher than the overall regression coefficient. The above results show that urban infrastructure development can not only directly affect local real estate market demand but also increase real estate prices in adjacent areas through the diffusion effect and affect the local real estate market again through the feedback effect.
Fifth, the direct and indirect effects of city size on real estate prices are the largest in the three spatial weight matrices. Urban scale enlargement means the agglomeration of the urban population. The demographic dividend directly increases the demand for urban housing. Population aggregation has brought a significant amount of labor to urban economic development and increased economic volume. The diffusion effect of the scale economy will also drive the economic development of surrounding areas and thus boost the housing market in the surrounding areas.
This study’s research results have reference value for the coordinated development of urban infrastructure and reasonable control of the real estate market in the Yangtze River Delta region. Considering the current development situation of infrastructure in the Yangtze River Delta region, we provide the following three suggestions.
First, the infrastructure in the Yangtze River Delta region is characterized by a low level of development and obvious regional differences. Therefore, to achieve high-quality infrastructure development, enhancing infrastructure investment in cities and accelerating weak infrastructure construction is necessary. The first key is to attract social private capital by expanding financing channels and the infrastructure market scale in cities with low-level regional infrastructure. The next step is strengthening the maintenance of existing infrastructure and planning construction cycles of various infrastructure reasonably instead of building some kind of infrastructure with high capital stock repeatedly in developed areas.
Second, the vigorous development of infrastructure is an important factor driving rising housing prices in the Yangtze River Delta region. Therefore, the driving effect of infrastructure construction on housing prices should be considered in real estate price regulations to implement city-specific policies. For the areas with poor infrastructure development, efforts should be made to build infrastructure with low stock and high demand to improve the life satisfaction of residents. Meanwhile, paying attention to the imbalance of supply and demand structures in the market caused by the rapid rise in housing prices leads to a large number of speculative behaviors and real estate market bubbles. In areas with a high level of infrastructure development, regulations and controls should focus on the transfer of residential land and bank credit. In particular, adjusting the structure of government fiscal revenue and restraining the flood of land finance to avoid a large amount of capital flooding the real estate investment market is essential.
Third, the real estate market in the Yangtze River Delta region has significant spatial linkage and heterogeneity. Hence, constructing a regional coordination and control mechanism for the real estate market from the macro level of urban agglomeration in the process of housing price regulation is necessary. Simultaneously, attention should be paid to the differential regulation of real estate prices. Excessive differences in real estate prices in urban agglomerations will lead to spatial arbitrage, which will spread virality with the spatial linkage of the housing market. Moreover, excessive price differences can stimulate a herd mentality in residents and further strengthen the imbalance of supply and demand structures in the whole market, making the real estate market unhealthy.
Author Contributions
Conceptualization, H.C. and N.Z.; methodology, Y.Z. and H.D.; software, Y.Z.; data curation, Y.Z. and N.Z.; writing—original draft preparation, H.C.; writing—review and editing, Y.Z.; supervision, H.C. and M.Z.; funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China Youth Science Foundation project, funder: Man Zhou, grant number: 51808559.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The case analysis data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Wang, S.J.; Wang, J.Y.; Wang, Y. Effect of land prices on the spatial differentiation of housing prices: Evidence from cross-county analyses in China. J. Geogr. Sci. 2018, 28, 725–740. [Google Scholar] [CrossRef] [Green Version]
- Nam, S.J. An Empirical Analysis on Determining Factors of Housing Prices in China. China Sinol. 2018, 33, 23–47. [Google Scholar]
- He, X.; Cai, X.J.; Hamori, S. Bank Credit and Housing Prices in China: Evidence from a TVP-VAR Model with Stochastic Volatility. J. Risk Financ. Manag. 2018, 11, 90. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.R.; Hui, E.C.M.; Sun, J.X. Population Aging, Mobility, and Real Estate Price: Evidence from Cities in China. Sustainability 2018, 10, 3140. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.; Ren, H.; Xiang, W.; Wu, K.; Cai, W. Nonlinear Influence of Public Services on Urban Housing Prices: A Case Study of China. Land 2021, 10, 1007. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Song, Y.; Wen, H.Z. Spatial Spillover of House Prices: An Empirical Study of the Yangtze Delta Urban Agglomeration in China. Sustainability 2019, 11, 544. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Rehm, M. Housing prices and speculation dynamics: A study of Auckland housing market. J. Prop. Res. 2021, 38, 286–384. [Google Scholar] [CrossRef]
- Liu, F.; Min, M.; Zhao, K.; Hu, W.Y. Spatial-Temporal Variation in the Impacts of Urban Infrastructure on Housing Prices in Wuhan, China. Sustainability 2020, 12, 1281. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.C.; Sun, P.Y. China’ s Infrastructure Development’ s Impact on China’ s Urbanization Process. China Popul. Resour. Environ. 2010, 20, 121–125. [Google Scholar]
- Kong, J.J.; Simonovic, S.P.; Zhang, C. Resilience Assessment of Interdependent Infrastructure Systems: A Case Study Based on Different Response Strategies. Sustainability 2019, 11, 6552. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.J.; Jiang, S.H. National Level Infrastructure Condition Assessment: Principles and Metrics. Appl. Mech. Mater. 2011, 71–78, 1622–1627. [Google Scholar]
- Xiang, Y.H.; Li, C.Y.; Li, P.C.; Zhang, T.T. The Infrastructure Security Evaluation of China’s Big Cities. Environ. Technol. Resour. Util. II 2014, 675–677, 1257–1261. [Google Scholar]
- Xu, Q.S.; Shi, J.G.; Zhang, Y.G. Evaluation on the Development of Shanghai Suburban Infrastructure Based on AHP-Entropy Method. Adv. Mater. Res. 2014, 919–921, 1451–1456. [Google Scholar]
- He, X.H.; Cao, Z.C.; Zhang, S.L.; Liang, S.M.; Zhang, Y.Y.; Ji, T.B.; Shi, Q. Coordination Investigation of the Economic, Social and Environmental Benefits of Urban Public Transport Infrastructure in 13 Cities, Jiangsu Province, China. Int. J. Environ. Res. Public Health 2020, 17, 6809. [Google Scholar] [CrossRef] [PubMed]
- Belke, A.; Keil, J. Fundamental Determinants of Real Estate Prices: A Panel Study of German Regions. Int. Adv. Econ. Res. 2018, 24, 25–45. [Google Scholar] [CrossRef] [Green Version]
- Abidoye, R.B.; Fam, F.; Oshodi, O.S.; Oyetunji, A.K. Impact of light rail line on residential property values–A case of Sydney, Australia. Int. J. Hous. Mark. Anal. 2021, 15, 691–708. [Google Scholar] [CrossRef]
- Stover, M.E. The Role of Infrastructure in The Supply of Housing. J. Reg. Sci. 1987, 27, 255–267. [Google Scholar] [CrossRef]
- Weisbrod, G.; Ben-Akiva, M.; Lerman, S. Tradeoffs in residential location decisions: Transportation versus other factors. Transp. Policy Decis.-Mak. 1997, 1, 55–145. [Google Scholar]
- Suen, I.S. Residential Development Pattern and Intraneighborhood Infrastructure Provision. J. Urban Plan. Dev. 2005, 131, 1–9. [Google Scholar] [CrossRef]
- Liang, J.; Koo, K.M.; Lee, C.L. Transportation infrastructure improvement and real estate value: Impact of level crossing removal project on housing prices. Transportatiom 2021, 48, 2969–3011. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, X.; Hang, J.; Yao, D.; Shi, G. Do Urban Rail Transit Facilities Affect Housing Prices? Evidence from China. Sustainability 2016, 8, 380. [Google Scholar]
- Yang, L.; Chau, K.W.; Szeto, W.Y.; Cui, X.; Wang, X. Accessibility to transit, by transit, and property prices: Spatially varying relationships. Transp. Res. Part D Transp. Environ. 2020, 85, 102387. [Google Scholar] [CrossRef]
- Zhang, D.; Jiao, J. How Does Urban Rail Transit Influence Residential Property Values? Evidence from An Emerging Chinese Megacity. Sustainability 2019, 11, 534. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Li, W.D.; Lownes, N.; Zhang, C.R. Estimating the Impacts of Proximity to Public Transportation on Residential Property Values: An Empirical Analysis for Hartford and Stamford Areas, Connecticut. Int. J. Geo-Inf. 2021, 10, 44. [Google Scholar] [CrossRef]
- Szczepanska, A.; Senetra, A.; Wasilewicz-Pszczolkowska, M. The Influence of Traffic Noise on Apartment Prices on the Example of a European Urban Agglomeration. Sustainability 2020, 12, 801. [Google Scholar] [CrossRef] [Green Version]
- Riccioli, F.; Fratini, R.; Boncinelli, F. The Impacts in Real Estate of Landscape Values: Evidence from Tuscany (Italy). Sustainability 2021, 13, 2236. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. Impacts of urban environmental elements on residential housing prices in Guangzhou (China). Landsc. Urban Plan. 2006, 78, 422–434. [Google Scholar] [CrossRef]
- Wu, C.; Ye, X.Y.; Du, Q.Y.; Luo, P. Spatial effects of accessibility to parks on housing prices in Shenzhen, China. Habitat Int. 2017, 63, 45–54. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Dong, R.C. Impacts of Street-Visible Greenery on Housing Prices: Evidence from a Hedonic Price Model and a Massive Street View Image Dataset in Beijing. Int. J. Geo-Inf. 2018, 7, 104. [Google Scholar] [CrossRef] [Green Version]
- Sohn, W.; Kim, H.W.; Kim, J.H.; Li, M.H. The capitalized amenity of green infrastructure in single-family housing values: An application of the spatial hedonic pricing method. Urban For. Urban Green. 2020, 49, 126643. [Google Scholar] [CrossRef]
- NRTEE. Cleaning Up the Past, Building the Future: Government of Canada Public Works & Government Services Canada; NRTEE: Ottawa, ON, Canada, 2003.
- Finger, E.M.; Yanar, N. The Elgar Companion to Urban Infrastructure Governance: Innovation, Concepts; Edward Elgar: Cheltenham, UK, 2022. [Google Scholar]
- Bertolini, L.; Spit, T. Cities on Rails. The Redevelopment of Railway Station Areas; E & FN Spon: London, UK; New York, NY, USA, 1998. [Google Scholar]
- Garcia-Mayor, C.; Marti, P.; Castano, M.; Bernabeu-Bautista, A. The unexploited potential of converting rail tracks to greenways: The Spanish Vias Verdes. Sustainbility 2020, 12, 881. [Google Scholar] [CrossRef] [Green Version]
- Degioanni, A.; Ferretti, V. How to support the design and evaluation of redevelopment projects for disused railways? A methodological proposal and key lessons learned. Transp. Res. Part D Transp. Environ. 2017, 52, 29–48. [Google Scholar]
- Davidson, M.; Lees, L. New-build ‘gentrification’ and London’s riverside renaissance. Environ. Plan. 2005, 37, 1165–1190. [Google Scholar] [CrossRef] [Green Version]
- Way, T. Landscapes of industrial excess: A thick sections approach to Gas Works Park. J. Lands. Archit. 2013, 8, 28–39. [Google Scholar] [CrossRef]
- Zhou, Y. The Beauty of The Ruins: An Analysis of The Northern Landscape Park in Duisburg. Archit. Cult. 2017, 3, 179–181. [Google Scholar]
- Bowman, A.; Folkman, P.; Froud, J.; Johal, S.; Law, J.; Leaver, A.; Moran, M.; Williams, K. The Great Train Robbery: Rail Privatisation and After; Centre for Research on Socio-Cultural Change: Manchester, UK, 2013. [Google Scholar]
- Hess, D.B.; Almeida, T.M. Impact of proximity to light rail rapid transit on station-area property values in Buffalo, New York. Urban Stud. 2007, 44, 1041–1068. [Google Scholar] [CrossRef]
- Liang, X.J.; Liu, Y.L.; Qiu, T.Q.; Jing, Y.; Fang, F.G. The effects of locational factors on the housing prices of residential communities: The case of Ningbo, China. Habitat Int. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Lan, F.; Wu, Q.; Zhou, T.; Da, H.L. Spatial Effects of Public Service Facilities Accessibility on Housing Prices: A Case Study of Xi’an, China. Sustainability 2018, 10, 4503. [Google Scholar] [CrossRef] [Green Version]
- Haider, M.; Miller, E.J. Effects of Transportation Infrastructure and Location on Residential Real Estate Values: Application of Spatial Autoregressive Techniques. Transp. Res. Rec. J. Transp. Res. Board 2000, 1722, 1–8. [Google Scholar] [CrossRef]
- Dorantes, L.M.; Paez, A.; Vassallo, J.M. Analysis of house prices to assess economic impacts of new public transport infrastructure: Madrid metro line 12. Transp. Res. Rec. J. Transp. Res. Board 2011, 2245, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Efthymiou, D.; Antoniou, C. How do Transport Infrastructure and Policies Affect House Prices and Rents? Evidence from Athens. Transp. Res. Part A Policy Pract. 2013, 52, 1–22. [Google Scholar] [CrossRef]
- Ouyang, Y.Y.; Chen, L.N.; Ll, Z.J. Infrastructure, urban and rural housing prices, rents: A micro-study based on Bayesian model averaging. Syst. Eng.—Theory Pract. 2020, 40, 2825–2838. [Google Scholar]
- Qin, Q.; Feng, W.B.; Yang, R.; Liang, Z.M. Study on evaluation characteristics of ecological infrastructure in four municipalities directly under the central government of China. Huazhong Shifan Daxue Xuebao 2008, 42, 471–476. [Google Scholar]
- Chen, Y.E.; Sun, Q. A Study on Calculation of Development of China’s Infrastructure and its Influencing Factors—The Empirical Research Based on Provincial Panel Data. Econ. Geogr. 2016, 36, 23–30. [Google Scholar]
- Tian, S.Z.; Sun, Y.G.N.; Zhan, Q.Y. Evaluation of lnfrastructure Development Level Based on Principal Component Analysis—Panel Data from 30 Provinces from 2007 to 2016. J. Chongqing Technol. Bus. Univ. (Nat Sci Ed) 2017, 34, 41–49. [Google Scholar]
- Lu, Y.F.; Zheng, F.H. Comprehensive evaluation on the municipal infrastructure development from the regional integration perspective: An empirical analysis based on the nine cities of the Pearl River Delta Area. Urban Problems 2014, 10, 2–9. [Google Scholar]
- Aycart Luengo, C. Vías verdes: La experiencia española. Proy. Rever. Ing. Territ. 2004, 69, 28–37. [Google Scholar]
- Foster, J. Off Track, In Nature: Constructing Ecology on Old Rail Lines in Paris and New York. Nat. Cult. 2010, 5, 316–337. [Google Scholar] [CrossRef]
- Keil, U.; Heimann, J. Berlins erster Naturerfalrungsraun: Ein Pilotprojekt im Park am Gleisdreieck. Stadt Grun 2012, 61, 39–44. [Google Scholar]
- Fu, Q.C.; Zheng, X.D. Regional Brownfields Regeneration Strategies Driven by the International Building Exhibition in the Ruhr. Chin. Landsc. Archit. 2018, 35, 21–26. [Google Scholar]
- Feng, S.; Hou, W.; Chang, J. Changing Coal Mining Brownfields into Green Infrastructure Based on Ecological Potential. Sustainbility 2019, 11, 2252. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.Y.; Wang, X.Y. The impact of structural adjustment on housing prices in China. Asian-Pac. Econ. Lit. 2018, 32, 108–119. [Google Scholar] [CrossRef]
- Jiang, Y.S.; Zhao, D.; Sanderford, A.; Du, J. Effects of Bank Lending on Urban Housing Prices for Sustainable Development: A Panel Analysis of Chinese Cities. Sustainbility 2018, 10, 642. [Google Scholar] [CrossRef]
- Yang, L.; Sun, Z.C. The Development of Western New-lype Urbanization Level Evaluation Based on Entropy Method. Econ. Probl. 2015, 3, 115–119. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit Region. Econ. Geogr. 1970, 46, 115–146. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, R.; Zhong, C.W. Research on Spatial Spillover Effects and Regional Differences of Urban Housing Price in China. Econ. Comput. Econ. Cyb. 2021, 55, 211–228. [Google Scholar]
- James, L.; Robert, K.P. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, H.; Zhou, S.J. The Analysis of the “Direct Effect” and “Indirect Effect” of Urbanization Affects on Real Estate Prices: Based on the Dynamic Spatial Durbin Model of Prefecture-level Cities. Nankai Econ. Stud. 2017, 2, 3–22. [Google Scholar]
- Lean, H.H.; Smyth, R. Regional House Prices and the Ripple Effect in Malaysia. Urban Stud. 2013, 50, 895–922. [Google Scholar] [CrossRef]
- Meen, G. Regional house prices and the ripple effect: A new interpretation. Hous. Stud. 1999, 14, 733–753. [Google Scholar] [CrossRef]
- Gray, D. District house price movements in England and Wales 1997–2007: An exploratory spatial data analysis approach. Urban Stud. 2012, 49, 1411–1434. [Google Scholar] [CrossRef]
- Chen, M.H.; Wang, S.; Liu, W.F.; Liu, Y.X. Measurement and Analysis of Correlation Effect of Urban Housing Price under the Nonlinear Perspective. China Soft Sci. 2020, 10, 96–106. [Google Scholar]
- Guo, G.L.; Su, X.R. Research on Mediating Effect of Municipal Infrastructure Construction on Housing Price—Based on Empirical Analysis of 35 Big and Medium-sized Chinese Cities. Future Dev. 2015, 39, 54–58. [Google Scholar]
- Boquet, Y. The renaissance of tramways and urban redevelopment in France. Misc. Geogr. 2017, 21, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Reis, A.C.; Lovelock, B. Linking tourism products to enhance cycle tourism: The case of the Taieri Gorge Railway and the Otago Central Rail Trail, New Zealand. Tour. Rev. Int. 2014, 18, 57–69. [Google Scholar] [CrossRef]
- Camerin, F. From “Ribera Plan” to “Diagonal Mar”, passing through 1992 “Vila Olímpica”. How urban renewal took place as urban regeneration in Poblenou district (Barcelona). Land Use Policy 2019, 89, 104226. [Google Scholar] [CrossRef]
- Franz, M.; Nathanail, P.; Okuniek, N. Sustainable development and brownfield regeneration. What defines the quality of derelict land recycling. Environ. Sci. 2006, 3, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Offner, J. ‘Territorial deregulation’: Local authorities at risk from technical networks. Int. J. Urban Reg. 2000, 24, 165–182. [Google Scholar] [CrossRef]
- Burinskiene, M.; Bielinskas, V.; Podviezko, A.; Gurskiene, V.; Maliene, V. Evaluating the Significance of Criteria Contributing to Decision-Making on Brownfield Land Redevelopment Strategies in Urban Areas. Sustainbility 2017, 9, 759. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, A.; Zhu, Y.M.; Shafait, Z.; Sahibzada, U.F.; Waheed, A. Critical barriers to brownfield redevelopment in developing countries: The case of Pakistan. J. Clean. Prod. 2019, 212, 1193–1209. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).