Competition and Heterogeneous Innovation Qualities: Evidence from a Natural Experiment
Abstract
:1. Introduction
2. Theoretical Framework
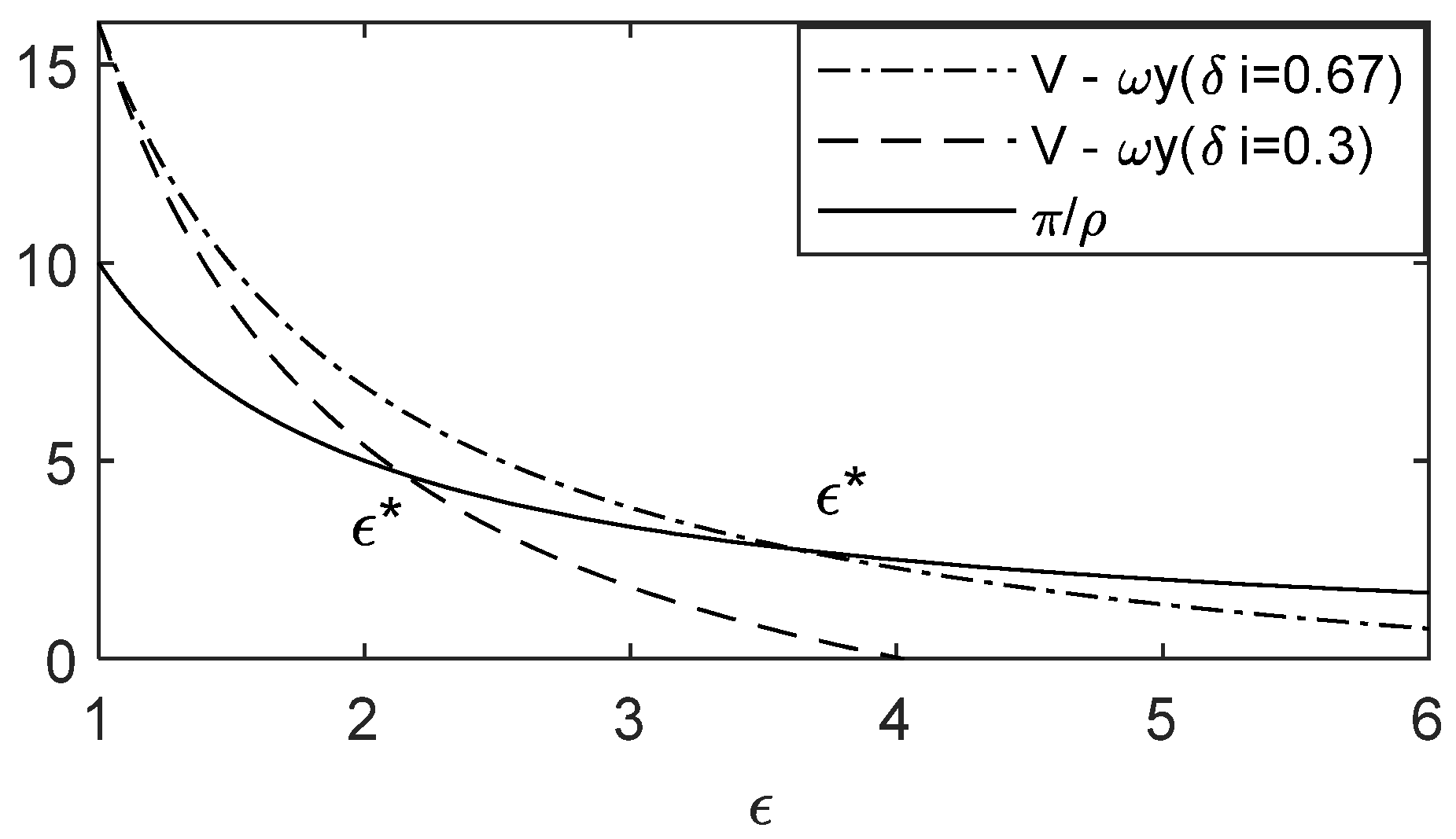
2.1. Incentives for Innovation
2.2. Innovation of Heterogeneous Firms
3. Materials and Methods
3.1. Identification Strategy
3.2. Empirical Method
3.3. Data
4. Results
4.1. Parallel Trend Test and Correlation Test on DID
4.2. Baseline Estimates
4.3. Placebo Test
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- Schumpeter, J.A. Capitalism, Socialism and Democracy; Harper and Row: New York, NY, USA, 1942. [Google Scholar]
- Arrow, K.J. Economic Welfare and the Allocation of Resources for Invention; Princeton University Press: Princeton, NJ, USA, 1962; p. 609. [Google Scholar]
- Greenstein, S.; Ramey, G. Market structure, innovation and vertical product differentiation. Int. J. Ind. Organ. 1998, 16, 285–311. [Google Scholar] [CrossRef]
- Chen, Y.; Schwartz, M. Monopoly vs. Competition: Product innovation incentives. J. Econ. Manag. Strat. 2013, 22, 513–528. [Google Scholar] [CrossRef]
- Aghion, P.; Bloom, N.; Blundell, R.; Griffith, R.; Howitt, P. Competition and innovation: An inverted-U relationship. Q. J. Econ. 2005, 120, 701–728. [Google Scholar]
- Bloom, N.; Draca, M.; Van Reenen, J. Trade Induced Technical Change? The Impact of Chinese Imports on Innovation, IT and Productivity. Rev. Econ. Stud. 2016, 83, 87–117. [Google Scholar] [CrossRef] [Green Version]
- Campbell, D.L.; Mau, K. On “Trade induced technical change: The impact of Chinese imports on innovation, IT, and productivity”. Rev. Econ. Stud. 2021, 88, 2555–2559. [Google Scholar] [CrossRef]
- Autor, D.; Dorn, D.; Hanson, G.H.; Pisano, G.; Shu, P. Foreign Competition and Domestic Innovation: Evidence from U.S. Patents; Social Science Electronic Publishing: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Hall, B.H.; Jaffe, A.; Trajtenberg, M. Market value and patent citations. Rand J. Econ. 2005, 36, 16–38. [Google Scholar]
- Akcigit, U.; Kerr, W.R. Growth through Heterogeneous Innovations. J. Politi-Econ. 2018, 126, 1374–1443. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D.; Akcigit, U.; Alp, H.; Bloom, N.; Kerr, W. Innovation, reallocation, and growth. Am. Econ. Rev. 2018, 108, 3450–3491. [Google Scholar] [CrossRef] [Green Version]
- Galaasen, S.M.; Irarrazabal, A. R&D Heterogeneity and the Impact of R&D Subsidies. Econ. J. 2021, 131, 3338–3364. [Google Scholar] [CrossRef]
- Lentz, R.; Mortensen, D.T. An Empirical Model of Growth Through Product Innovation. Econometrica 2008, 76, 1317–1373. [Google Scholar] [CrossRef]
- Raith, M. Competition, risk, and managerial incentives. Am. Econ. Rev. 2003, 93, 1425–1436. [Google Scholar] [CrossRef]
- Bauner, C. Mechanism choice and the buy-it-now auction: A structural model of competing buyers and sellers. Int. J. Ind. Organ. 2015, 38, 19–31. [Google Scholar] [CrossRef]
- Liu, T.X. All-pay auctions with endogenous bid timing: An experimental study. Int. J. Game Theory 2018, 47, 247–271. [Google Scholar] [CrossRef]
- Juang, W.-T.; Sun, G.-Z.; Yuan, K.-C. A model of parallel contests. Int. J. Game Theory 2020, 49, 651–672. [Google Scholar] [CrossRef]
- Da Silveira, B.S.; De Mello, J.M.P. Campaign Advertising and Election Outcomes: Quasi-natural Experiment Evidence from Gubernatorial Elections in Brazil. Rev. Econ. Stud. 2011, 78, 590–612. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y. Optimal capital structure, bargaining, and the supplier market structure. J. Financ. Econ. 2012, 106, 411–426. [Google Scholar] [CrossRef]
- Acemoglu, D.; Gancia, G.; Zilibotti, F. Competing engines of growth: Innovation and standardization. J. Econ. Theory 2012, 147, 570–601. [Google Scholar] [CrossRef]
- Deng, S.; Li, B.; Wu, K. Analysing the impact of high-tech industry on regional competitiveness with principal component analysis method based on the new development concept. Kybernetes 2022. [Google Scholar] [CrossRef]
- Nidumolu, R.; Prahalad, C.K.; Rangaswami, M.R. Why sustainability is now the key driver of innovation. Harvard Bus. Rev. 2009, 87, 56. [Google Scholar]
- Yao, M.; Di, H.; Zheng, X.; Xu, X. Impact of payment technology innovations on the traditional financial industry: A focus on China. Technol. Forecast. Soc. Chang. 2018, 135, 199–207. [Google Scholar] [CrossRef]
- Wei, T.; Zhu, Z.; Li, Y.; Yao, N. The evolution of competition in innovation resource: A theoretical study based on Lotka–Volterra model. Technol. Anal. Strat. Manag. 2018, 30, 295–310. [Google Scholar] [CrossRef]
- Heywood, J.S.; Wang, Z.; Ye, G. R&D rivalry with endogenous compatibility. Manch. Sch. 2022, 90, 354–384. [Google Scholar] [CrossRef]
- Braga, J.P.; Semmler, W.; Grass, D. De-risking of green investments through a green bond market–Empirics and a dynamic model. J. Econ. Dyn. Control 2021, 131, 104201. [Google Scholar] [CrossRef]
- Cozzolino, A.; Rothaermel, F.T. Discontinuities, competition, and cooperation: Coopetitive dynamics between incumbents and entrants. Strat. Manag. J. 2018, 39, 3053–3085. [Google Scholar] [CrossRef]
- Nunn, N.; Qian, N. The potato’s contribution to population and urbanization: Evidence from a historical experiment. Q. J. Econ. 2011, 126, 593–650. [Google Scholar] [CrossRef]
- Grimm, M.; Krüger, J.; Lay, J. Barriers to entry and returns to capital in informal activities: Evidence from sub-saharan africa. Rev. Income Wealth 2011, 57, S27–S53. [Google Scholar] [CrossRef] [Green Version]
- Lofstrom, M.; Bates, T.; Parker, S.C. Why are some people more likely to become small-businesses owners than others: Entrepreneurship entry and industry-specific barriers. J. Bus. Ventur. 2014, 29, 232–251. [Google Scholar] [CrossRef]
- Couto, A.; Barbosa, N. Barriers to entry: An empirical assessment of Portuguese firms’ perceptions. Eur. Res. Manag. Bus. Econ. 2020, 26, 55–62. [Google Scholar] [CrossRef]
- Kudová, D.; Chládková, H. Barriers to the entry into the fruit producing industry in the Czech Republic. Agric. Econ.–Czech 2008, 54, 413–418. [Google Scholar] [CrossRef] [Green Version]
- Jensen, C. Competition as an engine of economic growth with producer heterogeneity. Macroecon. Dyn. 2016, 20, 362–379. [Google Scholar] [CrossRef]
- Kim, N.; Min, S. Impact of Industry Incumbency and Product Newness on Pioneer Leadtime. J. Manag. 2012, 38, 695–718. [Google Scholar] [CrossRef]
- Gil, R.; Ruzzier, C.A. The Impact of Competition on “Make-or-Buy” Decisions: Evidence from the Spanish Local TV Industry. Manag. Sci. 2018, 64, 1121–1135. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Dai, H.; Cai, S. A research on the influence effect of innovation quantity and innovation quality on foreign trade export. Sci. Res. Manag. 2019, 40, 116–125. [Google Scholar]
- Jin, P.; Yin, D.; Jin, Z. Urban heterogeneity, institution supply and innovation quality. J. World Econ. 2019, 42, 99–123. [Google Scholar]
- Nickell, S.J. Competition and Corporate Performance. J. Politi-Econ. 1996, 104, 724–746. [Google Scholar] [CrossRef]
- Acemoglu, D.; Aghion, P.; Zilibotti, F. Distance to frontier, selection, and economic growth. J. Eur. Econ. Assoc. 2006, 4, 37–74. [Google Scholar] [CrossRef]
- Griffith, R.; Redding, S.; Simpson, H. Technological catch-up and geographic proximity. J. Reg. Sci. 2009, 49, 689–720. [Google Scholar] [CrossRef]
- Negassi, S.; Lhuillery, S.; Sattin, J.-F.; Hung, T.-Y.; Pratlong, F. Does the relationship between innovation and competition vary across industries? Comparison of public and private research enterprises. Econ. Innov. New Technol. 2019, 28, 465–482. [Google Scholar] [CrossRef]
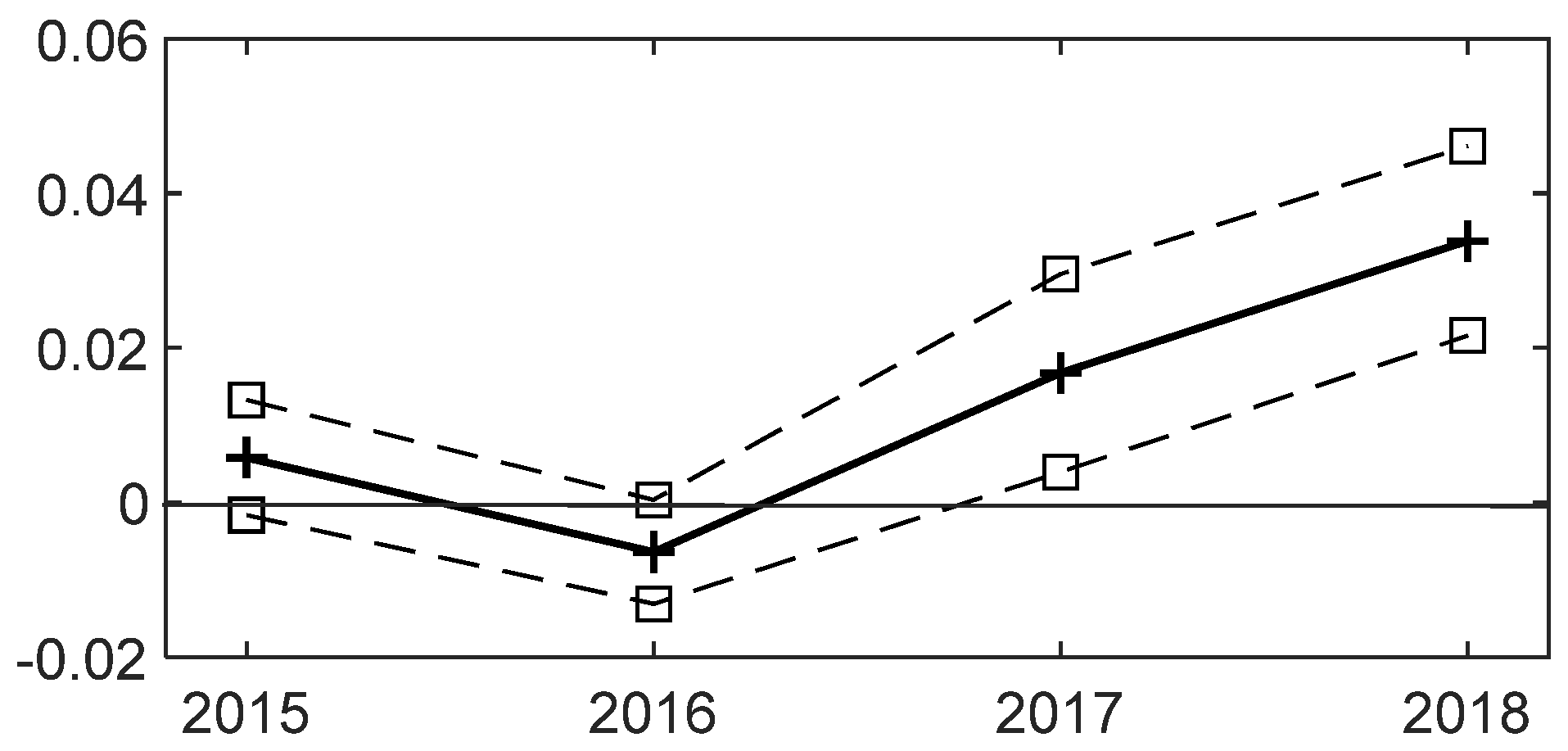
| Variable | (1) | (2) |
|---|---|---|
| Treat·D2015 | 0.0041 | 0.0058 |
| (0.0035) | (0.0038) | |
| Treat·D2017 | 0.0209 *** | 0.0167 ** |
| (0.0058) | (0.0065) | |
| Treat·D2018 | 0.0360 *** | 0.0338 *** |
| (0.0059) | (0.0063) | |
| Control variables | No | Yes |
| Individual fixed effects | Yes | Yes |
| Industry fixed effects | Yes | Yes |
| Regional fixed effects | Yes | Yes |
| Year fixed effects | Yes | Yes |
| 0.4417 | 0.4731 |
| Variable | Comp (1) | Comp (2) | Quality (3) | Quality (4) |
|---|---|---|---|---|
| 0.0049 *** | 0.0057 *** | 0.0275 *** | 0.0235 *** | |
| (0.0016) | (0.0017) | (0.0050) | (0.0056) | |
| RD | 0.0000 | 0.0000 | ||
| (0.0000) | (0.0000) | |||
| RDL | 0.0005 | 0.0070 *** | ||
| (0.0004) | (0.0020) | |||
| techBase | −0.0001 ** | 0.0050 *** | ||
| (0.0000) | (0.0007) | |||
| ROS | 0.0000 | −0.0001 ** | ||
| (0.0000) | (0.0001) | |||
| Age | −0.0102 | −0.0423 | ||
| (0.0128) | (0.0739) | |||
| Individual fixed effects | Yes | Yes | Yes | Yes |
| Industry fixed effects | Yes | Yes | Yes | Yes |
| Regional fixed effects | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| 0.5660 | 0.5789 | 0.4416 | 0.4729 |
| Variable | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| * | 0.0033 | 0.0026 | −0.0037 | −0.0067 |
| (0.0033) | (0.0035) | (0.0037) | (0.0041) | |
| RD | 0.0000 | 0.0000 | ||
| (0.0000) | (0.0000) | |||
| Researcher | 0.0070 *** | 0.0101 *** | ||
| (0.0022) | (0.0024) | |||
| techBase | 0.0049 *** | 0.0023 * | ||
| (0.0008) | (0.0014) | |||
| ROS | −0.0001 * | 0.0000 | ||
| (0.0000) | (0.0000) | |||
| Age | −0.0572 | 0.0266 | ||
| (0.0966) | (0.0222) | |||
| Individual fixed effects | Yes | Yes | Yes | Yes |
| Industry fixed effects | Yes | Yes | Yes | Yes |
| Regional fixed effects | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| 0.4581 | 0.4861 | 0.4668 | 0.4906 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Wu, X.; Li, J.; Liang, B. Competition and Heterogeneous Innovation Qualities: Evidence from a Natural Experiment. Sustainability 2022, 14, 7562. https://doi.org/10.3390/su14137562
Yan Z, Wu X, Li J, Liang B. Competition and Heterogeneous Innovation Qualities: Evidence from a Natural Experiment. Sustainability. 2022; 14(13):7562. https://doi.org/10.3390/su14137562
Chicago/Turabian StyleYan, Zhenjun, Xinyan Wu, Jing Li, and Bingqing Liang. 2022. "Competition and Heterogeneous Innovation Qualities: Evidence from a Natural Experiment" Sustainability 14, no. 13: 7562. https://doi.org/10.3390/su14137562
APA StyleYan, Z., Wu, X., Li, J., & Liang, B. (2022). Competition and Heterogeneous Innovation Qualities: Evidence from a Natural Experiment. Sustainability, 14(13), 7562. https://doi.org/10.3390/su14137562





