Estimation of Ground Thermal Properties of Shallow Coaxial Borehole Heat Exchanger Using an Improved Parameter Estimation Method
Abstract
:1. Introduction
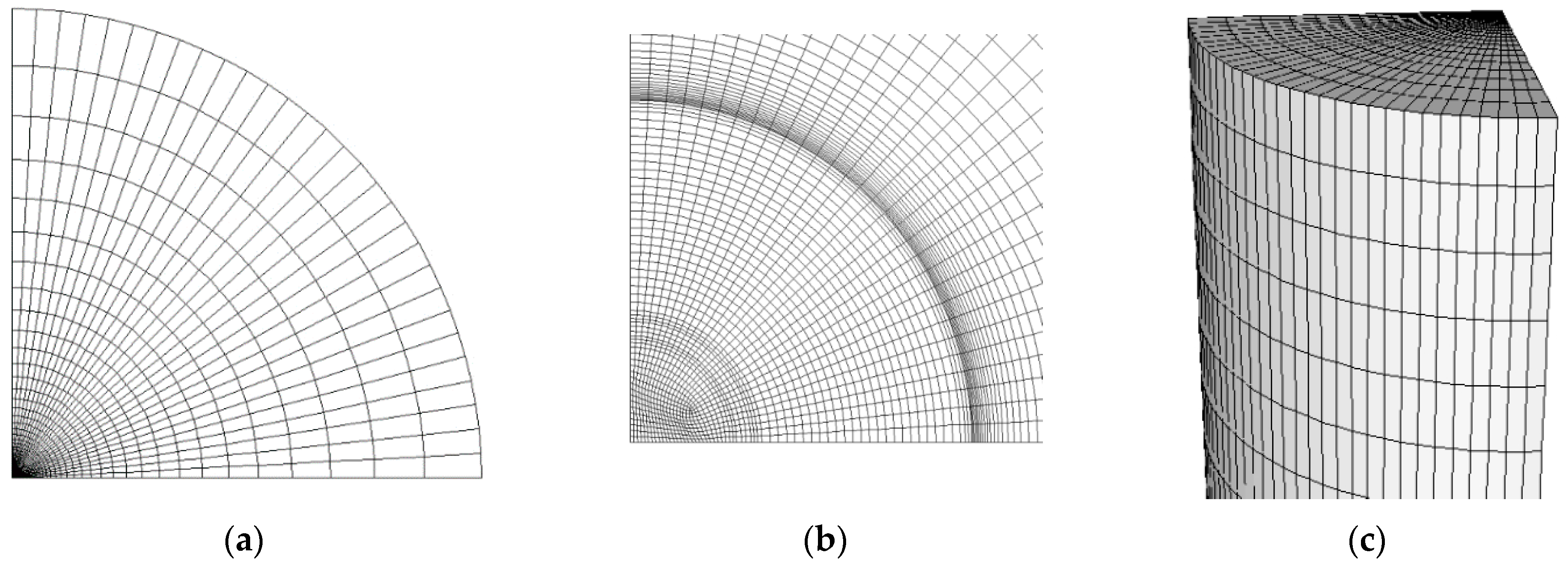
2. 3D Heat Transfer Model of SCBHE
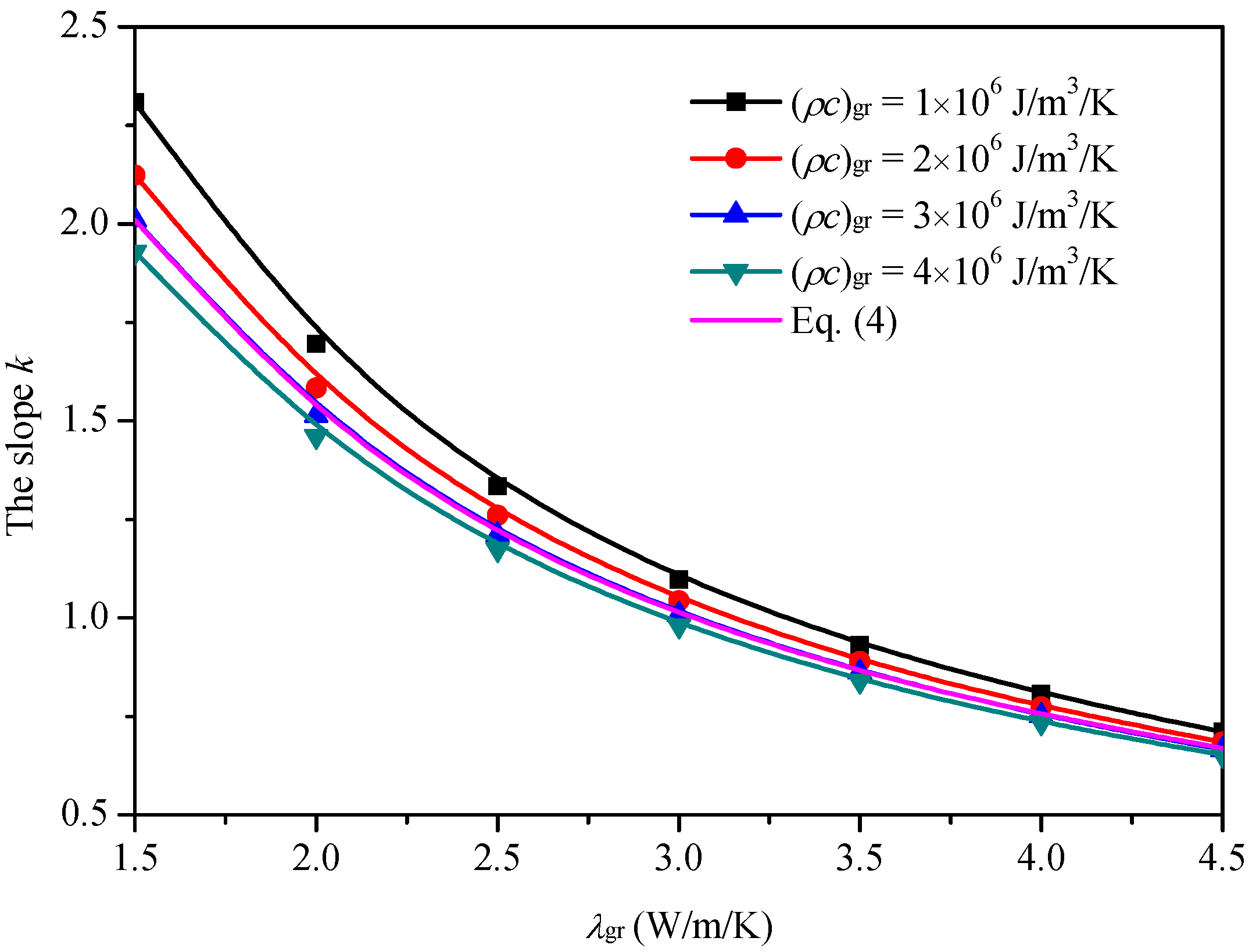
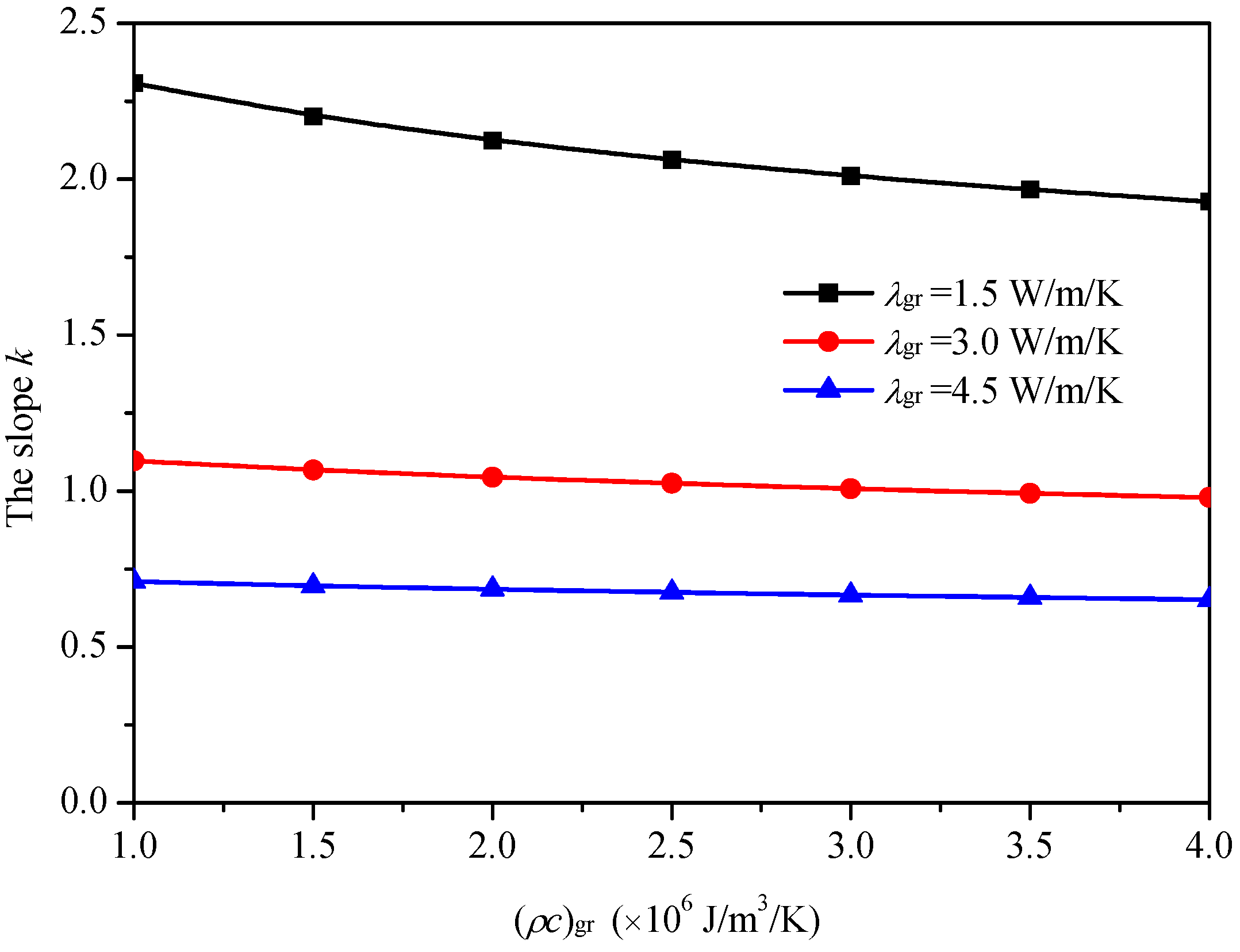
3. Effects of Ground Thermal Properties on the Slope
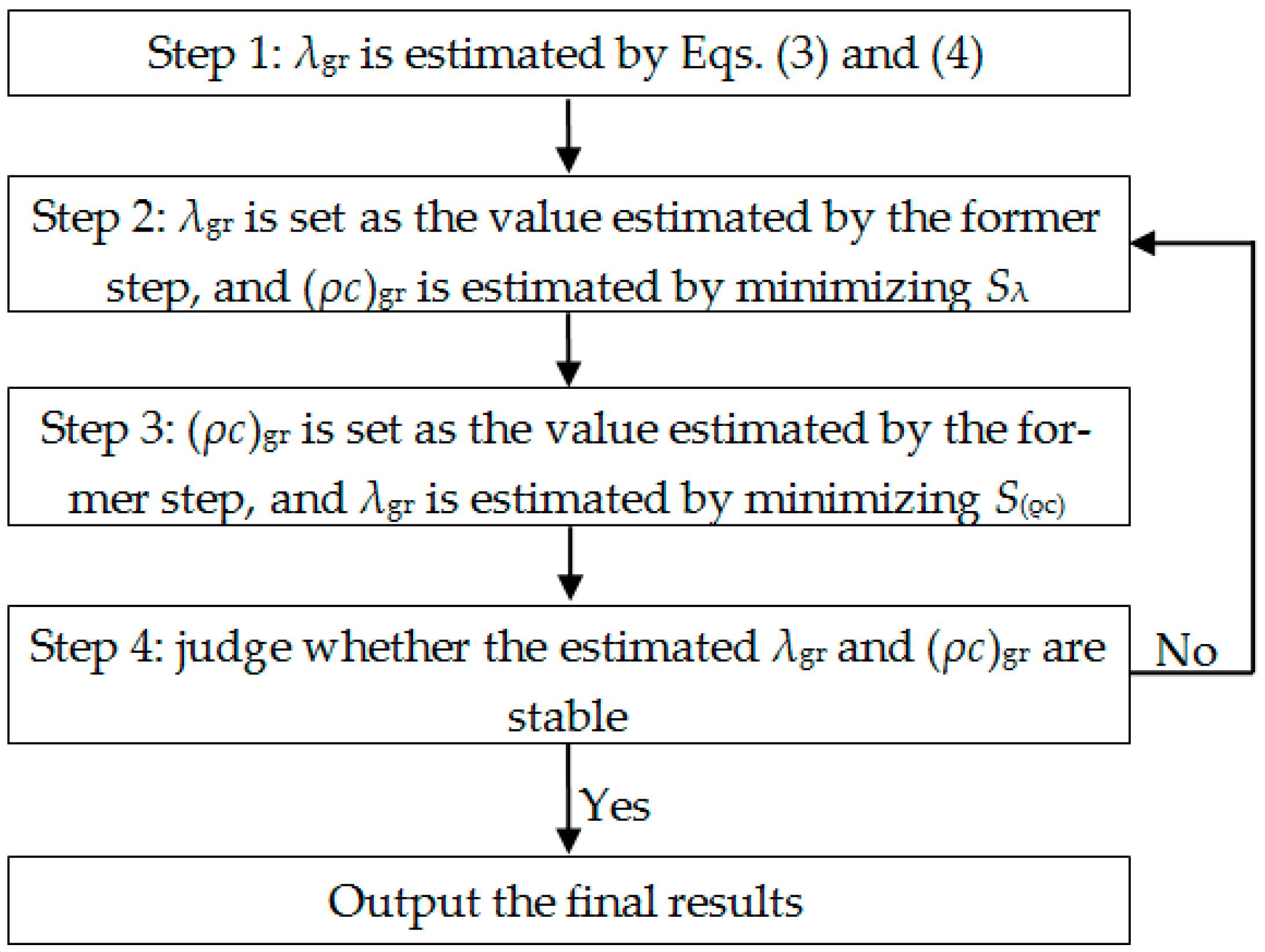
4. Improved Parameter Estimation Method
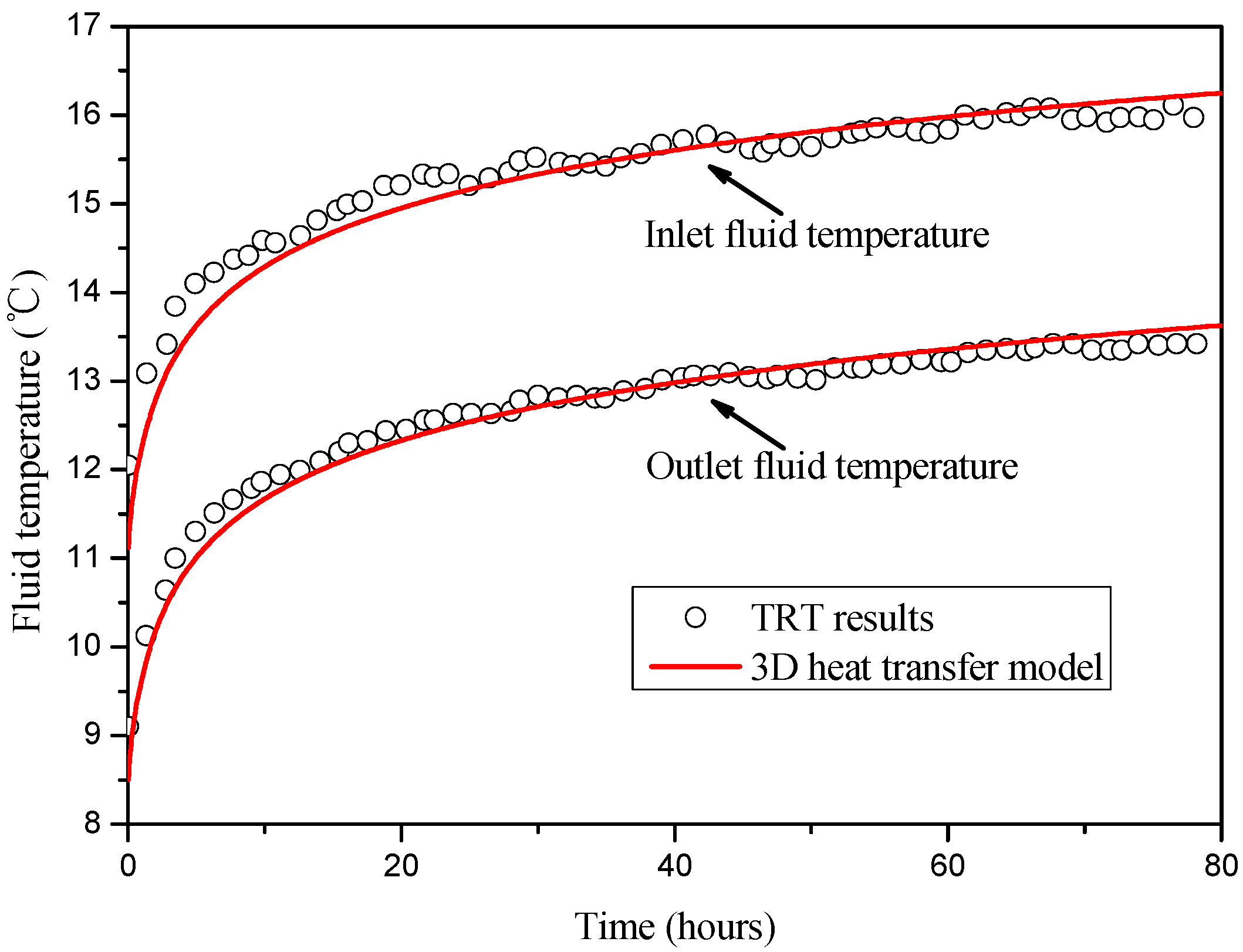
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Introduction to the Heat Transfer Model Used in the Paper
References
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Eswiasi, A.; Mukhopadhyaya, P. Performance of conventional and innovative single U-tube pipe configuration in vertical ground heat exchanger (VGHE). Sustainability 2021, 13, 6384. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Javadi, H.; Ajarostaghi, S.S.M.; Rosen, M.A.; Pourfallah, M. Performance of ground heat exchangers: A comprehensive review of recent advances. Energy 2019, 178, 207–233. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Z.; Liu, Y.; Cong, X.; Peng, D. A review on thermal response test of ground-coupled heat pump systems. Renew. Sustain. Energy Rev. 2014, 40, 851–867. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Huang, G.; Du, Y. A p(t)-linear average method to estimate the thermal parameters of the borehole heat exchangers for in situ thermal response test. Appl. Energy 2014, 131, 211–221. [Google Scholar] [CrossRef]
- Nikolaev, I.V.; Leong, W.H.; Rosen, M.A. Experimental investigation of soil thermal conductivity over a wide temperature range. Int. J. Thermophys. 2013, 34, 1110–1129. [Google Scholar] [CrossRef]
- Raymond, J. Colloquium 2016: Assessment of subsurface thermal conductivity for geothermal applications. Can. Geotech. J. 2018, 55, 1209–1229. [Google Scholar] [CrossRef] [Green Version]
- Beier, R.A. Insights into parameter estimation for thermal response tests on borehole heat exchangers. Sci. Technol. Built Environ. 2019, 25, 947–962. [Google Scholar] [CrossRef]
- Sapińska-Śliwa, A.; Sliwa, T.; Twardowski, K.; Szymski, K.; Gonet, A.; Żuk, P. Method of averaging the effective thermal conductivity based on thermal response tests of borehole heat exchangers. Energies 2020, 13, 3737. [Google Scholar] [CrossRef]
- Yang, H.; Cui, P.; Fang, Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Li, M.; Lai, A.C.K. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs): A perspective of time and space scales. Appl. Energy 2015, 151, 178–191. [Google Scholar] [CrossRef]
- Nian, Y.L.; Cheng, W.L. Insights into geothermal utilization of abandoned oil and gas wells. Renew. Sustain. Energy Rev. 2018, 87, 44–60. [Google Scholar] [CrossRef]
- Beier, R.A. Use of temperature derivative to analyze thermal response tests on borehole heat exchangers. Appl. Therm. Eng. 2018, 134, 298–309. [Google Scholar] [CrossRef]
- Pasquier, P.; Zarrella, A.; Marcotte, D. A multi-objective optimization strategy to reduce correlation and uncertainty for thermal response test analysis. Geothermics 2019, 79, 176–187. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, H.; Fan, J.; Sun, P.; Sun, S.; Kong, X. The coupled two-step parameter estimation procedure for borehole thermal resistance in thermal response test. Renew. Energy 2020, 154, 672–683. [Google Scholar] [CrossRef]
- Bozzoli, F.; Pagliarini, G.; Rainieri, S.; Schiavi, L. Estimation of soil and grout thermal properties through a TSPEP (two-step parameter estimation procedure) applied to TRT (thermal response test) data. Energy 2011, 36, 839–846. [Google Scholar] [CrossRef]
- Li, M.; Zhang, L.W.; Liu, G. Step-wise algorithm for estimating multi-parameter of the ground and geothermal heat exchangers from thermal response tests. Renew. Energy 2020, 150, 435–442. [Google Scholar] [CrossRef]
- Nian, Y.L.; Wang, X.Y.; Xie, K.; Cheng, W.L. Estimation of ground thermal properties for coaxial BHE through distributed thermal response test. Renew. Energy 2020, 152, 1209–1219. [Google Scholar] [CrossRef]
- Wang, C.; Fang, H.; Lu, J.; Sun, Y.; Zhang, P.; Wang, X. A two-step parameter estimation method for estimating soil thermal properties of coaxial ground heat exchangers. Geothermics 2021, 96, 102229. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Borehole resistance and vertical temperature profiles in coaxial borehole heat exchangers. Appl. Energy 2013, 102, 665–675. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Transient heat transfer in a coaxial borehole heat exchanger. Geothermics 2014, 51, 470–482. [Google Scholar] [CrossRef]
- Morchio, S.; Fossa, M. On the ground thermal conductivity estimation with coaxial borehole heat exchangers according to different undisturbed ground temperature profiles. Appl. Therm. Eng. 2020, 173, 115198. [Google Scholar] [CrossRef]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Y.; Chen, L.; Huang, Z.; Fang, H. A semi-analytical model for heat transfer in coaxial borehole heat exchangers. Geothermics 2021, 89, 101952. [Google Scholar] [CrossRef]
- Wang, C.; Fang, H.; Wang, X.; Lu, J.; Sun, Y. Study on the influence of the borehole heat capacity for deep coaxial borehole heat exchanger. Sustainability 2022, 14, 2043. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Lu, J.; Lu, Y.; Sun, Y.; Zhang, P. A semi-analytical heat transfer model for deep borehole heat exchanger considering groundwater seepage. Int. J. Therm. Sci. 2022, 175, 107465. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| SCBHE length L (m) | 168 |
| Borehole radius rb (m) | 0.0575 |
| Internal radius of internal pipe rii (m) | 0.0176 |
| External radius of internal pipe rie (m) | 0.020 |
| Internal radius of external pipe rei (m) | 0.0566 |
| External radius of external pipe ree (m) | 0.057 |
| Thermal conductivities of internal and external pipes λip, λep (W·m−1·K−1) | 0.4 |
| Thermal capacities of internal and external pipes (ρc)ip, (ρc)ep (J·m−3·K−1) | 1.8 × 106 |
| Grout thermal conductivity λg (W·m−1·K−1) | 0.59 |
| Grout thermal capacity (ρc)g (J·m−3·K−1) | 4.19 × 106 |
| Ground thermal conductivity λgr (W·m−1·K−1) | 3.28 |
| Ground thermal capacity (ρc)gr (J·m−3·K−1) | 2.24 × 106 |
| Fluid thermal conductivity λf (W·m−1·K−1) | 0.59 |
| Fluid thermal capacity (ρc)f (J·m−3·K−1) | 4.19 × 106 |
| Fluid Prandtl number Pr | 8.09 |
| Initial ground temperature T0 (℃) | 8.4 |
| Fluid flow rate V (m3·s−1) | 0.58 × 10−3 |
| Heat input rate of SCBHE Qin (W) | 6360 |
| Reference Values | Calculated Results of Direct Method | Calculated Results of the Improved PEM | |||||
|---|---|---|---|---|---|---|---|
| (ρc)gr (×106 J·m−3·K−1) | λgr (W·m−1·K−1) | λgr (W·m−1·K−1) | Error of λgr | λgr (W·m−1·K−1) | Error of λgr | (ρc)gr (×106 J·m−3·K−1) | Error of (ρc)gr |
| 1.0 | 1.5 | 1.306 | 12.9% | 1.490 | 0.7% | 1.001 | 0.1% |
| 1.0 | 2.0 | 1.777 | 11.2% | 1.987 | 0.7% | 1.008 | 0.8% |
| 1.0 | 2.5 | 2.258 | 9.7% | 2.489 | 0.4% | 1.005 | 0.5% |
| 1.0 | 3.0 | 2.746 | 8.5% | 2.985 | 0.5% | 1.002 | 0.2% |
| 1.0 | 3.5 | 3.239 | 7.5% | 3.485 | 0.4% | 1.005 | 0.5% |
| 1.0 | 4.0 | 3.737 | 6.6% | 3.985 | 0.4% | 1.006 | 0.6% |
| 1.0 | 4.5 | 4.239 | 5.8% | 4.482 | 0.4% | 1.011 | 1.1% |
| 2.0 | 1.5 | 1.419 | 5.4% | 1.491 | 0.6% | 2.013 | 0.7% |
| 2.0 | 2.0 | 1.903 | 4.9% | 1.990 | 0.5% | 2.002 | 0.1% |
| 2.0 | 2.5 | 2.392 | 4.3% | 2.490 | 0.4% | 1.999 | 0.1% |
| 2.0 | 3.0 | 2.887 | 3.8% | 2.987 | 0.4% | 2.007 | 0.4% |
| 2.0 | 3.5 | 3.388 | 3.2% | 3.485 | 0.4% | 2.019 | 1.0% |
| 2.0 | 4.0 | 3.893 | 2.7% | 3.980 | 0.5% | 2.021 | 1.1% |
| 2.0 | 4.5 | 4.401 | 2.2% | 4.480 | 0.4% | 2.026 | 1.3% |
| 3.0 | 1.5 | 1.499 | 0.1% | 1.495 | 0.3% | 3.005 | 0.2% |
| 3.0 | 2.0 | 1.991 | 0.5% | 1.992 | 0.4% | 3.007 | 0.2% |
| 3.0 | 2.5 | 2.488 | 0.5% | 2.490 | 0.4% | 3.010 | 0.3% |
| 3.0 | 3.0 | 2.990 | 0.3% | 2.990 | 0.3% | 3.004 | 0.1% |
| 3.0 | 3.5 | 3.496 | 0.1% | 3.490 | 0.3% | 3.012 | 0.4% |
| 3.0 | 4.0 | 4.007 | 0.2% | 3.990 | 0.3% | 3.016 | 0.5% |
| 3.0 | 4.5 | 4.522 | 0.5% | 4.481 | 0.4% | 3.038 | 1.3% |
| 4.0 | 1.5 | 1.563 | 4.2% | 1.502 | 0.1% | 3.971 | 0.7% |
| 4.0 | 2.0 | 2.063 | 3.1% | 1.998 | 0.1% | 3.979 | 0.5% |
| 4.0 | 2.5 | 2.567 | 2.7% | 2.496 | 0.2% | 3.980 | 0.5% |
| 4.0 | 3.0 | 3.075 | 2.5% | 2.995 | 0.2% | 3.996 | 0.1% |
| 4.0 | 3.5 | 3.587 | 2.5% | 3.492 | 0.2% | 4.009 | 0.2% |
| 4.0 | 4.0 | 4.103 | 2.6% | 3.988 | 0.3% | 4.027 | 0.7% |
| 4.0 | 4.5 | 4.623 | 2.7% | 4.480 | 0.4% | 4.056 | 1.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Fu, Q.; Fang, H.; Lu, J. Estimation of Ground Thermal Properties of Shallow Coaxial Borehole Heat Exchanger Using an Improved Parameter Estimation Method. Sustainability 2022, 14, 7356. https://doi.org/10.3390/su14127356
Wang C, Fu Q, Fang H, Lu J. Estimation of Ground Thermal Properties of Shallow Coaxial Borehole Heat Exchanger Using an Improved Parameter Estimation Method. Sustainability. 2022; 14(12):7356. https://doi.org/10.3390/su14127356
Chicago/Turabian StyleWang, Changlong, Qiang Fu, Han Fang, and Jinli Lu. 2022. "Estimation of Ground Thermal Properties of Shallow Coaxial Borehole Heat Exchanger Using an Improved Parameter Estimation Method" Sustainability 14, no. 12: 7356. https://doi.org/10.3390/su14127356
APA StyleWang, C., Fu, Q., Fang, H., & Lu, J. (2022). Estimation of Ground Thermal Properties of Shallow Coaxial Borehole Heat Exchanger Using an Improved Parameter Estimation Method. Sustainability, 14(12), 7356. https://doi.org/10.3390/su14127356





